
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier
Systems
Reem Melki
1 a
, Hassan Noura
2 b
and Ali Chehab
1 c
1
Department of Electrical and Computer Engineering, American University of Beirut, Beirut, Lebanon
2
Department of Computer Science, Arab Open University, Beirut, Lebanon
Keywords:
Physical Layer Security, Security and Performance Analysis, FBMC.
Abstract:
Future mobile systems support heterogeneous devices with diverse requirements and hence require flexible
and efficient allocation of available time-frequency resources. A promising multi-carrier modulation scheme
considered for 5G systems is the filter bank multi-carrier (FBMC) scheme. FBMC offers better spectral
characteristics compared to conventional orthogonal frequency division multiplexing (OFDM) by combining
individual or groups of sub-carriers and applying a shaping filter to achieve better spectral containment. While
current research on FBMC has mainly focused on reducing the signal processing complexity associated with
FBMC as well as coping with the issue of the increased symbol period, analysis of the security aspects of
FBMC systems remains largely unattempted. In this paper, we take the first step in this direction and propose
a new cipher scheme to guard against adversaries, while preserving the promised performance of FBMC.
The proposed cipher scheme is based on dynamic permutation of time-domain symbols, and a dynamic key
approach that generates session keys by exploiting the randomness of the underlying physical communication
channel. The randomness of the channel-dependent dynamic key ensures robustness of the cipher solution.
The cipher scheme is shown to be highly efficient since it requires only one iteration with one simple operation.
Experimental simulations demonstrate that the proposed scheme strikes a good balance between performance
and security.
1 INTRODUCTION
The quest for communication systems that support
stringent requirements such as low latency, high data
transmission rates, and better utilization of resources,
is constantly fueled by user demand for more ad-
vanced wireless services and more connected de-
vices. Multi-carrier modulation (MCM) is a promis-
ing scheme that has been shown to be an efficient
alternative to single-carrier modulation since it is
more resilient to multi-path channels (Gotthans et al.,
2015). So far, OFDM has been the most success-
ful MCM system, and is currently the modulation
scheme of choice in most of today’s communications
systems (He and Schmeink, 2015).
Among the many advantages of OFDM, the most
attractive properties are due to the orthogonality of
sub-carriers and the use of cyclic prefixes (CPs) to
a
https://orcid.org/0000-0002-0234-4419
b
https://orcid.org/0000-0003-1768-9193
c
https://orcid.org/0000-0002-1939-2740
mitigate the effects of inter-symbol interference (ISI)
and inter-carrier interference (ICI). Instead of using
empty guard intervals, the CP copies the last sam-
ples of the signal and inserts them at the beginning
of each symbol. However, this introduces redun-
dancy in transmitted signals and degrades the over-
all performance in terms of data rate, spectral and
power efficiency (Franzin and Lopes, 2017). Fur-
thermore, OFDM systems suffer from two major
drawbacks, namely high peak-to-average power ratio
(PAPR) and high out-of-band (OOB) emissions. Ba-
sically, all MCM waveforms experience high PAPR,
however, frequency confinement varies significantly
from one MCM waveform to another. OFDM uses
a rectangular-shape pulse, which results in poor con-
finement in the frequency domain, leading to high
OOB emission (Moles-Cases et al., 2017).
The filter-bank multi-carrier transmission scheme
(FBMC) (Schaich and Wild, 2014; Lin, 2015) has
been introduced as alternative modulation scheme
that overcomes the drawbacks of OFDM systems, and
enhances their performance, efficiency and flexibil-
Melki, R., Noura, H. and Chehab, A.
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier Systems.
DOI: 10.5220/0009852701330141
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - DCNET, OPTICS, SIGMAP and WINSYS, pages 133-141
ISBN: 978-989-758-445-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
133

ity. FBMC eliminates the CP and introduces filter
banks to the OFDM system. More specifically, in-
stead of using a CP, FBMC uses an array of filters to
reduce the OOB power leakage and increase the spec-
tral efficiency at low costs (He and Schmeink, 2015).
However, the security aspects of FBMC-based sys-
tems have not been addressed in the literature so far.
Contributions. In this paper, we leverage the
random nature of the physical layer to enhance
the security of FBMC systems without impacting
its performance. More specifically, we propose a
new channel-based link-to-link encryption technique
for FBMC systems based on a pseudo-random per-
mutation. The proposed cipher scheme depends
on the unique pseudo-random channel characteris-
tics between two communicating users, which in-
creases the security level and robustness against ad-
versaries. Specifically, after offset quadrature ampli-
tude modulation (OQAM), frequency-domain sym-
bols are transformed into time-domain symbols using
the inverse fast Fourier transform (IFFT). The result-
ing time-domain symbols are randomly shuffled, and
then, filtered using a poly-phase network (PPN) fil-
ter bank, which also acts as a diffusion layer. Conse-
quently, this leads to a more secure FBMC system, as
demonstrated through experimental simulations and
cryptanalysis. To the best of our knowledge, this is the
first work that addresses and analyzes possible physi-
cal layer security (PLS) solutions for FBMC systems.
The rest of this paper is organized as follows.
Section 2 presents some basic concepts of the filter
bank and its system model. Section 3 presents the
proposed confidentiality scheme for the filter bank
system based on PLS. Section 4 analyzes the se-
curity properties of the proposed scheme, and as-
sesses it performance against different security at-
tacks. Section 5 studies the performance of the pro-
posed scheme in terms of execution time and error
propagation. Finally, section 6 concludes this work
and discusses its future prospects.
2 BACKGROUND
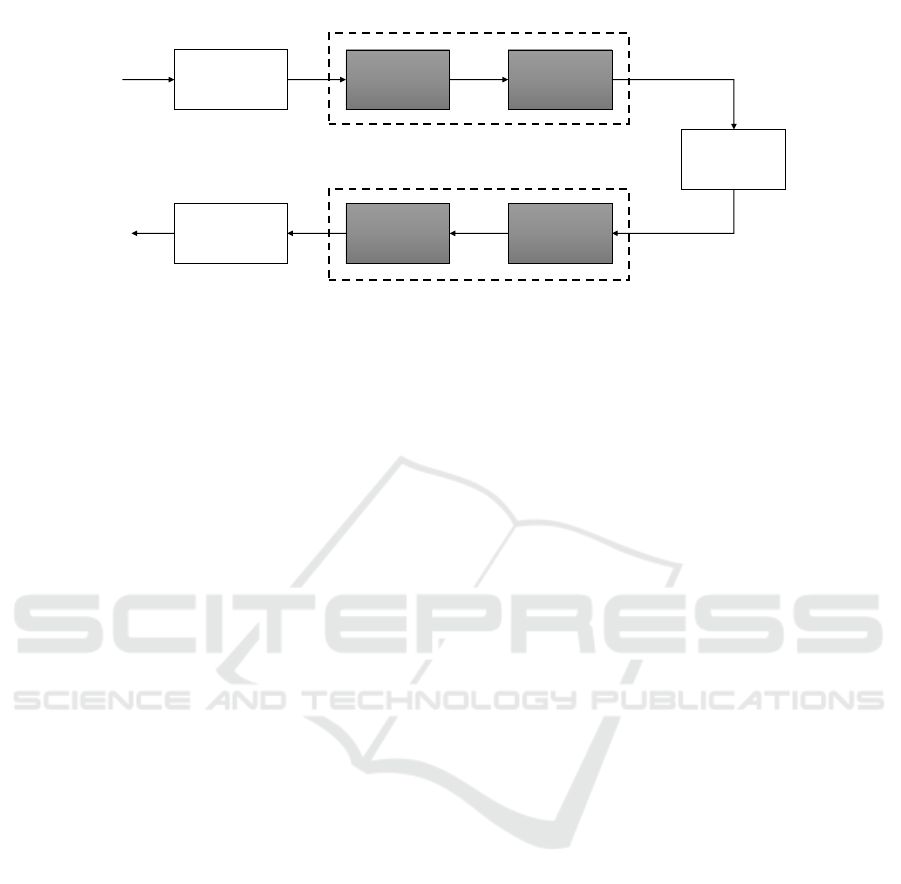
Figure 1 shows a block diagram of an FBMC sys-
tem. At the transmitter side, the symbols are first
modulated using offset QAM, and then, filtered us-
ing a Synthesis Filter Bank (SFB), which includes the
IFFT block and the poly-phase network. Similarly,
at the receiver, a reversed operation is performed, in
which time-domain symbols are recovered using an
Analysis Filter Bank (AFB) (which includes an FFT
block and PPN) and then demodulated (OQAM post-
processing). The SFB and AFB consist of an array of
filters equal in number to available sub-carriers.There
are two types of FBMC implementations—frequency
spreading (FS-FBMC) and poly-phase network (PPN-
FBMC). The latter is most common in the literature
as well as in this work, since it reduces the high
complexity that results from extra filtering (He and
Schmeink, 2015; Franzin and Lopes, 2017).
2.1 Offset Quadrature Amplitude
Modulation (OQAM)
In FBMC systems, orthogonality is achieved through
OQAM modulation where real and imaginary compo-
nents of symbols are transmitted in a staggered way.
The OQAM pre-processing block is based on a two-
step operation. The first step is converting complex
data into real data by separating the real and imag-
inary components of a complex-valued symbol into
two symbols. This increases the sample rate by a fac-
tor of 2 (Viholainen et al., 2009). Afterwards, the two
symbols are multiplied by the sequence θ
n,m
, given
by:
θ
n,m
= e
j
π
2
(n+m)
= j
n+m
(1)
where n is the sub-carrier index, and m is the time in-
dex at OQAM sub-symbol rate. Moreover, the time
index m depends on whether n is even or odd. If n is
even, then the time indices of the real and imaginary
parts of a complex symbol would be m and m + 1, re-
spectively. However, when n is odd, the time indices
of the real and imaginary components would be m+1
and m, respectively.
Accordingly, this technique avoids the interfer-
ence between consecutive sub-channels since in each
time interval, either the real or the imaginary part of
the original symbol is transmitted on a sub-carrier.
At the receiver, a reversed operation is performed
where the received symbols are multiplied by θ
∗
n,m
,
and the real part of the symbols are extracted. After-
wards, two consecutive real-value symbols are com-
bined to form the original complex-value symbol
(real-to-complex conversion).
2.2 Poly-Phase Network (PPN)
FBMC systems mainly depend on the poly-phase im-
plementation, which can be realized using different
filters such as finite impulse response filters (FIR)
or the more recent PHYDYAS prototype filters (Bel-
langer et al., 2010). In this paper, the PHYDYAS pro-
totype filter is considered since it reduces the high
complexity introduced by the extra filtering opera-
tions at the transmitter and receiver.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
134
OQAM Pre-
Processing
IFFT PPN
OQAM Post-
Processing
FFT PPN
Channel
SFB
AFB
Transmitted time-
domain symbols
Received time-
domain symbols
Input
Data
Output
Data
Figure 1: Block diagram of an FBMC system.
In general, a filter P(z) having a length equal to L =
KN (L coefficients), can be decomposed into N sub-
filters that represent the PPN, where K is the overlap-
ping factor.
Considering the PHYDYAS prototype filter, data
transmission consists of two steps:
1. After serial-to-parallel conversion, the OQAM
symbols enter the IFFT block. The IFFT out-
put is then duplicated K times and multiplied by
the impulse response of the prototype filter (time-
domain). It should be noted that convolution is
utilized in the frequency domain instead of multi-
plication.
2. Then, each of the filtered frames that result from
the previous step is shifted by half a symbol pe-
riod and added, forming the final transmission
frame.
At the receiver, the received symbols are multiplied
by the impulse response of the filter and then divided
into K frames. These K frames are then resized (over-
lapped) and summed up to form one symbol.
3 CIPHER SOLUTION FOR
FBMC SYSTEMS
In this section, the proposed dynamic key generation
algorithm and the proposed FBMC cipher scheme are
described.
3.1 Proposed Cipher Scheme for FBMC
Systems
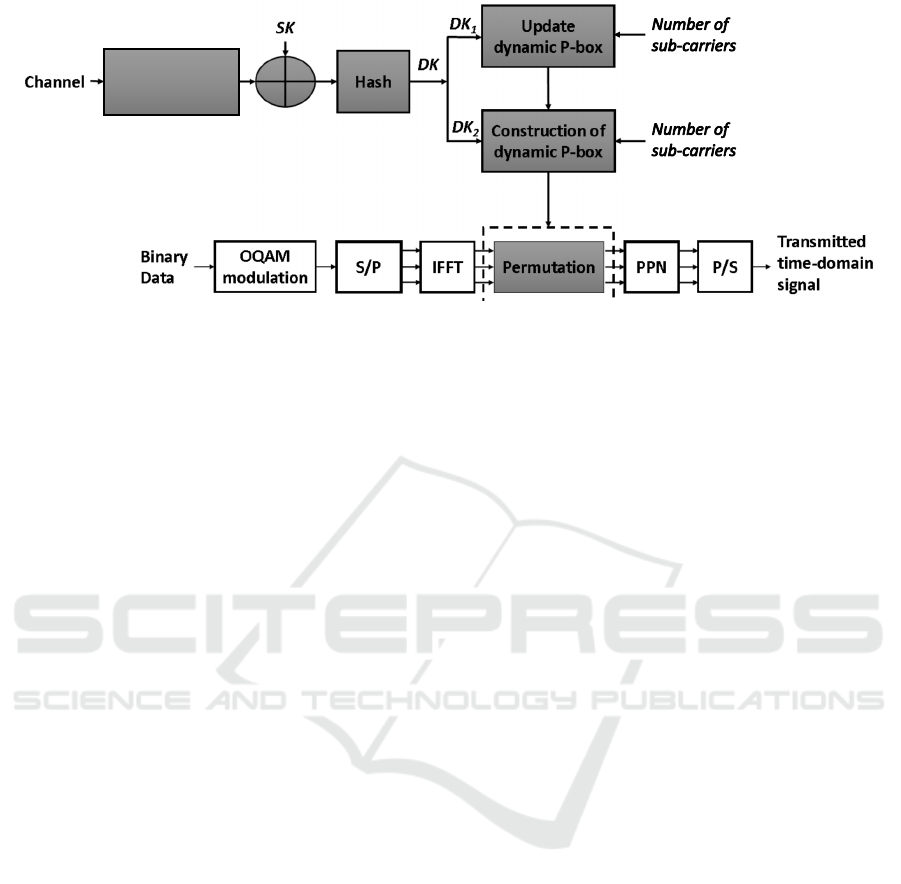
First, we consider the encryption process at the
FBMC transmitter side (refer to Fig. 2). Af-
ter serial-to-parallel conversion, the OQAM sym-
bols (frequency-domain) are transformed into time-
domain symbols via the IFFT block.
The IFFT output is then encrypted before entering
the PPN filter bank. The encryption process is simply
based on shuffling the post-IFFT symbols using the
permutation table, π, which changes the order of data
symbols. Here, π depends on two main parameters,
which are the pre-shared secret key and the common
physical channel characteristics between users.
Afterwards, the encrypted symbols are processed
with the prototype filter before being transmitted.
This procedure is accomplished in two steps: first, the
encrypted symbols are duplicated K times and then
multiplied by the impulse response of the filter (in
the time-domain). The resulting filtered frames are
shifted by half a symbol period and are then added all
together to form the final transmitted signal.
At the receiver side, the decryption process de-
pends on the inverse permutation table, π
−1
, where
the received signal is first processed by the PPN and
then decrypted using π
−1
. The resulting time-domain
symbols are transformed into frequency-domain sym-
bols using the FFT transformation and then demodu-
lated.
Note that having a static permutation table (π)
makes a cipher scheme vulnerable to chosen/known
plaintext/ciphertext attacks. Therefore, in the pro-
posed scheme, the permutation table is shuffled for
every input frame where a new permutation box is
generated to ensure robust security for FBMC sys-
tems. By dynamically changing the permutation table
using the proposed channel-based key, this method
becomes very effective and robust against several at-
tacks while maintaining a low complexity (one round
and one operation).
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier Systems
135
Extract Nonce
and perform
hashing
Figure 2: Block diagram of proposed FBMC-based cipher scheme.
3.2 Proposed Key Generation Scheme
Physical layer security (PLS) has emerged as a
promising methodology to secure current and future
networks. It depends mainly on the channel’s physical
characteristics and exploits its random nature. Sim-
ply, users sharing the same channel are able to extract
the same information (such as channel state informa-
tion (CSI)) without the need for relaying any useful
data. However, in some cases, channel-related infor-
mation can be acquired by non-legitimate users. More
specifically, adversaries present on a specific channel
can synchronize to the transmitted signals on that par-
ticular channel by performing preamble synchroniza-
tion. Therefore, the encryption keys should depend
not only on the pseudo-random channel characteris-
tics, but also on a secret only known to the communi-
cating users. In this work, users are assumed to have
pre-shared secret keys (after authentication).
Figure 2 illustrates the key derivation function,
which takes as input a secret key SK and a nonce N
o
.
• Secret Key SK. This secret key can be ex-
changed between the communicating entities after
the mutual authentication step or it can be origi-
nally embedded within a device during manufac-
turing such as via a physically uncloneable func-
tion (PUF).
• Nonce N
o
. This nonce is extracted from the
shared channel parameters between the legitimate
users. For each new session, a new nonce is gen-
erated. Moreover, we assume channel reciprocity
where both the transmitter and receiver are able to
extract the same nonce, separately.
The obtained SK and N
o
are XOR-ed and then hashed
(using SHA-512), to derive the dynamic key DK with
a size of 512 bits. DK is divided into two sub-keys
(DK
1
and DK
2
), one is used for data encryption and
the other is used to shuffle the permutation box. More
specifically, DK
1
is used to produce a dynamic key-
dependent permutation table (π), which allows the dy-
namic permutation of unfiltered time-domain symbols
(before PPN). The length of π depends on the size of
the IFFT output block. On the other hand, DK
2
is used
to shuffle π for every new input frame (updating the
permutation box).
The dynamic key is sensitive to any change that
occurs either to the channel or to the secret key, and
thus, its dynamic property guarantees a high level of
security.
4 SECURITY ANALYSIS
An efficient cipher scheme should resist most types
of known attacks such as the statistical, differential,
brute-force, and chosen/known plaintext and cipher-
text attacks. This section discusses and analyses the
proposed scheme in the context of these attacks and
quantifies its immunity against them.
Note that the adversary is assumed to have com-
plete knowledge of the channel characteristics and the
protocols used for transmission, and is able to in-
tercept the encrypted frames that are exchanged be-
tween the transmitter and receiver (a set of encrypted
FBMC symbols in addition to preamble symbols).
Moreover, the proposed cipher algorithm is consid-
ered public and the cryptanalyst is assumed to have
complete knowledge of all the required steps but none
regarding the secret key.
4.1 Immunity against Statistical Attacks
In general, a ciphertext should exhibit a high degree of
randomness in order to increase its resistance against
statistical attacks. Randomness, on the other hand,
can be achieved by ensuring 1) the uniformity of en-
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
136
0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000
0
50
100
150
200
250
(a) Symbol Amplitude
0 50 100 150 200 250
0
5
10
15
20
25
(b) Recurrence (c) PDF
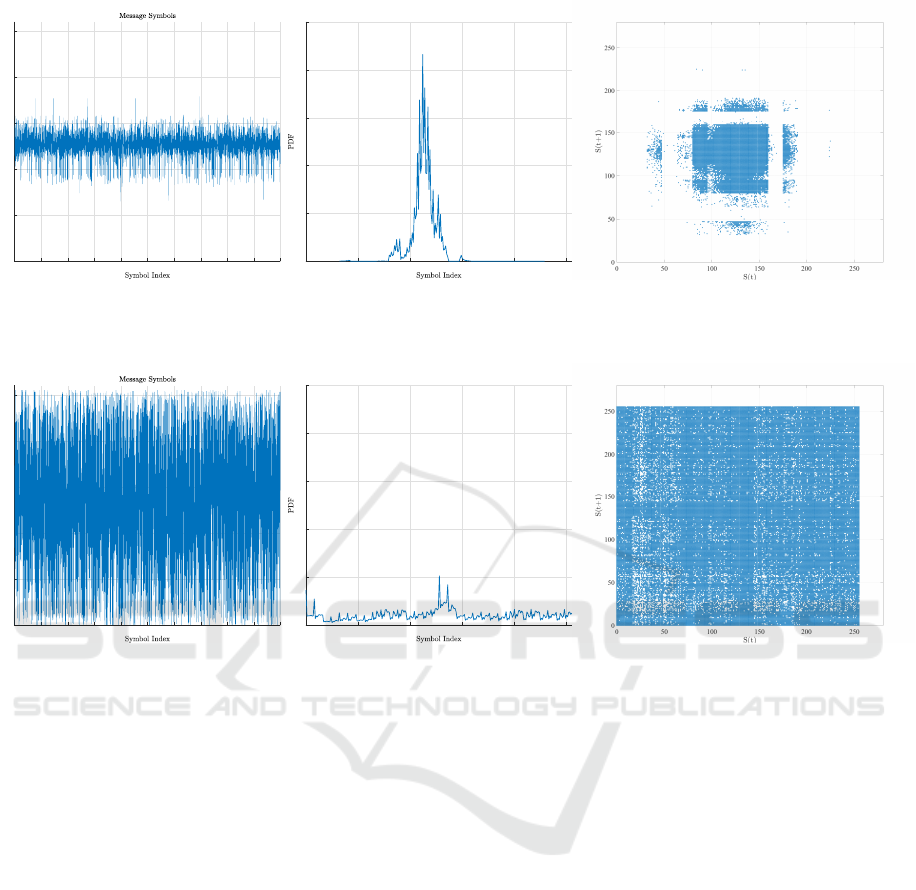
Figure 3: (a) Symbol amplitude, (b) PDF, and (c) recurrence plots of the chosen original message having a normal distribution.
0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000
0
50
100
150
200
250
(a) Symbol Amplitude
0 50 100 150 200 250
0
5
10
15
20
25
(b) PDF (c) Recurrence
Figure 4: (a) Symbol amplitude, (b) PDF, and (c) recurrence plots of the corresponding encrypted message of Fig. 3.
crypted frames, and 2) the independence property be-
tween the original and the encrypted frames.
Uniformity can be depicted visually by plotting
the probability density function (PDF), where the dis-
tribution of encrypted frames should be close to uni-
form. Also, uniformity can be tested by employing
several statistical tests such as the entropy test.
FBMC symbols are generated according to a nor-
mal distribution with a mean of 128 and a standard
deviation of 16. Hence, the generated data messages
have non-uniform distribution and non-random recur-
rence. The plots of distribution, recurrence, and the
symbol amplitude of the original FBMC frames and
their corresponding ciphertext are shown in Figure 3
and 4, respectively. Moreover, entropy is computed
for the original and encrypted FBMC blocks in or-
der to measure the level of uncertainty (Figure 5).
According to both results, the distribution of the en-
crypted FBMC symbols is close to a uniform distri-
bution, which is the desired outcome.
On the other hand, the independence criterion
can be visually verified by plotting the recurrence of
the encrypted frames. Statistically, this criterion can
also be validated by employing several statistical tests
such as the difference test (the percentage of differ-
ence at the bit level) and by quantifying the corre-
lation coefficient between the original and encrypted
FBMC symbols.
Figures 3-c and 4-c represent the recurrence of the
original and encrypted FBMC frames, respectively.
The recurrence of the encrypted frames is distributed
randomly, spanning all the available space unlike that
of the original frames, which is grouped in one region.
Consequently, the encrypted FBMC symbols have a
high level of randomness and no clear pattern can be
inferred after the encryption process.
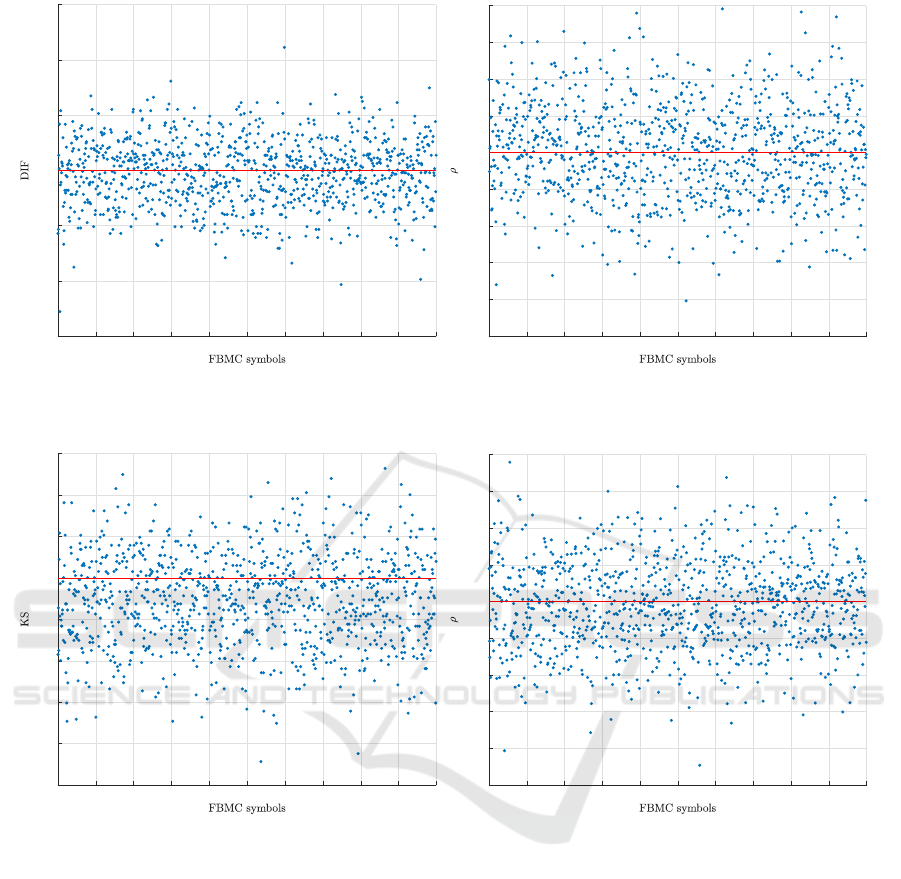
In order to satisfy the independence property, a se-
cure cipher scheme should attain a difference value
of at least 50%. Figure 6-a shows the difference of
1,000 pairs of original and encrypted FBMC symbols
at the bit level. The mean value is 50.01 and the stan-
dard deviation is close to zero. Moreover, the correla-
tion coefficient among 1,000 original and encrypted
FBMC symbols is close to the desired value of 0,
which is shown in Figure 6-b. As such, the proposed
cipher scheme satisfies the required randomness prop-
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier Systems
137
0 100 200 300 400 500 600 700 800 900 1000
4.5
5
5.5
6
6.5
7
7.5
Encrypted FBMC Symbol
Original FBMC Symbol
Figure 5: Entropy measurements for original and encrypted
FBMC symbols.
erties. Moreover, these results demonstrate that sta-
tistical attacks would not reveal any useful informa-
tion from the encrypted FBMC symbols and that the
proposed cipher scheme is highly resilient against all
types of statistical attacks.
4.2 Resistance against Key Attacks
The proposed cipher scheme employs a dynamic key
approach in contrast to upper-layer cipher schemes,
which are in most cases static and symmetric. In this
part, various attacks are studied and their correspond-
ing results are analyzed.
4.2.1 Weak Keys
The proposed key derivation function produces a set
of dynamic sub-keys with a high degree of random-
ness. Moreover, all cipher operations, such as the
generated permutation tables, are directly related to a
dynamic key that ensures the desirable cryptographic
performance. If any weakness exists in any of the dy-
namic keys, it will not affect the previous or future
processed data. Therefore, the proposed approach is
highly resistant against weak keys. In addition, the
variation of both permutations tables takes place for
each new input FBMC frame. The permutation ta-
ble used in symbol encryption is updated using the
second permutation table. Any weakness in any of
the two permutation tables can be avoided by using
the proposed approach. Moreover, the variation of
the dynamic key for each new input FBMC symbols
produces a different dynamic key and consequently, it
guards against the key disclosure accident.
4.2.2 Brute-force Attacks
The size of the secret key can be 128, 196, or 256 bits
such as the case in AES and the size of the dynamic
key is 512 bits, which is sufficient to make the brute
force attack unfeasible.
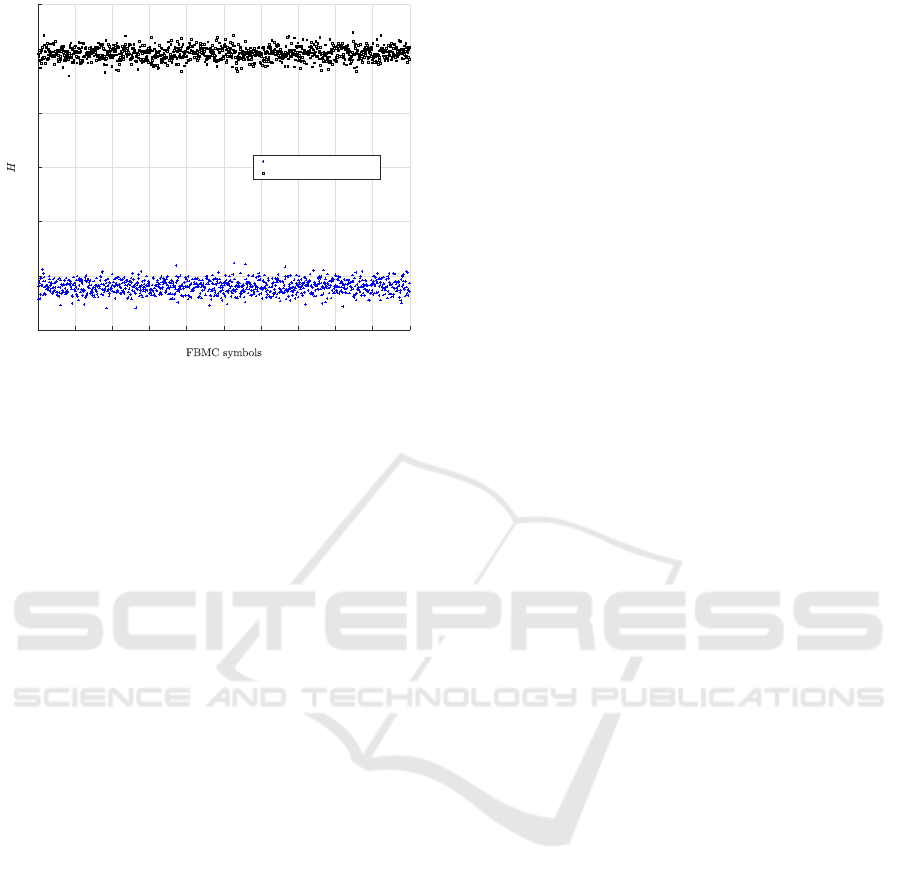
4.2.3 Key Sensitivity
The key sensitivity test calculates the difference be-
tween the encrypted symbols at the bit level after do-
ing a slight change in the secret key. A secure cipher
scheme should ensure a key sensitivity value close to
50%.Indeed, for this test, two secret keys are used (K
and K
0
) where all elements of K
0
and K are identi-
cal, except for one random bit. Figure 7 represents
the key sensitivity test for 1,000 iterations; the mean
value is close to 50% with a low standard deviation.
Therefore, the proposed cipher can ensure high resis-
tance against both, related-key attacks and linear and
differential attacks.
4.2.4 Resistance against Chosen/Known
Plaintext/Ciphertext Attacks
The proposed cipher scheme does not ensure the
avalanche effect. If the scheme was based on a static
key, it would be considered insecure against cho-
sen/known plaintext/ciphertext attacks. However, this
weak point is avoided in the proposed solution since
the scheme is based on a dynamic key structure.
Also, the proposed approach generates two per-
mutation tables that change for each new input FBMC
frame. The permutation table is changed for each
FBMC symbol by using the second permutation ta-
ble. This complicates the task of attackers and it is
very hard to recover the transmitted data using this
cipher scheme.
4.2.5 Resistance against More Powerful Attacks
The employment of the dynamic key approach will
ensure a high resistance degree and robustness against
powerful attacks. The presented discussion in this
section validates the safe employment of the proposed
cipher approach for FBMC systems and proves that
it can resist most well known attacks, such as brute
force attack, statistical attack, chosen/known plain-
text/ciphertext attack, linear and differential attacks
in addition to several key attacks. To the best of our
knowledge, this is the first work that proposes a dy-
namic approach for FBMC systems based on channel
characteristics and a shared secret key, leading to a ro-
bust symmetric cipher candidate with low latency and
resource requirements.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
138
0 100 200 300 400 500 600 700 800 900 1000
0.44
0.46
0.48
0.5
0.52
0.54
0.56
(a)
0 100 200 300 400 500 600 700 800 900 1000
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
(b)
Figure 6: (a) Difference measurements, and (b) correlation coefficients between original and encrypted FBMC symbols.
0 100 200 300 400 500 600 700 800 900 1000
0.45
0.46
0.47
0.48
0.49
0.5
0.51
0.52
0.53
(a)
0 100 200 300 400 500 600 700 800 900 1000
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
(b)
Figure 7: (a) Key sensitivity measurements, and (b) correlation coefficients between two encrypted FBMC symbols with one
bit difference in the secret key.
5 PERFORMANCE ANALYSIS
In order to verify that the proposed scheme enhances
the security level of FBMC systems without degrad-
ing their performance, we consider two metrics, the
effect of channel error and the execution time.
5.1 Effect of Channel Errors
An important criterion that should be considered by
any PLS cipher scheme is error tolerance, which
means that there should exist no error propagation
among encrypted symbols. Interference and noise,
which exist in transmission channels, are the main
causes of errors. A bit error means that a ’0’ bit is
substituted with a ’1’ bit or vice versa. Consequently,
this error may propagate and lead to the corruption
of data, which is a big challenge since there exists a
strong trade-off between the Avalanche effect and er-
ror propagation as seen in the upper-layer traditional
cryptographic algorithms (Massoudi et al., 2008).
Simulations are conducted in MATLAB for the
Bit Error Rate (BER), and in the presence of Additive
White Gaussian Noise (AWGN). The average num-
ber of symbols used in each simulation run is equal to
10
4
. QPSK symbol modulation is used.
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier Systems
139
−25 −20 −15 −10 −5 0 5 10
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
Signal−to−Noise Ratio(SNR) in [dB]
Bit Error Rate (BER)
Original
FBMC Encryption
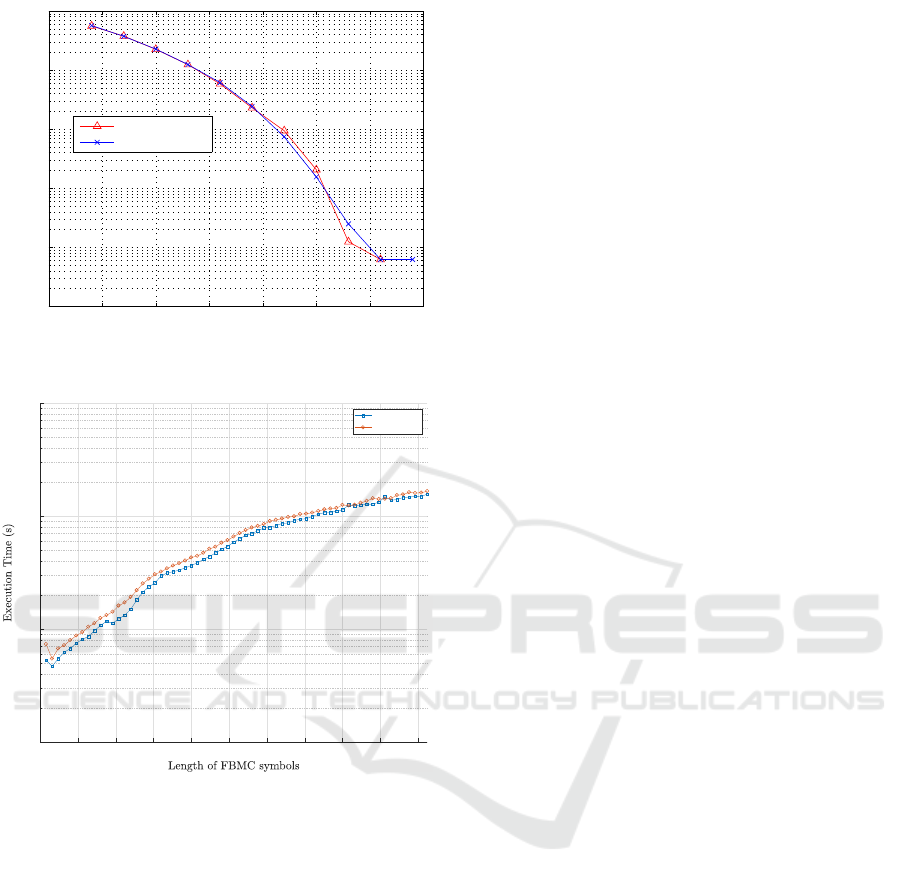
Figure 8: BER performance versus E
s
/N
0
.
200 400 600 800 1000 1200 1400 1600 1800 2000
10
-6
10
-5
10
-4
10
-3
Encryption
Decryption
Figure 9: Execution time versus the number of sub-carriers.
Figure 8 shows the BER curves of the original data
sent without encryption and the proposed encryption
scheme for different SNR values (E
s
/N
0
). It is clear
from the results that the proposed cipher scheme does
not affect the performance of FBMC since the en-
cryption is realized on the modulated symbol and no
chaining operation is introduced. In fact, The BER
curve without encryption is similar to the encrtpted
one.
Moreover, if a bit error appears in any of the sym-
bols in the encrypted data frame, it should not af-
fect other symbols. For the proposed scheme, the
effect of erroneous bits in the modulated symbol is
restricted to the same positions in the encrypted and
decrypted frames. This means that the error does not
propagate to other modulation symbols and it will not
affect neighboring modulation symbols. Hence, the
proposed cipher scheme is immune to error propaga-
tion.
5.2 Execution Time
Another way to assess the efficiency and performance
of a specific cipher scheme, is through calculating and
evaluating the execution time. In general, the execu-
tion time should be as low as possible, which results
in low energy consumption and fewer number of cal-
culations. This is very critical and important when
securing devices with limited power. For this pur-
pose, the average execution time (for 100, 000 itera-
tions) to encrypt a FBMC symbol having a flexible
size that varies from 32 to 1024 with a fixed step size
equal to 32, is calculated. This simulation uses the
following software and hardware environment Mat-
lab R2017a simulator, micro-computer Intel Core i7,
3.4 GHZ CPU, 2 GB RAM Intel and the Microsoft
Windows 10 operating system.
According to Figure 9, we can conclude that the
execution time of the encryption and decryption pro-
cesses varies linearly, where it increases with the with
the number of sub-carriers N. Moreover, it has been
shown that the proposed encryption scheme intro-
duces only 5% to 7% (for various FFT sizes) overhead
to the FBMC system in terms of execution time.
6 CONCLUSION
In this paper, a new cipher scheme for FBMC sys-
tems has been proposed. The scheme depends on dy-
namic permutation of time-domain symbols and on a
dynamic key derived from a secret key and physical
channel parameters between communicating users.
To the best of our knowledge, this paper is the first
work that aims at designing a secure FBMC cipher
scheme. It has been proven that the proposed cipher
scheme strikes a good balance between security and
performance in which desirable cryptographic perfor-
mance can be attained.
REFERENCES
Bellanger, M. et al. (2010). FBMC physical layer: a primer.
PHYDYAS, 25(4):7–10.
Franzin, R. and Lopes, P. (2017). A performance compari-
son between OFDM and FBMC in PLC applications.
In Proc. IEEE Ecuador Technical Chapters Meeting
(ETCM). IEEE.
Gotthans, T. et al. (2015). Experimental evaluation of
digital predistortion with FBMC and OFDM signals.
In Proc. IEEE Wireless and Microw. Technol. Conf.
(WAMICON), pages 1–3. IEEE.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
140

He, Q. and Schmeink, A. (2015). Comparison and eval-
uation between FBMC and OFDM systems. In Proc.
workshop on smart antennas (WSA), pages 1–7. VDE.
Lin, H. (2015). Filter bank OFDM: A new way of looking
at FBMC. In Proc. IEEE Int. Conf. Commun. (ICC),
pages 1077–1082. IEEE.
Massoudi, A. et al. (2008). Overview on selective en-
cryption of image and video: challenges and perspec-
tives. EURASIP Journal on Information Security,
2008(1):179290.
Moles-Cases, V. et al. (2017). A comparison of OFDM,
QAM-FBMC, and OQAM-FBMC waveforms subject
to phase noise. In Proc. IEEE Int. Conf. Commun.
(ICC), pages 1–6. IEEE.
Schaich, F. and Wild, T. (2014). Waveform contenders for
5G-OFDM vs. FBMC vs. UFMC. In Proc. IEEE Int.
Symp. on Commun., Control and Signal Process (IS-
CCSP), pages 457–460. IEEE.
Viholainen, A. et al. (2009). Prototype filter design for filter
bank based multicarrier transmission. In Proc. IEEE
European Signal Process. Conference, pages 1359–
1363. IEEE.
An Efficient and Secure Cipher Scheme for Filter Bank Multi-Carrier Systems
141
