
Efficient and Secure Cipher Scheme for Limited IoT Devices
Hassan N. Noura
1,2
, Ola Salman
1
and Ali Chehab
1
1
American University of Beirut, Department of Electrical and Computer Engineering, Lebanon
2
Arab Open University, Department of Computer Sciences, Beirut, Lebanon
Keywords:
Cryptanalysis, Data Confidentiality, Cipher Scheme, Avalanche Effect, Key Derivation Function, Binary
Diffusion Matrix, Security Analysis.
Abstract:
In this paper, an effective and robust cipher scheme is proposed to cater for the resource-constrained nature
of IoT devices. The proposed cipher scheme is a combination of static and dynamic cryptographic structures,
towards ensuring better resistance and resilience against existing security attacks. More precisely, the proposed
solution is designed to be a lightweight cipher scheme, iterating a round function just twice, along with a
dynamic key-dependent block permutation. The proposed round function satisfies the required confusion and
diffusion properties, and consequently, it guarantees the desired cryptographic aspects such as message and
key avalanche effects. Finally, the security and performance tests confirm the effectiveness and the robustness
of the proposed cipher solution in terms of security level, the associated delay and required resources.
1 INTRODUCTION
With the emergence of the Internet of Things (IoT),
billions of devices will be connected to the Internet.
Many of these devices are constrained in terms of
power consumption, memory capacity, and/or com-
putational capability. Such devices are used in an
IoT network to collect, monitor, and process data for
various types of applications. The ubiquitous con-
nectivity of these devices makes them prone to var-
ious security threats targeting main different secu-
rity aspects such as privacy, data confidentiality, in-
tegrity (data/system(s)), availability (data/system(s)),
and authentication (device/user and data origin au-
thentication). Therefore, protective mechanisms,
which can be based on either cryptographic or non-
cryptographic solutions, must be employed to pre-
serve data and network security. In this paper, we
aim at designing a lightweight cryptographic solution
to preserve data confidentiality in the IoT domain.
Given the huge amount of generated data and the lim-
itations of IoT devices, lightweight cipher algorithms
are needed to cope with the Big Data, time and re-
source constraints. The existing security solutions are
not suitable for constrained IoT devices. For exam-
ple, traditional cryptographic algorithms that provide
data confidentiality, such as the Advanced Encryp-
tion Standard (AES) (Daemen and Rijmen, 2013), re-
quire a high number of rounds and operations (Noura
et al., 2018), exhibiting a high overhead in terms
of latency and resources. To resolve this issue, al-
ternative chaotic cryptographic algorithms have been
recently proposed. However, these algorithms suf-
fer from several performance and security limitations
such as the need for floating-point computations, fi-
nite periodicity, and complex hardware implemen-
tation. Accordingly, and to respond better to real-
time IoT applications and tiny devices, recent works
proposed lightweight cipher algorithms with a rela-
tively low number of operations and rounds to mini-
mize the latency and resources (McKay et al., 2016;
Poschmann, 2009). Moreover, new lightweight cryp-
tographic algorithms that are based on the dynamic
key approach, with relatively small number of rounds,
were presented in (Noura et al., 2018; Melki et al.,
2018). In this context, this paper combines static
and dynamic cipher structures with a low number of
rounds to achieve a high level of security with mini-
mum delay and required resources. The proposed ci-
pher includes a simple round function that follows the
substitution-diffusion structure. This function is iter-
ated only twice to achieve the desired cryptographic
properties. The advantage of the proposed cipher,
compared to existing solutions (Noura et al., 2018;
Melki et al., 2018), is that it satisfies the avalanche
effect at the block level. The proposed cipher uses
a dynamic key to produce the required cryptographic
primitives for encryption/decryption. This dynamic
key is based on a device secret key and a nonce,
which complicates the attackers task in guessing and
breaking the proposed dynamic cryptographic algo-
rithm and the associated cryptographic primitives. Fi-
142
Noura, H., Salman, O. and Chehab, A.
Efficient and Secure Cipher Scheme for Limited IoT Devices.
DOI: 10.5220/0009858501420150
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - DCNET, OPTICS, SIGMAP and WINSYS, pages 142-150
ISBN: 978-989-758-445-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

nally, the security and performance analysis confirm
the effectiveness and the robustness of the proposed
cipher solution against several cryptographic attacks.
The rest of this paper is organized as follows. The
proposed key derivation scheme and cipher algorithm
are described in Section 2. The security analysis is
presented in Section 3. Then, the effectiveness of the
proposed cipher scheme is analysed and assessed in
Section 4. Finally, Section 5 concludes the paper.
2 PROPOSED CIPHER SCHEME
The majority of the existing cryptographic algorithms
(especially the standard ones) are based on a static
key and use static substitution and diffusion primi-
tives. The main originality of this work is combin-
ing static and dynamic cryptographic approaches to-
ward ensuring a good balance between performance
and security level. The proposed cipher scheme uses
the static AES substitution table which ensures the
strict avalanche criterion in addition to minimum lin-
ear and differential approximations (Koo et al., 2006;
Koo et al., 2003). Moreover, the proposed static bi-
nary diffusion in (Koo et al., 2006; Koo et al., 2003)
is used since it ensures a high linear branch number
(10 for h=16 and 12 for h=32). Furthermore, the pro-
posed algorithm uses dynamic addition round keys
and permutation tables. In the following, we detail the
proposed dynamic key and cryptographic primitives
derivation, cipher algorithm, and decryption process.
2.1 Dynamic Key and Cryptographic
Primitives Derivation
To generate the dynamic key (DK), the device secret
key SK is mixed with a Nonce for each set of mes-
sages (the number of messages can be configured ac-
cording to the IoT application requirements). Each
generated dynamic key DK is produced by hashing
the mix of the secret key and the Nonce as shown by
the following equation:
DK = h(SK ⊕ Nonce) (1)
Where h represents the secure cryptographic hash
function (SHA-512). The obtained dynamic key is
divided into 4 sub-keys (see Figure 1). Each of these
sub-keys is employed to produce a specific dynamic
key-dependent cryptographic primitive: round keys
and 3 permutation tables. The modified Key Setup
Algorithm (KSA) of RC4, presented in (Noura et al.,
2018), is used to produce the required permutation
and selection tables. The permutation table is used
in the block permutation process, which is denoted
BL − Pbox. The selection tables are generated us-
ing the technique in (Noura et al., 2019). Further-
more, two selection tables are employed, Pbox
SIV 1
and Pbox
SIV 2
, to select the round key for the first and
the second iterations, respectively. On the other hand,
a set of q round keys is required, and it can be gener-
ated using any stream cipher. For example, RC4 can
be used to produce these q round keys (called IV ),
where each round key has h bytes in length.
Algorithm 1: Proposed Encryption Algorithm.
1: procedure ENCR(M, S −
box, SIV 1, SIV 2, IV, Bl Pbox, h)
2: Ml ← reshape(M, 1, 1 → size(M, 1) ×
size(M, 2) × size(M , 3))
3: n ← length(M1)
4: α ← d
n
h
e
5: Ml ← padding(Ml, α × h −n)
6: B ← reshape(Ml, α, h)
7: for it ← 1 toα do
8: X ← B(it, 1 → h) + IV ( SIV 1(it), 1 →
h)%256
9: Y ← S −box(X )
10: Z ← Di f f usion(Y )
11: X ← Z ⊕ IV ( S I V 2(it), 1 → h)
12: Y ← S −box(X )
13: Z ← Di f f usion(Y )
14: T mp(it, 1 → h) ← Z
15: end for
16: Cp ← T mp(Bl Pbox, 1 → h)
17: C ← reshape(Cp, 1, α × h)
18: return C
19: end procedure
2.2 Encryption Algorithm
The proposed cipher algorithm deals with a flexible
block size (h bytes). If the number of bytes in a given
message is not a multiple of h (8, 16 and 32), padding
is required. Then, the input message is divided into
α blocks {B
1
, B
2
, . . . , B
α
}, where each block has a
length of h bytes.
The proposed cipher scheme is illustrated in Fig-
ure 2, while its pseudo-code is included in Algo-
rithm 1. The encryption scheme consists of two main
steps. First, the round function is iterated for two
times. Second, a block permutation process is in-
troduced to randomize the sequential order of the en-
crypted blocks. In fact, the round function consists of
three operations, byte addition with a round key, byte
substitution and binary byte diffusion, as described
next.
• The first operation mixes an input message block
Efficient and Secure Cipher Scheme for Limited IoT Devices
143
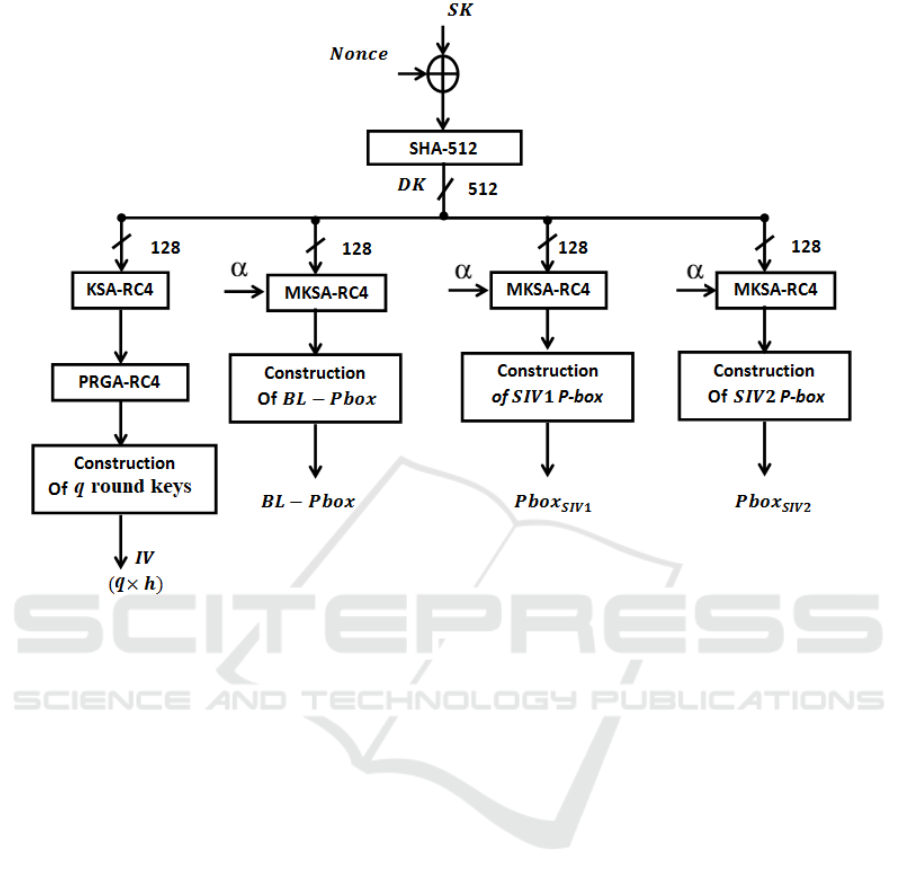
Figure 1: Architecture of the proposed key derivation function.
with a round key represented by the Initial Vec-
tor (IV), which is dynamically selected, according
to the first selection table Pbox
SIV 1
, for the first
round and to the second selection table Pbox
SIV 2
,
for the second round. In this operation, the arith-
metic addition modulo 256 is used in the first
round and the logical ”exclusive or” is used in the
second one.
• Next, the substitution operation is performed
based on AES S-box.
• Then, a diffusion operation is performed based on
a static binary mixing matrix, G.
In fact, running the proposed cipher for two rounds
achieves a high level of randomness in addition to
message and key avalanche effects (a slight bit change
in the plain-block or dynamic key must produce com-
pletely different encrypted blocks). In the follow-
ing, we summarize the different steps of the proposed
round function.
2.2.1 Addition with a Round Key Operation
The proposed addition with a round key operation
uses two different instructions. The arithmetic ad-
dition modulo 256 is used for the first round, while
the logical ’exclusive or’ is used for the second one.
The addition is performed between an input block and
a selected IV (SIV ), representing the round key, as
shown in the following equations.
Equation 2 illustrates the addition process.
x = A(B, SIV ) =
B + SIV mod 256 r =1
B ⊕ SIV r =2
(2)
Equation 3 illustrates the inverse addition operation
that should be employed in the decryption process.
B = A
−1
(X, SIV )
(
X ⊕ S I V r = 1
X − S I V mod 256 r = 2
(3)
B, X, SIV have each a length of h bytes. B and
X represent the input plain and encrypted blocks re-
spectively, while S I V is dynamically chosen for each
block and for each round according to two permuta-
tion tables (Pbox
SIV 1
, and Pbox
SIV 2
) from a set of q
different IVs.
2.2.2 Substitution Operation
Mainly, this step is introduced to ensure the confusion
property. The static AES substitution table is used to
substitute the addition block X, as indicated by the
following equation.
Y = AES − Sbox(X) (4)
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
144
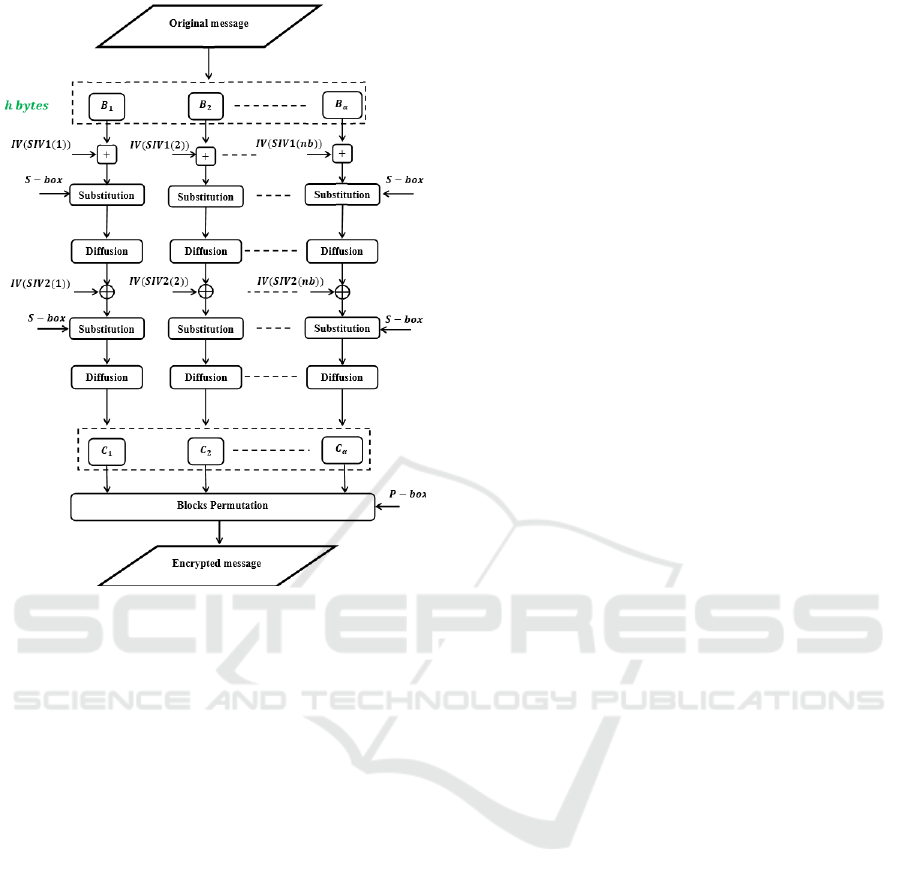
Figure 2: Architecture of the proposed encryption algo-
rithm.
2.2.3 Binary Diffusion Matrix Form
The diffusion process is applied in the binary finite
field. We select a static binary diffusion matrix G
for each value of h since it only requires the logi-
cal ”exclusive or” operation and consequently, lower
execution time compared to other diffusion opera-
tions (Noura et al., 2019; Koo et al., 2006; Koo et al.,
2003).
Figure 3-(a) shows a visual representation of the
selected binary matrix G for h=32 (Koo et al., 2006)
and its corresponding inverse matrix G
−1
is shown in
Figure 3-(b). For The visual representation of G and
G
−1
, the blue color indicates that the index is equal
to 0, otherwise it is 1. Note that the employed ma-
trix should have a maximum linear branch number.
Therefore, for h = 8, the Camellia binary diffusion
matrix is chosen (Aoki et al., 2000), while for h =
16 and 32, the binary matrix of (Koo et al., 2003)
and (Koo et al., 2006) are chosen, respectively. The
methods proposed in (Koo et al., 2003; Koo et al.,
2006) offer some optimization by finding common
patterns in the diffusion matrix, which enables the re-
duction of the required diffusion computational com-
plexity. This will consequently decrease the required
execution time of the diffusion and inverse diffusion
operations. On the other hand, the proposed solution
requires only 2 iterations and consequently less exe-
cution time compared to (Koo et al., 2003) and (Koo
et al., 2006), which require 8 and 6 iterations, respec-
tively.
In fact, the different index values in each vector
(G
i
) should be equal to 1 corresponding to the byte
introduced in the diffusion process (see (Koo et al.,
2006; Noura et al., 2019) for more details about the
binary diffusion process). The diffused byte is the re-
sult of m XORed bytes, where m represents the num-
ber of elements of the diffusion vector with the corre-
sponding index is equal to 1.
2.3 Blocks Permutation
This step consists of permuting the encrypted blocks.
It is designed to randomize the order of encrypted
blocks independently of the employed operation
mode. The block permutation operation is performed
using the produced dynamic P − box that has a length
of α elements.
2.4 Decryption Algorithm
The decryption process consists of applying the in-
verse block permutation first, then two rounds of the
inverse round function. The inverse round function
consists of applying the round function in the reverse
order and using the inverse AES substitution table in
addition to the inverse diffusion matrix G
−1
. The in-
verse addition operation is already defined previously
and the same round keys should be used. Algorithm 2
details the decryption steps to recover the plain block.
3 SECURITY ANALYSIS
In this section, a comprehensive security analysis is
conducted to demonstrate that the proposed cipher is
immune against several attacks such as statistical, dif-
ferential, chosen/known plain-text, and brute-force at-
tacks. In the following tests, the chosen plaintext mes-
sages follow the normal distribution with mean equal
to 128 and standard deviation equals to 16.
3.1 Resistance against Statistical
Attacks
A ciphertext should exhibit a high degree of random-
ness to resist statistical attacks (Noura et al., 2018;
Noura et al., 2017). The proposed cipher scheme
should therefore ensure the independence and unifor-
mity criteria. The uniformity of the ciphertext can be
Efficient and Secure Cipher Scheme for Limited IoT Devices
145

(a) Binary Diffusion Matrix (b) Corresponding Invertible matrix of (a)
Figure 3: The binary diffusion matrix presented in (Koo et al., 2006) (a) and its corresponding inverse one (b).
Algorithm 2: Proposed decryption algorithm.
1: procedure DECR(C, Inv − S −
box, SIV 1, SIV 2, IV, Inv − Bl Pbox, h)
2: Cl ← reshape(M, 1, 1 → size(C, 1) ×
size(C, 2) × size(C, 3))
3: n ← length(C1)
4: α ← d
n
h
e
5: Cl ← reshape(Cl, α, h)
6: Cp ← T mp(Cl Pbox , 1 → h)
7: for it ← 1 toα do
8: Z ← Inverse Di f f usion(Cp(it, 1 → h))
9: Y ← Inv − S − box(Z)
10: X ← Y ⊕ IV ( SIV 2(it), 1 → h)
11: Z ← Inverse Di f f usion(X)
12: Y ← Inv − S − box(Z)
13: X ← Y − IV ( SIV 1(it), 1 → h)%256
14: T mp(it, 1 → h) ← X
15: end for
16: D ← reshape(T mp, 1, α × h)
17: D ← Eliminate Padding(D)
18: D ← reshape(D, L, C, P)
19: return D
20: end procedure
shown visually by analyzing the corresponding Prob-
ability Density Function (PDF) and it can be validated
using several statistical tests such as the entropy test.
In addition, a visual presentation of the encrypted
message recurrence can verify the independence cri-
terion of the ciphertext. Moreover, the difference per-
centage between the original and encrypted messages
can also be used to prove the independence between
plaintext and ciphertext. These tests were applied and
the results, as shown next, clearly confirm that the
proposed scheme achieves the required properties and
consequently, can guard against statistical attacks.
3.1.1 Uniformity Analysis
To resist common statistical attacks, the encrypted
messages should satisfy the randomness property.
Therefore, we employ the PDF test to analyze the
distribution of the encrypted messages. The PDF of
the encrypted messages indicate whether or not the
ciphertext distribution is uniform. If the ciphertext
distribution is uniform, then each symbol (here each
byte) has an occurrence probability close to
1
n
, where
n is the number of symbols (here is equal to 256).
The amplitude, the corresponding PDF, and the recur-
rence of selected original messages are shown in Fig-
ure 4 a-c. Additionally, the corresponding encrypted
messages amplitude, PDF, and recurrence are shown
in Figure 4 d-f. It can be observed from the PDF
of the encrypted messages, using the proposed ci-
pher scheme, that each symbol has a uniform distri-
bution. Furthermore, the numerical results of cipher-
text symbols occurrence probability ( Figure 4 e) are
very close to 0.039, which represents the ideal value
for this test
1
256
.
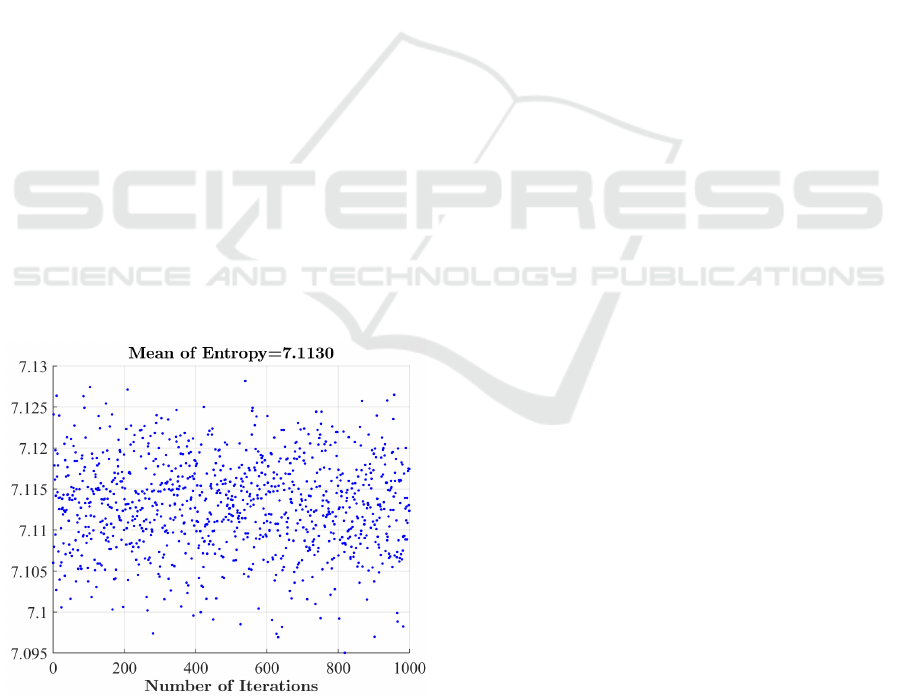
Moreover, the entropy analysis of the encrypted
messages is computed and presented in Figure 5.
Here, the entropy is computed for each original mes-
sage of 256 bytes. The results indicate that the en-
crypted messages have an entropy close to the ideal
value, which is equal to log
2
(n) =8 (Noura et al.,
2018). Therefore, the proposed cipher algorithm is
sufficiently secure against entropy attacks.
On the other hand, the independence (probability
of difference at the bit level) between plain and en-
crypted messages are computed and shown in Fig-
ure 6-a). The resulting difference average value is
nearly 50%, which is the ideal value. Hence, the en-
crypted messages are totally different compared to the
original ones. As such, the proposed approach satis-
fies the desired independence propriety.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
146
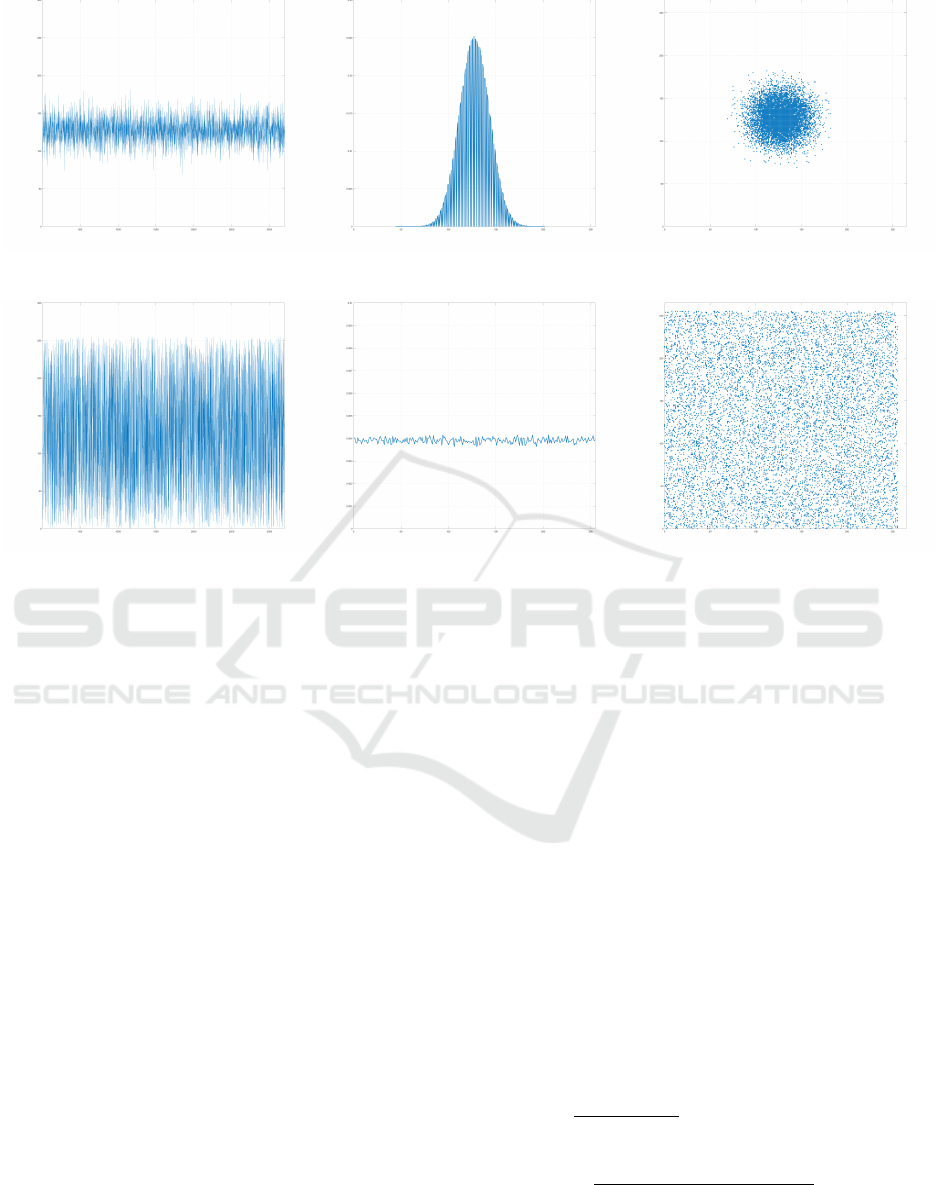
(a) (b) (c)
(d) (e) (f)
Figure 4: Amplitude variation of the original message (a) in addition to its corresponding probability density function (b),
and the original message recurrence (c). Amplitude variation of the obtained corresponding ciphertext (d) in addition to its
corresponding probability density function (e), and the ciphertext recurrence for a random dynamic key(h = 32) (f).
3.2 Resistance against Key-related
Attacks
In this section, we assess the proposed cipher scheme
against different sorts of key-related attacks. In the
following, we present the key sensitivity test results
in addition to analyzing the effect of weak keys on
the proposed scheme security.
3.2.1 Weak Key Effect
Unlike the static structure used by the standard sym-
metric cipher algorithms, the proposed cipher scheme
relies on the dynamic key structure. The proposed
cipher uses a pseudo-random function to produce a
dynamic key, which is used to produce several cryp-
tographic primitives (permutation and selection tables
in addition to round keys). Then, at each interval
(depending on the configuration), the dynamic secret
key is updated and consequently a new set of crypto-
graphic primitives is generated. Thus, if in one inter-
val, there is a weakness in the dynamic key, this will
not affect the previous or next ciphertext messages se-
curity. This limits the effects of weak dynamic session
keys.
3.2.2 Key Sensitivity Test
This test aims at evaluating the secret key sensitiv-
ity against any slight change. In fact, the proposed
key derivation function is based on a secret key and a
cryptographic nonce. In this test, two dynamic keys
are used: DK
1
and DK
2
that differ in only one ran-
dom bit. Next, the plain-message (a) of Figure 4 is
encrypted using these keys. To evaluate the difference
between the obtained cipher-messages using DK
1
and
DK
2
, the Hamming distance of the corresponding en-
crypted cipher-messages C
1
and C
2
is computed and
illustrated in Figure 6-(c) for 1,000 iterations, each
time with different DK
1
and DK
2
. The Hamming dis-
tance between these two cipher-messages is computed
as follows:
KS =
∑
T
k=1
C
1
⊕C
2
T
× 100% (5)
=
∑
T
k=1
(E
DK
1
(I)) ⊕ (E
DK
2
(I))
T
× 100%
Where, T is the bits length of the plain and encrypted
messages. It is clear from Figure 6-c that the majority
Efficient and Secure Cipher Scheme for Limited IoT Devices
147
of difference percentage values are close to the opti-
mal value (50 %). These results indicate that the pro-
posed encryption algorithm is robust and can with-
stand any adjustment(s) in the secret key or nonce.
Thus, the proposed cipher can resist key-related at-
tacks.
3.3 Resistance against Linear and
Differential Attacks
The plain-text/ciphertext sensitivity test aim at eval-
uating the ability of cipher scheme to resist against
linear and differential attacks (chosen/known plain-
text/ciphertext attacks). In other words, this test
demonstrates the level of sensitivity of the proposed
cipher against any variation(s) on the plain-block
message. Hence, the following scenario is realized:
First, two plain blocks B
1
and B
2
, which have only
one bit difference, are encrypted separately to produce
two cipher blocks C
1
and C
2
. Then, the Hamming dis-
tance between these two cipher-blocks is computed as
shown in Eq 5.
This test is iterated for 1, 000 random plain-blocks
as shown in Figure 6-(b). The obtained mean value is
close to 50%, which means that more than 50% of the
corresponding cipher-block changes. Therefore, the
proposed approach exhibits a high block sensitivity
against any change(s) on the plain-block, producing
a totally different encrypted block. Therefore, ensur-
ing the avalanche effect in a dynamic pseudo-random
manner helps in resisting linear and differential at-
tacks.
Figure 5: Entropy analysis of encrypted messages (each 256
bytes) using 1,000 random dynamic keys.
3.4 Discussion and Cryptanalysis
The proposed cipher approach ensures both the diffu-
sion and confusion properties. Moreover, it satisfies
the randomness and uniformity statistical character-
istics, which guarantees immunity against statistical
attacks.
Furthermore, the proposed cipher approach ren-
ders differential and linear attacks ineffective and in-
feasible since the avalanche effect at the block level
is attained along with a high key sensitivity, in a dy-
namic manner. In fact, any change(s) in any bit of
the secret key or Nonce can cause a significant differ-
ence in the encrypted messages as seen in Figure 6.
Moreover, the key space of the secret key can be
2
128
, 2
256
or 2
512
, which is sufficiently large to ren-
der brute-force attacks infeasible. Additionally, the
key space of the dynamic key is 2
512
, which can also
be considered large enough to overcome brute-force
attacks. Hence, a secret key and a dynamic key are
employed in the proposed cipher approach to make
the cipher-text-only attack impossible and there is no
way to retrieve any useful information from the en-
crypted messages. Therefore, the proposed cipher can
guard against any cipher-text attack. Besides, the use
of a dynamic key-dependent cryptographic primitives
limits the ability of the attackers to break the proposed
cipher scheme, especially when conducting side chan-
nel attacks.
4 PERFORMANCE ANALYSIS:
COMPUTATIONAL DELAY
In this section, the computational delay of the pro-
posed cipher is evaluated. The main objective of the
proposed cipher approach is to achieve a high level
of security with the minimum number of operations
and round iterations to reduce the computational com-
plexity and consequently, the latency and resource re-
quirements.
To asses the total associated delay of the proposed
scheme, we define the following delay components:
1. T
S
denotes the required substitution execution
time for a block of h bytes.
2. T
D
denotes the required diffusion execution time
for a block of h bytes.
3. T
xor
denotes the required logical ”exclusive or”
execution time between two blocks of h bytes.
4. T
add
denotes the required arithmetic ”addition
modulo 256” execution time between two blocks
of h bytes.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
148
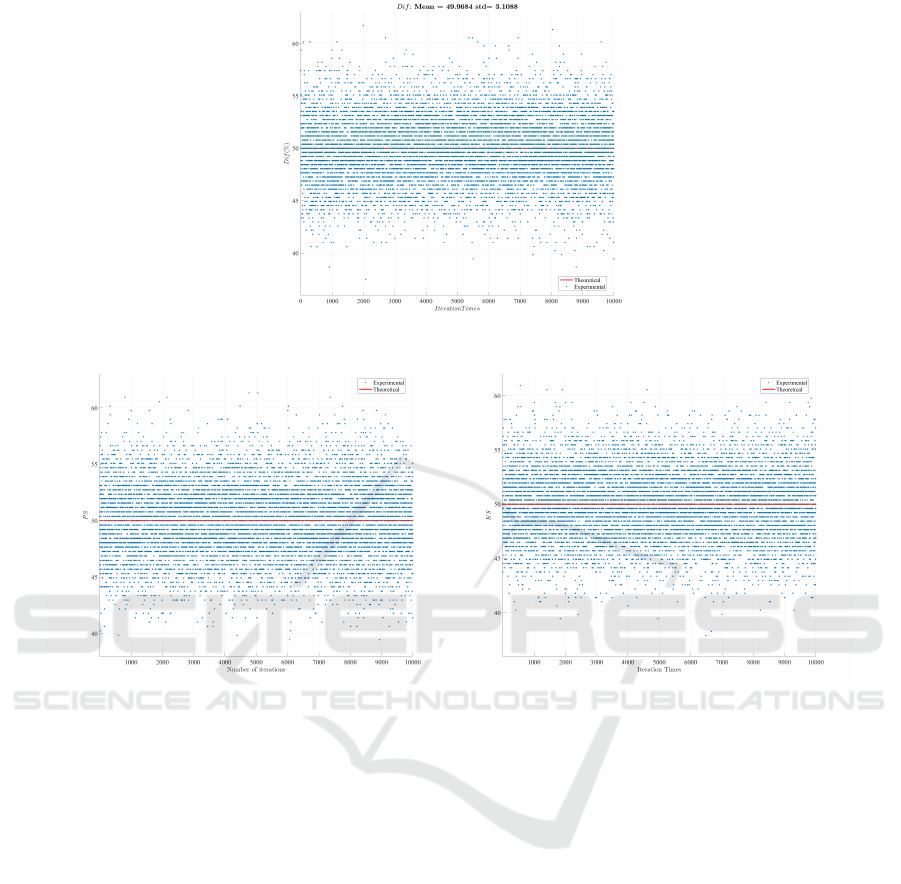
(a) DIF
(b) PS (c) KS
Figure 6: Independence tests (a), plain-block sensitivity (b) and key sensitivity (c) against 1,000 random keys for the proposed
cipher.
5. T
π
denotes the required time to permute an input
block.
Therefore, the total Computational Delay (CD) of the
proposed scheme to encrypt two blocks is:
CD
D−ECB
= 2 × T
S
+ 2 × T
D
+ ×T
xor
+ ×T
add
+ T
π
(6)
while the total computation delay of the standard AES
in (Daemen and Rijmen, 2013) to encrypt one block
is:
CD
AES
= rT
S
+ (r + 1)T
xor
+ (r − 1)T
D
+ rT
SR
(7)
where T
D
represents the required delay for the AES
diffusion mix-column operations (for all 4 columns),
representing the highest delay compared to the other
AES operations. T
SR
represents the required delay
for the AES permutation ”Shift-rows” operation and r
represents the number of rounds. The minimum value
of r is 10 for 128 bits secret key. Hence, the minimum
AES computation delay is given by:
CD
AES(r=10)
= 10T
S
+ 11T
xor
+ 9T
D
+ 10T
SR
(8)
Consequently, the AES computational delay is larger
compared to the proposed one. Moreover, the pro-
posed solution uses an optimized binary diffusion
operations minimize the computational complexity
compared to mix-columns of AES, which reduces fur-
ther the required diffusion delay.
Accordingly, the proposed scheme requires less
computational complexity compared to the AES stan-
dard cipher for 128-bit length secret key.
5 CONCLUSION
In this paper, a novel cipher scheme is presented and
analyzed based on different criteria such as crypto-
graphic robustness and performance. The obtained
results show that the proposed solution provides a
high level of security with low resources and latency
requirements. This is achieved due to the low re-
quired number of operations and rounds. In addition,
Efficient and Secure Cipher Scheme for Limited IoT Devices
149

the proposed cipher scheme is based on a combina-
tion of static (that can ensure maximum cryptographic
performance) and dynamic cryptographic primitives.
Additionally, all of its associated operations can be
realized in parallel. The diffusion operation is flexi-
ble and depends on the block size, which can be cho-
sen according to the device limitations. Moreover, its
permutation operation is performed at the block level
and not at the byte level, which reduces the overhead
of permutation in terms of memory consumption and
latency.
REFERENCES
Aoki, K., Ichikawa, T., Kanda, M., Matsui, M., Moriai,
S., Nakajima, J., and Tokita, T. (2000). Camel-
lia: A 128-bit block cipher suitable for multiple plat-
forms—design andanalysis. In International Work-
shop on Selected Areas in Cryptography, pages 39–
56. Springer.
Daemen, J. and Rijmen, V. (2013). The design of Rijndael:
AES-the advanced encryption standard. Springer Sci-
ence & Business Media.
Koo, B., Jang, H., and Song, J. (2006). On constructing of a
32× 32 binary matrix as a diffusion layer for a 256-bit
block cipher. Information Security and Cryptology–
ICISC 2006, pages 51–64.
Koo, B. W., Jang, H. S., and Song, J. H. (2003). Con-
structing and cryptanalysis of a 16× 16 binary ma-
trix as a diffusion layer. In International Workshop
on Information Security Applications, pages 489–503.
Springer.
McKay, K. A., Bassham, L., Turan, M. S., and Mouha, N.
(2016). Report on lightweight cryptography. NIST
DRAFT NISTIR, 8114.
Melki, R., Noura, H. N., Mansour, M. M., and Chehab, A.
(2018). An efficient ofdm-based encryption scheme
using a dynamic key approach. IEEE Internet of
Things Journal.
Noura, H., Chehab, A., Sleem, L., Noura, M., Couturier,
R., and Mansour, M. M. (2018). One round cipher al-
gorithm for multimedia iot devices. Multimedia tools
and applications, 77(14):18383–18413.
Noura, H., Sleem, L., Noura, M., Mansour, M. M.,
Chehab, A., and Couturier, R. (2017). A new efficient
lightweight and secure image cipher scheme. Multi-
media Tools and Applications.
Noura, H. N., Chehab, A., and Couturier, R. (2019). Ef-
ficient & secure cipher scheme with dynamic key-
dependent mode of operation. Signal Processing: Im-
age Communication, 78:448–464.
Poschmann, A. Y. (2009). Lightweight cryptography: cryp-
tographic engineering for a pervasive world. In PH.
D. THESIS. Citeseer.
WINSYS 2020 - 17th International Conference on Wireless Networks and Mobile Systems
150
