Ammonium Sensor Fault Detection in Wastewater Treatment Plants

David Tena

, Ignacio Pe

narrocha-Al

, Roberto Sanchis

and Rub

en Moliner-Heredia

Industrial Systems Engineering and Design Department, Universitat Jaume I, Castell

o, Spain

Keywords:

Fault Detection, Waste Treatment, Optimal Filtering, Trade-offs.

Abstract:

We develop a fault detection strategy for the output ammonium sensor present in wastewater treatment plants.

The only assumed measurements are the output ammonium concentration, the aeration of the reactor and the

incoming volumetric ﬂow to the plant. The incoming ammonium concentration is not measured, resulting in

an important source of uncertainty. We use a IIR model based on Volterra series for predicting the ammonium

measurement and we design a fault detector based on a ﬁlter applied on the prediction error and a threshold

comparator to decide whether the sensor is faulty or not. The faults in the sensor are assumed to produce a

slowly decreasing gain due to dirtiness in its surface. The fault detector design is based on the trade-off be-

tween fault detection sensitivity and disturbance rejection (due to measurement noise and model uncertainty).

The design parameters are based in understandable fault indices: time needed to detect the fault, gain deviation

at the time of detection, and poured volume of ammonium until the fault is detected. We use the benchmark

BSM1 to validate the results as a common frame in the study of waste water treatment plants.

1 INTRODUCTION

As one of the results of human activity, wastewater

must be treated before it returns to the environment.

The aim of Wastewater Treatment Plants (WWTPs)

is treating and cleaning wastewater to achieve an ac-

ceptable healthy state before being returned, being,

therefore, crucial agents in an environment-friendly

society. One of the critical aspects in its operation is

the concentration of ammonium of the treated water.

For that purpose, several control strategies have been

developed.

One of the most important technologies that en-

able those control strategies are the ammonium sen-

sors, that allow a tight control of ammonium concen-

tration of the poured water. However, those sensors

are not as reliable as would be desirable due to the

difﬁcult conditions in which they operate. Quite fre-

quently, wrong measurements provided by faulty am-

monium sensors lead to polluted water at the WWTP

output. Sudden faults are usually quite easy to de-

tect, as the measurement is suddenly zero or out of

range. The most difﬁcult faults are those that pro-

duce a slow drift of the measurement due to, for ex-

ample, a progressive accumulation of dirt in the sen-

https://orcid.org/0000-0002-0549-1844

https://orcid.org/0000-0002-7502-2787

https://orcid.org/0000-0003-3385-7548

sor membranes. The detection of this kind of slow

sensor faults is specially difﬁcult because WWTPs

are complex non-linear dynamic systems subjected

to large disturbances and uncertainties; these systems

deal with wide variations of the inlet wastewater, and

the biochemical and physical processes that happen

in their inside feature limits and saturations. The

detection of sensor faults is an active research area

in WWTPs in different sensor technologies (Kazemi

et al., 2020) and in industrial networked environ-

ments (Pinto et al., 2016).

In (Dovzan et al., 2011), a fault detection algo-

rithm is presented for the ammonium sensor of a

WWTP, using a Fuzzy prediction model. Several vari-

ables are assumed to be measured, including the input

ammonium concentration and the dissolved oxygen in

the reactors. While the dissolved oxygen is a com-

mon measurement in WWTP, the input ammonium

concentration is difﬁcult to be measured in practice,

because the input water is very dirty. A direct com-

parison of the prediction error (with no ﬁltering) with

a threshold is proposed to detect the fault. This has

several drawbacks due to high uncertainties and pe-

riodical patterns in the inlet water behavior. Other

works as (Nagy-Kiss et al., 2012; Garc

ıa et al., 2017;

Behzad et al., 2018; Jia et al., 2018) also use both

nonlinear models and nonlinear observers to address

the problem of fault detection.

In this work, trying to decouple the model iden-

Tena, D., Peñarrocha-Alós, I., Sanchis, R. and Moliner-Heredia, R.

Ammonium Sensor Fault Detection in Wastewater Treatment Plants.

DOI: 10.5220/0009875406810688

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 681-688

ISBN: 978-989-758-442-8

681

tiﬁcation problem from the fault detection mecha-

nism design problem, we assume that we have a given

model from which we can obtain some characteristic

values to validate it. From that starting point, this pa-

per presents a fault detection strategy to detect slow

drift type faults of the ammonium sensor in a WWTP.

The plant is assumed to be controlled in closed loop

using the ammonium measurement, and using the aer-

ation as the control action, as in (Moliner-Heredia

et al., 2019). The input ﬂow is also measured, but

not the input ammonium concentration since its mea-

surement is difﬁcult due to the dirt of the input water.

In the literature, many papers about control of

WWTP, as (Zeng and Liu, 2015), (Revollar et al.,

2016; Revollar et al., 2015; Revollar et al., 2017), are

based on the model that the Benchmark Simulation

Model n

1 offers (see(Alex et al., 2008)). In this pa-

per, the BSM1 model is used to simulate the behavior

of a WWTP and to test the developed fault detection

algorithm. Some other works try to make the control

tolerant to different faults (Nagy-Kiss et al., 2015).

The proposed fault detection strategy compares

the ammonium output concentration measurement

and a prediction of this variable. This prediction is

based on a relatively simple non-linear Volterra model

with two inputs: the aeration and the input ﬂow. The

error (difference between measurement and predic-

tion) is low pass ﬁltered to reject the ﬂuctuations due

to the daily and weekly patterns of input ammonium

concentration and the input ﬂow. The paper studies

the relation between the ﬁlter time constant, the time

needed to detect a fault and the deviation of the mea-

surements at the detection time, leading to the selec-

tion of the ﬁlter that minimizes the volume of poured

ammonium that is out of control.

The paper is structured as follows. First, the prob-

lem of ammonium sensor fault detection in WWTP is

described. Then the prediction model used is detailed.

The fault detection algorithm is then developed, fol-

lowed by extensive simulation results to test the va-

lidity of the approach. Finally, some conclusions are

summarized.

2 PROBLEM STATEMENT

This paper deals with the problem of detecting slow

drift type faults in the output ammonium concentra-

tion sensor in waste water treatment plants, in which

the output ammonium is controlled in closed loop us-

ing that ammonium sensor as output measurement,

and the aeration as control action. We have used a

realistic simulation model of the WWTP to test the

fault detection algorithm. This model is the widely

known Benchmark Simulation Model nº 1 (BSM1)

(Alex et al., 2008). This model describes the behavior

of a biological reactor with two non-aerated compart-

ments followed by three aerated compartments. The

equations that regulate this reactor come from the Ac-

tivated Sludge Model nº 1 (ASM1, see (Henze et al.,

1987)). The BSM1 also describes the behavior of the

secondary clariﬁer. An explanation of these equations

can be found in (Vilanova et al., 2017).

As it can be seen in Figure 1, inlet wastewater

) enters the bioreactor and crosses all the com-

partments. In the meanwhile, bacteria stored in the

reactor treat the wastewater, eliminating some com-

ponents and generating some others. In the last com-

partment, there is a bifurcation, where some of the

ﬂow (Q

int

) is recycled back to the ﬁrst compartment,

and the other part ﬂows to the secondary clariﬁer

). Here, wastewater is subjected to a settling pro-

cess, and the ﬂow is yet divided into the efﬂuent (Q

which may be dumped directly into the river, and the

underﬂow (Q

), which is rich in particulate compo-

nents. This ﬂow is partially purged to eliminate some

of these particles, which results in the generation of

sludge (Q

). The rest of the ﬂow (Q

) is also recycled

back to the ﬁrst compartment of the biological reac-

tor.

The differential equations that model the BSM1

use 13 different internal states for each compartment,

which correspond with 12 components and a measure

of alkalinity. In this paper, due to the recent improve-

ments in the ﬁeld of ammonium sensors, we have cho-

sen the ammonium concentration in the efﬂuent ﬂow

NH,e

) as the measured variable. In correspondence

with the BSM1 example, the oxygen transfer coefﬁ-

cient in the ﬁfth compartment (k

) is the main con-

trollable input. A controller (denoted by C in Fig-

ure 2) is assumed to be operating in closed loop, mea-

suring the output ammonium, and modifying the aer-

ation (the oxygen transfer coefﬁcient) in order to pour

the water with a given prescribed ammonium concen-

tration. The control algorithm is not relevant for this

paper, but we assume that the closed loop behavior is

stable.

The fault of the sensor to be detected is assumed

to be a slow negative ramp variation of the sensor gain

(K, being equal to 1 in normal conditions), which

presents progressively smaller measurements, lower

than the real output concentration, i.e., K < 1. This

kind of fault is more difﬁcult to detect that a step like

fault, specially in this process since it has very com-

plex non-linear dynamics. There is also an important

uncertainty in the ammonium concentration of the in-

put ﬂow, which is not measured (denoted as distur-

bance d in Figure 2). Note that the controller only

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

682

int

m = 10

m = 1

m = 6

Control

Unit 1 Unit 2 Unit 3

Unit 4

Unit 5

Anoxic section Aerated section

Biological rea ctor Secondary clari ﬁ er

NH,e

Figure 1: BSM1 Model Adaptation.

knows the concentration given by the sensor, not its

real value. The fact that the sensor shows lower val-

ues than the real concentration makes the controller to

actuate in such a way that the real ammonium may be

over the desired constraints.

The proposed fault detection strategy is based on a

predictor that estimates the value of the output ammo-

nium, using as input data the input ﬂow and the con-

trol action (the oxygen transfer coefﬁcient). The error

(difference between measurement and prediction) is

evaluated to conclude if a fault occurs in the sensor.

In the following sections we explain in detail the pre-

diction model and the fault detection mechanism.

3 PREDICTION MODEL

We propose a simple inﬁnite impulse response (IIR)

non-linear model based on Volterra series to com-

pute the prediction of the output ammonium concen-

tration, at 1 minute sampling period. The inputs of

the model are the input ﬂow (Q) and the control ac-

tion (u, the oxygen transfer coefﬁcient), and its output

is the WWTP output ammonium concentration (y).

The equation (1) shows the structure of the proposed

model:

ˆy[k] = y

∑

i=1

ˆy[k − i] +

∑

i=1

u[k − i] +

∑

i=1

u[k − i]

∑

i=1

Q[k − i] +

∑

i=1

Q[k − i]

∑

i=1

Q[k − i]u[k − i] (1)

The model is linear in the parameters (y

, a

,.. ., f

and they are obtained through least squares identiﬁ-

cation from simulated data without sensor fault. The

simulations are run with the BSM1 model and the in-

cluded input ﬂow data. Several models can be used

to predict the value of the sensor, as well as identi-

ﬁcation techniques. In this work, we focus on the

problem of detecting a fault on the sensor from a

given model (the one presented here or another one)

by means of ﬁltering the estimation error and deﬁn-

ing a threshold. This threshold is computed taking

into account that the predicted values have some error

due to both modelling errors and sensor noises, and

the ﬁltered error takes into account its effect on the

ability to detect faults.

4 FAULT DETECTION

MECHANISM

The fault detection strategy consists of low pass ﬁl-

tering the error between the measurement of ammo-

nium and the prediction given by equation (1) and

then compare it with a given threshold at each period

k. Figure 2 shows the complete detection diagram.

We propose to use a low pass ﬁlter because

there are modeling errors and important uncertainties

that have a quasi periodical shape, mainly daily and

weekly variations of the incoming water ammonium

concentration. This means that, in absence of sensor

faults, the error will have an important quasi periodic

variation that should be ﬁltered to get a smoother sig-

nal. On the other hand, the modeling error produces

a bias in the error signal, i.e. the average is not zero.

Note that the identiﬁcation of the parameters in (1)

with a least squares method does not guarantee a zero

mean estimation error.

The proposed ﬁlter is detailed in equation (2), in

which y[k] is the measurement at period k and ˜y

[k] is

the ﬁltered error. Filter time constant τ is deﬁned in

minutes.

˜y

[k] = e

−

˜y

[k − 1] + (1 − e

−

)(y[k] − ˆy[k]) (2)

Ammonium Sensor Fault Detection in Wastewater Treatment Plants

683

re f

Plant

Model

Sensor

−

Filter (τ)

Comparison

˜y

(τ)

Fault

˜y

ˆy

Figure 2: Fault detection mechanism (y

re f

: ammonium reference, u: aeration, d: disturbances, Q: input ﬂow, K: sensor gain,

y: measured ammonium, ˆy: estimated ammonium, ˜y

: ﬁltered estimation error, ˜y

: threshold).

The detection logic (3) is simply a comparison of this

ﬁltered error with a threshold ˜y

(

if | ˜y

[k]| > ˜y

: fault,

otherwise : no fault.

(3)

This threshold must be deﬁned from fault free data to

avoid false alarms (or more precisely to reach a given

low rate of false alarms), ﬁltering these data (i.e., es-

timation error) from a sufﬁcient large time window

(the one needed to stabilize the behavior of the ﬁltered

data for the chosen time constant) and computing its

maximum value, i.e.,

˜y

= max

k∈[1,N]

˜y

[k]|, (4)

where m

is a security margin (m

≥ 1) to avoid false

alarms in the case that errors are different in other op-

eration points or control situations. Obviously, this

threshold is a function of the ﬁlter time constant (the

higher the time constant, the lower the threshold).

However, it does not converge to zero; it has a lower

bound because of the inherent bias in the error signal

due to modeling errors.

We deﬁne the detection time (t

) as the time

elapsed since the gain of the sensor starts the descent

until our ﬁltered prediction error reaches the thresh-

old. The time constant of the ﬁlter (τ) affects the value

of the threshold as well as the evolution of the ﬁltered

signal, and, therefore, affects the achieved detection

time as well as the value of the fault (the gain in the

sensor due to dirty) at the instant of detection.

If we assume a slowly varying ramp like fault, a

very high value of τ will lead to a threshold close to

the lower bound determined by the error bias and the

ﬁltered error will change very slowly because of the

high τ what, altogether, will cause a high detection

time. On the other hand, a very low value of τ will

also lead to a high detection time because of the high

value of the corresponding threshold.

Thus, we can ﬁnd an intermediate value of τ that

minimizes the detection time or other interesting in-

dices that measure the performance of the fault de-

tector. As the ammonium sensor is used to control

the concentration of ammonium that is poured and it

0 2 4

t (days)

mg/l

ˆy

Figure 3: Measured ammonium and its estimation during

one week.

must be under control to avoid environmental or le-

gal problems, a good performance index can be the

amount of poured ammonium that is over the legally

allowed concentration, between the time of fault ap-

pearance and the instant of detection of the fault.

5 SIMULATION RESULTS

In this section we present the proposed algorithm re-

sults applied to data from the BSM1. First, we have

excited the system with the inlet ﬂow included in the

BMS1 and several random operations on the control

action that keep the ammonium between a certain op-

eration range and excite sufﬁciently the plant to per-

form an identiﬁcation. Then, we extract a data set to

apply least squares and to get the model parameters,

and another data set to validate the model predictions.

Figure 3 shows the measured ammonium and the es-

timated one during a particular week in the validation

set.

The estimation error (difference between mea-

sured and estimated ammonium) has some random

behavior and a signiﬁcant periodical pattern due to

the daily and weekly variations of the inlet ﬂow. Fig-

ure 4 shows the frequency spectrum of the estimation

error showing the important peaks that appear in the

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

684

0 2 4

frequency (days

−1

)

power

Figure 4: Frequency spectrum of the estimation error, show-

ing the high effect of periodical disturbances.

−3

−2

−1

0.2

0.4

0.6

0.8

τ (days)

˜y

(mg/l)

˜y

(τ)

Figure 5: Computed threshold with fault-free data with dif-

ferent time constants.

frequency related with one week and their harmonics,

and in the frequency related with one day and their

harmonics.

We have ﬁltered the fault free estimation error

with several time constants, obtaining the thresh-

olds (4) with m

= 2. Figure 5 exhibits the relation

between the ﬁlter time constant τ and the threshold

obtained. There is a maximum threshold of 0.83 mg/l

for fast ﬁltering and a minimum threshold of 0.047

mg/l for slow ﬁltering (related with the mean estima-

tion error of the proposed model).

Then, we have simulated several ramp faults in the

BSM1 benchmark. For that, we have modiﬁed the

output ammonium concentration measurement multi-

plying it by a time varying gain that starts initially in

1 and then has a constant decay. Since that measure-

ment is used in the control algorithm, the fault implies

that real ammonium concentration does not track the

reference of the controller (it is higher than the am-

monium reference). We have simulated gains with

100

150

0.5

t (days)

sensor gain (K)

Figure 6: Sensor gain evolution for the four simulated sce-

narios.

4 decay ratios: r

= 0.7%, r

= 2.8%, r

= 7% and

= 28% per week. Figure 6 shows the different time

varying gains simulated.

Then, we apply comparison (3) to the obtained

faulty signals for different time constants (τ) of the

ﬁlter. Figure 7 shows the ﬁltered estimation error for

time constants of 0.02, 1, 10 and 120 days (0.02 days

≈ 30 min) under the fault with the lower gain decay

, and the corresponding computed threshold by ﬁl-

tering fault free data with that time constant. We see

that for low values of the time constants (i.e., practi-

cally no ﬁltering), the threshold is high and that im-

plies a large detection time. For high values of the

time constant, the absolute ﬁltered error changes very

slowly and that also generates a large detection time.

For intermediate time constants we obtain lower de-

tection times.

Figure 8 shows the obtained detection times t

for

the four simulated gain decays with time constants

from 10

−3

days (i.e., 1.4 min) to 10

days. We see

that for time constants between 0.4 days to 10 days

we have a different minimum detection time for each

situation. Figure 9 shows the value of the simulated

sensor gain reduction at the time of detection for each

explored time constant.

In a real application we do not know a priori which

will be the real decay for the faulty sensor, so we

cannot directly decide an optimum value for the time

constant from the analysis of detection time and the

value of the gain at that instant. In order to decide

a ﬁltering time constant that gives good results in all

cases, we analyze now the poured volume of ammo-

nium that is out of the control speciﬁcations in each

situation; this can be computed as the integral of the

product between real ammonium concentration and

the ﬂow during the time from fault appearance until

fault detection. That value is proportional to the prod-

Ammonium Sensor Fault Detection in Wastewater Treatment Plants

685

−1

(mg/l)

τ = 0.02 (days)

τ = 0.02 (days) τ = 1 (days)

τ = 1 (days)

ˆy

threshold

0 20 40

80 100 120 140

−1

t (days)

(mg/l)

τ = 10 (days)

0 20 40

80 100 120 140

t (days)

τ = 120 (days)

Figure 7: Filtered error and threshold for different time constants in the experiment with lower gain decay rate (r

). Fault

starts at t = 10 days.

−3

−2

−1

τ (days)

(days)

Figure 8: Achieved detection time for different experiments

and time constants.

uct between detection time and simulated sensor gain

reduction at the time of detection (ﬁgures 8 and 9).

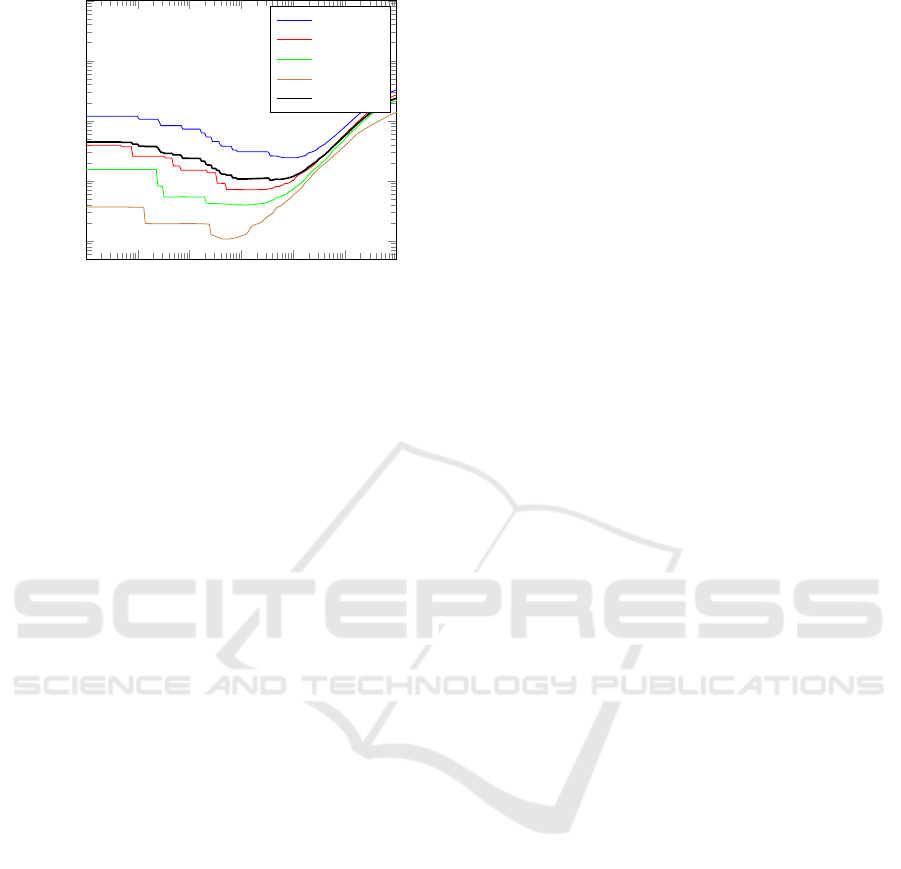
Figure 10 shows that value, evincing that the min-

imum values for each of the simulated sensor gain de-

cays are closer (in terms of τ) than the ones for the de-

−3

−2

−1

0.2

0.4

0.6

0.8

τ (days)

Gain deviation

Figure 9: Sensor gain deviation at the time of detection with

different time constants.

tection time. We have also included in the ﬁgure the

average of the poured ammonium for the four simu-

lated scenarios. The conclusion is that time constants

in the range [1,10] days are a good choice to minimize

the estimated poured volume.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

686

−3

−2

−1

τ (days)

average

Figure 10: Estimated ammonium mass that is out of speci-

ﬁcation until the detection of the fault.

6 CONCLUSIONS

A fault detection strategy has been proposed to detect

faults in the output ammonium sensor of waste water

treatment plants. The plant is assumed to be oper-

ated in closed loop by a controller that measures the

ammonium, and changes the aeration of the reactor.

The faults are assumed to be a slow drift of the mea-

surement. The only signals that are assumed to be

measured are the ammonium sensor, the aeration and

the incoming volumetric water ﬂow. The input am-

monium concentration is not measured. The BSM1

model is used to simulate the behavior of the plant

and validate the proposal.

The fault detection scheme is based on a predic-

tion model that predicts the output ammonium, and

the comparison of the ﬁltered prediction error with a

threshold. The predictor is based on a Volterra se-

ries based IIR model, whose parameters are obtained

through least squares identiﬁcation.

Despite the modeling errors that produce a bias

in the prediction error, plus the important uncertainty

in the input ammonium concentration, that follows a

quasi periodic daily and weekly pattern, the proposed

fault detector detects the slow varying fault. The pa-

per shows that the detection time depends on the time

constant of the ﬁlter, and concludes that there is an

optimum value that minimizes the fault detection time

for a given sensor drift. This optimum value depends

on the magnitude of the fault, so we have proposed

to use the constant time that minimizes the estimated

poured volume of ammonium out of control speciﬁca-

tions for the range of proposed faults. Future research

lines come from studying the behavior of our proposal

in other scenarios as rainy days or storms.

ACKNOWLEDGEMENTS

Supported by MICINN project number TEC2015-

69155-R from the Spanish government, Uni-

versitat Jaume I (UJI-B2018-39) and the grant

ACIF/2018/245 from Generalitat Valenciana.

REFERENCES

Alex, J., Benedetti, L., Copp, J., Gernaey, K., Jeppsson, U.,

Nopens, I., Pons, M., Rieger, L., Rosen, C., Steyer,

J., et al. (2008). Benchmark simulation model no. 1

(bsm1). Report by the IWA Taskgroup on benchmark-

ing of control strategies for WWTPs, pages 19–20.

Behzad, H., Casavola, A., Tedesco, F., Sadrnia, M. A., and

Gagliardi, G. (2018). A fault-tolerant sensor reconcil-

iation scheme based on self-tuning lpv observers. In

ICINCO (1), pages 121–128.

Dovzan, D., Logar, V., Hvala, N., and Skrjanc, I. (2011).

Monitoring and sensor fault detection in a waste-water

treatment process based on a fuzzy model. Elek-

trotehniski Vestnik, 78(3):142–146.

Garc

ıa, C. M., Puig, V., and Astorga-Zaragoza, C.-M.

(2017). Fault estimation using a takagi-sugeno in-

terval observer: Application to a pem fuel cell. In

ICINCO.

Henze, M., Grady Jr, C. L., Gujer, W., Marais, G., and

Matsuo, T. (1987). A general model for single-

sludge wastewater treatment systems. Water research,

21(5):505–515.

Jia, X., Cheng, Q., and Hou, Y. (2018). Sensor fault

detection based on state estimation observer in dis-

crete nonlinear systems. In 2018 International Con-

ference on Control, Automation and Information Sci-

ences (ICCAIS), pages 542–547. IEEE.

Kazemi, P., Giralt, J., Bengoa, C., and Steyer, J.-P. (2020).

Data-driven fault detection methods for detecting

small-magnitude faults in anaerobic digestion process.

Water Science and Technology.

Moliner-Heredia, R., Pe

narrocha-Al

os, I., and Sanchis-

Llopis, R. (2019). Economic model predictive control

of wastewater treatment plants based on bsm1 using

linear prediction models. In 2019 IEEE 15th Interna-

tional Conference on Control and Automation (ICCA),

pages 73–78. IEEE.

Nagy-Kiss, A. M., Ichalal, D., Schutz, G., and Ragot, J.

(2015). Fault tolerant control for uncertain descrip-

tor multi-models with application to wastewater treat-

ment plant. In 2015 American Control Conference

(ACC), pages 5718–5725. IEEE.

Nagy-Kiss, A. M., Marx, B., Mourot, G., Schutz, G., and

Ragot, J. (2012). Observer synthesis for uncertain

nonlinear systems. application to waste-water treat-

ment plants. IFAC Proceedings Volumes, 45(13):485–

490.

Pinto, R., Rossetti, R. J., and Gonc¸alves, G. (2016). Wire-

less sensor network simulation for fault detection in

industrial processes. In 2016 6th International Con-

ference on Simulation and Modeling Methodologies,

Ammonium Sensor Fault Detection in Wastewater Treatment Plants

687

Technologies and Applications (SIMULTECH), pages

1–6. IEEE.

Revollar, S., Vega, P., Francisco, M., Vilanova, R., and

Sant

ın, I. (2016). Optimization of economic and envi-

ronmental objectives in a non linear model predictive

control applied to a wastewater treatment plant. In

2016 20th International Conference on System The-

ory, Control and Computing (ICSTCC), pages 318–

323. IEEE.

Revollar, S., Vega, P., and Vilanova, R. (2015). Economic

optimization of wastewater treatment plants using non

linear model predictive control. In 2015 19th Inter-

national Conference on System Theory, Control and

Computing (ICSTCC), pages 583–588. IEEE.

Revollar, S., Vega, P., Vilanova, R., and Francisco, M.

(2017). Optimal control of wastewater treatment

plants using economic-oriented model predictive dy-

namic strategies. Applied Sciences, 7(8):813.

Vilanova, R., Sant

ın, I., and Pedret, C. (2017). Con-

trol y operaci

on de estaciones depuradoras de

aguas residuales: modelado y simulaci

on. Revista

Iberoamericana de Autom

atica e Inform

atica indus-

trial, 14(3):217–233.

Zeng, J. and Liu, J. (2015). Economic model predictive con-

trol of wastewater treatment processes. Industrial &

Engineering Chemistry Research, 54(21):5710–5721.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

688