Ensemble Clustering based Semi-supervised Learning for Revenue
Accounting Workflow Management
Tianshu Yang
1,2
, Nicolas Pasquier
1
and Frederic Precioso
1
1
Université Côte d’Azur, CNRS, I3S, France
2
Amadeus, Sophia-Antipolis, France
Keywords: Ensemble Clustering, Consensus Clustering, Closed Sets, Multi-level Clustering, Semi-supervised Learning,
Amadeus Revenue Management, Revenue Accounting, Anomaly Corrections.
Abstract: We present a semi-supervised ensemble clustering framework for identifying relevant multi-level clusters,
regarding application objectives, in large datasets and mapping them to application classes for predicting the
class of new instances. This framework extends the MultiCons closed sets based multiple consensus clustering
approach but can easily be adapted to other ensemble clustering approaches. It was developed to optimize the
Amadeus Revenue Management application. Revenue Accounting in travel industry is a complex task when
travels include several transportations, with associated services, performed by distinct operators and on
geographical areas with different taxes and currencies for example. Preliminary results show the relevance of
the proposed approach for the automation of Amadeus Revenue Management workflow anomaly corrections.
1 INTRODUCTION
Amadeus is the leading provider of IT solutions to the
global travel and tourism industry. Amadeus creates
solutions that enable airlines, airports, hotels,
railways, search engines, travel agencies, tour
operators and other stakeholders to operate and
improve travel management worldwide.
Revenue Accounting refers to the process of
managing and dispatching to the different suppliers
involved the amount collected from customer’s
payment for their travel. This process involves multiple
successive treatments of the data in input represented
as a ticket calculation code sequence for each travel.
The Amadeus Revenue Management application
helps customer performing revenue accounting. It
consists of a sequence of modules, each one
performing a computation from its input and sending
its output to the next module, that generates the
different amounts related to a journey and the
different travels it involves: Calculation of fees,
commissions and taxes, proration between
transportation operators, etc. This sequence of
modules, referred to as the Revenue Management
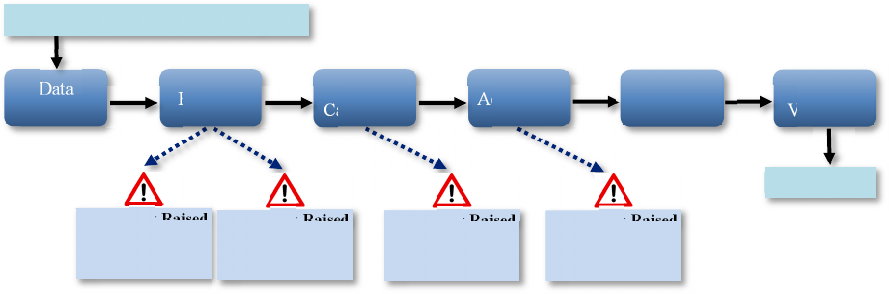
Workflow, is illustrated in Figure 1. The first stage of
the
process is to validate input data. Next, amounts
Figure 1: Example Revenue Management Workflow and Error Tasks Raised by Anomalies.
Error Task Raised
ID: ******
Type: *******
…
BOM
Before
BOM
After
Error Task Raised
ID: ******
Type: *******
…
BOM
Before
BOM
After
Error Task Raised
ID: ******
Type: *******
…
BOM
Before
BOM
After
Error Task Raised
ID: ******
Type: *******
…
BOM
Before
BOM
After
Data
Validation
Proration
Tax
Calculation
Accounting
Output
Validation
•••
In
p
ut Ticket Calculation Code Se
q
uence
Out
p
ut Status

are prorated to travel coupon level. Then, taxes, fees,
charges and other values are calculated based on these
prorated coupon amounts and local government laws.
Finally, the accounting module checks if the amounts
are balanced, which means credit should be equal to
debit to avoid calculation errors.
This process involves complex management
constraints and is automated unless an error occurs.
Errors are defined by domain experts and refer to
situations where the input and/or the output of a
module is abnormal. Such anomalies are identified by
comparing the Business Object Model (BOM) values
before and after each module to generate Error Tasks
described by their associated Error Ticket. During
each module computation, one or several anomalies,
such as an incorrect amount computed due to
erroneous values in input, can occur.
The main limitation of the current Error Tasks
handling system is that each task is treated as
independent, even if similar errors have already been
corrected. The analysis of 2 000 sample tasks from
the Task Handling Module have shown up to 40%
similar tasks. This results in an important waste of
efforts and machine learning techniques are
considered to help in decreasing costs and time spent
on similar error tickets due to their required
individual correction.
The application of machine learning techniques
thus aims to improve the automation of the error
correction process with the automatic identification
of anomaly patterns in the Amadeus Revenue
Management workflow, and the automatic or semi-
automatic, depending on the type of the anomaly
pattern, correction of the error. This application
involves the two main steps described hereafter.
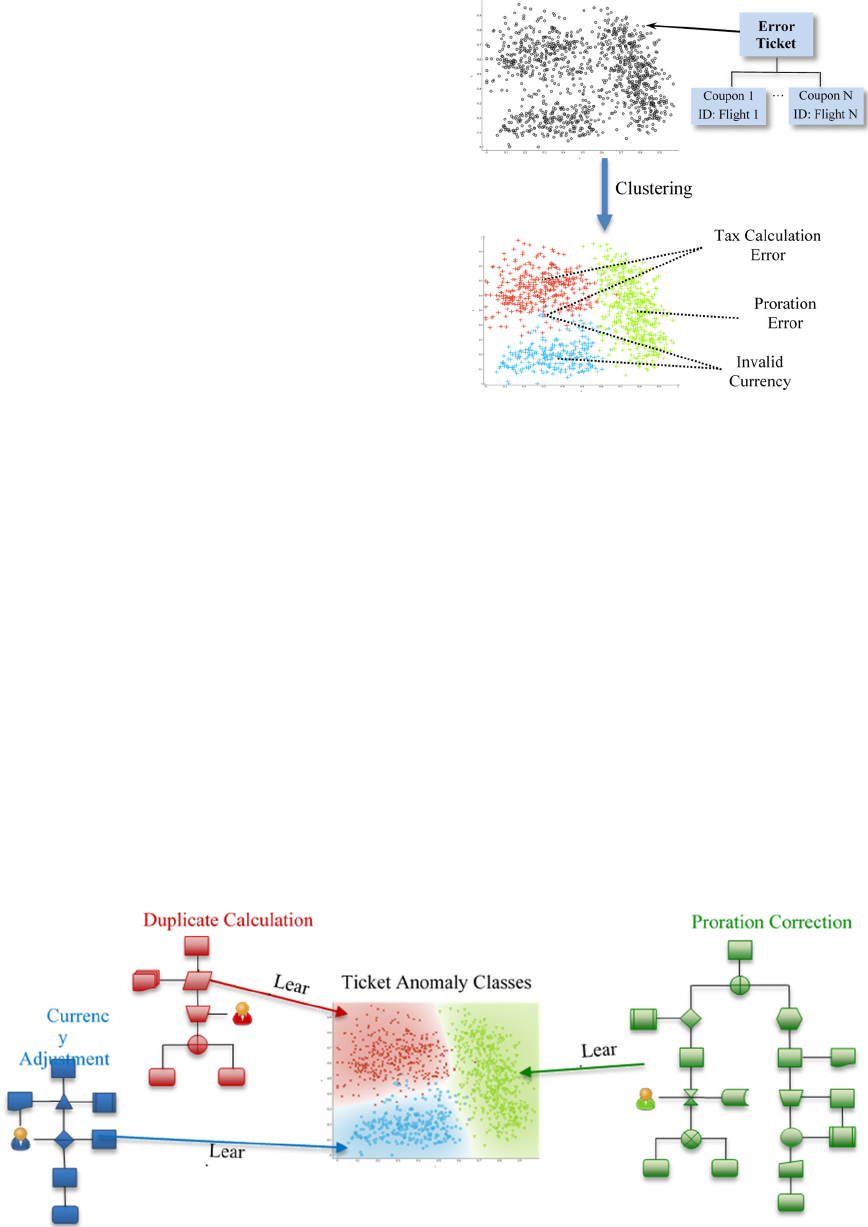
The first step is the identification of relevant
anomaly patterns, i.e., error distinctive features,
through the unsupervised classification, or
clustering,
of error tickets to form clusters of tickets
Figure 2: Clustering Anomaly Pattern Correction Tasks.
corresponding to similar anomalies and requiring
similar correction processes. Error tickets containing
information about the transportation coupons of a
travel are then grouped into clusters corresponding
each to a type of anomaly, e.g., a tax calculation or a
proration anomaly, as illustrated in Figure 2.
The second step is the learning of the correction
processes associated to each cluster of tickets, by the
analysis of logs of correction actions taken by the
correctors, for the automation of the error correction
processes. By this analysis, automatic processes of
anomaly correction can be defined for each type of
error pattern corresponding to a cluster of error
tickets. As illustrated in Figure 3, these correction
processes can require the intervention of the end-user.
The article is organized as follows. Section 2
reviews the central issues of classical clustering
approaches for semi-supervised learning and the most
recent
algorithmic developments to address these
Figure 3: Learning of Correction Processes for Anomaly Pattern Classes.

issues. In Section 3, we present the proposed semi-
supervised framework and the technical and scientific
challenges addressed during its development. Section
4 concludes the article.
2 CLUSTERING ALGORITHMS
Clustering, or unsupervised classification, is the
computational process that aims to discover clusters
(groups) of instances in a dataset. A cluster is a set of
instances, e.g., individuals, that are as much as
possible similar among themselves within the group
and different from one group to another regarding
their features represented as variable values. See
(Fahad et al., 2014), (Kriegel et al., 2009) and (Xu
and Tian, 2015) for surveys of clustering algorithms.
Algorithmic Configuration Choice Issue. Different
algorithmic configurations, i.e. a specific algorithm
with a specific parameterization, can provide
different clustering solutions. Hence, each algorithm
relies on a particular assumption on the distribution
model of instances in the data space, and each
parameterization defines a manner to put in practice
this model. The quality of the resulting clustering will
depend to which extent they are adequate to the
analysed data space properties, as studied in (Xu and
Wunsch, 2005) and (Hennig, 2016).
Cluster Internal Validation Issue. A distinctive
characteristic of clustering applications regarding
machine learning issues is the absence of initial prior
knowledge about the data space properties and of
labelled, i.e., annotated, data to help choosing an
algorithmic configuration that is appropriate for the
analysed dataset.
Moreover, the problem of choosing an adequate
algorithmic configuration and obtaining a meaningful
clustering is exacerbated by the current difficulty of
objectively assessing the quality of the resulting
clusters. If several internal validation measures have
been proposed, each measure also relies on a specific
assumption on the distribution model of instances in
the data space and can thus overrate clustering results
of algorithms based on the same model, e.g., centroid
or density based. See (Dalton et al., 2009), (Halkidi
et al., 2001), (Rendón et al., 2011) and (Tomasini et
al., 2017) for studies on clustering validation
measures.
Cluster Characterization to Application Class
Issue. The objective of the characterization of
clusters to application classes is to connect consensus
clusters and application classes, e.g., accounting
anomaly correction classes, so that each cluster is as
much as possible representative, i.e., distinctive in the
data space, of an application class. This procedure
implies the development of semi-supervised
algorithmic solutions combining unsupervised
internal validation of consensus clusters and
supervised external validation of consensus clusters
based on Amadeus business metrics. See (Färber et
al., 2010), (Halkidi et al., 2001) and (Xiong and Li,
2014) for theoretical and experimental comparisons
and studies on internal and external validation
measures.
2.1 Multi-level Clustering
The use of clustering techniques in this context aims
to discriminate the application classes according to
their properties in the data space, and potentially
refine them by distinguishing different sub-classes of
a class according to the different modeling properties
of each cluster in the data space. In the context of the
Amadeus Revenue Management workflow, clusters
can distinguish sub-classes of predefined anomaly
correction processes and overlapping clusters can
also distinguish correction action sequences that are
common to several classes of anomaly correction
processes. Indeed, one class of correction process can
correspond to several error ticket clusters, and each
cluster can correspond to several correction process
classes.
Multi-level Clustering generates a hierarchical
decomposition of clusters, where a cluster at a level
in the hierarchy can be decomposed into several
smaller clusters in the sub-levels of the hierarchy.
Such a hierarchical clustering can provide a relevant
framework for the identification of correction process
classes and sub-classes as illustrated in Figure 4 in
which the proration correction process is divided into
two sub-classes corresponding to two sub-clusters in
the data space (Färber et al., 2010).
Correction Process Class Prediction Model. Once
the most relevant multi-level clusters have been
identified, regarding internal and external validations,
their evaluation by the user is based on the statistical
and analytical exploration of cluster structures,
properties and relationships in the data space and their
adequation to the application through business related
criteria.
The validated clusters are then characterized by
the analysis of discriminative features regarding
internal and external validation results to identify
features that distinguish each of them in the data
space and to rank them from a business application
perspective.

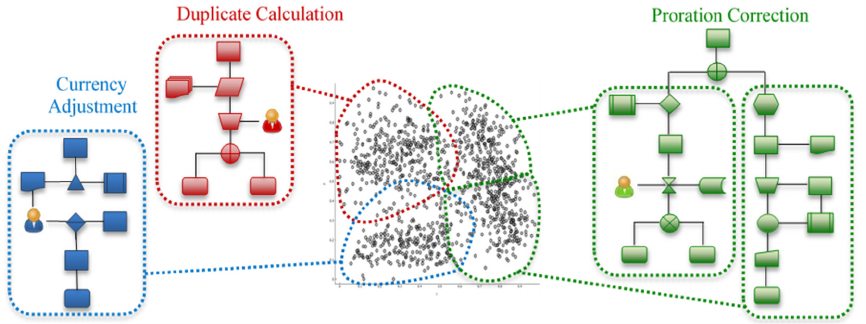
Figure 4: Detection of Ticket Anomaly Correction Classes and Sub-classes Based on Clusters.
A comparative analysis of the characterizations of
clusters, to identify the features that distinguish each
cluster from the others in the data space, is then be
performed to learn a class prediction model of
instances. In the Amadeus Revenue Management
workflow context, the learned classifier aims to
predict error ticket classes and sub-classes for
automating the learned correction processes and
provide the corrector with indicators and potential
external references to support and optimize the
correction process of the ticket anomaly.
2.1.1 Ensemble Clustering
Ensemble Clustering, or Consensus Clustering,
approaches combine multiple clustering results,
called base clusterings, each generated by a different
algorithmic configuration, for generating more robust
consensus clusters corresponding to agreements
between base clusters.
Existing ensemble clustering approaches can be
classified into the four following categories:
 Approaches considering the clustering ensemble
problem as a clustering of categorical data.
 Approaches based on the generation of an
instance co-association matrix depicting the
number of assignments of each pair of objects to
the same cluster in a clustering solution.
 Approaches that rely on the generation of a
cluster association matrix based on the number of
objects that were commonly assigned to the
clusters in a clustering solution.
 Approaches that consider the problem as a graph,
or hypergraph, partitioning problem.
However, these approaches have some limitations
in this context. Indeed most of them require the user
to define the number of clusters to generate prior to
the execution, and approaches based on instance to
instance relationships require to generate large
association matrices (N
2
size for N instances) which
is unfeasible for very large datasets (e.g., millions of
objects) due to space and time complexities of the
matrix computation and manipulation.
Once a consensus clustering is generated, its
quality is evaluated using an internal validation
measure based on the analysis of the properties of
clusters in the clustering solution relatively to the
clusters in all the base clusterings. This evaluation is
usually based either on the Adjusted Rand Index
(ARI) measure or on the Normalized Mutual
Information (NMI) measure that assess the quality of
the resulting clustering by its average similarity with
all base clusterings.
See (Boongoen and Iam-On, 2018), (Ghosh and
Acharya, 2016) and (Vega-Pons and Ruiz-
Shulcloper, 2011) for extensive reviews and studies
on ensemble clustering algorithmic approaches.
2.2 Multiple Consensus Clustering
The proposed framework is an extension of the
MultiCons multiple consensus clustering approach
described in (Al-Najdi et al., 2016) with five
algorithmic variants of the approach, based each on a
different consensus creation process (merge/divide
based, graph based, etc.), and comparative studies of
their properties in different application contexts and
for datasets with distinct data space properties.
The MultiCons approach makes use of closed set
mining to discover clustering patterns among the
different base clustering solutions, each defining an
agreement between a set of clusters to group a set of
instances. These patterns are then processed by a
split/merge strategy to generates multiple consensus
clusterings
represented in the ConsTree tree-like

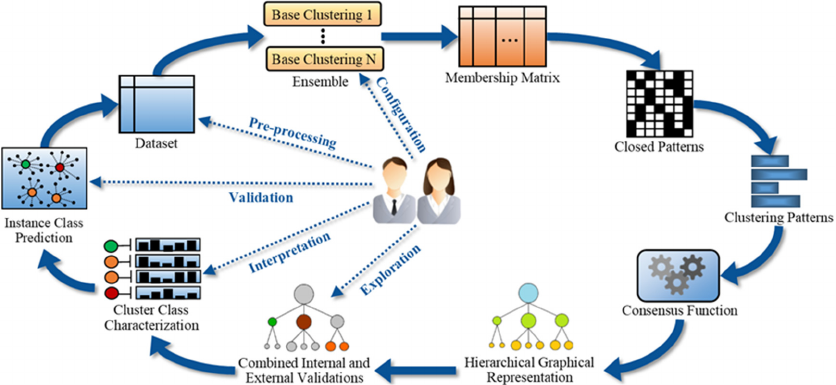
Figure 5: Semi-MultiCons Approach for Cluster Learning and Characterization for Class Prediction.
structure that helps understanding the clustering
process and data space subjacent intrinsic structures.
3 PROPOSED FRAMEWORK
The Semi-MultiCons approach proposed here is a
novel semi-supervised consensus clustering
algorithmic framework. It extends the MultiCons
approach to semi-supervised clustering, with a new
constraint-based iterative consensus creation process
and a new strategy for selecting the most relevant
consensus clusters in the ConsTree tree-like structure.
The Semi-MultiCons process is presented in Figure 5.
Starting from the dataset, the base clusterings are
generated and then combined in a membership matrix
representing the assigned cluster for each dataset
instance. Closed patterns, depicting each an
agreement between a set of base clusterings to group
a set of instances into the same cluster, are extracted
from the membership matrix and combined to
generate relevant clustering patterns of different
sizes. These patterns are processed by the consensus
function to generate the ConsTree hierarchical
graphical representation of the multi-level clusters
and identify the most relevant ones using internal and
external validations. These clusters are then
characterized and mapped to application classes to
predict the class of new instances using a neighbour-
based or model-based approach. Validated instance
class predictions can then be integrated in the process
as new constraints for the semi-supervised aspect.
This interactive process requires from the end-user to
configurate the data pre-processing step and the base
clustering algorithmic configurations, and to explore,
interpret and validate the results, i.e., the selected
multi-level clusters and their associated application
classes and sub-classes. Application domain expertise
is indeed required to optimize these tasks.
3.1 Semi-supervised Multiple
Consensus Clustering
Semi-supervised learning approaches combine
unsupervised classification, i.e., clustering, and
supervised classification, that is the subsequent
learning of classes from clusters, when partial prior
knowledge about the data is available, i.e., when
some dataset instances are annotated with class
labels. Short surveys on semi-supervised clustering-
based learning can be found in (Agovic and Banerjee,
2013), (Grira et al., 2005) and (Jain et al., 2016).
Studies of the Amadeus Revenue Management
workflow data and semi-supervised learning concepts
lead to the development of three new closed pattern
consensus-based semi-supervised algorithmic
approaches. These approaches extend the MultiCons
approach by integrating supervised information
represented as cannot-link and must-links constraints
between annotated dataset instances, i.e., pairs of
instances with different and identical class labels
respectively. Each approach integrates these
constraints in a different phase of the consensus
clustering process.
In the first proposed approach, depicted in Figure
6, cannot-link and must-link constraints are integrated
during the creation of the base clusterings by using
semi-supervised clustering algorithms.
In the second approach, depicted in Figure 7,
cannot-link
and must-link constraints are integrated

Figure 6: Integrating Constraints by using Semi-Supervised Clustering for Base Clusterings Creation.
during the processing of base clusterings to generate
the clustering ensemble, that can be represented as a
co-association matrix or a membership matrix
depending on the consensus function that will be used
to generate consensus clusters.
In the third approach, depicted in Figure 8,
cannot-link and must-link constraints are integrated
during the processing of the clustering ensemble by
the consensus function to generate consensus clusters,
so that the resulting consensus clusterings comply as
far as possible with the integrated constraints.
Different experimental protocols were defined
using reference benchmark datasets to study and
compare the three proposed approaches and other
classical single unsupervised and semi-supervised
clustering approaches. Datasets corresponding to
different ratios of annotated dataset instances and
different ratios of cannot-link and must-link
constraints among annotated dataset instances were
generated to assess the effect of these ratios on the
efficiency of the process and the relevance of the
clustering results. Results of this theoretical and
experimental study show the relevance of the three
proposed approaches for semi-supervised learning.
They also show that the integration step can be
adapted to the available prior knowledge and the
eventual integration restrictions, for example
regarding technical constraints on the use of semi-
supervised algorithms for generating base clusterings
or the use of constraints in the internal and external
validation measures applied for generating the
clustering ensemble and/or the consensus clusters.
Error ticket annotations by the end-users will be
converted to cannot-link and must-link constraints to
conduct experiments comparing classical and
ensemble semi-supervised approaches proposed in
the literature with the three developed approaches
from the viewpoints of the efficiency and the
scalability of the approaches, and of the quality of the
resulting clustering solutions.
3.2 Technical Challenges
3.2.1 Source Data Pre-processing
This challenge encompasses the representation,
storage, specialization and/or generalization and
manipulation of source data. Data collected from the
Figure 7: Integrating Constraints in the Ensemble Creation Process.

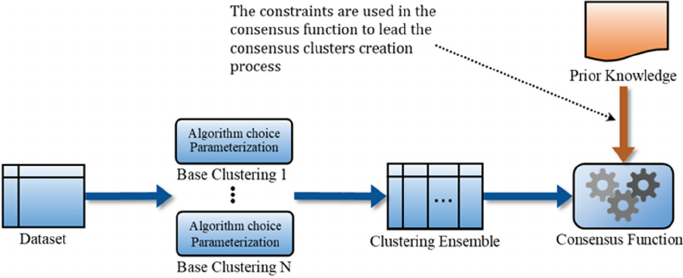
Figure 8: Integrating Constraints in the Clustering Function for Generating Consensus Clusters from the Ensemble.
Amadeus Revenue Management workflow contain
all accounting information required for processing a
travel that is coded internally as a ticket in input of
the workflow. Each ticket is a hierarchical data
structure representing the complete travel and its
associated coupons, each coupon corresponding to a
flight connection and related commercial treatments
in the travel. For each ticket, general data on the travel
(distance of travel, total duration, number of
connections, etc.) are included as well as data on each
coupon (departure and arrival airports, air operator,
duration, price, taxes, etc.). This study of the
Amadeus Revenue Management workflow data
shows that both the heterogeneity and number of
features associated with each ticket presents a great
variability, depending on the corresponding travel
and commercial treatments.
Different pre-processing steps were tested in
order to represent in a relevant format the information
on tickets regarding the applicability of unsupervised
and supervised algorithms versus the heterogeneity,
the number of objects and the number of variables in
the processed datasets.
3.2.2 Data Space Understanding
This challenge covers the analytical exploration and
identification of structural properties of the data space
regarding the issue of the parameterizations of base
clustering algorithms, to generate relevant base
clusterings in the ensemble. After the data exploration
and visualization phase, the initial datasets
constructed represent each ticket in input of the
Amadeus Revenue Management workflow as an
instance, i.e., a row, in the dataset. For this, the
hierarchical data structure representing tickets and
associated coupons was flattened: Each dataset
instance contains both data on ticket and its
associated coupons. This flattened representation of
tickets allows the applicability of all clustering
algorithms, whereas the heterogeneity of initial data
encoding does not allow to apply certain categories or
implementations of clustering algorithms.
Tickets in the dataset correspond to both tickets
with normal output, i.e., no anomaly detected, and
with error output, i.e., anomaly detected. These
datasets were sampled in order that tickets of both
classes, i.e., normal or error ticket, are sufficiently
balanced to ensure that the different classes can be
identified and segregated in the data space.
The first dataset contains 2 000 tickets, with 1 000
normal tickets and 1 000 error tickets of the anomaly
class ‘FOP Reconciliation, Unsettled Payment’.
Among these 2 000 tickets, 1 785 tickets are correctly
annotated (true class labels) while the 215 other
tickets represent noise in the data space (incorrect
class labels that were automatically generated by the
workflow, representing false positives). The second
dataset integrates with the data processed by the
Amadeus Revenue Management workflow the data
generated by the successive modules of the workflow
for the management of error tickets. This dataset
contains 20 000 tickets, with 10 000 normal tickets
and 10 000 error tickets of the anomaly class ‘FOP
Reconciliation, Unsettled Payment’.
These pre-processing operations show that a high
number of attributes are manipulated during the
Amadeus Revenue Management workflow, with up
to 39 889 features (variable values) per ticket in the
first dataset and up to 83 698 features per ticket in the
second dataset. However, this high dimensional data
space is sparse, meaning that only a small proportion
of the corresponding variables are filled in for most
tickets. If this flattened representation of ticket
features induces the applicability of all clustering
algorithms, high-dimensional data spaces impose
restrictions on the applied algorithmic configurations
regarding space and time complexities of the
computation as shown in the baseline experiments.

3.3 Scientific Challenges
3.3.1 Data Representation and Encoding
This challenge concerns the representation,
formatting and encoding of the heterogeneous data in
input of the workflow considering the applicability of
base clustering algorithms and their time and space
complexity classes relatively to the dataset size.
If the maximal number of features manipulated
for each ticket during the Amadeus Revenue
Management workflow is important, in the order of
tens of thousands, the analytical exploration of these
data and the application of supervised classification
and regression approaches show that only a small
proportion is relevant for the detection and the
prediction of classes of anomalies.
The use of feature selection techniques allows to
reduce the maximal number of features for each ticket
to the order of hundreds by removing irrelevant data
regarding the distinction of ticket classes in the data
space. This pre-processing both extends the list of
clustering algorithms that are applicable considering
their time and space complexities and to enhance the
quality of the result by reducing the negative impact
of the high-dimensionality of the data space on the
capabilities of distance measures to precisely assess
the similarity between objects in the data space
(Curse of Dimensionality issue).
3.3.2 Definition of Base Clustering
Algorithmic Configurations
The development of the semi-supervised clustering
approach integrating prior knowledge in the
generation of the base clusterings from which the
clustering ensemble is created is based on an
extensive study of semi-supervised clustering
algorithms. This study encompasses the different
algorithmic approaches and their variants that can be
divided into the following categories regarding the
underlying model they are based on: Semi-supervised
K-means, semi-supervised metric learning, semi-
supervised spectral clustering, semi-supervised
ensemble clustering, collaborative clustering,
declarative clustering, semi-supervised evolutionary
clustering and constrained expectation-maximization.
Diverse criteria were considered for determining
the best semi-supervised algorithmic approaches to
integrate for the generation of the base clusterings.
These criteria consider in first place the quality of the
clustering results, the efficiency and scalability of the
approach regarding dataset size, the applicability of
the approach to datasets containing heterogeneous
and missing data, and the robustness of the approach
to noise and outliers in the data. Considering reported
theoretical and experimental results in the literature,
and both the availability and the results of tests of
implementations, the COP K-means (Constraint-
Partitioning K-means), the MPCK-means (Metric
Pairwise Constrained K-means) and the LCVQE
(Constrained Vector Quantization Error) algorithmic
approaches were integrated. Their algorithmic
configurations are defined using an interval of values
for the K parameter (number of clusters) to comply
with the diversity required for the search space of the
consensus clustering function. This interval is
centered on the number of classes defining the
cannot-link and must-link constraints to improve the
robustness of consensus solutions.
3.3.3 Ensemble Definition and Formatting
This challenge addresses the problem of the
representation of base clustering results in the
ensemble. That is how resulting instance cluster
assignments are represented for partitioning,
overlapping and fuzzy based clustering algorithms.
The design of a semi-supervised clustering
approach integrating prior knowledge in the
generation of the clustering ensemble required to
develop new algorithmic approaches. This prior
knowledge consists of partial class label annotations
in the dataset, that is some dataset instances are of
known classes while others are not. These annotations
are used to generate cannot-link constraints between
instances of different classes and must-link
constraints between instances of identical classes.
The generated cannot-link and must-link constraints
are used to evaluate the quality of base clusters and
base clusterings by considering the number of
constraints that are violated and met in each cluster.
The results of this evaluation are used either to delete
from the clustering ensemble the base clusterings
with a low score, or to assign a reduced weight to base
clusterings with a low score and an increased weight
to base clusterings with a high score.
Depending on the consensus function used and
the data representation it requires as input, different
processes are defined to generate the clustering
ensemble. For co-association matrix-based consensus
functions, the co-association matrix can be generated
from the base clusterings with a sufficiently high
score only, or a weighted co-association matrix can
be generated using evaluation scores to weight co-
association values. For membership matrix-based, a
binary membership matrix can be generated from the
base clusterings with a sufficiently high score only, or

a weighted membership matrix can be generated
using constraint-based evaluation score of clusters to
weight cluster assignments with confidence degrees.
3.3.4 Definition of Clustering Patterns
This challenge concerns the definition of the criteria
used during the analysis of agreements between base
clusterings by the consensus function to identify
clustering patterns. A clustering pattern is a group of
instances that verifies some properties, e.g., based on
the number of base clustering agreements or
constraints it satisfies and violates, to form a cluster.
New algorithmic techniques were developed
during the design of the Semi-MultiCons approach to
integrate prior knowledge in the generation of
consensus clusters by the consensus function. The
prior knowledge, represented as partial annotations,
is used to generate cannot-link and must-link
constraints that are integrated during the processing
of the clustering ensemble by the consensus function
to obtain consensus clusters and consensus
clusterings that comply as far as possible with the
constraints.
The proposed approach first extracts closed
patterns from the membership matrix representing the
clustering ensemble and iteratively combine these
closed patterns to define clustering patterns, each one
representing a relevant agreement between base
clusterings on grouping a set of instances. These
clustering patterns, that can overlap, are evaluated
and compared to create the multi-level consensus
clusters using a constraints-based merging/splitting
method. The key step of this phase is to access a
normalized score that evaluates whether two
overlapping patterns should be merged or spitted. We
introduced three new constraints-based normalized
measures, that consider the reflexive property of the
cannot-link constraint type and the symmetrical,
reflexive and transitive properties of the must-link
constraint type, that are used to decide how to split or
merge patterns. Each measure corresponding to a
different situation from the viewpoint of the prior
knowledge available for the considered patterns.
When no prior knowledge is available, the classical
unsupervised measure of the approach, based on the
relative and absolute sizes of the overlapping and
distinct subsets of objects for the two patterns, is used.
Once the hierarchical structure of consensus
clusterings is created, the candidate consensus
clustering that satisfies the highest number of
constraints is selected as the recommended solution.
4 CONCLUSIONS
Figure 9: Principal Component Analysis Results for Task
Type Classes.
Figure 10: Principal Component Analysis Results for Semi-
MultiCons Clusters.
Both theoretical and experimental results obtained
during the initial phase of the Semi-MultiCons
development have demonstrated both the feasibility
and the relevance of semi-supervised learning
approaches relying on closed patterns-based multi-
level consensus clustering for improving processes
such as the Amadeus Revenue Management
workflow. Moreover, generating multi-level
consensus clusters, such as generated by the Semi-
MultiCons approach, can support the refinement of
application classes into more adequate sub-classes
regarding the application objectives, for example by
decomposing anomaly correction processes into sub-
processes, that can be common to several processes.
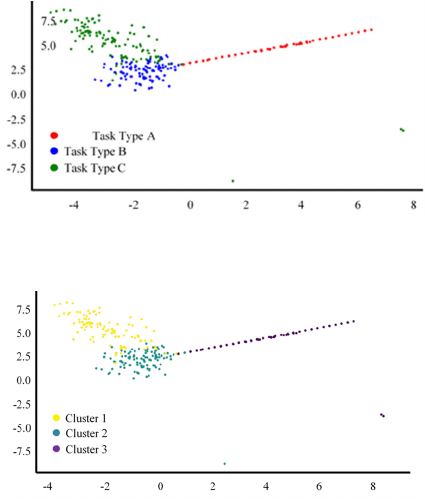
Initial experiments were conducted on a sample
dataset of 474 error tasks raised by the Accounting
module of the workflow. These tasks are annotated
with three different types: 94 tasks of type A, 210
tasks of type B and 170 tasks of type C. Figure 9
shows the result of the application of the Principle
Component Analysis approach for transforming raw
data into two-dimensional points, where horizontal
and vertical axes represent principal components
calculated by the approach. Each point in this scatter
plot represents a task which true label, i.e., type of
task, is represented in color. The scatter plot obtained
by the application of the same Principle Component

Analysis approach to the output of Semi-MultiCons
for this dataset is shown in Figure 10, where the
assigned cluster for each task is represented in color.
Using Jaccard index to compare true classes and
assigned clusters for the 474 tasks, an accuracy of
82% was calculated. It should be noted that these
initial results were obtained without tuning the
parameters of each step of the Semi-MultiCons
approach. In a second time, the Semi-MultiCons
approach was applied to a dataset of 303 064 error
tasks containing all error tasks raised by the Proration
module between January 2019 and September 2019
for a medium sized airline customer. Due to the size
of dataset, only partial information was available for
supervised validation of the results. However,
assuming clustering result is correct, the assessed rate
of tasks that are similar is 39.5%. With an estimated
average manual correction duration for tasks of more
than one minute, identifying similar tasks for their
simultaneous anomaly correction may save up to
2 000 hours of manual correction activity for these
303 064 tasks.
These achievements have also shown the
necessity for a speciation of semi-supervised
approaches to take into account the heterogeneous
internal and external available information, i.e., data
and prior knowledge, in input and the application
objectives from the perspective of the classes that are
to be distinguished: The potential overlapping
properties of classes in the data space, a hierarchical
structure of application classes, the availability of
prior knowledge such as data partially annotated with
application classes, the complex processing of logs of
sequential correction actions requiring deep learning
techniques, etc. Examples of recent applications with
similar considerations in the domains of ontology
matching and document classification can be found in
(Boeva et al., 2018) and (Ippolito and Júnior, 2016).
ACKNOWLEDGMENTS
This project was carried out as part of the IDEX
UCA
JEDI
MC2 joint project between Amadeus and the
Université Côte d'Azur. This work has been
supported by the French government, through the
UCA
JEDI
Investments in the Future project managed
by the National Research Agency (ANR) with the
reference number ANR-15-IDEX-01.
REFERENCES
Agovic A., Banerjee A. Semi-supervised Clustering. In
Data Clustering: Algorithms and Applications, Chapter
20, pp. 505-534, 2013, Chapman & Hall.
Al-Najdi A., Pasquier N., Precioso F. Frequent Closed
Patterns Based Multiple Consensus Clustering. In
ICAISC'2016 International Conference on Artificial
Intelligence and Soft Computing, pp. 14-26, June 2016,
LNCS 9693, Springer.
Al-Najdi A., Pasquier N., Precioso F. Using Frequent
Closed Pattern Mining to Solve a Consensus Clustering
Problem. In SEKE'2016 International Conference on
Software Engineering & Knowledge Engineering, pp.
454-461, July 2016, KSI Research Inc. SEKE'2016
Third Place Award.
Al-Najdi A., Pasquier N., Precioso F. Multiple Consensuses
Clustering by Iterative Merging/Splitting of Clustering
Patterns. In MLDM'2016 International Conference on
Machine Learning and Data Mining, pp. 790-804, July
2016, LNAI 9729, Springer.
Al-Najdi A., Pasquier N., Precioso F. Using Frequent
Closed Itemsets to Solve the Consensus Clustering
Problem. In International Journal of Software
Engineering and Knowledge Engineering,
26(10):1379-1397, December 2016, World Scientific.
Boeva V., Angelova M., Lavesson N., Rosander O.,
Tsiporkova, E. Evolutionary Clustering Techniques for
Expertise Mining Scenarios. In ICAART’2018
International Conference on Agents and Artificial
Intelligence, pp. 523-530, January 2018, SciTePress.
Boongoen T., Iam-On N. Cluster Ensembles: A Survey of
Approaches with Recent Extensions and Applications.
In Computer Science Review, vol. 28, pp. 1-25, 2018.
Dalton L., Ballarin V., Brun M. Clustering Algorithms: On
Learning, Validation, Performance, and Applications to
Genomics. In Current Genomics, 10(6):430-445, 2009,
Bentham Science Publisher.
Fahad A., Alshatri N., Tari Z., Alamri A., Khalil I., Zomaya
A., Foufou S., Bouras A. A Survey of Clustering
Algorithms for Big Data: Taxonomy and Empirical
Analysis. In IEEE Transactions on Emerging Topics in
Computing, 2(3):267-279, September 2014, IEEE
Computer Society.
Färber I., Günnemann S., Kriegel H.-P., Kröger P., Müller
E., Schubert E., Zimek A. On Using Class-Labels in
Evaluation of Clusterings. In KDD MultiClust
International Workshop on Discovering, Summarizing
and Using Multiple Clusterings, 2010.
Ghosh J., Acharya A. A Survey of Consensus Clustering.
In Handbook of Cluster Analysis, Chapter 22, pp. 497-
518, 2016, Chapman and Hall/CRC.
Grira I., Crucianu M., Boujemaa N. Unsupervised and
Semi-supervised Clustering. A Brief Survey. In A
Review of Machine Learning Techniques for
Processing Multimedia Content, vol. 1, pp. 9-16, 2005.
Halkidi M., Batistakis Y., Vazirgiannis, M. On Clustering
Validation Techniques. In Journal of Intelligent
Information Systems, vol. 17, pp. 107-145, 2001,
Springer.

Hennig C. Clustering Strategy and Method Selection. In
Handbook of Cluster Analysis, Chapter 31, pp. 703-
730, 2016, Chapman and Hall/CRC.
Ippolito A., Júnior J.R. Ontology Matching based on Multi-
Aspect Consensus Clustering of Communities.
ICEIS'2016 International Conference on Enterprise
Information Systems, Volume 2, pp. 321-326, April
2016, SciTePress.
Jain A., Jin R., Chitta R. Semi-supervised Clustering. In
Handbook of Cluster Analysis, Chapter 20, pp. 443-
468, 2016, Chapman and Hall/CRC.
Kriegel H.-P., Kröger P., Zimek A. Clustering High-
dimensional Data: A Survey on Subspace Clustering,
Pattern-based Clustering, and Correlation Clustering. In
ACM Trans. Knowl. Discov. Data, vol. 3, num. 1,
article 1, March 2009, ACM Publisher.
Vega-Pons S., Ruiz-Shulcloper J. A Survey of Clustering
Ensemble Algorithms. In International Journal of Pat-
tern Recognition and Artificial Intelligence, 25(3):337-
372, 2011.
Rendón E., Abundez I., Arizmendi A., Quiroz E.M. Internal
versus External Cluster Validation Indexes. In
International Journal of Computers and
Communication, 5(1):27-34, 2011.
Tomasini C., Borges E.N., Machado K., Emmendorfer L.R.
A Study on the Relationship between Internal and
External Validity Indices Applied to Partitioning and
Density-based Clustering Algorithms. In ICEIS'2017
International Conference on Enterprise Information
Systems, Volume 3, pp. 89-98, April 2017, SciTePress.
Xiong H., Li Z. Clustering Validation Measures. In Data
Clustering Algorithms and Applications, Chapter 23,
pp. 571-605, 2014, CRC Press.
Xu D., Tian A. A Comprehensive Survey of Clustering
Algorithms. In Annals of Data Science, 2(2):165-193,
2015, Springer.
Xu R., Wunsch D. Survey of Clustering Algorithms. In
IEEE Transactions on Neural Networks, 16(3):645-
678, 2005, IEEE Computer Society.