
Damage Detection and Diagnosis for Offshore Wind Foundations
Bryan Puruncajas
1,2 a
, Yolanda Vidal
2 b
and Christian Tutiv
´
en
1 c
1
Mechatronics Engineering, Faculty of Mechanical Engineering and Production Science (FIMCP),
Escuela Superior Polit
´
ecnica del Litoral (ESPOL), Guayaquil, Ecuador
2
Department of Mathematics, Control, Modeling, Identification and Applications (CoDAlab),
Universitat Polit
`
ecnica de Catalunya (UPC), 08019 Barcelona, Spain
Keywords:
Structural Health Monitoring, Offshore Wind Turbine, Structural Vibration, Data-driven, Convolutional
Neural Network.
Abstract:
Structural health monitoring for wind turbines (WT) in remote locations, as offshore, is crucial (Presencia
and Shafiee, 2018). Offshore wind farms are increasingly realized in water depths beyond 30 meters, where
lattice foundations (as jacket-type) are a highly competitive substructure type (Moulas et al., 2017). In this
work, a methodology for the diagnosis of structural damage in jacket-type foundations is stated by means
of a small-scale structure -an experimental laboratory tower modeling an offshore-fixed jacket-type WT. In
the literature, a lot of methodologies for damage detection can be found (Li et al., 2015). Among them,
the vibration-based methods are one of the most prolific ones. However, they are, primarily, focused on
the case of measurable input excitation and vibration response signals, with only few recent studies focused
on the vibration–response–only case, the importance of which stems from the fact that in some applications
the excitation cannot be imposed and often is not measurable. This work aims to contribute in this area, as
the vibration excitation is given by the wind and analyzed by a convolutional neural network (CNN), with a
classification accuracy result of 93 %.
1 INTRODUCTION
Wind energy is one of the best sources of fuel, as it
is clean, relatively cheap and inexhaustible. In or-
der to increase the energy produced by these means,
more offshore wind farms have been installed (Selot
et al., 2018). Given the location of wind turbines and
the sea conditions, new problems related to inspec-
tion, maintenance and repair work arise (Zhang et al.,
2016). To reduce logistics and maintenance costs, as
well as to minimize turbine downtime, it is crucial that
wind turbines are continuously monitored (Breteler
et al., 2015). In particular, a structural health moni-
toring system (SHM) is needed to verify the state of
the structure to guarantee its correct operation and de-
termine whether the wind turbine needs some mainte-
nance.
There are different types of WT foundations, see
Figure 1, depending on the depth at which the WT
will be installed. In general, monopiles are used in
a
https://orcid.org/0000-0002-2194-6853
b
https://orcid.org/0000-0003-4964-6948
c
https://orcid.org/0000-0001-6322-4608
installations at depths below 15 meters, gravity foun-
dations are preferred when depth is less than 30 me-
ters, and jackets are the option used for greater depths,
(Klijnstra et al., 2017). This work proposes a com-
plete methodology for SHM (damage detection and
classification) of a jacket-type foundation tested in a
laboratory offshore-fixed wind turbine model. The
only excitation of the WT is assumed to be given
by wind turbulence, so the input excitation is as-
sumed to be unknown. The proposed method is vi-
bration–response–only and can be summarized in the
following steps: (i) the wind excitation is simulated
as a Gaussian white noise and the data coming from
the WT is collected using a set of accelerometers; (ii)
the raw data are pre-processed and converted into im-
ages using as many channels as sensors; (iii) a con-
volutional neural network is stated as a classifier. The
damage detection strategy is applied to different types
of predefined damage. The obtained results demon-
strate the reliability of the proposed approach.
Puruncajas, B., Vidal, Y. and Tutivén, C.
Damage Detection and Diagnosis for Offshore Wind Foundations.
DOI: 10.5220/0009886101810187
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 181-187
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

Figure 1: Types of foundations (Association et al., 2012).
2 RELATED WORK
The first SHM study dates back 50 years ago. In
70s and 80s, the oil industry faced the problem of
identifying damage in offshore platforms (Martinez-
Luengo et al., 2016). They struggled to develop meth-
ods based on identifying vibrations to locate the dam-
age. At the same time, the aerospace community
began investigating the use of vibration-based strate-
gies. This approach has continued with the current
research of the National Aeronautics and Space Ad-
ministration (Seshadri et al., 2016). Currently, SHM
has been developed in the fields of civil aviation in-
dustry (Khan et al., 2014) and civil structures (Song
et al., 2017). SHM is highly multidisciplinary, and
advances in other areas of study can probably be re-
cruited for SHM’s progress.
Figure 2 shows a general classification for differ-
ent types of strategies for SHM.
Figure 2: Algorithms classification (Martinez-Luengo et al.,
2016).
The methodology implemented in this work is based
on supervised learning algorithms. Specifically on
neural networks (NN), which are recently used in
structural health monitoring to identify, locate, and
quantify damage in different types of structures (Liu
et al., 2017). One of the best-known deep NNs is
the convolutional neural network (CNN). A CNN is
commonly used to recognize objects in images given
their ability to exploit spatial or temporal correlation
in the data (Albawi et al., 2017). A CNN has multi-
ple layers; including fully connected layers, grouping
layers, convolutional and nonlinear layers. Fully con-
nected layers and convolutional layers have parame-
ters, however non-linearity and grouping layers have
no parameters.
Some research has been conducted related to CNN
in the field of SHM. For example, (Tabian et al., 2019)
proposes to collect impact waves using piezoelectric
sensors (PZT) to detect and locate impacts (this ap-
proach was tested on a rigid panel). Another method
with piezoelectric sensors is used in (De Oliveira
et al., 2018), where the signals from the sensors are
transformed to RGB images. A different study fo-
cused on transfer learning (TL) techniques to train
with discrete histogram data (compressed data) is pre-
sented in (Azimi and Pekcan, 2019). Their results in-
dicate that deep TL can be effectively implemented
for SHM of similar structural systems with different
types of sensors. However, these previous works used
known-input vibration signals. In this work, it is pro-
posed to use CNN for damage diagnosis in wind tur-
bines foundations by using only vibration-response
data. The strategy consists on transforming the vi-
bration signals into images (with as many channels as
sensors), and then classify the images with its corre-
sponding structural state label.
3 EXPERIMENTAL SET-UP
The general overview of the experimental testbed is
given in Figure 3 and explained as follows.
The experiment starts with a white noise signal
given by the function generator. This signal is am-
plified and passed to the inertial shaker. This is re-
sponsible for generating vibrations (similar to those
produced by gusts of wind on the blades) to the lab-
oratory tower structure. The shaker is placed at the
upper part of the structure, thus simulating the nacelle
mass. The simulation of different wind speed is also
simulated with this shaker, by changing the amplitude
of the input electrical signal. In particular, multiply-
ing it by the factors 0.5, 1, 2, and 3. Finally, the struc-
ture is monitored by 8 triaxial accelerometers which
are connected to the data acquisition system. Thus,
data from 24 sensors is collected. The nomenclature
used for each sensor is given in Table1.
The real structure used in this work is a tower model.
From Figure 3 (offshore platform) it can be seen the
components of the structure: jacket, tower and na-
celle. As a whole, this structure is 2.7 m high. The
tower is composed of three sections joined with bolts.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
182

Figure 3: General overview of the experimental testbed.
Table 1: Nomenclature used to refer to each available sen-
sor. Note that i = 1,...,8, as there are eight accelerometers.
Sensor
A
x
i
Acceleration in x-direction for accelerometer number i
A
y
i
Acceleration in y-direction for accelerometer number i
A
z
i
Acceleration in z-direction for accelerometer number i
The jacket is composed with several sections, all of
them joined with bolts, with a torque of 12 Nm. The
different studied damages are introduced in one of
these sections. The top piece (representing the na-
celle) is 1 m long and 0.6 m width.
Two types of damage are introduced at the jacket
support: a 5 mm crack in one of the bars; and loos-
ening one of the bolts in the jacket. Also a healthy
replica of the studied bar has been considered, as the
proposed strategy should be able to detect and clas-
sify the studied types of damage, but also be robust
to the replacement of one bar by a new healthy one
(avoiding false alarms).
4 DAMAGE DETECTION AND
CLASSIFICATION
METHODOLOGY
The proposed SHM methodology is composed by the
following steps. First, the data is collected from
the experiment and reshaped. Second, the data is
pre-processed in order to obtain a data set of multi-
channel images. Third, a CNN with 24 channel in-
puts is designed and trained for classification of the
different types of damage.
4.1 Data Collection and Reshape
The time window for each experimental test is 60 sec-
onds with a sampling frequency of approximately 257
Hz. Thus, each experiment obtains 16517 data mea-
surements from each of the 24 sensors. In this work,
a total of 25 experimental tests are conducted for each
different white noise amplitude. In particular:
• 10 tests with the original bar.
• 5 tests with the replica bar.
• 5 tests with a 5 mm crack damaged bar.
• 5 tests with an unlocked bolt damage.
That is 100 experiments in total, as there are 25 ex-
periments for each one of the 4 different considered
white noise amplitudes. Given the k-th experimen-
tal test, the data is initially stored in a matrix Y
(k)
∈
M
16517×24
(R) such that:
Y
(k)
=
y
(k)
1,1
y
(k)
1,2
· · · y
(k)
1,24
y
(k)
2,1
y
(k)
2,2
· · · y
(k)
2,24
.
.
.
.
.
.
.
.
.
.
.
.
y
(k)
16517,1
y
(k)
16517,2
· · · y
(k)
16517,24
, (1)
where the number of rows is given by the number of
time stamps in each experimental test and the number
of columns is equal to the number of sensors. Note
that data in the first, second and third columns (A
x
1
,A
y
1
,
A
z
1
) come from accelerometer 1; fourth, fifth and sixth
columns are related to the second accelerometer, and
so on until the last accelerometer.
To convert the data into images, the dimensions
of matrix Y
(k)
have been chaned. In particular, the
data coming from the k-th experimental test, Y
(k)
, is
reshaped to a matrix Z
(k)
∈ M
64×(256·24)
(R), that is a
matrix with 64 rows and 256 · 24 = 6144 columns as
detailed in Table 2. Note that the last samples (from
16385 to 16517) of each sensor are discarded.
4.2 Signal to Image Conversion
The damage diagnosis method converts time-domain
signals, from the 24 measured sensors, into 2D gray
level images to exploit texture information from the
converted images. The data conversion process is in-
spired in reference (Ru
´
ız et al., 2018) but here it is
enhanced by using multi-channel images.
Damage Detection and Diagnosis for Offshore Wind Foundations
183

In particular, first the values in matrix Z
(k)
are
scaled between 0 and 255. This will allow an easy
conversion into gray scale images. The image size
used for signal to image conversion is 16 × 16 (256
pixels) with 24 channels (one per sensor) and it is con-
structed as follows. For each sensor (different blocks
of matrix Z
(k)
, see Table 2) the first 16 data-points
determine the first row of the gray-scale image; im-
mediately after, the next 16 data points determine the
second row and finally the data points 240 to 256 de-
termine the last row of the image. That is, each row
of matrix Z
(k)
is converted to 24 gray-scale images
(one per sensor) with size 16 × 16. In fact, in order to
apply convolutional neural networks, it is proposed to
shape these data as one image with 24 channels (one
per sensor), similarly to RGB images (with 3 chan-
nels). Note that, considering that the sampling time
is 1/257 seconds, each image contains approximately
one second of data from all the sensors, which ensures
to capture all the system dynamics. The total number
of images in the data set is 6400, as there are 64 im-
ages coming from each one of the 100 experiments.
Figure 4 shows one of the multi-channel images.
Figure 4: Multi-channel gray-scale image corresponding to
the 24 sensors (size 16 × 16).
4.3 Convolutional Neural Network
(CNN)
The next step of the proposed damage diagnosis
method is to use a convolutional neural network
(CNN) in order to detect and classify the damage
state. The input data to the CNN are the multi-channel
gray-scale images obtained from the signal-to-image
conversion explained in the previous section.
The proposed CNN architecture is shown in Fig-
ure 5 and the most significant characteristics are
given in Table 3. Briefly explained, first, the gray-
scale images (16 × 16 × 24) are applied to the first
convolutional module. This module is composed of
32 filters (kernel 5 × 5) and padding of 1, resulting
in an output size of 14 × 14 × 32. Next, the second
and the third convolutional layers have the same ker-
nel and same padding, resulting in an output size of
12 × 12 × 64 and 10 × 10 × 32, respectively. Then, a
fully connected layer of size 1 × 1 × 4 is connected
and finally, the softmax layer outputs the predicted
structural condition. The data set is split into 70% for
training and 30% for validation.
The parameters have been optimized with Adam,
which is an adaptive learning rate method. This
method is easy to implement, is computationally ef-
ficient, has few memory requirements, and hyper-
parameters have intuitive interpretations and gener-
ally require little tuning (Kingma and Ba, 2014). The
selected hyper-parameter values are an initial learning
rate of α
0
= 0.01, a gradient decay factor of β
1
= 0.9,
a squared gradient decay factor of β
2
= 0.992, and a
value ε = 10
−7
. Moreover, the learning rate is drop
every 2 epochs by multiplying with factor 0.5, and fi-
nally, L2 regularization with λ = 10
−6
is employed.
Finally, a flowchart of the proposed approach is
shown in Figure 6. When a WT has to be diagnosed,
the accelerometers data are scaled, reshaped and con-
verted into gray-scale images that are fed into the al-
ready trained CNN. A classification is obtained to pre-
dict the condition of the structural state.
5 RESULTS
A comprehensive decomposition of the error between
the true classes and the predicted classes is shown by
means of the so-called confusion matrix in Table 4.
Each row represents the instances in a true class while
each column represents the instances in a predicted
class. The first row is labeled as 1 and corresponds to
Table 2: Data reshape for each experimental test k = 1,...,100.
Sensor 1 Sensor 2 . . . Sensor 24
Z
(k)
=
y
(k)
1,1
· · · y
(k)
256,1
y
(k)
257,1
· · · y
(k)
512,1
.
.
.
.
.
.
.
.
.
y
(k)
16129,1
· · · y
(k)
16384,1
y
(k)
1,2
· · · y
(k)
256,2
y
(k)
257,2
· · · y
(k)
512,2
.
.
.
.
.
.
.
.
.
y
(k)
16129,2
· · · y
(k)
16384,2
· · ·
y
(k)
1,24
· · · y
(k)
256,24
y
(k)
257,24
· · · y
(k)
512,24
.
.
.
.
.
.
.
.
.
y
(k)
16129,24
· · · y
(k)
16384,24
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
184
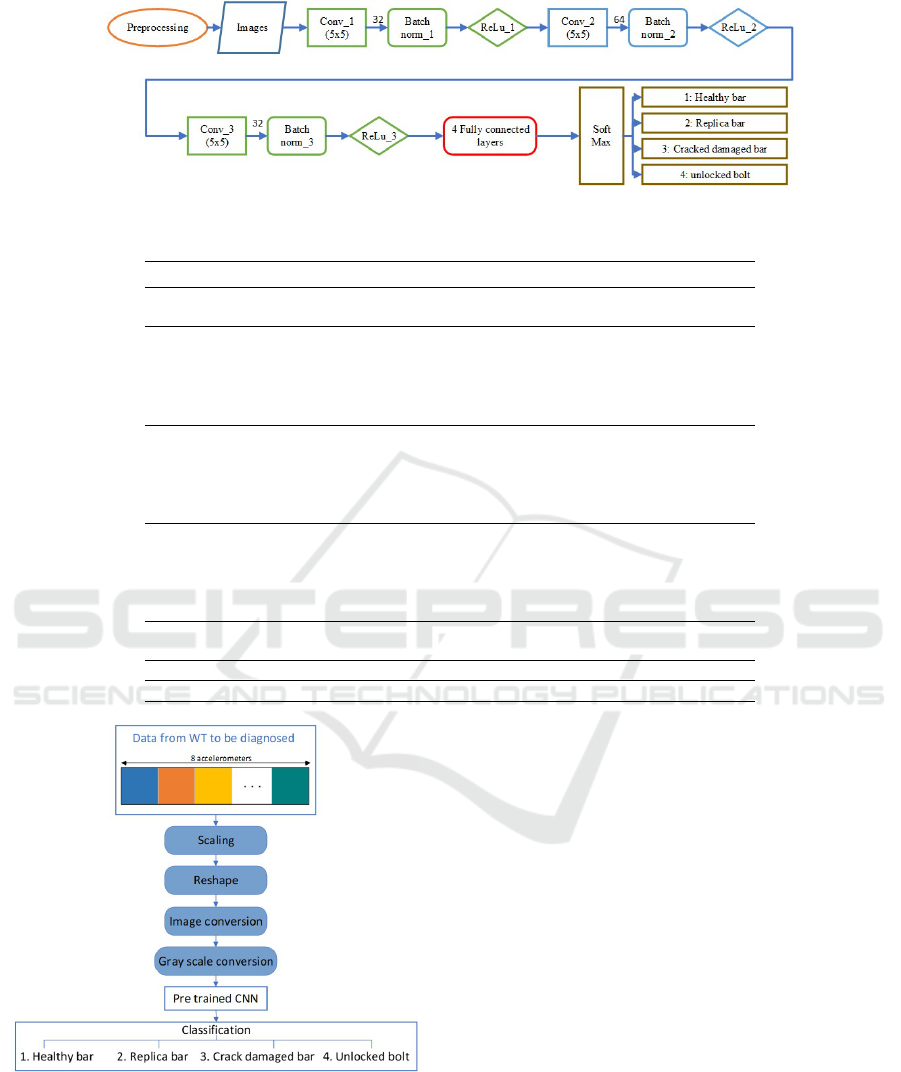
Figure 5: Architecture of the developed CNN.
Table 3: Detailed characteristics of each CNN layer.
Layer Ouput size Parameters
Input
16×16×24 images
16×16×24 -
Convolution#1
32 filters of size 5×5×24 with padding [1 1 1 1]
14×14×32
Weight 5×5×24×32
Bias 1×1×32
Batch Normalization#1 14×14×32
Offset 1×1×32
Scale 1×1×32
ReLu#1 14×14×32 -
Convolution#2
64 filters of size 5×5×24 with padding [1 1 1 1]
12×12×64
Weight 5×5×24×64
Bias 1×1×64
Batch Normalization#2 12×12×64
Offset 1×1×64
Scale 1×1×64
ReLu#2 12×12×64 -
Convolution#3
32 filters of size 5×5×24 with padding [1 1 1 1]
10×10×32
Weight 5×5×24×32
Bias 1×1×32
Batch Normalization#3 10×10×32
Offset 1×1×32
Scale 1×1×32
ReLu#3 10×10×32 -
Fully connected layer#1 1×1×4
Weight 4×3200
Bias 1×1
Softmax - -
classoutput - -
Figure 6: Flowchart to illustrate how the proposed SHM
strategy is applied when a WT has to be diagnosed.
the original healthy bar, the next rows are labeled with
2, 3 and 4, corresponding to the replica bar, the crack
damaged bar and the unlocked bolt, respectively.
After 64 epochs of training on a laptop running
Windows 10 with an Intel Core i7-9750H, 16 GB of
RAM and a graphic card (GeForce RTX 2060) of 6
GB of GPU, the obtained overall accuracy perfor-
mance is 93%. A high true positive rate (TPR) of
94.04% for the original healthy bar is reached, fol-
lowed by a 93.06% of TPR for the replica bar. The
results for the crack damaged bar and unlocked bolt
are 92.23% and 91.88% respectively. Furthermore,
the obtained average recall is 92.8%, the average pre-
cision is 92.3% and, finally, a F1-score of 92.55% is
achieved.
Figure 7 shows the accuracy and loss curves dur-
ing the CNN training. Note that the training data set
reached 100% accuracy while the validation set only
obtained an accuracy of 93%. This variance could be
improved with more data. However, the results con-
firm the viability of the proposed methodology.
5.1 Conclusions
This work proposes a SHM methodology for jacket-
type wind turbine foundations using only accelerome-
ter information. The strategy is validated experimen-
tally for different types of predefined damages on a
Damage Detection and Diagnosis for Offshore Wind Foundations
185
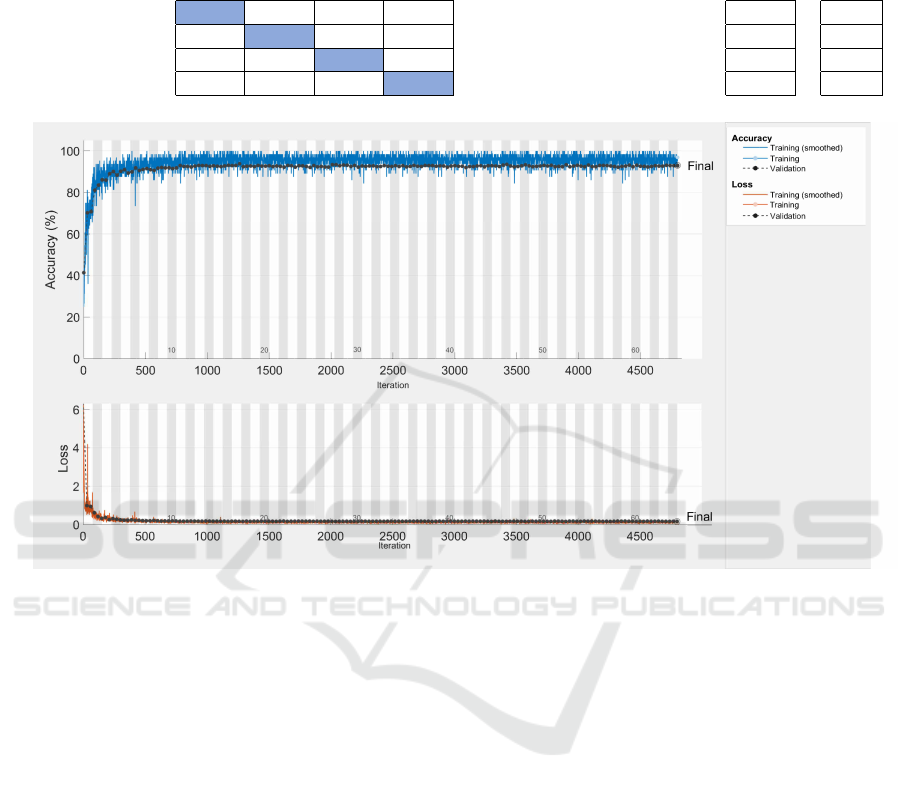
Table 4: Validation set confusion matrix. The first row is labeled as 1 and corresponds to the original healthy bar, the next
rows are labeled with 2, 3 and 4, corresponding to a replica bar, crack damaged bar and unlocked bolt, respectively. True
positive rate (TPR) and false negative rate (FNR) of each class are given.
Predicted class TPR FNR
True class
94.04 2.14 1.99 1.83 1. Healthy bar 94.04 5.96
3.47 93.06 3.15 0.32 2. Replica bar 93.06 6.94
0.65 2.91 92.23 4.21 3. Crack damaged bar 92.23 7.77
3.75 0.63 3.75 91.88 4. Unlocked bolt 91.88 8.13
Figure 7: Accuracy and loss curves. The accuracy is represented by blue lines, the loss is represented by orange lines and the
validation results are represented by black dotted lines.
small-scale laboratory tower. In a nutshell, this work
applies the idea to represent time domain accelera-
tion signals to multi-channel gray-scale images and
then utilize convolutional neural networks for classi-
fication of the different structural states. The obtained
results, with an overall accuracy of 93%, demonstrate
the viability of the proposed approach. Future work
will deal with data augmentation in order to reduce
the validation error with respect to the train set error.
REFERENCES
Albawi, S., Mohammed, T. A., and Al-Zawi, S. (2017).
Understanding of a convolutional neural network. In
2017 International Conference on Engineering and
Technology (ICET), pages 1–6. IEEE.
Association, W. S. et al. (2012). Steel solutions in the green
economy-wind turbines. Brussels, Belgium.
Azimi, M. and Pekcan, G. (2019). Structural health moni-
toring using extremely compressed data through deep
learning. Computer-Aided Civil and Infrastructure
Engineering.
Breteler, D., Kaidis, C., Tinga, T., and Loendersloot, R.
(2015). Physics based methodology for wind turbine
failure detection, diagnostics & prognostics. EWEA
2015 Annual Event.
De Oliveira, M. A., Monteiro, A. V., and Vieira Filho, J.
(2018). A new structural health monitoring strategy
based on pzt sensors and convolutional neural net-
work. Sensors, 18(9):2955.
Khan, A. A., Zafar, S., Khan, N., and Mehmood, Z. (2014).
History current status and challenges to structural
health monitoring system aviation field. Journal of
Space Technology, 4(1):67–74.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Klijnstra, J., Zhang, X., van der Putten, S., and R
¨
ockmann,
C. (2017). Technical risks of offshore structures.
In Aquaculture Perspective of Multi-Use Sites in the
Open Ocean, pages 115–127. Springer, Cham.
Li, D., Ho, S.-C. M., Song, G., Ren, L., and Li, H.
(2015). A review of damage detection methods for
wind turbine blades. Smart Materials and Structures,
24(3):033001.
Liu, W., Wang, Z., Liu, X., Zeng, N., Liu, Y., and Alsaadi,
F. E. (2017). A survey of deep neural network ar-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
186

chitectures and their applications. Neurocomputing,
234:11–26.
Martinez-Luengo, M., Kolios, A., and Wang, L. (2016).
Structural health monitoring of offshore wind tur-
bines: A review through the statistical pattern recog-
nition paradigm. Renewable and Sustainable Energy
Reviews, 64:91–105.
Moulas, D., Shafiee, M., and Mehmanparast, A. (2017).
Damage analysis of ship collisions with offshore wind
turbine foundations. Ocean Engineering, 143:149–
162.
Presencia, C. E. and Shafiee, M. (2018). Risk analysis of
maintenance ship collisions with offshore wind tur-
bines. International Journal of Sustainable Energy,
37(6):576–596.
Ru
´
ız, M., Mujica, L. E., Alf
´
erez, S., Acho, L., Tutiv
´
en, C.,
Vidal, Y., Rodellar, J., and Pozo, F. (2018). Wind tur-
bine fault detection and classification by means of im-
age texture analysis. Mechanical Systems and Signal
Processing, 107:149–167.
Selot, F., Fraile, D., and Brindley, G. (2018). Offshore wind
in europe-key trends and statistics 2018.
Seshadri, B. R., Krishnamurthy, T., and Ross, R. W. (2016).
Characterization of aircraft structural damage using
guided wave based finite element analysis for in-flight
structural health management.
Song, G., Wang, C., and Wang, B. (2017). Structural health
monitoring (shm) of civil structures.
Tabian, I., Fu, H., and Sharif Khodaei, Z. (2019). A convo-
lutional neural network for impact detection and char-
acterization of complex composite structures. Sen-
sors, 19(22):4933.
Zhang, J., Fowai, I., and Sun, K. (2016). A glance at off-
shore wind turbine foundation structures. Brodograd-
nja: Teorija i praksa brodogradnje i pomorske
tehnike, 67(2):101–113.
Damage Detection and Diagnosis for Offshore Wind Foundations
187
