Practically Efficient Attribute-based Encryption for Compartmented
Access Structures
Ferucio Lauren¸tiu ¸Tiplea
1,2 a
, Alexandru Ioni¸t
˘
a
1 b
and Anca Maria Nica
1 c
1
Department of Computer Science, Alexandru Ioan Cuza University of Ia¸si, Ia¸si, Romania
2
Simion Stoilow Institute of Mathematics of the Romanian Academy, Bucharest, Romania
Keywords:
Compartmented Access Structure, Attribute Based Encryption.
Abstract:
Compartmented access structures (CASs) regulate the access control by requesting the consent of various com-
partments. Thus, they are particularly useful to Internet of Things or Wireless Sensor Networks applications
with cloud support. The construction of practically efficient attribute-based encryption (ABE) schemes for
CASs is faced with the fact that these access structures cannot be represented by Boolean formulas. The use of
multilinear map based ABE schemes for general Boolean circuits is not only impractical but also suffers from
the lack of secure multilinear map candidates. Also, the schemes based on lattice cryptography, even if they
are secure, are highly inefficient in practice. We show in this paper that for CASs we can construct practically
efficient ABE schemes based on secret sharing and just one bilinear map. The construction can also be applied
to multilevel access structures.
1 INTRODUCTION
Recent developments in wireless sensor networks
(WSN), internet of things (IoT), and cloud comput-
ing are raising increasing problems over access con-
trol. Standard access control techniques, such as dis-
cretionary access control (DAC), mandatory access
control (MAC), or role-based access control (RBAC),
prove to be inappropriate in such cases. For instance,
DAC is not well suited for large-scale networks with
high security requirements mainly because it does not
offer any mechanism or method to manage the im-
proper access control: if the software fails to restrict
the user from predefined permissions then any hacker
can hack into the system, can have access to the con-
fidential files, and can also perform all the actions
like read, write, or delete. Neither MAC does bet-
ter in such cases. For instance, it is difficult to deploy
MAC in cloud systems because it does not support
separation of duties, delegation, or inheritance. Al-
though RBAC alleviates some of the security issues
with DAC and MAC, it is still not very well suited
for cloud computing because it does not scale eas-
ily to systems with large number of users and roles
a
https://orcid.org/0000-0001-6143-3641
b
https://orcid.org/0000-0002-9876-6121
c
https://orcid.org/0000-0002-3808-572X
where the user’s roles change frequently. Moreover,
it is difficult to extended RBAC across administrative
domains as it is difficult to decide a role’s privileges.
Attribute based Access Control (ABAC) is one of
the techniques that can overcome the shortcomings
mentioned above. ABAC uses attributes (of users,
objects, actions, environment) and defines policies
based on them. Attributes make ABAC a more fine-
grained access control model than RBAC. However,
when working with encrypted data for example in
cloud, it is good to have the access control policy di-
rectly embedded in data and the decryption be carried
out only by authorized access structures. One of the
best methods to do that is by attributed-based encryp-
tion (ABE) that allows us to define fine-grained access
control on the decryption process.
Diversifying the roles of users and managers, in-
creasing the number of resources and their type, sub-
sidiaries and departments of companies, leads to the
orientation of the access control more on groups of
attributes than on individual objects. For instance, the
Oracle Cloud Infrastructure (Jakóbczyk, 2020) uses
compartments to group related cloud resources. Com-
partments provide logical isolation, which makes it
much easier to govern the management permission
policies and track the costs incurred by the related
groups of resources.
Often, compartments must be considered in a cer-
Laurentiu Tiplea, F., Ionit
˘
a, A. and Nica, A.
Practically Efficient Attribute-based Encryption for Compartmented Access Structures.
DOI: 10.5220/0009887202010212
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 201-212
ISBN: 978-989-758-446-6
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
201

tain (partial or total) order, regardless of whether they
consist of users or resources. The supply chain with
products grouped in compartments must follow a cer-
tain order (which can be partial), the decision pro-
cess often follows a total order between compart-
ments, etc. The access control structures should then
be defined by means of compartments. Existing ap-
proaches for such access structures include multilevel
access structures (MASs) and compartmented access
structures (CASs) (Simmons, 1988; Ghodosi et al.,
1998; Tassa, 2007; Tassa and Dyn, 2008; Yu and
Wang, 2011; Pramanik et al., 2018; ¸Tiplea and Dr
˘
a-
gan, 2018).
Contribution. Access control through ABE has
proven to be a necessary and important technology
in the current context. There are two basic policies
in using ABE: the key policy (KP-ABE) and the ci-
phertext policy (CP-ABE). In a KP-ABE, each mes-
sage is encrypted together with a set of attributes and
the decryption key is computed for the entire access
structure; in a CP-ABE, each message is encrypted
together with an access structure while the decryption
keys are given for specific sets of attributes.
In this paper we focus on the KP-ABE paradigm.
The most efficient KP-ABE scheme from the prac-
tical point of view is that in (Goyal et al., 2006),
which uses linear secret sharing and a single bilin-
ear map. Unfortunately, the access structures sup-
ported by this scheme are only those that can be de-
scribed by Boolean formulas, while compartmented
access structures cannot be described by Boolean for-
mulas (Proposition 3.1 in our paper). The extension of
KP-ABE to Boolean circuits by means of multi-linear
maps as proposed in (Garg et al., 2013) is not secure
due to the fact that no candidate multi-linear map pro-
posed so far is secure (Albrecht and Davidson, 2017;
¸Tiplea, 2018). The extension of KP-ABE to Boolean
circuits by means of lattice cryptography as proposed
for instance in (Boneh et al., 2013) is rather unpracti-
cal due to the large expansion of the ciphertext and the
decryption key. The KP-ABE scheme in ( ¸Tiplea and
Dr
˘
agan, 2015) may accommodate Boolean circuits.
However, it is efficient in practice only if the fan-out
gates it uses do not lead to an exponential increase of
the size of the decryption key.
In this paper we prove first that CASs cannot be
described by Boolean formulas. Then, we show that
the KP-ABE scheme proposed in ( ¸Tiplea and Dr
˘
agan,
2015) can be applied quite efficiently to CASs. The
ciphertext has the same size as in the case of the KP-
ABE scheme in (Goyal et al., 2006), while the size of
the decryption key is four times larger than the one in
(Goyal et al., 2006). This is even far more efficient
than the scheme in (Garg et al., 2013) if it were to be
secure with any multi-linear map candidate.
Due to the particularity of the CASs we show then
that the fan-out gates can be removed, leading to an
even more efficient KP-ABE scheme in which the size
of the decryption key is only two times larger than the
one in (Garg et al., 2013). The same technique is also
applied to MASs.
Related Work. During the last decade there has
been a continuous increase in the use of ABE tech-
nology in IoT and WSN with cloud support. One
of the most cited papers (Yu et al., 2010) addresses
the problem of defining and enforcing access policies
based on data attributes and, on the same time, allow-
ing the data owner to delegate most of the computa-
tion tasks involved in fine-grained data access control
to untrusted cloud servers without disclosing the un-
derlying data contents.
(Touati and Challal, 2016) proposes a KP-ABE
scheme for IoT applications based on cloud, with col-
laborative encryption. When a node with low compu-
tational capabilities must encrypt some message, it is
assisted by more powerful neighboring nodes.
In order to have an efficient decryption cost and
at the same time to offer protection to sensitive data,
(Green et al., 2011) came with the solution of out-
sourcing the decryption process in the case of ABE
schemes to the cloud. Since then, this new paradigm
presented a high interest, having several extensions
and new systems being constructed upon it. A few
examples of the extensions include support for veri-
fication of the decryption process (Qin et al., 2015),
remote auditing (Yu et al., 2016), keyword search (Li
et al., 2016), and efficiency improvements (Liao et al.,
2020).
The authors of (Wang et al., 2017) combine
searchable encryption along with ABE, resulting in
a multiple keyword search ABE scheme. Their sys-
tem also supports attribute revocation without chang-
ing the ciphertext. The system uses a linear secret
sharing scheme as access structure.
Another recent work on ABE in cloud system
is presented in (Wang et al., 2018), where an ABE
scheme with multiple functionalities is proposed: the
scheme provides malicious user traceability, attribute
revocation for malicious users, and updates over se-
cret key and ciphertext in order to provide security
against collusion attack between users. However, the
system is limited to Boolean formulas as access struc-
tures.
In (Chatterjee and Das, 2015), a password-based
user access control scheme with ABE support has
been proposed to provide access control over WSNs.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
202

Because most ABE schemes are computationally
heavy, sensor requests are grouped under cluster
heads, where they are encrypted under some set of
attributes, specific for the sensor information. Then
each user is assigned a smart card, which stores an ac-
cess tree. If a user’s access structure is satisfied by the
attributes from some ciphertext, then it can decrypt
the information from the sensor. However, complex
real life situations such as healthcare systems where
the sensors must contain medical data, may require
advanced access control structures that could be un-
able to express with Boolean formulas.
The necessity of using compartments to define ac-
cess control policies has already been advocated by
many researchers. (Brenner et al., 2017) proposes a
secure platform, called TrApps, to offer solutions for
secure execution in untrusted cloud systems. The ap-
plications are divided in small trusted compartments
in order to protect sensitive data.
We have already mentioned that the Oracle cloud
infrastructure (Jakóbczyk, 2020) uses a compart-
mented hierarchical form of grouping together related
applications. One of the reasons for this is to facilitate
access control granting of the resources. Such a sys-
tem could benefit from an ABE scheme with compart-
mented access structure: each resource is assigned
some attributes, and each application has its own ac-
cess structure, based upon which it is granted access
to resources.
(Hyla et al., 2014) have proposed MobInfoSec, a
system to protect sensitive information on mobile de-
vices. The authors recognize the importance of mul-
tilevel access structures in order to have a good ac-
cess control system, and tries to combine certificate
public-key cryptography with general access struc-
ture.
One of the papers that tries to design ABE
schemes for multi-level access control policies is
(Kaaniche and Laurent, 2017). The access control
policy is based on a Boolean tree whose root is a
threshold gate and the set of its children is partitioned
into sets called security levels. A message is viewed
as a vector of components, each of which being en-
crypted by a standard CP-ABE scheme. So, message
components can be obtained by decryption depending
on the security level of the user. The scheme does not
offer a threshold multi-level access on security lev-
els. So, the decryption entity has to satisfy a precise
set of attributes to be able to decrypt a given sub-sets
of data blocks with respect to a given security level.
This aspect is somehow fixed in (Kaaniche and Lau-
rent, 2018) by using two bilinear maps. We empha-
size that the access control structures in these papers
are different from MASs and CASs. A similar idea is
used in (Li, Zhao and Huan, Shuiyuan, 2018), where
the access control architecture is built on five entities:
data owner, cloud service provider, center authority,
department user, and user. Nor does this scheme use
policies such as MAS or CAS.
Paper Structure. The paper is divided into five sec-
tions. The next one fixes the basic terminology and
notation used throughout the paper. Section 3 in-
cludes our main contribution. It starts by motivat-
ing our work on practically efficient ABE schemes for
CASs and shows that CASs cannot be represented by
Boolean formulas. Then, it proves efficiency of the
KP-ABE scheme in ( ¸Tiplea and Dr
˘
agan, 2015) when
applied to CASs. An improvement of this scheme is
also proposed and it is shown that the technique can
also be applied to the case of multilevel access struc-
tures. Section 4 discusses on the implementation of
our scheme, and the last section concludes the paper.
2 PRELIMINARIES
We recall in this section the basic terminology and
notation that is to be used throughout this paper.
The set of integers is denoted by Z. A positive
integer a > 1 is a prime number if the only positive
divisors of it are 1 and a. Two integers a and b are
called congruent modulo n, denoted a ≡ b mod n or
a ≡
n
b, if n divides a − b (n is an integer too). The
notation a = b mod n means that a is the remainder
of the integer division of b by n. The set of all con-
gruence classes modulo n is denoted Z
n
. For a set A,
a ← A means that a is uniformly at random chosen
from A.
Access Control Structures. Given a non-empty fi-
nite set U whose elements are called attributes in our
paper, an access structure over U is any set S of
non-empty subsets of U (Stinson, 2005). S is called
monotone if it contains all subsets B ⊆ U with A ⊆ B,
whenever A ∈ S. The subsets (of U) that are in S are
called authorized sets, while those not in S, unautho-
rized sets.
It is customary to represent (monotone) access
structures by (monotone) Boolean circuits (for more
details about Boolean circuits the reader is referred to
(Bellare et al., 2012)). We only consider monotone
Boolean circuits that have a number of input wires
(which are not output wires of any other gates), just
one output wire (which is not input wire of any gate),
and arbitrarily many logic (k, n)-gates. A (k, n)-gate,
where 1 ≤ k ≤ n, has n input wires and one or more
output wires. That is, the fan-in of the gate is n, while
Practically Efficient Attribute-based Encryption for Compartmented Access Structures
203

the fan-out may be arbitrarily large but at least one. If
the input wires of a (k,n)-gate are assigned Boolean
values and at least k of them are 1, the output wires of
the gate will get the value 1; otherwise they will get 0.
(1,2)- and (2,2)-gates are usually referred to as OR-
and AND-gates, respectively.
The fan-out of a Boolean circuit is the maximum
fan-out of its gates. Boolean circuits of fan-out one
correspond to Boolean formulas.
If the input wires of a Boolean circuit C are in a
one-to-one correspondence with the elements of U,
we will say that C is a Boolean circuit over U. Each
A ⊆ U evaluates the circuit C to one of the Boolean
values 0 or 1 by simply assigning 1 to all input wires
associated to elements in A, and 0 otherwise; then the
Boolean values are propagated bottom-up to all gate
output wires in a standard way. C(A) stands for the
Boolean value obtained by evaluating C for A. The
access structure defined by C is the set of all A with
C(A) = 1.
Key-policy Attribute based Encryption. A key-
policy attribute based encryption (KP-ABE) scheme
consists of four probabilistic polynomial-time (PPT)
algorithms (Goyal et al., 2006):
Setup(λ): this is a PPT algorithm that takes as input
the security parameter λ and outputs a set of pub-
lic parameters PP and a master key MSK;
Enc(m, A, PP): this is a PPT algorithm that takes as
input a message m, a non-empty set of attributes
A ⊆ U , and the public parameters, and outputs a
ciphertext E;
KeyGen(C, MSK): this is a PPT algorithm that takes
as input an access structure C (given as a Boolean
circuit) and the master key MSK, and outputs a
decryption key D (for the entire Boolean circuit
C);
Dec(E, D): this is a deterministic polynomial-time
algorithm that takes as input a ciphertext E and
a decryption key D, and outputs a message m or
the special symbol ⊥.
The following correctness property is required to
be satisfied by any KP-ABE scheme: for any
(PP,MSK) ← Setup(λ), any Boolean circuit C over
a set U of attributes, any message m, any A ⊆ U,
and any E ← Enc(m, A,PP), if C(A) = 1 then m =
Dec(E, D), for any D ← KeyGen(C, MSK).
We consider the standard notion of selective se-
curity for KP-ABE (Goyal et al., 2006). Specifically,
in the Init phase the adversary (PPT algorithm) an-
nounces the set A of attributes that he wishes to be
challenged upon, then in the Setup phase he receives
the public parameters PP of the scheme, and in Phase
1 oracle access to the decryption key generation or-
acle is granted for the adversary. In this phase, the
adversary issues queries for decryption keys for ac-
cess structures defined by Boolean circuits C, pro-
vided that C(A) = 0. In the Challenge phase the ad-
versary submits two equal length messages m
0
and m
1
and receives the ciphertext associated to A and one of
the two messages, say m
b
, where b ← {0,1}. The ad-
versary may receive again oracle access to the decryp-
tion key generation oracle (with the same constraint
as above); this is Phase 2. Eventually, the adversary
outputs a guess b
0
← {0,1} in the Guess phase.
The advantage of the adversary in this game is
P(b
0
= b) − 1/2. The KP-ABE scheme is secure
(in the selective model) if any adversary has only a
negligible advantage in the selective game described
above.
Bilinear Maps and the Decisional BDH Assump-
tion. Given G
1
and G
2
two multiplicative cyclic
groups of prime order p, a map e : G
1
× G
1
→ G
2
is
called bilinear if it satisfies:
• e(x
a
,y
b
) = e(x,y)
ab
, for any x,y ∈ G
1
and a,b ∈
Z
p
;
• e(g,g) is a generator of G
2
, for any generator g of
G
1
.
G
1
is called a bilinear group if the operation in G
1
and e are both efficiently computable.
The Decisional Bilinear Diffie-Hellman (DBDH)
problem in the bilinear group G
2
is the problem to
distinguish between e(g,g)
abc
and e(g,g)
z
given g, g
a
,
g
b
, and g
c
, where g is a generator of G
1
and a, b,
c, and z are randomly chosen from Z
p
. The DBDH
assumption for G
2
states that no PPT algorithm A
can solve the DBDH problem in G
2
with more than a
negligible advantage.
3 OUR CONTRIBUTION
3.1 Motivation and Main Goal
Compartmented Access Structures. Threshold
access structures (Barzu et al., 2013; ¸Tiplea and
Dr
˘
agan, 2014; Dr
˘
agan and ¸Tiplea, 2018) are suit-
able when participants have the same degree of trust.
However, many real-world applications such as cloud
storage, healthcare systems, wireless sensor networks
and so on need more complex access structures based
on different degrees of trust and privileges associated
to participants. Compartmented access structures can
cope with this problem. Within such structures the set
SECRYPT 2020 - 17th International Conference on Security and Cryptography
204

of participants is partitioned into groups called com-
partments, and thresholds are assigned on whose basis
authorized sets are defined.
A compartmented access structure (Simmons,
1988) over a finite set U = {1,...,n} of attributes is a
tuple (U,c,t,S), where:
• U = (U
1
,...,U
k
) is a partition of U into k ≥ 1 non-
empty subsets called compartments (the number
of participants in U
i
is n
i
, for all 1 ≤ i ≤ k);
• c = (t
1
,...,t
k
) is a vector of strictly positive in-
tegers called thresholds that satisfy t
i
≤ n
i
for all
1 ≤ i ≤ k;
• t is a global threshold satisfying
∑
k
i=1
t
i
≤ t ≤ n;
• S is the set of all authorized sets defined by
S = {A ⊆ U|(∀1 ≤ i ≤ k)(|A ∩U
i
| ≥ t
i
) ∧
(|A| ≥ t)}.
That is, an authorized set in such an access struc-
ture should include enough attributes from each com-
partment and should also be large enough (please see
( ¸Tiplea and Dr
˘
agan, 2018) for more details.)
The importance of CASs has been recognized by
many researchers, as we have already mentioned in
the first section of the paper.
CASs and Boolean Formulas. The ABE scheme in
(Goyal et al., 2006) is the most practically efficient
scheme known so far when it comes to access struc-
tures defined Boolean formulas. Unfortunately, CASs
cannot be described by Boolean formulas, as the fol-
lowing proposition shows.
Proposition 3.1. Compartmented access structures
cannot be defined by Boolean formulas.
Proof. Assume that CASs can be represented by
Boolean formulas (that is, by Boolean circuits with
fan-out of one). Consider then the following CAS:
• U = {1,2,3,4,5};
• U
1
= {1,2,3}, U
2
= {4,5};
• t
1
= 1, t
2
= 1, and t = 3.
Let C be a Boolean circuit of fan-out one that rep-
resents this CAS. This circuit has five input gates,
namely the attributes 1, 2, 3, 4, and 5. We remark that
at least two input gates must be directly connected.
We have then the following cases:
1. There is a gate Γ that connects directly inputs
only from the same compartment. Let us assume
that Γ connects directly 1 and 2 and, moreover, Γ
is evaluated to 1 whenever one of these two in-
puts is assigned to 1. Remark that {1,4,5} and
{2,4,5} are authorized, but {1, 4}, {1,5}, {2,4},
and {2,5} are not. As the circuit is of fan-out
one, the gates 1 and 2 cannot be connected to
other logic gates. Therefore, the gates 4 and 5
must be connected to logic gates in such a way
that the circuit is evaluated to one only if these
two gates are simultaneously assigned to one. But
then, C(1, 2,4) = 0 = C(1,2,5) because it does
not matter that 1 or 2 or both evaluate Γ to 1 as
long as these inputs have fan-out one. Therefore,
we have arrived at a contradiction;
2. There is a gate Γ that connects directly inputs only
from the same compartment. Let us assume that
Γ connects directly 1 and 2 and, moreover, Γ is
evaluated to 1 whenever at least two of its inputs
are assigned to 1. As C(1, 4,5) = 1, C(2, 4,5) = 1,
and in both cases Γ is evaluated to 0, the fact that
the circuit is of fan-out one leads to the conclusion
that the evaluation of C to 1 does not depend on
the value of Γ. But then we get C(4, 5) = 1, which
is a contradiction;
3. The other cases, when Γ connects input only from
the second compartment or when it connects in-
puts from both compartments, are treated in a sim-
ilar way.
As in all possible cases we were led to a contradic-
tion, we conclude that CASs cannot be represented
by Boolean formulas.
CASs can however be described by Boolean cir-
cuits of fan-out two. Before showing this let us
adopt the following notation for CASs, which will be
used throughout our paper. If the set of attributes is
U = {1,... , n} and there are k compartments, then
these will be denoted by U
i
= {i.1,...,i.n
i
}, for all
1 ≤ i ≤ k. All the compartments’ attributes are taken
in order from 1 to n and, therefore, i. j refers to the
attribute i. j = j +
∑
i−1
`=1
n
`
, for all 1 ≤ j ≤ n
i
. The
threshold for U
i
is denoted t
i
, and the global thresh-
old is t.
Given a CAS as above, it can be described by a
Boolean circuit with input gates of fan-out two, as it
is shown in Figure 1(a). For the sake of readability,
we have used a generalized AND-gate with more than
two input wires; it can be regarded as the threshold
(k + 1,k + 1)-gate.
Our Main Goal. Due to Proposition 3.1, the ABE
scheme in (Goyal et al., 2006) cannot be applied to
CASs. The options we have then are the following:
1. Use the ABE scheme in (Garg et al., 2013) or
even the more efficient one in (Dr
˘
agan and ¸Ti-
plea, 2016b). Unfortunately, both of them are
Practically Efficient Attribute-based Encryption for Compartmented Access Structures
205

Level
3
2
1
0
1.1
1.n
1
k.1
k.n
k
(t
1
,n
1
) (t
k
,n
k
) (t,n)
AND
··· ···
···
···
(a) Boolean circuit for CASs
1.1
1.n
1
k.1
k.n
k
FO FO FO FO
(t
1
,n
1
) (t
k
,n
k
) (t,n)
AND
··· ···
···
···
(b) Boolean circuit with FO-gates for CASs
Figure 1: Boolean circuit representation of compartmented access structure.
based on multi-linear maps and the recent results
show clearly that no candidate multi-linear map
proposed so far is secure (Albrecht and Davidson,
2017; ¸Tiplea, 2018);
2. Use ABE schemes based on lattice cryptography,
such as (Boneh et al., 2013). They are secure
schemes but, unfortunately, they generate very
large ciphertexts and keys;
3. Use the ABE scheme in ( ¸Tiplea and Dr
˘
agan,
2015). This is a solution based on secret sharing
and just one bilinear map. Under this scheme, the
sharing process produces multiple shares on the
gates with fan-out greater than two. If such gates
are chained, then the input gates may get too many
shares, which means a large increase in the size of
the decryption key. However, for certain access
structures, the gates with fan-out greater than two
are in a limited number and without overlapping.
In such cases, the decryption key might have rea-
sonable size and the scheme becomes, in terms
of efficiency, comparable to that in (Goyal et al.,
2006).
In this paper we will show that the ABE scheme in
( ¸Tiplea and Dr
˘
agan, 2015) can efficiently be used for
CASs. In this context, the scheme produces a decryp-
tion key of size 2nlog p, together with a public key
of the same size, where n is the number of attributes
and p is a prime. Recall that the scheme in (Goyal
et al., 2006) produces a smaller decryption key of size
nlog p, but it is limited to Boolean formulas.
Then, we will also show how to simplify the
scheme above to one that does not need any public
key. In this way, we probably get the most efficient
ABE scheme, based on secret sharing and just one bi-
linear maps, for compartmented access structures.
3.2 Our Scheme
The aim of this section is to show that the ABE
scheme in ( ¸Tiplea and Dr
˘
agan, 2015) can efficiently
be used to accommodate CASs. Then, a more effi-
cient ABE scheme will be derived.
Recall first the scheme in ( ¸Tiplea and Dr
˘
agan,
2015) adapted to CASs. The Boolean circuit for a
CAS, as it is required in ( ¸Tiplea and Dr
˘
agan, 2015),
looks like in Figure 1(b). As one can see, the Boolean
circuit uses FO-gates that simply multiple the output
of the gates to which they are associated. These gates
are just a technical ingredient used to help us better
understand the secret sharing process.
The ABE scheme uses a secret sharing procedure
Share(y,C ) that on a Boolean circuit C as above and
a value y ∈ Z
p
, where p is a prime, shares y top-down
on C as follows:
• Initially, y is assigned to the output wire of the
circuit (the output wire of the AND-gate);
• Uniformly at random choose y
1
,..., y
k
← Z
p
,
compute y
k+1
= y − (y
1
+···+y
k
) mod p, and as-
sign y
i
to the i-th input wire of the AND-gate, for
all 1 ≤ i ≤ k + 1 (from left to right);
• Share y
1
at the (t
1
,n
1
)-gate as follows. If
t
1
= 1, then y
1
is “copied” at all its input
SECRYPT 2020 - 17th International Conference on Security and Cryptography
206

wires. Otherwise, choose uniformly at random
a
1,1
,..., a
1,t
1
−1
← Z
p
and define the polynomial
f
1
(x) = y
1
+ a
1,1
x + · ·· + a
1,t
1
−1
x
t
1
−1
mod p
Then, assign to the input wires of the gate the
shares f
1
(1),... , f
1
(n
1
) (from left to right).
Share then y
2
,..., y
k
in the same way y
1
was
shared. For y
k+1
we choose uniformly at random
a
1
,..., a
t−1
← Z
p
and define the polynomial
f
k+1
(x) = y
k+1
+ a
1
x + · ·· + a
t−1
x
t−1
mod p
Then, assign to the input wires of the gate the
shares f
k+1
(i. j) in lexicographic order on i and
j (please remark that y
k+1
has to be shared at the
(t, n)-gate which has n input wires);
• The FO-gate that splits the output of the input gate
i. j (1 ≤ i ≤ k, 1 ≤ j ≤ n
i
) gets two shares: f
i
( j)
and f
k+1
(i. j). Each of them is shared down as
follows. Uniformly at random choose a
1
i, j
,a
2
i, j
←
Z
p
and compute b
1
i, j
= f
i
( j) − a
1
i, j
mod p, b
2
i, j
=
f
k+1
(i. j) − a
2
i, j
mod p, g
b
1
i, j
, and g
b
2
i, j
. The values
a
1
i, j
and a
2
i, j
are passed down to the input gate i. j
as shares, while g
b
1
i, j
and g
b
2
i, j
are public keys as-
sociated to the FO-gate.
At the end of the sharing procedure, each gate i. j
gets two shares denoted S(i. j, 1) and S(i. j,2), while
its associated FO-gate is assigned two public values
denoted P(i. j, 1) and P(i. j,2) (please see Figure 2).
Now, the ABE scheme can be described as follows
(we will name it SSBM_1 as an acronym for secret
sharing and bilinear map based ABE scheme).
SSBM_1 ABE Scheme
Setup(λ, n): the setup algorithm uses the security pa-
rameter λ to choose a prime p, two multiplicative
groups G
1
and G
2
of prime order p, a generator
g of G
1
, and a bilinear map e : G
1
× G
1
→ G
2
.
Then, it chooses y ∈ Z
p
and, for each attribute i. j,
chooses r
i, j
← Z
p
(please see the notation above).
Finally, the algorithm outputs the public parame-
ters
PP = (p, G
1
,G
2
,g,e,n,Y = e(g,g)
y
,
(T
i, j
= g
r
i, j
|i, j))
and the master key MSK = (y,r
i, j
| i, j);
Encrypt(m,A,PP): the encryption algorithm en-
crypts a message m ∈ G
2
by a non-empty set A
of attributes as follows:
• s ← Z
p
;
• output E = (A,E
0
= mY
s
,(E
i, j
= T
s
i, j
=
g
r
i, j
s
|i. j ∈ A),g
s
);
KeyGen(C, MSK): the decryption key generation al-
gorithm generates a decryption key (D,P) for the
CAS defined by the Boolean circuit C as follows:
• (S, P) ← Share(y,C) (please see the notation
above);
• output (D, P), where D(i. j,`) = g
S(i. j,`)/r
i, j
for
all 1 ≤ i ≤ k, 1 ≤ j ≤ n
i
, and ` = 1, 2;
Decrypt(E,(D,P)): given E and (D,P) as above, the
decryption works as follows:
• Compute V
A
(i. j, `) for all attributes i. j and ` =
1,2 by
V
A
(i. j, `) =
(
e(g,g)
S(i. j,`)s
, if i. j ∈ A
⊥, otherwise
where e(g,g)
S(i. j,`)s
= e(g
r
i, j
s
,g
S(i. j,`)/r
i, j
) and
⊥ means “undefined”;
• For each attribute i. j use the public key P(i. j, 1)
to compute F
A
(i. j, 1) = e(g,g)
f
i
( j)s
by
F(i. j,1) = V
A
(i. j, 1) · e(P(i. j, 1),g
s
).
In a similar way, F
A
(i. j, 2) = e(g,g)
f
k+1
(i. j)s
is
computed by means of P(i. j, 2). Remark that
F
A
(i. j, `) = ⊥, whenever i. j 6∈ A;
• If (t
1
,n
1
)-gate is satisfied (i.e., at least t
1
at-
tributes from the first compartment are in A),
then use the Lagrange interpolation formula
to derive e(g,g)
y
1
s
from the corresponding at-
tributes’ F
A
-values (as computed before). If the
gate is not satisfied, then the value will be ⊥.
Do the same for all gates on the first level;
• If the values for the gates on the first level are
all different than ⊥, then multiply them and get
O = e(g,g)
ys
as the value of the output wire of
the AND-gate. Otherwise, O = ⊥;
• m := E
0
/O.
The correctness of the SSBM_1 scheme simply
follows from its description (one may also consult
( ¸Tiplea and Dr
˘
agan, 2015) for the general case), and
its security follows from the general approach in ( ¸Ti-
plea and Dr
˘
agan, 2015) (the scheme we have de-
scribed above is just an instantiation of the general
case in ( ¸Tiplea and Dr
˘
agan, 2015)).
As with respect to its efficiency, we may say that
the SSBM_1 scheme is quite efficient:
1. The size of the secret key is 2nlog p, and so is the
size of the public key;
2. The secret sharing phase needs to randomly split
y in k + 1 shares, to apply Shamir’s secret sharing
for each of them, and to split 2k secrets at the FO-
gates, each in exactly two shares;
Practically Efficient Attribute-based Encryption for Compartmented Access Structures
207

1.1
1.n
1
k.1
k.n
k
FO
g
b
1
1,1
/g
b
2
1,1
FO
g
b
1
1,n
1
/g
b
2
1,n
1
FO
g
b
1
k,1
/g
b
2
k,1
FO
g
b
1
k+1,1
/g
b
2
k+1,1
(t
1
,n
1
)
a
1
1,1
a
2
1,1
a
1
n
1
,1
a
2
n
1
,1
f
1
(1) f
1
(n
1
)
(t
k
,n
k
)
a
1
k,1
a
2
k,1
a
1
k,n
k
a
2
k,n
k
f
k
(1) f
k
(n
k
)
(t,n)
f
k+1
(1.1)
f
k+1
(1.n
1
)
f
k+1
(k.1)
f
k+1
(k.n
k
)
AND
y
1
y
k
y
k+1
y
··· ···
···
···
Figure 2: Sharing procedure.
3. The decryption phase needs 4n computations of
the map e, k + 1 secret reconstruction by polyno-
mial interpolation, and 2n + k multiplications.
Even if the SSBM_1 scheme is quite efficient for
CASs, we may still improve its efficiency. The fun-
damental observation is that the FO-gates only dupli-
cate the outputs of the input gates. As a result, it is no
longer necessary for the shares coming to them from
top to bottom be once again shared (this statement
will be rigorously argued a little bit later). Therefore,
the secret sharing scheme can be simplified as it is
illustrated in Figure 3. That is, the FO-gates are re-
moved and the shares from the (t
i
,n
i
)-gate and from
the (t, n)-gate come directly to the attribute i. j. In
this way, the public keys are completely removed and
each attribute i. j gets the shares S(i. j,1) = f
i
( j) and
S(i. j,2) = f
k+1
(i. j). We denote this new secret shar-
ing procedure by Share
0
(y,C).
Thus, we arrive at the following ABE scheme.
SSBM_2 ABE Scheme
Setup(λ, n): the same as in SSBM_1 scheme;
Encrypt(m,A,PP): the same as in SSBM_1 scheme;
KeyGen(C, MSK): the decryption key generation al-
gorithm generates a decryption key D for the CAS
defined by the Boolean circuit C as follows:
• S ← Share
0
(y,C) (please see the notation
above);
• output D, where D(i. j, `) = g
S(i. j,`/r
i, j
for all
1 ≤ i ≤ k, 1 ≤ j ≤ n
i
, and ` = 1, 2;
Decrypt(E,D): given E and D as above, the decryp-
tion works as follows:
• Compute F
A
(i. j, `) for all attributes i. j and ` =
1,2 by
F
A
(i. j, `) =
(
e(g,g)
S(i. j,`)s
, if i. j ∈ A
⊥, otherwise
where e(g,g)
S(i. j,`)s
= e(g
r
i, j
s
,g
S(i. j,`)/r
i, j
) and
⊥ means “undefined”;
• If (t
1
,n
1
)-gate is satisfied (i.e., at least t
1
at-
tributes from the first compartment are in A),
then use the Lagrange interpolation formula
to derive e(g,g)
y
1
s
from the corresponding at-
tributes’ F
A
-values (as computed before). If the
gate is not satisfied, then the value will be ⊥.
Do the same for all gates on the first level;
• If the values for the gates on the first level are
all different than ⊥, then multiply them and get
O = e(g,g)
ys
as the value of the output wire of
the AND-gate. Otherwise, O = ⊥;
• m := E
0
/O.
It is straightforward to prove the correctness of
this new scheme. Just remark that the recovering pro-
cedure produces the same result at the threshold gates
on the first level as in the case of the SSBM_1 scheme.
The security of the SSBM_2 scheme is subject of
the following theorem.
Theorem 3.1. The SSBM_2 ABE scheme is secure
in the selective model under the decisional bilinear
Diffie-Hellman assumption.
Proof. Assume that the SSBM_2 ABE scheme is not
secure in the selective model, and let A be an adver-
sary that has a non-negligible advantage against this
scheme (when applied to CASs).
SECRYPT 2020 - 17th International Conference on Security and Cryptography
208

1.1
1.n
1
k.1
k.n
k
(t
1
,n
1
)
f
1
(1)
f
1
(n
1
)
(t
k
,n
k
)
f
k
(1)
f
k
(n
k
)
(t,n)
f
k+1
(1.1)
f
k+1
(1.n
1
)
f
k+1
(k.1)
f
k+1
(k.n
k
)
AND
y
1
y
k
y
k+1
y
··· ···
···
···
Figure 3: Simplified secret sharing procedure.
We define an adversary A
0
against the SSBM_1
ABE scheme and we show that it has a non-negligible
advantage against this scheme, which is a contradic-
tion (this scheme is an instance of the scheme in ( ¸Ti-
plea and Dr
˘
agan, 2015), which is secure in this se-
curity model). From a technical point of view, if C
denotes a Boolean circuit in the SSBM_2 scheme (as
it is, for instance, the circuit in Figure 1(a)), then the
corresponding circuit with FO-gates in the SSBM_1
scheme (as it is the one in Figure 1(b)) is denoted by
C
0
. The adversary A
0
does as follows:
• A
0
announces the set A of attributes that he wishes
to be challenged upon;
• In the Setup phase A
0
receives the public param-
eters PP of the scheme;
• In Phases 1 and 2 oracle access to the decryption
key generation oracle is granted for the adversary
A
0
. Querying this oracle for a Boolean circuit
¯
C
(that represents some CAS) with
¯
C(A) = 0, the
adversary gets the decryption key (D
0
,P
0
) as it
is given in the description of the SSBM_1 ABE
scheme. Using the notation in this scheme, A
0
computes F
A
(i. j, 1) = e(g,g)
f
i
( j)s
and F
A
(i. j, 2) =
e(g,g)
f
k+1
(i. j)s
, for all attributes i. j.
If we look now to the SSBM_2 scheme, we see
that the F
A
-values computed by A
0
are exactly the
F
A
-values computed by A if A had interrogated
the key decryption oracle of the SSBM_2 scheme
with the circuit C and the secret sharing would
have been done in the same way at the logic gates
(remark that C(A) = 0);
• In the Challenge phase the adversary A
0
submits
two equally length messages m
0
and m
1
and re-
ceives the ciphertext associated to A and one of
the two messages, say m
b
, where b ← {0,1}.
It is clear that A
0
can compute at least the same in-
formation as A. Therefore, A
0
may guess b with at
least the same probability as A. This shows that A
0
has a non-negligible advantage against the SSBM_1
scheme, which is a contradiction.
3.3 Variations on the Same Theme
Multilevel Access Structures. are another exam-
ple of access structures that cannot be described by
Boolean formulas. This was shown in ( ¸Tiplea and
Dr
˘
agan, 2015), where the most efficient ABE scheme
(at that time) for such access structures was proposed.
However, the SSBM_2 scheme can also be adapted
for multilevel access structures, leading to an even
more efficient solution than the one in ( ¸Tiplea and
Dr
˘
agan, 2015). But, let us first recall the multilevel
access structures.
A disjunctive multilevel access structure (DMAS)
(Simmons, 1988) over a set U = {1, . ..,n} of at-
tributes is a tuple (t, U,S), where t = (t
1
,...,t
k
) is a
vector of positive integers satisfying 0 < t
1
< · · · < t
k
,
U = (U
1
,..., U
k
) is a partition of U (U
i
is the i-th
level of U), and S is defined by:
S = {A ⊆ U|(∃1 ≤ i ≤ k)(|A ∩ (∪
i
j=1
U
j
)| ≥ t
i
)}.
If we replace “∃” by “∀” in the above definition, we
obtain the concept of conjunctive multilevel access
structure (CMAS) (Tassa, 2007).
If we adopt the same notations for attributes as in
the case of CASs, then the Boolean circuit used in
( ¸Tiplea and Dr
˘
agan, 2015) to represent multilevel ac-
cess structures looks like the one in Figure 4(a). If
we remove the FO-gates we get the Boolean circuit
in Figure 4(b) to which we can apply Share
0
. In this
case, the attribute i. j will get k − i + 1 shares denoted
S(i. j,`), with 1 ≤ ` ≤ k − i + 1 (remark that the num-
ber of shares only depends on the level i). The ABE
scheme SSBM_2 can be applied in this case too, with
Practically Efficient Attribute-based Encryption for Compartmented Access Structures
209

1.1
1.n
1
(k − 1).1 (k − 1).n
k−1
k.1
k.n
k
FO FO FO FO
(t
1
,n
1
) (t
k−1
,n
k−1
) (t
k
,n
k
)
(z,k)
··· ··· ···
···
···
(a) Boolean circuit with FO-gates
1.1
1.n
1
(k − 1).1 (k − 1).n
k−1
k.1
k.n
k
(t
1
,n
1
) (t
k−1
,n
k−1
) (t
k
,n
k
)
(z,k)
···
···
···
···
···
(b) Boolean circuit without FO-gates
Figure 4: Boolean circuit representation of multilevel access structure: z = 1 for the disjunctive case, and z = k for the
conjunctive case.
the only difference that ` takes values as above. Re-
mark also that for DMAS, z = 1 means that the (z,k)-
gate is a generalized OR-gate and, therefore, the se-
cret y is “copied” on all its input wires. When z = k,
the (z, k)-gate is a generalized AND-gate as in the
case of CASs.
The decryption key size produced by the ABE
scheme SSBM_2 for multilevel access structures is
k · n
1
+ (k − 1) · n
2
+ · · · + n
k
· 1
which gives on average n(k +1)/2 (just take all levels
of the same size). The approach in ( ¸Tiplea and Dr
˘
a-
gan, 2015) generates a public key too of the same size.
Therefore, we get a substantial improvement over the
approach in ( ¸Tiplea and Dr
˘
agan, 2015) which, besides
the one proposed in this paper, was the most efficient
one (please see ( ¸Tiplea and Dr
˘
agan, 2015) for details).
Can FO Gates Always be Removed? FO-gates
have been used in ( ¸Tiplea and Dr
˘
agan, 2015) to spec-
ify a kind of secret sharing at the gates of fan-out
greater than two, in order to defeat the backtracking
attack (Goyal et al., 2006). As we have seen so far,
we were able to successfully remove the FO-gates
whenever they were attached to the circuit’s input
gates (where the secret sharing process is completed).
However, if FO-gates are attached to gates inside the
circuit, removing them may be more complex. An
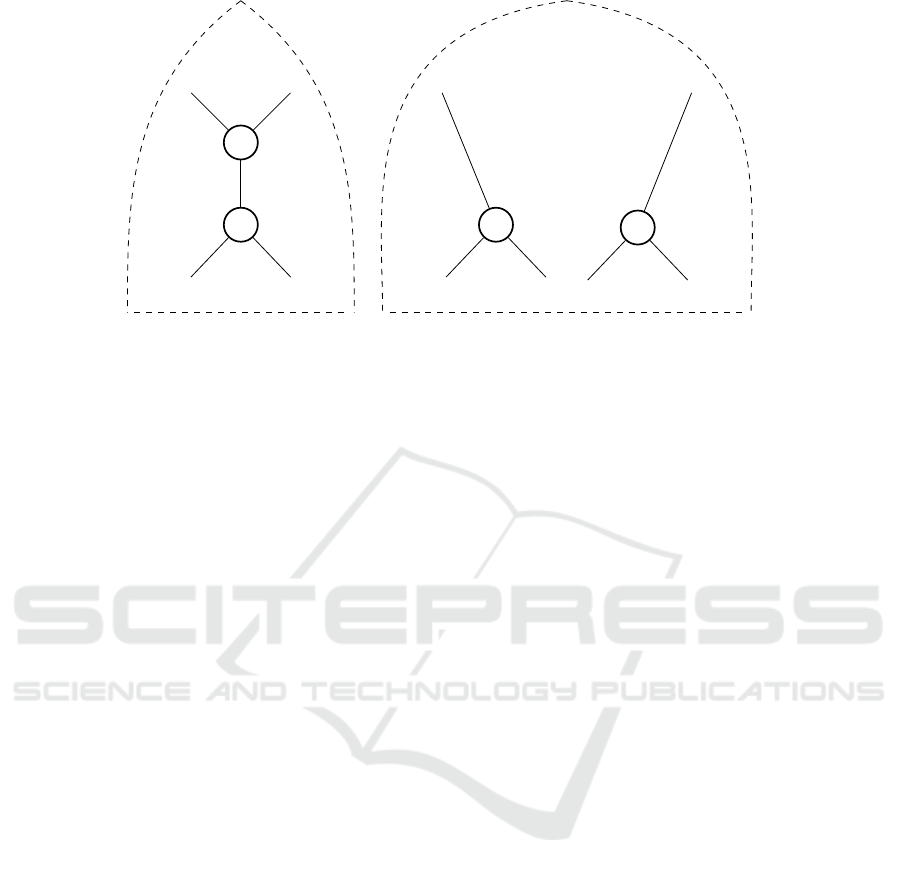
idea of how we could do it would be to duplicate the
sub-circuits whose roots are logic gates with fan-out
greater than two, as suggested in Figure 5.
As one can see, the sub-circuit with the OR-gate as
root (in the left hand side picture) must be duplicated.
Clearly, this can lead to a very large increase of the
final circuit compared to the original one (just think
that the duplicated sub-circuits contain another gates
with fan-out greater than two, which means that the
duplicating process must be repeated).
4 IMPLEMENTATION
An implementation of our SSBM_2 ABE scheme can
be found at https://github.com/Juve45/abe-cas. The
programs are written in C for better portability. For
bilinear map support we have used the PBC library
(Lynn, 2007) and also the GMP library for multi pre-
cision arithmetic. Thus, our system should run în any
operating system that supports GMP and PBC. The
implementation was tested în Linux (Linux 4.9, De-
bian 9.12) and Windows 10.
5 CONCLUSIONS
Building access control policies based on compart-
ments plays an important role in today’s technologies,
such as IoT and WSN with cloud support. In addition,
the need to work with encrypted data in the cloud
requires that such access policies be integrated with
encryption techniques. Attribute-based Encryption
(ABE) is an encryption technique that integrates ac-
cess control policies defined in the most general way,
namely, through Boolean circuits. However, ABE
schemes developed to date are practically efficient
SECRYPT 2020 - 17th International Conference on Security and Cryptography
210

FO
g
b
1
g
b
2
OR
x
y
(a
1
,a
2
)
(a
1
,a
2
) (a
1
,a
2
)
OR
x
x x
OR
y
y y
Figure 5: Removing FO-gates.
only for Boolean formulas, while compartmented ac-
cess structures cannot be expressed by Boolean for-
mulas.
In this paper we have shown that for the case
of compartmented access structures we can construct
practically efficient ABE schemes. We started from
the scheme in ( ¸Tiplea and Dr
˘
agan, 2015) and we have
refined it to a new scheme that is likely to achieve the
maximum possible efficiency. Also, by applying the
same technique, the case of multilevel access struc-
tures presented in ( ¸Tiplea and Dr
˘
agan, 2015) has been
made more efficient.
We believe that multilevel and compartmented ac-
cess structures, along with access structures that can
be defined by Boolean formulas, cover most of the
practical needs. Possibly, there could be a certain
interest for weighted or distributed access structures
such as those of (Dr
˘
agan and ¸Tiplea, 2016a).
ACKNOWLEDGEMENTS
This project is funded by the Ministry of Research and
Innovation within Program 1 – Development of the
national RD system, Subprogram 1.2 – Institutional
Performance – RDI excellence funding projects, Con-
tract no.34PFE/19.10.2018.
REFERENCES
Albrecht, M. and Davidson, A. (2017). Are graded encod-
ing schemes broken yet? https://malb.io/are-graded-
encoding-schemes-broken-yet.html.
Barzu, M., ¸Tiplea, F. L., and Dr
˘
agan, C. C. (2013). Com-
pact sequences of co-primes and their applications to
the security of CRT-based threshold schemes. Infor-
mation Sciences, 240:161 – 172.
Bellare, M., Hoang, V. T., and Rogaway, P. (2012). Founda-
tions of garbled circuits. In Proceedings of the 2012
ACM Conference on Computer and Communications
Security, CCS ’12, pages 784–796, New York, NY,
USA. ACM.
Boneh, D., Nikolaenko, V., and Segev, G. (2013). Attribute-
based encryption for arithmetic circuits. IACR Cryp-
tology ePrint Archive, 2013:669.
Brenner, S., Goltzsche, D., and Kapitza, R. (2017). TrApps:
Secure compartments in the evil cloud. In Proceed-
ings of the 1st International Workshop on Security
and Dependability of Multi-Domain Infrastructures,
XDOMO’17, New York, NY, USA. Association for
Computing Machinery.
Chatterjee, S. and Das, A. K. (2015). An effective ECC-
based user access control scheme with attribute-based
encryption for wireless sensor networks. Sec. and
Commun. Netw., 8(9):1752–1771.
¸Tiplea, F. L. (2018). Multi-linear maps in cryptography. In
Proceedings of 4th International Conference on Math-
ematical Foundations of Informatics, pages 241–258.
¸Tiplea, F. L. and Dr
˘
agan, C. C. (2014). A necessary and suf-
ficient condition for the asymptotic idealness of the
GRS threshold secret sharing scheme. Information
Processing Letters, 114(6):299 – 303.
¸Tiplea, F. L. and Dr
˘
agan, C. C. (2015). Key-policy attribute-
based encryption for Boolean circuits from bilinear
maps. In Ors, B. and Preneel, B., editors, Cryptog-
raphy and Information Security in the Balkans - First
International Conference, BalkanCryptSec 2014, Is-
tanbul, Turkey, October 16-17, 2014, Revised Selected
Papers, volume 9024 of Lecture Notes in Computer
Science, pages 175–193, Istanbul, Turkey. Springer.
¸Tiplea, F. L. and Dr
˘
agan, C. C. (2018). Asymptotically ideal
CRT-based secret sharing schemes for multilevel and
compartmented access structures. IACR Cryptology
ePrint Archive, 2018:933.
Dr
˘
agan, C. C. and ¸Tiplea, F. L. (2016a). Distributive
weighted threshold secret sharing schemes. Informa-
tion Sciences, 339:85 – 97.
Dr
˘
agan, C. C. and ¸Tiplea, F. L. (2016b). Key-policy
attribute-based encryption for general Boolean cir-
Practically Efficient Attribute-based Encryption for Compartmented Access Structures
211

cuits from secret sharing and multi-linear maps. In
Pasalic, E. and Knudsen, L. R., editors, Cryptography
and Information Security in the Balkans: Second In-
ternational Conference, BalkanCryptSec 2015, Koper,
Slovenia, September 3-4, 2015, Revised Selected Pa-
pers, pages 112–133. Springer International Publish-
ing.
Dr
˘
agan, C. C. and ¸Tiplea, F. L. (2018). On the asymptotic
idealness of the Asmuth-Bloom threshold secret shar-
ing scheme. Information Sciences, 463 - 464:75 – 85.
Garg, S., Gentry, C., Halevi, S., Sahai, A., and Waters, B.
(2013). Attribute-based encryption for circuits from
multilinear maps. In Canetti, R. and Garay, J., editors,
Advances in Cryptology – CRYPTO 2013, volume
8043 of Lecture Notes in Computer Science, pages
479–499. Springer Berlin Heidelberg.
Ghodosi, H., Pieprzyk, J., and Safavi-Naini, R. (1998). Se-
cret sharing in multilevel and compartmented groups.
In Boyd, C. and Dawson, E., editors, Third Aus-
tralasian Conference on Information Security and Pri-
vacy (ACISP ’98), volume 1438 of Lecture Notes in
Computer Science, pages 367–378. Springer.
Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).
Attribute-based encryption for fine-grained access
control of encypted data. In ACM Conference on
Computer and Communications Security, pages 89–
98. ACM.
Green, M., Hohenberger, S., and Waters, B. (2011). Out-
sourcing the decryption of abe ciphertexts. In Pro-
ceedings of the 20th USENIX Conference on Security,
SEC’11, page 34, USA. USENIX Association.
Hyla, T., Pejas, J., Fray, I. E., Macków, W., Chocianowicz,
W., and Szulga, M. (2014). Sensitive information pro-
tection on mobile devices using general access struc-
tures. In ICONS 2014.
Jakóbczyk, M. T. (2020). Practical Oracle Cloud Infras-
tructure: Infrastructure as a Service, Autonomous
Database, Managed Kubernetes, and Serverless.
Apress, 1 edition.
Kaaniche, N. and Laurent, M. (2017). Attribute based en-
cryption for multi-level access control policies. In
Proceedings of the 14th International Joint Confer-
ence on e-Business and Telecommunications - Volume
4: SECRYPT, (ICETE 2017), pages 67–78. INSTICC,
SciTePress.
Kaaniche, N. and Laurent, M. (2018). SABE: A selective
attribute-based encryption for an efficient threshold
multi-level access control. In Samarati, P. and Obai-
dat, M. S., editors, Proceedings of the 15th Interna-
tional Joint Conference on e-Business and Telecom-
munications, ICETE 2018 - Volume 2: SECRYPT,
Porto, Portugal, July 26-28, 2018, pages 321–333.
SciTePress.
Li, J., Lin, X., Zhang, Y., and Han, J. (2016). KSF-OABE:
outsourced attribute-based encryption with keyword
search function for cloud storage. IEEE Transactions
on Services Computing, 10(5):715–725.
Li, Zhao and Huan, Shuiyuan (2018). Multi-level attribute-
based encryption access control scheme for big data.
MATEC Web Conf., 173:03047.
Liao, Y., Zhang, G., and Chen, H. (2020). Cost-efficient
outsourced decryption of attribute-based encryption
schemes for both users and cloud server in green cloud
computing. IEEE Access, 8:20862–20869.
Lynn, B. (2007). PBC library. https://crypto.stanford.edu/
pbc/.
Pramanik, J., Roy, P. S., Dutta, S., Adhikari, A., and Saku-
rai, K. (2018). Secret sharing schemes on compart-
mental access structure in presence of cheaters. In
Proceedings of the International Conference on Infor-
mation Systems Security, pages 171–188.
Qin, B., Deng, R. H., Liu, S., and Ma, S. (2015). Attribute-
based encryption with efficient verifiable outsourced
decryption. IEEE Transactions on Information Foren-
sics and Security, 10(7):1384–1393.
Simmons, G. J. (1988). How to (really) share a secret.
In Goldwasser, S., editor, 8th Annual International
Cryptology Conference on Advances in Cryptology
(CRYPT ’88), volume 403 of Lecture Notes in Com-
puter Science, pages 390–448. Springer.
Stinson, D. (2005). Cryptography: Theory and Practice.
Chapman and Hall/CRC, 3 edition.
Tassa, T. (2007). Hierarchical threshold secret sharing.
Journal of Cryptology, 20(2):237–264.
Tassa, T. and Dyn, N. (2008). Multipartite secret shar-
ing by bivariate interpolation. Journal of Cryptology,
22(2):227–258.
Touati, L. and Challal, Y. (2016). Collaborative KP-ABE
for cloud-based Internet of things applications. In
2016 IEEE International Conference on Communica-
tions (ICC), pages 1–7.
Wang, S., Guo, K., and Zhang, Y. (2018). Traceable
ciphertext-policy attribute-based encryption scheme
with attribute level user revocation for cloud storage.
PLOS ONE, 13(9):1–23.
Wang, S., Zhao, D., and Zhang, Y. (2017). Searchable
attribute-based encryption scheme with attribute revo-
cation in cloud storage. PLOS ONE, 12(8):1–20.
Yu, J., Ren, K., and Wang, C. (2016). Enabling cloud stor-
age auditing with verifiable outsourcing of key up-
dates. IEEE transactions on information forensics and
security, 11(6):1362–1375.
Yu, S., Wang, C., Ren, K., and Lou, W. (2010). Achieving
secure, scalable, and fine-grained data access control
in cloud computing. In 2010 Proceedings IEEE IN-
FOCOM, pages 1–9.
Yu, Y. and Wang, M. (2011). A probabilistic secret shar-
ing scheme for a compartmented access structure. In
Qing, S., Susilo, W., Wang, G., and Liu, D., editors,
Information and Communications Security - 13th In-
ternational Conference, ICICS 2011, Beijing, China,
November 23-26, 2011. Proceedings, volume 7043 of
Lecture Notes in Computer Science, pages 136–142.
Springer.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
212