Approaches to Parameter Identiﬁcation for

Hybrid Multilinear Time Invariant Systems

Aadithyan Sridharan

1 a

, Gerwald Lichtenberg

1 b

, Antonio Correcher Salvador

2 c

and Carlos Vargas Salgado

3 d

Faculty of Life Sciences, University of Applied Sciences, Ulmenliet 20, 21033 Hamburg, Germany

Instituto Universitario de Autom

atica e Inform

atica Industrial (ai2),

Universitat Polit

ecnica de Val

encia, 46022, Valencia, Spain

Department of Electrical Engineering, Universitat Polit

ecnica de Val

encia, 46022, Valencia, Spain

Keywords:

Multilinear Systems, Parameter Identiﬁcation, Tensor Decomposition, Industrial Building Modelling.

Abstract:

Industrial buildings often have interacting continuous- and discrete-valued signals. Hybrid multilinear time

invariant (MTI) models have been shown to be able to describe this hybrid dynamics appropriately for many

cases. White box modelling methods from ﬁrst principles have been used in this application domain before.

The parameters of these models can be efﬁciently represented by higher order tensors. This paper introduces

as alternatives black and grey box approaches for the parameter identiﬁcation of MTI models from data. The

methods are tested with the help of simulation data produced from a multilinear model of an industrial hall. It

is assumed that all state variables are measured with additative noise and the input and disturbances are exactly

measured, too. Two black box methods obtain either the full parameter tensor or a rank-r decomposition of it.

Numerical examples using the industrial building model show the principle applicability of these approaches

for real data.

1 INTRODUCTION

Systems in many application areas as buildings engi-

neering show discrete-valued as well as continuous-

valued signals, e.g. if a continuous state like a temper-

ature depends on the switching ON/OFF of a binary

input like a gas heater. This example can be sufﬁ-

ciently good described by multilinear time invariant

(MTI) models, as well as many more from other ap-

plication areas, (Lichtenberg, 2011).

There are three traditional approaches in order to

obtain a state space model depending on the avail-

able information about the system. If no sufﬁcient

prior knowledge about the system is available, then

the black box identiﬁcation approach is chosen (Cha-

van and Talange, 2018), (Tayamon, Zambrano, Wi-

gren and Carlsson, 2011), (Royer, Thil, Talbert and

Polit, 2014). On the contrary, in some cases through

ﬁrst principles like laws of physics, sufﬁcient infor-

https://orcid.org/0000-0002-1237-3125

https://orcid.org/0000-0001-6032-0733

https://orcid.org/0000-0002-2443-9857

https://orcid.org/0000-0002-9259-8374

mation about the system can be obtained. In these

cases, white box techniques are used. However, if the

information through ﬁrst principles is incomplete, in

the sense that there are unknown parameters in the

system, the grey box identiﬁcation approach is used

(Bacher and Madsen, 2011).

In (Batselier, Ko, Phan, Cichoki and Wong, 2018),

the system identiﬁcation problem of multilinear state

space models has been considered. In this work, the

coefﬁcients of the state space matrices have been es-

timated by representing them as tensor train matrices.

The computational complexity is reduced by repre-

sentation as tensor train matrices. The contribution of

this paper are different methods for parameter identi-

ﬁcation of an MTI state space model. In order to solve

the identiﬁcation problem, both the grey and black

box methods are considered. The grey box problem

involves ﬁnding the unknown physical parameters of

the system. In this case the structure of the model is

known beforehand.

On the other hand, the black box problem involves

no prior knowledge about the system. The identiﬁ-

cation problem is to ﬁnd parameters of a multilinear

state space model, given a set of input state data and

Sridharan, A., Lichtenberg, G., Salvador, A. and Salgado, C.

Approaches to Parameter Identiﬁcation for Hybrid Multilinear Time Invariant Systems.

DOI: 10.5220/0009887502550262

In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 255-262

ISBN: 978-989-758-444-2

255

a speciﬁc system order. The ﬁrst black box method

shows how the parameter identiﬁcation problem can

be transformed to a linear least squares problem and

thus solved efﬁciently. The parameters of the MTI

state space model increase exponentially with respect

to the order of the system and the number of inputs.

As the parameters of MTI state space models can nat-

urally be represented as tensors, decomposition meth-

ods can be used to compute low rank approximations,

which need only a remarkable less number of param-

eters, especially for the case of canonical polyadic

(CP) decompositions, (Kruppa, 2017). The second

approach to black box parameter identiﬁcation given

in this paper is a direct estimation method for the CP

decomposition factors of the parameter tensor from

data. Throughout the paper, discrete time models are

used and the inputs as well as state signals are as-

sumed to be sampled with a ﬁxed sampling time. The

effects of measurement noise are not dealt with by a

formal approach. However, simulation results are pre-

sented by adding noise as well.

The paper is organized as follows. Firstly, a brief

introduction to tensor calculus and MTI systems is

given. Thereafter, the identiﬁcation problem is setup

and is dealt with by the methods described above. Fi-

nally, a numerical example simulated using MATLAB

Simulink is presented, followed by conclusion and fu-

ture scope.

2 TENSOR BASICS

The state space model of an MTI system can be for-

mulated in a tensor framework. Thereby, in this sec-

tion, some basic concepts about tensors and tensor de-

compositions are presented (Kolda and Bader, 2009).

Deﬁnition 1 (Tensor). A multidimensional n-way ar-

ray

X ∈ R

×I

×···×I

(1)

where (I

, I

, ..., I

) ∈ N

is called a real tensor of or-

der n.

Although such a structure can store complex val-

ues as well, in the current work, only real values are

dealt with. An element

x(i) = x(i

, i

, ..., i

) ∈ R

of the tensor X can be selected by the index vector

i = (i

, i

, ..., i

For tensors, numerous arithmetic operations exist

and two of them are used in this paper: the contracted

product of two tensors A, B is denoted by h A |B i

whereas the outer product is denoted by A ◦ B. In

depth information on these products can be found in

(Kolda and Bader, 2009).

Tensors can have very high storage demands,

since the number of elements of a tensor depends

exponentially on the number of dimensions of the

tensor. In order to address this problem, tensor de-

composition methods have been developed over the

last decades, (Cichocki, Zdunek, Phan and Amari,

2009). Decomposition methods range from canoni-

cal polyadic (CP), Tucker, tensor trains to hierarchi-

cal decompositions. Because of their superior storage

effort savings and suitability to MTI models, CP de-

compositions are used in this paper. The simplest of

it is given in the next deﬁnition.

Deﬁnition 2 (Rank One Tensor). An n dimensional

tensor

X = x

◦ x

◦ ··· ◦ x

∈ R

×I

×···×I

(2)

has rank one if it can be computed by the outer prod-

uct of n vectors x

∈ R

∀i = 1, ..., n.

All full tensors are representable by a sum of rank

one tensors, which is given in the next deﬁnition.

Deﬁnition 3 (CP Tensor). A canonical polyadic rep-

resentation

K = [X

, X

, ..., X

] · λ (3)

∑

l=1

λ(l)x

(:, l)◦ ·· · ◦ x

(:, l) (4)

of a real tensor of dimension I

× I

× ··· × I

is given

by a sum of rank 1 tensors.

The elements are computed by the sums of

the outer products of the column vectors of fac-

tor matrices X

∈ R

×r

. The introduction of a

weighting vector λ ∈ R

allows to normalize the

column vectors of the factor matrices. The minimum

number of rank 1 tensors required to reproduce the

original tensor K is called the CP rank of the tensor K.

Example 1. Figure 1 visualizes a 3rd order CP ten-

sor

K = [X

, X

] · λ

∑

l=1

λ(l)X

(:, l)◦ X

(:, l)

Figure 1: CP tensor (Kruppa and Lichtenberg, 2017).

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

256

3 MULTILINEAR MODELS

MTI systems are described by multilinear functions

depending on states and inputs. Multilinearity means

that the function is linear if all but one variables are

held constant. Thus, they are polynomials of order n

but showing a maximum order of one for each vari-

able, (Pangalos, Eichler and Lichtenberg, 2015).

Deﬁnition 4 (Multilinear Function). The function

f (x) = α

m(x) (5)

where

α =



·· · α



∈ R

is a coefﬁcient row vector and

m(x) =





⊗ ··· ⊗





∈ R

is a column vector of monomial is called multilinear.

Here, ⊗ is the well known Kronecker product.

Deﬁnition 5 (MTI Matrix Model). A discrete-time

multilinear model is represented by a next state equa-

tion

x(k + 1) = F · m(x(k), u(k)) (6)

where m(x(k), u(k)) is given by



(k)



⊗·· ·⊗



(k)



⊗



(k)



⊗·· ·⊗



(k)



i.e. the monomial vector containing all multiplicative

combinations of states and inputs at time k.

The transition matrix F ∈ R

n×2

n+m

holds the

parameters of the model as the following example

shows.

Example 2. A MTI state space model of order two

(k + 1) = f

+ f

(k) + f

(k)x

(k)

(k + 1) = f

+ f

(k) + f

(k)x

(k)

has a transition matrix and monomial vector given by

F =





m(x

(k), x

(k)) =







(k)

(k)x

(k)







Next, the multilinear structure of the functions can be

exploited to represent the next state equation in a ten-

sor format.

Deﬁnition 6 (MTI Tensor Model). The next state

equation (6) can equivalently be written by

x(k + 1) = hF |M(x(k), u(k))i (7)

where F ∈ R

(n+m)

2×n

contains the parameters of the

model arranged as a tensor and M(x, u) ∈ R

(n+m)

a monomial tensor. The notation ×

(n+m)

2 stands for

2 × 2 × ... × 2

{z }

(n+m)times

Example 3. An autonomous MTI state space model

of order two in tensor form is given by



(k + 1)



= h F | M(x

(k), x

(k)) i .

For this example, the contracted product of the tran-

sition tensor F ∈ R

2×2×2

and the monomial tensor

M ∈ R

2×2

leads to the same next state equations as

in the matrix case of Example 2.

The monomial tensor is already rank one and thus,

minimal. The parameter tensor can be decomposed as

CP tensor

F = [F

, .., F

, F

, .., F

, F

] · λ

(8)

which is e.g. discussed in (Pangalos, 2016).

With the parameter tensor (8), the next state equa-

tion (7) can be simpliﬁed

x(k + 1) = F

~ F



(k)



~ ···~



(k)



~ F



(k)



~ · ··~ F



(k)



(9)

The element wise multiplication, also known as the

Hadamard product is denoted as ~ operation and ma-

trix vector multiplication has precedence here.

Example 4. The previous example in decomposed

tensor representation has the next state equation

x(k + 1) = F

~ F



(k)





(k)



(10)

the weighting vector



. . . f



Approaches to Parameter Identiﬁcation for Hybrid Multilinear Time Invariant Systems

257

and the factor matrices



1 1 1 1 0 0 0 0

0 0 0 0 1 1 1 1





1 0 1 0 1 0 1 0

0 1 0 1 0 1 0 1





1 1 0 0 1 1 0 0

0 0 1 1 0 0 1 1



4 IDENTIFICATION PROBLEM

In this section, the identiﬁcation problem is formu-

lated for both grey and black box methods. Within

black box identiﬁcation, the problem is tackled by two

different approaches.

4.1 Grey Box Identiﬁcation

In this sub-section, it is assumed that a model from the

laws of physics is already available, albeit with un-

known parameters. Considering the following model

with n states, m inputs and l disturbances in discrete

time domain







(k + 1)













+ f

(k) + .. + f

n+m+l

∏

i=1

∏

i=1

∏

i=1

+ f

(k) + .. + f

n+m+l

∏

i=1

∏

i=1

∏

i=1







(11)

The discrete time MTI state space model for the

system in (11) is of order n with state vector x ∈ R

having an input vector u ∈ R

inputs and disturbances

d ∈ R

x(k + 1) = Fm (x(k), u(k), d(k)) (12)

where F ∈ R

n×2

n+m+l

is the matrix containing the

parameters ( f

, .., f

n+m+l

) of the MTI state space

model. m(x(k), u(k), d(k)) is the monomial vector as

already introduced in section 3.

Assuming that the states of the MTI state space

model in (12) can be measured, then the parameter es-

timation problem can be formulated as, given an ini-

tial state x(0), a set of inputs u(k), set of disturbance

inputs d(k) and a set of real measured data

x(k) where

k = 0, 1, .., T , ﬁnd the parameter matrix F containing

the parameters ( f

, .., f

n+m+l

) in the sense that the

sum J of squared errors e is minimum.

min

J (13)

J =

Qe) (14)

where Q ∈ R

nT ×nT

is a diagonal, positive semi def-

inite weighting matrix for normalization of the mea-

sured signals.

Q = diag(q

, q

, .., q

)

e =







x(1) −

x(1)

x(T ) −

x(T )







(15)

For i = 1..T , the states x(i) are the one step ahead

predictions from the model (12) using the measured

states

x(i−1), the inputs u(i−1) and the disturbances

d(i − 1) in the previous time step. The objective is

to ﬁnd the parameters set that minimizes the error

between the measured state

x(i) and predicted state

x(i) from the MTI model in (12). The assumption

is that the parameters are constants and not varying

with time. The parameter matrix can be determined

in a straight forward way by simply solving an inverse

problem. Considering the MTI state space model in

matrix form introduced in the equation (12). Given

the data-set (

x(k), u(k), d(k) for all k = 0, 1, .., T ), for

a model order n, with m inputs and l disturbances

X = F · M (16)

where

X ∈ R

n×T

, F ∈ R

n×2

n+m+l

and M ∈ R

n+m+l

×T







x(1)

x(2)

x(T )







(17)







m(x(0), u(0), d(0))

m(x(1), u(1), d(1))

m(x(T − 1), u(T − 1), d(T − 1))







(18)

Assuming T is large enough such that the given sys-

tem of equations is over-determined, the solution is:

F =

X · M

−1

(19)

Solving the equation (19) will also minimize the sum

of squared errors as mentioned in (13).

4.2 Black Box Identiﬁcation

For this case, no prior knowledge about the system

is available from the laws of physics. Thereby, the

problem now is to ﬁnd a state space model of order n,

from a given a input-state data set, instead of ﬁnding

the unknown physical parameters of the system.

We solve the problem in two ways. First, the pa-

rameter matrix F is calculated by solving an inverse

problem. Thereafter, as shown in the section 3, MTI

state space model can be written in tensor form as well

and hence, the problem is solved by calculating the

CP factors of the parameter tensor F.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

258

4.2.1 Inverse Problem

The inverse problem approach is similar to the solu-

tion discussed for the grey box problem in the equa-

tion (19). It follows from the solution in (19) that, for

a solution to exist, MM

must be non-singular and

thereby, full rank. For this to have full rank, all the

dynamic modes of the system must be excited. Since

the only set of inﬂuence-able variables of the T sam-

ple monomial matrix are the inputs, they must be rich

enough to excite all the modes of the system. This

is the well known concept of persistence excitation

(Ljung, 1999).

4.2.2 Estimation of Tensor Factors

In (7), it is shown how an MTI state space model can

be written in tensor form and thereafter, in (8) the CP

decomposed form of the tensor model is shown. The

objective here is to estimate the CP factors of the pa-

rameter tensor directly from the measurements. As-

suming a rank r CPD of the parameter tensor F such

that

F = [F

, .., F

, F

, .., F

, F

] · λ

(20)

where all of F

, .., F

, F

, .., F

∈ R

2×r

, F

∈ R

n×r

and λ

∈ R

The one step ahead predicted states x(k) as shown

in the error vector in (15) can be calculated from (9).

Using the error vector in (15), the least squares op-

timization problem in (13) can be solved for the un-

known factors of the parameter tensor. The optimiza-

tion problem is:

min

,..,F

,λ

J (21)

The problem (21) turns out to be a nonlinear opti-

mization problem. Solutions to such problems can

be found by using the nonlinear optimization solvers

in the simulation environment of MATLAB Simulink.

An important variable in the given problem is the as-

sumed rank r of the CPD. The more the multilinear

terms present to calculate the state in the next time

step, the denser the parameter tensor becomes and

thereby, the CP rank of the parameter tensor also in-

creases. Hence, while choosing the rank of the CPD

one must consider that there is a trade off between the

savings in storage effort and the accuracy of the de-

composed tensor with respect to the original tensor.

5 APPLICATION

In this section, the simulation results of the MTI state

space model identiﬁcation are presented. The identi-

ﬁcation will be performed for the heating system of

an industrial building.

5.1 Heating System

Figure 2: Heating system.

In ﬁgure 2, the schematic diagram of the heating sys-

tem of three heat zones of an industrial building is

clearly shown. Each heat zone has one heating device

which is a gas heater denoted by Hi, i=1..3. Depend-

ing on the input u

(k) ∈ E, i = 1..3, where E ∈ {0, 1, 2}

to the valves Vi, i=1..3, a volume of gas g

, i = 1..3

goes into the gas heater. The gas heater emits heat

ﬂow q

, i = 1..3, depending on the gas inlet. Natu-

rally, the heat ﬂow causes changes in the temperature

(k) ∈ R, i = 1..3 of the zone. The absolute temper-

ature of each the zones is measured by the respective

sensors Si, i=1..3. Additionally, there are three exter-

nal inﬂuences on the heating system as well. Two of

the three inﬂuences (d

(k) and d

(k)) are binary sig-

nals corresponding to the opening and closing of the

doors and one of the doors (d

(k)) is in between the

zones and the other between the zone and the open

area outside the industrial building, both the doors

have been marked in red in the schematic. The d

(k)

inﬂuence is the external temperature. The multilinear-

ity in the model comes through the presence of these

external disturbances. The equations describing the

temperatures t

(k + 1), t

(k + 1) and t

(k + 1) of the

three zones in the next time step are

(k + 1) = t

(k) + p

(k)

− p

(k) − d

(k))

− p

(k)(t

(k) − t

(k))

(22)

(k + 1) = t

(k) + p

(k)

− p

(k) − d

(k))

− p

(k)(t

(k) − t

(k))

− p

(k)(t

(k) − d

(k))

(23)

Approaches to Parameter Identiﬁcation for Hybrid Multilinear Time Invariant Systems

259

(k + 1) = t

(k) + p

(k)

− p

(k) − d

(k))

− p

(k)(t

(k) − t

(k))

(24)

The constants p

∀(i = 1..3) are the heat ﬂow con-

stants corresponding to the heating devices in the zone

i. The p

∀(i = 1..3) constants are the heat ﬂow con-

stants between the respective zone and the outside.

The constants p

∀(i = 1..3) are corresponding to the

heat ﬂow between zones when the door between them

is open. Furthermore, the constant p

is the heat

ﬂow constant between the second zone and the out-

side when the door is open.

For the given heating system, the identiﬁcation

problem will be solved by three approaches. Firstly,

the grey box identiﬁcation problem is tackled. The

MTI state space model can be deduced from the equa-

tions in (22), (23) and (24). Hence, the grey box iden-

tiﬁcation problem is to identify the unknown param-

eters p

, p

∀(i = 1..3) and p

from the given

input-state data set. From the equations (22), (23),

(24) we can write the model in the following form

t(k + 1) =

m(t(k), u(k), d(k))

(25)

where t(k) ∈ R

is the state vector comprising of the

the temperatures of the respective zones

t(k) =





(k)





u(k) ∈ E

is the input vector

u(k) =





(k)





and d(k) ∈ B

∪ R is the disturbance inputs vector

d(k) =





(k)





F ∈ R

3×12

contains the unknown parameters corre-

sponding to the terms in the monomial vector

m ∈

The second approach is the black box identiﬁca-

tion of the MTI state space model for the heating sys-

tem. It is assumed that a model of order three is to

be identiﬁed. Assuming that no information is avail-

able about the heating system, the task is to ﬁnd the

parameter matrix F ∈ R

3×512

. This objective can be

achieved by solving an inverse problem as mentioned

in the previous section.

The ﬁnal approach is the estimation of a low rank

approximation of the parameter tensor F, by ﬁnding

the CP factors of the parameter tensor directly from

the measurements (virtual data).

Due to unavoidable circumstances, real measure-

ment data from the building is not available in this

moment. Hence, to generate the temperature state

data for solving the identiﬁcation problem using all

methods, a Simulink model is constructed with the

help of information in equations (22), (23) and (24).

The unknown parameters are set to certain values.

Thereafter, the model constructed in Simulink is sim-

ulated to obtain the temperature response. The data

is collected for one whole day and the sample time of

the model is one minute. Thereby, in total T = 1440

samples are collected. The signals in the heating sys-

tem (u

, u

, d

and measurement noise) are

generated in the following way:

• u

, u

and u

: Random integers between 0 and 2.

• d

(external temperature): Temperatures for the

day 30.03.2020 in Hamburg, Germany have been

used. This day in particular is chosen, because

substantial variations in temperature could be ob-

served. The maximum and minimum recorded

temperatures on this day were 8.25 and -3.46 de-

gree celsius respectively. The JEVis platform

(Palensky, 2003) was used to obtain the data,

which in turn uses the data from Germany’s Na-

tional Meteorological Service to obtain the tem-

peratures. The data is available only in 15 minute

intervals in JEVis. Since the sample time of the

model is one minute, it is assumed that the temper-

ature is constant for every minute of the 15 minute

time interval.

• d

(door between two zones): It is assumed that

between 9:00 and 17:00 (core working hours) on

the particular day, the door is opened and closed

randomly by the workers. Hence, between the

mentioned time interval, random integers between

0 and 1 are generated.

• d

(door between zone and outside open area): It

is assumed that between 12:00 and 14:00 on the

particular day, the door has to remain open for

loading of the manufactured goods. Hence, be-

tween the mentioned time interval, d

= 1, other-

wise d

= 0.

• Noise: The band limited white noise block is used

to add measurement noise to the temperatures. A

noise power of 100 is chosen.

5.2 Identiﬁcation Results

The simulated responses in ﬁgures 3, 4, 5 and 6

show the results of all the approaches to identiﬁca-

tion discussed so far. The validation of the respective

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

260

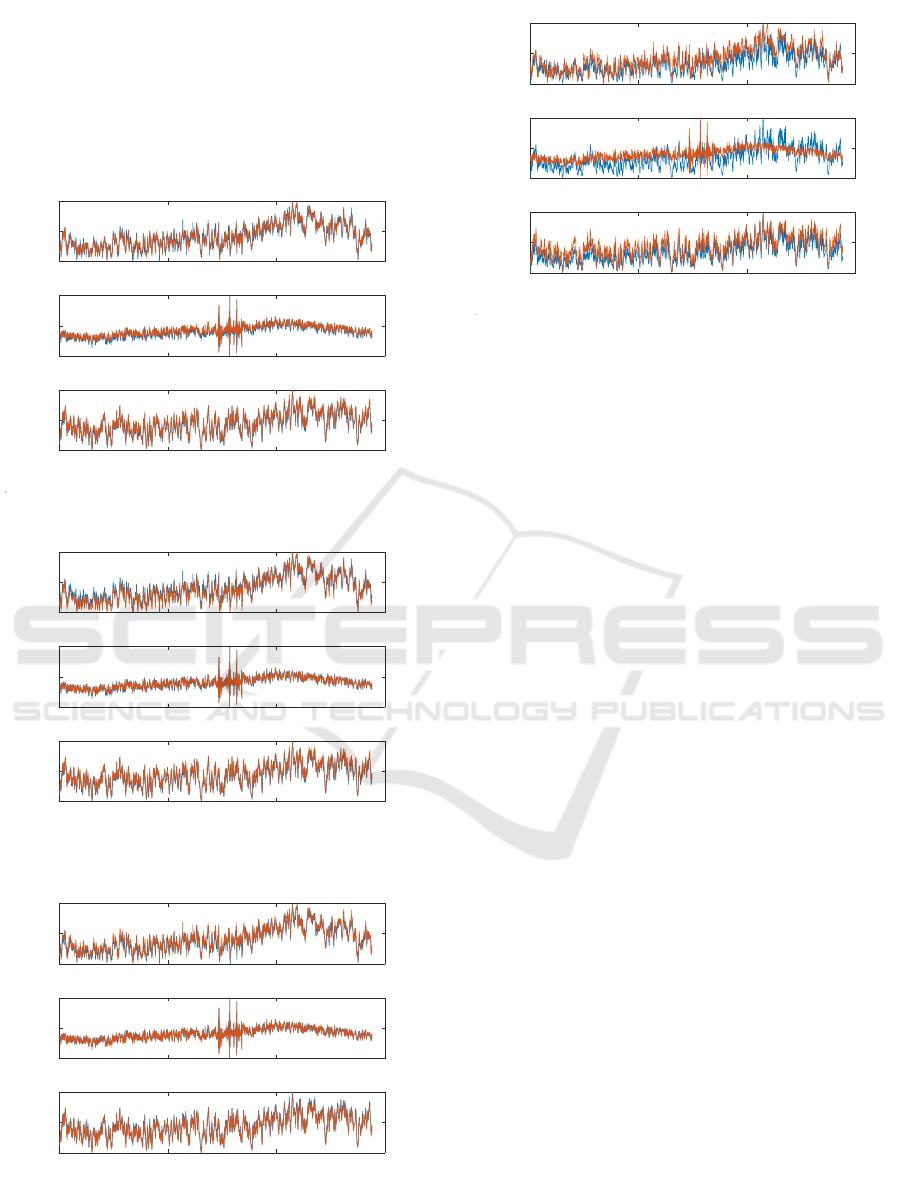
identiﬁcation approaches are presented by displaying

the plots of the temperatures generated through the

Simulink model and the temperatures predicted by the

identiﬁed model. Under the approach of estimating

the low rank approximation of the parameter tensor in

ﬁgures 5 and 6, two cases are considered. Case one

with r = 1 and second case with r = 10.

0 500 1000 1500

Sample Number

0.5

Normalized t

0 500 1000 1500

Sample Number

0.5

Normalized t

0 500 1000 1500

Sample Number

0.5

Normalized t

Figure 3: Grey box: measured (red) vs estimated (blue).

0 500 1000 1500

Sample Number

0.5

Normalized t

0 500 1000 1500

Sample Number

0.5

Normalized t

0 500 1000 1500

Sample Number

0.5

Normalized t

Figure 4: Black box: measured (red) vs estimated (blue).

0 500 1000 1500

Sample Number

0.5

Normalized State t

0 500 1000 1500

Sample Number

0.5

Normalized State t

0 500 1000 1500

Sample Number

0.5

Normalized State t

Figure 5: Black box rank 10 approximation: measured (red)

vs estimated (blue).

0 500 1000 1500

Sample Number

0.5

Normalized State t

0 500 1000 1500

Sample Number

0.5

Normalized State t

0 500 1000 1500

Sample Number

0.5

Normalized State t

Figure 6: Black box rank 1 approximation: measured (red)

vs estimated (blue).

From the ﬁgures 3, 4 and 5, it is clear that the tem-

peratures predicted by the identiﬁed models and the

temperatures generated through the Simulink model

are in agreement. A similar accuracy in identiﬁca-

tion is not seen in ﬁgure 6. This means that the pa-

rameter tensor of the model to be identiﬁed has a CP

rank substantially higher than 1. Therefore, a rank 1

CP parameter tensor does not adequately represent the

model. The ﬁgures 5 and 6 also illustrate the trade off

that is storage effort (r = 1 has 22 elements and r = 10

has 220 elements) and accuracy of the decomposed

tensor with respect to the original parameter tensor.

6 CONCLUSIONS

The paper presents the system identiﬁcation of an

MTI state space model of a given order using both the

grey and black box identiﬁcation methods. Within the

black box method, two different approaches are pre-

sented. The ﬁrst approach focuses on solving an in-

verse problem. The result of this approach is a full

parameter matrix of the state space model. The sec-

ond approach focuses on ﬁnding a low rank approxi-

mation of the parameter tensor directly from the mea-

surements.

A numerical example of identiﬁcation of MTI

state space model for a heating system of an industrial

building was also presented where, state space models

of order three were identiﬁed for the corresponding

input-output data sets. Real measurement data was

not available, therefore, virtual data was generated

by simulating a known model of the heating system

in MATLAB Simulink. The data was collected for a

whole day, with signals as close to reality as possible.

The future work should be towards making the es-

timation process more robust to noises. Furthermore,

identiﬁcation could be carried out for larger systems

with real measurement data.

Approaches to Parameter Identiﬁcation for Hybrid Multilinear Time Invariant Systems

261

ACKNOWLEDGEMENTS

This work was partly supported by the project

SIOSTA of the Federal Ministry of Education and Re-

search, Germany (Grant-No.: 01LY1812B).

REFERENCES

Lichtenberg, G. (2011). Hybrid tensor systems. Habilita-

tion, Hamburg University of Technology, 152.

Chavan, S. L., & Talange, D. B. (2018). System identiﬁ-

cation black box approach for modeling performance

of PEM fuel cell. Journal of Energy Storage, 18, 327-

332.

Tayamon, S., Zambrano, D., Wigren, T., & Carlsson, B.

(2011). Nonlinear black box identiﬁcation of a se-

lective catalytic reduction system. IFAC Proceedings

Volumes, 44(1), 11845-11850..

Royer, S., Thil, S., Talbert, T., & Polit, M. (2014). Black-

box modeling of buildings thermal behavior using sys-

tem identiﬁcation. IFAC Proceedings Volumes, 47(3),

10850-10855.

Bacher, P., & Madsen, H. (2011). Identifying suitable mod-

els for the heat dynamics of buildings. Energy and

Buildings, 43(7), 1511-1522.

Batselier, K., Ko, C. Y., Phan, A. H., Cichocki, A.,

& Wong, N. (2018). Multilinear state space system

identiﬁcation with matrix product operators. IFAC-

PapersOnLine, 51(15), 640-645.

Kruppa, K. (2017). Comparison of tensor decomposition

methods for simulation of multilinear time-invariant

systems with the MTI toolbox. IFAC-PapersOnLine,

50(1), 5610-5615.

Kolda, T. G., & Bader, B. W. (2009). Tensor decompositions

and applications. SIAM review, 51(3), 455-500.

Cichocki, A., Zdunek, R., Phan, A. H., & Amari, S. I.

(2009). Nonnegative matrix and tensor factorizations:

applications to exploratory multi-way data analysis

and blind source separation. John Wiley & Sons.

Pangalos, G., Eichler, A., & Lichtenberg, G. (2015). Hybrid

multilinear modeling and applications. In Simulation

and Modeling Methodologies, Technologies and Ap-

plications (pp. 71-85). Springer, Cham.

Pangalos, G. (2016). Model-based controller design meth-

ods for heating systems. Technische Universit

at Ham-

burg.

Kruppa, K., & Lichtenberg, G. (2017). Decentralized State

Feedback Design for Multilinear Time-Invariant Sys-

tems. IFAC-PapersOnLine, 50(1), 5616-5621.

Ljung, L. (1999). System identiﬁcation: theory for the user.

PTR Prentice Hall, Upper Saddle River, NJ, 1-14.

Palensky, P. (2003). The JEVis system-An advanced

database for energy-related services. na.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

262