Towards Fully Automated Inspection of Large Components with UAVs:

Ofﬂine Path Planning

Constantin Wanninger

, Raphael Katschinsky, Alwin Hoffmann

, Martin Sch

orner

and Wolfgang Reif

Institute for Software and Systems Engineering, University of Augsburg, Augsburg, Germany

Keywords:

UAV, Visual Inspection, Trajectory Planning, Ant Colony Optimization.

Abstract:

Automation mechanisms are increasingly established in the ﬁeld of visual inspections. UAVs can be used

for particularly large components, such as those used in ship production and for critical infrastructures. This

paper concentrates on the problem of visual inspection in the ﬁeld of perspective-dependent route planning.

It is shown how the requirements for such a system can be implemented and elaborated. Furthermore we

investigate how sensor positions can be calculated ofﬂine, based on optical and geometrical requirements

and how a trajectory can be planned which contains the found sensor positions for each given area on the

component. It is shown how the systems architecture can be designed in order to be able to adapt it to

different requirements for the planning of sensor positions and trajectory. The implementation was tested in

a simulation environment, evaluated using a benchmark data set and it was shown how above-average results

can be achieved on this data set.

1 INTRODUCTION

The development progress and the strongly increased

availability of unmanned aerial vehicles (UAVs) in

the last years open up more and more possibilities

for civil and scientiﬁc applications. For example, the

use of UAVs for the inspection and measurement of

infrastructures is being investigated, as they enable

image-based observation from almost any perspec-

tive. Among others, the Competence Center Multi-

copter of (Deutsche Bahn AG, 2020) offers a com-

prehensive portfolio in the infrastructure sector. This

includes the inspection of rail tracks, buildings and

bridges as well as construction progress and condition

documentation, to name just a few.

A still little explored area, is the fully automated

visual inspection of large technical components by

UAVs, to which this work is dedicated. The com-

ponents considered here are assemblies according to

DIN-199, i.e. self-contained objects consisting of at

least two individual parts or assemblies of lower or-

der. Currently, visual inspection of large technical

components is still mostly carried out manually. For

https://orcid.org/0000-0001-8982-4740

https://orcid.org/0000-0002-5123-3918

https://orcid.org/0000-0001-6237-222X

this purpose, an inspector checks the attached individ-

ual parts whether the present situation corresponds to

the normal conditions of the component. This form of

inspection, however, is associated with longer inspec-

tion times, increased personnel expenditure, human

error susceptibility, and thus with overall increased ﬁ-

nancial costs, which can be addressed by the full au-

tomation of the visual inspection.

The ofﬂine path planning within a fully automated

inspection is usually divided into two subproblems,

ﬁnding sensor positions, so-called viewpoints, and

ﬁnding a collision-free route through all viewpoints.

When planning viewpoints, it must be ensured that

they can be reached by the UAV and that no obsta-

cles block the view of the component to be examined,

or more generically expressed point of interest (POI).

In order for a POI, e.g, to be optimally located in the

picture, the desired resolution, focus and the camera’s

angle of aperture must be taken into account when

choosing the location of the viewpoint in relation to

the POI. When selecting the position, the orientation

of the visual sensor to the normal of the POI must

also be taken into account. However, this desired ori-

entation cannot necessarily be achieved with a UAV,

since the tilt and inclination angle of the UAV can-

not be selected at will and the camera is statically

attached to the copter or the degree of freedom of a

Wanninger, C., Katschinsky, R., Hoffmann, A., Schörner, M. and Reif, W.

Towards Fully Automated Inspection of Large Components with UAVs: Ofﬂine Path Planning.

DOI: 10.5220/0009887900710080

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 71-80

ISBN: 978-989-758-442-8

swivel-mounted camera is limited. Therefore, it must

be considered to what extent the angle between the

normal of the POI and the vector of the optical axis

of the camera may deviate. In addition, a minimum

distance between the copter and the component may

be required for safety reasons.

The route should contain all viewpoints from

which all POIs can be inspected. Therefore, it is im-

portant to keep the route through all the viewpoints as

short as possible and optimize the route lenght. Since

the search for the shortest route in three-dimensional

space is NP-hard (LaValle, 2006), procedures must be

considered that offer an almost optimal solution for

this problem in polynomial time. In the course of op-

timizing the route length, it is therefore important to

keep the number of viewpoints as small as possible,

while still ensuring an optimal view of all POIs.

This work is dedicated to exactly these two parts,

the viewpoint and trajectory planning. This involves

the fully automated inspection of predeﬁned areas on

the component. It is examined how viewpoints can be

planned ofﬂine on the prerequisites mentioned above

and a route based on them. The designed procedure

is tested simulatively and the results of the trajectory

planning are evaluated using benchmark data sets.

2 RELATED WORK

Work that is speciﬁcally dedicated to the fully auto-

mated inspection of technical infrastructures by UAVs

usually aims to achieve complete visual coverage

of the entire surface of the respective infrastructure,

which is the aim of the Coverage Path Planning (Gal-

ceran and Carreras, 2013; Danner and Kavraki, 2000).

A detailed summary of the current inspection scenar-

ios provided by UAVs is provided by (Jordan et al.,

2018). According to the work of (Bircher et al.,

2015), the most adaptable approaches to the inspec-

tion scenario are those that use two-step optimiza-

tion. In a ﬁrst step, viewpoints are computed that

cover the entire surface of the infrastructure, which

can be achieved by solving the Art Gallery problem

(O’Rourke, 1987; Gonz

alez-Banos, 2001). In a sec-

ond step, a route or trajectory is calculated that con-

nects all viewpoints, which can be modeled by solv-

ing the Traveling Salesman Problem (Laporte, 1992).

A concrete CPP solution for UAVs is described

by (Bircher et al., 2015), in which the surface of

the infrastructure is represented by a triangle mesh

and a viewpoint is calculated for each triangle, from

which the triangle is completely visible. In the sec-

ond step a route through all viewpoints is planned.

To do this, viewpoints are connected directly to each

other if there is no obstacle between them, otherwise

the RRT* search algorithm (Karaman and Frazzoli,

2011) is used to connect both viewpoints. RRT* is

an extension of the Rapidly Exploring Random Tree

(RRT) search algorithm by (LaValle, 2006).

(Englot and S. Hover, 2014) also show a two-step

procedure for the inspection of ship hulls, which has

already been successfully tested on the object. Al-

though the procedure was designed for the use of au-

tonomous underwater vehicles, it is still noteworthy

because it deals with the automated ofﬂine planning

of sensor positions relative to a component in three-

dimensional space. In the ﬁrst phase, conﬁgurations

are randomly sampled by the Redundant Roadmap

Algorithm until the surface is covered. In the sec-

ond phase, an iterative solution of the RRT over all

goal-to-goal routes calculates a route that connects all

goals. Here, goal-to-goal means that the route ends at

the conﬁguration where it started. The Local Cover-

age Algorithm (LCA) optimizes the route in terms of

length: Therefore (P, C) is the set system. The surface

to be observed depends on a ﬁnite set of geometric

primitives p

∈ P (i.e., POIs to be covered) and from

each conﬁguration q

∈ Q (i.e., a viewpoint) a set of p

can be observed. The LCA is passed a coverage route

which is not yet optimized. The algorithm se-

lects any goal q

∈ W

per iteration and tries to ﬁnd a

conﬁguration q

that observes all primitives, that also

observes q

and at the same time reduces the costs

for the route section W

q−1,q+1

. Finding an optimized

route stage is done by RRT

∗

, a variant of the RRT*

algorithm by (Karaman and Frazzoli, 2011). To get

an optimized route section W

q−1,q+1

with q

as inter-

mediate conﬁguration, RRT

∗

will calculate in parallel

an optimal collision free route from q

j−1

to q

and

one from q

to q

j+1

. For this purpose two RRT* trees

are built with q

j−1

and q

j+1

as the root. This method

was evaluated at USCGC Seneca and it was shown

that the feasible route with 192 viewpoints and 246

m could be improved to an optimized route with 169

viewpoints and 157 m length.

Works dealing with ﬁnding viewpoints usually

assume that any pose of the camera can be taken.

According to (Alarcon-Herrera et al., 2014) optimal

viewpoints can be found for a POI if the optical axis

of the camera runs along the normal vector of the POI

and a so-called standoff distance to the POI is main-

tained. The standoff distance is calculated from the

desired resolution of the POI in the image, the height

and width of the image sensor and the angle of aper-

ture of the camera. By aligning the optical angle along

the normal of the POI, the POI is centered in the pic-

ture, which ensures maximum visibility of the POI.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

This also prevents the POI from being distorted in

the picture. By positioning the viewpoint around the

standoff distance along the normal of the POI, an al-

most optimal resolution of the picture can be guaran-

teed. If a desired padding in pixels around the POI is

desired, this can be taken into account in the calcula-

tion of the standoff distance.

(Malandrakis et al., 2018) present an already suc-

cessfully tested procedure for the complete inspection

of aircraft wings by penetration testing. For this pur-

pose, a copter was equipped with a wide-angle cam-

era with digital image stabilization and UV light. To

ensure that the viewpoints are evenly distributed over

the wing and that each area of the wing can be opti-

mally inspected by the camera and UV light over the

course of the trajectory, the viewpoints are planned

so that the light cones from adjacent viewpoints over-

lap on the surface of the wing. The trajectory is then

planned so that the copter travels row by row through

all viewpoints.

3 CONCEPT

This chapter addresses the conceptual viewpoint and

trajectory planning, in particular how the require-

ments for visual inspection of speciﬁed areas on the

assembly can be achieved. As a basis, the required

concepts are ﬁrst introduced and then described how

the position and orientation of a viewpoint can be

planned depending on the camera’s ﬁeld of view. Fi-

nally, the concept behind trajectory planning is de-

scribed, in which, for example, the traveling salesman

problem can be solved with Ant Colony Optimization.

3.1 Orientation in Space

The calculation of the sensor positions and the tra-

jectory planning is done in the coordinate space R

which is based on a Cartesian coordinate system.

The coordinate axes and coordinate frames follow the

right-hand rule with the z-axis pointing upwards.

3.2 Workspace

The workspace is the State-Space (LaValle, 2006)

considered here and builds on the underlying coordi-

nate space. It deﬁnes the planning environment for

the viewpoints and the trajectory. The size of the

workspace is determined by the size of the compo-

nent and any padding around it. The most important

terms concerning the workspace are explained below.

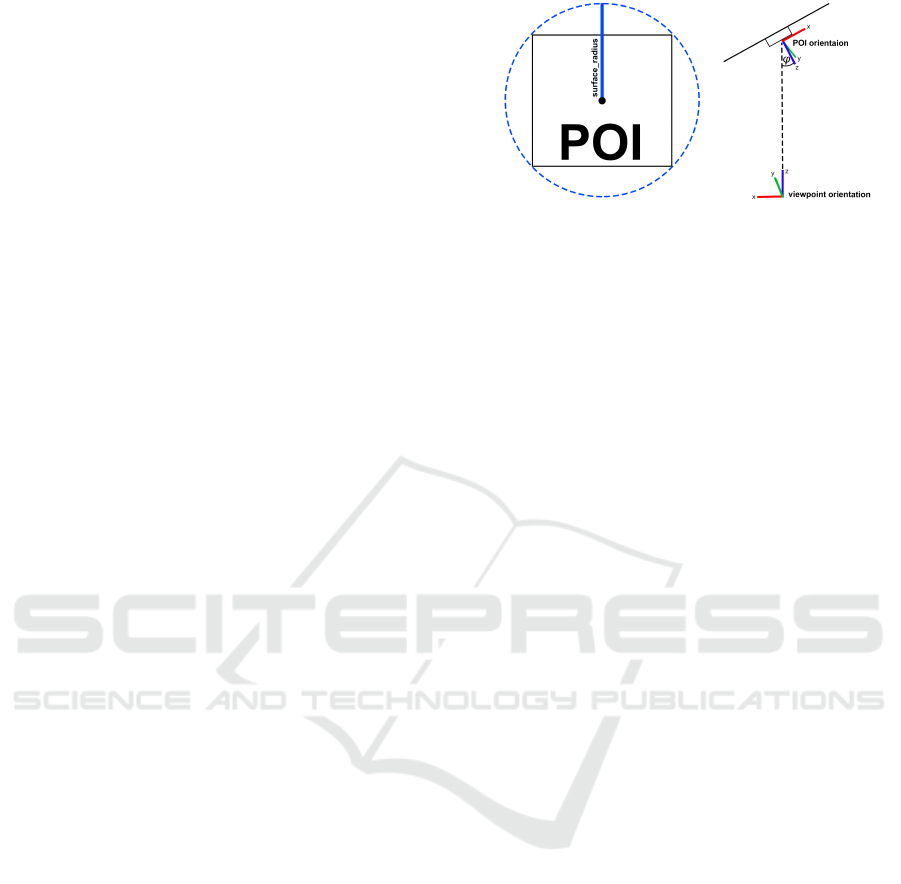
(a)

(b)

Figure 1: (a) Example POI with corresponding surface ra-

dius. (b) Deviation angle ϕ between the normal of the POI

and the optical axis of the camera.

3.3 Point of Interest

A Point-of-Interest, POI for short, is an individual

part or a low-order assembly on the component to

be inspected. POIs are described by its ID, position,

orientation, maximum deviation angle, semantic An-

notation and a surface radius. The position of the

POI in the workspace is indicated by its coordinates

x, y, z and its orientation x

, y

, z

, w

. The orientation

of the copter is deﬁned over the division ring of the

quaternions H. The position speciﬁes the center of

the POI. The maximum deviation angle ϕ

max

speci-

ﬁes the maximum deviation of the angle ϕ between

the normal of the POI and the optical axis of the cam-

era, as shown in ﬁgure 1b. Each POI has a semantic

annotation that describes the low-order part or com-

ponent. To determine the camera position, the surface

radius is also needed. It describes the radius of the

POI on the surface of the part and is an approxima-

tion of the complex structure of the POI to a circle, as

shown in ﬁgure 1a.

3.4 Viewarea

A POI is visible to the UAVs camera from a certain

area, the so-called Viewarea. A Viewarea is calcu-

lated depending on the Angle-of-View (AoV) and the

focus of the camera, as well as the surface radius of

the POI to which the Viewarea is assigned. It is de-

scribed by the radii va

min

and va

max

. Where va

min

describes the minimum distance between the visual

sensor and the POI. It indicates the lower limit from

which a POI is no longer completely visible in the

image. However, if the required minimum distance to

the component is greater than this lower limit, va

min

represents the required minimum distance to the com-

ponent. The va

max

represents the upper limit, from

which on the POI is no longer visible in the picture.

Both parameters thus indicate a lower and upper limit

of the effectively usable viewarea.

Towards Fully Automated Inspection of Large Components with UAVs: Ofﬂine Path Planning

3.5 Viewpoint

Each POI has at least one viewpoint from which sen-

sor data can be collected. In the best case, it lies on the

inverted z-axis of the camera orientation, ﬁxed at the

position of the POI. A viewpoint vp

that observes a

POI poi

with associated viewarea VA

is calculated

so that vp

∈ V P

. Here V P

contains all viewpoints

in the following form:

V P

= {vp

∈ VA

: va

min

≤

||poi

− vp

≤ va

max

}

(1)

Furthermore, it can happen that two Viewareas are not

disjoint, i.e. there is a set A with Viewareas VA

⊇ V P

, VA

⊇ V P

and viewpoint vp

, so that the following

applies: A = {vp

: vp

∈ V P

∩V P

}. If A contains

viewpoints that maintain the maximum angle of de-

viation ϕ

max

for each POI they can theoretically ob-

serve, it is possible to use such sets A in the case of

optimizing the trajectory length between three adja-

cent viewpoints. A viewpoint is described by its ID,

position, orientation, a boolean parameter that indi-

cates whether the viewpoint lies in the middle of its

viewarea, three radii and a list of all POIs which it

observes. The position is given by the coordinates

x, y, z and the orientation by x

, y

, z

, w

. The orien-

tation of the viewpoints is deﬁned above the division

ring of the quaternions H. Position and orientation

represent the position and orientation of the camera

lens relative to the origin of the coordinate space. If

the viewpoint cannot be optimally positioned (on the

inverted z-axis of the camera orientation ﬁxed to the

position of the POI), the boolean parameter indicates

that it is an alternative viewpoint. The radii vp

min

and

max

represent the effectively usable viewarea in the

xy-plane at the viewpoint position, depending on the

AoV of the camera. The radius r

represents the ef-

fective viewarea in the xy-plane at the viewpoint po-

sition, depending on the deviation angle ϕ of the POI.

3.6 Key Viewpoint

If at least one viewpoint is found for each POI, the

number of viewpoints should be kept to a minimum.

As described in the previous paragraph, alternative

viewpoints can be calculated that can inspect more

than one POI. However, this may result in a worse

view on the POIs that vp

observes. Therefore, a

good trade-off between optimal viewpoint positions

and trajectory length must be found in the course of

optimization. In the end there should be at most one

viewpoint for each POI that observes it. The set of

these viewpoints are the so-called key viewpoints.

3.7 Trajectory

A UAV has so-called holonomic properties, i.e. its

controllable degree of freedom with respect to its

position corresponds to its total degree of freedom

with respect to its position. Therefore viewpoints can

be accessed directly and the trajectory between two

viewpoints can be described as a linear motion (LIN).

For this purpose, this paper assumes that there are no

obstacles between two adjacent viewpoints. Finally,

the trajectory contains a permutation of all key view-

points and represents a shortest route.

3.8 Planning of Viewpoints

Before the trajectory can be calculated, viewpoints

must be planned depending on the camera’s ﬁeld of

view. The following section describes the require-

ments that need to be considered when planning view-

points and how viewpoints can be planned in detail:

3.8.1 Requirements for Viewpoint Planning

As stated by Alarcon et al. (Alarcon-Herrera et al.,

2014), a POI is optimally positioned in the image if

the optical axis of the camera runs along the normal

vector of the POI and a standoff-distance to the POI

is maintained (here: va

min

≤ stando f f distance ≤

max

). Since the tilt and inclination angle of the UAV

is not arbitrary selectable and the camera is statically

attached to the UAV, viewpoints have to be found so

that ϕ (see ﬁgure 1b) is within the given tolerance

range ϕ

max

and the standoff-distance is kept.

3.8.2 Planning

When planning a viewpoint, the radii of the viewarea

to a POI must be calculated and the orientation of the

camera must be taken into account. The minimum-

and maximum distance va

min

, va

max

between the

viewarea and a POI is calculated as follows:

min

poi

tan(

min(AoV )

)

(2)

max

= f ·

(poi

· φ)

[mm]

poi

[px]

(3)

Where f is the focal length of the camera, A

poi

the

minimum size of the POI in pixels in the picture so

that the POI can be identiﬁed and poi

the surface ra-

dius of Poi poi

. The constant φ indicates to which

extent A

poi

may be exhausted.

To examine the planning of the viewpoints under

ideal conditions ﬁrst, the orientation of the POIs and

the camera was chosen so that the optical axis of the

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

camera runs along the normal vector of the POI and

is therefore valid:

∀vp

, poi

(vp

, poi

) ∈ V P

× POI

⇒ ϕ = 0 (4)

Where POI

is the set of all POIs for a single part

or an assembly of lower order. V P

is the set as de-

scribed in Eq.1. If the z-axes of the camera, POI and

workspace are parallel to each other, the orientation

of the camera can be taken as the orientation of the

viewpoint. The position of the viewpoint is then a

translation around the standoff-distance along the z-

axis of the POI. Thus the POI is located on the optical

axis of the camera and the viewpoint is located in the

middle of the viewwarea. The radii of the Viewarea

at the position of the viewpoint are calculated as fol-

lows:

max

(poi

, vp

) =

= tan(

max(AoV )

) · d(poi

, vp

) − poi

(5)

min

(poi

, vp

) =

= tan(

min(AoV )

) · d(poi

, vp

) − poi

(6)

(poi

, vp

) =

= tan(ϕ

max

) · d(poi

, vp

) − poi

(7)

d(poi

, vp

) = ||poi

− vp

(8)

The radii vp

min

and vp

max

are especially important if a

POI cannot be identiﬁed from a viewpoint during the

inspection. If a POI cannot be identiﬁed from a POI

during inspection, one of the radii can be used during

inspection to circle around the viewpoint in a spiral

ﬂight. If the POI still cannot be identiﬁed, it will be

marked as not present.

3.9 Planning the Trajectory

After key viewpoints have been found for all POIs,

a trajectory containing all key viewpoints must be

planned. For this purpose, the following describes

which requirements have to be considered when plan-

ning a trajectory and how these can be fulﬁlled by

modelling the Travelings-Salesman-Problem as Ant

Colony Optimization.

3.9.1 Requirements for Trajectory Planning

For the ofﬂine planning of the trajectory there are

three main requirements: For each POI to be in-

spected, each key viewpoint must be located on the

trajectory. For easy handling of the UAV during the

inspection, the trajectory should end at the position

where it started. To minimize the time needed for the

inspection, the trajectory through all key-viewpoints

should be planned as short as possible.

3.9.2 Planning

The Ant Colony Optimization (ACO), a method for

solving the Travelings-Salesman-Problem, was used

to fulﬁll the requirements. This method is particularly

well suited for a large number of nodes (viewpoints)

because it provides a near-optimal solution (Chaud-

hari and Thakkar, 2019), as shown in table 1. Fur-

thermore, a near-optimal route can be found in a short

time by using ACO.

ACO is inspired by the behaviour of ants in ﬁnd-

ing a shortest possible route from their nest to a food

source. For this purpose, ants leave pheromones on

their route when they have found a food source. Other

ants follow this pheromone trail with a certain prob-

ability, whereby the probability increases with the in-

tensity of the pheromone on the trail. After a certain

time, more and more ants follow the strongest/opti-

mal pheromone trail. Since more pheromones can be

deposited in the same time on a shorter route than on

a longer one, the intensity of the pheromone trace in-

creases most on the shorter route. Over time, the in-

tensity of the pheromone trace of less used routes de-

creases again.

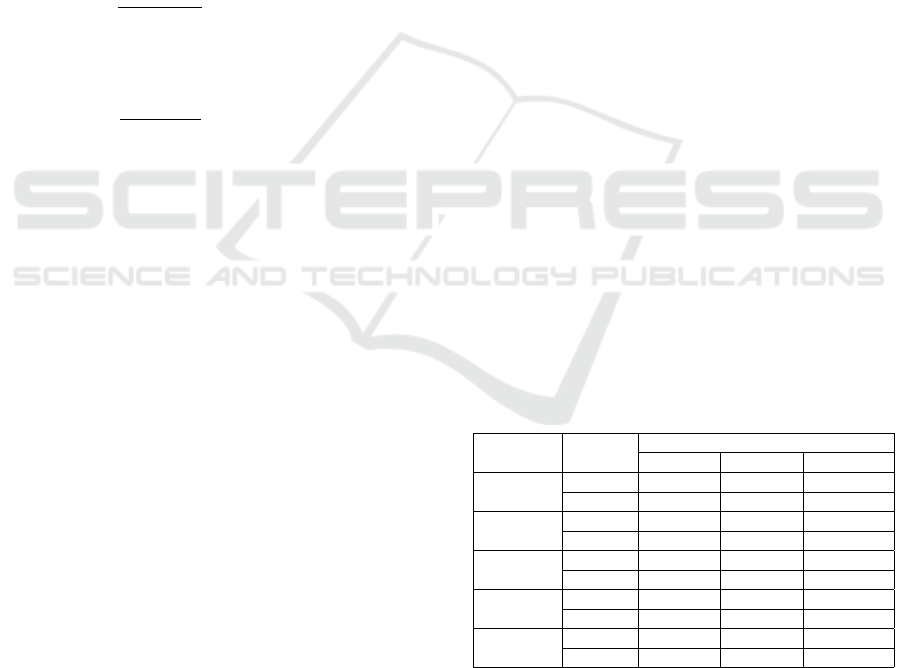
Table 1: Source: Chaudhari et al. (Chaudhari and Thakkar,

2019). Comparison of average and best found distances (in

km) of Ant Colony Optimization (ACO), Particle-Swarm-

Optimization (PSO), Artiﬁcial-Bee-Colony (ABC), Fireﬂy

Algorithm (FA) and Genetic Algorithm (GA). Burma14 rep-

resents 14 cities in Burma, Bayg29 29 cities in Bavaria and

Att48 cities in the USA.

Algorithm Route

Few of the benchmark TSPs

Burma14 Bayg29 Att48

ACO

Average 31,05 9274,79 35043,34

Best 30,88 9195,22 34600,71

PSO

Average 32,34 15047,83 109979,87

Best 30,88 14036,75 91237,09

ABC

Average 32,36 17404,62 107883,76

Best 30,88 16658,30 101985,88

Average 31,80 14283,51 81182,32

Best 30,88 13062,40 78479,69

Average 31,49 11023,70 50753,50

Best 30,88 10018,10 46362,05

To imitate this behavior, ﬁrst deﬁne the pheromone

update formula (Eq. 9) for each edge c

i j

in a graph

G = (V, E).

i j

= (1 − ρ) · τ

i j

∑

k=1

∆τ

i j

(9)

Towards Fully Automated Inspection of Large Components with UAVs: Ofﬂine Path Planning

Where ρ is the pheromone evaporation rate, m the

number of ants and ∆τ

i j

(Eq. 10) the pheromone in-

tensity left by ant k at edge c

i j

∆τ

i j







i f c

i j

is on the Route o f ant k

0 else

(10)

Where Q is a constant and L

is the route length of ant

k in the current iteration. The probability of taking the

edge c

i j

at node i to node j is given by Eq. 11.

i j











i j

· η

i j

∑

∈N(s

)

· η

i f c

i j

∈ N( j

)

0 otherwise

(11)

Where j

is the route taken by ant k so far and N( j

)

are the edges (i, l) to not yet visited nodes l. The pa-

rameters α, β control the inﬂuence of the pheromone

i j

and the heuristic information η

i j

(Eq.12).

i j

(12)

In this work the Ant Colony System (ACS) (Gam-

bardella and Dorigo, 1996; Stuetzle and Dorigo,

1999; Dorigo et al., 1999), a variation of the ACO,

was used. With ACS, only pheromone from the

globally best ant is deposited on an edge c

i j

and

the pheromone update formula changes to a Global

Pheromone Update Formula (Eq.13).

i j

= (1 − ρ) · τ

i j

+ ρ · ∆τ

best

i j

(13)

Additionally, a local pheromone update formula (Eq.

14) is deﬁned for each ant. This makes already visited

edges less interesting for other ants and increases the

exploration of not yet visited edges.

i j

= (1 − ρ) · τ

i j

+ ρ · τ

(14)

n · L

(15)

Where n is the number of key viewpoints and L

the length of a route according to the nearest neighbor

heuristic. In addition, formula (Eq. 11) is reformu-

lated to calculate the probability of which node will

be visited next by ant k. For this purpose, q ∈ [0, 1]

is randomly determined and q

is ﬁxed as a constant.

The constant q

determines whether the focus should

be on the exploration of G or the exploitation of good

pheromone traces. Ant k then selects the next node j,

according to the formula (Eq. 16)

j =







argmax

i j

∈N( j

)

{τ

i j

· η

i j

} i f q ≤ q

J otherwise

(16)

i j











i j

· η

i j

∑

∈N(s

)

· η

i f c

i j

∈ N( j

)

0 otherwise

(17)

Here J is a random node j which has not yet been

visited by ant k and according to Eq. 17: This cal-

culation gives preference to nodes that are connected

to the current node i by a short edge and have a high

pheromone intensity.

The underlying graph G = (V, E) is a complete

graph, i.e. each key viewpoint is connected to each

by an edge. Since the trajectory consists of LINs be-

tween the key-viewpoints, the edge weights are equal

to the Euclidean distance between the key-viewpoints.

4 REALIZATION AND

IMPLEMENTATION

This chapter deals with the realization and implemen-

tation of the concept presented in chapter 3. For the

realization of the ofﬂine planning of the viewpoints

and the trajectory a software architecture was devel-

oped, which allows to deﬁne different requirements to

the viewpoint and trajectory planning and to extend

the system component by component. For trajectory

planning, it is shown how the Ant Colony System can

be implemented.

4.1 System Architecture

The elaboration of all presented concepts was ab-

stracted to a necessary level in order to ﬁrst investigate

the suitability of UAVs for fully automated inspection

of given areas on the component. The design of the

system was therefore chosen in such a way that the

realization within the scope of this paper is limited

to the complete concept and can be extended beyond

that. For this reason, the software architecture placed

great emphasis on the scalability and interchangeabil-

ity of the viewpoint and trajectory planning compo-

nents with the aim of adapting the system to different

viewpoint and trajectory requirements. If, for exam-

ple, a trajectory is to be planned for multiple com-

ponents of the same type, a strategy can be selected

that keeps the length of the trajectory as short as pos-

sible, thus saving time and costs in visual inspection.

If, on the other hand, a trajectory is to be planned for

individual components, a much less computationally

intensive strategy can be used to plan the trajectory if

a fast calculation of the trajectory is essential. In or-

der to plan viewpoints and trajectory, camera parame-

ters, minimum distance of the UAV to the component

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

and the desired planning strategy are transferred to the

system. The camera parameters necessary for the sys-

tem are the orientation of the camera lens relative to

the orientation of the UAV, angle of view, focal length

and the desired minimum size of a POI in the image

in pixels. The strategy for viewpoint and trajectory

planning is then instantiated via an abstract factory.

Which factory should be used is determined by the

implementation of the strategy pattern: The strategy

for viewpoint planning is determined using the trans-

ferred parameters and the corresponding factory is se-

lected. If a new strategy is to be added to the system, a

new factory can be added by implementing the corre-

sponding interface. The system outputs the trajectory

and the key viewpoints in serialized form. Afterwards

the planned trajectory can be tested simulatively with

ROS, Gazebo and Rviz or the key viewpoints can be

sent to a UAV via mavlink.

4.2 Viewpoint and Trajectory Planning

The viewpoint and trajectory planning component

were realized and implemented in Python 3. The ex-

act elaboration is described below.

4.2.1 Viewpoint Planning

When planning the viewpoints, the radii were calcu-

lated according to the formulas in chapter 3.8.2. To

calculate the position of the viewpoint, the x and y

position of the POI was taken and the position of the

viewpoint along the z-axis of the POI was shifted by

the va max radius of the associated viewarea. The

va max radius distance between the viewpoint and

the POI was chosen to allow the UAV to initially

maintain a certain safety distance to the component.

The orientation of the camera has been adopted as

the viewpoint orientation. This is possible for the

case under consideration because the z-axis of the

workspace, the optical axis of the camera and the nor-

mal of the POI are parallel to each other.

4.2.2 Trajectory Planning

The implementation of the ACS is based on the con-

cept of Trevlovett (trevlovett, ). The implementation

of the ACS is multithreaded, i.e. each ant was imple-

mented as a single thread. The distance between the

key viewpoints and the pheromone intensity on the

edges are created as two separate matrices. The Eu-

clidean distance between the key-viewpoints is used

as the distance measure, since the trajectory is deﬁned

as LINs between the key-viewpoints. The pheromone

intensity on each edge is initially set to τ

∑

i j

||i − j||

(18)

where N is the number of key viewpoints. The calcu-

lation of the global and local pheromone update for-

mula was done as in Eq. 13 and Eq. 14 and the heuris-

tic information η

i j

as in Eq. 12. The formula for the

pheromone intensity at edge c

i j

was calculated as fol-

lows:

∆τ

best

i j

||i − j||

best

(19)

Where ||i − j|||

best

is the Euclidean distance of the

edge c

i j

on the best route and L

best

is the distance of

the best route.

The implementation of the formula as in Eq. 17, was

implemented as a roulette wheel-style selection pro-

cedure. This is done by taking the average value of

the pheromone and heuristic information of all edges

∈ N( j

avg =

∑

∈N(s

)

· η

(20)

Where N

is the number of viewpoints not yet visited.

The edge to the ﬁrst viewpoint in the list of unvisited

viewpoints whose pheromone and heuristic informa-

tion value of the edge is greater than avg is taken. The

implementation is based on the ROS infrastructure

and can be visualized with Rviz. Gazebo was used

to simulate the behavior of the UAVs and the visual

sensors. For illustrative purposes we provide videos

of the implementation of the simulation environment

as well as the processing of the trajectory (ros, ; rvi, ).

5 EVALUATION

For the evaluation, nine POIs were considered, which

are attached to a component. The orientation of the

POIs were chosen so that their normals are parallel to

the z-axis of the workspace. For the additional evalu-

ation of the trajectory planning, the results of the im-

plementation were evaluated using a TSP-benchmark

data set. The trajectory through the nine key view-

points was tested with Gazebo, Rviz and ROS. The

results of the evaluation are shown below.

5.1 Results of Trajectory Planning

As described in chapter 3.9, the trajectory is planned

in a complete graph G = (V, E). For each of the nine

POIs, a viewpoint has been planned which is located

in the middle of the POI’s Viewarea. The optical axis

of the camera is always on the normal of the POI, so

Towards Fully Automated Inspection of Large Components with UAVs: Ofﬂine Path Planning

that for all pairs (vp

, poi

) ∈ V P

×POI

the deviation

angle ϕ is 0. An almost optimal route of 11.78 me-

ters through all nine key viewpoints was found after

twenty iterations of the procedure described in section

4.2.2. The found route in G, as well as the course of

the route through all key viewpoints including the as-

sociated POIs, their normals and the z-orientation of

the key viewpoints can be seen in ﬁgure 2.

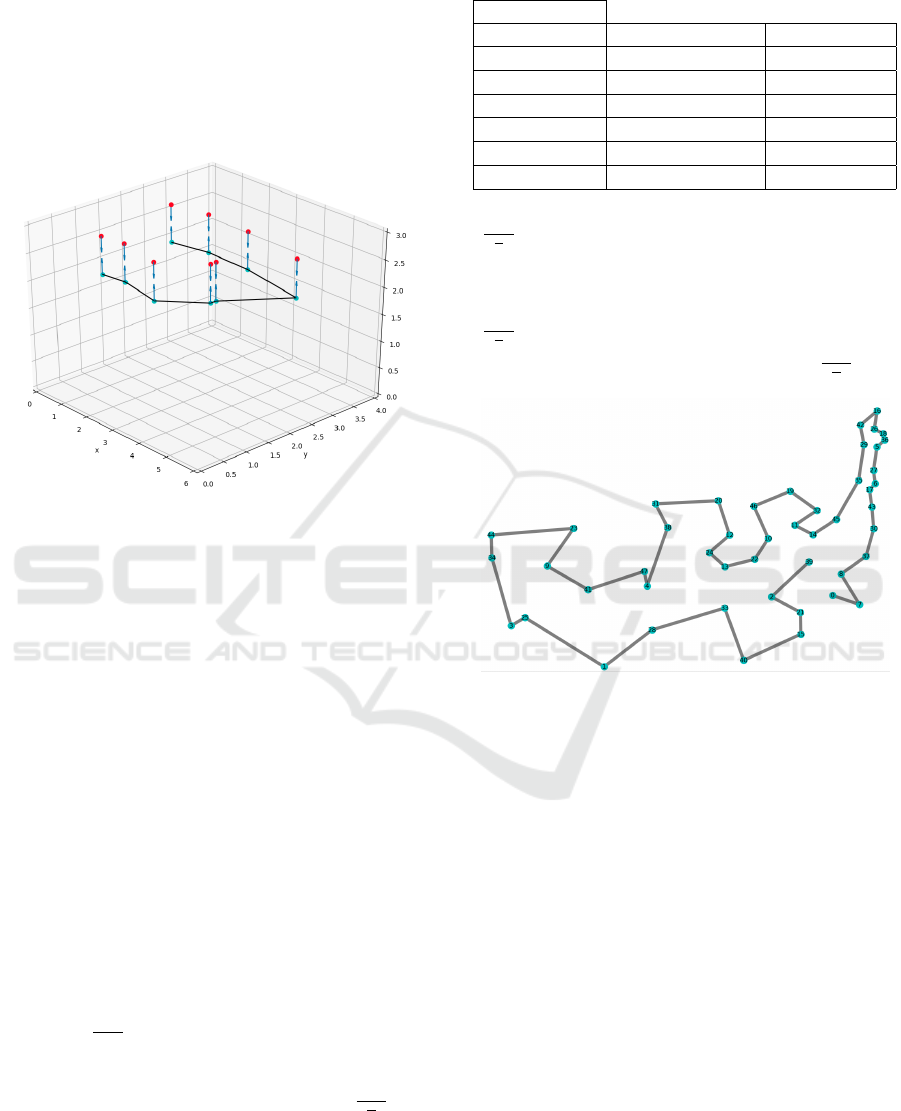
Figure 2: Planned trajectory through all key viewpoints to

their corresponding POIs. The vectors of the POIs corre-

spond to the z-orientation and those of the viewpoints to the

optical axis of the camera.

5.1.1 Evaluation of the ACS Implementation

The implementation of the ACS was evaluated on the

Att48 benchmark dataset. (att, ) Att48 consists of the

distance relationships between 48 cities in the USA.

For the number of ants, as well for the parameters β

and ρ the results of the work of Pettersson et al. (Pet-

tersson and Lundell Johansson, 2018) are used:

β = 5, ρ = 0, 5, m = b0, 3 · Nc (21)

Where m is the number of ants and N is the number

of key viewpoints. The implementation was evaluated

using the Att48 dataset and it was examined which

ratio of ants to iterations yields a good trade-off of

found distance to required computing time. The num-

ber of iterations was calculated based on the num-

ber of ants, which in turn, as in Eq. 21, depends

on the number of key viewpoints. For this purpose,

the value b

2000

c by Pettersson et al. (Pettersson and

Lundell Johansson, 2018) were used and examined to

what extent better results can be achieved by increas-

ing the number of iterations. The values b

2000

c for

i ∈ {2, 3, 4, 5, 6, 7} were tested. With each value, ten

passes were performed. The average result for each

value can be seen in Table 2. The best distance on

the Att48 record of 34023.35 km was achieved with

Table 2: Comparison of the results with different choice of

iterations.

Att48

iterations ∅ lenght [in km] ∅ time [in s.]

2000 / (m / 2) 36483.416 84.262

2000 / (m / 3) 35937.116 124.487

2000 / (m / 4) 36261.336 173.377

2000 / (m / 5) 36031.142 217.897

2000 / (m / 6) 36061.551 247.518

2000 / (m / 7) 35929.504 293.229

2000

c iterations. This result undercuts the result ob-

tained by Chaudhari et al. The course of the best dis-

tance found in this work on the Att48 data set is shown

in ﬁgure Although the best results were obtained with

2000

c iterations, no signiﬁcant better results were ob-

tained by increasing the iterations beyond b

2000

Figure 3: Course of the route for the distance of 34023.35

km.

5.2 Results in Simulation

To check the trajectory in the simulation, the trajec-

tory, consisting of the nine key viewpoints, was trans-

ferred to the ROS node. As can be seen in ﬁgure 4,

the trajectory could be followed through the nine key

viewpoints. Here it can be observed that the move-

ment between the key viewpoints is not always linear.

The exact reason for this is unknown, but it is most

likely due to the local-planner, which requires sev-

eral attempts to get to the viewpoint using Adaptive

Monte Carlo Localization. Another reason could be

the deﬁned speed of the UAV. It was observed that the

higher the speed was deﬁned, the longer it took the

UAV to reach a viewpoint. Since the deceleration be-

havior of the UAV was not deﬁned near a viewpoint,

it is possible that the UAV ﬂies over viewpoints, then

decelerates and tries to reach the viewpoint again.

This procedure may be repeated several times.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

Figure 4: Performed trajectory in the simulation.

6 CONCLUSION AND FUTURE

WORK

Within the scope of this paper the feasibility of ofﬂine

trajectory planning for fully automated visual inspec-

tion of predeﬁned areas on a component was inves-

tigated. It was shown how viewpoints to predeﬁned

parts on the component can be planned and what has

to be considered during the planning. The planning of

viewpoints was examined for the use of UAVs. Fur-

thermore, it was shown how the Ant-Colony-System

can be used to plan a trajectory that contains all key-

viewpoints and can be planned in short time and has

a nearly optimal length. However, a number of mile-

stones still need to be reached before fully automated

visual inspection can be performed by UAVs for large

components:

First of all, the planning of optimal viewpoints

of any orientation of the POIs has to be more inves-

tigated.If the maximum deviation radius allows the

viewpoint to be off the optical axis, it is important

to check how to plan viewpoints that observe multi-

ple POIs simultaneously and shorten the overall tra-

jectory length. Furthermore, it must be possible for

the system to evaluate viewpoints that have already

been found ofﬂine: First of all, it must be checked

whether a viewpoint is located in the area of a static

obstacle on the component, whether the ﬁeld of view

on the POI is blocked by a static obstacle or whether

the viewpoint is otherwise not accessible by the UAV.

Also, light conditions and shading can make it dif-

ﬁcult to inspect a POI. It is therefore necessary to

investigate how to take into account difﬁcult inspec-

tion conditions when planning ofﬂine and how to plan

viewpoints so that difﬁcult conditions can be dealt

with more easily during the inspection.

In section 3.8, a strategy was presented for how

to proceed if a POI cannot be identiﬁed from a view-

point during the inspection. However, this is only one

way to deal with such a situation. It is also possible

to consider procedures that already plan and provide

alternative viewpoints to a POI ofﬂine. Furthermore,

when inspecting predeﬁned areas of the component,

the Coverage Planning must also be considered. This

is necessary if geometrically complex and/or large

POIs on the part are to be inspected and a single view-

point per POI is no longer sufﬁcient.

The existence check examined in this paper is only

one use case for the inspection of predeﬁned areas on

the component. Further use cases, which have to be

investigated in the future, are the relative orientation

of a POI in the component, as well as the attachment

of the POI to the component.

There are also areas of trajectory planning that can

be optimized. As in viewpoint planning, obstacles

must also be taken into account when planning the

trajectory. Therefore it must be possible to check in

the context of trajectory planning whether adjoining

key viewpoints can be reached by a linear trajectory

of the UAV and how the obstacles between adjoining

key viewpoints can be avoided. Another point of opti-

mization is the current view of the trajectory as LINs

between the key viewpoints. Depending on the in-

spection scenario, point-to-point or trajectory control

could also be considered.

The automated visual inspection of large compo-

nents by UAVs is still in its infancy, but it is a nec-

essary step to make visual inspections of components

more precise, easier and more efﬁcient in the future.

REFERENCES

Localization using laser-based slam. last access: 29.03.20.

Mp-testdata - the tsplib symmetric traveling salesman prob-

lem instances. last access: 25.04.20.

Trajectory trough all viewpoints. last access: 29.03.20.

Alarcon-Herrera, J. L., Chen, X., and Zhang, X. (2014).

Viewpoint selection for vision systems in industrial in-

spection. In 2014 IEEE International Conference on

Robotics and Automation (ICRA), pages 4934–4939.

Bircher, A., Alexis, K., Burri, M., Oettershagen, P., Omari,

S., Mantel, T., and Siegwart, R. (2015). Structural in-

spection path planning via iterative viewpoint resam-

pling with application to aerial robotics. In 2015 IEEE

International Conference on Robotics and Automation

(ICRA), pages 6423–6430.

Chaudhari, K. and Thakkar, A. (2019). Travelling salesman

problem: An empirical comparison between aco, pso,

abc, fa and ga. In Shetty, N. R., Patnaik, L. M., Na-

garaj, H. C., Hamsavath, P. N., and Nalini, N., editors,

Emerging Research in Computing, Information, Com-

munication and Applications, pages 397–405, Singa-

pore. Springer Singapore.

Towards Fully Automated Inspection of Large Components with UAVs: Ofﬂine Path Planning

Danner, T. and Kavraki, L. E. (2000). Randomized planning

for short inspection paths. In Proceedings 2000 ICRA.

Millennium Conference. IEEE International Confer-

ence on Robotics and Automation. Symposia Proceed-

ings (Cat. No.00CH37065), volume 2, pages 971–976

vol.2.

Deutsche Bahn AG (2020). Kompetenzcenter Multicopter

DB.

Dorigo, M., Caro, G. A. D., and Gambardella, L. M. (1999).

Ant algorithms for discrete optimization. Artiﬁcial

Life, 5:137–172.

Englot, B. and S. Hover, F. (2014). Sampling-based cov-

erage path planning for inspection of complex struc-

tures. ICAPS 2012 - Proceedings of the 22nd In-

ternational Conference on Automated Planning and

Scheduling.

Galceran, E. and Carreras, M. (2013). A survey on coverage

path planning for robotics. Robotics and Autonomous

Systems, 61:1258–1276.

Gambardella, L. M. and Dorigo, M. (1996). Solving sym-

metric and asymmetric tsps by ant colonies. In Pro-

ceedings of IEEE International Conference on Evolu-

tionary Computation, pages 622–627.

Gonz

alez-Banos, H. (2001). A randomized art-gallery al-

gorithm for sensor placement. Proc. 17th ACM Symp.

Comp. Geom., pages 232–240.

Jordan, S., Moore, J., Hovet, S., Box, J., Perry, J., Kirsche,

K., Lewis, D., and Tse, Z. T. H. (2018). State-of-the-

art technologies for uav inspections. IET Radar, Sonar

Navigation, 12(2):151–164.

Karaman, S. and Frazzoli, E. (2011). Sampling-based algo-

rithms for optimal motion planning. The International

Journal of Robotics Research, 30(7):846–894.

Laporte, G. (1992). The traveling salesman problem: An

overview of exact and approximate algorithms. Euro-

pean Journal of Operational Research, 59:231–247.

LaValle, S. M. (2006). Planning Algorithms. Cambridge

University Press.

Malandrakis, K., Savvaris, A., Domingo, J. A. G., Avde-

lidis, N., Tsilivis, P., Plumacker, F., Fragonara, L. Z.,

and Tsourdos, A. (2018). Inspection of aircraft wing

panels using unmanned aerial vehicles. In 2018

5th IEEE International Workshop on Metrology for

AeroSpace (MetroAeroSpace), pages 56–61.

O’Rourke, J. (1987). Art Gallery Theorems and Algorithms.

Oxford University Press, Inc., New York, NY, USA.

Pettersson, L. and Lundell Johansson, C. (2018). Ant

colony optimization - optimal number of ants.

Stuetzle, T. and Dorigo, M. (1999). Aco algorithms for the

traveling salesman problem.

trevlovett. Python ant colony tsp solver. last access:

10.10.2019.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics