Formal Accuracy Analysis of a Biometric Data Transformation and Its

Application to Secure Template Generation

Shoukat Ali

, Koray Karabina

2,3

and Emrah Karagoz

University of Calgary, Canada

Florida Atlantic University, U.S.A.

National Research Council, Canada

Keywords:

Secure Biometric Templates, Face Recognition, Keystroke Dynamics.

Abstract:

Many of the known secure template constructions transform real-valued feature vectors to integer-valued vec-

tors, and then apply cryptographic transformations. Throughout this two-step transformation, the original

biometric data is distorted, whence it is natural to expect some loss in the accuracy. As a result, the ac-

curacy and security of the whole system should be analyzed carefully. In this paper, we provide a formal

accuracy analysis of a generic and intuitive method to transform real-valued feature vectors to integer-valued

vectors. We carefully parametrize the transformation, and prove some accuracy-preserving properties of the

transformation. Second, we modify a recently proposed noise-tolerant template protection algorithm and com-

bine it with our transformation. As a result, we obtain a secure biometric authentication method that works

with real-valued feature vectors. A key feature of our scheme is that a second factor (e.g., user password, or

public/private key) is not required, and therefore, it offers certain advantages over cancelable biometrics or

homomorphic encryption methods. Finally, we verify our theoretical ﬁndings through implementations over

public face and keystroke dynamics datasets and provide some comparisons.

1 INTRODUCTION

Convenience and fraud prevention requirements in

systems create a growing demand for biometric au-

thentication. A biometric authentication system con-

sists of two phases: enrollment and veriﬁcation. In

the enrollment phase, a user’s biometric sample is

collected via a sensor, and distinctive characteristics

are derived using a feature extraction algorithm. A

digital representation of these characteristics (the fea-

ture vector or the template) is stored in the system

database. In the veriﬁcation phase, a matching algo-

rithm takes a pair of templates as input, and outputs a

score. A decision (accept or reject) is made based on

the matching score. Therefore, biometric templates

should be stored in some protected form to guard

against adversarial attacks. Since 1994 (Bodo, 1994;

Schmidt et al., 1996), there have been tremendous

research and development efforts for creating secure

biometric schemes. In the most general terms, we can

classify biometric template protection methods under

four main categories: biometric cryptosystems (BC)

cancelable biometrics (CB), secure multiparty com-

putation based biometrics (SC), also known as keyed

biometrics (KB), and hybrid biometrics (HB) We re-

fer the reader to (Natgunanathan et al., 2016) for more

details on biometric template protection methods.

In BC and SC (whence in HB), cryptographic

functions and transformations are the main tools to

create secure templates. By construction, the under-

lying cryptographic primitives are deﬁned over some

particular discrete domains, and therefore, feature

vectors are supposed to be some binary, or integer-

valued vectors. For example, the BC- and SC-based

secure ﬁngerprint and iris identiﬁcation algorithms in

(Blanton and Gasti, 2011; Karabina and Canpolat,

2016; Tuyls et al., 2005) assume that feature vec-

tors are represented as ﬁxed length binary vectors,

and the Hamming distance (and some variants of the

Hamming distance) is used as a way of measuring

the similarity between feature vectors. More gener-

ally, a large class of template protection algorithms

assume that feature vectors are integer-valued, and

the similarity scores are calculated based on Ham-

ming distance, set difference distance, or edit dis-

tance; see (Natgunanathan et al., 2016). On the

other hand, biometric data, in general, is represented

through real-valued feature vectors as in the case of

Ali, S., Karabina, K. and Karagoz, E.

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation.

DOI: 10.5220/0009888604850496

In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 485-496

ISBN: 978-989-758-446-6

485

face recognition (Huang et al., 2007; Kanade et al.,

2009; Rathgeb et al., 2014) and keystroke dynamics

(Banerjee and Woodard, 2012; Bours and Barghouthi,

2009; Fairhurst and Da Costa-Abreu, 2011; Killourhy

and Maxion, 2009). Therefore, many of the known

secure template constructions, including the exam-

ples given above, would not be immediately applica-

ble when feature vectors are composed of non-integer,

real numbers.

Contributions and Organization of the Paper.

1. Provable Accuracy. In Section 2, we recall a

generic method to transform real-valued feature

vectors to integer-valued vectors. This method is

derived from a simple and intuitive transforma-

tion. However, the actual challenge is to carefully

parametrize the transformation and rigorously

prove that the method is accuracy-preserving. In

summary, given a (non-cryptographic) biometric

authentication system that takes real-valued vec-

tors as input, our construction yields a new sys-

tem that now takes integer-valued vectors as input.

Our key result Corollary 1 proves that the rates of

the new system can be made arbitrarily close to

the rates of the original system.

2. Accuracy Evaluation. For practical purposes, we

evaluate our theoretical ﬁndings over two publicly

available biometric datasets: the LFW face dataset

(Huang et al., 2007) and the keystroke-dynamics

dataset (Killourhy and Maxion, 2009). Our re-

sults are competetive with previously reported ac-

curacy results derived from the same datasets us-

ing some state-of-the-art biometric recognition al-

gorithms. For more details, please refer to Sec-

tion 3.

3. Cryptographic Implementation. As stated pre-

viously, a major advantage of transforming real-

valued feature vectors to integer-valued vectors

is the ability to cryptographically secure biomet-

ric templates. In order to evaluate the practi-

cal impact of our results, we modify a recently

proposed noise tolerant secure template genera-

tion and comparison algorithm NTT-Sec (Kara-

bina and Canpolat, 2016) and combine it with our

transformation. As a result, we obtain a secure

biometric authentication method that works with

real-valued feature vectors. A key feature of our

scheme is that a second factor (e.g., user pass-

word, or public and private key) is not required,

and therefore, it offers certain advantages over

cancelable biometrics or homomorphic encryp-

tion methods. We verify our theoretical ﬁndings

through implementations over the LFW dataset

(Huang et al., 2007) and the keystrokes-dynamics

dataset (Killourhy and Maxion, 2009). For more

details, please refer to Section 4 and Table 4 for

comparison.

As a result, we expect that our new construction

and its explicit accuracy analysis will enable cryp-

tographic techniques to secure biometrics at a larger

scale.

2 AN ACCURACY-PRESERVING

TRANSFORMATION

Let s be a positive real number called scaling factor.

We deﬁne the following scale-then-round transforma-

tion StR

that maps a real-valued vector of length n to

an integer-valued vector of the same length.

Deﬁnition 1 (The Scale-then-Round transformation

StR

). For a real-valued vector x = (x

,...,x

the map StR

: R

→ Z

is deﬁned as

StR

(x) = (

,...,

)

where

is the nearest integer function.

Now, let d : R

× R

→ R be a distance function that

satisﬁes the homogeneity and translation properties:

for any x,y ∈ R

and u ∈ R, d(ux,uy) = |u|d(x,y)

and d(x,y) = d(x + u, y + u). We have the following

lemma:

Lemma 1. Let the transformation StR

: R

→ Z

and the distance function d be deﬁned as above. Let

x,y ∈ R

be any real-valued vectors and denote their

transformations as the integer valued vectors X =

StR

(x) and Y = StR

(y) in Z

. Then

d(X,Y) − sd(x,y)

≤ 2ε

max

where ε

max

= max

u∈R

d(su,StR

(u)). Equivalently,

sd(x,y) − 2ε

max

≤ d(X,Y ) ≤ sd(x,y) + 2ε

max

and

d(X,Y) − 2ε

max

≤ d(x,y) ≤

d(X,Y) + 2ε

max

Proof. Using the triangular inequality on both

d(sx,sy) and d(X,Y) we have

d(X,Y) ≤ d(X, sx) + d(Y, sy) + d(sx,sy) and

d(sx,sy) ≤ d(X,sx) + d(Y,sy) + d(X,Y ).

Since d(sx,sy) = sd(x, y) and both d(X,sx) and

d(Y, sy) are bounded above by ε

max

, we have the de-

sired results.

Remark 1. Lemma 1 shows that given a pair of vec-

tors x,y ∈ R

, d(X ,Y )/s lies in the neighborhood of

the distance d(x,y) up to an error margin of 2ε

max

/s.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

486

In the next theorem, we observe that if the Minkowski

distance d

(x,y) = (

∑

i=1

− y

)

1/p

is deployed,

then d

(X,Y )/s converges to d

(x,y). This result will

later be used in Theorem 2 where we compare the er-

ror rates of our new system (with integer valued vec-

tors) and the original system (with real valued vec-

tors).

Theorem 1. Let d

be the Minkowski distanced de-

ﬁned on R

× R

, and let X = StR

(x), Y = StR

(y),

as deﬁned before. For a given ε > 0, if a scalar s is

chosen such that s ≥ n

1/p

/ε, then

d(X,Y)/s − d(x,y)

≤ ε ∀x,y ∈ R

Proof. Note that

max

= max

u∈R

(su,StR

(u)) (1)

≤

∑

i=1

(1/2)

1/p

where the last inequality follows because |su

−

| ≤ 1/2 for all i. Now, for a given ε >

0, choose s such that s ≥ n

1/p

/ε. This implies

1/p

/s ≤ ε, and it follows from Lemma 1 and (1) that

d(X,Y)/s − d(x,y)

≤ 2ε

max

/s ≤ n

1/p

/s ≤ ε, as re-

quired.

Next, we provide some theoretical estimates on the

new system’s False Accept Rate (FAR) and False Re-

ject Rate (FRR) as a function of the original system’s

error rates. Let GenP and ImpP denote the list of

genuine pairs and the list of impostor pairs, respec-

tively. Corresponding to these lists, let GenP

and

ImpP

denote the lists of transformed version of GenP

and ImpP respectively, deﬁned as

GenP

= {(StR

(x),StR

(y)) : (x,y) ∈ GenP}

ImpP

= {(StR

(x),StR

(y)) : (x,y) ∈ ImpP}

Thus, #GenP = #GenP

and #ImpP = #ImpP

where

the symbol # represents the number of pairs. Note

that all of them are lists, not sets. Therefore it is

possible to see identical pairs, especially in the lists

GenP

and ImpP

because there may be several identi-

cal pairs which are the transformation of different pair

of vectors, i.e. there may exists (x

),(x

) such

that (x

) 6= (x

) but (StR

),StR

)) =

(StR

),StR

)).

For a distance function d on R

and t ∈ R

, the

FAR (t) and FRR (t) are deﬁned as follows:

FAR (t) =

#{(x,y) ∈ ImpP : d(x, y) ≤ t}

#ImpP

FRR(t) =

#{(x,y) ∈ GenP : d(x, y) > t}

#GenP

Now we can deﬁne the corresponding rates for T ∈

FAR

(T ) =

#{(X,Y ) ∈ ImpP

: d(X,Y ) ≤ T }

#ImpP

FRR

(T ) =

#{(X,Y ) ∈ GenP : d(X,Y) > T }

#GenP

We have the following lemma:

Lemma 2. Let s be the scaling factor in transfor-

mation StR

and deﬁne ε

max

= max

u∈R

d(su,StR

(u)).

Then FAR



t −

2ε

max



≤ FAR

(st) ≤ FAR



t +

2ε

max



FRR



t +

2ε

max



≤ FRR

(st) ≤ FRR



t −

2ε

max



Proof. For the ﬁrst inequality, deﬁne (X,Y ) =

(StR

(x),StR

(y)) for an impostor pair (x, y) in the

list ImpP. Then by using the inequalities in Lemma

1, we have

d(x,y) ≤ t −

2ε

max

=⇒ d(X,Y ) ≤ s



t −

2ε

max



+ 2ε

max

= st

=⇒ d(x,y) ≤

st + 2ε

max

= t +

2ε

max

These inequalities mean that

• Any impostor pair (x,y) having distance less than

or equal to t −

2ε

max

, which is already counted in

the rate FAR



t −

2ε

max



, has its transformed pair

(X,Y ) with a distance less than or equal to st.

Therefore, this transformed pair (X,Y ) is needed

to be counted in the rate FAR

(st). Thus,

FAR



t −

2ε

max



≤ FAR

(st).

• Any pair (X,Y ) in the list ImpP

having distance

less than or equal to st, which is already counted

in the rate FAR

(st), has its pre-transformed im-

postor pair (x,y) in the list ImpP with a distance

less than or equal to t +

2ε

max

. Therefore, this im-

poster pair (x,y) is needed to be counted in the

rate FAR



t +

2ε

max



. Thus,

FAR

(st) ≤ FAR



t +

2ε

max



For the second inequality, now let (X,Y ) denote the

transformation (StR

(x),StR

(y)) for a genuine pair

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation

487

(x,y) in the list GenP. Then by using the inequalities

in Lemma 1, we have

d(x,y) > t +

2ε

max

=⇒ d(X,Y ) > s



t +

2ε

max



− 2ε

max

= st

=⇒ d(x,y) >

st − 2ε

max

= t −

2ε

max

These inequalities mean that

• Any genuine pair (x,y) in the list GenP having

distance greater than t +

2ε

max

, which is already

counted in the rate FRR



t +

2ε

max



, has its trans-

formed pair (X,Y ) with a distance greater than st.

Therefore, this transformed pair (X,Y ) is needed

to be counted in the rate FRR

(st). Thus,

FRR



t +

2ε

max



≤ FRR

(st).

• Any pair (X ,Y ) in the list GenP

having distance

greater than st, which is already counted in the

rate FRR

(st), has a pre-transformed genuine pair

(x,y) in the list GenP with a distance greater than

t −

2ε

max

. Therefore, this genuine pair (x, y) is

needed to be counted in the rate FRR



t −

2ε

max



Thus,

FRR

(st) ≤ FRR



t −

2ε

max



Theorem 2. Let d

be the Minkowski distance deﬁned

on R

×R

, and let X = StR

(x), Y = StR

(y), as de-

ﬁned before. For a given ε > 0, if a scalar s is chosen

such that s ≥ n

1/p

/ε, then

FAR (t − ε) ≤ FAR

(st) ≤ FAR (t + ε), and

FRR(t + ε) ≤ FRR

(st) ≤ FRR (t − ε) .

Proof. Let ε > 0 be given and choose s such that

s ≥ n

1/p

/ε. We already observed in the proof of Theo-

rem 1 that 2ε

max

/s ≤ n

1/p

/s ≤ ε. Using this inequality

together with the inequality

FAR

(st) ≤ FAR



t +

2ε

max



from Lemma 2, and the fact that FAR(t

) ≥ FAR (t

)

for t

≥ t

, we obtain

FAR

(st) ≤ FAR



t +

2ε

max



≤ FAR(t + ε).

This proves one of the four inequalities in the state-

ment, and the other three inequalities can be proved

similarly.

Corollary 1. For any given

ε > 0, there exists T ≥

0 ∈ R such that

FAR (t) −

ε ≤ FAR

(T ) ≤ FAR(t) +

ε, and (2)

FRR(t) −

ε ≤ FRR

(T ) ≤ FRR (t)+

ε (3)

Proof. Given

ε > 0 as in the statement of the corol-

lary, one can choose ε > 0 such that

FAR (t + ε) ≤ FAR(t)+

ε,

FAR (t) −

ε ≤ FAR(t − ε),

FRR(t − ε) ≤ FRR(t) +

ε,

FRR(t) −

ε ≤ FRR (t + ε),

because FAR(t) and FRR (t) can be modelled as a

continuously increasing and decreasing function pa-

rameterized by t, respectively. Now, choosing s as

suggested by Theorem 2, and combining the inequal-

ities of Theorem 2 with the inequalities above, we can

write

FAR (t) −

ε ≤ FAR(t − ε) ≤ FAR

(st)

≤ FAR(t + ε) ≤ FAR(t) +

ε, and

FRR(t) −

ε ≤ FAR(t + ε) ≤ FRR

(st)

≤ FRR (t − ε) ≤ FRR(t) +

ε.

Finally, setting T = st, we conclude

FAR (t) −

ε ≤ FAR

(T ) ≤ FAR(t) +

ε, and (4)

FRR(t) −

ε ≤ FRR

(T ) ≤ FRR (t)+

ε (5)

Remark 2. Given a biometric authentication system

that takes real-valued feature vectors as input, de-

ploys Minkowski distance d

in its matching algo-

rithm, and runs at false accept rate FAR (t) and false

reject rate FRR(t), Theorem 2 and its Corollary 1 as-

sure the existence of a scalar s (and T = st) that can

be used to transform the system to integer-valued vec-

tors, deploys the same d

in its matching algorithm,

and runs at false accept rate FAR

(T ) and false reject

rate FRR

(T ) that are arbitrarily close to FAR(t) and

FRR(t) of the original system.

Remark 3. Smaller values of s would be preferred in

cryptographic secure template generation algorithms

due to the smaller size of the resulting feature vec-

tors and the smaller threshold values. However, it

seems challenging to ﬁnd a tight lower bound for s

in Theorem 2, one can address this gap between the-

ory and practice as we explain in the following re-

mark. One should also be careful to choose s sufﬁ-

ciently large to prevent dictionary attacks. Therefore,

in the light of Theorem 2, we outline a procedure in

Algorithm 1 to determine a suitable scalar s

and a

threshold T

from a given original system. We assume

SECRYPT 2020 - 17th International Conference on Security and Cryptography

488

Algorithm 1: To determine suitable parameters s and T .

Input: t

,n, p,

ε,I

FAR

FRR

,DS,MinScalar

Output: s

≥ MinScalar and T

such that FAR

) ∈

FAR

and FRR

) ∈ I

FRR

1: Set a and b as the corresponding thresholds of



FAR (t

) −



and



FRR(t

) +



, respectively

2: t

← Max



a,b



3: Set c and d as the corresponding thresholds of



FAR (t

) +



and



FRR(t

) −



, respectively

4: t

← Min



c,d



5: ε ← Min



−t

),(t

−t

)



6: s

← bn

1/p

/εe

7: while s

> MinScalar and



FAR

((s

− 1)t

) ∈

FAR

and FRR

((s

− 1)t

) ∈ I

FRR

over DS



8: s

← s

− 1

9: end while

that the original system deploys the distance function

(x,y) = (

∑

− y

)

1/p

, and has some some de-

sired rates FAR(t

), FRR(t

), where FAR (t), FRR (t)

are measured over some dataset DS. For example,

one may ﬁx t

so that the system runs at the equal er-

ror rate EER = FAR(t

) = FRR (t

). Our procedure

outputs a value of s

≥ MinScalar and a threshold

value T

for which the new system’s accuracy is in a

close neighborhood of the original system’s accuracy.

More particularly, new parameters will assure that

FAR

) ∈ I

FAR

= [FAR(t

) −

ε,FAR (t

) +

ε] and

FRR

) ∈ I

FRR

= [FRR(t

) −

ε,FRR(t

) +

ε] for a

given

ε > 0, where d

(X,Y ) is used to compute the

distance between integer-valued vectors X = StR

(x)

and Y = StR

(y). In practice,

ε should be chosen so

that the new rates FAR

) and FRR

) are close

to FAR(t

) and FRR (t

), respectively. The correct-

ness of Algorithm 1 follows from Theorem 2.

3 APPLICATIONS OF THE NEW

TRANSFORMATION

In this section, we evaluate our theoretical ﬁndings

over two publicly available biometric datasets: the

LFW dataset (Huang et al., 2007) for face recogni-

tion, and the keystrokes-dynamics dataset (Killourhy

and Maxion, 2009). Our reasoning for choosing these

datasets is that they are widely referenced in the lit-

erature, and the biometric features in both of these

datasets are represented as real-valued vectors. As

an application of our construction, we propose some

concrete system parameters to convert these feature

vectors into integer-valued vectors, and verify its ac-

curacy preserving property.

3.1 Labeled Faces in the Wild

We use one of the most popular public face datasets

that was presented by Gary B. Huang et. al. (Huang

et al., 2007) and named “Labeled Faces in the Wild”

(LFW). The dataset comprises more than 13,000 face

images of 5,749 people collected from the web and

1,680 of them have two or more images. Among the

four different available versions of the datasets, we

use the original version of the LFW in our experiment.

In our implementation, we have used the face

recognition (Python) module of Adam Geitgey (Geit-

gey, 2017) which he built using the face recognition

model in the Dlib library of Davis E. King (King,

2011) where the model was trained on a dataset of

about 3 million face images (King, 2017). The His-

togram of Oriented Gradients (HOG) and the Convo-

lutional Neural Network (CNN) are the two methods

that we used for face detection in our experiment. The

HOG is faster than the CNN method but less accu-

rate in detecting faces from the images. For example,

we found that CNN only failed to detect the face in

Jeff Feldman 0001.jpg while the HOG failed to de-

tect faces in 57 images in the LFW. Therefore, we uti-

lize CNN detector in our experiments and report the

results that we found.

In the pre-trained model of Davis E. King, the

Euclidean Distance (ED) is measured between two

128-dimensional facial vectors. If the distance is less

than or equal to 0.6, then two images are considered

a match otherwise, it is a mis-match. The match and

mis-match are returned as “True” and “False”, respec-

tively, by Adam Geitgey in his face recognition mod-

ule. In other words, False implies correct identiﬁca-

tion of impostors in the set of ImpP. Here, the accu-

racy is measured as follows

Accuracy =

#True in GenP + #False in ImpP

#GenP + #ImpP

(6)

#GenP × (1 − FRR) + #ImpP × (1 − FAR)

#GenP + #ImpP

Each image in the dataset is labelled with a person’s

name and contains that person’s face image. In addi-

tion, some images contain faces of people other than

the person in the label. In our experiments, we as-

sume that the ﬁrst detected face is the face of the

labelled person. Under this assumption, for GenP,

we ﬁnd #True and #False as 231,752 and 10,505,

respectively. On the other hand, for ImpP, we ﬁnd

#True and #False as 515, 817 and 86,778,222, respec-

tively. So the sizes of GenP and ImpP are 242,257

and 87,294,039, respectively. Hence, our evaluation

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation

489

yields 99.40% accuracy using the CNN method and

threshold t = 0.6 with ED; see Table 1. Note that our

accuracy evaluation conﬁrms the results reported by

Davis E. King and Adam Geitgey (King, 2017; Geit-

gey, 2017), and also it is comparable to other state-of-

the-art models; see (Huang et al., 2007) for an exten-

sive list of results and comparisons.

3.1.1 Transforming LFW Feature Vectors

As mentioned before, a (detected) face in the image

is represented by a 128-dimensional real-valued vec-

tor, and the accuracy evaluations are performed us-

ing the ED function. In this section, we apply our

proposed transformation to obtain 128-dimensional

integer-valued feature vectors. We further replace the

ED by the Manhattan distance (MD) function. This

latter modiﬁcation allows us to simplify the quadratic

distance formula to a linear one, which eventually

yields better efﬁciency in crpytographic computations

for secure template comparison.

In our analysis, we focus on three critical thresh-

old values t = 0.54, t = 0.6, and t = 0.66 as shown in

Table 1. These three thresholds capture FAR values

near 0.001, FAR values near 0.005, and the equal

error rate FAR = FRR ≈ 0.03; with respect to the use

of the ED function. The threshold t = 0.6 provides a

basis for comparing our results to previously reported

results in (King, 2017; Geitgey, 2017). We should

ﬁrst emphasize that switching from the ED to MD has

almost negligible impact on FAR and FRR as shown

in the ﬁrst two rows of Table 1. The critical part is

Table 1: ED = Euclidean Distance, MD = Manhattan Dis-

tance, MD

100

, MD

1376

= MD where the feature vector com-

ponents are scaled-then-rounded by integer 100 and 1376,

respectively.

Method FAR ≈ 0.001 FAR ≈ 0.005 EER

t = 0.54 t = 0.6 t = 0.66

FRR = 0.091159 FRR = 0.043363 FRR = 0.033427

FAR = 0.000897 FAR = 0.005909 FAR = 0.033630

Accuracy = 0.9989 Accuracy 0.99399 Accuracy = 0.96637

t = 4.846 t = 5.393 t = 5.941

FRR = 0.100096 FRR = 0.044989 FRR = 0.03358

FAR = 0.00087 FAR = 0.005896 FAR = 0.03365

Accuracy = 0.99885 Accuracy = 0.993995 Accuracy = 0.96635

100

t = 485 t = 539 t = 594

FRR = 0.099105 FRR = 0.04497 FRR = 0.033617

FAR = 0.00091 FAR = 0.006007 FAR = 0.03428

Accuracy = 0.99882 Accuracy = 0.993886 Accuracy = 0.965718

1376

t = 6668 t = 7421 t = 8175

FRR = 0.100088 FRR = 0.044973 FRR = 0.033555

FAR = 0.000873 FAR = 0.005908 FAR = 0.033702

Accuracy = 0.99885 Accuracy = 0.99398 Accuracy = 0.966299

to determine a suitable scalar s using Algorithm 1 so

as to preserve the accuracy after the StR

transforma-

tion. We explain the process in detail for t

= 5.941

(i.e. FAR(t

) = 0.03365 and FRR (t

) = 0.03358)

over the dataset DS = LFW. First, we choose

ε = 0.01 so that the new system’s error rates

would satisfy FAR

) ∈ I

FAR

= [FAR(5.941) −

ε,FAR (5.941) +

ε] = [0.02365,0.04365], and

FRR

) ∈ I

FRR

= [FRR(5.941) −

ε,FRR(5.941) +

ε] = [0.02358, 0.04358].

Following the steps 1 to 4 in Algorithm 1,

we ﬁnd the smallest ε = 0.093 such that

[FAR (5.941 − ε) , FAR(5.941 + ε)] ⊆ I

FAR

, and

[FRR(5.941 + ε),FRR(5.941 − ε)] ⊆ I

FRR

. The step

5 in Algorithm 1 initializes s

as shown below. Note

that p = 1 in the MD function.

= bn

1/p

/εe = b128/0.093e = 1376.

Next, we need to choose a suitable value for

MinScalar. For this, we compute the average fea-

ture vector a = [a

,...,a

128

] over all 13233 fea-

ture vectors in the LFW dataset, where a

is the

average of the absolute values of the i’th com-

ponents of the feature vectors. We ﬁnd that

min(a) = min({a

}) = 0.035,max(a) = max({a

}) =

0.37, with an average of Mean(a) =

∑

/128 =

0.098. We choose s = MinScalar = 100, and obtain

min(StR

(a)) = 4,max(StR

(a)) = 37, with an aver-

age of Mean(StR

(a)) = 10. This ensures that creat-

ing a dictionary for the set of transformed feature vec-

tors is an infeasible task for an attacker because 10

128

feature vectors are expected on average. Finally, the

Algorithm 1 returns

= 100 and T

= bs

e = 594,

and the new system’s rates become FAR

(594) =

0.03428 and FRR

(594) = 0.033617, which are ex-

tremely close to the original system’s rates. Please

see the results in the last two rows of Table 1 for

the new system derived from the original system with

the threshold values of t

= 4.846, t

= 5.393, and

= 5.941. As expected, the new system’s rates are

close to the original system’s rates.

In Figure 1, we show the Receiver Operating

Characteristic (ROC) curve and the Area Under Curve

(AUC) for ED, MD, MD

100

and MD

1376

. In all the

following ﬁgures, the False Positive Rate and True

Positive Rate represent FRR and (1 − FAR), respec-

tively. The curves in Figure 1a depict that the dif-

ferences among the used techniques are very small

which is further supported by AUC. It shows that the

AUC of ED and MD are 0.98604 and 0.98601, re-

spectively. In other words, the area differ by 0.00003

only. Furthermore, we ﬁnd the AUC of MD

100

and MD

1376

as 0.98595 and 0.98602, respectively.

Clearly, MD

1376

is a better choice than MD

100

terms of accuracy. However, note that the loss of

0.00006 in accuracy, if MD

100

is used, is actually very

small, and it may be tolerable in practice given the ef-

ﬁciency gains in choosing smaller scalars. The ROC

SECRYPT 2020 - 17th International Conference on Security and Cryptography

490

(a) Normal ROC. (b) Zoomed in near EER.

Figure 1: ROC curve and the area underneath called Area under curve (AUC).

curves differences among our used techniques near

the EER neighborhood are shown in Figure 1b, which

conﬁrm that relative differences are not signiﬁcant.

3.2 Keystroke-dynamics

The public keystroke-dynamics dataset of Killourhy

and Maxion (Killourhy and Maxion, 2009) contains

the keystroke-timing of 51 subjects typing the same

password in 8 different sessions where each session

consists of 50-repetition and only one session per day

was performed. From each (password) typing event,

31 timing features were extracted. The authors imple-

mented 14 anomaly-detection algorithms using the R

statistical programming language. The performance

of each detector was measured by generating an re-

ceiver operating characteristic (ROC) curve using the

anomaly scores. The authors have reported 0.153 as

the average equal error rate (EER) using MD func-

tion. Note that the subject identiﬁers are not in the

range of s001 to s051 and for further details please

see (Killourhy and Maxion, 2009).

Using the MD, we compute the error rates and se-

lect the two subjects that exhibit minimum and maxi-

mum equal error rate (EER). Actually, these two sub-

jects are tantamount to the best- and worst-case which

we believe are the best candidates to show the impact

of our transformation. If the two extreme error rates

satisfy the conditions, then do all the other values be-

cause they lie in the range of the two extremes. Using

the Python programming language, we ﬁnd the aver-

age EER to be 0.153, that matches the rate as reported

in (Killourhy and Maxion, 2009).

3.2.1 Transforming Keystroke Feature Vectors

After computing the error rates for each of the

51-subject, our implementation results show that

subjects s055 and s049 have minimum and maximum

EER, respectively. In Table 2, the error rates of

both s055 and s049 are provided at EER threshold

points. In this context the length of the feature

vector is 31. We ﬁnd t

= 1.509 and t

= 6.718

as the EER threshold for s055 and s049, respec-

tively. Using the FRR and FAR values at EER

threshold, for s055, we choose

ε = 0.005 such that

FAR

) ∈ I

FAR

= [FAR (1.509) −

ε,FAR (1.509) +

ε] = [0.007,0.017], and FRR

) ∈ I

FRR

[FRR(1.509) −

ε,FRR(1.509) +

ε] = [0.005,0.015].

Similarly, for s049, we choose

ε = 0.02 such that

FAR

) ∈ I

FAR

= [FAR (6.718) −

ε,FAR (6.718) +

ε] = [0.46,0.50], and FRR

) ∈ I

FRR

[FRR(6.718) −

ε,FRR(6.718) +

ε] = [0.46, 0.50].

Following the steps 1 to 4 in Algorithm 1, we

ﬁnd the smallest ε = 0.061 and ε = 0.032 for s055

and s049, respectively, such that FAR

and FRR

lie

in the range of the error rates of the corresponding

subjects. The step 5 in Algorithm 1 initializes the

corresponding s

for s055 and s049 as b31/0.061e =

508, and b31/0.032e = 969, respectively.

Next, we need to choose a suitable value for

MinScalar. For this, we compute the average fea-

ture vector a = [a

,...,a

] over all 400 feature vectors

of each subject, where a

is the average of the abso-

lute values of the i’th component of the feature vec-

tors. For s055, we ﬁnd min(a) = 0.0184, max(a) =

0.2344 and Mean(a) =

∑

/31 = 0.0964. We choose

s = MinScalar = 100, and obtain min(StR

(a)) = 2,

max(StR

(a)) = 23 and Mean(StR

(a)) = 10. This

ensures that creating a dictionary for the set of trans-

formed feature vectors is an infeasible task for an at-

tacker because 10

≈ 2

feature vectors are expected

on average. Finally, the Algorithm 1 returns

= 100 and T

= bs

e = 151.

On the other hand, we ﬁnd the new system’s rates

become FAR

(151) = 0.012 and FRR

(151) = 0.010

that are the same as the original system’s EER. Please

see the two-column MD

in Table 2 for a complete

list of parameters for the new system (integer-valued)

derived from the original system (real-valued). As ex-

pected, the new system’s rates are close to the origi-

nal system’s rates. Similarly, we perform the same

operations for s049 and the results are provided in

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation

491

(a) ROC curve for s055 and s049. (b) Variation near EER. (c) Variation near EER.

Figure 2: ROC curve, AUC and the curve variation near EER for s055 and s049.

Table 2: The FRR and FAR values for the subjects s055 and

s049 by computing the MD using both real- and integer-

valued feature vectors and using the EER threshold as point

of reference.

Method

MD MD

EER

s055

s = 100 s = 500

t = 1.510 t = 151 t = 755

FRR = 0.010 FRR

= 0.010 FRR

= 0.010

FAR = 0.012 FAR

= 0.012 FAR

= 0.012

s049

s = 100 s = 969

t = 6.718 t = 672 t = 6510

FRR = 0.480 FRR

= 0.470 FRR

= 0.480

FAR = 0.480 FAR

= 0.464 FAR

= 0.480

Table 2. Note that the use of smallest scalar s does

not necessarily yield EER threshold in the new sys-

tem and the result of s049 depicts such a scenario for

s = 100. But if one is interested in EER, then any

scalar greater than the smallest scalar can be used and

Algorithm 1 guarantees that those scalars satisfy the

error rates range.

Like the LFW dataset, we provide the ROC curve

and AUC for keystroke in Figure 2. Both the ROC

curve and AUC of s055 are much better than s049

as shown in Figure 2a and we ﬁnd the AUC of s055

and s049 as 0.99894 and 0.55172, respectively. It is

evident that all the other subjects’ curves and AUCs

lie between the two curves in Figure 2a. In order to

show the effects of our choice of scalars, we provide

the ROC curves near the EER of s055 and s049 in

Figure 2b and Figure 2c, respectively. In case of s055,

we have the AUC value of 0.99897 and 0.99892 by

using s = 100 and s = 500, respectively. Similarly, we

ﬁnd the AUC value of 0.55455 and 0.55156 by using

s = 100 and s = 969, respectively. The AUC values of

s = 100 are greater than s = 500 and s = 969 for both

s055 and s049. As expected, larger scalars preserve

the accuracy of the original system better, however,

the loss in accuracy is not signiﬁcant when smaller

scalars are used as shown in Figure 2b and Figure 2c.

4 A CASE ANALYSIS

We have so far proposed and analyzed a method for

transforming biometric authentication systems based

on real-valued feature vectors into biometric au-

thentication systems based on integer-valued feature

vectors. This allows real-valued feature vectors to

be used as input to some cryptographic algorithms,

whence to enhance the security of the matching al-

gorithms while preserving the accuracy rates of the

original (non-cryptographic) systems. Our proposed

biometric authentication system (Enrollment and Ver-

iﬁcation Phase) is shown in Figure 3. In the following

sections, we make our ideas more concrete by imple-

menting a previously proposed algorithm NTT-Sec

(Karabina and Canpolat, 2016) over the face (Huang

et al., 2007) and keystroke-dynamics (Killourhy and

Maxion, 2009) datasets. We choose NTT-Sec in our

implementation because a second factor (e.g. user

password, or public/private key) is not required in

the system, and therefore it offers certain advantages

over cancelable biometrics or homomorphic encryp-

tion methods. NTT-Sec also seems to be more ad-

vantageous than some of the known biometric cryp-

tosystems (e.g. fuzzy extractors) because it is highly

non-linear, which yields some built-in security against

distinguisahbility and reversibility attacks. For more

details about the technical details on NTT-Sec and its

security analysis, we refer the reader to (Karabina and

Canpolat, 2016).

4.1 Modifying NTT-Sec to NTT-Sec-R

NTT-Sec was originaly proposed to work with bi-

nary feature vectors. On the other hand, the face

and keystroke-dynamics datasets (Huang et al., 2007;

Killourhy and Maxion, 2009), consists of real-valued

feature vectors. Therefore, we ﬁrst need to modify

NTT-Sec to NTT-Sec-R so it can handle real-valued

vectors.

The original NTT-Sec is based on two algorithms

called Proj (project) and Decomp (decompose). The

Proj algorithm maps (projects) a length n binary vec-

SECRYPT 2020 - 17th International Conference on Security and Cryptography

492

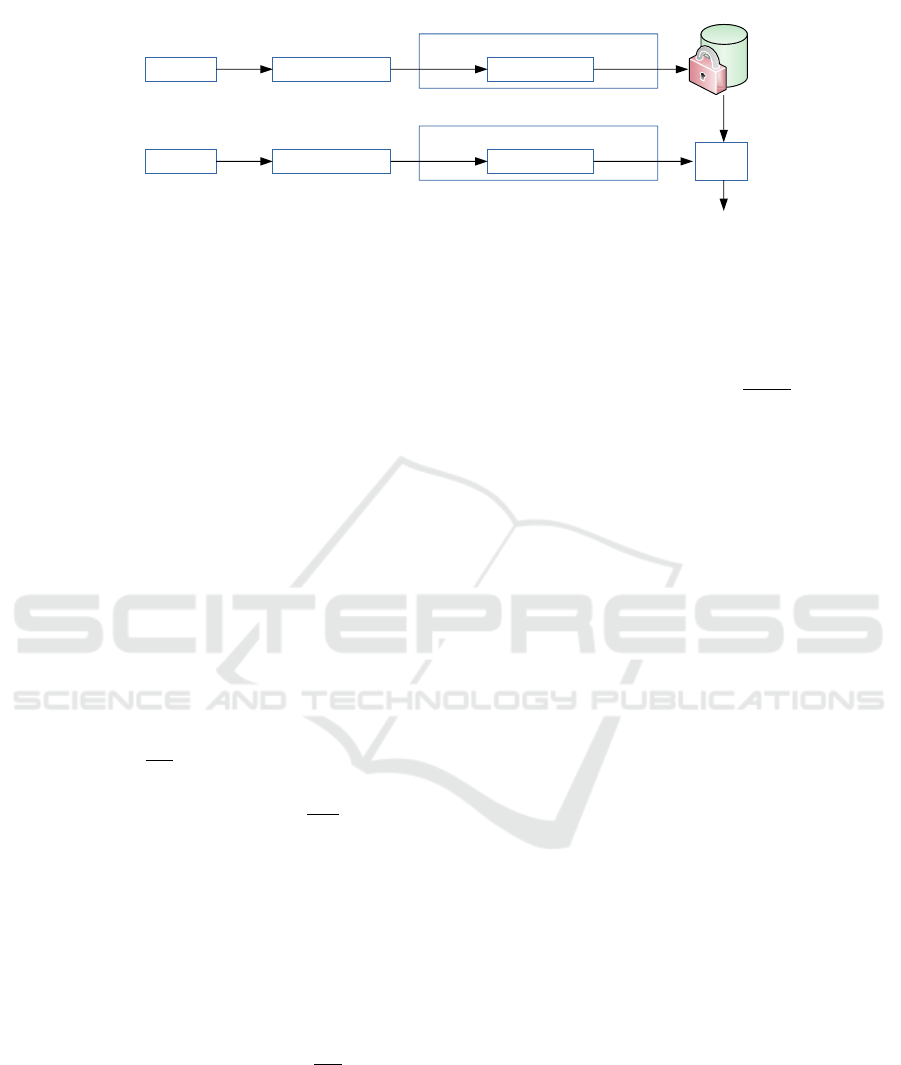
Biometric Trait

Feature Extraction

(real-valued vector)

Integer-valued vector

Ntt-Sec-R

Enrollment Phase

StR

Transformation

Cryptographic

Algorithm

Biometric Trait

Feature Extraction

(real-valued vector)

Integer-valued vector

Ntt-Sec-R

StR

Transformation

Cryptographic

Algorithm

Matching

Algorithm

Match/Mismatch

Verification Phase

Figure 3: Block Diagram of the proposed system.

tor (considered as the feature vector) to a ﬁnite ﬁeld

element (considered as its secure template) using a

priori-ﬁxed set of public parameters and a factor ba-

sis. Given a pair of secure templates, the Decomp

algorithm can detect whether the templates originate

from a pair of binary feature vectors that differ in

at most t indices for some priori-ﬁxed error thresh-

old value t. In Decomp, the detection is achieved

by checking whether a particular ﬁnite ﬁeld element

can be written (decomposed) as a product of the fac-

tor basis elements in a certain form. Computations in

NTT-Sec are performed in a cyclotomic subgroup G

of the multiplicative group of a ﬁnite ﬁeld. We adapt

the same group structure in our modiﬁcation. More

speciﬁcally, let F

be a ﬁnite ﬁeld with q elements

where q = p

. Let c ∈ F

be a non-quadratic residue

with minimal polynomial of degree m over F

. Let

= F

(σ) be a degree two extension of F

where

σ is a root of x

− c. F

has a cyclotomic subgroup

G of order q and every non-identity element in G can

be represented as

a+σ

a−σ

for some a ∈ F

. Moreover, we

say an element a ∈ G is k-decomposable over F

if it

can be written as a product a =

∏

i=1



+σ

−σ



for some

-elements a

,...a

Modiﬁcations. Now, assume that n and t are some

ﬁxed values that represent the length of feature vec-

tors and the system threshold value, respectively. We

choose a scaling factor s (to be used in StR

transfor-

mation) and let T =

be the new threshold value.

As in NTT-Sec, we choose a prime number p such

that p > 2n, an integer m such that m ≥ T , a set

B = {g

,...,g

} such that 1 ≤ g

≤

p−1

for each i.

We further choose m to be prime in order to avoid any

potential attacks exploiting subﬁelds. We deﬁne new

functions NTT-Hash-R and NTT-Match-R as a re-

placement of the original Proj and Decomp functions

in NTT-Sec.

The algorithm NTT-Hash-R maps (or hashes) a

given real-valued feature vector x = (x

,...,x

) to

a group element in G as follows: It ﬁrst computes X =

,...,X

) = StR

(x) using the StR

transformation.

Then using the basis B = {g

,...,g

}, it computes

the hash value

NTT-Hash-R(x) =

∏

i=1



+ σ

− σ



We note that the output of NTT-Hash-R serves as the

secure template for x. The main difference between

the modiﬁed NTT-Hash-R and the original Proj is

that NTT-Hash-R can handle real-valued vectors.

The algorithm NTT-Match-R works very sim-

ilar to Decomp. Assume a hash value h

NTT-Hash-R(x) for some x = (x

,...,x

), a real-

valued vector y = (y

,...,y

), and a positive real num-

ber t are given. The goal of NTT-Match-R is to

decide whether

∑

i=1

− y

| ≤ t or not. To achieve

this goal, the following process is performed: It com-

putes h

= NTT-Hash-R(y) using NTT-Hash-R, and

then it decides whether the G-element h/h

decomposable. Furthermore, if the retreived F

elements belong to the basis B, NTT-Match-R re-

turns Match, otherwise Mismatch.

We pack all of these parameters under the set

SP = {n,t,s, p, m, B}, and call this as the system

parameter set. Note that SP can be made pub-

lic, and commonly used in the NTT-Hash-R and

NTT-Match-R algorithms.

4.2 Implementation Results, Security

Analysis, and Comparisons

First, we discuss the implementation details of the

NTT-Sec-R algorithm over the LFW dataset (Huang

et al., 2007) and the keystroke-dynamics dataset (Kil-

lourhy and Maxion, 2009). For the LFW dataset, we

align our parameter set with the parameters from Ta-

ble 1. We set n = 128, t = 5.941, and s = 100. Then,

we set p = 257 (smallest prime p ≥ 2n) and m = 599

(smallest prime m ≥ T =

= 594). The param-

eters for the keystroke-dynamics datasets are chosen

similarly, and they are same as in Table 2; see Ta-

ble 3 for a complete list of the parameters. In Ta-

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation

493

Table 3: The systems parameters (SP), secure template

bit size, and timing results in millisecond (ms) using

the NTT-Sec-R algorithm on face and keystroke public

datasets.

Template size (Bit)

Time (ms)

n t s p m Hash Match

Face 128 5.941 100 257 599 5391 68.17 309.07

Keystroke

s055 31 1.510 100 67 157 1099 3.68 9.21

s049 31 6.718 100 67 673 4711 21.65 322.63

ble 3, we also report on the bit size of secure biomet-

ric template. Recall that a secure template (the out-

put of NTT-Hash-R) is represented as an F

element

with m × (blog

pc + 1) bits. Hashing (secure tem-

plate generation) and matching times are also reported

in Table 3. We conﬁrm that NTT-Sec-R does not

alter the accuracy-preserving properties of our con-

struction and our experimental results conﬁrm that the

FRR and FAR values of the NTT-Sec-R algorithm are

same as that of the MD when integer-valued feature

vectors are used. All the codes are written in C pro-

gramming language. The results are obtained on an

Intel Core i7 − 7700 CPU @ 3.60GHz desktop com-

puter that is running Ubuntu 16.04 LTS. The timings

are based on a high level implementation of the al-

gorithms and only the GCC compiler is utilized for

optimization using the argument -O3.

A Security Analysis. The security of NTT-Sec-R

should be discussed with respect to the irreversibility

and indistinguishability notions as deﬁned in (Kara-

bina and Canpolat, 2016). They are formally mod-

elled between a challenger and a computationally

bounded adversary. For irreversibility, several at-

tacks have been considered in (Karabina and Canpo-

lat, 2016), including guessing attack, brute force at-

tack, and discrete logarithm attack. It was also ar-

gued in (Karabina and Canpolat, 2016) that reversing

the templates is the best strategy for an adversary in

a distingushing attack. Following the security analy-

sis in (Karabina and Canpolat, 2016), we inspect that

the best strategy for an adversary to attack our mod-

iﬁed NTT-Sec-R (with respect to both irreversibility

and indistinguisahbility notions) is to solve the dis-

crete logarithm problem in the underlying cyclotomic

group. We provide some details in the following.

Assuming g is a generator of G, the adversary

solves e := log

h and e

:= log

for each i = 1, . . . , n

using a discrete-logarithm solver. Then the adversary

gets an equation

e =

∑

i=1

mod p

since |G| = p

. Using a Knapsack-solver, the adver-

sary ﬁnds a solution X

,...,X

; and recovers X. As-

suming the cost of computing the discrete logarithm

of an element in G is C

DLP

and the cost of solving the

above modular Knapsack problem is C

Knapsack

, then

the total cost is

(n + 1)C

DLP

Knapsack

Discrete logarithms in F

can be computed in a

time bounded by (max(p,m))

O(log

; see Theorem

3 in (Barbulescu et al., 2014). Ignoring the cost

Knapsack

of the underlying Knapsack problem, we es-

timate the cost of this discrete logarithm attack to be

(n+1)(max(p,m))

log

. Therefore, based on the val-

ues of n, p and m from Table 3, we estimate that cost

of discrete logarithm based attacks over the LFW face

dataset, the Subject s055, and the Subject s049 are

, 2

, and 2

, respectively.

Revocability of Templates. Another im-

portant security property is the cancella-

bility/revocability/renewability of templates.

NTT-Sec-R naturally allows this property as follows.

Instead of using the same public system parameters

for each user, one can make the system parameters

user speciﬁc. This can be achieved in (at least) two

different ways. First, the server can generate a public

system parameter set per user. If a user’s template is

stolen or revoked, then a new set of parameters can

be generated for that user, and a new template can be

enrolled. This would also provide an extra advantage

for the indistinguishability of the templates, because

now template spaces (F

) become algebraically

independent of each other. As a second method,

each user can derive his own system parameter set

from a secret password or a token. Then the user

can generate and enroll his template in the server. At

the time of authentication, the user can regenerate

the parameter set, compute his template, and send

them to the server as part of his query. The server

proceeds as before and can authenticate the user.

This second approach makes the reversibility and

distinguishability problems much harder because now

an attacker has to search for p and an ordered base

elements g

, i = 1, ..., n, which belong to a set of size

approximately (p/2)(p/2 − 1)···(p/2 − (n − 1)).

Comparisons. We provide a comparison between our

method and four other relevant and recently proposed

methods for face template protection. In (Feng et al.,

2010), Feng et al. combine distance preserving di-

mensionality reduction transformation, a discriminal-

ity preserving transformation, and a fuzzy commit-

ment scheme. The method in (Feng et al., 2010) re-

quires assigning a random secret token to each user

(namely, a random projection matrix) during enroll-

ment; and users need to provide their token dur-

ing authentication. Therefore, the scheme in (Feng

et al., 2010) can be seen as a two factor authentica-

tion scheme.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

494

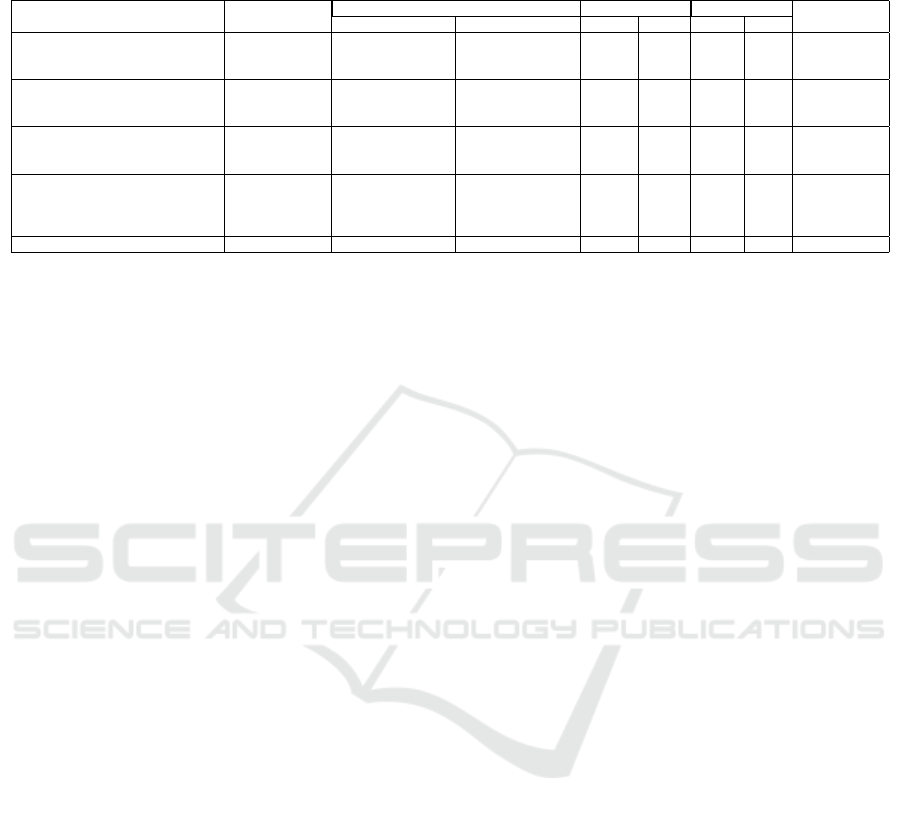
Table 4: Before/After = No/Using cryptographic algorithm, N/P = Not provided, Enroll = Enrollment, and Auth = Authen-

tication. For the LFW dataset, before and after results show the MD results using the respective scalar recommended by

Algorithm 1.

Dataset

GAR@FAR EER Secret Multifactor

Before After Before After Enroll. Auth. Authentication

Feng et al. (Feng et al., 2010)

FERET

N/P N/P

21.66% 3.62%

Yes Yes YesCMU-PIE 18.18% 8.26%

FRGC 31.75% 9.13%

Pandey et al. (Pandey et al., 2016)

Extended Yale B

N/P

96.49%@0FAR

N/P

0.71%

Yes No NoCMU-PIE 90.13%@0FAR 1.14%

Multi-PIE 97.12%@0FAR 0.90%

Jindal et al. (Jindal et al., 2019)

FEI

N/P

99.98%@0FAR

N/P

0.01%

Yes Yes YesCMU-PIE 99.98%@0FAR 1.14%

Color FERET 99.24%@0FAR 0.38%

Boddeti (Naresh Boddeti, 2018)

LFW 94.56%@0.1FAR 94.53%@0.1FAR

N/P N/P Yes Yes No

IJB-A 45.92%@0.1FAR 45.78%@0.1FAR

FaceNet and FHE (2 decimal digits) IJB-B 48.31%@0.1FAR 48.31%@0.1FAR

CASIA 84.70%@0.1FAR 84.68%@0.1FAR

Our method LFW 89.99%@0.1%FAR 90.09%@0.1%FAR 3.36% 3.39% No No No

The scheme in (Pandey et al., 2016) uses deep Convo-

lutional Neural Network (CNN) to map face images

to maximum entropy binary (MEB) codes. Each user

is assigned a unique random MEB code during en-

rollment, and a deep CNN is used to learn a robust

mapping of users’ face images to their MEB codes. A

cryptographic hash of the MEB code is stored on the

server side, which represents the secure template of

the underlying biometric data. Plain MEB codes are

not needed during authentication, because a queried

face image goes through the already trained CNN, and

the hash of its output is compared to the stored hash

value. It is claimed in (Pandey et al., 2016) that even

if an attacker knows the CNN parameters of a user,

he cannot obtain signiﬁcant advantage to attack the

system.

The method by Jindal et al. in (Jindal et al., 2019)

also uses deep CNN similar to the method in (Pandey

et al., 2016), but (Jindal et al., 2019) improves the

matching performance over (Pandey et al., 2016) by

using user speciﬁc random projection matrices. Sim-

ilar to the method in (Feng et al., 2010), each user

is assigned a random secret token during enrollment;

and users need to provide their token during authenti-

cation.

The method in (Naresh Boddeti, 2018) uses fully

homomorphic encryption (FHE), where each user has

to generate and manage her public and private key

pair. In a typical application, a user stores her private

key on his device, encrypts her biometric informa-

tion under her private key, and enrolls this encrypted

template through a server. At the time of authentica-

tion, the server receives another encrypted template

and uses the homomorphic encryption properties to

compute the (encrypted) distance between two tem-

plates.

Our scheme does not require using user speciﬁc

secret, or public/private keys. As a result, it can be

thought as a single factor authentication scheme. User

speciﬁc secrets can easily be adopted in our scheme to

obtain extra security (e.g., cancelable templates); see

our revocability of templates discussion in the security

analysis part above for more details. This would also

increase the matching accuracy of the system similar

to the improvements gained in earlier work due to use

of user-speciﬁc secrets.

In summary, our proposed scheme provides rea-

sonable security levels with comparable performance

with respect to previously known systems but comes

with an advantage of not requiring any user speciﬁc

secrets or training during enrollment and authentica-

tion. Our comparisons are summarized in Table 4.

Finally, we should note that it is challenging to

make a global comparison between the matching ac-

curacy of different methods. This is mainly because

of the use of different datasets, feature extraction al-

gorithms, and accuracy measures. For example, er-

ror rates over LFW are not reported in (Feng et al.,

2010; Pandey et al., 2016; Jindal et al., 2019). And

the reason for the difference between our error rates

and the error rates as reported in (Naresh Boddeti,

2018) over LFW is that (Naresh Boddeti, 2018) uses

FaceNet and we use ResNet for feature extraction. We

chose ResNet in our implementation because ResNet

has been more commonly used for comparisons over

LFW, and that ResNet and FaceNet are comparable in

terms of their accuracy. It should be clear from the ac-

curacy preserving properties of our construction that

deploying FaceNet in our scheme would yield error

rates which are arbitrarily close to the rates in (Naresh

Boddeti, 2018).

Formal Accuracy Analysis of a Biometric Data Transformation and Its Application to Secure Template Generation

495

5 CONCLUSION

We presented a method to create secure biometric

templates from real-valued feature vectors. We ver-

iﬁed our theoretical ﬁndings by implementing a re-

cently proposed secure biometric template generation

algorithm over face and keystroke public data sets.

We expect that our new construction and its explicit

accuracy analysis will enable known cryptographic

techniques to protect biometric templates at a larger

scale.

ACKNOWLEDGEMENTS

This work was supported by the U.S. National Sci-

ence Foundation (award number 1718109). The state-

ments made herein are solely the responsibility of the

authors.

REFERENCES

Banerjee, S. P. and Woodard, D. L. (2012). Biometric au-

thentication and identiﬁcation using keystroke dynam-

ics: A survey. Journal of Pattern Recognition Re-

search, 7(1):116–139.

Barbulescu, R., Gaudry, P., Joux, A., and Thom

e, E. (2014).

A heuristic quasi-polynomial algorithm for discrete

logarithm in ﬁnite ﬁelds of small characteristic. In

Advances in Cryptology – EUROCRYPT 2014, pages

1–16.

Blanton, M. and Gasti, P. (2011). Secure and efﬁ-

cient protocols for iris and ﬁngerprint identiﬁcation.

ESORICS’11, European Symposium on Research in

Computer Security, pages 190–209.

Bodo, A. (1994). Method for producing a digital signature

with aid of a biometric feature. German patent DE,

42(43):908.

Bours, P. and Barghouthi, H. (2009). Continuous authen-

tication using biometric keystroke dynamics. In The

Norwegian Information Security Conference (NISK),

volume 1, pages 1–12.

Fairhurst, M. and Da Costa-Abreu, M. (2011). Using

keystroke dynamics for gender identiﬁcation in social

network environment. In 4th International Conference

on Imaging for Crime Detection and Prevention 2011

(ICDP 2011), pages 1–6.

Feng, Y. C., Yuen, P. C., and Jain, A. K. (2010). A hy-

brid approach for generating secure and discriminat-

ing face template. IEEE Transactions on Information

Forensics and Security, 5(1):103–117.

Geitgey, A. (2017). Face recognition. https://github.

com/ageitgey/face recognition, last accessed: May

18, 2020.

Huang, G. B., Ramesh, M., Berg, T., and Learned-Miller,

E. (2007). Labeled faces in the wild: A database for

studying face recognition in unconstrained environ-

ments. Technical Report 07-49, University of Mas-

sachusetts, Amherst. http://vis-www.cs.umass.edu/

lfw/, last accessed: May 18, 2020.

Jindal, A. K., Chalamala, S. R., and Jami, S. K. (2019). Se-

curing face templates using deep convolutional neu-

ral network and random projection. In IEEE Inter-

national Conference on Consumer Electronics, ICCE

2019, pages 1–6.

Kanade, S., Petrovska-Delacr

etaz, D., and Dorizzi, B.

(2009). Cancelable iris biometrics and using error cor-

recting codes to reduce variability in biometric data.

In IEEE Conference on Computer Vision and Pattern

Recognition, CVPR 2009, pages 120–127.

Karabina, K. and Canpolat, O. (2016). A new cryptographic

primitive for noise tolerant template security. Pattern

Recognition Letters, 80:70 – 75.

Killourhy, K. S. and Maxion, R. A. (2009). Comparing

anomaly-detection algorithms for keystroke dynam-

ics. In IEEE/IFIP International Conference on De-

pendable Systems & Networks, 2009, DSN’09, pages

125–134.

King, D. E. (2011). Dlib library. http://dlib.net/, last ac-

cessed: May 18, 2020.

King, D. E. (2017). High quality face recognition with

deep metric learning. http://blog.dlib.net/2017/02/

high-quality-face-recognition-with-deep.html, last

accessed: May 18, 2020.

Naresh Boddeti, V. (2018). Secure face matching using

fully homomorphic encryption. In 2018 IEEE 9th In-

ternational Conference on Biometrics Theory, Appli-

cations and Systems (BTAS), pages 1–10.

Natgunanathan, I., Mehmood, A., Xiang, Y., Beliakov, G.,

and Yearwood, J. (2016). Protection of privacy in bio-

metric data. IEEE Access, 4:880–892.

Pandey, R. K., Zhou, Y., Kota, B. U., and Govindaraju, V.

(2016). Deep secure encoding for face template pro-

tection. In 2016 IEEE Conference on Computer Vision

and Pattern Recognition Workshops (CVPRW), pages

77–83.

Rathgeb, C., Breitinger, F., Busch, C., and Baier, H. (2014).

On application of bloom ﬁlters to iris biometrics. IET

Biometrics, 3(4):207–218.

Schmidt, G., Soutar, C., and Tomko, G. (1996). Fingerprint

controlled public key cryptographic system (1996).

US Patent, 5541994.

Tuyls, P., Akkermans, A., Kevenaar, T., Schrijen, G.-J.,

Bazen, A., and Veldhuis, R. (2005). Practical bio-

metric authentication with template protection. Audio-

and Video-Based Biometric Person Authentication,

Lecture Notes in Computer Science, 3546:436–446.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

496