
A CART-based Genetic Algorithm for Constructing Higher Accuracy
Decision Trees
Elif Ersoy
a
, Erinç Albey
b
and Enis Kayış
c
Department of Industrial Engineering, Özyeğin University, 34794, Istanbul, Turkey
Keywords: Decision Tree, Heuristic, Genetic Algorithm, Metaheuristic.
Abstract: Decision trees are among the most popular classification methods due to ease of implementation and simple
interpretation. In traditional methods like CART (classification and regression tree), ID4, C4.5; trees are
constructed by myopic, greedy top-down induction strategy. In this strategy, the possible impact of future
splits in the tree is not considered while determining each split in the tree. Therefore, the generated tree cannot
be the optimal solution for the classification problem. In this paper, to improve the accuracy of the decision
trees, we propose a genetic algorithm with a genuine chromosome structure. We also address the selection of
the initial population by considering a blend of randomly generated solutions and solutions from traditional,
greedy tree generation algorithms which is constructed for reduced problem instances. The performance of
the proposed genetic algorithm is tested using different datasets, varying bounds on the depth of the resulting
trees and using different initial population blends within the mentioned varieties. Results reveal that the
performance of the proposed genetic algorithm is superior to that of CART in almost all datasets used in the
analysis.
1 INTRODUCTION
Classification is a technique that identifies the
categories/labels of unknown observations/data
points, and models are constructed with the help of a
training dataset whose categories/labels are known.
There are many different types of classification
techniques such as Logistic Regression, Naive Bayes
Classifier, Nearest Neighbor, Support Vector
Machines, Decision Trees, Random Forest,
Stochastic Gradient Descent, Neural Networks, etc.
Classification techniques are divided into two groups:
(1) binary classifiers that classify two distinct classes
or two possible outcomes and (2) multi-class
classifiers that classify more than two distinct classes.
Also, many of these methods are constructed with a
greedy approach. Hence, these approaches always
make the choice that seems to be the best at each step.
However, these greedy approaches may not result in
an optimal solution.
Decision trees (DT) are one of the most widely-
used techniques in classification problems. They are
a
https://orcid.org/0000-0003-1126-213X
b
https://orcid.org/0000-0001-5004-0578
c
https://orcid.org/0000-0001-8282-5572
guided by the training data (x
i
, y
i
), i = 1, . . . , n.
(Bertsimas and Dunn, 2017). DTs recursively
partition the training data’s feature space through
splits and assign a label(class) to each partition. Then
created tree is used to classify future points according
to these splits and labels. Since, conventional decision
tree methods are creating each split in each node with
greedy approaches and top-down induction methods,
which may not capture well the underlying
characteristics of the entire dataset. The possible
impact of future splits is not considered while
determining each split in the tree. Thus, attempts to
construct near-optimal decision trees have been
discussed for a long time (Safavian and Landgrebe,
1991).
The use of heuristics in creating decision trees
with the greedy approach is discussed widely in the
literature. Heuristic algorithms will be applied to
construct decision trees from scratch or to improve
the performance of constructed trees. Kolçe and
Frasheri (2014) study on the greedy decision trees and
focus on four of the most popular heuristic search
328
Ersoy, E., Albey, E. and Kayı¸s, E.
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees.
DOI: 10.5220/0009893903280338
In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 328-338
ISBN: 978-989-758-440-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

algorithms, such as hill-climbing, simulated
annealing, tabu search, and genetic algorithms (Kolçe
and Frasheri, 2014). For continuous feature data,
evolutionary design is suggested in Zhao and
Shirasaka (1999) and an extreme point tabu search
algorithm is proposed in Bennett and Blue (1996).
There are some examples for optimal decision
trees. For example, Blue and Bennett (1997) use a
Tabu Search Algorithm for global tree optimization.
In their paper, they mention that “Typically, greedy
methods are constructed one decision at a time
starting at the root. However, locally good but
globally poor choices of the decisions at each node
can result in excessively large trees that do not reflect
the underlying structure of the data”. Gehrke et al.
(1999), develop a bootstrapped optimistic algorithm
for decision tree construction.
The genetic algorithm (GA) have been proposed
to create decision trees in the literature and have been
discussed in two different ways to find near-optimal
decision trees. One method is for selecting features to
be used to construct new decision trees in a hybrid or
preprocessing manner (Bala et al., 1995) and others,
applies algorithm directly to constructed decision
trees to improve them (Papagelis and Kalles, 2000).
Also, additionally, Chai et al. (1996) construct a
linear decision binary tree with constructing
piecewise linear classifiers with the GA. Therefore,
we choose to use a GA to construct highly accurate
decision trees to expand the search area so as not to
get stuck in local optima and get close to the near-
optimal tree.
In GA literature, different approaches are used to
construct an initial population. Most of them use
randomly generated populations (Papagelis and
Kalles, 2000; Jankowski and Jackowski, 2015) and
some of them use a more intelligent population with
the help of greedy algorithms (Fu et al., 2003; Ryan
and Rayward-Smith, 1998). In Fu et al. and Ryan et
al.’s works, C4.5 is used as a greedy algorithm to
construct the initial population. An intelligent
population helps to start the algorithm with better
fitness values. Also, in their paper, they discussed that
using C4.5 is a bit computationally expensive.
In this work, we develop a GA to construct high
accuracy decision trees. Also, we use greedy
algorithm CART trees in the initial population to
improve these trees’ performance. In GA, to
implement evolutionary operations, decision trees
must be represented as chromosome structures. In this
work, we propose a structure to encode a decision tree
to a chromosome and to generate the initial
population, we divide the original dataset into subsets
with reasonable size and generate trees with these
subsets on CART. Then in GA full-size dataset and
the initial population are used to create more accurate
trees. So, we want to use the power of CART trees in
our algorithm and we are trying to improve the
performance of greedy CART solutions.
The rest of the paper is organized as follows. In
Methodology section, you can find a more detailed
explanation of our implementation of GA,
chromosome structure and generated initial
populations. Subsections of the Methodology section
present the encoding/decoding decision trees to/from
chromosomes, genetic operators like mutation and
crossover, fitness functions. Experiment and
Computational Result section explains the
experimental details and results. Finally, Conclusion
section concludes all of this work.
2 GENETIC ALGORITHM AS A
SOLUTION METHOD
In this paper, we discuss GA to improve the
performance of decision trees. For the GA
implementation, we concentrate on the following
facts: (1) new chromosome structure, (2) initial
population, (3) fitness function, (4) selection
algorithm, (5-6) genetic operations, (7) generation
and (8) stopping condition and overall flow of GA.
These are explained in detail in following subsections
to understand the essentials of our GA.
2.1 Encoding the Solution
Representation (Chromosome
Structure)
The representation of a solution using the
chromosome is critical for relevant search in solution
space and tree-based representation for the candidate
solution is the best one (Jankowski and Jackowski,
2015). A chromosome must contain all split decisions
and rules to decode it into a feasible decision tree.
Figure 1: Tree structure and split rules at depth 3.
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees
329

Decision trees are constructed based on split rules
and in each node, split occurs with a rule, and data-
points are following the related branch based on that
rule. Also, in this paper, we concentrate on binary
split trees so there are only two branches in each node
splits, which means splits are bidirectional. Left
branch refers less than operation and the right branch
refers greater than or equal to operation (see Figure
1). So, in GA’s solution representation if we encode
which feature is used as a rule in which branch node,
and their threshold values we will construct a tree
with this linear representation. Then the fitness value
will be calculated easily. To encode that
representation, we use a modification of Jankowski
and Jackowski (2015) as follows.
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
𝑏
𝑏
𝑏
𝑏
𝑏
𝑏
𝑏
Figure 2: Chromosome structure for depth 3 tree.
Each branch node is stored in a depth-first manner
as an implicit data structure in two arrays (see Figure
2). All feature IDs are maps to an integer and each
feature values are maps to normalized continuous
values between [0,1], so each component is numeric.
The dimension of a chromosome is 2x(2
D
-1). We
use 2 rows where first-row stores split feature
information and second-row stores threshold values
for the related feature. Number of columns equal to
the number of total branch nodes, 2
D
-1, where D is
the depth of a tree. Also, in our algorithm D is used
as a fixed parameter, thus chromosome dimension is
also fixed. We define a tree if and only if the right
branch always follows the “>=” rule and left branch
follow “<” rule. Thus, if the related feature of the
node’s rule and the threshold for that rule is known,
they are enough to construct a tree easily. So, the
chromosome structure of depth 3 is presented below.
One of the decision trees at depth 3 is represented
in Figure 3. To explain it in detail, split feature at the
root node is 15
th
feature and threshold is 0.295. So, in
Figure 3: Example chromosome and related decision tree at
depth 3.
training data, datapoints whose 15
th
feature is less
than 0.295, follow left branch, accumulated in node 2
and points greater than or equal to 0.295, follow right
branch and accumulated in node 5. Second column of
the chromosome represents the rule of left node, node
2, then split feature is 9
th
feature and threshold is
0.843. Thus, data points accumulated in node 2
follows that rule, they are split according to their 9
th
feature and if the value is less than 0.843 they follow
left branch, accumulated in node 3 and points greater
than or equal to 0.843 follows right branch and
accumulated in node 4. Then 3
rd
column of the
chromosome is the left branch of the node 2 and split
feature is 17
th
one, threshold is 0.149. Then if 17
th
features of data points in the node 2 are less than
0.149 datapoints assign to Leaf #1 and others assign
to Leaf #2.
2.2 Generation of Initial Population
To generate initial solutions/populations for the GA,
CART (Breiman et al., 1984) is used as a constructive
algorithm. But GA needs an initial population that has
more than 1 solution, so as Fu et. al (2003) used in
their paper, some sub-trees are created for the initial
population. In this paper, we generate sub-trees using
two ways: randomly and with the CART algorithm.
For random trees, we generate a tree with randomly
chosen features for each node of a tree with given
depth and random threshold values within the
normalized values between 0 and 1. For sub-CART
trees, a whole size data set is divided into some
number of subsets randomly with a decided instance
size (explained in Section 3.3) and CARTs are
generated for these subsets. Some data points can be
in multiple subsets. When subsets of this dataset are
used in CART, a solution will be found for these
subsets and we call them as sub-trees. Then original
data will be classified using these subtrees and fitness
value for each subtree is calculated for the whole
dataset. Fitness is defined as the total
misclassification error, which will be discussed in
more detail later.
We use two different initial population mixtures
(1) random trees only and (2) random trees, subtrees
generated via CART, and 1 full CART solutions.
Details for these population types and effects of these
selections are discussed in Section 3.
2.3 Fitness Value
Fitness Value will be calculated as total number of
misclassified points or total correctly classified points
of each individual tree. A misclassification is number
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
330

of points that are labeled incorrectly. In other words,
in classification trees, leaf nodes are labeled with the
majority points’ class labels after split rules.
Therefore, other minority points are labeled
incorrectly, and the total number of that minority
points is equal to the misclassification error and
others are labeled correctly. Aim of our algorithm and
all other classification algorithms are minimizing
number of misclassification or maximizing number of
correctly classified points, which are almost the same
things.
In our algorithm, we choose maximizing correctly
classified points as an objective. Thus, our fitness
value is equal to total number of correctly classified
points. We choose this one because of the working
principle of our selection algorithm, we explain it in
the following section in more detail.
When a new tree is reproduced after evolutionary
operations, fitness value needs to be updated. Firstly,
points are assigned to related leaf nodes according to
new split rules. Then, each leaf is labeled with
majority class, we call poin ts labeled incorrectly
according to their real class labels, as misclassified
points and others labeled as correctly classified
points.
In the GA algorithm, we calculate the fitness
function value of each individual sub-tree with the
whole dataset instead of the related subset, because,
in this paper, the classification tree must be generated
for the whole dataset which considers all data points
completely.
2.4 Parent Selection
In GA, during children production, the algorithm uses
the current generation to create children that make up
the next generation based on the fitness value. In GA
and other evolutionary algorithms, to select parents,
some well-known selection methods are tournament
selection, roulette wheel selection, rank-based
selection, etc. In these selection methods, each
individual in the population can be selected more than
once, so each individual spread its genes to possibly
more than one child.
In our implementation of the GA, we use roulette
wheel (RW) selection. Roulette wheel selection is
under the title of Fitness Proportionate Selection
Methods. In these methods, every solution has a
probability of being selected according to their fitness
values proportion. In roulette wheel, fitness values of
each tree in the current generation take a place in the
wheel according to their weighted fitness value. Thus,
higher fitness takes wider proportion and it will be
selected with a higher probability. Furthermore, we
want to choose high accuracy trees as a parent to
spread its genes to the next generations. This will help
us to reproduce stronger children. If fitness value is
used as a total number of correctly classified points,
the roulette wheel works well and will chooses high
accurate trees with higher probability. So, to select
stronger parents, which has less number of misclassed
points and more correctly classified ones, roulette
wheel method is the proper one. That’s why we
choose our objective as maximize fitness function
which is total number of correctly labeled points.
2.5 Crossover Operation
The algorithm creates crossover children by
combining pairs of selected parents in the current
population. Firstly, two individuals (parents) are
chosen using the RW method. From chosen trees, a
random cut point is selected according to a randomly
generated number which can take values between 1
(root node) to n (total number of tree nodes). After
identifying the random cut points in both parents, new
individuals (offspring) are created by replacing sub-
part form the first parent by the one from the second
parent. We cut each parent from the exact same
point/node and replace the remaining part with a same
sized sub-parts. Figure 6 illustrates an example of the
crossover operation.
Also, in this paper’s algorithm, crossover is applied on
linear chromosome in two ways, 1-point, and 2-point
crossover. In 1-point crossover, the sub-part starting from
the cutting node (and runs through the last node of the
selected parent) is exchanged; whereas in 2-points
crossover, we exchange interior sub-parts. In more detail,
we cut sub-trees at the same level from each parent. In
Figure 4, possible cut points for depth 2 trees are shown. 1-
point crossover is applied when parents are cut from the 1
st
or 2
nd
cut points and crossed each other. 2-point crossover
is applied when the part between the 1
st
and 2
nd
cut point
Figure 4: Possible crossover cut points in depth 2; 1 or 1-2
or 2.
Figure 5: Possible crossover cut points in depth 3; 1 or 1-4
or 2-3 or 3-4 or 4 or 5-6 or 6.
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees
331
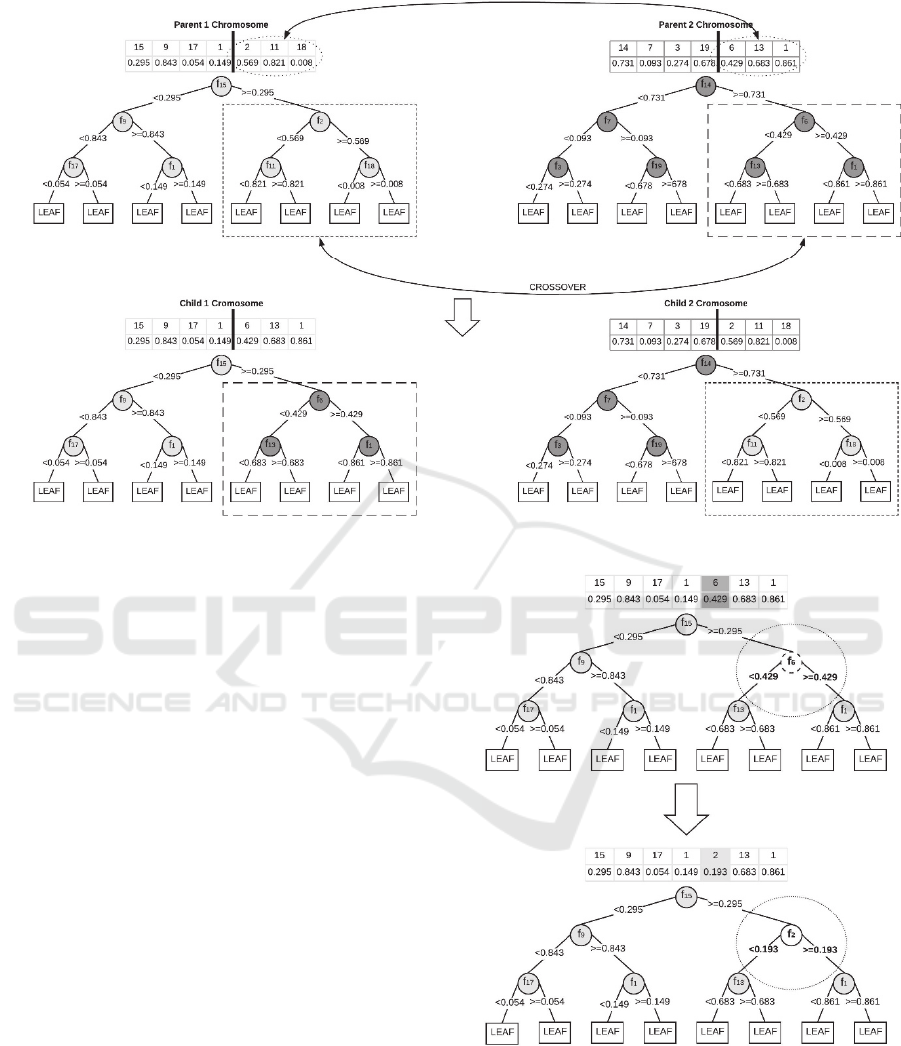
Figure 6: Crossover operation on selected parent and generated children in depth 3 trees.
is crossed. To be more precise, after the crossover
operation, depth of the tree cannot change because we
cut each parent from the exact same point. Figure 5
shows cut points for depth 3. For 1-point crossover at
depth 3, possible cut points will be 1, 4 or 6 and for
2-point crossover, possible parts will be between 1-4,
2-3, 3-4 or 5-6. These specific cut-parts represent
each meaningful sub-tree in a maximal tree. This
specification also prevents depth change in the
crossover.
In Figure 6, you can see the illustration of 1-point
crossover on the depth 3 tree. We cut each parent
from the 4
th
cut point, which is decided randomly in
the algorithm, and cut parts crossing between each
other.
2.6 Mutation Operation
Mutation operation makes changes on the individual
tree in the population. In the proposed algorithm, this
change is applied, based on mutation rate, on to the
generated children`s randomly selected node to create
a mutated child. With the help of mutation, GA
enables us to search a broader space with providing
genetic diversity. In our implementation, we use node
base mutation similar to Jankowski and Jackowski
(2015), we randomly change both feature and split
threshold of a randomly selected node (see Figure 7).
Figure 7: Tree node mutation.
Figure 7 illustrates how mutation operation
applied on Child 1, which comes from the crossover.
In this mutation, 5
th
node is selected randomly, and
this node’s feature ID and threshold value are
changed with randomly chosen feature ID and
threshold value. With mutation, the class assignment
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
332
of leaf nodes may also change based on the majority
class on each node because split rule is changed. Also,
there is a restriction, mutation will be applied to all
branch nodes except the root node.
2.7 Replacement and New Generation
To generate a new generation of the GA, we applied
the elitism procedure. Elitism keeps a proportion
known as elite rate, of the fittest candidates into the
next generation. For example, given a population of
100 individuals, if you have an elite rate of 5%, you
choose to keep the five best individuals of the current
generation to the next generations and you apply
crossover and mutation to generate the rest of the new
generation.
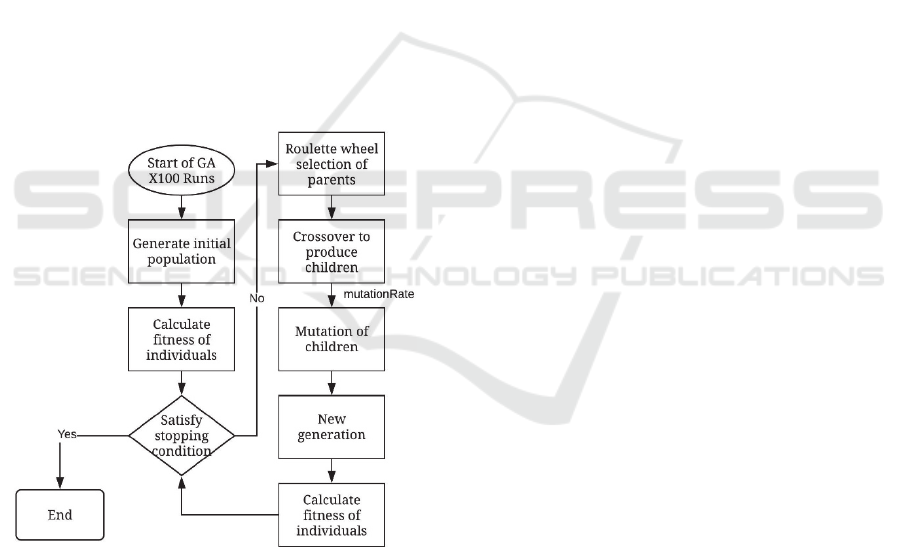
2.8 Stopping Criteria and Overall
Algorithm
In the literature, there are many different applications
of GA implementation. The flowchart in Figure 8
shows the general steps of our GA implementation.
Figure 8: Flow of GA.
To explain our algorithm in more detail, the steps
of GA implementation is as follows:
Repeat below steps TotalRun times:
Generate an initial population (first generation)
of size N with the selected mixture.
Initialize a variable, Iter, for keeping track of
successive iterations where the best tree found in
each generation has not changed.
Repeat while Iter < MaxIter:
o Select eliteRate*N best individual from
the previous generation and keep them
into the new generation.
o Repeat until the new generation is
fulfilled to size N.
- Randomly select two members from
the previous generation based on
roulette wheel method.
- Run the crossover operator: input
selected two members and obtain two
children.
- Add new children to the new
generation
- Run the mutation operator: input one
of the currently generated children
from crossover and apply mutation if
mutationRate is satisfied.
- Replace mutated child in the new
population.
- If the new generation cannot provide
a better tree and fitness value than the
previous generation’s best, increase
Iter by 1.
Select the best tree in the final generation
and its fitness.
We repeat these steps TotalRun times in order to
minimize the effects of randomization on overall
performance. Also, we choose the final solution as the
best tree found in all TotalRun runs.
3 COMPUTATIONAL RESULTS
In this section, we explain our datasets, parameters,
initial populations, then the computational results of
the proposed approach on different variations of
datasets are discussed. We compare the performance
of our GA to that of CART.
3.1 Datasets
To evaluate the effects of data size, number of
features and class we use six different datasets with
different dimensions and characteristics. These
datasets are obtained from the UCI machine learning
repository (Lichman, 2013). Some of these datasets
are used in other classification studies as well, such
as study about optimal classification tree (Bertsimas
and Dunn, 2017). Details about each dataset are
described below (see Table 1).
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees
333
Table 1: Details of datasets used in experiments.
Data Set
Name
Number of
Points (n)
Number of
Classes (K)
Number of
Features (p)
Wine 173 3 13
Chess 3196 2 36
Image
Segmentation
210 7 19
Avila 20867 12 10
Parkinson 756 2 754
Madelon 2600 2 500
We are given each dataset to GA in the form of
(X, Y). To be more general, each dataset containing n
observations, each observation is defined with p
features and K possible class label. The x values for
each feature across the data are normalized between
0 and 1, which means each x
i
∈
[0, 1]
p
.
We apply 5-fold cross-validation to estimate the
performance of our algorithm to minimize the
overfitting problem. We split each dataset as 80% for
training and 20% for testing sets. And then we take
an average of 5 runs` accuracies.
3.2 Parameters
In our proposed GA, we use four parameters: (1)
maxIter which is used for restricting the ineffective
improvement moves to stop algorithm, (2) Elite Rate
represents the proportion of best individual to keep in
next generation, (3) Mutation Rate is the proportion
for mutation operation applied on children and (4)
TotalRun which is the total number of replications.
For maxIter, in each ineffective generation, iteration
counter increases but if the new generation improves
the best solution and updates the best tree so far,
iteration does not increase and iteration counter is
reset. If the iteration counter reaches maxIter, GA
terminates. We take TotalRun amounts of replications
because, in the applied algorithm, there are lots of
randomization in reproduction operators as selection,
crossover and mutation. So, we apply some
replications and decrease the effect of randomness
over each procedure. In this work, we use the
parameter values as shown in Table 2. Sensitivity
analysis is applied to these parameters and final
values are selected as the values that yield the best
performance.
Table 2: Values of each parameter.
Parameter Value
MaxIter 10
Elit Rate 0.2
Mutation Rate 0.1
Total Run 100
3.3 Initial Population
As mentioned before, this work aims to improve the
performance of GA by using a specific initial
population. We use two different population blends
for initializing our algorithm. These mixtures include
random trees, sub-CART trees which are generated
with sub-sets of the whole datasets and 1 CART tree
which is constructed with the full-size training set.
Table 3: Content of population blends.
Population Content
MIX_V1 30 Random Trees
MIX_V2
30 Random + 30 Sub-CART + 1 full-
CART Trees
We generate each random tree by assigning
random rules for a given depth. Random feature ID
for each node, which is integer, is assigned between
[0, p] and threshold value, which is continuous,
between [0,1]. For constructing CART trees, we used
the rpart package (Therneau et al. 2019) in the R
programming language version 3.5.3 (R Core Team
2019). In the rpart function, there is a control
parameter called minbucket, which limits the
minimum number of observations in any leaf node to
prevent overfitting. We use this parameter as
(0.05*n).
We add CART based decision trees into the initial
population and our aim is to beat CART
performances with the help of GA. We will evaluate
the contributions of CART based initial population in
the next subsection.
3.4 Experimental Analysis and Result
As mentioned in previous subsections, we use 6
different datasets with different sizes, and we divide
them into 5 folds. We aim to find more accurate trees
rather than the CART. As an initial population, we
use 2 different population mixtures with different size
(see Table 3).
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
334

Our first initial population includes 30 different
random trees with a given depth. And second initial
population type includes the same 30 random trees
plus 30 sub-CART and 1 full-sized CART solution.
Also, we train each dataset at 4 different depths as {2,
3, 4, 5}.
We take 100 replication runs to minimize effects
of randomization. So, to compare our GA results we
take best tree found in overall 100 runs as a final
solution. In the below tables, “mean out-sample
accuracy” is refer to average out-sample accuracy of
the best tree found in 100 runs of 5 folds.
We use average out-sample accuracies across 5
folds to compare the performance of our algorithm
against CART in cross-validation manner. Also, to
show the exact improvement performance of our
Table 4: Full results at depth 2.
DATASET
Mean Out-Sample
Accuracy
Mean In-Sample
Accuracy Improvement
Time(sec)
Wine
CART 88.78% 0.112
GA MIX_V1 88.19% +12.22% 0.460
GA MIX_V2 88.21% +2.67% 0.767
Chess
CART 76.69% 0.131
GA MIX_V1 86.64% +17.47% 7.543
GA MIX_V2 86.92% +0.52% 7.700
Segment
CART 37.14% 0.169
GA MIX_V1 57.14% +8.10% 0.566
GA MIX_V2 58.10% +3.10% 0.645
Avila
CART 50.10% 0.257
GA MIX_V1 51.14% +3.14% 32.721
GA MIX_V2 51.97% +0.78% 41.768
Parkinson
CART 79.89% 0.349
GA MIX_V1 79.10% +2.71% 1.697
GA MIX_V2 81.88% +0.07% 1.872
Madelon
CART 65.19% 0.783
GA MIX_V1 57.00% +5.45% 7.248
GA MIX_V2 66.38% +0.77% 11.629
The best performing solutions for each dataset are highlighted in bold.
Table 5: Full results at depth 3.
DATASET
Mean Out-Sample
Accuracy
Mean In-Sample
Accuracy Improvement
Time(sec)
Wine
CART 91.02% 0.214
GA MIX_V1 96.60% +8.01% 0.733
GA MIX_V2 91.57% +2.53% 1.464
Chess
CART 90.43% 0.249
GA MIX_V1 90.43% +12.64% 11.192
GA MIX_V2 93.80% +3.38% 12.466
Segment
CART 52.38% 0.254
GA MIX_V1 68.57% +17.38% 0.984
GA MIX_V2 80.48% +10.36% 1.150
Avila
CART 52.43% 0.278
GA MIX_V1 51.08% +3.26% 59.846
GA MIX_V2 54.70% +1.33% 92.289
Parkinson
CART 80.95% 0.526
GA MIX_V1 78.44% +3.11% 3.120
GA MIX_V2 82.80% +1.03% 3.887
Madelon
CART 69.04% 1.004
GA MIX_V1 60.00% +6.31% 14.336
GA MIX_V2 69.27% +0.37% 16.901
The best performing solutions for each dataset are highlighted in bold.
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees
335

algorithm over training set, we share average in-
sample accuracy improvement as the difference
between the accuracy of the best accurate tree out of
100 run and the initial best accurate tree in the initial
generation. Table 4 presents these in-depth direct
comparisons at depth 2 and Table 5 at depth 3. Result
tables for depth 4 and 5 are provided in the Appendix.
`Time` is the total time in seconds for population
initialization plus GA execution time.
GA is codded in Java language (Java version
1.8.0) and computed on Eclipse IDE version 4.14.0.
These computations are done in a PC with Intel Core
i7-8550U 1.8GHz, 8GB RAM.
In Table 4, at depth 2, 5 out of 6 datasets show GA
with CART based initial population (MIX_V2) is
stronger than CART with an improvement over
CART of about 1% to 10% nominal improvement
depending on the dataset. Also, in some datasets, the
performance of the GA with random initial
population ( MIX_V1) is also stronger than the pure
CART performance but in general GA with MIX_V2
population has the best performance over CART and
GA with MIX_V1.
Improvement amounts of GA with MIX_V2
increases at higher depths. Moreover, at higher
depths, GA with MIX_V2 population is always the
best one. Especially at depth 5 (see Appendix 2), for
all the 6 datasets, GA with MIX_V2 is always the best
method.
For more detail, let's analyze the results of Avila
dataset at depth 2-3-4 and 5. When depths are getting
deeper, out-sample accuracies are also increased.
Although, in-sample accuracy improvements are
almost same for all depths. But, more crucial point is
difference between the MIX_V1 and MIX_V2. At all
depths, MIX_V2 is always outperformed CART and
MIX_V1. Only Wine dataset at depth 2 cannot
outperform CART at MIX_V1 and MIX_V2. But in
higher depths, we can beat CART performance as
well.
These results show that our GA can outperform
CART in all datasets when depth 3. On the other
hand, in mean in-sample perspective, GA with
MIX_V1 shows higher average in-sample accuracy
improvement. This metric shows effect of GA over
the initial population with the training set. In
MIX_V1 initial population we use only random trees
and their initial accuracies are very low over the
training set. After the GA implementation, we can
increase the accuracy of these random trees
dramatically. This shows, our GA works well to
increase the initial fitness of the provided problem
within a reasonable execution time for small and
medium size datasets.
We conclude that GA found trees with higher
prediction accuracy compared to greedy CART
algorithm in a reasonable time for small and medium
size datasets. For large size datasets (n>20,000), the
execution time increases, especially when we
increase the population size along with the data size.
But in all dataset sizes, we can observe at least 1%
accuracy improvement, which is crucial in
classification problems. Thanks to GA to improve the
performance of the given initial population and find
trees with better accuracies.
4 CONCLUSIONS
In this article, we describe and evaluate an
evolutionary algorithm, GA, for decision tree
induction. In conclusion, because of the
disadvantages of greedy approaches, some heuristics
will be combined to improve their performances.
Genetic algorithm is chosen in this work to combine
with CART. So, we use random initial population as
well to compare the performance of including CART
subtrees into the initial population. In GA, crossover
is applied to all parents, and mutation is applied only
for the given proportion of the children coming from
the crossover. In mutation, the randomly chosen node
is mutated.
Results show GA improves the performance of
given trees in the initial population. But if the initial
population contains random trees only, GA cannot
outperform CART solution usually. So, when we
include CART solutions to the population we can
improve their performances and outperform CART.
Results show MIX_V2 initial population is better
than de MIX_V1 population 5 out of 6 datasets at
depth 2, 3 and MIX_V2 is always the better one at
depth 4 and 5.
For future work, some additional steps will be
applied to this presented heuristic to observe more
improvements and some other heuristic methods will
be experienced to construct more accurate trees. For
example, in presented GA, some additional
operations and improvement moves will be tested and
selected according to their contribution. Also, we will
consider pruning steps in GA implementation and we
will be limiting some parameters like minbucket and
complexity parameter, which are used in constructing
CART. Additionally, we will generate different initial
population mixtures with the help of different
decision tree induction strategies and compare their
performance with the proposed ones.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
336

REFERENCES
Bertsimas, D., & Dunn, J., 2017. Optimal classification
trees. Machine Learning, 106(7), 1039-1082.
Safavian, S. R., & Landgrebe, D., 1991. A survey of
decision tree classifier methodology. IEEE transactions
on systems, man, and cybernetics, 21(3), 660-674.
Gehrke, J., Ganti, V., Ramakrishnan, R., & Loh, W. Y.,
1999. BOAT—optimistic decision tree construction. In
Proceedings of the 1999 ACM SIGMOD international
conference on Management of data (pp. 169-180).
Kolçe, E., & Frasheri, N., 2014. The use of heuristics in
decision tree learning optimization. International
Journal of Computer Engineering in Research Trends,
1(3), 127-130.
Zhao, Q., & Shirasaka, M., 1999. A study on evolutionary
design of binary decision trees. In Proceedings of the
1999 Congress on Evolutionary Computation-CEC99
(Cat. No. 99TH8406) (Vol. 3, pp. 1988-1993). IEEE.
Bennett, K. P., & Blue, J. A.,1996. Optimal decision trees.
Rensselaer Polytechnic Institute Math Report, 214, 24.
Bennett, K., & Blue, J., 1997. An extreme point tabu search
method for data mining. Technical Report 228,
Department of Mathematical Sciences, Rensselaer
Polytechnic Institute.
Bala, J., Huang, J., Vafaie, H., DeJong, K., & Wechsler, H.,
1995. Hybrid learning using genetic algorithms and
decision trees for pattern classification. In IJCAI (1)
(pp. 719-724).
Papagelis, A., & Kalles, D., 2000. GA Tree: genetically
evolved decision trees. In Proceedings 12th IEEE
Internationals Conference on Tools with Artificial
Intelligence. ICTAI 2000 (pp. 203-206). IEEE.
Chai, B. B., Zhuang, X., Zhao, Y., & Sklansky, J., 1996.
linear decision tree with genetic algorithm. In
Proceedings of 13th International Conference on
Pattern Recognition (Vol. 4, pp. 530-534). IEEE.
Ryan, M. D., & Rayward-Smith, V. J., 1998. The evolution
of decision trees. In Proceedings of the Third Annual
Conference on Genetic Programming (pp. 350-358).
San Francisco, CA.: Morgan Kaufmann.
Fu, Z., Golden, B. L., Lele, S., Raghavan, S., & Wasil, E.
A., 2003. A genetic algorithm-based approach for
building accurate decision trees. INFORMS Journal on
Computing, 15(1), 3-22.
Jankowski, D., & Jackowski, K., 2015. Evolutionary
algorithm for decision tree induction. In IFIP
International Conference on Computer Information
Systems and Industrial Management (pp. 23-32).
Springer, Berlin, Heidelberg.
Breiman, L., Friedman, J., Stone, C. J., & Olshen, R. A.,
1984. Classification and regression trees. CRC press.
Lichman, M., 2013. UCI machine learning repository.
http://archive.ics.uci.edu/ml.
Therneau, T., Atkinson, B., & Ripley, B., 2019. rpart:
Recursive partitioning and regression trees.
http:/CRAN.R-project.org/package=rpart, R package
version 4.1-15.
R Core Team., 2019. R: A language and environment for
statistical computing. Vienna: R Foundation for
Statistical Computing. http://www.R-project.org/.
APPENDIX
Appendix 1: Full results for depth 4.
DATASET
Mean Out-
Sample Accuracy
Mean In-Sample
Accuracy Improvement
Time(sec)
Wine
CART 91.02% 0.214
GA MIX_V1
92.11%
10.67% 1.654
GA MIX_V2 91.03% 3.09% 2.653
Chess
CART 89.86% 0.391
GA MIX_V1 90.49% 15.09% 22.899
GA MIX_V2
94.09%
0.23% 18.734
Segment
CART 69.05% 0.222
GA MIX_V1 77.14% 22.02% 1.994
GA MIX_V2
84.29%
7.02% 1.890
Avila
CART 55.20% 0.303
GA MIX_V1 50.56% 2.23% 145.270
GA MIX_V2
57.04%
0.86% 188.793
Parkinson
CART 80.95% 0.715
GA MIX_V1 77.51% 3.11% 5.952
GA MIX_V2
83.20%
1.49% 7.657
Madelon
CART 69.27% 1.109
GA MIX_V1 58.73% 2.55% 25.317
GA MIX_V2
70.04%
0.60% 28.863
The best performing solutions for each dataset are highlighted in bold.
A CART-based Genetic Algorithm for Constructing Higher Accuracy Decision Trees
337

Appendix 2: Full results for depth 5.
DATASET
Mean Out-Sample
Accuracy
Mean In-Sample
Accuracy Improvement
Time(sec)
Wine
CART 91.02% 0.237
GA MIX_V1 91.60% 9.70% 4.140
GA MIX_V2
94.40%
3.37% 3.300
Chess
CART 89.86% 0.427
GA MIX_V1 94.15% 15.81% 55.128
GA MIX_V2
94.40%
0.66% 36.076
Segment
CART 77.14% 0.253
GA MIX_V1 77.14% 15.48% 3.150
GA MIX_V2
84.76%
4.52% 3.546
Avila
CART 58.82% 0.529
GA MIX_V1 50.32% 6.71% 139.102
GA MIX_V2
60.04%
1.08% 314.508
Parkinson
CART 80.95% 0.767
GA MIX_V1 81.08% 2.15% 6.699
GA MIX_V2
83.86%
1.69% 14.384
Madelon
CART 69.27% 1.164
GA MIX_V1 58.58% 5.30% 38.731
GA MIX_V2
70.85%
1.13% 53.497
The best performing solutions for each dataset are highlighted in bold.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
338
