
Deep Learning with Transfer Learning Method for Error Compensation
of Cable-driven Robot
Aydar Akhmetzyanov
a
, Maksim Rassabin
b
, Alexander Maloletov
c
, Mikhail Fadeev
d
and Alexandr Klimchik
e
Center for Technologies in Robotics and Mechatronics Components, Innopolis University, Innopolis, Russia
Keywords:
Cable-driven Robot, Kinematics Compensation, Deep Learning, Transfer Learning, Robotics.
Abstract:
This paper proposes the application of Deep Learning methods for kinematic error compensation. Particular
attention is paid to simulation-based error estimation and the use of the Transfer Learning method for error
compensation to reduce physical experiments with a real robot. The obtained results were applied and vali-
dated for 4-dof (degrees of freedom) cable-driven parallel robot. The problem of error compensation for the
cable-driven parallel robot is highly non-linear. Nevertheless, deep learning-based methods for a considerable
training dataset provides better accuracy than simple linear error compensators. To overcome this drawback,
we applied the transfer learning method and used the knowledge of robot kinematics simulated in Unity. Unity
cable-driven robot simulation was implemented, and the central hypothesis was verified first in the simulated
environment. The proposed Transfer Learning method allowed to speed up the process of robotics system
integration and recalibration due to the significant sample efficiency improvement.
1 INTRODUCTION
The cable-driven parallel robot is a wide class of
robots that find their application in many areas, for
example, warehousing (Alias et al., 2018), (Rasheed
et al., 2020), 3D printing (Izard et al., 2017), surgery
(Wang et al., 2016), etc. Their advantages include
larger workspace (Morris and Shoham, 2009), rela-
tively small robot mass, ability to handle large pay-
load, ability to operate with high speed and accel-
eration. The main disadvantage of parallel cable-
controlled robots is associated with the complexity of
physical modeling and, as a result, with the complex-
ity of non-linear compensation of geometric and non-
geometric errors. In this paper, we address the prob-
lem of non-linear inverse kinematics error of cable-
driven robot.
In an industrial environment, additional on-line or
off-line error compensation methods are used to im-
prove robot positioning accuracy (Wu et al., 2015). In
the cable-driven parallel robot, the error compensa-
a
https://orcid.org/0000-0003-3698-2977
b
https://orcid.org/0000-0002-3468-9331
c
https://orcid.org/0000-0002-7312-2944
d
https://orcid.org/0000-0002-9503-1242
e
https://orcid.org/0000-0002-2244-1849
tion algorithm can be realized employing adjustment
cable lengths, which change the end-effector position.
In this case, the error compensation algorithm is rela-
tively simple, since it does not require controller mod-
ification while updating higher-level inputs only. To
achieve the desired positioning accuracy, it is often
required to give as input reference trajectory that dif-
fers from the target one (Klimchik et al., 2013). In
this case, the input trajectory is usually changed on
the value of correction, which is computed either it-
eratively using the kinematic model or based on the
Jacobian matrix (Klimchik et al., 2014).
In general, the error compensation algorithms can
be split into two big groups: based on some sophis-
ticated model (Klimchik et al., 2014) or model-free
compensation (Zhao et al., 2019). The first group can
be easily adopted within the robot workspace but it is
not able to take into account any factor that is not de-
scribed by the model. The second group does not need
any preliminary knowledge on the robot, may take
into account all possible factor influences on the robot
positioning accuracy, but frequently requires either a
considerable amount of data for training (for machine
learning-based algorithms) or real-time estimation of
the end-effector position. Real-time estimation of the
end-effector position is usually not possible on the in-
dustrial floor; that is why this approach is commonly
Akhmetzyanov, A., Rassabin, M., Maloletov, A., Fadeev, M. and Klimchik, A.
Deep Learning with Transfer Learning Method for Error Compensation of Cable-driven Robot.
DOI: 10.5220/0009905605530559
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 553-559
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
553
used for some validations in the lab only. Recent re-
search in kinematic error compensation shows the ef-
ficiency of Deep learning and Reinforcement learn-
ing methods (Pane et al., 2019). The most straight-
forward approach to compensate robot positioning er-
rors is based on the simple linear regression model
which provides acceptable results for the majority of
real cases.
Deep learning is also related to representation or
feature learning term, the process of finding an ap-
propriate representation of data. In our case, the
neural network can learn inverse kinematics without
predefined knowledge of the robot structure. This
method first proved its efficiency on image classifica-
tion tasks (Krizhevsky et al., 2017) and later was ex-
panded to other functions including robot kinematics
(Duka, 2014). The primary drawback of deep learn-
ing compensation methods is the requirement of the
extensive training dataset, resulting in increased cal-
ibration time. In this paper, we address the Transfer
Learning paradigm to reduce the demand for the train-
ing set with real robots for neural network training.
Transfer learning is the improvement of learning
in a new task through the transfer of knowledge from
a related task that has already been learned (Torrey
et al., 2009). Transfer learning also can be character-
ized as a process of knowledge transfer from one task
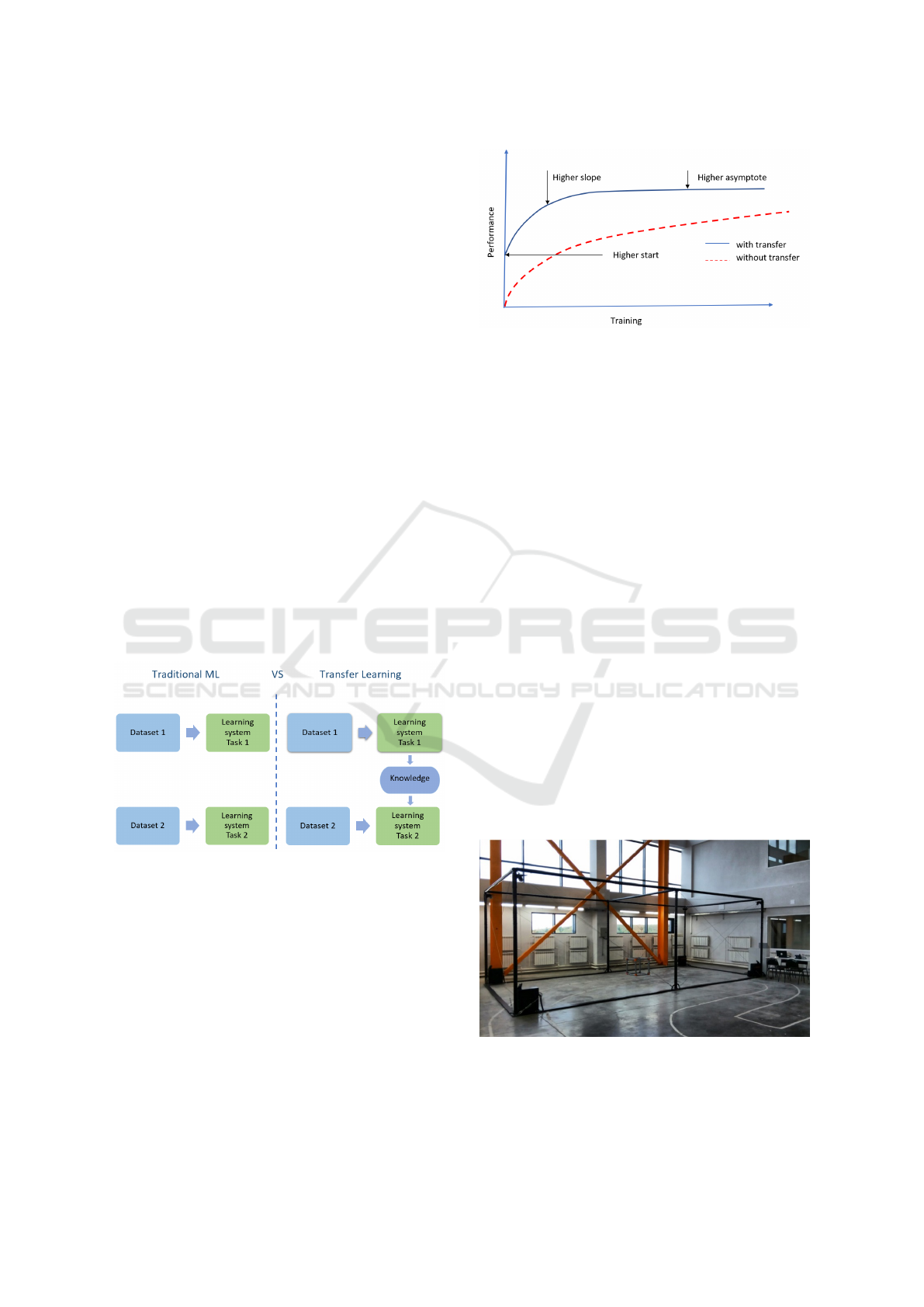
to another, which is visualized in Fig 1.
Figure 1: Traditional ML and transfer learning scheme.
Transfer learning is a broad research field. Its
application includes the Natural Language Process-
ing field with word2vec (Mikolov et al., 2013), Re-
inforcement learning with Curriculum (Narvekar and
Stone, 2018), etc. The benefit of transfer learning
is visualized in Fig. 2 (Torrey et al., 2009). It al-
lows us to improve initial accuracy, improve the slope
of the training curve, or increase the asymptote. In
our robotics case, transfer learning can be potentially
used to compensate different payload applied to our
robot or to speed up the process of regular robot re-
calibration.
Employing testing the initial idea of applying a
Figure 2: Learning performance.
transfer learning approach for cable-driven robot cal-
ibration, we modeled the robot in Unity with an inte-
grated Nvidia PhysX simulation engine. The original-
ity of this work corresponds to the reduction of train-
ing set size required for the neural network through
Transfer Learning application and validation of the
proposed approach on 4-dof cable-driven robot.
2 SYSTEM OVERVIEW
2.1 Cable-driven Robot Description
The approach developed in this paper is tested on a
prototype of the cable-driven parallel robot presented
in Fig.3. The cable robot consists of a frame, sev-
eral winches with cables, and a mobile platform (Fig
4). Winch mechanisms are located at the bottom of
the frame. The cables are thrown through the guide
rollers in the upper part of the frame. Mountings of
guide rollers can rotate around a vertical axis, pro-
viding an orientation of the cables in the direction of
the mobile platform. The free ends of the cables are
attached to a mobile platform on which various equip-
ment can be placed.
Figure 3: Photo of cable-driven parallel robot prototype
used for validation.
The 4-cable robot is an underactuated system. In
this system, it is possible to control the position of the
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
554
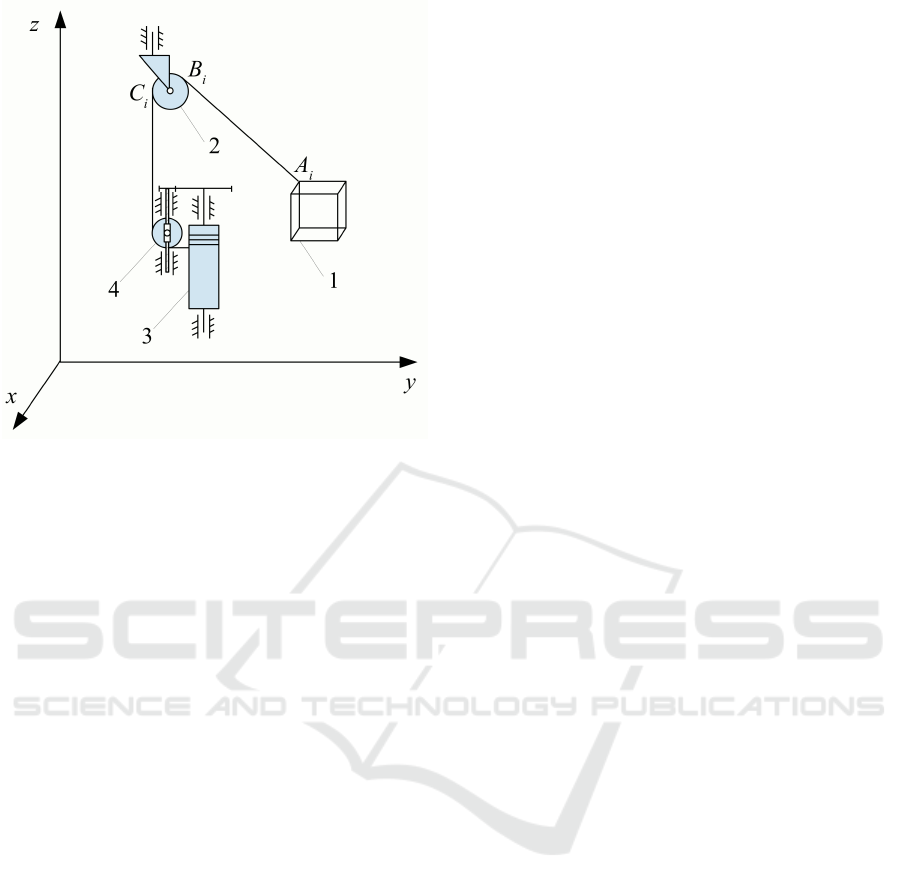
Figure 4: The design scheme of the cable robot: 1 - mobile
platform, 2 - guide roller, 3 - spool, 4 - movable guide roller.
mobile platform, but it is impossible to control its ori-
entation. In addition, cables sagging affects the end-
effector positioning accuracy of the mobile platform.
Formally, 4 actuators should provide control of
4 degrees of freedom, for example, they should al-
low to control the position of the mobile platform and
the angle of rotation around a certain axis. However,
the cables are non-restraining geometric connections,
which are closed only due to external forces acting on
the mobile platform. In other words, cables can only
work in tension. Therefore, using 4 cables, control
of 4 generalized coordinates is possible only in such
configurations of the cable system in which one of the
cables is an antagonist for the other three cables and
at the same time its tension is ensured by the external
forces of the system. In the configuration of the cable
robot under consideration, the mobile platform is sus-
pended from 4 cables. Therefore, none of the cables
can be as an antagonist to the rest. And this means
that to control 4 generalized coordinates, at least one
of the cables must work in compression, which is im-
possible.
The robot control system solves the inverse kine-
matics problem by determining the cable lengths ac-
cording to the given position of the mobile platform,
taking into account the peculiarities of the winding
mechanism and the guide rollers construction (Malo-
letov et al., 2019). However, this system does not take
into account sagging cables and other possible factors
affecting the positioning accuracy of the mobile plat-
form.
The control system provides the ability to enter a
compensating factor to improve the accuracy of robot
control (Fadeev and Maloletov, 2019). But the prob-
lem is the complexity of a fairly accurate estimate of
the value of the compensating factor. Direct measure-
ment of the positioning error of the mobile platform
during the operation of the robot is not always pos-
sible. A more accurate dynamic model of the robot,
taking into account many parameters, requires large
computational costs during the operation of the robot
and the time required for calibration to determine the
values of these parameters. Accordingly, a high-speed
neural network is a good solution, provided that due
the Transfer Learning the time spent on retraining the
network on a particular robot will be comparable to
the time spent on calibrating the dynamic model.
In the experiments, we used a mobile platform,
in which all 4 cables are attached to a single point
and the position of the mobile platform is determined
by the coordinates of this point. To obtain the real
position of the mobile platform, the VantageE laser
tracker is used, which measures the absolute reflector
position with the accuracy of 20 µm + 5 µm/m. To
measure the coordinates of the mobile platform, the
reflector was mounted on the platform above the ca-
bles’ attachment point.
Test positions of a mobile platform were measured
for 1183 points located in nodes of a regular grid of
13x13x7 points. Sizes of the investigated working
space: ξ ∈ [-3500 mm, 3500 mm], η ∈ [-1500 mm,
1500 mm], ζ ∈ [0 mm, 1200 mm]. Experimental stud-
ies were carried out for 3 different payloads: for the
masses equal to 5, 17 and 33 kg. The difference be-
tween the target and obtained positions of the mobile
platform corresponds to the error that should be com-
pensated in the control loop.
2.2 Unity Robot Simulation
To collect data for transfer learning we created the
unity simulation of the cable-driven parallel robot that
integrated the physical engine. The robot structure
screenshot is available in Fig. 5. The robot consists of
4 elastic prismatic joints, the end-effector, and cable
end object which connects prismatic joints to the end-
effector. We can control joint lengths and thus move
the end-effector inside the robot workspace. The end
effector mass influences the tension of robot springs
and changes the kinematics of the robot.
To collect the dataset for the transfer learning ex-
periment we defined a set of the target position and
estimated their end-effector positions in the simulated
environments (Fig. 6). The randomly generated joint
length allowed to collect the dataset for different situ-
ations. We performed the data collection for 2 differ-
ent masses which allowed to estimate the advantage
Deep Learning with Transfer Learning Method for Error Compensation of Cable-driven Robot
555

Figure 5: Cable-driven parallel robot structure in the Unity
environment.
from neural network weight transfer for the training
of the new error compensator.
Figure 6: Unity model parallel simulation.
The resulting dataset consists of the tar-
get and the measured positions in the unity
frame for 2 different masses and available un-
der simulated kinematicsMass1.csv and simu-
lated kinematicsMass2.csv files in the dataset folder
(Akhmetzyanov, 2019). To further apply this dataset
to the real robot, the coordinate frame should be
converted to the robot coordinate system.
3 IMPLEMENTATION AND
RESULTS
To check the transfer learning viability for robot cal-
ibration tasks, we implemented the following exper-
iments. In the first one, we modeled a robot with
Unity and implemented simple inverse kinematics.
Using this simulator, we collected the inverse kine-
matics reference error dataset. In the second one, we
trained the error compensator on it. In the third one,
we modified robot parameters to simulate the uncali-
brated robot behavior with additional weight applied
to the end-effector and used transfer learning to speed
up the process of compensatory training. In the fourth
experiment, we tried to verify the viability of transfer
learning to train compensators on the data from real
robots. Finally, we applied different weighed pay-
loads on the robot and recalibrated the compensator
in a new usage scenario. The results, the dataset, the
source code, and the unity project are available in the
GitHub repository (Akhmetzyanov, 2019).
3.1 Unity Model Compensation
We developed a neural network model that is capable
to fit kinematics and outperform linear model that has
been taken as a baseline. We implemented our model
with Keras framework with a TensorFlow backend.
We provide XYZ coordinates as the input to the net-
work (3 float inputs). Output in our case is a correc-
tion signal for XYZ coordinates (3 float outputs). The
best results were obtained with the neural network
model with one hidden layer containing 7 neurons,
the hyperbolic tangent activation function, and input
normalization. We provided the target position as in-
put and kinematic error as a prediction target. Thus,
our neural network must accept the coordinates of the
position of the mobile platform and provide the pre-
dicted value of the positioning error, which we can
use as a compensating factor in the control system of
the cable robot.
We tested sigmoid, linear, tanh, and ReLU acti-
vation functions with different neural network archi-
tectures. The Hyperbolic tangent activation function
gave the best results, because of its range symmetry
around zero which is true for linear activation as well.
We provide the visualization of kinematics error
data (Fig. 7) as a difference between reference (trian-
gular dots) and measured (round dots) positions. The
codirected shift in positions exists and can be com-
pensated. Errors are not linear relative to the position
in the workspace and thus the non-linear model is re-
quired to compensate errors. MAE for the weight #1
dataset is 25.09 mm, for the weight #2 is 33.93 mm.
Training history is available in Figure 8. After com-
pensation mean error reduced to 0.8 mm.
3.2 Unity Model Transfer Learning
Low error for compensator training is possible due to
unlimited data availability from the simulation. It al-
lows us to estimate optimal model architecture. For
further experiments, we will use only a limited sub-
set of available simulation data. To verify our trans-
fer learning hypothesis, we are comparing sample re-
quirements for model training from scratch and with
inherited neural network weights from the previous
payload type. Besides, we will compare both models
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
556
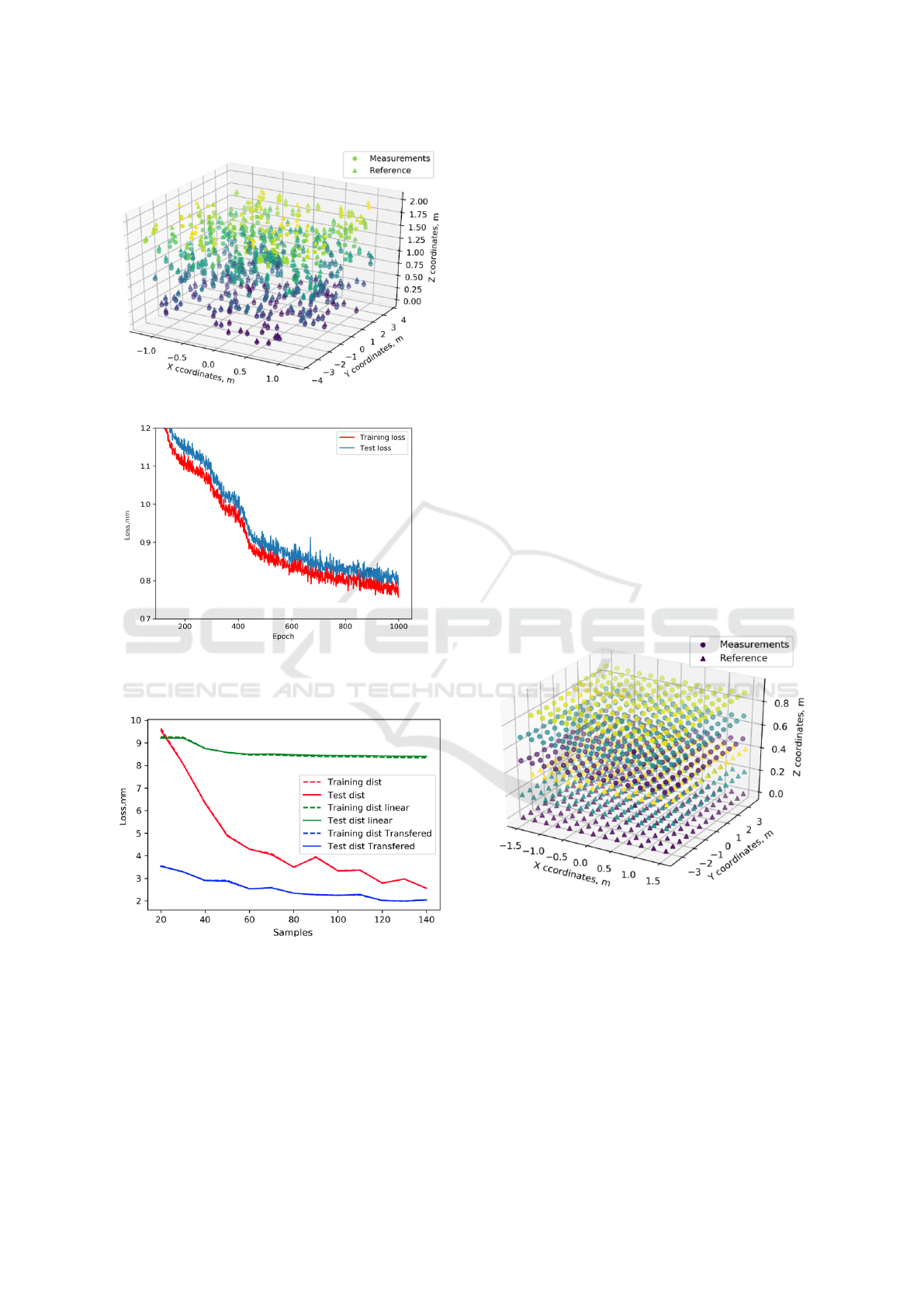
Figure 7: Kinematic errors on simulated data.
Figure 8: Training history on simulated data.
with a linear compensator as a baseline.
Figure 9: Train and test errors on Unity data.
The results of the experiments are presented in
Fig. 9. Here we present the error distance (training
and test set dist) for different training set sizes. The
Hypothesis was confirmed and it seems that weight
transfer is more efficient in terms of sample efficiency.
We see that 22 samples are enough to outperform
the linear model. But with transfer learning, 22 are
enough to adapt the previous model to the new task
with 2.5 times accuracy increase. The same accuracy
can be achieved with 100 samples for training from
scratch. We also increasing the number of training
epochs while increasing the number of training sam-
ples to improve training performance.
In our figures, we use epochs and loss dimensions.
In artificial neural network terms, an epoch stands for
one cycle of gradient descent and backpropagation
through the full training dataset. For the loss term,
we use mean absolute error or L1 Loss which value
is measured in millimeters, thus, naturally describes
the accuracy of our model. Our loss is the arithmetic
mean of absolute differences between our target ref-
erence and predicted values.
3.3 Real Robot Compensation
We collected 2000 samples from real robots for 17
and 33 kg masses. Visualizations of errors for 17 kg
payload available in Fig. 10. In the real robot dataset,
the linear shift of error also explicit. For 5 kg payload,
we have a 1.117m mean Z position and 1.085 m for
33 kg, which means that the bigger mass pulls the end
effector down. Our total error for 5kg: 0.198 m and
error for 33kg: 0.186 m. The training process is avail-
able in Fig. 11. Test error is 8.1 mm after training.
Figure 10: Kinematic error data based on real measure-
ments.
3.4 Real Robot to Real Robot with
Different Mass Compensation
In the production environment, we need to recalibrate
our robot or adapt our controller for the new pay-
load. This is the common application scenario of our
method. From our experiment, in the case of differ-
ent mass adaptation for real robots, transfer learning
strongly reasonable. The results are available in Fig.
Deep Learning with Transfer Learning Method for Error Compensation of Cable-driven Robot
557
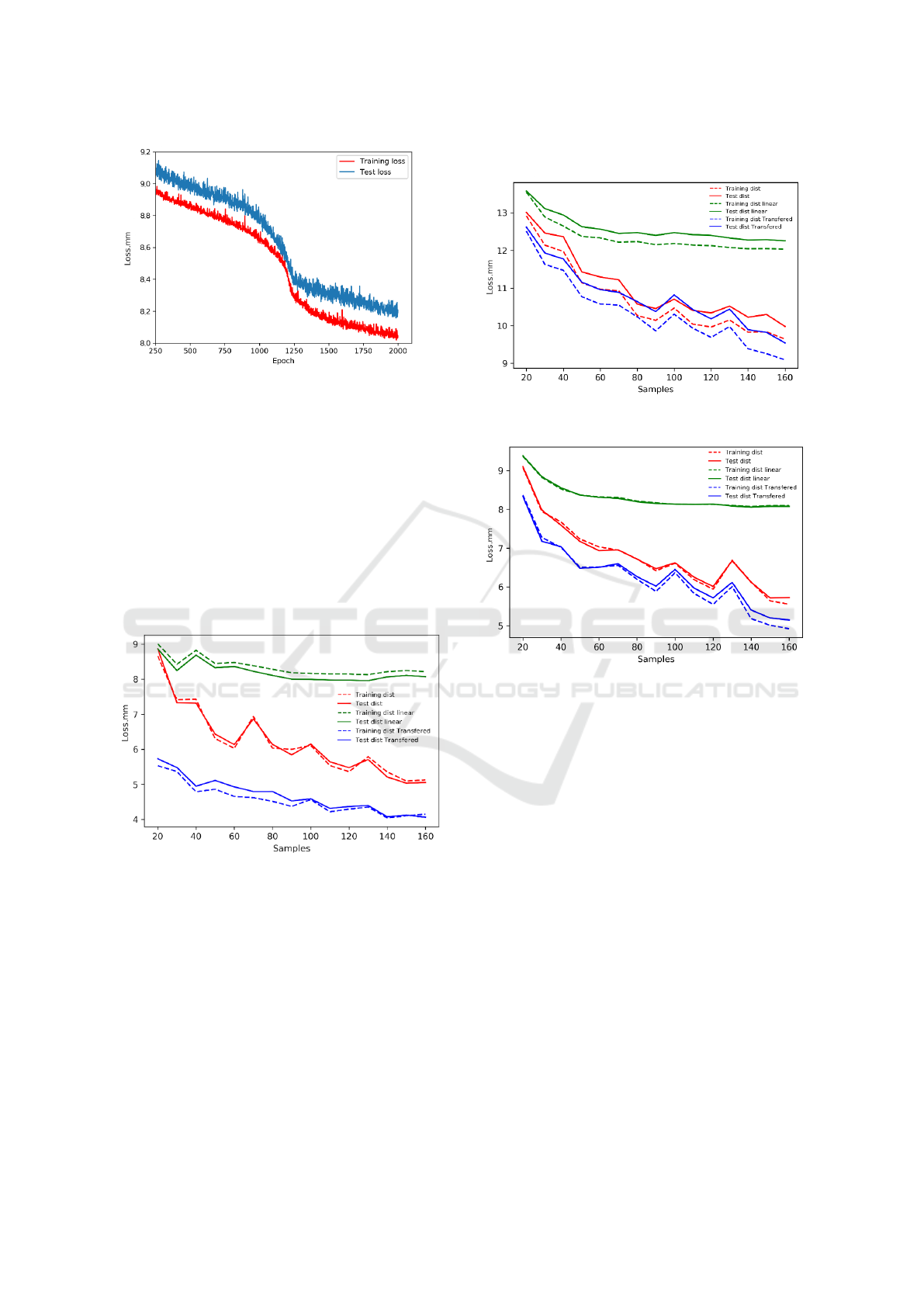
Figure 11: Training history with real data.
12. This experiment proved that it is efficient to apply
transfer learning when we need to speed up the pro-
cess of robot calibration or adaptation to a new end-
effector payload.
In Fig. 12 we see that for 20 samples we achieve
the same performance for linear and neural network
based compensator. For the same training set size
we achieved 30% in accuracy using proposed trans-
fer learning method. To achieve the same accuracy
we need 120 samples to train the neural network from
scratch which shows sample efficiency increase by the
order of magnitude.
Figure 12: Training and test errors.
3.5 Unity Simulation to Real Robot
Transfer Learning
Our experiments showed that in some cases, it is pos-
sible to improve the training process even when the
environment dynamics is different. In our case, we
used weights from simulated environments to train
the real robot error compensator. As a result, some
constraints emerge. For example, the frames should
be co-directed, and scales should be the same. Nor-
malization with zero mean and one standard deviation
help to achieve this task. Fig. 13 and Fig. 14 shows
these results.
Figure 13: Training and test errors for 5 kg.
Figure 14: Training and test errors for 33 kg.
4 CONCLUSIONS
Since modern manipulators is a complex non-linear
kinematic system, a system on neural networks can
be used to compensate for the errors of the displace-
ment of the end effector. However, for this type of
calibration, a large dataset is usually required, which
is an undoubted problem when calibrating with vari-
able parameters, such as mass, at the end of the end
effector. However, as discussed above, the use of sim-
ulation and a part of real data, in conjunction with the
use of the transfer learning technique, allows increas-
ing the accuracy of the manipulator operation with-
out increasing data collection. It is worth noting that
this work examined the application of the method us-
ing only one type of a manipulator - a cable-driven
robot, however, this area in the field of robotics has
prospects and requires further study.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
558

ACKNOWLEDGEMENTS
Work was supported by the RFBR (Russian Founda-
tion for Basic Research)(Grant No. 19-08-01234).
REFERENCES
Akhmetzyanov, A. (2019). Github repository.
https://github.com/AydarAkhmetzyanov/Deep-
Learning-based-cable-driven-robot-kinematics-
error-compensation-with-Transfer-Learning.
Alias, C., Nikolaev, I., Correa Magallanes, E. G., and
Noche, B. (2018). An overview of warehousing appli-
cations based on cable robot technology in logistics.
In 2018 IEEE International Conference on Service
Operations and Logistics, and Informatics (SOLI),
pages 232–239.
Duka, A.-V. (2014). Neural network based inverse kinemat-
ics solution for trajectory tracking of a robotic arm.
Procedia Technology, 12:2027.
Fadeev, M. and Maloletov, A. (2019). Control of the four-
cable-driven parallel robot with the help of the inverse
kinematic model. In Proceedings of the 6th Inter-
national Young Scientists Conference on Information
Technologies, Telecommunications and Control Sys-
tems (ITTCS 2019).
Izard, J.-B., Dubor, A., Herv, P.-E., Cabay, E., Culla, D.,
Rodriguez, M., and Barrado, M. (2017). Large-scale
3d printing with cable-driven parallel robots. page
6976.
Klimchik, A., Bondarenko, D., Pashkevich, A., Briot, S.,
and Furet, B. (2014). Compliance error compensation
in robotic-based milling. CoRR, abs/1409.6231.
Klimchik, A., Pashkevich, A., Chablat, D., and Hovland,
G. (2013). Compliance error compensation tech-
nique for parallel robots composed of non-perfect se-
rial chains. Robotics and Computer-Integrated Manu-
facturing, 29(2):385 – 393.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Im-
agenet classification with deep convolutional neural
networks. Commun. ACM, 60(6):8490.
Maloletov, A., Fadeev, M., and Klimchik, A. (2019). Error
analysis in solving the inverse problem of the cable-
driven parallel underactuated robot kinematics and
methods for their elimination. IFAC-PapersOnLine,
52:1156–1161.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).
Efficient estimation of word representations in vector
space.
Morris, M. and Shoham, M. (2009). Applications and the-
oretical issues of cable-driven robots.
Narvekar, S. and Stone, P. (2018). Learning curriculum
policies for reinforcement learning.
Pane, Y., Nageshrao, S., Kober, J., and Babuska, R. (2019).
Reinforcement learning based compensation methods
for robot manipulators. Engineering Applications of
Artificial Intelligence, 78:236–247.
Rasheed, T., Long, P., and Caro, S. (2020). Wrench-
Feasible Workspace of Mobile Cable-Driven Parallel
Robots. Journal of Mechanisms and Robotics, 12(3).
031009.
Torrey, L., Shavlik, J., Walker, T., and Maclin, R. (2009).
Transfer Learning via Advice Taking, volume 262,
pages 147–170.
Wang, H., Zhang, R., Chen, W., Wang, X., and Pfeifer, R.
(2016). A cable-driven soft robot surgical system for
cardiothoracic endoscopic surgery: preclinical tests in
animals. Surgical Endoscopy, 31:3152–3158.
Wu, Y., Klimchik, A., Caro, S., Furet, B., and Pashkevich,
A. (2015). Geometric calibration of industrial robots
using enhanced partial pose measurements and design
of experiments. Robotics and Computer-Integrated
Manufacturing, 35:151 – 168.
Zhao, G., Zhang, P., Ma, G., and Xiao, W. (2019). System
identification of the nonlinear residual errors of an in-
dustrial robot using massive measurements. Robotics
and Computer-Integrated Manufacturing, 59:104 –
114.
Deep Learning with Transfer Learning Method for Error Compensation of Cable-driven Robot
559
