Detection and Estimation of Helicopters Vibrations by Adaptive Notch
Filters
∗
Antoine Monneau
1,2
, Nacer K. M’Sirdi
1 a
, S
´
ebastien Mavromatis
1
, Guillaume Varra
2
, Marc Salesse
2
and Jean Sequeira
1
1
Aix Marseille Universit
´
e, Universit
´
e de Toulon, CNRS, LIS, LIS UMR CNRS 7020, Marseille, France
2
Airbus Helicopters, Marignane, France
Keywords:
Adaptive Spectral Analysis, Vibration detection, Adaptive Notch Filters, Aerospace Systems.
Abstract:
This paper addresses online vibration detection in helicopters using Adaptive Filters. Adaptive Notch Filters
(ANF) are used to estimate and track the time varying frequencies of the vibrations. We estimate and track the
amplitudes and phases of time varying frequencies of the vibrations. This allows the detection of abnormal
oscillations in the helicopter flight to keep control of the aircraft. In the application presented, we show the
detection of severe vibrations that occurred during a helicopter flight test. This proves the effectiveness of
proposed ANF to track and reject narrow band perturbations.
1 INTRODUCTION
1.1 Mechanical Vibrations of
Helicopters
Within helicopters structure, the excitation’s stresses
are relatively important considering the mass of the
fuselage and its flexibility. The large number of ro-
tating parts aboard a helicopter generates vibrations
that can be fed back into the flight loop by the aircraft
flight control system (AFCS) (see in (NTSB, 2018)).
For example, the main rotor of an Airbus H125 rotates
at 390 rpm, which generates vibrations of frequency
6.5Hz and 19.5Hz within the air-frame.
When excitation go near to natural frequencies of
the helicopter, this may lead to constraints in the me-
chanical parts and increase the vibrations. The in-
creasing need of comfort on board helicopters lead
manufacturers to develop anti-vibration systems. The
consequences of vibrations aboard a helicopter can
range from the discomfort of the crew to the complete
destruction of the aircraft.
The last case occurred on July 6, 2016 with the
first prototype of the Bell 525 Relentless. Accord-
ing to the US National Transportation Safety Board
(NTSB), the in-flight breakup of the aircraft was
a
https://orcid.org/0000-0002-9485-6429
∗
This work is supported by the SASV of the LIS (UMR
CNRS 7020) and Airbus Helicopters.
18
16
14
12
Time [s]
10
8
6
4
2
14
12
10
Frequency [Hz]
8
6
4
2
0
0.02
0.04
0.06
0.08
0
Power Spectral Density [abs]
Figure 1: Power Spectral Density of the helicopter lateral
acceleration Γ
Y pilot
.
caused by severe vibration during a flight test at 185 kt
(342 km/h), (see figure 1 (NTSB, 2018)). The vibra-
tion at 6Hz was so high in the cockpit (17mm of dis-
placement with a vertical load factor up to 3g) that the
pilots were probably unable to see the control panel
nor exit the flight case. Moreover, vibrations caused
unintentional vertical control inputs by the pilot that
further amplified the phenomenon. A secondary feed-
back loop was set by the aircraft’s attitude and head-
ing reference system (AHRS). This system attempted
Monneau, A., M’Sirdi, N., Mavromatis, S., Varra, G., Salesse, M. and Sequeira, J.
Detection and Estimation of Helicopters Vibrations by Adaptive Notch Filters.
DOI: 10.5220/0009910302010207
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 201-207
ISBN: 978-989-758-442-8
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
201

to correct the airframe’s vertical vibration, however it
responded to the 6Hz vibration and exacerbated ro-
tor blades modes. While the rotor was losing speed,
the excessive flapping of the blades became uncon-
trollable and caused the main rotor to strike the heli-
copter’s tail boom. This led to the crash of the aircraft.
Passive systems such as suspensions or active con-
trol systems help to decrease significantly the level of
vibration. The design of such anti-vibration systems
is based on mechanical models of the structure for
damping oscillations near to the natural frequencies.
The perturbation can be filtered based on the mechan-
ical features (see (Krysinski and Malburet, 2007)).
Passive damping and compensations can also be con-
sidered.
Sensors like accelerometers capture these vibrations
and using feedback stabilization or classical con-
trollers generates controls which contain these oscil-
lations. As a consequence, vibrations can be ampli-
fied by the closed loop. The excitation must also be
modeled, which is not an easy task for aerodynamic
processes, but it can help to design active vibration
compensation approaches.
In this paper we focus on fast detection and robust
adaptive estimation of the perturbation, for its com-
pensation. After a spectral analysis of the vibration
(measured by accelerometers) on board helicopters,
the first conclusion was that vibration can appear sud-
denly (see figure 1) with a narrow spectrum with and
changing frequency.
1.2 Objective and Contribution
We propose the use of a narrow band signal model
to describe the perturbation like in (Nehorai, 1985)
or in (M’Sirdi and Landau, 1987). A notch filter
can be considered for perturbation detection and fil-
tering (see figure 2). We propose the use of a band-
width monitored in an Adaptive Notch Filter. Then
we propose an Adaptive Narrow Band Signal predic-
tion method to perform online fast detection of the
vibration frequency. This will generate an alarm and
will track the time varying frequency.
This allow us to develop an efficient and very fast
converging frequency estimation algorithm and adap-
tive filter (see figure 3).
It is worthwhile to note that the notch bandwidth
depends on the parameter 0 < r < 1. When r goes
near to one the notch becomes very narrow. for es-
timation, we will start with r small (wide notch) and
make it go to one for a narrow notch.
The third and last contribution, of this paper, is
the estimation of the amplitudes and phase of the vi-
bration in order to allow its compensation. The dis-
Normalized frequency f/f
s
0 0.1 0.2 0.3 0.4 0.5
Amplitude [dB]
-50
-40
-30
-20
-10
0
10
r=0.5
r=0.7
r=0.8
r=0.9
r=0.95
Figure 2: Frequency response of notch filter H
i
centered
on the normalized frequency
f
f
s
= 0.2 with different notch
bandwidth parameter r.
crete transfer function representation do not catch the
information of the signal power or amplitude. So it
is necessary for detection to estimate either the signal
power (output of the ANF) or the amplitude and phase
of each frequency component.
This is developed assuming not only one but sev-
eral frequencies in the vibrations. Note that the pro-
posed Adaptive Notch Filters may be cascaded to de-
tect and estimate several vibration components.
This paper is organized as follows. After this in-
troduction, section 2 is devoted to some related previ-
ous works in literature and background definition.
In section 3, we present the use of Adaptive Notch
Filters (ANF) for online frequency estimation using a
recursive maximum likelihood (RML) adaptation al-
gorithm. This is followed by a recursive least squares
(RLS) estimation of the amplitudes and phases of the
vibration components. Section 4 presents an applica-
tion of the proposed ANF and amplitude and phases
estimation (APE) method on real data acquired from
an helicopter flying in critical vibration conditions.
This study emphasizes the interest of using the pro-
posed method based on ANF for online spectral es-
timation of vibrations and shows the effectiveness of
the proposed methods.
Figure 3: Frequency estimation using ANF.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
202

2 PREVIOUS WORKS
Vibration spectral analysis is a commonly used tool
in the field of industrial rotating machinery. In fact,
with online processing of vibration signals, it is pos-
sible to extract the current status of the machine. In
case of fault, the machine produces distinctive vibra-
tion patterns that can be compared with those of ref-
erence, thus enabling the fault detection, see (Betta
et al., 2002).
The characteristic patterns of vibratory signals are
often represented in the frequency domain. Most
spectral signal analyzer uses the fast Fourier trans-
form (FFT) to extract the frequency characteristics of
the vibratory signal. An important limitation to the
use of the FFT is its application to non stationary sig-
nals. The windowing of the signal over a fixed period
makes it impossible to obtain the correlation between
time and frequency components.
If the frequencies vary significantly during this pe-
riod, the FFT will generate an error for building the
signal spectrum. Varying frequencies are frequent on
a helicopter, for example when rotors are speeding up.
The wavelet transform is a powerful alternative to
the Fourier transform, which is adapted to the study
of non-stationary signals. In particular, it is able to
perform local spectral analysis over any time inter-
val (zoom) without losing its frequency information.
An application using continuous wavelets transform
(CWT) to the study of vibrations of rotating machines
is presented in (Al-Badour et al., 2011) and (Qin et al.,
2011).
An auto-regressive model can be used to charac-
terize the vibrations of a mechanical assembly. For
example in (Wang and Wong, 1986), an AR filter is
set to output a low residual signal during nominal op-
eration of a helicopter transmission box. When a fault
occurs, for example when a tooth fatigue crack devel-
ops, the residual signal increases because of the vari-
ation of the vibration spectrum. In fact, the AR filter
is no longer centered on the nominal frequencies.
3 REAL TIME SPECTRAL
ANALYSIS
Mechanical vibrations in a helicopter may results
from numerous rotating parts that generate oscillatory
motions. This appear when a transmission shaft is
unbalanced or the pressure on the blades of the heli-
copter varies alternately.
3.1 Frequency Components Estimation
and Tracking
The signals describing the vibrations can be seen as a
sum of sinusoidal components with time varying fre-
quencies f
i
(k), amplitudes C
i
(k) and phases β
i
(k) :
y
k
=
n
∑
i=1
C
i
k
sin(2π f
i
k
T
s
k + β
i
k
) (1)
Counteracting these oscillatory signals in noise relies
on accurate online detection by means of estimation
of their time varying parameters. The recently pro-
posed adaptive identification algorithm deduces the
frequency estimation of narrow band signals based
on Adaptive Notch Filters (ANF), see (M’Sirdi and
al., 2018). Online amplitudes and phases estimation
are made using Weighted Recursive Least-Squares
(WRLS) algorithm on a Fourier series decomposition
of the signal.
3.2 Frequencies Estimation
Adaptive Notch Filters are well known to be very ef-
ficient for extracting frequencies of signals composed
of sinusoidal components, see (M’Sirdi and Landau,
1987). For example, the following second order ANF
H
i
(z
−1
) is proposed to catch the i
th
sinusoidal compo-
nent (frequency f
i
) of a given signal:
H
i
(z
−1
) =
1 + a
i
z
−1
+ z
−2
1 + ra
i
z
−1
+ r
2
z
−2
(2)
• a
i
= −2cos(2π f
i
T
s
) is the notch filter parameter
with T
s
as the signal sampling period
• 0 < r < 1 the notch bandwidth parameter
Figure 2 shows the amplitude of the frequency re-
sponse of H
i
with different r. A small value of this
parameter is associated with a large filter bandwidth
whereas r close to 1 is associated with thin filtering
for an accurate frequency detection.
The ANFs are cascaded when there are several
sinusoidal components to be removed. The transfer
function can be written
∏
p
i=1
H
i
(z
−1
) with i ∈ [1; p],
for p components to estimate. When the ANFs have
converged, each cell will remove one component.
When using the ANFs cascaded of equation:
∏
p
i=1,i6= j
H
i
(z
−1
) with i ∈ [1; p] and i 6= j, all sinu-
soidal components are removed except the one of the
frequency f
j
.
Consequently, the remaining signal noted
e
y
j
k
is
written:
e
y
j
k
=
p
∏
i = 1
i 6= j
1 + a
i
z
−1
+ z
−2
1 + ra
i
z
−1
+ r
2
z
−2
· y
k
(3)
Detection and Estimation of Helicopters Vibrations by Adaptive Notch Filters
203

Filtering of the remaining signal
e
y
j
k
with the last notch
filter H
j
(z
−1
) will give us the prediction error for the
estimation of the frequency component f
j
:
ε
j
k
= H
j
(z
−1
)
e
y
j
k
=
1 + a
j
z
−1
+ z
−2
1 + ra
j
z
−1
+ r
2
z
−2
·
e
y
j
k
(4)
Minimization of this prediction error ε
j
k
will lead to
estimate the error gradient:
ψ
j
k−1
= −
dε
j
k
da
j
=
(1 − r)(1 − rz
−2
)
(1 + ra
j
z
−1
+ r
2
z
−2
)
2
·
e
y
j
k−1
(5)
Real time implementation of the frequency estimation
leads to use the following Recursive Maximum Like-
hood (RML) algorithm for an output Prediction Error
Method (PEM):
f or j = 1,..., p do
1) compute the prediction ε
j
k
2) ˆa
j
k
= ˆa
j
k−1
+ F
j
k−1
ψ
j
k−1
ε
j
k
3) F
j
k
=
F
j
k−1
(λ+ψ
j
k−1
F
j
k−1
ψ
j
k−1
)
(6)
for each time instant k, where:
• ˆa
j
k
= −2cos(2π
ˆ
f
j
k
T
s
)
• F
j
k
is the adaptation gain
• 0 < λ < 1 is the forgetting factor
Several second order notch filter cells are applied in a
cascaded way to removed the frequency components
successively from the prediction equation error. The
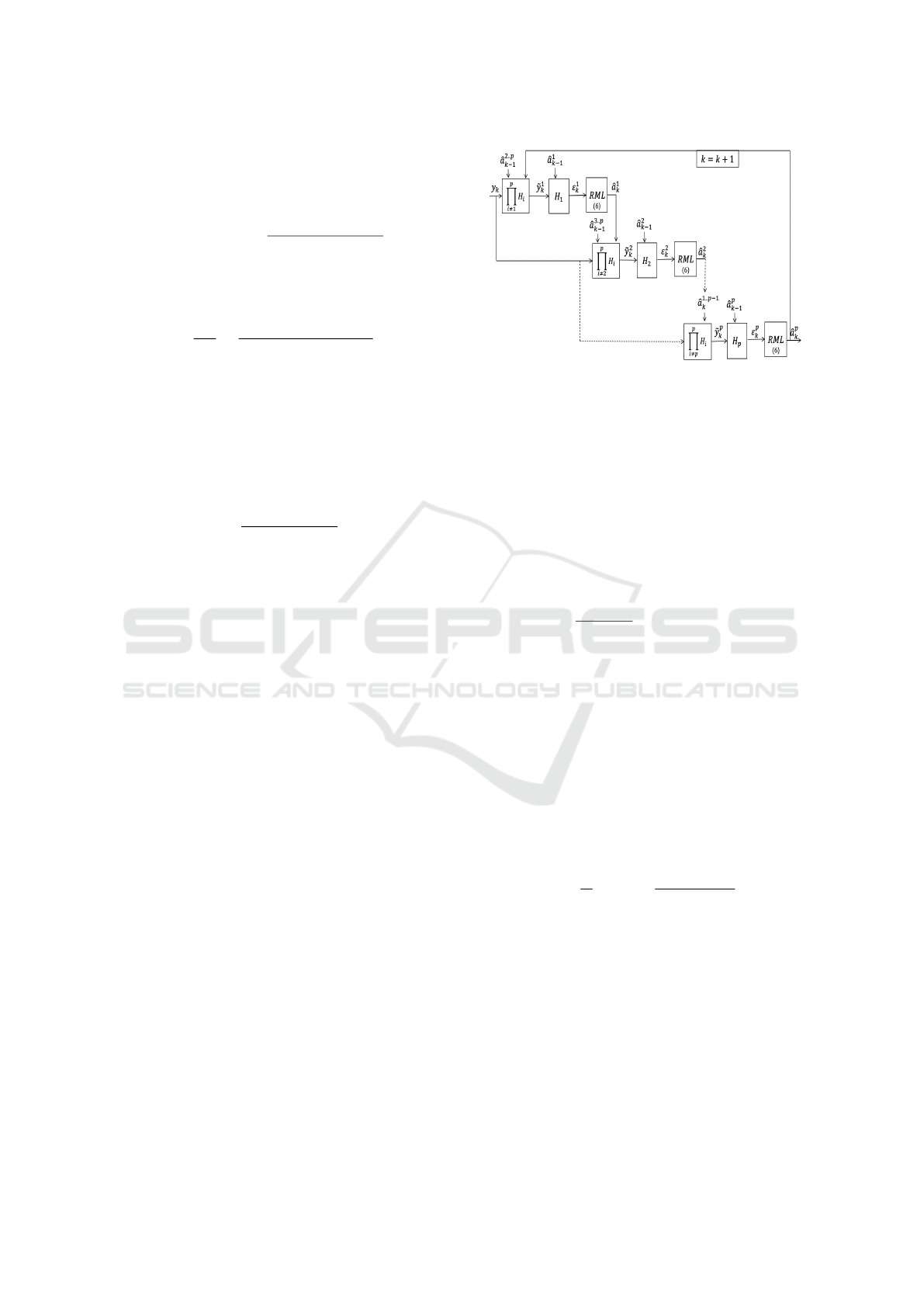
implementation structure is shown on the figure 4.
The cascaded cells are adapted in a recursive manner.
In fact, the current cell input is the output prediction
error of the previous ones.
3.3 Tracking Capabilities
The notch filter bandwidth parameter r
k
is time vary-
ing: starting from a value r
0
to r
f
according to the
following expression:
r
k
= r
d
r
k−1
+ (1 − r
d
)r
f
(7)
0 < r
k
< 1 defines the position of the filter poles along
frequency radials in the z plan. r
k
≈ 0 means that
poles are close to the origin whereas r
k
≈ 1 means
that poles are close to the unit circle (narrow band-
width). r
d
is the exponential coefficient of the filter
bandwidth evolution, it is typically 0.99. The conver-
gence and performance of frequency estimation us-
ing ANF are developed in (M’Sirdi and al., 2018) and
(M’Sirdi et al., 1988).
Figure 4: Frequencies estimation stage of ANF algorithm.
3.4 Amplitudes and Phases Estimation
Once the frequencies of the signal components f
i
are
known or estimated, we can use a Weighted Recur-
sive Least Squares (WRLS) to estimate amplitude and
phase of each component.
The signal defined in equation 1 can be decom-
posed in a Fourier basis as follows:
y
k
=
p
∑
i=1
[g
i
k
cos(2π f
i
k
T
s
k) + h
i
k
sin(2π f
i
k
T
s
k)] + v
k
(8)
where C
i
k
=
q
g
i
k
2
+ h
i
k
2
is the amplitude of the ith
frequency component and β
i
k
its phase, at time k
(tan(β
i
k
) = g
i
k
/h
i
k
).
The parameter vector
ˆ
θ
k
and regression vector Φ
k
are
defined as follows:
ˆ
θ
k
=

g
1
k
g
2
k
... g
p
k
h
1
k
h
2
k
... h
p
k

T
and Φ
k
= [C
k
,S
k
]
T
C
k
=

cos(2π
ˆ
f
1
k
T
s
k) · · · cos (2π
ˆ
f
p
k
T
s
k)

S
k
=

sin(2π
ˆ
f
1
k
T
s
k) · · · sin (2π
ˆ
f
p
k
T
s
k)

(9)
The Fourier parameters g
i
and h
i
are estimated using
the WRLS:
ε
0
k
= y
k
−
ˆ
θ
T
k−1
Φ
k
G
k
=
1
λ
0

G
k−1
−
G
k−1
Φ
T
k
Φ
k
G
k−1
λ
0
+Φ
T
k
G
k−1
Φ
k

ˆ
θ
k
=
ˆ
θ
k−1
+ G
k
Φ
k
ε
0
k
(10)
where ε
0
k
is the a priori prediction error, G
k
the adapta-
tion gain and λ
0
the exponential forgetting factor typ-
ically chosen between 0.98 and 0.995.
The exponential convergence of this algorithm has
been proved, provided that the data are informative
(persistent excitation condition). The proof uses the
results in (Johnson and col., 1982) and (M’Sirdi and
al., 2018). This means the existence narrow band
components in the signal.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
204

4 APPLICATION
In order to test the performance of the online spectral
estimation algorithm, we apply the signals measured
on board of a prototype helicopter during a flight test.
The objective is to determine if the algorithm is able
to detect the predominant frequency (6Hz) and its as-
sociated amplitude.
4.1 Helicopter Lateral Vibration Case
We focus here on the lateral acceleration signal mea-
sured by the accelerometer placed under the pilot’s
seat (Γ
Y pilot
). This location is one of the most sensi-
tive to vibrations, it is far from the center of gravity
of the helicopter and subjected to the lateral bending
mode excitations. This mode of the fuselage includes
left/right yawing motion of the main rotor mast and
lateral motion of the forward cabin. The motions of
the airframe are illustrated in figure 5, that shows an
overlay of the fuselage at its minimum and maximum
displacement for the first lateral bending mode. The
forward part of the cabin (which includes the pilot
seat and the attitude heading reference system) sees
mainly 6 Hz right-left lateral motion.
Figure 5: Helicopter first lateral bending mode (exaggerated
for comprehension).
When looking at the evolution of the spectrum of lat-
eral acceleration over time on figure 1, no significant
vibration is present on the first seconds of the flight
test record. From 6s, we observe a small oscilla-
tion varying around 8Hz. At 13s a 6Hz vibration is
perceived and its amplitude increases strongly until
reaching 0.5g at 16s. Then the vibration decreases
because the test pilot changed the flight case to avoid
damaging the structure of the helicopter.
It is certain that the pilot felt this vibration from
the 13th second, given its amplitude and frequency.
At this moment, the problem of the crew was no
longer the detection of the anomaly but to leave the
Figure 6: Helicopter first vertical bending mode (exagger-
ated for comprehension).
current flight case. Given the low amplitude of the
vibrations (3mm of amplitude at 6Hz), the pilot was
able to recover. But in some extreme case, the severity
of vibrations prevents the pilot to act on the controls.
Only automatic system could recover the helicopter to
safe flight conditions.
Two automatic actions could be envisaged:
• Exit the flight case after the detection of severe
vibrations (for example: automatic action on the
controls to increase the rotational speed of the
main rotor)
• Filter the AFCS output controls to eliminate the
abnormal oscillations amplified by the feedback
loops.
We present in the results the online spectral analy-
sis of the lateral acceleration Γ
Y pilot
performed with
adaptive notch filters. Severe lateral vibrations can be
detected when the amplitude of the Γ
Y pilot
frequency
components exceeds a given threshold. In parallel all
controls sent to actuators can be analysed, in partic-
ular the yaw control δ
ped
(tail rotor collective pitch
control). If a strong vibration is detected on Γ
Y pilot
and its frequency is present in the controls spectrum,
it could be filtered using the associated notch filter.
The detection and tracking of significant oscilla-
tions and the estimation of their frequencies must be
fast enough to be able to filter them efficiently. The
adaptive notch filter method is particularly suited to
the filtering of unexpected vibration since it directly
gives the notch filter to be used and thus eliminate the
propagation of corresponding oscillations in the con-
trol loop.
4.2 Methods Setting
ANF. The parameter estimates ˆa
j
are set to zero ini-
tially. For the ANF bandwidths, r
0
is 0.5, and r
f
is
chosen such that the poles of H
i
are as close as possi-
Detection and Estimation of Helicopters Vibrations by Adaptive Notch Filters
205

Time [s]
0 2 4 6 8 10 12 14 16 18 20
Lateral Acceleration [g]
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Γ
Y pilot
Amplitude estimate ˆa
1
Amplitude estimate ˆa
2
Time [s]
0 2 4 6 8 10 12 14 16 18 20
Frequencies [Hz]
0
2
4
6
8
10
12
14
Frequency estimate
ˆ
f
1
Frequency estimate
ˆ
f
2
Time [s]
0 2 4 6 8 10 12 14 16 18 20
ANF Output [g]
-0.1
-0.05
0
0.05
0.1
ANF Output ǫ
Figure 7: Online spectral estimation of helicopter lateral
acceleration Γ
Y pilot
.
ble to the unit circle. We use r
f
= 0.85. We choose
p = 2 to study the frequency content of Γ
Y pilot
and
p = 3 for δ
ped
.
WRLS. The initial value of the adaptation gain is set
to a large value, typically G
0
= 100. The forgetting
factor λ
0
is set to 0.99, and the parameters vector
ˆ
θ(0)
is initially set to 0.
4.3 Results
We present on figure 7 the online spectral analysis
of the lateral acceleration signal Γ
Y pilot
. The second
curve of this figure depicts the frequencies estimate of
the two main oscillations using ANF algorithm. We
Time [s]
0 2 4 6 8 10 12 14 16 18 20
Yaw control [%]
2
4
6
8
10
12
14
Yaw control δ
ped
measured
Yaw control δ
ped
filtered by ANF
Time [s]
0 2 4 6 8 10 12 14 16 18 20
Frequencies [Hz]
0
2
4
6
8
10
12
14
Frequency estimate
ˆ
f
1
Frequency estimate
ˆ
f
2
Frequency estimate
ˆ
f
3
Figure 8: Online spectral estimation of helicopter yaw con-
trol δ
ped
.
observe that the first frequency estimate
ˆ
f
1
is vary-
ing until 6s where it converges to 8.2Hz. In parallel,
the weighted recursive least squares algorithm esti-
mates the amplitude of this first oscillation using the
current frequency estimate. Amplitude estimate ˆa
1
is
showed in green on the first curve, it never exceeds
0.1g. A second frequency band is tracked by
ˆ
f
2
and
converges to 6Hz from the 13th second. The ampli-
tude estimate ˆa
2
of this frequency band shows a rapid
increase from 14s to 16s when it reaches 0.28g. The
third curve represents the output of the filter, we ob-
serve that it gradually increases from 11s to 16s, this
is due to the presence of others frequency components
than 8.2Hz and 6Hz. In fact when looking at the spec-
trum evolution, other frequency components appear
from 11s at higher frequencies. This is due to main
rotor modes that develops during this high dynamical
phase. These frequencies are not estimated by the two
notch filters, they appear as error. This spectral analy-
sis can be used to detect exaggerate vibration and exit
the current flight conditions. For example, at 15s, the
information of exceedance of 0.2g at 6Hz can be send
to the autopilot computer which would act on the ac-
tuators to change the main rotor states and therefore
decrease the level of vibration.
We present on figure 8 the online spectral analysis
of the yaw control signal δ
ped
. The second graphic
of this figure shows the 3 frequencies estimates of
the signal. Note that the 6Hz oscillation (in red) is
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
206

present from 11s. The first graphic shows δ
ped
mea-
sured (in blue) and its filtered counterpart (in red) us-
ing the notch filter centered on the second frequency
estimate
ˆ
f
2
. In practice, we could trigger the filter-
ing of 6Hz at 15s after severe vibration detection on
Γ
Y pilot
.
5 CONCLUSION AND
PERSPECTIVES
Online estimation of the spectral component of vi-
brations has been proposed based on use of Adaptive
Notch Filters. Frequency tracking is done using a Re-
cursive Maximum Likelihood (RML) algorithm and
Amplitudes and Phases Estimation (APE) adapted by
a Weighed Recursive Least Square (WRLS) algo-
rithm. This method allows on estimation and tracking
of the narrow band frequencies and their amplitudes
and phases.
The main interest of the ANF is the fast tracking
of time-varying frequencies and allows to get directly
accurate prediction of the vibration components to be
compensated. Moreover, this algorithm, being very
fast and with reduced complexity can be easily imple-
mented on computing resources of an aircraft thanks
to its low number of coefficients to estimate (one coef-
ficient for each frequency component). The proposed
approach has been applied to the case of an helicopter
flying in flight test conditions and having a severe vi-
bration.
The application results validate the good perfor-
mance and efficiency of the proposed algorithms to
characterize and track oscillations. Moreover, a strat-
egy based on detection and filtering has been sug-
gested to prevent propagation of abnormal oscilla-
tions in the flight control loop. The proposed APE al-
lows predictions of the vibrations in case where large
prediction horizon can be needed.
The experimental validations on helicopters and
the integration with active vibration control systems
is in progress. Extensions of this work will be done in
case of longer prediction horizon is needed (e.g. for
integration of the compensation in the control loop)
and for model prediction control of the helicopter.
The main concern of the future work will be in-
tegration of the ANF in the helicopter autonomous
flight robust control, to enhance the robustness versus
perturbations.
REFERENCES
Al-Badour, F., Sunar, M., and Cheded, L. (2011). Vibration
analysis of rotating machinery using time frequency
analysis and wavelet techniques. In Mechanical Sys-
tems and Signal Processing, volume 25, pages 2083–
2101.
Betta, G., Liguori, C., and al. (2002). A dsp-based fft-
analyzer for the fault diagnosis of rotating machine
based on vibration analysis. In IEEE Transactions on
Instrumentation and Measurement, volume 51, pages
1316–1322.
Johnson, R. M. and col. (1982). Exponential convergence
of rls with exponential forgetting factor. System and
control letters.
Krysinski, T. and Malburet, F. (2007). Mechanical Vibra-
tions: Active and Passive Control. ISTE.
M’Sirdi, N. and al. (2018). Adaptative notch filters for pre-
diction of narrow band signals. In 7th International
Conference on Systems and Control, Valencia, Spain.
M’Sirdi, N. and Landau, I. (1987). Adaptive evolutionary
spectrum analysis for narrow band signals. In ICASSP,
IEEE International Conference on Acoustics, Speech
and Signal Processing.
M’Sirdi, N. K., Tjokronegoro, H. R., and Landau, I. D.
(1988). An rml algorithm for retrieval of sinusoids
with cascaded notch filters. In ICASSP-88., Interna-
tional Conference on Acoustics, Speech, and Signal
Processing, volume 4, pages 2484–2487.
Nehorai, A. (1985). A minimal parameter adaptive notch
filter with constrained poles and zeros. In Proceed-
ings of ICASSP 85, IEEE International Conference on
Acoustics, Speech, and Signal Processing, volume 10,
pages 1185–1188.
NTSB (2018). Bell 525 crash report dca16fa199. Techni-
cal report, The National Transportation Safety Board
(NTSB), Washington, USA.
Qin, Z., Chen, L., and Bao, X. (2011). Continuous wavelet
transform for non-stationary vibration detection with
phase-otdr. In Optics express, volume 20, pages
20459–20465.
Wang, W. and Wong, A. (1986). Autoregressive model-
based gear fault diagnosis. Journal of Vibration and
Acoustics, 1274:172–179.
Detection and Estimation of Helicopters Vibrations by Adaptive Notch Filters
207