Influence and Evaluation of Potential Fractured Zone by

Surrounding Rockmass Deformation during Deep Tunneling Blasting

Excavation

Jixue Zhou

1,2

, Junhong Huang

1,3,4

, Yi luo

and Xinping Li

Hubei Key Laboratory of Roadway Bridge and Structure, Wuhan University of Technology, Wuhan, China

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, China

School of Safety Science and Emergency Management, Wuhan University of Technology, Wuhan, China

School of Resource, Environmental Science and Engineering, Hubei University of Science and Technology,

Xianning, China

Keywords: Deep Tunnel, Rockmass Excavation, Longitudinal Deformation Curve, Fractured Band, Settlement

Monitoring.

Abstract: Daliang tunnel on Lanzhou-Xinjiang high-speed railway is a typical tunneling project with adverse geological

conditions, especially fractured zones during blasting excavation. A major collapse disaster was caused due

to an unexpected fractured zone, which was excavated and supported improperly. Field test data of

surrounding rockmass displacement is analyzed for changes alone tunnel axis and with time. Deformation

curve versus time for tunnel sections with surrounding rockmass in consistent and relatively high integrity

shows one inflection point, where deformation rate changes from increase to decrease. It revealed by

numerical analysis that before exposed by blasting excavation, rockmass near fractured zone has shown much

deformation. Inflection point can always by observed on the total deformation curve, while it appears earlier

when nearer to the fractured zone. When the inclination angle of the fractured zone is small, the location of

inflection point on deformation-time curve is more sensitive to the change of inclination angle. Existence of

a fractured zone in vicinity ahead can be evaluated for choosing proper blasting excavation and support

method.

1 INTRODUCTION

With the continuous development of the Belt and

Road initiative, construction of Chinese

transportation projects have been further developed.

High-speed railway network are extending in West

China along the Silk Road and through Qinghai-Tibet

Plateau and Xinjiang, where geological conditions are

complex. Deformation and stability of deep-buried

tunnels in complicated geological conditions are

often controlled by fault fractured zone (Lenz et al,

2017), such as similar cases in the world-famous

Tauern Tunnel and the Arlberg Tunnel (Austria), and

the Enasan Tunnel (Japan), during excavation. Fault

fractured zone problems are also often encounter

during tunnel blasting excavation in recent years. Kun

and Onargan (2013) studied the influence of fractured

zone for Izmir Metro Tunnel, and determined risky

area in the tunnel. A Case Study on Nowsoud Tunnel

fractured zones would determine the stress

distribution in adjacent tunnel section, and predicted

squeezing potential for a critical zone (Fatemi et al,

2016). Zhao et al (2013) studied highly risky tunnels

in Guiyang-Guangzhou high-speed railway, and

developed a method for detecting fractured zone in

karst area. Zhang et al (2014) have focused on issues

in excavating the deep and long Taining tunnel, South

China, where several squeezing fault zones have to be

tunneled through, and large deformations were

frequently encountered during excavation. It is

demonstrated by previous studies that, fractured

zones have great influence on surrounding rockmass

integrity in vicinity, thus surrounding rockmass

deformation characteristic is different.

Lisjak et al (2015) argued that the characteristics

of rockmass have great influence on the characteristic

of near field deformation base on the analysis of the

monitoring data about deformation from Mont Terri

underground research laboratory. Moffat et al (2015)

studied the axial strain of roadway and distribution

law based on fiber grating equipment. Lin et al (2017)

Zhou, J., Huang, J., luo, Y. and Li, X.

Inﬂuence and Evaluation of Potential Fractured Zone by Surrounding Rockmass Deformation during Deep Tunneling Blasting Excavation.

DOI: 10.5220/0009968802790286

In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 279-286

ISBN: 978-989-758-444-2

279

investigated the characteristics of strike-slip faults

and displacement in Yanmenguan Tunnel, and

revealed that quality of surrounding rock masses

should be carefully identified, since it can be greatly

influenced by faults nearby and is critical to rockmass

deformation.

In the aspect of calculating the deformation

distribution of longitudinal profile, many scholars

have studied the deformation release coefficient

method and the support force coefficient method (Cai

et al, 2015; Lu et al, 2014). Alejano et al (2012)

calculated the numerical calculation of the rockmass

within a certain GSI (geological strength index) based

on the ideal elasto-plastic assumption, and proposed

a simplified formula for calculating the radius of the

plastic zone of the surrounding rockmass to optimize

the Calculation method of deformation distribution of

strain softening longitudinal section. Vlachopoulos

and Diederichs (2009) optimized the deformation

energy analysis calculation about the longitudinal

profile of surrounding rock, which is based on the

further study of the final radial plastic deformation

calculation method.

In the numerical analysis, Zhao et al (2015)

analyzed the variation of surrounding rockmass

deformation along with the tunnel axis during soft

rock tunneling based on numerical calculation.

Basarir et al (2010) considers the influence of rock

mass characteristics, tunnel size and force state of

surrounding rockmass of the face tunnels, and uses

the Three-Dimensional Finite Element Analysis to

calculate the deformation distribution of the

longitudinal profile of the tunnel and put forward the

fitted formula.

This paper is aiming at the fault fractured zone

with smaller thickness and strike perpendicular to the

axis of the tunnel, so as to explore the deformation

evolution characteristics of surrounding rockmass

caused by tunnel blasting excavation near a fault, by

analyzing field test data and numerical calculation of

surrounding rock deformation.

2 DEFORMATION

CHARACTERISTICS OF

DALIANG TUNNEL BLASTING

EXCAVATION

Lanzhou-Xinjiang high-speed railway (from Lanzhou

to Urumqi), also known as The "Iron Silk Road", is

the longest railway ever built in the world with full

length for 1776 km. Along this railway, Daliang

tunnel starts from DK328+820 and ends at

DK335+370, with length for 6550m. It’s a double-

line tunnel with large section,the excavation height is

13m and the excavation span is 15m. The track

gradient inside the tunnel lies between 6 ‰－9 ‰.

Apart from the entrance point located on the curve,

the rest are located on straight line. Tunnel goes

through the Qilian Mountain (elevation more than

4000m) ,with the maximum buried depth for more

than 600m.

At the time of assisting main tunnel construction,

the tunnel section in 465m depth has faced serious

large abrupt deformation due to blasting excavation.

The maximum deformation rate reached 41mm/d,

which led to cracking of initial support and dropping

of concrete. Deformation of surrounding rockmass is

not convergent. Design reports show that surrounding

rockmass of this section should be Class IV, but in

fact it is crashed thin layer black slate with developed

joints. Surrounding rockmass has obvious tectonic

extrusion characteristic, and is in poor stability

(Figure 1). Large deformation was observed in

surrounding rockmass after application of original

construction design.

Figure 1: The actual surrounding rockmass exposed by

excavation.

Figure 2: Longitudinal section of exit section of Daliang

tunnel.

Maximum daily settlement of DK331+885

section is 56mm, maximum daily convergence value

is 30.8mm. Maximum settlement and convergence of

DK331+766 section values are up to 197.5mm and

151.3mm for 4 days, with maximum daily settlement

and convergence value of 45.8mm and 29.9mm.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

280

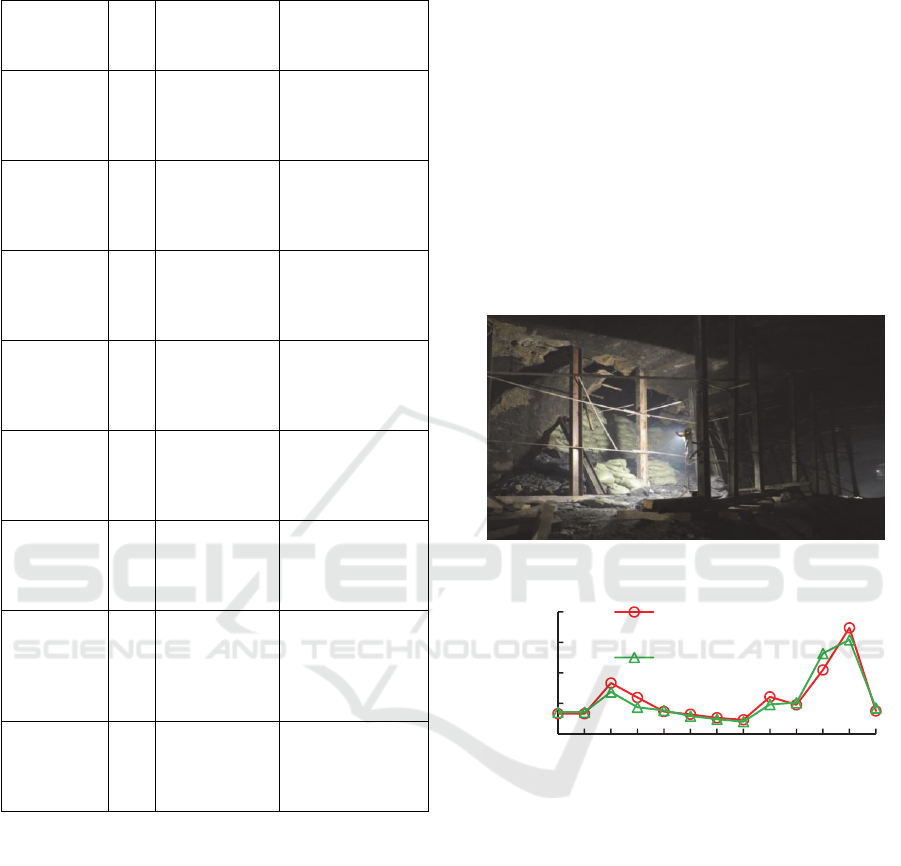
Table 1: Classification and design excavation method for

surrounding rockmass of Daliang tunnel (2010).

Tunnel

Section

Rock

Class

Geological

Feature

Excavation and

Support Method

DK332+040

~DK332+750

III

Deep buried

limestone slate

in good integrity

Bench blasting,

Grade III support

DK332+750

~DK333+250

III

Deep buried

limestone slate

in good integrity

Short bench

blasting. Enhanced

Grade III lining

DK333+250

~DK333+780

III

Deep buried

limestone slate

in good integrity

Bench blasting,

Grade III support

DK333+780

~DK334+300

Deep buried

limestone slate

in good integrity

Full-face blasting,

Grade II support

DK334+300

~DK334+590

III

Deep buried

limestone slate

in good integrity

Bench blasting,

Grade III support

DK334+590

~DK334+790

III

Deep buried

limestone slate

in good integrity

Short bench

blasting. Grade III

lining.

DK334 +790

~DK334+840

Influenced by

Fault F5.

Limestone slate

rich of fractures

Three-bench

blasting in seven

steps. Grade IV

lining.

DK334+840

~DK335+370

Fractured zone

at Fault F5.

Fault breccia

CRD blasting

method. Grade V

lining.

As described in the Tunnel Risk Assessment

Report (Figure 2 and Table 1), the exit of Daliang

Tunnel at DK334+300 ~ DK333+780 was initially

designed for Middle Ordovician limestone sandwich

plate and Class II surrounding rockmass in good

integrity, using full-face method and Class II

rockmass lining. However, during the excavation

process, obvious loosening and broken rockmass is

found after blasting excavation. Even after adopting

bench method and Class III lining conservatively, it

still generated large deformation in surrounding

rockmass after excavation.

When blasting excavating to DK334+241 section,

collapse of surrounding rockmass took place in

17~24m distance to excavation face. The primary

supporting frame squeezed off, with about 185m

rockmass fragments swarmed into the tunnel (Figure

3), forming a cavity 3.5m in depth, 6m in height and

7m in length. The collapse section showed obvious

crushed carbonaceous slate layers formed by strong

tectonic movement, which constantly collapsed in an

unstable state. Within 10m distance to the collapse

area, shot concrete layer cracked in several locations,

including severe dropping off at the dome. The

maximum convergence value for side wall was 1m,

and primary support had intruded the limit.

Monitoring measurement on the sidewall shows that

collapse in surrounding rockmass had led to large

deformation. Settlement and the convergence value

raise up to 36.4mm and 57.6mm on the same day, 5m

distance to the collapse.

Figure 3: Collapse due to a fractured zone.

Figure 4: The surrounding rockmass deformation in vicinity

of the fractured zone.

From long-term observation of accumulative

settlement and convergence deformation values

around the surrounding rockmass in this section

(Figure 4), the accumulated deformation in

surrounding rock mass of this section is much larger

than that of other tunnel sections. Obviously, accurate

judgment on the type of rockmass and identifying

potential fractured zone ahead is significant in

choosing proper blasting excavation methods,

applying advanced support and controlling

surrounding rockmass deformation and stability.

100

200

300

400

DK334+244

DK334+260

DK334+270

DK334+280

DK334+390

DK334+400

DK334+410

DK334+420

DK334+430

DK334+440

DK334+450

DK334+460

Deformation / mm

Settlement

Deformation

Side Convergence

Deformation

Inﬂuence and Evaluation of Potential Fractured Zone by Surrounding Rockmass Deformation during Deep Tunneling Blasting Excavation

281

3 DEFORMATION

DISTRIBUTION

CHARACTERISTICS OF

TUNNEL EXCAVATION

3.1 Abrupt Deformation Mechanism

Induced by Integrity Change of

Tunnel Surrounding Rockmass

Previous studies on deformation distribution caused

by tunnel blasting excavation have more concern to

tunnel cross section. According to the Kastner

Equation 1 (Cui et al, 2014), plastic zone boundary

deformation u* and tunnel wall deformation u can be

calculated in Equation 2 and 3, if the shear expansion

of surrounding rocks is ignore.



)

sin2

sin1

(exp

cossin1

























cctgp

ctgcc

(1)







cossin





 cR

(2)

)(

RRK





(3)

where, R

is tunnel radius, R

is plastic zone radius, σ

is initial in-situ stress, P

is support resistance, φ is

internal friction angle, μ is Poisson's ratio, E is elastic

modulus, and K is plastic zone shear coefficient.

It can be seen that tunnel wall deformation is

approximately proportional to the square of the radius

of the plastic zone, and the deformation of the

surrounding rock is larger when angle of internal

friction is small or in-situ stress is larger. During

tunnel excavation, the sudden encountering of a

fractured zone is actually a sudden change in

rockmass integrity in the longitudinal profile, thus

will induce a large and rapid increase in deformation.

3.2 Abrupt Deformation Mechanism

Induced by Integrity Change of

Tunnel Surrounding Rockmass

Studies on longitudinal deformation curve (LDC)

were mainly limited by the three-dimensional

characteristics of this subject. Studies on convergence

deformation induced by tunnel excavation were

mainly about radial deformation (Carranza-Torres

and Fairhurst, 2000). Under the assumption of linear

elastic assumption, the radial deformation of

surrounding rockmass of circular tunnel can be

expressed in polar coordinate equation:



 

































 2θcos

μ14λ1λ1

2Er

1+μRσ



(4)

where, λ is the lateral pressure coefficient, μ is

poisson's ratio, σ

is the maximum overburden

pressure, η is the constraint loss.

Panet (1995) put forward:































max

-1-1

RZm



(5)

Hoek (1988) proposed:

7.1

max

1.1

exp1































(6)

Most empirical formulas for longitudinal

deformation variation were established based on a

large amount of monitored deformation data. They

can describe variation of radial deformation along

unsupported tunnels. However, after considering the

influence of a fractured zone in front of tunnel face,

the deformation distribution on longitudinal profile is

more complicated, thus numerical calculation method

is adopted to carry out a three-dimensional analysis

(Basarir, 2010).

4 ANALYSIS OF DEFORMATION

CHARACTERISTICS OF

SURROUNDING ROCKMASS

NEAR FRACTURED BAND

4.1 Physical and Mechanical

Parameters of Rockmass and

In-situ Stress Field

Laboratory tests of the sample of rock mass were

carried out. Results showed that the rockmass of

fractured band was mostly formed under tectonic

movement, of which the unit weight was 18.2~19.6

KN/m

. Rockmass in the fractured band has a

relatively uniform gradation. Its coarse particle size

filled with fine particles, thus has a higher internal

friction angle and cohesion force. So, in original

stable state, it can be regarded as equivalent

elastoplastic body, thus the Drucker-Prager yield

criterion is used to calculate the physical and

mechanical parameters of the rockmass as Table 2.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

282

Table 2: Classification and design excavation method for

surrounding rockmass of Daliang tunnel.

Parameter Fractured zone Slate

Elastic Modulus / GPa 2.2 6.8

Poisson's Ratio 0.4 0.31

Cohesion / MPa 0.3 0.64

Internal Friction Angle / ° 27 47

Unit Weight / KN/m

18.9 26.2

Based on the field test, the effective in-situ stress

test data were obtained in the borehole at depth of

15.0m, 18.5m, 19.0m and 27.0m in the inclined shaft,

as shown in Table 3. It is shown that the maximum

value of maximum horizontal principal stress at the

measured depth is 25.14MPa, and is approximately

perpendicular to the borehole axis. The maximum

value of the minimum horizontal principal stress is

13.77MPa. The maximum vertical stress is 12.30MPa.

The lateral pressure coefficient is between 1.89 and

2.08, and is consistent to strata curvature observed on

tunnel face. The in-situ stress is applied to the

calculation model based on test results.

Table 3: Vertical drilling water pressure fracturing results

(2012).

Parameter

Test section depth / m

15 18.5 22 27

Maximum Horizontal

Principal Stress / MPa

23.55 25.14 23.04 24.81

Minimum Horizontal

Principal Stress / MPa

12.95 13.45 13.77 13.37

Vertical Principal

Stress / MPa

12 12.09 12.18 12.3

Lateral Pressure

Coefficient

1.96 2.08 1.89 2.02

4.2 The Finite Element Analysis and

Comparison of the Deformation

Due to Influence of Fractured Zone

A three-dimensional finite element calculation model

is established for practical engineering. The length of

the model is 100m and the width is 200m. The model

is meshed into 117,872 eight-node elements and

120,098 nodes. The fractured zone is meshed by

smaller elements as shown in Figure 5. Element live-

and-kill method is adopted in simulating excavation

process, with excavation footage of 1m. Deformation

evolution of surrounding rockmass at each measuring

points are calculated for the process of tunneling into

the fractured zone.

Figure 5: Finite element model.

Blasting excavation to the vicinity of the tunnel

collapse section is analyzed. Judging by collapse area

width and strata dip angle, the thickness of the

fractured band is about 7m, and the inclination is

about 66° inclination. The strike of the fractured zone

is perpendicular to the excavation direction, and dip

is in the same direction as excavation direction. Based

on the actual excavation process, the excavation rate

is 1m/d, the deformation and evolution of the

surrounding rockmass of each measuring point are

calculated in the process of heading into the fractured

zone and compared with the measured data, as shown

in Figure 6.

Figure 6: The calculative results compared with the

measured data.

Comparison between calculated results and the

measured data of the settlement of the top arch of the

distance crushing zone 38m shows small difference.

On the one hand, in the calculated deformation curve,

obvious deformation rate increases can be observed

about 1 days after the excavation of the measuring

section, showing obvious inflection point on the

deformation-time curve. However, no inflection point

can be observed on the monitored curve. On the other

2013/1/28 2013/2/4 2013/2/11 2013/2/18

Deformation at Arch / mm

Monitored Data

Calculation Result

Calculation Result with Delay

Inﬂuence and Evaluation of Potential Fractured Zone by Surrounding Rockmass Deformation during Deep Tunneling Blasting Excavation

283

hand, the accumulative deformation value of the two

curves show up to 10 mm difference on the 31st day.

However, in actual excavation, when the measuring

section has just been exposed, installation of

monitoring points could be very risky near tunnel face.

Therefore, the actual monitoring process usually

starts several days after the section was exposed.

Considering the above fact, the calculated excavation

curve is shifted leftwards. The new curve shows

consistence with the monitored curve in deformation

trend and value.

Figure 7: The accumulative settlement of the measured

points as tunneling proceeding.

Figure 8: Calculated values for accumulative subsidence

after exposure at different locations.

Variation of arch settlement of each measuring

point during tunneling into the fractured band is

further analyzed, and a three-dimensional surface

map is drawn as shown in Figure 7. The accumulated

settlement distribution of each measuring section is

plotted in as tunnel face is advancing. The negative

value in distance between the monitored section and

the fractured zone indicates that the monitored section

is located behind the fractured zone. The distance

between tunnel face and the fractured zone varies

from 48m to 0. Result shows that when the tunnel face

is constantly advancing to the fractured zone, the

settlement of surrounding rockmass is quite different

on each monitoring section.

Given the ideal situation in the actual monitoring,

in which monitoring starts once the section is exposed

by excavation, the settlement variation of the

monitored sections in different distance to the

fractured zone are plotted as separate curves.

Accumulative settlement deformation of each

monitoring section is shown in Figure 8. Observation

shows the accumulative deformation value of the

monitored section 51m away from the fractured zone

is the largest, while that 21m away from the fractured

zone is the smallest. As shown in Figure 7, the total

accumulative deformation of the monitored section

closer to the fractured zone is larger (including the

deformation before the monitored section is exposed).

On the other hand, the complete deformation time

curve of the monitored section should have an

inflection point. In the deformation accelerating

period from the beginning of the deformation, the

deformation rate is increasing, while the deformation

rate will be decreasing, after the inflection point. If

the deformation curve of the monitored section at

different distances from the fractured zone is a

function of time as Equation 7.





txfx ,





(7)

When x is determined, the function should have

an inflection point at t > 0, and the inflection point

would not be monitored when there is a fractured

zone at a certain distance in front.

Figure 9: Statistical analysis of accumulative deformation

measured at different monitoring sections.

The relationship between monitoring date and

accumulative settlement deformation of different

sections is shown in Figure 9, from which

comprehensive analysis is carried out on the

monitored data of the tunnel sections between

DK330+029 and DK330+115. Rockmass quality

change is very small among there sections, while no

fractured zone was found. On February 18, 2013, the

0 5 10 15

Accumulated

Deformation / mm

Days after Exposure by Excavation / d

100

150

200

0 10203040506070

Accumulated

deformation / mm

Days Monitored / d

Accumulated Deformation/ mm

Cubic Polynomial Fitting

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

284

accumulative settlement value of the top arch has a

significant inflection point in the fitting curve.

Cubic polynomial is used to fit monitored

deformation, for further study on identifying the

inflection point on the deformation curve, as Equation

8, with correlation coefficient of 98.6%.

Y = －0.0012x

+0.1117x

+0.1866x (8)

Given the second derivative of Y(x) being 0, the

inflection point position X ≈ 31d. It means that on the

deformation curve, deformation rate changes from

continuously increasing to reducing on the 31st day.

However, compared with Figure 6, it is found that the

inflection point was not observed in the deformation-

time curve monitored after the section around the

fractured zone is exposed. It is indicated that the

deformation of this section has already been

influenced by the excavation area before this section

being exposed by excavation. Actual accumulative

deformation should be larger. It can also be seen from

Figure 7 that the inflection point in the deformation-

time curve on the section closer to the fractured zone

should occur before the section is exposed by

excavation, i.e. X

< 0.

4.3 Influence of Inclined Angle on

Deformation Curve of Surrounding

Rockmass

The deformation of the surrounding rockmass caused

by tunnel excavation through fractured zone in

different inclinations are analyzed. As analyzed by

similar method as shown in Figure 9, the position of

the inflection point on the settlement deformation

curves of sections in various axial distances to the

fractured zone are shown in Table 4.

As observed, under the influence of specific

inclination angle of the fractured zone, the inflection

point would appear sooner after the section is exposed,

when the section is closer to the fractured zone. The

change in inclination angle of the fractured zone has

a great influence on when the inflection point would

appear. When the inclination angle is small, the

inclination change has a greater effect on the change

of the inflection point position on time domain. When

the inclination angle is close to 90°, the inflection

position is not sensitive to inclination angle. However,

when the inclination angle is smaller, the location of

inflection point on the deformation-time curve is

much more sensitive. For example, when the

inclination angle is 100°, if the section is monitored

right after exposure, the inflection point can still be

monitored a few days later. So as to determine a

possible existence of a fractured zone several tens of

meters ahead the monitored section. Thus timely

adjustment can be applied to excavation and support

parameters, to avoid a potential large-scale

construction disasters.

Table 4: Inflection point position of different monitoring

sections due to inclination change of fractured zone.

Distance to

Fractured

Zone / m

Inclination angle of fractured zone / °

40 50 60 70 80 90 100 110 120 130 140

51 -6 -1 3 6 7 8 10 11 12 13 15

42 -9 -4 0 2 4 6 8 9 10 12 14

33 -13-8-40 1 3 5 7 8 1012

21 -18 -12 -7 -3 -1 1 3 5 6 8 11

5 CONCLUSION

Analysis of the collapse disaster during the blasting

excavation of the Lanzhou-Xinjiang high-speed

railway, due to the existence of a fractured zone. The

selection of reasonable blasting parameters is of great

significance to avoid the construction disaster caused

by fractured zone. Following conclusions can be

drawn based on theoretical and numerical analysis on

the monitored data of surrounding rockmass

deformation in different tunnel section.

(1) The deformation rate of surrounding rockmass

in increases first and then decreases along tunnel axis,

when rockmass integrity is high and even. And there

is an inflection point on the deformation-time curve.

By observing the occurrence date of the inflection

point after section exposure, the possibility of

fractured zone ahead can be estimated, and

reasonable adjustment can be applied to excavation

and support blasting excavation parameters to avoid

construction disasters.

(2) The deformation process of the surrounding

rockmass is obviously affected by fractured zone in

vicinity, which makes a sooner appearance of the

inflection point on deformation-time curve. Under the

same circumstance, the surrounding rockmass near

the fractured zone may even generate a large portion

of deformation before excavation, and the inflection

point may disappear in the monitored deformation

curve from the exposure of the section. And the

deformation rate might only be reducing after the

excavation.

Inﬂuence and Evaluation of Potential Fractured Zone by Surrounding Rockmass Deformation during Deep Tunneling Blasting Excavation

285

(3) When the inclination angle of the fractured

zone is small, the location of inflection point on

deformation-time curve is more sensitive to the

change of inclination angle. And it is much less

sensitive to the inclination angle, when it is close to

90°.

ACKNOWLEDGEMENTS

This work was supported by the Postdoctoral

Innovation Research Post in Hubei Province

(20201jb001), the Fundamental Research Funds for

the Central Universities (WUT: 2019IVA098), the

Youth Talent Project of Science and Technology

Research Program of Hubei Provincial Department of

Education (Q20192801), and the Fundamental

Research Funds for the National Natural Science

Foundation of China (

51779197, 51979208,

51774222

REFERENCES

Alejano, LR., Rodriguez-Dono, A., Veiga, M., 2012.

Plastic radii and longitudinal deformation profiles of

tunnels excavated in strain-softening rock masses.

Tunnelling and Underground Space Technology, 30:

169-182.

Basarir, H., Genis, M., Ozarslan, A., 2010. The analysis of

radial displacements occurring near the face of a

circular opening in weak rock mass. International

Journal of Rock Mechanics and Mining Sciences, 47(5):

771-783.

Cai, Y., Jiang, Y., Djamaluddin, I., Iura, T., Esaki, T., 2015.

An analytical model considering interaction behavior of

grouted rock bolts for convergence-confinement

method in tunneling design. International Journal of

Rock Mechanics and Mining Sciences, 76: 112-126.

Carranza-Torres, C., Fairhurst, C., 2000. Application of the

convergence-confinement method of tunnel design to

rock masses that satisfy the Hoek-Brown failure

criterion. Tunnelling and Underground Space

Technology, 15(2): 187-213.

China Railway First Surver and Design Institute Group CO.,

LTD. 2010. Risk Evaluation Report for Daliang Tunnel

of Gansu-Qinghai Section on New Second Lanzhou-

Urumqi Double-track Railway.

Cui, L., Zheng, J., Zhang, R., Zhang, W., 2014. Study of

support pressure and surrounding rock deformation of a

circular tunnel with an elastoplastic softening model.

Rock and Soil Mechanics, 35(3): 717-722+728.

Fatemi Aghda, S., Ganjalipour, K., Esmaeil Zadeh, M.,

2016. Comparison of Squeezing Prediction Methods: A

Case Study on Nowsoud Tunnel. Geotechnical and

Geological Engineering, 34(5): 1487-1512.

Hoek, E., 1988. In The Hoek-Brown failure criterion-a

1988 update, Proc. 15th Canadian Rock Mech. Symp,

'Ed.' Toronto, Dept. Civil Engineering, University of

Toronto, p: 31-38.

Institute of Rock and Soil Mechanics, Chinese Academy of

Sciences, 2012. High In-situ Stress and Surrounding

Rockmass Deformation Report for Daliang Tunnel of

Gansu-Qinghai Section on New Second Lanzhou-

Urumqi Double-track Railway.

Kun, M., 2013. Onargan T. Influence of the fault zone in

shallow tunneling: A case study of Izmir Metro Tunnel.

Tunnelling and Underground Space Technology, 33:

34-45.

Lenz, G., Kluckner, A., Holzer, R., Stadlmann, T.,

Schachinger, T., Gobiet, Gl., 2017. Prediction of fault

zones based on geological and geotechnical

observations during tunnel construction. Geomechanics

and Tunnelling, 10(4): 366-379.

Lin, D., Yuan, R., Shang, Y., Bao, W., Wang, K., Zhang,

Z., Li, K., He, W., 2017. Deformation and failure of a

tunnel in the restraining bend of a strike-slip fault zone:

an example from Hengshan Mountain, Shanxi Province,

China. Bulletin of Engineering Geology and the

Environment, 76(1): 263-274.

Lisjak, A., Garitte, B., Grasselli, G., Muller, HR., Vietor, T.,

2015. The excavation of a circular tunnel in a bedded

argillaceous rock (Opalinus Clay): Short-term rock

mass response and FDEM numerical analysis.

Tunnelling and Underground Space Technology, 45:

227-248.

Lu, AZ., Chen HY., Qin, Y., Zhang, N., 2014. Shape

optimisation of the support section of a tunnel at great

depths, Computers and Geotechnics, 61: 190-197.

Moffat, R., Sotomayor, J., Beltran, JF., 2015. Estimating

tunnel wall displacements using a simple sensor based

on a Brillouin optical time domain reflectometer

apparatus. International Journal of Rock Mechanics and

Mining Sciences, 75: 233-243.

Panet, M., 1995. Le calcul des tunnels par la méthode

convergence-confinement. 'Ed.' Presses ENPC.

Vlachopoulos, N., Diederichs, MS., 2009. Improved

Longitudinal Displacement Profiles for Convergence

Confinement Analysis of Deep Tunnels. Rock

Mechanics and Rock Engineering, 42(2): 131-146.

Zhang, G., Jiao, Y., Wang, H., 2014. Outstanding issues in

excavation of deep and long rock tunnels: a case study.

Canadian Geotechnical Journal, 51(9): 984-994.

Zhao, K., Bonini, M., Debernardi, D., Janutolo, M., Barla,

G., Chen, GX., 2015. Computational modelling of the

mechanised excavation of deep tunnels in weak rock.

Computers and Geotechnics, 66: 158-171.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

286