
Overview on Modeling for Control of Autonomous Road Vehicles Platoon
Nacer K. M’Sirdi
1 a
, Abdelhak Dahmani
1
and Habib Nasser
2,†
1
Aix Marseille University, Universit
´
e de Toulon, CNRS, LIS UMR 7020, SASV, Marseille, France
2
RDI’UP (Innovative Research), 2 Rue Louis Bl
´
eriot, 78130 Les Mureaux, France
†
https://www.rdiup.com/
Keywords:
Vehicles Fleet, Fleet Modeling, Modelling and Control Approach.
Abstract:
This is an overview on the models used to control fleets of road vehicles. In general, simplified vehicle models
are used and their coupling features are introduced through the (individual) controllers. The robustness and
precision of motion control needs geometric, kinematic and dynamic descriptions. We propose a modeling
methodology for robots platooning to introduce specific features in the platoon behavior. This overview pro-
poses reference models to link the fleet vehicles and assign a character to the group independent from control.
1 INTRODUCTION
1.1 Context and Objectives
To increase the capacity of the infrastructures while
improving the safety and the comfort, vehicle pla-
tooning is of interest. Several solutions are consid-
ered, in the urban environment and on the highway,
by automating vehicles driving and autonomous fleet
control (Nouveliere et al., 2002; Alcala et al., 2018;
Allou and Zennir, 2018). This can be a very efficient
means of transportation for passengers and freight and
for increasing traffic capacity. For example, a convoy
of trucks carries goods, with only one driver (Bauer
and Tomizuka, 1996; M’Sirdi, 2018). Other benefits,
such as reducing fuel consumption and minimizing la-
bor, may exist in piggybacking or truck-mounted cars.
The convoy consists of a leading vehicle and trailing
trucks. The leader can be autonomous or manually
driven, other vehicles follow him with a safety dis-
tance to avoid collisions between vehicles.
Depending on the application purpose, a lot of ve-
hicle models have been considered in the literature
(Nouveliere et al., 2002; Alcala et al., 2018; Allou
and Zennir, 2018). The representation is, in general,
simplified and the fleet control is at a level higher than
the one of the embedded feedback (local level of the
DoF or actuators). Robust control laws, can avoid the
use of precise models, but this means that all efforts
are done in control (Menhour et al., 2015).
a
https://orcid.org/0000-0002-9485-6429
The nonlinear robust control approaches give the
fleet a better controlled and more robust behavior
against uncertainties (Szanto et al., 2020; Lenain,
2005; Guillet et al., 2014). In this type of ap-
proach, the disadvantages are the availability of in-
formation on the vehicles of the chain, the need for
sensors, the communication of the data, and the ob-
servability. There is still a lack of inter vehicles rela-
tions,environment interactions and global strategy.
There is no general modelling methodology. The
main focus of this paper is the fleet modeling and in-
formation contained in the models. It is well known
that there exists also robust control approaches, avoid-
ing models or considering only integrators in the pro-
cess (Menhour et al., 2015). Indeed, the entire vehicle
dynamic controllability must be mobilized to perform
safe driving and emergency maneuvers like an obsta-
cle or slipping avoidance and urgent controlled brak-
ing (Ali et al., 2015; M’Sirdi, 2018). The models used
for fleets control focus on the representation of rela-
tive trajectories of the vehicles. Some of them con-
sider only longitudinal motion (1D) and few of them
are 2D. Each modeling approach suggests or more ap-
propriate control approaches (M’Sirdi, 2020).
The organization of this paper is as follows. Af-
ter this introduction, the section 2 presents the convoy
models used in fleets control. This is followed by a
general overview of the most often used control archi-
tectures (local and global). In section 3, inspired from
the nature, we propose a new modeling approach to
represent a fleet of vehicles. This will allow to assign
a special character to the group and application of sev-
208
M’Sirdi, N., Dahmani, A. and Nasser, H.
Overview on Modeling for Control of Autonomous Road Vehicles Platoon.
DOI: 10.5220/0009971302080216
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 208-216
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

eral non linear control approaches for the autonomous
fleet driving. Then we conclude and give some per-
spectives on our work on observation and control of
robots platooning.
2 CONVOY MODELS USED IN
CONTROL
Table 1: Table of state variables and Acronyms.
L distance between the vehicle axles
G
i
The gravity center of vehicle i
l
f
distance from the front axle to G
l
r
distance from the rear axle to G
m
i
mass of vehicle i plus 2 wheels
X
i
Longitudinal position of vehicle i in R
0
Y
i
Lateral position of vehicle i in R
0
ψ
i
Angular position of vehicle i in R
0
ψ
Γ
Orientation at M of ref Trajectory in R
0
x
v
Longitudinal vehicle position in R
v
y
v
Lateral vehicle position in R
v
δ
i
Front Steering angle (input vehicle i)
δ
r
rear Steering angle (d
r
= 0 in general)
e
i,i−1
longit distance inter vehicles i and i-1
ε
i, j
lateral distance between vehicles i and j
u
i
input of the vehicle i
d
i, j
desired distance between vehicles
d
i
IVD: Inter Vehicles Distance
h IVSD Inter Vehicle Safety Distance
s
i
Curvilinear abcissa of the vehicle i
LDI Londitudinal Double Integrator
LUM Longitudinal Unidirectional Model
LBM Longitudinal Bidirectional Model
ACM Anti-Collision Margin
L distance between the vehicle axles
G
i
The gravity center of vehicle i
l
f
distance from the front axle to G
l
r
distance from the rear axle to G
c(s) Curvature tangent to Γ at M
B
f
,K
f
Damping and Stifness of RM-IVDR
f , r, l, d Indices for front, rear, left and right sides
RM- Reference Model
IVDR Inter Vehicles Dynamic Relations
2.1 Longitudinal Control Models (1D)
In general, a set of simplified and individual 1D mod-
els are considered. The only interest of 1D models is
the study of the IVSD (Inter-Vehicle Safety Distance).
This type of model and its controls ignore the lateral
movement and curvatures of the trajectory. Note that
there is no relation between the vehicles equations ex-
cept by the relative distance variables e
i
, which is used
in the control only.
2.1.1 Longitudinal Unidirectional Models
(LUM)
The most used model, for the longitudinal control of
the convoy is the double Integrator (Swaroop, 1994).
The input u
i
is the force applied to the vehicle i.
¨x
i
= u
i
(1)
For the Longitudinal Unidirectional Model, some au-
thors add a mass and a damper (Avanzini, 2010). m
is the vehicle mass and b a damper. Many parameters
are neglected. The vehicles are considered indepen-
dent and linked only by the control.
m ¨x
i
+ b ˙x + k(x − d
r
) = u
i
(2)
The desired relative Inter-Vehicle Distance IVD (see
figure 1) d
r
is considered in the control with the error
or relative distance to the preceding vehicle e
i,i−1
.
e
i, j
= x
j
− x
i
− (i − j)d (3)
Figure 1: LDI and LUM Mass-Spring-Damper.
2.1.2 Longitudinal Bidirectional Models (LBM)
The LBM is a second-order system and the distances
to the neighbors (preceding e
i,i−1
and following e
i,i+1
)
are fed back through the control (Avanzini, 2010). In
this scheme, the individual vehicle models are cou-
pled with the control interaction forces. Figure 1
shows a bidirectional longitudinal (mass, spring and
damper) model which link each vehicle to its neigh-
bors (previous and follower one).
2.1.3 LBM-VISD with Inter Vehicles Safety
Distance (IVSD)
The model dynamic equations, for a fleet of n vehi-
cles, may be written as follows:
m ¨x
1
= k(x
1
− x
2
− d
1,2
) − c(˙x
1
− ˙x
2
) − h ˙x
1
+ u
1
m ¨x
i
= k(x
i−1
− x
i
− d
i−1,i
) − k(x
i
− x
i+1
− d
i,i+1
)+
+c( ˙x
i−1
− 2 ˙x
i
+ ˙x
i+1
) − h ˙x
i
+ u
i
. . . . . .
m ¨x
n
= k(x
n−1
− x
n
− d
n−1,n
) − c(˙x
n−1
− ˙x
n
) − h ˙x
n
+ u
n
(4)
where k is the coefficient of stiffness, c the damping
coefficient and d the length of the spring (inter-vehicle
distance). The leading vehicle is driven by force input
control u
1
. It receives the forces of constraints trans-
mitted by the links springs - dampers, on the chain of
Overview on Modeling for Control of Autonomous Road Vehicles Platoon
209

the vehicles of the convoy. The inputs u
2
,...u
n
(not
used in the literature) may be zero or some comple-
mentary control inputs that we have added to enhance
the controllability.
• with either d
i−1,i
= d = constant and h = 0 ∀i.
This imposes an IVD. To ensure the stability of
the fleet, according to the authors (Yanakiev and
Kanellakopoulos, 1996) (Avanzini, 2010), the ra-
tio c
2
/km must be greater than constants that in-
crease proportionally to the vehicle index i in the
convoy.
• or d
i−1,i
chosen for each vehicle i and h = 0 ∀i.
Another IVD has been proposed, to improve the
stability (Contet et al., 2009). It consists of choos-
ing, for each vehicle, a distance command d
i−1,i
between the vehicles of the convoy, according to
the state of the fleet and stability constraints
• or d
i−1,i
= d = constant and h 6= 0. The Anti-
Collision Margin (ACM) h is added as a time dis-
tance margin to avoid collisions between vehicles
(Mu’azu et al., 2017).
The study of stability in (Contet et al., 2009), shows
that the bidirectional control architecture gives good
theoretical results when the number of vehicles of the
convoy is limited. In general, these models are used
for convoys that move at low speeds, do not take into
account the risk of failures, or the effects of errors
and noise measurement (Avanzini, 2010). Adding a
dynamics in the model has benefits.
2.2 2D Convoy Models for Control
2.2.1 Unicycle Model (UCM)
A unicycle uses a minimal kinematic representation.
v
i
is the linear velocity of the vehicle i and ψ
i
is the
orientation angle of the vehicle wheel i (Samson and
Ait-Abderrahim, 1990; Xiang and Braunl, 2010; Ri-
cardo et al., 2008).
˙
X
i
= v
x
vi
.cos(ψ
i
)
˙
Y
i
= v
x
vi
sin(ψ
i
)
˙
ψ
i
= w
i
K
γ
γ
i
(5)
A study of chain transformation for a convoy is pro-
posed, to determine the Inter-Vehicle Distances (d
v
)
and the relative caps (γ) between the neighboring ve-
hicles. The control applied to the convoy vehicles is
based on a tangential linearization; The overall stabil-
ity has been proven for the linearized model.
2.2.2 Use of the Kinematic Models (KM)
Several applications use only a kinematic model, in a
2D space with limited speeds in the urban frame.
This is not advisable for a truck convoy
on the highway. Using a bidirectional con-
trol can alleviate the problem (Avanzini et al.,
2010). The model equations are presented
in equation (6). One can see a demo of this
model in open loop, by M Compere, in https:
//ch.mathworks.com/matlabcentral/fileexchange/
67034-simple-animation-for-n-vehicles?focused=
9173618&tab=function
˙
X
i
= v
x
vi
.cos(ψ
i
) −
L
2
.
˙
ψ
i
.sin ψ
i
˙
Y
i
= v
x
vi
.sin(ψ
i
) +
L
2
.
˙
ψ
i
.cos ψ
i
˙
ψ
i
=
v
x
vi
.δ
i
L
i
(6)
2.2.3 Kinematics Bicycle Model (KBM)
Geometric Convoy Model. Now we need to local-
ize the vehicle with regard to the reference trajectory
to be followed. The road reference path is noted Γ.
Figure 2 shows the geometric scheme of the vehicles
with regard to the path Γ in the absolute frame R
0
.
The vehicle is modeled with respect to the reference
path Γ (Lenain, 2005; Cartade et al., 2005). The ge-
ometric model defines the relations between vehicle
variables (in the vehicle frame R
v
) to Cartesian ones
and to the reference trajectory.
Figure 2: Bicycle Model.
Let us recall that ψ
i
is the orientation in the ab-
solute reference R
0
and l
d
i
denotes the desired IVSD
distance between 2 vehicles. Let s
i
be the curvilinear
abscissa of the vehicle i. This abscissa is at a distance
d
i
from the reference (desired) trajectory Γ (at point
M).
c(s): the curvature of the trajectory Γ at the point M
ψ
Γ
(s): Orientation of the tangent at M, in the absolute
frame R
0
(desired vehicle orientation)
˜
ψ
i
= ψ
i
−ψ
Γ
(s) is the angular deviation of the vehicle
i relative to Γ.
e
s
i
= s
i−1
− s
i
− l
d
i
is the curvilinear spacing error, or
difference between 2 vehicles with a kinematic model
expressed as follows (see fig 2).
˙
X = v.cos(ψ
i
+ β)
˙
Y = v.sin(ψ
i
+ β)
(7)
β denotes the side slip Angle
δ
i
and δ
r
i
are the front and rear steering
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
210

δ
v
= Ψ
i
+ β is the vehicle motion angle
β = tan
−1
(
l
r
.tan(δ)+l
f
.tan(δ
r
)
l
f
+l
r
)
˙
Ψ =
v.cos(β)
l
f
+l
r
.(tan(δ) − tan(δ
r
)
(8)
Assuming that δ
r
= 0 and β = 0, the Kinematics of
the system can be written as in equation (6)
Now, to be able to follow a trajectory (Γ) let us
define the desired position (Fig2) for the vehicle as
(X
d
,Y
d
). We get ψ
d
ψ
d
= tan
−1
(
(Y
d
−Y )
(X
d
− X)
) (9)
For the control, that there are two control inputs
(steering and velocity), we then define the curvilinear
trajectory errors (for the distance and the angle):
e
d
=
p
(X
d
− X)
2
+ (Y
d
−Y )
2
e
ψ
= ψ
d
− ψ
(10)
For the longitudinal and lateral control (in Carte-
sian space R
0
) of a train of two vehicles following a
leader, in (Allou and Zennir, 2018), the authors use
multi-PID controllers (Optimized by PSO and Fuzzy
Logic) to compute the orientation and velocity of the
vehicle:
Ψ
c
= PID(e
Ψ
) = (K
p
1
+
K
i
1
s
+ K
d
1
.s)e
ψ
v
c
= PID(e
d
) = (K
p
2
+
K
i
2
s
+ K
d
2
.s)e
d
(11)
The two PID control parameters (K
x
i
) are optimized
by Particle Swarm (PSO) technique and by a fuzzy
approach. The parameter optimization is based on
a fitness weight function Time Square Error (ITSE).
The drawback of this approach is the lack of dynam-
ics and that precise measurements of the absolute po-
sition variables is needed.
2.2.4 Dynamics Bicycle Model (DBM)
Also known as the Ackermann model, the DBM is
a Longitudinal and lateral model describing dynamic
and kinematic vehicle motions (Martinez et al., 2004;
Sprinkle et al., 2008). Its formulation varies from
one author to others (Daviet and Parent, 1996; Khatir
and Davidson, 2005; Bascetta et al., 2016; Zin et al.,
2004; Song et al., 2017; Huang et al., 2016).
DBM Decentralized Control. The simplified dy-
namic model (as presented in (Khatir and Davison,
2004)) is written in a three DoF system where v
x
i
de-
note the linear velocity of the vehicle i and θ
i
its wheel
orientation angle and β
i
the vehicle’s steering angle i.
m ˙v
x
i
= f
xi
cos(β)
i
+ f
yi
sin(β
i
)
˙
β
i
= −
1
mv
i
f
xi
sin(β
i
) +
1
mv
i
f
yi
cosβ
i
− ψ
i
˙
ψ
i
=
1
I
f
τ
(12)
The bicycle Kinematics model is:
˙
X
i
= v
x
i
cos(θ
i
+ β
i
)
˙
Y
i
= v
x
i
sin(θ
i
+ β
i
)
˙
θ
a
i
= ψ
i
(13)
Platoon of Autonomous Buses. In (Stanley and
Katupitiya, 2013b; Stanley and Katupitiya, 2013a),
the authors use the DBM with a different formulation
for each bus of a platoon dynamics. Their work is fo-
cused on the multi-agent systems to demonstrate the
ability for platoons to cooperatively maneuver around
each other. The kinematic equations are the same as
in eq 6:
˙
X
i
= v
x
i
cosψ −
L
2
˙
ψ
i
cosψ
i
˙
Y
i
= v
x
i
sinψ +
L
2
˙
ψ
i
sinψ
i
(14)
with r=L/2 is the distance between the effective center
of rotation in the vehicle and the definite origin of the
vehicle, ψ as the vehicle orientation in a reference co-
ordinate system, and ω = ˙y as the vehicle body turning
rate. The dynamic equations, for each vehicle, are
m(
¨
X −
˙
Y
˙
ψ) = R
r
− sinδF
f
− cosδ(T
f
− R
f
) − T
r
m(
¨
Y +
˙
X
˙
ψ) = − cos δ.F
f
+ F
r
+ sinδ.(T
f
− R
f
)
J
¨
ψ = −l
f
.cos δ.F
f
+ l
r
.F
r
+ l
f
.sin δ.(T
f
− R
f
)
(15)
T represents traction or propulsion, R the rolling re-
sistance and F the lateral forces on the wheels. The
slip angles are shown as the β
s
.
2.2.5 Robotics Models
The longitudinal and lateral positions and orientation
(X,Y,θ) of each vehicle i (with mass m
i
and inertia I
i
)
of the convoy are represented in a Cartesian frame R
0
.
G
i
is the gravity center of the vehicle, (v
xi
,v
yi
) are its
longitudinal and lateral velocities.
Robotic Models are composed of Dynamic equa-
tions (eq 16, Kinematic transformation (see equation
6, and a geometric representation. This is why they
are more precise and advisable.
Dynamic Equations. The Lagrange method leads
to a set of dynamic equations (2.2.5) to describe the
motion of one vehicle (see the left scheme of figure
3), in the vehicle reference frame R
v
= (G
i
,x
vi
,y
vi
)
(Rabhi, 2005; DeSantis, 1995; Chebly, 2017). δ
i
is
the steering front wheel angle and ψ: the yaw angle.
The input force is F
xr
i
= F
mot
i
and F
res
i
gathers
the resistance forces from the slope gravity and aero-
dynamics. The rolling resistance is ρ
vi
and the road
slope is ζ.
F
res
i
= mg sin ζ +
ρAC
d
I
˙v
2
x
v
sgn( ˙v
x
v
) − ρ
vi
Overview on Modeling for Control of Autonomous Road Vehicles Platoon
211
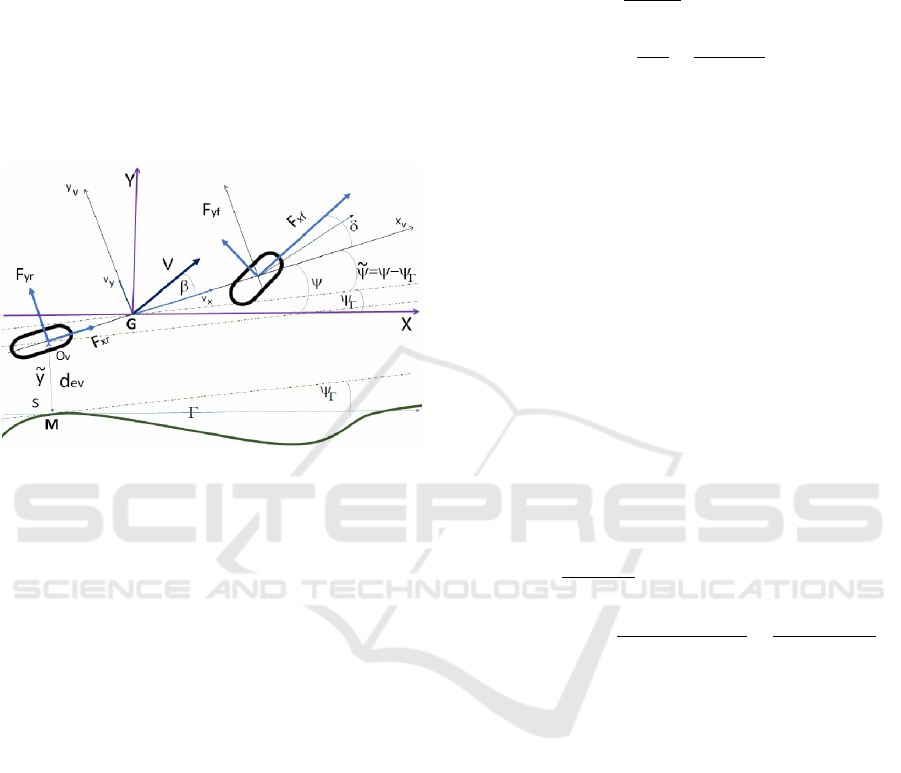
The longitudinal and lateral wheel forces are noted
F
x f
i
,F
xr
i
,F
y f
i
,F
yr
i
. They can be got either trough the
wheel-road contact modeling or considering simply
longitudinal and lateral cornering stiffness for each
wheel (Rabhi, 2005) ( I
i
= I
z
+ 2I
w
+ m
w
(l
2
f
+ l
2
r
)).
m
i
. ˙v
x
vi
= F
x f
i
.cosδ
i
− F
y f
i
.sinδ
i
+ F
xr
i
− F
res
i
m
i
. ˙v
y
vi
+ a.m
w
¨
ψ = F
x f
i
.sinδ
i
+ F
y f
i
.cosδ
i
+ F
yr
i
I
i
.
¨
ψ
i
+ a.m
w
˙v
y
= l
f
(F
x f
i
sinδ
i
+ F
y f
i
cosδ
i
− F
y f
i
) − F
yr
i
.l
r
(16)
l
f
and l
r
are distances to G
i
from the front wheel and
from the rear wheel (respectively); a = l
f
− l
r
.
Figure 3: Bicycle Model and trajectory Γ.
The actuation dynamics when considered can be
written as follows, where J
x
,r
x
,T
x
are the wheels in-
ertia, rays, and motor torques. For a rear traction ve-
hicle T
m
f
i
= 0 and T
m
r
i
6= 0.
J
f
.
˙
ω
f i
= (T
m
f
i
− r
f i
.F
x f
)
J
r
.
˙
ω
ri
= (T
m
r
i
− r
ri
.F
xr
)
(17)
Let us recall that the process has only 2 inputs (the
torque and the steering).
Geometric Model. The figure 3 shows the geomet-
ric scheme of the vehicles with the reference path γ in
the absolute frame R(0xy).
Let us note s
i
, the curvilinear abscissa (position
M) of vehicle i. The abscissa s
i
is located with respect
to a desired trajectory or trajectory Γ and we note d
the Side linear deviation of the vehicle i with respect
to the desired trajectory Γ.
O
i
is the center of the rear axle of the ith vehicle and
s
i
is the distance traveled (curvilinear abscissa) by the
closest point to O
i
on the path Γ. c(s
i
) is the curvature
of the Γ path in s
i
.
Recall that d
i
is the desired curvilinear distance be-
tween vehicles and c(S) is the curvature of the tra-
jectory C at the point M. The Curvilinear spacing be-
tween 2 vehicles is then: e
s
i
= s
i−1
− s
i
− d
i
˜
ψ
i
= ψ−ψ
Γ
is the angular deviation of the vehicle
i relative to reference trajectory Γ.
The Kinematic equations are needed to get the
Curvilinear velocities ( ˙s
i
) to follow the motion of the
vehicle i and determine its orientation. The curvilin-
ear kinematic model can be written:
˙s
i
=
cos(
˜
ψ
i
)
1− ˜y
i
.c(s)
v
x
v
i
˙
˜y
i
= sin(
˜
ψ
i
).v
x
v
i
˙
˜
ψ
i
= (
tanδ
i
L
−
c(s)cos(
˜
ψ
i
)
1− ˜y
i
.c(s)
)v
x
v
i
(18)
The kinematic modeling of vehicles, describes the
velocities based on the geometry of these vehicles.
The kinematic model alone does not completely rep-
resent the physical reality (Cordesses, 2000). The half
vehicle model, known as the bicycle, is an acceptable
representation for the dynamics of the convoy and is
most often used (Nadji, 2007; Nouveliere et al., 2002;
Lenain, 2005; Cartade et al., 2005).
These equations represent a non-holonomic sys-
tem, the state vector has three dimensions and two
dimensional control. The mathematical singularity
(d
c
(s) = 1) will never appear because the point O
v
is
not at the center of the curve of the desired trajectory.
O
i
is the center of the rear axle of the ith vehicle. c(s
i
)
is the curvature of the Γ path in s
i
(Cordesses, 2000)
(see figures 3).
Some authors, to be complete, add to this model a
representation of wheel slip and drift angles (Lenain,
2005; Cartade et al., 2005; Petrov, 2009). If we con-
sider β
F
i
and β
R
i
the drift angles (front and back) of
the robot. The kinematics becomes then
˙s
i
= v
i
cos(
˜
ψ
i
+β
R
i
)
1−c(s
i
) ˜y
i
˙
˜y
i
= v
i
sin(
˜
ψ
i
+ β
R
i
)
˙
˜
ψ
i
= cos(β
R
i
)
tan(δ
i
+β
F
i
)−tan(β
R
i
)
L
−
c(s
i
)cos(
˜
ψ
i
+β
R
i
)
1−c(s
i
) ˜y
i
(19)
2.2.6 Conclusion on Vehicles Models
We have presented the models used for the control of
vehicle fleets ranging from the simplest to the most
complete one. Several architectures have been used,
but there is still a lack of clear strategies non depen-
dent of the control laws used. For control of the vehi-
cle chain, the robotics models are the most appropri-
ate for the good motion control of the vehicles while
taking into account their dynamics and kinematic re-
lations. They involve correctly the transformations
from the vehicles operational variables to the Carte-
sian space representation.
Note that up to now, only the individual model of
one vehicle of the fleet are considered and there is no
criteria on the global behaviour or the fleet shape.
In section 3, we will propose a more complete
model, by adding to the robotics equations, a clear
description of the links and couplings of the vehicles
within the fleet and with their environment.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
212

2.3 Control Architectures for Fleets
The existing control architectures can be classified
into several categories: Kinematic / Dynamic, Local /
Global, Uni or Bi-directional. This is related to the in-
formation used to control each vehicle. They are local
or global depending on sensor information they use to
control (Global: from all the vehicles, or Local only
neighbors). The two approaches can be unidirectional
(preceding neighbors) or bidirectional (neighbors in
front and behind).
2.3.1 Global Fleet Control Architecture
For the global or centralized architecture (GUC,
GBC), the control law applied to each vehicle of the
fleet is based on the data (positions, velocities, ...) of
all the vehicles of the convoy (Yazbeck, 2014). Some-
times it can be partial, with data limited to the leader
and some of the neighboring vehicles, if the con-
voy chain is too long. For example, in partial GBC,
one uses the states variables of the leader and the 4
(front and rear plus left and right if any) or only 2
neighboring vehicles. This approach has been used
in (Caicedo et al., 2003), for a convoy moving in a
straight line. This makes global approaches more ex-
pensive(Ali et al., 2015).
2.3.2 Local or Decentralized Control
Architecture
In general, the most of vehicle pilots use only the in-
formation of the previous vehicle and possibly (only
partially) that of the following one (LUC, LBC). This
decentralized control (LUC) approach requires fewer
sensors and and very little information exchange be-
tween vehicles of the convoy, than the centralized ap-
proach. It also requires less computations and infor-
mation. The control is based on the data restricted to
neighbours in the convoy, to minimize the numbers of
the sensors used. (Qian et al., 2016; Nouveliere et al.,
2002; Sheikholeslam and Desoer, 1993).
2.3.3 Local Bidirectional Control Architecture
(LBC)
In bidirectional architecture, we are interested in in-
formation about the two neighbors,the previous vehi-
cle and the follower one. Each vehicle is controlled
targeting the previous one with regard to its followers
and leaders.
In this case, the disadvantages are the availability
of information on the vehicles of the chain, the need
for sensors, the communication of the data, and the
observability.
2.3.4 Local Unidirectional Control (LUC)
Each vehicle is controlled targeting the previous one
regardless to its follower. The driven vehicle in LUC
is slaved to follow its predecessor (Avanzini et al.,
2010). Tracking errors, introduced by sensors, actu-
ators, and delays accumulate from the leader vehicle
to the last one, in the convoy chain and affect the sta-
bility of the convoy motion. This causes oscillations
due to accumulated errors (Ali et al., 2015). This also
causes unacceptable disturbances if the string is long
(Avanzini, 2010). These problems are only partially
avoided in the global architecture.
3 NEW MODELING APPROACH
PROPOSED FOR PLATOONING
The robotic modeling approach seems more suitable
for driving fleets of vehicles, robots or mobile de-
vices. Let us first, discuss some observations of the
nature groups and then, we will use a more complete
architecture with a strategy that will consider models
including the group characteristics which is inspired
by the behavior of animals.
3.1 Modeling for Platooning
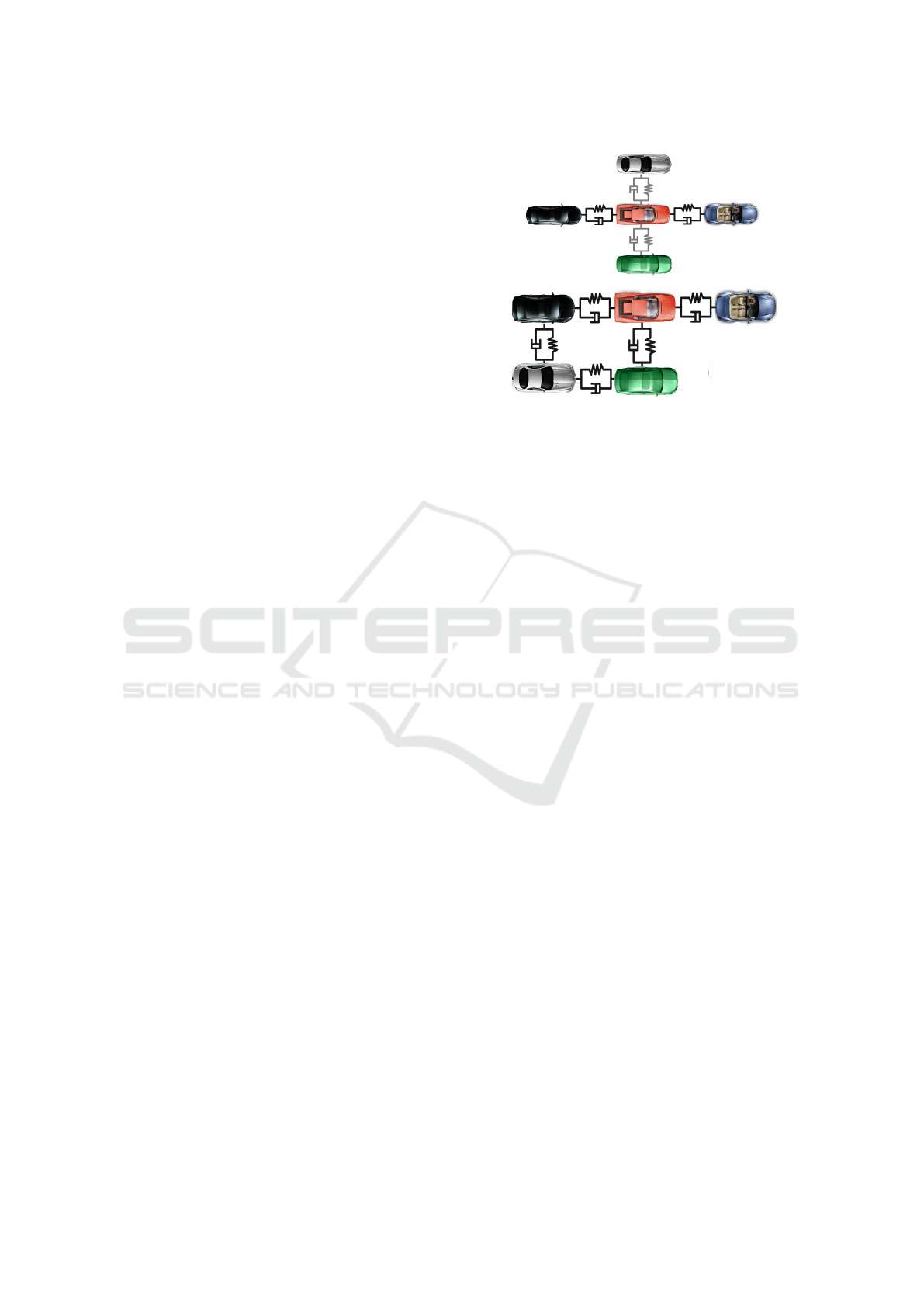
Two examples of fleets of 5 vehicles will be used to il-
lustrate our modeling approach. They are represented
in figure (4). We will define the geometric model of
each vehicle and for the global fleet. Using the five
gravity centers of the 5 vehicles we will define the
geometric form of the fleet. Then, each vehicle is lo-
calized regard to the gravity center or the red vehicle
chosen as being the leader. Therefore the kinemat-
ics and finally the dynamic equations for each vehicle
will be considered.
Geometric Models in R
v
. If the red vehicle is the
leader of the fleet 1 of the figure 4, its position is q
0
=
[x
v
0
,y
v
0
,ψ
0
]
T
, the preceding vehicle is at q
1
= q
0
+
[d,0,0]
T
the rear one at q
2
= q
0
+ [−d,0,0]
T
, the left
one at q
3
= q
0
+ [0,d
y
,0]
T
and the right one at q
4
=
q
0
+ [0,−d
y
,0]
T
, where d and d
y
are the longitudinal
and lateral IVSD. The geometric transformationis
T
kin
i
=
cosψ
i
−sin ψ
i
0
sinψ
i
cosψ
i
0
0 0 1
(20)
Kinematics Models. The Kinematic transforma-
tion matrix, for each vehicle, is the same as previously
Overview on Modeling for Control of Autonomous Road Vehicles Platoon
213
given (eq 6). We then get here:
˙
X
0
= T
kin
0
. ˙q
0
,
˙
X
1
= T
kin
1
. ˙q
1
˙
X
2
= T
kin
2
. ˙q
2
,
˙
X
3
= T
kin
3
. ˙q
3
,
˙
X
4
= T
kin
4
. ˙q
4
Dynamic Models. The Lagrange method can be
used to get the (Inverse or Direct) Dynamic Model
equations, in the vehicle frame R
v
, (M’Sirdi et al.,
2007) for each vehicle, knowing it is related to its
neighbours (by τ
r
j
).
InverseDM U
i
= M
i
(q
i
). ¨q
i
+ H
i
( ˙q
i
,q
i
)
DirectDM ¨q
i
= M
i
(q
i
)
−1
(−H
i
( ˙q
i
,q
i
) +U
i
)
where U
i
= u
i
− τ
f
i+1
− τ
r
i−1
− τ
l
i
− τ
d
i
...
(21)
with the operational variables q
i
= [x
v
i
,y
v
i
,ψ
i
]
T
as
the position vector for vehicle i, and ˙q
i
, ¨q
i
the velocity
and acceleration vectors. To this model we can add
the actuators (equation 17) and wheel ground contact
models (ignored here for the sake of simplicity and
considered in another control step).
Inter Vehicles Dynamic Relations (IVDR)
We introduce here the IVDR as a Reference Model
to include the constraints defining the vehicles inter-
action dynamics (instead of only an intervehicle dis-
tance (constant or not); (τ
r
i−1
,τ
f
i+1
) are rear and front
constraints and (τ
l
i
,τ
d
i
) are from the left and right ve-
hicles in the fleet 1 of the figure (4). We can have four
Reference Models (RM) for one vehicle and more RM
if we need. We can also relate all the vehicles to the
leader. We can also share a percentage of leading.
The forces τ
x
j
, represents the constraints (attrac-
tion/repulsion) from the nearby vehicles (front, rear,
left and right). This is the description of the relation
of the vehicle i to the other ones in the group (or pla-
toon). As an example, the relation with the preceding
vehicle could be, with a simple mass-spring-damper
model (for simplicity):
τ
f
i+1
= M
i
. ¨e
i,i+1
+ B
f
i. ¨e
i,i+1
+ K
f
i.e
i,i+1
+ w
f
i+1
(22)
where e
i, j
is the distance between two vehicles.
A virtual control input w
f
i+1
is introduced to
keep control of any variation which can be done on
the fly on the reference model character. It is also
worthwhile to note that this virtual input will proba-
bly enhance the platoon controllability. It can be used
by a high control level to manage the character of the
fleet and change its features depending the operational
state, the environment and the road conditions.
The constraints torques are linked by pairs
through the desired Reference Models for the Inter
Vehicles Dynamic Relations (RM-IVDR). In the fig-
ure (4) we see that these torques are generated by
damping and springs reference models.
Figure 4: Fleets of 5 Vehicles.
Please note that for the first fleet (of figure (4)) we
need Four reference models (2 longitudinal and 2 lat-
eral) and for the second one 5 RM-IVDR are needed.
We can also consider that all the vehicles are also
linked to the leader. Why not adding, for all the vehi-
cles a link to the blue one (first) or the last one.
In addition, note that the RM-IVDR models
(mass-spring-damper) are considered here for sim-
plicity. We can choose more complex models and use
nonlinear stiffness (rigidity for the front and flexible
for the rear). The parameters are not obligatorily lin-
ear, nor constant and bidirectional. A vehicle, (in-
teresting or not) for the fleet, may be attached to the
platoon or left if it goes too far. We can consider also
holonomic or non-holonomic constraints (with equal-
ities or inequalities C(X) ≥ c
0
).
This is the main difference with the previous
approaches where vehicles are related only through
the controllers. We include specific reference models
to define the character of the dynamic relations
between vehicles.
The proposed Dynamic Model for the Platoon
The model can be expressed in the operational frame
or in the Cartesian frame by geometric and kinematic
transformations. Let us note ε
r
and ε
l
the distance be-
tween the vehicle and the right or the left one. The
parameters indexed f, r, l, d, corresponds to the Ref-
erence model with regard to the front, rear, left and
right vehicle (respectively).
The proposed dynamic model for the platoon is
then
For i = 1,...N,
U
i
= M
¨
X
i
+ H(
˙
X
i
,X
i
)
τ
f
i+1
= M
i
. ¨e
i,i+1
+ B
f
i
. ˙e
i,i+1
+ K
f
i
.e
i,i+1
+ w
f
i+1
τ
r
i−1
= M
i
. ¨e
i,i−1
+ B
r
i
. ˙e
i,i−1
+ K
r
i
.e
i,i−1
+ w
r
i−1
τ
l
i
= M
i
.
¨
ε
i,i
l
+ B
l
i
.
˙
ε
i,i
l
+ K
l
i
.ε
i,i
l
+ w
l
i
τ
d
i
= M
i
.
¨
ε
i,i
r
+ B
d
i
.
˙
ε
i,i
r
+ K
d
i
.ε
i,i
r
+ w
d
i
(23)
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
214

In fact the reference models (RM-IVDR), add to
the system degrees of freedom (DoF) corresponding
to the relative motions. This will make the control
more admissible and more realistic. Those DoF are
added, in our model, with the corresponding virtual
control inputs to enhance the process observability
controllability. The system can be considered in a
triangular form to assign to the system mechanical
impedance features to the different DoF.
4 CONCLUSIONS
There is no general theory for modeling platoons of
vehicles, drones or robots. This paper has considered
the fleets or groups modeling as an open problem for
autonomous global driving.
An overview of the modeling approaches used for
platooning control is presented. The reported applica-
tions in literature consider separate and simple vehicle
models and link their behaviour only through the con-
trol laws. This means that there is no a priory defined
relation between the group elements (except the inter
vehicles distance) and then there is no optimal strat-
egy through the control. To much efforts are left to
the control.
The proposed model gives more clearly the global
description of the fleet and separate definitions of
the control objective and the behaviour (Reference
Model) for Inter Vehicles Dynamic Relations. It al-
lows more flexibility for the control laws and respect
the constraints using an appropriate Reference Model
for the behaviour (which copes with the control ad-
missibility). In our ongoing research, we will show
that the Platoon observability and controllability is
enhanced when using the new proposed model.
In perspectives the platoon Observability and con-
trollability will be analysed and non linear control
techniques will be applied to control the global pla-
toon behavior.
REFERENCES
Alcala, E., Puig, V., Quevedo, J., and Escobet, T. (2018).
Gain-scheduling lpv control for autonomous vehi-
cles including friction force estimation and compen-
sation mechanism. IET Control Theory Applications,
12(12):1683–1693.
Ali, A., Garcia, G., and Martinet, P. (2015). Urban pla-
tooning using a flatbed tow truck model. In Intelligent
Vehicles Symposium (IV), 2015 IEEE, pages 374–379.
IEEE.
Allou, S. and Zennir, Y. (2018). A comparative study of
pid-pso and fuzzy controller for path tracking control
of autonomous ground vehicles. In Proceedings of the
15th International Conference on Informatics in Con-
trol, Automation and Robotics - Volume 1: ICINCO,,
pages 306–314. INSTICC, SciTePress.
Avanzini, P. (2010). Mod
´
elisation et commande d’un convoi
de v
´
ehicules urbains par vision. PhD thesis, Univer-
sit
´
e Blaise Pascal-Clermont-Ferrand II.
Avanzini, P., Thuilot, B., and Martinet, P. (2010). Accu-
rate platoon control of urban vehicles, based solely on
monocular vision. In Intelligent Robots and Systems
(IROS), 2010 IEEE/RSJ International Conference on,
pages 6077–6082. IEEE.
Bascetta, L., Cucci, D. A., and Matteucci, M. (2016). Kine-
matic trajectory tracking controller for an all-terrain
ackermann steering vehicle. IFAC-PapersOnLine,
49(15):13 – 18. 9th IFAC Symposium on Intelligent
Autonomous Vehicles IAV 2016.
Bauer, M. and Tomizuka, M. (1996). Fuzzy logic traction
controllers and their effect on longitudinal vehicle pla-
toon systems. Vehicle System Dynamics, 25(4):277–
303.
Caicedo, R. E., Valasek, J., and Junkins, J. L. (2003). Pre-
liminary results of one-dimensional vehicle formation
control using a structural analogy. In American Con-
trol Conference, 2003. Proceedings of the 2003, vol-
ume 6, pages 4687–4692. IEEE.
Cartade, P., Lenain, R., Thuilot, B., and Berducat, M.
(2005). Algorithmes pour la commande d’une forma-
tion de robots mobiles. In Conf
´
erence Internationale
Francophone d’Automatique (CIFA2012) Grenoble,
France. 4-6 Juillet 2012, pages 2159–2165. IEEE.
Chebly, A. (2017). Trajectory planning and tracking for au-
tonomous vehicles navigation. PhD thesis, Universit
´
e
de Technologie de Compi
`
egne.
Contet, J.-M., Gechter, F., Gruer, P., and Koukam, A.
(2009). Bending virtual spring-damper: a solution to
improve local platoon control. In International Con-
ference on Computational Science, pages 601–610.
Springer.
Cordesses, L. (2000). Commande de robots holonomes
et non holonomes. Application au guidage d’engins
agricoles par GPS. PhD thesis, Universit
´
e Blaise Pas-
cal - Clermont II.
Daviet, P. and Parent, M. (1996). Longitudinal and lat-
eral servoing of vehicles in a platoon. In Intelligent
Vehicles Symposium, 1996., Proceedings of the 1996
IEEE, pages 41–46. IEEE.
DeSantis, R. (1995). Path-tracking for car-like robots with
single and double steering. IEEE Transactions on ve-
hicular technology, 44(2):366–377.
Guillet, A., Lenain, R., Thuilot, B., and Martinet, P. (2014).
Adaptable robot formation control: Adaptive and
predictive formation control of autonomous vehicles.
IEEE Robotics Automation Magazine, 21(1):28–39.
Huang, C., Naghdy, F., and Du, H. (2016). Model predic-
tive control based lane change control system for an
autonomous vehicle. In Region 10 Conference (TEN-
CON) 2016 IEEE, pages 3349–3354. IEEE.
Khatir, M. E. and Davidson, E. (2005). Decentralized
control of a large platoon of vehicles operating on
Overview on Modeling for Control of Autonomous Road Vehicles Platoon
215

a plane with steering dynamics. In Proceedings of
the American Control Conference, 2005, pages 2159–
2165. IEEE.
Khatir, M. E. and Davison, E. J. (2004). Decentralized con-
trol of a large platoon of vehicles using non-identical
controllers. In American Control Conference, 2004.
Proceedings of the 2004, volume 3, pages 2769–2776.
IEEE.
Lenain, R. (2005). Contribution
`
a la mod
´
elisation et
`
a la
commande de robots mobiles en pr
´
esence de glisse-
ment: application au suivi de trajectoire pour les en-
gins agricoles. PhD thesis, Universit
´
e Blaise Pascal-
Clermont-Ferrand II.
Martinez, J.-J., Avila, J.-C., and de Wit], C. C. (2004). A
new bicycle vehicle model with dynamic contact fric-
tion. IFAC Proceedings Volumes, 37(22):625 – 630.
IFAC Symposium on Advances in Automotive Con-
trol 2004, Salerno, Italy, 19-23 April 2004.
Menhour, L., D’Andr
´
ea-Novel, B., Fliess, M., Gruyer, D.,
and Mounier, H. (2015). A new model-free design for
vehicle control and its validation through an advanced
simulation platform. In 14th annual European Control
Conference - ECC 2015, Linz, Austria.
M’Sirdi, N. K. (2018). Vehicle platooning: an overview on
modelling and control approaches. In International
Conference on Applied Smart Systems (ICASS’18).
Medea University.
M’Sirdi, N. K. (2020). Autonomous vehicle platooning and
motioncontrol: Overview on models and control ap-
proaches; features and characters. In springer, P. I.,
editor, International Conference on Electronic Engi-
neering and Renewable Energy (ICEERE’2020), vol-
ume 1, Oujda, Morocco.
M’Sirdi, N. K., Rabhi, A., and Naamane, A. (2007). Vehicle
models and estimation of contact forces and tire road
friction. In ICINCO 2007, Proceedings of the Fourth
International Conference on Informatics in Control,
Automation and Robotics, Robotics and Automation
1, Angers, France, May 9-12, 2007, pages 351–358.
Mu’azu, J. M., Sudin, S., Mohamed, Z., Yusuf, A., Us-
man, A. D., and Hassan, A. U. (2017). An improved
topology model for two-vehicle look-ahead and rear-
vehicle convoy control. IEEE 3rd International Con-
ference on Electro-Technology for National Develop-
ment (NIGERCON), 6:0.
Nadji, M. (2007). Ad
´
equation de la dynamique de v
´
ehicule
`
a la g
´
eom
´
etrie des virages routiers: apport
`
a la
s
´
ecurit
´
e routi
`
ere. PhD thesis, Villeurbanne, INSA.
Nouveliere, L., Marie, J. S., and an N K M’Sirdi, S. M.
(2002). Controle longitudinal de v
´
ehicules parcom-
mande sous optimale. In CIFA 2002, pages 906–911.
Nantes Juillet.
Petrov, P. (2009). Nonlinear adaptive control of a two-
vehicle convoy. Open Cybernetics & Systemics Jour-
nal, 3:70–78.
Qian, X., de La Fortelle, F. A. A., and Moutarde, F. (2016).
A distributed model predictive control framework for
road-following formation control of car-like vehicles.
In arXiv:1605.00026v1 [cs.RO] 29 Apr 2016.
Rabhi, A. (2005). Estimation de la dynamique du v
´
ehicule
en interaction avec son environnement. PhD thesis,
Versailles-St Quentin en Yvelines.
Ricardo, C., Aguiar, A. P., and Gaspar, J. (2008). Control
of unicycle type robots tracking, path following and
point stabilization. In Proc. of IV Jornadas de Engen-
haria Electr
´
onica e Telecomunicac¸
˜
oes e de Computa-
dores, pages 180–185. Lisbon Portugal.
Samson, C. and Ait-Abderrahim, K. (1990). Mobile robot
control. Part 1 : Feedback control of nonholonomic
wheeled cart in cartesian space. Research Report RR-
1288, INRIA.
Sheikholeslam, S. and Desoer, C. A. (1993). Longitudi-
nal control of a platoon of vehicles with no commu-
nication of lead vehicle information: A system level
study. IEEE Transactions on vehicular technology,
42(4):546–554.
Song, L., Guo, H., Wang, F., Liu, J., and Chen, H. (2017).
Model predictive control oriented shared steering con-
trol for intelligent vehicles. In Control And Decision
Conference (CCDC), 2017 29th Chinese, pages 7568–
7573. IEEE.
Sprinkle, J., Eklund, J. M., Gonzalez, H., Grotli, E., San-
keti, P., and Moser, M. (2008). Recovering mod-
els of a four-wheel vehicle using vehicular system
data. Technical Report UCB/EECS-2008-92, EECS
Department, University of California, Berkeley.
Stanley, J. L. and Katupitiya, J. (2013a). Cooperative
autonomous platoon maneuvers on highways. In
IEEE/ASME International Conference on Advanced
Intelligent Mechatronics (AIM), Wollongong, Aus-
tralia.
Stanley, J. L. and Katupitiya, J. (2013b). Modeling and con-
trol of a platoon of autonomous buses; project: Au-
tonomous vehicle transportation. In IVS, editor, Con-
ference: Intelligent Vehicles Symposium (IV), 2013
IEEE.
Swaroop, D. (1994). String Stability of Interconnected Sys-
tems : An application to platooning in AHS. PhD the-
sis, University of California at Berkeley.
Szanto, A., Hajdu, S., and Deak, K. (2020). Survey of the
application fields and modeling methods of automo-
tive vehicle dynamics models. International Journal
of Engineering and Management Sciences (IJEMS)
Vol. 5. (2020). No. 2, 5(2):196–209.
Xiang, J. and Braunl, T. (2010). String formations of mul-
tiple vehicles via pursuit strategy. IET control theory
and applications, 4(6):1027–1038.
Yanakiev, D. and Kanellakopoulos, I. (1996). A simplified
framework for string stability analysis in ahs1. IFAC
Proceedings Volumes, 29(1):7873–7878.
Yazbeck, J. (2014). Accrochage immat
´
eriel s
ˆ
ur et pr
´
ecis
de v
´
ehicules automatiques. PhD thesis, Universit
´
e de
Lorraine.
Zin, A., Sename, O., and Dugard, L. (2004). Active
comfort and handling improvement with a 3d bicycle
model. IFAC Proceedings Volumes, 37(22):619 – 624.
IFAC Symposium on Advances in Automotive Con-
trol 2004, Salerno, Italy, 19-23 April 2004.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
216
