
Towards Quantitative Trade-off Analysis in Goal Models with Multiple
Obstacles using Constraint Programming
Christophe Ponsard
1
and Robert Darimont
2
1
CETIC Research Centre, Charleroi, Belgium
2
Respect-IT SA, Louvain-la-Neuve, Belgium
Keywords:
Requirements Engineering, Obstacle Analysis, Risk Minimisation, Search-based Software Engineering,
Quantitative Reasoning, Pareto Front, Attack Trees, Case Study, Tool Support.
Abstract:
Goal Models capture system goals and their decomposition into operational requirements assigned to human,
hardware or software agents. This refinement process supports alternatives both when refining goals processes
but also when reasoning and refining obstacles to goals. This leads to large design space to explore in order
to select a specific solution fulfilling a set of set of non-functional requirements (e.g. reliability, security,
performance) or business goals (e.g. costs, satisfaction). This paper investigates how optimisation techniques
can be used to efficiently explore the design space where multiple objectives have to be met simultaneously.
This works extends previous work by allowing one not only to select a single alternative but also to combine
different alternatives together to produce a more robust design. In order to explore the potentially very large
design space, we show how to translate a model with many goals and obstacle alternatives, expressed in the
KAOS notation, into a constraint programming (CP) problem. The OscaR.CP engine is then used to compute
a set of Pareto-optimal solutions regarding the targeted evaluation objectives. Our method is implemented as a
tool plugin of a requirements engineering platform and is benchmarked on a security case study close to attack
trees.
1 INTRODUCTION
Requirements Engineering (RE) is concerned with
the elicitation, evaluation, specification, consolida-
tion, and evolution of the objectives, functionalities,
qualities, and constraints of a software-based system
(van Lamsweerde, 2009). RE is a crucial phase and
the failure of many projects can be related to flaws
in requirements. In addition to dealing with require-
ments quality, RE also support the process of taking
high-level design decisions related to alternative ways
to achieve the system goals or avoid obstacles to reach
such goals, generally also resulting in different trade-
offs in terms of Non-Functional Requirements (NFR)
such as performance, security and usability, in addi-
tion to more global cost constraints. Such alterna-
tive designs can be precisely modelled using Goal-
Oriented Requirements Engineering (GORE) nota-
tions like KAOS (Dardenne et al., 1993), i* (Yu and
Mylopoulos, 1997) or GRL (ITU, 2012).
The design of a complex system is the combina-
tion of many choices leading to a potentially combi-
natorial explosion of possible solutions which must
meet various constraints about feasibility or specific
properties to optimise, especially NFR. The process
leading to the selection of an adequate design can ac-
tually be described as a multi-objective optimisation
problem over the system design space (Mogk, 2014).
This leads to computing a set of solutions known as
Pareto-optimal from which trade-offs can be explic-
itly evaluated (Zhang et al., 2008). To support this
activity, a specialised field of software engineering
concerned with the application of optimisation tools
is Search-Based Software Engineering (SBSE). A fa-
mous problem in this field is the Next Release Prob-
lem which is NP-Hard (Bagnall et al., 2001).
This paper explores how to use SBSE to tackle the
problem of alternative selections in a multi-objective
context by efficiently computing the Pareto front con-
taining all solutions and then selecting from it. Our
approach is to translate a GORE model into an op-
timisation model to perform the search phase. Our
work builds upon previous work by us (Ponsard and
Darimont, 2020) and other research teams in this
field using different GORE notations and optimisa-
tion tools (Heaven and Letier, 2011; Calderon et al.,
Ponsard, C. and Darimont, R.
Towards Quantitative Trade-off Analysis in Goal Models with Multiple Obstacles using Constraint Programming.
DOI: 10.5220/0009972105370543
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 537-543
ISBN: 978-989-758-443-5
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
537
2012; Nguyen et al., 2018). Our proposed contribu-
tion here is twofold:
• we extend the reasoning beyond goals to also cope
with the concept of obstacles to reason in terms of
risks for applications in security and safety areas.
Concretely, our generic framework is applied to
the study of attack trees.
• we allow to combine different alternatives to build
a more robust solution. This makes a lot of sense
when considering obstacles because different re-
duction strategies can be mixed to reach the re-
quired assurance level. In our security context,
multiple countermeasures may be combined to
make sure a critical asset is well protected.
We rely on the KAOS notations but our work can
easily be applied to the other GORE notations men-
tioned above. On the SBSE side, we consider the use
of Constraint Programming (CP) which is a power-
ful paradigm for solving combinatorial search prob-
lems by expressing constraints in a declarative way
and letting the system search the solution space, e.g.
using backtracking or branch and bound algorithm
combined with inference that propagates information
from one constraint to neighbouring ones in order to
efficiently reduce the size of the search space (van
Harmelen et al., 2008). More specifically we use the
Open Source OscaR library which provide support for
multi-objective problems (OscaR Team, 2012). In or-
der to illustrate our approach, we have focused on a
security case study inspired by a malicious insider
case study adapted from (Butts et al., 2005).
Our paper is structured as follows. Section 2
presents our case study and our notations. Section
3 illustrates how we map a GORE model into a CP
model. Section 4 then exploits the model to perform
single and multi-objective searches and illustrate the
result on our case study. Section 5 discusses our ap-
proach in the light of related work. Finally, Section 6
concludes and identifies our future work.
2 MODELLING OF THE
MALICIOUS INSIDER
This section presents key modelling concepts and our
supporting security case related to reasoning on attack
trees.
2.1 Key Concepts
Goals prescribe, at different levels of abstrac-
tion, key properties the considered system should
achieve. Goal models refine high-level strategic
goals. Such goals are related to the global sys-
tem for example in a banking system: Main-
tain[RapidAndSecureBankOperations]. It contains
a security NFR which is made explicit when re-
fining it into a lower level goal such as Main-
tain[ProtectionState] which will be considered here.
When a goal can be controlled by an agent (such as
SecurityPatching by the Operating System agent), it
becomes a requirement. Obstacle is the dual concept
of a goal; it defines a set of undesirable behaviours
(van Lamsweerde and Letier, 2000). Obstacles can
occur from the environment (like a safety hazard) or
be deliberately caused by an attacker in the security
area considered here, e.g. insider sending a forged
banking order. Like goals, obstacles can be refined
using AND/OR trees, leading to decomposition struc-
tures that are quite similar to attack trees in security
(Weiss, 1991; Schneier, 1999).
2.2 Attack Tree Modelling
When applied to security goals, obstacle analysis is
very close to Attack Trees (AT) and provides a me-
thodical way of describing the security of systems,
based on varying attacks. They represent attacks
against a system in a tree structure, with the goal as
the root node and different ways of achieving that
goal as leaf nodes. There are two kinds of nodes:
an AND node requires the achievement of all its sub-
goals while an OR node only requires one (but possi-
bly multiple can be tried, e.g. for raising chances of
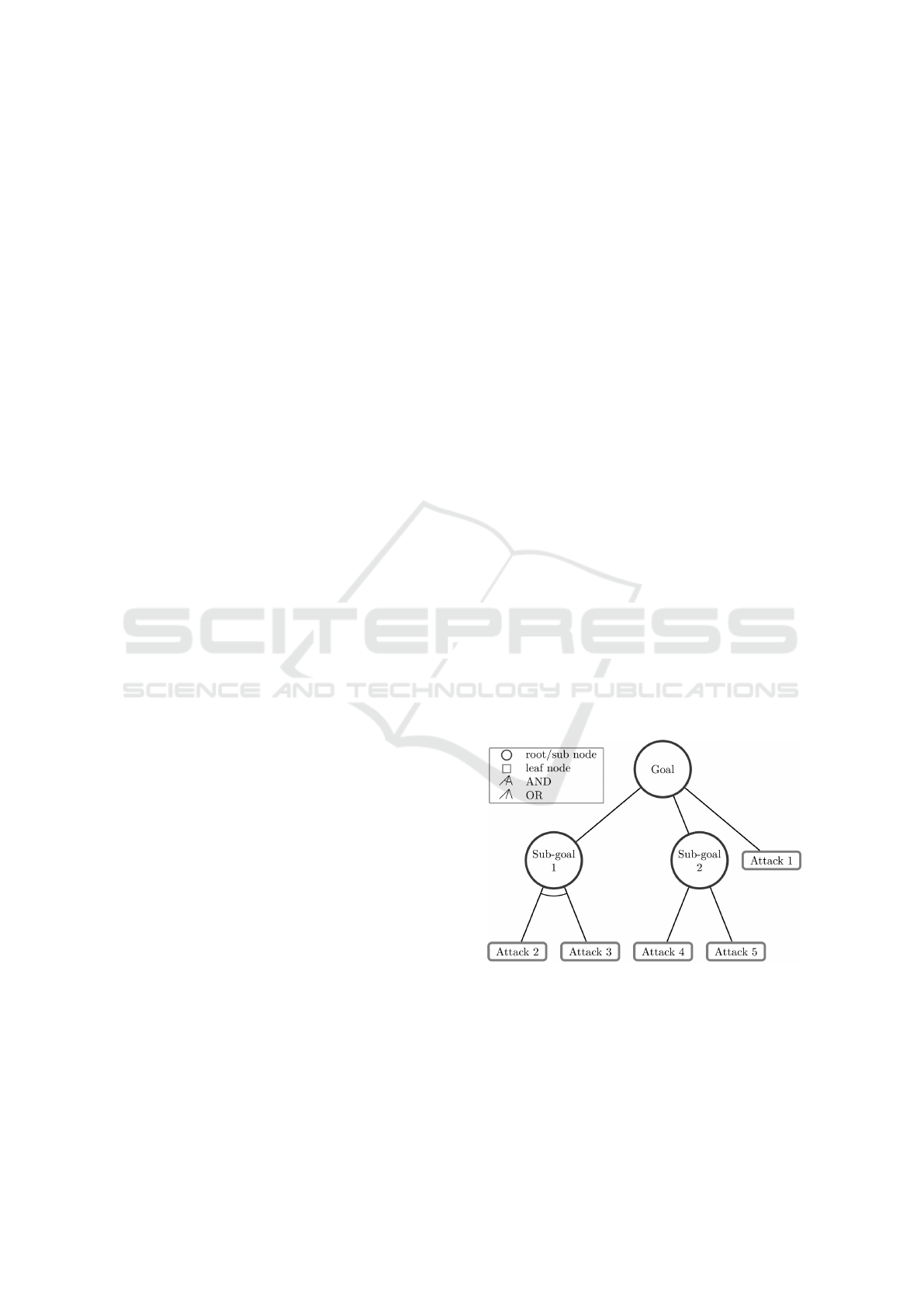
success). A typical AT structure is shown in Figure 1.
Figure 1: Example of Attack Tree (Siddiqi et al., 2018).
Our Malicious Insider case was developed with the
goal to provide a quite generic and reusable tax-
onomy of attacks against the Protection State of a
system which encompasses all activities that are al-
lowed according to organisation policy or system
access controls. In Figure 2, we represent this
as as the top goal, depicted using a blue parallel-
ICSOFT 2020 - 15th International Conference on Software Technologies
538
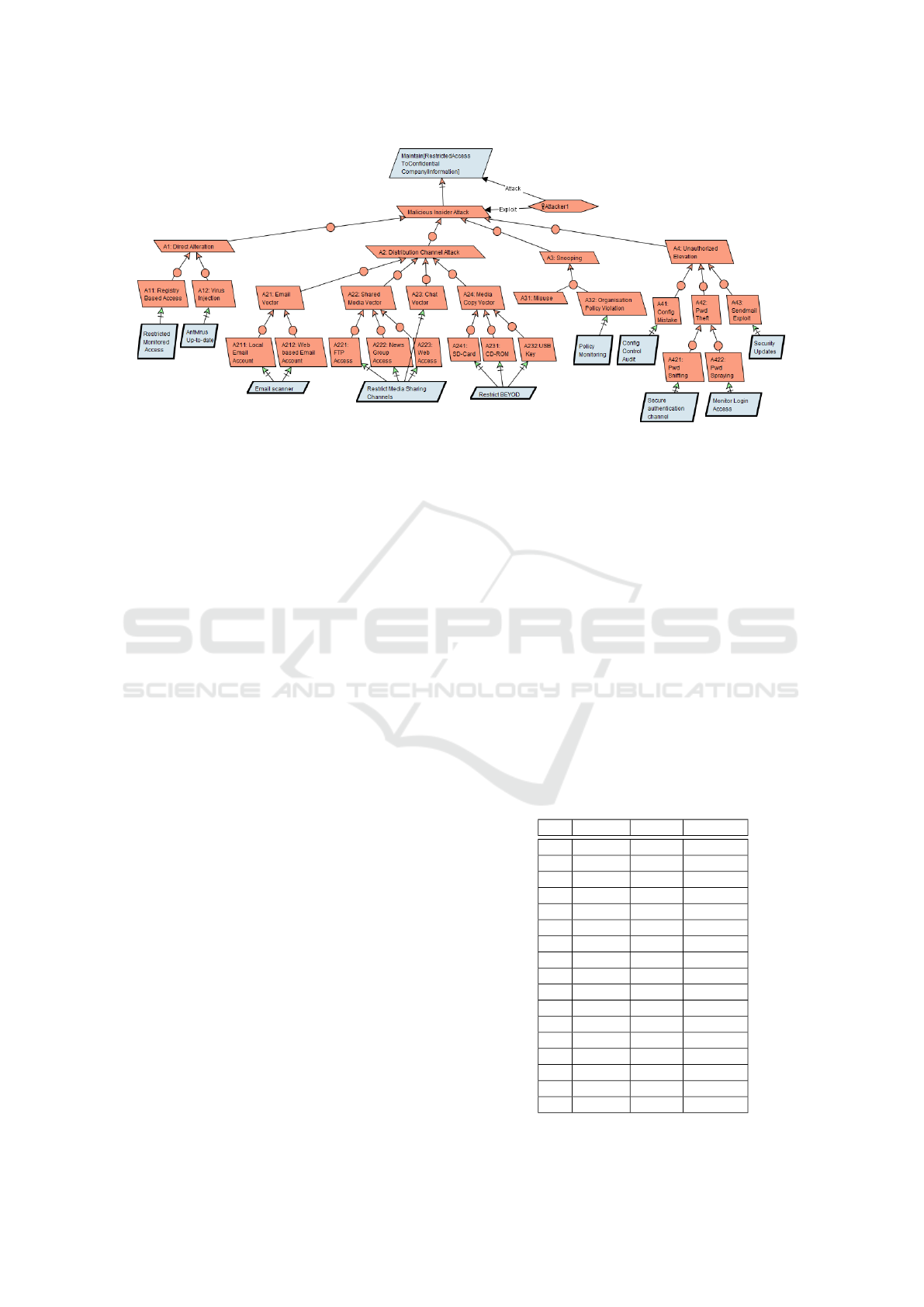
Figure 2: Attack Tree for a Malicious Insider.
ogram. Note this Maintain[ProtectionState] goal
could be instantiated more specifically, e.g. Main-
taint[RestrictedAccessToConfidentialInformation]
The malicious insider is the attacker whose goal
is to violate the Protection State of the system as de-
picted the threat as a red parallelogram just below the
top-goal in Figure 2. The attacker is also depicted
with its links with both the goal and the threat (also
called obstacle or anti-goal in the general KAOS no-
tation used here (van Lamsweerde, 2009)). A num-
ber of possible ways to violate the Protection State
are the following and compose the first level of OR-
refinement of our AT:
• Change another user or object’s rights (Alteration)
• Leak user or object information to an unautho-
rised entity (Distribution)
• Obtain protected information about another user
or object (Snooping)
• Change the rights on themselves (Elevation)
Note than our notations use AND-OR relationship
modelling: AND nodes are depicted as circular nodes
while OR nodes are defined by the presence of multi-
ple AND nodes. In Figure 2, all refinements are done
through OR nodes, except one: threat “A3: snooping”
is AND-refined into two children: “A31: misuse” and
“A32: Organisation Policy Violation”. We will not
detail the whole decomposition process which is fully
described in (Butts et al., 2005).
2.3 Attack Tree Attributes
In our case, we will focus on the following attributes:
• Probability of success in the threat by the attacker
• Cost of the effort required the deploy the threat
• Impact of the threat, i.e. company loss related to
the success of the specific threat by the attacker
Values for leaf nodes are expert estimations possibly
based on recorded history of each kind of threat. They
are of course subject to some level of imprecision
whose impact is not studied in the scope of this paper.
Typical figures are presented in Table 1. Intermediary
values are computed using propagation rules:
• Probability are propagated with the assumption
of threat independence resulting in a formula of
the form p
a
. p
b
for two AND nodes and 1 − (1 −
p
a
).(1 − p
b
) for two OR-nodes (Ketel, 2008).
• Cost is the sum of the costs of the selected chil-
dren of the OR-node (at least one child must be
selected but more than one is possible).
• Impact is also estimated using a summation.
Table 1: Attributes values for leaf nodes.
ID Probability Cost (K$) Impact (M$)
A11 0.08 50 200
A12 0.1 60 130
A211 0.15 70 100
A212 0.2 100 300
A221 0.1 150 250
A222 0.4 190 275
A223 0.1 100 300
A213 0.1 110 150
A241 0.1 90 225
A242 0.25 250 250
A243 0.3 275 275
A31 0.2 100 100
A32 0.15 120 120
A41 0.15 100 300
A421 0.3 30 200
A422 0.2 40 150
A43 0.5 170 50
Towards Quantitative Trade-off Analysis in Goal Models with Multiple Obstacles using Constraint Programming
539

3 TRANSLATING AN AT MODEL
INTO A CP MODEL
A CP model is composed of a set of declarations, a set
of constraints among those variables and one or sev-
eral variables that will be optimised. OscaR.CP sup-
ports a wide variety of variables (Int, Bool, Set) and
constraints (equality, inequality, arithmetic/logic ex-
pression, set inclusion/exclusion, etc) which will be
detailed in the translation process. As we use quite
standard CP features, the proposed mapping can eas-
ily be adapted to other CP frameworks.
The translation process of the AT model into an
OscaR.CP model requires the following three main
steps detailed in the rest of this section:
• transposing nodes as variables of the CP model
• generating specific constraints across alternatives
• for each target quality: producing an objective
function
3.1 Extracting Nodes
Extracting nodes is done by performing a query on
our model repository. In our experimental setting,
we used the Objectiver tool which can be queried us-
ing OCL based on an EMF meta-model (Respect-IT,
2005). E.g. OR nodes can be collected using:
Goal.allInstances()->reject(g:Goal |
GRefinement.allInstances()-> collect(parent)
->size()<2)
Such queries can easily be adapted to other model
variants. The result matches the content of Table 1.
In order to encode an OR-Node (also called al-
ternative in what follows), we use a OrVar which is
a sequence of CPBoolVar, i.e. an array of boolean
variables (or bits). The number of variables matches
the number of children in the OR node. For exam-
ple, the 4 nodes at the top level are mapped to an ar-
ray of 4 bits, meaning there are 16 possibles config-
urations, 0000 means nothing selected (which is not
valid here), 0110 means only alternative 2 and 3 are
selected, 1111 means all alternatives are selected. In
addition, some utility functions are defined in order to
ease the expression of constraints:
• no(v : OrVar) returns true iff there is no alterna-
tive selected (i.e. all bits are set to 0)
• one(v : OrVar) returns true iff there is exactly one
alternative selected (i.e. one bit is set to 1)
• some(v : OrVar) returns true iff there is at least
one alternative selected (i.e. one or more bits are
set to 1)
• isIn(n : Int; v : OrVar) returns true iff the n
th
alter-
native is selected (i.e. the n
th
bit is set to 1)
3.2 Generating Constraints
In what follows, we will call sub −alternative, an al-
ternative in the subtree of another alternative.
The following constraints are generated:
• all top level alternatives are enabled (i.e.
some(G))
• if an alternative is not selected, all its sub-
alternatives should be disabled (by recursion, it is
enough to disable the closest sub-alternatives us-
ing refinement links)
• if an alternative is selected, its sub-alternatives
should be enabled (again the same recursion re-
mark holds)
• domain specific constraints are generated, for ex-
ample if some alternatives need to be selected to-
gether or if two alternatives are mutually exclu-
sive.
The expression of those constraints is easy to translate
using the operators defined previously and result in
the model of Listing 1.
Listing 1: CP model for MI attack tree.
var G = c r e a t e ( 4 , ”G” )
var A1 = c r e a t e ( 2 , ”A1” )
v a l A2 = c r e a t e ( 4 , ”A2” )
v a l A4 = c r e a t e ( 3 , ”A4” )
v a l A21 = c r e a t e ( 2 , ”A21 ” )
v a l A22 = c r e a t e ( 3 , ”A22 ” )
v a l A24 = c r e a t e ( 3 , ”A24 ” )
v a l A42 = c r e a t e ( 2 , ”A42 ” )
/ / t o p l e v e l a t l e a s t one
add ( some (G ) )
/ / c o n s t r a i n t s on G
add ( ! i s I n ( 1 ,G) ==> no (A1 ) )
add ( ! i s I n ( 2 ,G) ==> no (A2 ) )
add ( ! i s I n ( 4 ,G) ==> no (A4 ) )
add ( i s I n ( 1 ,G) ==> some ( A1 ) )
add ( i s I n ( 2 ,G) ==> some ( A2 ) )
add ( i s I n ( 4 ,G) ==> some ( A4 ) )
/ / c o n s t r a i n t s on A2
add ( ! i s I n ( 1 , A2 ) ==> no ( A21 ) )
add ( ! i s I n ( 2 , A2 ) ==> no ( A22 ) )
add ( ! i s I n ( 4 , A2 ) ==> no ( A24 ) )
add ( i s I n ( 1 , A2 ) ==> some ( A21 ) )
add ( i s I n ( 2 , A2 ) ==> some ( A22 ) )
add ( i s I n ( 4 , A2 ) ==> some ( A24 ) )
/ / c o n s t r a i n t s on A4
add ( ! i s I n ( 2 , A4 ) ==> no ( A42 ) )
add ( i s I n ( 2 , A4 ) ==> some ( A42 ) )
Using a binaryStatic search on all the variables with-
ICSOFT 2020 - 15th International Conference on Software Technologies
540

out any objective will enumerate all combinations
(see Listing 2). There are more than 65000 combina-
tions with multiple alternatives, while only 16 if only
one alternative can be selected for each OR node, i.e.
by replacing constraints some by one in our model.
This illustrates the importance of the combinatorial
explosion when mixing variants.
Listing 2: Optimisation search.
s e a r c h {
b i n a r y S t a t i c (G++A1++A2++A4++
A21++A22++A24++A42 )
} o n S o l u t i o n {
p r i n t S o l ( Seq (G, A1 , A2 , A4 ,
A21 , A22 , A24 , A42 ) )
n s o l s = n s o l s +1
} s t a r t ( )
3.3 Objective Function
Objective functions are encoded as CPIntVar and can
be expressed using expressions involving our OrVar
variables. The rules described in Section 2 are ap-
plied to produce evaluations at all levels enabling leaf
values to propagate up to the top level. The alter-
native selection operator is simply our isIn operator
which will evaluate to 0 when false and to 1 when
true. Based on the data of Table 1, the impact evalua-
tion function can be encoded as shown in Listing 3.
Listing 3: Optimisation search.
d e f i m pa ct G =
i s I n ( 1 ,G)
*
impa c t A 1 + i s I n ( 2 ,G)
*
impa c t A 2 +
i s I n ( 3 ,G)
*
impa c t A 3 + i s I n ( 4 ,G)
*
impa c t A 4
d e f i m p ac t A 1 = i s I n ( 1 , A1)
*
200+ i s I n ( 2 , A1)
*
130
d e f i m p ac t A 2 =
i s I n ( 1 , A2 )
*
impac t A 2 1 + i s I n ( 2 , A2)
*
impac t A 2 2 +
i s I n ( 3 , A2)
*
150+ i s I n ( 4 , A2)
*
impac t A 2 4
d e f i m p a ct A 2 1 = i s I n ( 1 , A21 )
*
100+ i s I n ( 2 , A21 )
*
300
d e f i m p a ct A 2 2 = i s I n ( 1 , A22 )
*
250+ i s I n ( 2 , A22)
*
275+
i s I n ( 3 , A22 )
*
300
d e f i m p a ct A 2 3 = 150
d e f i m p a ct A 2 4 = i s I n ( 1 , A24 )
*
225+ i s I n ( 2 , A24)
*
250+
i s I n ( 3 , A24 )
*
275
d e f i m p ac t A 3 = 100 + 120 / / AND
d e f i m p ac t A 4 = i s I n ( 1 , A4)
*
300+
i s I n ( 2 , A4 )
*
impac t A 4 2 + i s I n ( 3 , A4)
*
50
d e f i m p a ct A 4 2 = i s I n ( 1 , A42 )
*
200+ i s I n ( 2 , A42 )
*
150
At this point, it is easy to perform a single objec-
tive search. Trying to maximising the impact can
be done through the command maximize(Impact_G)
but will without surprise yield a configuration where
all possible attacks are selected. Using an objec-
tive combining some conflicting attributes such as
maximize(impact_G-cost_G*3) will identify a few
threats resulting in a good ROI (A11, A421, A422) as
depicted in Listing 4.
Listing 4: Optimisation search.
o b j e c t i v e t i g h t e n e d t o 190 l b : −6136
G={1 4} A1={1} A2={} A4={2}
A21={} A22={} A24={} A42={1 2}
4 MULTI-OBJECTIVE
OPTIMISATION
Encoding the cost objective is simply achieved by
adapting the numbers from Table 1. The probability
combination function is a bit more tricky for two rea-
sons. First, it requires computing independent prob-
abilities. Second, as we are restricted to integers, the
probabilities are encoded in percents and the multipli-
cation introduces a 100 factor that needs to be com-
pensated using a division constraint as shown in List-
ing 5. An additional utility function for OR nodes
with more than two children is also introduced.
Listing 5: Multi-objective search (for costs see Listing 5.
d e f c o st G = i s I n ( 1 ,G)
*
c o st A 1 + i s I n ( 2 ,G)
*
c o st A 2 +
i s I n ( 3 ,G)
*
c o st A 3 + i s I n ( 4 ,G)
*
c o st A 4
d e f c o s t A 1 = i s I n ( 1 , A1)
*
50+ i s I n ( 2 , A1)
*
60
. . .
d e f p r U n io n ( a : CPIntVar , b : CPIntVar ) : CPIntVar = {
v a l c a l c : CPIntVar = ( a −10 0)
*
( b −100)
*
( −1)+10000
v a l r e s =CPIntVar ( 0 , 1 0 0 )
add ( new I n t D i vi s i o nA C ( r e s , c al c , 1 0 0 ) )
r e s
}
d e f p r o b a G = p r U n i o n ( i s I n ( 1 ,G)
*
pro ba A1 ,
i s I n ( 2 ,G)
*
pro ba A2 , i s I n ( 3 ,G)
*
pro ba A3 ,
i s I n ( 4 ,G)
*
proba A 4 )
d e f p r o b a A1 = p r U n i o n ( i s I n ( 1 , A1)
*
8 , i s I n ( 2 , A1)
*
1 0 )
. . .
v a l o bj1 =proba G
*
imp a c t G
v a l o bj2 = c os t G
*
( −1)+1000
s o l v e r . p ar e t oM a x im i ze ( obj 1 , o b j2 )
var t a b v a r s =Seq (G, A1 , A2 , A4 , A21 , A22 , A24 , A42 )
s e a r c h {
b i n a r y S t a t i c ( t a b v a r s )
} o n S o l u t i o n {
p a r e t o P l o t . i n s e r t ( o bj1 . v a lue , o b j2 . v a l u e )
} s t a r t ( )
Performing a multi-objective search is quite easy us-
ing the multi-objective search function and Pareto
Towards Quantitative Trade-off Analysis in Goal Models with Multiple Obstacles using Constraint Programming
541
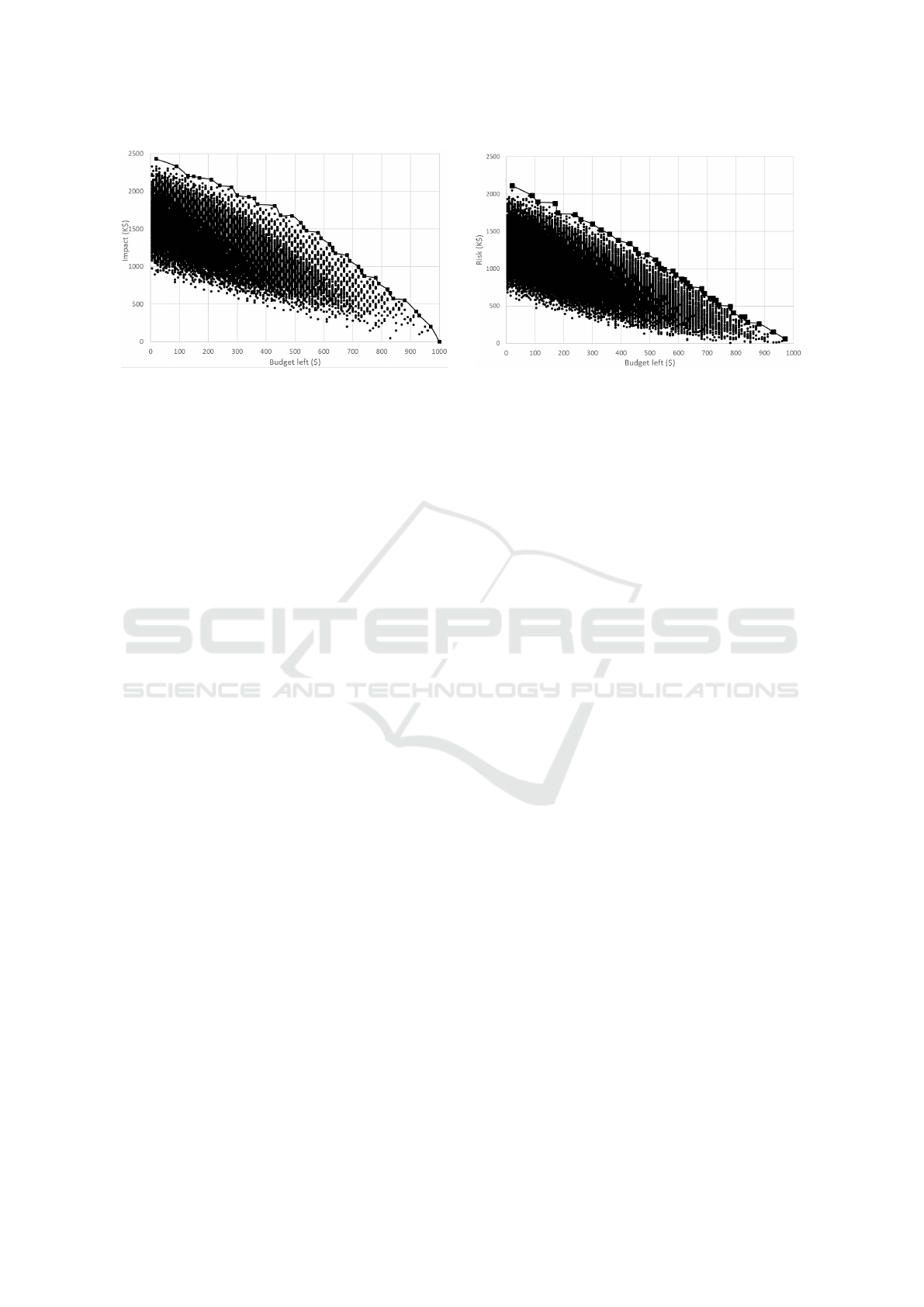
Figure 3: Structure of search space (points) and Pareto front (top line) for Budget vs Cost (left) and Budget vs Risk (right).
visualisation (Hartert and Schaus, 2014). Af-
ter defining a second objective function, the op-
timisation command before the search becomes
paretoMaximize(obj1, obj2) as shown in the sec-
ond part of Listing 5. Note the first objective function
was turned into a budget left function to maximise.
The two plots of Figure 3 depict two different
searches. The complete cloud of points is shown to
illustrate the respective size of the search space and
of the resulting Pareto front (located above) assum-
ing a maximal budget of 1000$. The left plot shows
the budget left vs impact analysis while the right plot
shows the budget vs risk (i.e. impact x probability)
analysis. In both cases, a low budget means high
spending and thus also more impact/risk. On the con-
trary, there is no possible attack thus impact when the
total budget (1000$) is left. The Pareto front could
be analysed further, e.g. to identify some common
threats. It could also be restricted based on specific
attacker assumptions (e.g. expertise or budget) but
we did not performe such analysis at this point.
5 RELATED WORK
This section focuses on works using CP or multi-
objective analysis of obstacles and attack trees.
First, it is interesting to point that a seminal pa-
per about attack trees also describes a system se-
curity engineering process where candidate architec-
tures are selected based on security cost vs resid-
ual risk (Parero) optimisation (Weiss, 1991). In our
work, we investigated such trade-off although not at
the residual risk level given we have not yet included
countermeasures.
In order to analyse an attack tree, a composi-
tional semantics in terms of priced timed automata
has been proposed by (Kumar et al., 2015). The Up-
paal CORA model checker is then used to evaluate
security queries expressed in weighted CTL and to
infer optimal attack paths from the resulting cost op-
timal traces. Like our work, it supports ranking of
attacks and evaluation of Pareto-optimal curves that
show trade-offs when multiple conflicting objectives.
The translation is closer to the denotational semantics
of AT however far more complex than ours. It can
also take the attack timing into consideration. The
attribute propagation seems however limited to accu-
mulation and less general than our approach.
Constraint satisfaction is considered by (Buldas
et al., 2020) in order to give a formulation of the
attack-tree decoration problem as a constraint satis-
faction problem. The purpose is different than ours:
CP is used to infer values in incomplete AT, e.g. using
data measured in intermediary nodes to infer missing
data in some leaf nodes. In our work, we implicitly
focused on bottom-up inference. However, we could
also generalise our approach to post such constraints.
The need to consider multiple parameters for
the successful selection of adequate measures from
attack-defence trees is stressed in (Fila and Wideł,
2019) which proposes a sound framework for multi-
parameter security analysis. A mathematical founda-
tions is presented as well as a python-based imple-
mentation related to the ATDtool and a case study
validation (electricity theft). The technique used for
optimisation is not discussed but is linear program-
ming. Like us, the focus is on the attacker although
the defender point of view could also be considered.
In a wider scope, the problem of efficiently de-
ploying security countermeasures to simultaneously
stay within the budget and minimise the residual dam-
age is addressed by (Dewri et al., 2007). It is also
formulated as a multi-objective optimisation problem
and relies on evolutionary algorithm to solve it. At-
tack graphs are also used to optimally deploy security
countermeasures w.r.t. risks associated with potential
cyber-attacks modelled using probabilities (Bhuiyan
et al., 2016). A sample average approximation al-
gorithm is proposed in conjunction with the Benders
ICSOFT 2020 - 15th International Conference on Software Technologies
542

decomposition algorithm. It also enables to perform
sensitivity analysis on different parameters such as
defender budget and uncertainty in probability esti-
mations. In our work, we did not cover counter-
measure optimisation but we could consider how to
model the residual risk and try to minimise it from the
point of view of the defender, including using multi-
objective approach.
6 CONCLUSION & NEXT STEPS
In this paper, we extended our approach to explore
the design space by allowing combination of alterna-
tives using model-based approach more specifically
goal-oriented. We focused our work on the concept
of obstacles as they generate many alternatives which
need to be combined to reach a good assurance level.
We illustrated the approach on a security context to
explore an attack tree. In order to investigate multi-
ple risk and cost factors, we showed how to imple-
ment a multi-objective approach computing a Pareto
front. Our work was implemented with the Objectiver
toolset and using the OscaR.CP optimisation library.
Our future work will focus on enriching our ap-
proach. First, we plan to analyse in deeper details
the composition of a Pareto front. Then, we aim at
supporting specialised forms of obstacle refinement
for the safety and security contexts, possibly in a co-
engineering approach. Finally, we would like to ex-
tend our work to cover the resolution step which can
introduce more alternatives. Based on this, different
optimisations can be investigated to propose how to
best control and improve the design of a system.
REFERENCES
Bagnall, A., Rayward-Smith, V., and Whittley, I. (2001).
The next release problem. Information and Software
Technology, 43(14):883 – 890.
Bhuiyan, T. H. et al. (2016). Minimizing expected max-
imum risk from cyber-attacks with probabilistic at-
tack success. In IEEE Symposium on Technologies
for Homeland Security.
Buldas, A. et al. (2020). Attribute evaluation on attack trees
with incomplete information. Computers & Security,
88.
Butts, J. W., Mills, R. F., and Baldwin, R. O. (2005). De-
veloping an insider threat model using functional de-
composition. In Computer Network Security.
Calderon, A. et al. (2012). Webred: A model-driven tool
for web requirements specification and optimization.
In Web Engineering.
Dardenne, A., van Lamsweerde, A., and Fickas, S. (1993).
Goal-directed requirements acquisition. Sci. Comput.
Program., 20(1-2):3–50.
Dewri, R. et al. (2007). Optimal security hardening using
multi-objective optimization on attack tree models of
networks. In Proc. of the 14th ACM Conference on
Computer and Communications Security.
Fila, B. and Wideł, W. (2019). Efficient attack-defense tree
analysis using pareto attribute domains. In IEEE 32nd
Computer Security Foundations Symposium (CSF).
Hartert, R. and Schaus, P. (2014). A support-based algo-
rithm for the bi-objective pareto constraint. In Proc.
of the 28th AAAI Conference on Artificial Intelligence,
July 27-31, Qu
´
ebec, Canada.
Heaven, W. and Letier, E. (2011). Simulating and optimis-
ing design decisions in quantitative goal models. In
IEEE 19th Int. Requirements Engineering Conference.
ITU (2012). Z.151 (10/12), User Requirements Notation
(URN) - Language Definition.
Ketel, M. (2008). It security risk management. In Proceed-
ings of the 46th Annual Southeast Regional Confer-
ence on XX, ACM-SE 46.
Kumar, R., Ruijters, E., and Stoelinga, M. (2015). Quanti-
tative attack tree analysis via priced timed automata.
In Formal Modeling and Analysis of Timed Systems.
Mogk, N. W. (2014). A requirements management system
based on an optimization model of the design process.
Procedia Computer Science, 28:221 – 227. 2014 Con-
ference on Systems Engineering Research.
Nguyen, C. M. et al. (2018). Multi-objective reasoning with
constrained goal models. Requir. Eng., 23(2).
OscaR Team (2012). OscaR: Operational Research in Scala.
https://bitbucket.org/oscarlib/oscar.
Ponsard, C. and Darimont, R. (2020). Towards multi-
objective optimisation of quantitative goal models us-
ing constraint programming. In Proc. of the 9th Int.
Conf. on Operations Research and Enterprise Sys-
tems, ICORES, Valletta, Malta, Feb. 22-24.
Respect-IT (2005). The Objectiver Goal-Oriented Require-
ments Engineering Tool. http://www.objectiver.com.
Schneier, B. (1999). Attack trees. Dr. Dobb’s journal,
24(12).
Siddiqi, M. A. et al. (2018). Attack-tree-based threat mod-
eling of medical implants. In PROOFS 2018, 7th Int.
Workshop on Security Proofs for Embedded Systems,
Amsterdam, The Netherlands.
van Harmelen, F., Lifschitz, V., and Porter, B. (2008).
Handbook of Knowledge Representation. ISSN. El-
sevier Science.
van Lamsweerde, A. (2009). Requirements Engineering -
From System Goals to UML Models to Software Spec-
ifications. Wiley.
van Lamsweerde, A. and Letier, E. (2000). Handling obsta-
cles in goal-oriented requirements engineering. IEEE
Trans. on Software Engineering, 26(10):978–1005.
Weiss, J. (1991). A System Security Engineering Process.
Yu, E. S. K. and Mylopoulos, J. (1997). Enterprise mod-
elling for business redesign: The i* framework. SIG-
GROUP Bull., 18(1):59–63.
Zhang, Y., Finkelstein, A., and Harman, M. (2008). Search
based requirements optimisation: Existing work and
challenges. In Requirements Engineering: Founda-
tion for Software Quality.
Towards Quantitative Trade-off Analysis in Goal Models with Multiple Obstacles using Constraint Programming
543
