
Autonomous Braking and Throttle System: A Deep Reinforcement
Learning Approach for Naturalistic Driving
Varshit Dubey
a
, Ruhshad Kasad
b
and Karan Agrawal
c
Department of Electronics and Telecommunication Engineering, College of Engineering Pune, Pune, India
Keywords:
Autonomous Systems, Collision Avoidance System, Deep Reinforcement Learning, Naturalistic Driving,
Simulation.
Abstract:
Autonomous Braking and Throttle control is key in developing safe driving systems for the future. There exists
a need for autonomous vehicles to negotiate a multi-agent environment while ensuring safety and comfort. A
Deep Reinforcement Learning based autonomous throttle and braking system is presented. For each time step,
the proposed system makes a decision to apply the brake or throttle. The throttle and brake are modelled as
continuous action space values. We demonstrate 2 scenarios where there is a need for a sophisticated braking
and throttle system, i.e when there is a static obstacle in front of our agent like a car, stop sign. The second
scenario consists of 2 vehicles approaching an intersection. The policies for brake and throttle control are
learned through computer simulation using Deep deterministic policy gradients. The experiment shows that the
system not only avoids a collision, but also it ensures that there is smooth change in the values of throttle/brake
as it gets out of the emergency situation and abides by the speed regulations, i.e the system resembles human
driving.
1 INTRODUCTION
The past decade has seen exponential growth in tech-
nologies associated with autonomous vehicles. Ma-
jor technology companies and vehicle manufacturers
have invested in autonomous vehicles. Autonomous
vehicles are exposed to countless dynamic scenarios
involving multiple agents such as vehicles, pedestri-
ans and signs. Autonomous vehicles require reliable
control systems to deal with such uncertainty. Active
safety measures such as collision avoidance systems
are becoming increasingly popular on cars.
Autonomous Braking systems are already available
on most cars. Such systems detect an impending crash
and take corrective action in time to avoid accidents.
These systems work independent of the driver and ap-
ply brakes to decelerate and stop the vehicle avoiding
incidents or reduce impact. Autonomous Braking sys-
tems work in the narrow zone between braking early
to avoid accidents and braking late to conserve perfor-
mance.
Advanced cruise control systems use a combina-
a
https://orcid.org/0000-0001-6238-217X
b
https://orcid.org/0000-0002-6864-9506
c
https://orcid.org/0000-0001-6600-0044
tion of throttle and braking to maintain a constant
velocity following a vehicle. Such features elevate
vehicles to Level 1 of driving automation. However,
they fall short of creating a high level of automation.
Traditionally rule-based control systems are unable
to adapt to the dynamic environment autonomous ve-
hicles have to operate in. Rule-based systems specify
a distance threshold or a speed threshold and often
require human assistance in complex situations. An
intelligent system is required to cover a wide spectrum
of scenarios.
Intelligent algorithms are required to make such
systems viable. Autonomous Throttle and Braking
Systems need to be accurate in a high percentage of
scenarios. False-alarm scenarios erode driver confi-
dence and can be dangerous. Such systems cannot be
programmed for the near infinite scenarios which may
occur, therefore there exists a need for such systems
to be able to learn and adapt. Driving and specifically,
scenarios requiring emergency brake action can be
considered a multi-agent problem with only a partial
observable space at any given instant.
The death of a pedestrian due to collision with an
Uber self-driving car highlights the need for evolved
braking and throttle systems. Despite detecting the
pedestrian early, the system failed to act and exceeded
Dubey, V., Kasad, R. and Agrawal, K.
Autonomous Braking and Throttle System: A Deep Reinforcement Learning Approach for Naturalistic Driving.
DOI: 10.5220/0010157401730180
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 173-180
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
173

its assured clear distance ahead.
Reinforcement Learning is a methodology allow-
ing an agent to learn by interacting and participating in
an environment. The aim of using such methods is to
obtain an optimal policy which maximizes the reward
when the agent interacts with the environment. Policy
Gradient methods optimizes the policy directly. The
ability of Policy Gradient methods to learn stochas-
tic policy is integral in implementing a throttle and
braking control system. (Sutton and Barto, 2018)
In this paper a throttle and braking control sys-
tem is developed using Deep Reinforcement Learning.
Specifically, policy gradient methods are utilized to
dictate discrete brake and throttle inputs. The perfor-
mance of the system is tested in two scenarios which
are simulated in CARLA simulator. (Dosovitskiy et al.,
2017)
The rest of the paper is organized as follows. Sec-
tion 2, will include a brief review of research into
braking control systems implemented using Deep Re-
inforcement Learning.Section 3 presents the scenarios
and simulation environment to test the proposed brak-
ing and throttle system. Section 4 contains details
regarding the reinforcement learning methods used
and the proposed reward function. Section 5 contains
the result of conducted experiments and Section 6 dis-
cusses future work.
2 RELATED WORK
Simulation is integral in the development of au-
tonomous vehicles. Developing algorithms to navigate
in dense urban environments has been a key focus area.
Dosovitskiy (Dosovitskiy et al., 2017) noted that there
are obstacles to real-life research such as government
regulation, logistical difficulties and the possibility of
accidents. Training an agent for the possibility of a
rare event such as jaywalkers is also a necessity. One
way to resolve the testing and training of autonomous
vehicles is the use of simulation software. CARLA
open-source simulator provides an urban environment
for simulation with the ability to generate pedestrians,
vehicles and common road signs. The ability to gather
data such as velocity, coordinates and distance to other
vehicles reduces the effort in acquiring specialized
data. Moreover, the ability to set up an environment
for scenarios to train is beneficial.
According to 2007 statistics for road accidents in
Germany, 14 % of accidents occur between a vehicle
following a moving vehicle ahead or a static vehicle.
Analysis of frontal collisions with stationary obsta-
cles exhibited that 21% of the drivers do not brake
at all prior to the accident. Kaempchen (Kaempchen
et al., 2009) proposes an emergency braking system
which generates potentially dangerous scenarios after
detecting an object or vehicle. The paper analyses
all possible trajectories of the host and object, while
calculating the possibility of a collision. Specifically,
it provides insight in two common scenarios, rear-end
collision and collisions at cross-sections.
Traditionally rule-based systems were utilized to
create braking and throttle control systems. Such sys-
tems had limited scope and needed specific protocols
for specific scenarios and would be handicapped in
the real-world. Chae (Chae et al., 2017) concludes
that a learning-based system is likely to achieve better
results in adapting to new and dynamic scenarios than
rule-based systems. The paper realizes braking control
systems as a discrete Markov Decision Process. More-
over the braking decision is initiated at a trigger point
which is calculated.
However such an approach is counterintuitive to
real-life driving since, braking decision can be decided
at any point during the approach. The author has used
DQN to design a braking system with 4 discrete action
values,
a
0
,
a
low
,
a
mid
,
a
high
(Chae et al., 2017). The
main drawback of this approach is that DQN works
on discrete state space whereas braking is continuous
value in the real world, which makes it difficult for
DQN to find optimal policy. This paper considers the
continuous space of the brake/throttle and uses DDPG
which is similar to DQN, but uses different subroutines
to find the optimal policy and works for continuous
action spaces. The details of DDPG will be explained
in the subsequent section.
Reinforcement Learning considers the problem of
an agent trying to achieve a goal while interacting with
an unknown environment, therefore it is well-suited to
deal with the problem of a vehicle navigating in traffic.
Talpeart (Talpaert. et al., 2019) focuses on teaching an
agent to establish a policy while interacting with an
environment to maximize a numerical reward.
Vasquez (Vasquez and Farooq, 2019). focuses on
emergency braking to avoid accidents with pedestri-
ans. A key aspect of the paper is modelling comfort
as reduction of jerk while braking and creating a nat-
uralistic dataset which closely mimics pedestrian be-
haviour. Early-braking methods combined with the
throttle action as discussed in this paper are designed
to reduce jerk. However the idea of creating datasets to
mimic real-world behaviour can be extended to driving
policies in order to make policies more naturalistic.
Y.Fu (Fu et al., 2020). examines Deep Determinis-
tic Policy Gradient (DDPG) algorithm based on Actor-
Critic infrastructure to reduce the difficulty of learning
in more complex environments. The paper proposes
that a reward function should accommodate multiple
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
174
objectives, such as safety, comfort. A DDPG system
consisting of only braking action outperforms similar
braking systems based on fuzzy logic and DQN. An-
other key criteria examined is reducing the probability
of exceeding comfortable deceleration or experiencing
jerk. On the same count, DDPG systems exceed com-
fortable deceleration limits on fewer occasions than
DQN or fuzzy logic systems.
There has been an increased interest in using a
DRL method for emergency braking scenarios. The
reward function penalizes early braking and collisions
with other vehicles and pedestrians. A Deep Deter-
ministic Policy Gradient method allows the agent to
rapidly discover optimal policies in simulation by us-
ing stochastic policies for exploration to learn a deter-
ministic policy.(Porav and Newman, 2018)
Previous research largely focuses on braking action
as a final resort to either prevent or mitigate collisions.
Such measures are limited in scope. Braking action
along with throttle control is more closely related with
real-world driving practices. This paper focuses on 2
scenarios. The first scenario tests the control systems
braking ability while scenario 2, works with throttle
action necessary after an emergency situation.
3 SYSTEM DESCRIPTION
Society of Automotive Engineering defines 6 levels
of driving automation from level 0 to level 5. Level
5 of driving automation can drive a vehicle anywhere
under all possible conditions. A driver is not required
to take control at any point and vehicles provide a safe
and comfortable journey. The biggest challenge in
achieving driverless cars is safety. A broad overview
of braking and throttle system using reinforcement
learning is shown in figure 1. A car should detect
the surrounding objects and take decisions such as
deciding velocity,steering angle and braking to avoid
accidents. An object in the surrounding environment
of the vehicle could be a static obstacle, pedestrian, a
stop sign or a moving car.
Figure 1: High level overview of Autonomous Brak-
ing/throttle system.
Once the object is detected, different parameters of
the car and the object will be passed into the neural
network (Goodfellow et al., 2016) and then via rein-
forcement learning an output will be generated. The
output can be a throttle or brake value which should
be applied by the car as shown in figure 1. The pa-
rameters to be passed into the network as input can be
initial velocity of car, relative position of the object to
the car, relative velocity etc.
In this paper we are considering 2 common scenarios,
where there is a need for effective braking and throttle
system to avoid accidents.
Figure 2: System description for Scenario 1.
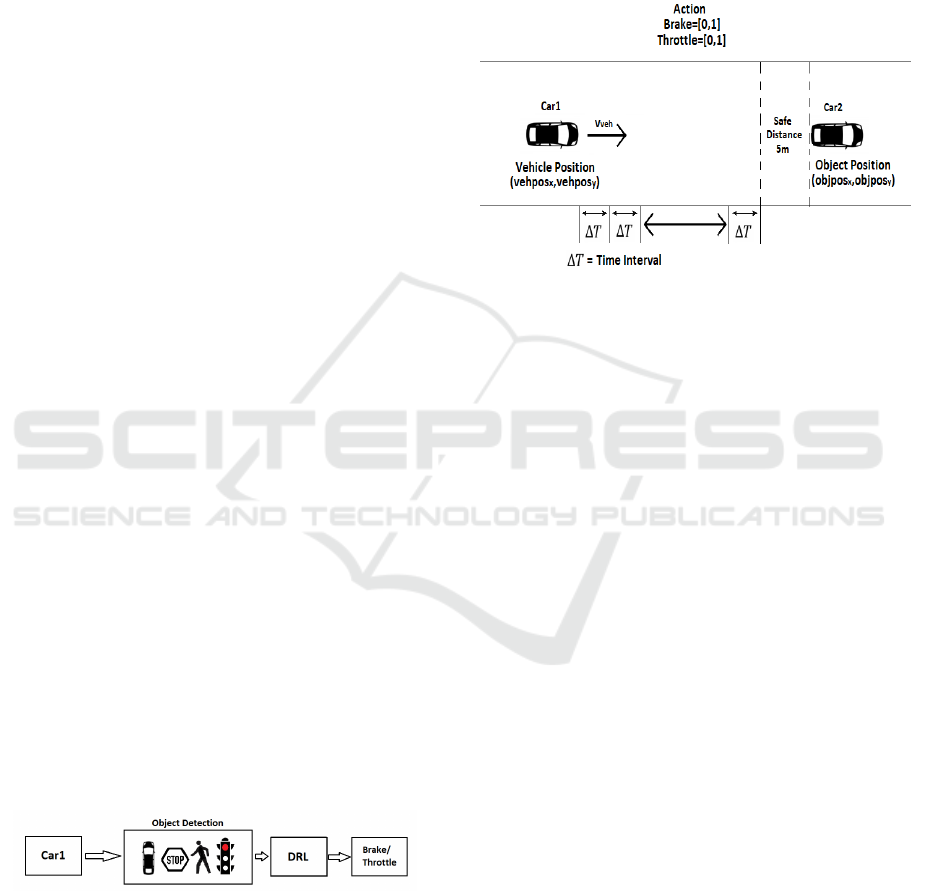
3.1 Scenario 1
The first scenario is shown in figure 2. There is
a static obstacle in front of the car at some dis-
tance. The static obstacle can be another vehicle, stop
sign etc. The autonomous agent is moving with the
velocity of
v
veh
from a position
(vehpos
x
,vehpos
y
)
.
As soon as the static object is detected, the vehi-
cle receives the relative position of the object, i.e
(ob j pos
x
− vehpos
x
,ob jpos
y
− vehpos
y
)
. From the
coordinates, the relative distance and direction from
the agent vehicle is calculated. Utilizing this infor-
mation, the agent decides whether to apply brake or
throttle at each time step. The brake and throttle values
are between [0,1].
3.2 Scenario 2
In the second scenario, 2 cars are approaching the in-
tersection. We consider that the other car approaching
the intersection is not abiding by traffic rules. This cre-
ates a scenario in which an agent is required to make
a quick decision to apply brakes to avoid an accident.
After we avoid this emergency situation, we can again
apply throttle to move forward. We will try to make
our autonomous agent learn this policy. Here, the au-
tonomous agent and the object are moving with veloci-
ties
v
veh
and
v
ob j
respectively. When the episode starts,
the agent starts from position
(vehpos
x
,vehpos
y
)
and
the other car starts from
(ob j pos
x
,ob jpos
y
)
. We as-
sume that at a certain time, using sensors, our agent
Autonomous Braking and Throttle System: A Deep Reinforcement Learning Approach for Naturalistic Driving
175
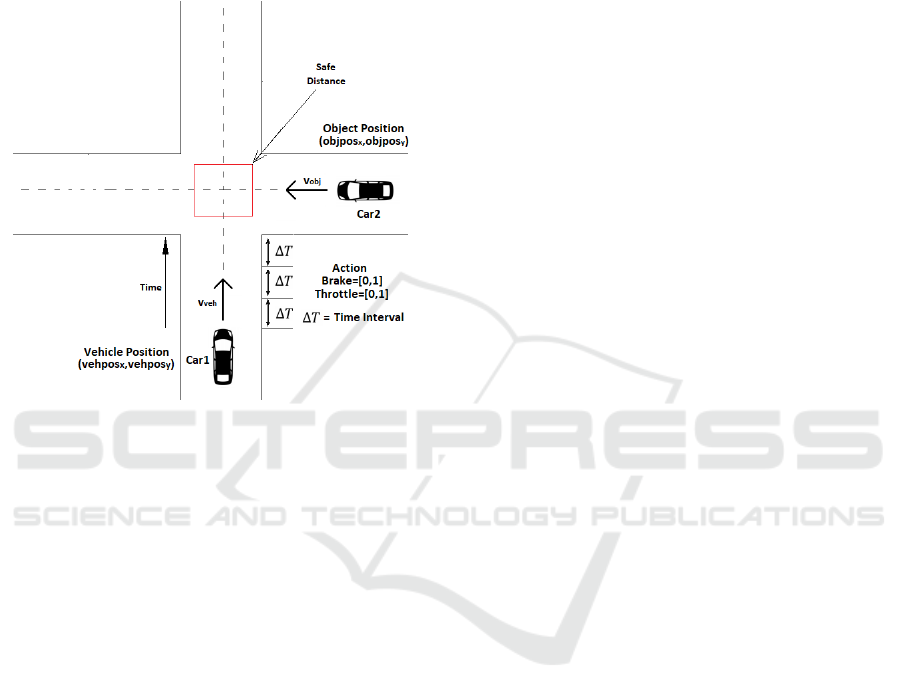
gets information about the object approaching the in-
tersection. Our agent after receiving useful parameters
such as relative distance and also relative velocities
makes the decision whether to apply brake or throt-
tle. A similar scenario can be applied to pedestrians
suddenly crossing the road. Figure 3 explains the pro-
posed scenario.
Figure 3: System description for Scenario 2.
4 DEEP REINFORCEMENT
LEARNING
In this section we present the details of our DRL-
based braking and throttle system. The aim of re-
inforcement learning algorithms is to learn a pol-
icy which maximizes the expected cumulative award
which will be received in the future. The agent per-
forms an action
a
t
given the state
s
t
under policy
π
. After performing the action, the agent receives
a new state and a reward
r
t
. Here the state consists
of relative position of the vehicle and the object, i.e
(ob j pos
x
− vehpos
x
,ob jpos
y
− vehpos
y
)
and relative
velocity of the vehicle and object for the past 10 steps.
The action that the agent takes consists of brake or
throttle. Brake and Throttle control are both real val-
ued with values in range [0,1].
The initial position of the agent and the objects is
fixed for all the simulation. The values of
v
veh
(velocity
of agent) and
v
ob j
(velocity of other car) are set as
random so that our reinforcement learning agent learns
a wide variety of cases.
For each scenario, there exists a set of events which
will result in the termination of the episode. For sce-
nario 1, the episode will end if there is:
•
Collision: The agent vehicle has breached the safe
distance limit of the object.
•
Early stop: The agent vehicle moving stops too
early, i.e the static object is very far away from the
agent.
The events for scenario 2 are mentioned below:
•
Collision: The agent vehicle has breached the safe
distance limit of the object.
•
Early Stopping: Similar to scenario 1, if our ve-
hicle stops very early compared to the distance to
the object in the environment.
•
High speed at intersection: The velocity of our
autonomous agent is very high during crossing at
intersection.
4.1 Deep Deterministic Policy Gradient
Policy methods (Sutton et al., 2000) are preferred for
numerous reasons. First, they do not compute the
immediate maximum reward and instead rely on total
rewards. Secondly, for a continuous action space, such
as braking or throttle control, we cannot calculate the
Q value (Watkins and Dayan, 1992), of each action, as
the action space will grow exponentially, which makes
Policy methods more appealing.
Deep Deterministic Policy Gradient is a determin-
istic, model-free, off-policy method which is used in
situations where the action space is continuous. It
is inspired by DQN and Deterministic Policy Gradi-
ents(DPG). DQN (Mnih et al., 2013) calculates the
Q function for all actions, using a neural network
and selects the action with maximum Q value. DPG
uses actor-critic style and learns a deterministic pol-
icy, i.e. for each state there is a fixed action defined.
For continuous action space, we need a differentiable
action-value function approximator to avoid calcula-
tion of Q value for each action. DDPG is thus an al-
gorithm which combines both the deterministic policy
approach and the neural network as function approxi-
mators. DDPG also has a target actor and target critic
along with actor and critic networks. The important
steps in the algorithm are shown as follows. First, the
current state is given as input to actor network and
a = µ(s; θ
µ
) + N
t
is computed, where
a
is the output
action for state
s
and
θ
µ
is the weights of the actor net-
work.
N
is the random process chosen for exploration
of action space. We will be using Ornstein-Uhlenbeck
process to add noise to the action output. (Uhlenbeck
and Ornstein, 1930). Next, the updated Q value, i.e
y
i
is computed as the sum of the immediate reward
r
i
and the outputs of the target actor and target critic
networks for the next state.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
176

y
i
= r
i
+ γQ
0
(s
i+1
,µ
0
(s
i+1
|θ
µ
0
)|θ
Q
0
) (1)
Here,
γ
is the discounting factor. The critic network
is updated by minimizing the mean-squared loss be-
tween
y
i
and the original Q value calculated using
critic network, i.e
Q(s
i
,a
i
|θ
Q
)
. Since DDPG is an off-
policy method, for a mini-batch, we take the mean
of the sum of policy gradients while updating actor
network (Lillicrap et al., 2015). The target networks
are time-delayed copies of the original networks and
they help bring stability to the system by only moving
a factor
τ
from the original networks at each step, i.e
θ
0
← τθ + (1 − τ)θ
0
,τ << 1
, where
θ
is the original
weight of the actor/critic network and
θ
0
is the weight
of the corresponding target network.
DDPG makes use of a finite buffer to store each
step of every episode as a tuple
(s
t
,a
t
,r
t
,s
t+1
)
. These
tuples are randomly sampled, thus they remain undif-
ferentiated between episodes during learning (Lillicrap
et al., 2015).
4.2 Reward Function for Scenario 1
The reward function is the most important component
of the reinforcement learning algorithm. It must be
formulated such that it closely resembles the proposed
braking and throttle system. The main objective which
our control system should achieve are:
• Collision must be avoided at all costs
•
The car should apply control smoothly instead of
sudden brake/throttle, so that the driving is more
realistic to human driving.
•
The car should not stop very early as it makes
no sense if the obstacle is very far away from the
agent.
•
The car should not cross the intersection at very
high speed.
To achieve the above objectives, we propose the fol-
lowing reward function for scenario 1:
r
t
=
−(αdistance
2
+ β)abs(action)
−(ηv
2
veh
+ λ), if Collision
−(αdistance
2
+ γ), if Early Stopping
+δ, otherwise
(2)
where
distance
2
= (ob jpos
x
− vehpos
x
)
2
+
(ob j pos
y
− vehpos
y
)
2
,
α,β,η, λ,γ,δ > 0
,
v
veh
is
the velocity of the vehicle, and action is the value of
throttle or brake taken by agent at any instant of time.
The first condition is proposed by Chae (Chae et al.,
2017). It suggests that the penalty in case of collision
is proportional to the square of the velocity of the ve-
hicle. The second and third part of the reward function
are proposed by us. We want the agent to decide when
to apply brakes once the obstacle is detected, we don’t
want our vehicle to stop if the obstacle is far away
from the vehicle. So the second condition gives the
penalty proportional to the square of the distance be-
tween obstacle and vehicle. Finally if we are in a safe
state, i.e there is neither collision or early stopping, we
simply give a constant positive reward for being in a
safe state. In an episode, we want our agent to gather
as much positive reward as possible.
4.3 Reward Function for Scenario 2
The reward function for the scenario where both the
agent and the car is moving towards an intersection is:
r
t
=
−(αdistance
2
+ β)abs(action)
−(η(v
veh
− v
ob j
)
2
+ λ), if Collision
−(αdistance
2
+ γ), if Early Stopping
−(αv
2
veh
+ µ), if High speed at intersection
+δ, otherwise
(3)
Here
distance
is the same as the one defined in sce-
nario 1 and α,β,η, λ,γ,δ,µ > 0.
The reward function looks very similar to the one
proposed for scenario 1. There is one additional condi-
tion. In a real-world scenario, we do not drive at very
high speed while driving through an intersection. We
give a penalty proportional to the square of the velocity
of agent. These conditions will ensure that our agent
will avoid a collision and also take decisions which
closely resemble human driving. The values of weight
parameters
α,β,η
etc, should be carefully chosen as
they serve as a trade-off between each objective. We
can assign each of these objectives a certain priority.
We give collision avoidance the highest priority, hence,
we assign maximum penalty in case of collision. Next
comes early stopping and high speed at intersection
which are given equal priority. However, the penalty is
lower as compared to collision avoidance. Considering
this argument, we conclude λ > γ,µ.
5 EXPERIMENT
5.1 Simulation Setup
We use CARLA (Car Learning to act) (Dosovitskiy
et al., 2017), an open-source driving simulator which
provides an environment to create scenarios commonly
Autonomous Braking and Throttle System: A Deep Reinforcement Learning Approach for Naturalistic Driving
177
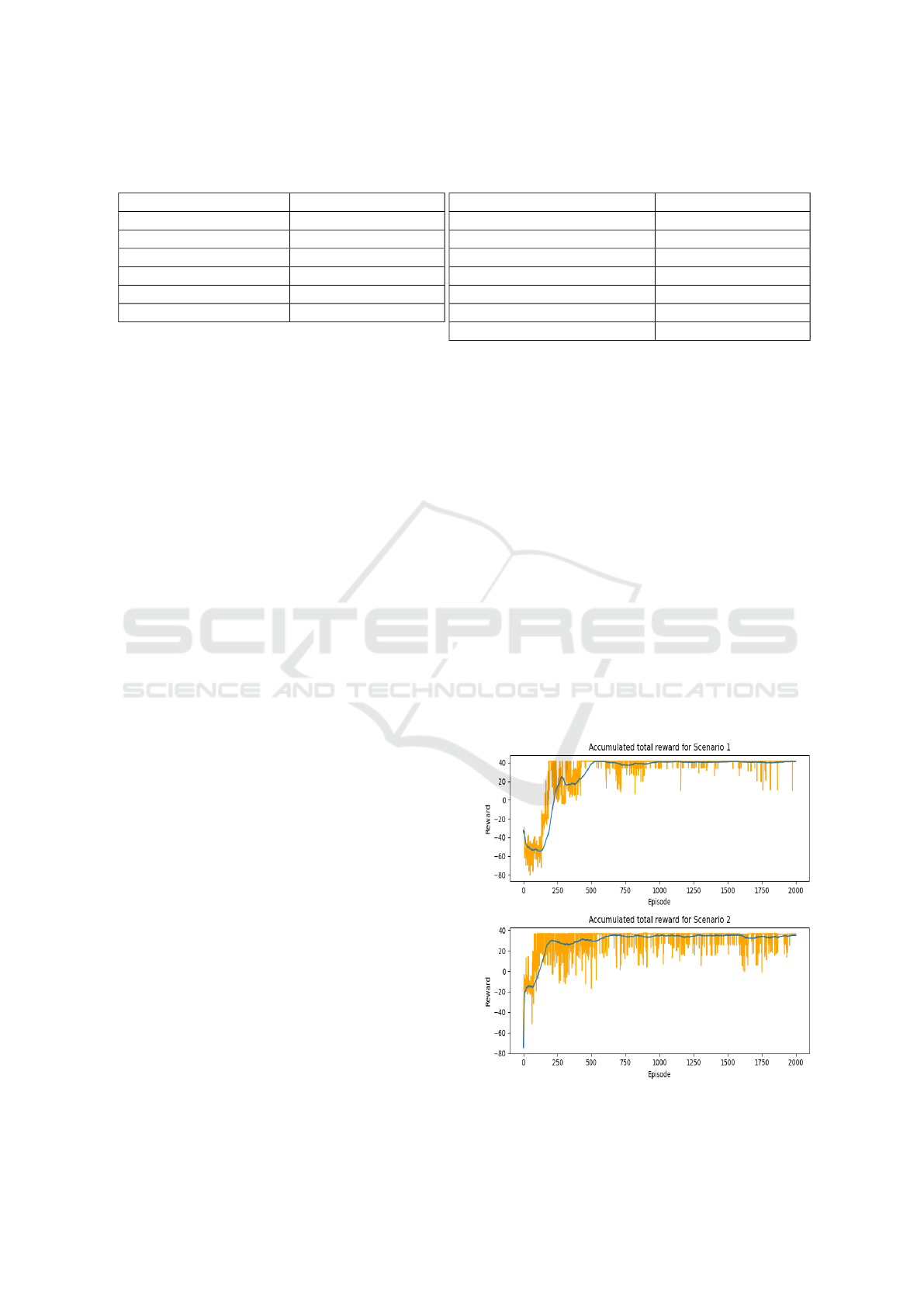
Table 1: Simulation Setup for experiment.
(a) Scenario 1.
v
init
of agent U(8.33, 27.77) m/s
v
init
of obstacle 0 m/s
Rel. Position of obstacle 60 m
Safety Distance 5 m
Throttle ∈ IR with values [0,1]
Brake ∈ IR with values [0,1]
∆T 0.1 s
(b) Scenario 2.
v
init
of agent U(8.33, 27.77) m/s
v
init
of obstacle U(8.33, 27.77) m/s
Pos. of agent from junction 45 m
Pos. of obstacle from junction 45 m
Safety Distance 5 m
Throttle ∈ IR with values [0,1]
Brake ∈ IR with values [0,1]
∆T 0.1 s
encountered by vehicles and allow the agent to learn
from the interactions. We simulated our environment
by spawning vehicles according to the scenario men-
tioned in figure 2 and 3. In the simulations it is as-
sumed that the relative distance of the other objects
like cars, stop sign to the agent is known. For each
simulation the agent will be spawned at the same lo-
cation. The 2 scenarios which we simulated to make
models are:
•
Scenario 1: Static obstacle in front of agent. (Car,
Stop sign).
•
Scenario 2: Dynamic Obstacle, i.e both cars mov-
ing towards an intersection.
For scenario 2, we also want our agent to start again
after emergency braking, so we do not end the episode
once the agent avoids the collision. We keep a maxi-
mum limit of 7.5 seconds for an episode to end. Time
to collision(TTC) is chosen within this maximum limit.
For both the scenarios, the time to collision (TTC)
is chosen to be between 1.5 s to 5 s. Also the safety
distance to the obstacle is kept to be 5
m
. For scenario
2, a safety distance box is made as shown in figure 3.
The velocity of agent is sampled from uniform dis-
tribution, with
v
min
init
= 8.33m/s(30km/h)
and
v
max
init
=
27.77m/s(100km/h)
. The wide range of values will
make our agent learn to apply brake/throttle in most
extreme cases also. The detailed simulation setup for
both of these scenarios is shown in Table 1
5.2 Training
The neural network architecture consists of a fully
connected feed-forward neural network with 5 hidden
layers for both the actor and critic networks. We use
the same architecture for both of the scenarios, the
difference is in their reward functions. Adam optimizer
is used for both actor and critic networks. (Kingma and
Ba, 2014). A total of 2000 episodes have been trained
for both scenarios.The details of the architecture is
shown below:
• State buffer size : n = 10
•
Network architecture - Fully connected feed-
forward network with 5 hidden layers
•
Number of nodes for each layers: [40(Input layer),
400, 200, 100, 200, 400, 1(Output Layer)]
• Non linear Function - leaky ReLU.
• Actor learning rate - 0.00005
• Critic learning rate - 0.0005
• Replay buffer size - 20000
• Minibatch size - 16
• Gamma - 0.99
• Tau - 0.001
•
Reward function -
α = 0.01
,
β = 0.1
,
η = 0.01
,
λ = 50
,
γ
(Scenario 1) = 15,
γ
(Scenario 2) = 20,
µ = 30 ,δ = 0.5.
Figure 4: Value function during training.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
178

Figure 5: Trajectory of action and velocity of agent during 1 episode.
There is one neuron at the output. We have used
tanh activation layer at the output, so that the network
outputs the value between -1 and 1. If the output is less
than 0, we apply the brake and if the value is greater
than 0, we apply throttle.
5.3 Results
Figure 4 depicts the accumulated reward for scenario
1 and 2. For scenario 1,we can see that our model
makes quite an improvement in the accumulated re-
ward after 200 episodes, from 200 episodes to 700-750
episodes, it follows an increasing curve and later the
curve remains more or less the same. Occasionally
the curve shows some small spikes which is expected
since we are sampling the initial velocity of a car to
be 100 km/hr which is very high and even if we apply
full braking action from the start of the episode, we
cannot avoid the collision. The accumulated reward
curve for scenario 2 follows a similar trend as scenario
1. But there are more spikes as compared to scenario
1. This can be attributed to scenario 2 being more
complex and the agent needing to take into account
the high speed at intersection, which makes it hard to
learn a good policy. Now we consider one test episode
of scenario 2. Figure 5 shows the velocity of the car
as the agent takes braking or throttle decisions during
one episode. We observe that as the car approaches
the intersection, the agent slowly decreases throttle, so
there is very less decrease in velocity, but after 3 sec-
onds, it detects the object crossing the intersection at
high speed, so it applies brakes till the vehicle reaches
a speed of 0. Once the car avoids an emergency situ-
ation (collision), it again applies throttle to speed up
the car. This explains the valley like curve of velocity
in figure 5, between 2 and 6 seconds of the episode.
At last, when the vehicle achieves desired velocity, it
reduces the throttle input to make it constant. This
Autonomous Braking and Throttle System: A Deep Reinforcement Learning Approach for Naturalistic Driving
179

curve closely resembles human driving while cross-
ing intersections. The inclusion of early stopping and
avoiding high speed at intersections ensures the car is
always in a safe state. Since we are using real values
of brake and throttle as compared to previous study by
Chae (Chae et al., 2017) where the author proposes
discrete values of deceleration, we get a smooth de-
crease/increase in velocity. Also the velocity is in the
safety limits as we have imposed penalties for high
speed.
6 CONCLUSION AND FUTURE
WORK
We have demonstrated the braking and throttle control
system for 2 scenarios. One where braking is very
important, while the other scenario needs both braking
and throttle action. DDPG is used to ensure that the
values of brake and throttle are smoothly changing in-
stead of a sudden change. We have proposed measures
to avoid early stopping and high speed movement at
an intersection, making autonomous driving similar
to human driving. This work can be further extended
to other such situations, where the vehicle must apply
brake or throttle to avoid emergency situations. An
interesting study would be to see the effect of braking
and throttle actions along with steering of the vehicle
in these situations. One can create a unified model
for all these scenarios with a singular reward func-
tion. Also, the effect of change of weather conditions
can also be considered so as to make the model more
realistic.
ACKNOWLEDGEMENTS
The authors would like to thank Dr. Prashant P. Bar-
takke, Department of Electronics and Telecommuni-
cation Engineering, College of Engineering Pune, for
guiding us throughout the project.
REFERENCES
Chae, H., Kang, C. M., Kim, B., Kim, J., Chung, C. C.,
and Choi, J. W. (2017). Autonomous braking system
via deep reinforcement learning. In 2017 IEEE 20th
International Conference on Intelligent Transportation
Systems (ITSC), pages 1–6.
Dosovitskiy, A., Ros, G., Codevilla, F., Lopez, A., and
Koltun, V. (2017). CARLA: An open urban driving
simulator. In Proceedings of the 1st Annual Conference
on Robot Learning, pages 1–16.
Fu, Y., Li, C., Yu, F. R., Luan, T. H., and Zhang, Y. (2020).
A decision-making strategy for vehicle autonomous
braking in emergency via deep reinforcement learn-
ing. IEEE Transactions on Vehicular Technology,
69(6):5876–5888.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. The MIT Press.
Kaempchen, N., Schiele, B., and Dietmayer, K. (2009).
Situation assessment of an autonomous emergency
brake for arbitrary vehicle-to-vehicle collision scenar-
ios. IEEE Transactions on Intelligent Transportation
Systems, 10(4):678–687.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2015). Continu-
ous control with deep reinforcement learning.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M. (2013).
Playing atari with deep reinforcement learning.
Porav, H. and Newman, P. (2018). Imminent collision miti-
gation with reinforcement learning and vision. In 2018
21st International Conference on Intelligent Trans-
portation Systems (ITSC), pages 958–964.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. A Bradford Book, Cambridge,
MA, USA.
Sutton, R. S., McAllester, D. A., Singh, S. P., and Mansour,
Y. (2000). Policy gradient methods for reinforcement
learning with function approximation. In Advances
in neural information processing systems, pages 1057–
1063.
Talpaert., V., Sobh., I., Kiran., B. R., Mannion., P., Yoga-
mani., S., El-Sallab., A., and Perez., P. (2019). Ex-
ploring applications of deep reinforcement learning
for real-world autonomous driving systems. In Pro-
ceedings of the 14th International Joint Conference
on Computer Vision, Imaging and Computer Graphics
Theory and Applications - Volume 5: VISAPP,, pages
564–572. INSTICC, SciTePress.
Uhlenbeck, G. E. and Ornstein, L. S. (1930). On the theory
of the brownian motion. Phys. Rev., 36:823–841.
Vasquez, R. and Farooq, B. (2019). Multi-objective au-
tonomous braking system using naturalistic dataset. In
2019 IEEE Intelligent Transportation Systems Confer-
ence (ITSC), pages 4348–4353.
Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine
learning, 8(3-4):279–292.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
180
