
Comparing Elementary Cellular Automata Classifications with a
Convolutional Neural Network
Thibaud Comelli
1
, Fr
´
ed
´
eric Pinel
2
and Pascal Bouvry
2
1
Polytech Lille, University of Lille, France
2
Faculty of Science, Technology and Medicine, University of Luxembourg, Luxembourg
Keywords:
Cellular Automata, Cellular Automata Classification, Convolutional Neural Network.
Abstract:
Elementary cellular automata (ECA) are simple dynamic systems which display complex behaviour from
simple local interactions. The complex behaviour is apparent in the two-dimensional temporal evolution of a
cellular automata, which can be viewed as an image composed of black and white pixels. The visual patterns
within these images inspired several ECA classifications, aimed at matching the automatas’ properties to
observed patterns, visual or statistical. In this paper, we quantitatively compare 11 ECA classifications. In
contrast to the a priori logic behind a classification, we propose an a posteriori evaluation of a classification.
The evaluation employs a convolutional neural network, trained to classify each ECA to its assigned class
in a classification. The prediction accuracy indicates how well the convolutional neural network is able to
learn the underlying classification logic, and reflects how well this classification logic clusters patterns in the
temporal evolution. Results show different prediction accuracy (yet all above 85%), three classifications are
very well captured by our simple convolutional neural network (accuracy above 99%), although trained on a
small extract from the temporal evolution, and with little observations (100 per ECA, evolving 513 cells). In
addition, we explain an unreported ”pathological” behaviour in two ECAs.
1 INTRODUCTION
This paper reports our findings when comparing ex-
isting classifications of elementary cellular automata
(ECA) from the perspective of a convolutional neural
network (CNN). We will introduce in the next para-
graphs ECAs and their classifications, but as a first
approximation, we can say that the representation of
a cellular automata’s temporal evolution (for exam-
ple: Figure 1) forms an image, which reveals patterns
that inspired several researchers to classify the differ-
ent ECAs under a few classes of behaviour. Figure 2
shows temporal evolutions of three ECAs belonging
to different classes in an early and well-known classi-
fication (Wolfram, 1984).
The different published ECA classifications are
like definitions: their underlying logic is their sole
justification, there is no a posteriori validation. We
propose to quantitatively compare these classifica-
tions, thus, we need a comparison method. The image
representation of the ECA’s temporal evolution sug-
gests the use of convolutional neural networks (CNN)
as a judge, this is further explained in Section 2. Next,
we introduce the various concepts used in this paper.
Figure 1: Rule 184 (Bach, 2020).
Elementary Cellular Automata. A cellular au-
tomata (Von Neumann et al., 1951; Moore and Burks,
1970; Wolfram, 1984) (CA) is the application of one
Boolean function, called the CA rule, which maps
the next value of a cell, from its previous value and
its neighbours’ values. The rule is individually ap-
plied to an array of cells, also called a configuration.
While the rule defines the behaviour of a CA, addi-
tional information is needed to fully execute a CA.
Here, we are concerned with elementary cellular au-
tomata: one-dimensional (the configuration is one-
dimensional), each cell takes the value 0 or 1 (white
Comelli, T., Pinel, F. and Bouvry, P.
Comparing Elementary Cellular Automata Classifications with a Convolutional Neural Network.
DOI: 10.5220/0010160004670474
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 467-474
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
467

or black), the rule’s domain are three cells, the cen-
tral cell and its left and right neighbours. Additional
information is further required to fully compute the
evolution of a CA, the full definition is presented in
Section 4.1. As an example, rule 30’s truth table is
presented below:
7→ = 0 7→ = 1
7→ = 0 7→ = 1
7→ = 0 7→ = 1
7→ = 1 7→ = 0
The decimal representation of the mapped values is
used to name the rule: 00011110
2
= 30
10
in this case.
The image representation of the temporal evolution is
obtained by placing the next value of each cell in the
cell array below its previous value.
Classification. The simplicity of the ECA is mis-
leading, as its simple local interactions can gener-
ate complex behaviours or patterns. Because of this,
some authors write (Wuensche et al., 1992) ”cellu-
lar automata are for complex systems theorists what
E. coli are for the biologist: a system simple enough
to manipulate experimentally, but complex enough
to suggest insights for real-world problems.” Some
ECAs are shown to be capable of universal compu-
tation (Cook, 2004). In addition, ECA behaviours
can be clustered, or classified, according to the sim-
ilar patterns their evolution reveals. This has lead to
several classifications of ECA behaviour. Wolfram’s
classification (Wolfram, 1984) defines 4 classes, class
I for ECA that converge to uniform configurations,
class II when converging to periodic configurations,
class III for generating apparent random configura-
tions and class IV for complex configurations, mostly
random but with pattern formation. Figure 2 high-
lights three of those classes, the first (leftmost) rule
is considered periodic, the second chaotic and the
last (rightmost) complex (Wolfram, 1984; Berto and
Tagliabue, 2017). It was also noted that some ECA
display different behaviours depending on their initial
configuration.
In contrast, other classifications have sought quan-
titative tools to form classes, instead of the more vi-
sual pattern recognition. Wuensche et al. (Wuen-
sche et al., 1992) have further examined the Wol-
fram classification with basins of attraction fields.
Normal Compression (Zenil and Villarreal-Zapata,
2013) base their classification on Kolmogorov com-
plexity (approximated with a lossless compression ra-
tio) and a probabilistic complexity measure, black
entropy (Wolfram, 2002). Surface Dynamics (Seck
Tuoh Mora et al., 2014) rely on statistics, density and
Figure 2: Rules 4, 30 and 110 (Berto and Tagliabue, 2017).
binary values (to further split equal density configu-
rations), predicted with nearest-neighbour interpola-
tion. The statistical model is then used to capture long
term effects.
Convolutional Neural Networks. The hypothesis
behind the choice of the convolutional neural network
as the comparison method is that if human pattern
recognition or statistical measures inspired the design
of a CA classification, then a CNN should also be ca-
pable of learning it. Section 4 shows if this hypothesis
holds.
To summarize, we aim to compare how well the
previously published ECA classifications capture the
temporal patterns of the ECA across different config-
urations. A convolutional neural network is trained
for each ECA classification, and its predictive accu-
racy (of the expected class under that classification)
on different ECA configurations is then used to com-
pare the ECA classifications.
2 PROPOSED APPROACH
Over time, multiple classifications for ECAs have
been proposed. Mart
´
ınez (Mart
´
ınez, 2013) provides
an exhaustive summary.
In this paper, we propose to quantitatively com-
pare the different ECA classifications through the lens
of a neural network: how well can a neural network
learn the logic behind an ECA classification. To this
end, we will define the input data, a neural network
architecture, training and test data sets. The classes
defined by each classification represent the expected
output, to be predicted by the CNN.
Most ECA classifications derive from the analy-
sis of the two-dimensional representation of the tem-
poral evolution of an ECA, as we saw from Fig-
ure 2. Therefore, the chosen neural architecture is
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
468

the convolutional neural network (LeCun et al., 1995)
(CNN), which has demonstrated its capability for pat-
tern recognition in images (Krizhevsky et al., 2012;
Russakovsky et al., 2015), matching and often ex-
ceeding human ability (He et al., 2015). The input
data to training and testing of the CNN are images:
black and white pixels of predetermined fixed size,
extracted from the representation of the temporal evo-
lution of an ECA. The executions start from a random
initial configuration, which permits the generation of
as much data as needed, for training and testing. A
common CNN architecture will be trained on each of
the ECA classification, then tested for prediction ac-
curacy on unseen ECA executions (from a different
initial configuration).
Each classification will then be judged on how ac-
curate the corresponding CNN can predict this classi-
fication’s classes: how does it grasp the concept un-
derlying that particular classification. We will analyse
these results and expose distinctive characteristics of
these classifications when possible.
3 RELATED WORK
To our best knowledge, there is no previous work
comparing ECA classifications. Therefore there is
no such comparison based on CNN either, neverthe-
less, casting the comparison as an instance of the im-
age classification problem suggests the use of a CNN,
given its demonstrated capability (see references in
Section 2).
Related work includes the proposal of new clas-
sification, based or not on previous classification, but
relies on a new indicator: a new observed behaviour.
Wuensch et al. (Wuensche et al., 1992) have estab-
lished the concept of equivalence classes between
CA. He used the left/right and black/white symme-
tries and has shown that they follow the same be-
haviour, and therefore should not be assigned to dif-
ferent classes in a classification (equivalent rules are
enumerated in (Mart
´
ınez, 2013)). Langton (Langton,
1990) introduces an indicator λ called activity. This
represents the ratio of the number of transformation
in the rule that lead to a quiescent state. This num-
ber has shown to be correlated with Wolfram’s clas-
sification (Wolfram, 1984). Others, such as Blinder
and Oliveira (Binder, 1993) suggest a better analysis
of CA behaviour by defining sensitivity, absolute ac-
tivity, neighbourhood dominance and activity propa-
gation (Oliveira et al., 2001b; Oliveira et al., 2001a;
de Oliveira et al., 2000). In our work, the CNN is
not used as an indicator, or discriminator, that leads
to a new classification, rather we employ a CNN as
a observer to determine which of those classifications
produce more accurate predictions.
Some previous works make use of neural net-
works, not for comparison but to automatically clas-
sify CAs within a specific classification. Kun-
kle (Kunkle, 2003) justifies seven parameters used as
input data to a neural network. The neural network
returns the class in Li and Packard’s classification (Li
and Packard, 1990) where the rule should belong.
The author aims to show the impact of those param-
eters, however dismissing the visual and random as-
pect that inspired Wolfram’s classification (Wolfram,
1984). Although multiple behaviours of the CA have
been described, it says nothing of the capability of al-
ternatives neural networks, such as CNN. Also, the
neural network is used to predict a class within a clas-
sification, and not to compare classifications, as pre-
sented here.
Silverman (Silverman, 2019) used a CNN as a
proof of accuracy: his goal was to study ECAs of
class IV in Wolfram’s classification, ECAs of this
class being difficult to categorise. He used a CNN
directly on the temporal evolution of cellular au-
tomata, as in our paper. After training, the CNN was
able to predict the class IV more than 90% even on
some higher-complexity spaces. However, Silverman
makes no mention of CNN to compare classifications,
which is the goal of our paper.
4 RESULTS
We begin this section with the experimental setup,
Section 4.1, followed by the complete description of
an unexpected behaviour for two specific ECAs, Sec-
tion 4.2. Finally, all results and noteworthy findings
are presented in Section 4.3.
We compare 11 known elementary CA classi-
fications: Wolfram, Li and Packard, Wuensche,
ECAM, Index complexity, Communication complex-
ity, Topological, Topological dynamics, Normalised
compression, Surface dynamics, Spectral. These
classifications were gathered in a survey paper by
Mart
´
ınez (Mart
´
ınez, 2013). However some minor er-
rors remain in that survey paper, so we recommend
referring back to the cited reference for each individ-
ual classification to avoid mis-classifications.
As mentioned, a CNN will be trained for each
classification. All CNNs share the same architecture
and will be trained and tested on the same data
1
,
where only the class each ECA belongs to varies from
one classification to another. Note that the number
1
Training and test data are different.
Comparing Elementary Cellular Automata Classifications with a Convolutional Neural Network
469

of classes also varies per classification (but remains
low). The data is composed of the temporal evolution
of a CA, starting from a randomly generated initial
configuration. More details are found in Section 4.1.
After training the CNN for each CA in each classifi-
cation, we observe the classification errors on the test
data set, which serves as the basis for the compari-
son among different classifications. Additionally, the
predicted classes for each CA in each classification is
recorded for further analysis (the raw data is not in-
cluded in the paper).
4.1 Detailed Setup
The CNN is defined by its structure and the train-
ing data. The training data is generated as follows.
We generate 100 ECA temporal evolutions for each
of the 256 ECAs (there are only 256 ECAs, as can
be deducted from Section 1). Each ECA evolves an
initial configuration of 512+1 cells, the configuration
is cyclic (Wolfram, 2002) (the right neighbor of the
rightmost cell is the leftmost cell, and vice versa).
Cyclic configurations are sometimes called wrapped
around (Wuensche et al., 1992).
The ECA iterations start from a random initial
configuration, and each new configuration produced
in an iteration is represented immediately below the
previous configuration values, to form a 2D represen-
tation (for example, Figure 1). After 512 iterations,
a fixed 32 × 32 area is selected, and the cells’ values
serve as the input image to the CNN. Other classifi-
cations have also relied on a small cell area (Wuen-
sche et al., 1992; Seck Tuoh Mora et al., 2014; Zenil
and Villarreal-Zapata, 2013). The different random
initial configurations aim to capture the ECA average
behaviour (Zenil and Villarreal-Zapata, 2013).
A cyclic configuration produces interference
faster (half the iterations) than without. We opted to
include the full behaviour of the CA, with interfer-
ence. Alternatives are: a fixed value (either 0 or 1)
at the edges of the array, or a random value. The ar-
ray length is 513 cells. The typical 512 = 2
9
was ini-
tially considered, however initial executions showed
that rules 60, 90 and their equivalent are nilpotent
2
from random initial configurations, despite Wolfram,
Li and Packard classifying them as chaotic. A proof
sketch is provided below, Section 4.2, for configura-
tions of 2
k
cells.
The CNNs trained for each classification share
the same architecture. The chosen architecture is a
straightforward sequential model of only 6 layers with
a input of a 32 × 32 binary type:
1. 3 × 3 convolution 2D layer,
2
Configuration cells are all 0 or 1 after several iterations.
2. 2 × 2 max pooling layer,
3. 3 × 3 convolution 2D layer,
4. input flattening layer,
5. 64 dense layer
3
6. dense layer, where the number of nodes matches
the number of classes in the classification being
fit.
The activation function is the ReLU, and the opti-
mizer algorithm is Adam. The only difference be-
tween CNNs trained for different classifications is the
class in the classification each rule belongs to. The
same ECA executions (starting from the same ran-
dom initial configuration) are used across the different
classifications.
We have deliberately opted for a simple CNN.
Deeper architectures are of course possible, and train-
able with the large amount of data that can be gener-
ated. Adding convolution layers could capture more
elaborate pattern classifications. Also, by considering
the ECA rule as spatial pattern, operating on a config-
uration (at one iteration, or one time step), and con-
sidering the cells’ interference as a temporal pattern,
we could decompose the CNN into two components,
where first a representation of the ECA rule would be
inferred from the ECA output, then followed by a rule
representation-to-class classifier. The size of the ex-
tracted data from the ECA’s output would guide the
length of the second classifier, while the first is dic-
tated by the number of possible rules (256 for ECA)
and the feature extraction of the convolution layers.
Such CNN designs would be much larger than the
one chosen above, which, as we shall discuss in Sec-
tion 4.3, achieves significant accuracy.
The testing data is of the same type as the training
data, but contains 200 unseen 32 ×32 images for each
of the 256 rules, for a total of 51,200 observations.
4.2 Nilpotency of Rules 90 and 60
In this section we propose a proof of the ’patholog-
ical’ behaviour of two ECA, under specific configu-
ration. The behaviour is that rules 60 and 90 have
a nilpotency behaviour when they operate from an
cyclic configuration of 2
k
cells. The proof also applies
to the equivalents of rule 60 (rules 102, 153, 195) and
rule 90 (rule 165) (Mart
´
ınez, 2013).
4.2.1 Notation
The following notation is used in the proof:
3
Fully-connected layer.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
470

• Symbols and describe the value of a cell, re-
spectively white (0) and black (1).
• Variables x, y and z describe the variable value of
a specific cell.
• C
k
represents any configuration of 2
k
− 1 cells,
whose exact values are ignored in the reasoning.
We define the operator =⇒
i
between a sub-array of
k + 2 ∗ i cells and a sub-array of k cells to represent
the transformation which defines the k values of the
k cells. The i in =⇒
i
indicates the number or CA
iterations. These k values that can be fully deter-
mined, despite ignoring other cells to the left or right
of the input (left-hand side) sub-array. This explains
the smaller output sub-array. The intent is to identify
the fully known values after the CA iterations. The
configuration on the right-hand side of =⇒
i
leads to
the value of the central cell after i iterations.
For example, for rule 90:
=⇒
1
and
=⇒
2
=⇒
1
4.2.2 Rule 90
Rule 90 implements the Boolean XOR operator on the
left and right neighbour. We can express rule 90 with
our introduced operator =⇒
1
:
xyz =⇒
1
n
i f x = z
otherwise
We start with a proof by induction, on k ≥ 1, that:
xC
k
y =⇒
2
k−1
n
i f x = y
otherwise
(1)
For the initial case, k = 1: by definition, C
k
consists
of one cell, and according to the definition of rule 90,
the inductive hypothesis holds for k = 1.
Let’s assume (1) holds for some k ≥ 1. For the
inductive step, k + 1, we start by establishing the fol-
lowing:
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
C
k
=⇒
2
k−1
C
k
=⇒
2
k−1
C
k
xC
k
consists of 2
k+1
− 1 cells, and from the above
expressions, it can be rewritten as:
xC
k+1
y =⇒
2
k
n
i f x = y
otherwise
Thus (1) is proved.
By definition of C
k
, x and y in xC
k
y are separated
by 2
k
−1 cells. So in the specific case of a 2
k
cyclic ar-
ray the rightmost (y) and leftmost neighbour (x) point
to the same cell. From (1), after 2
k−1
iterations, each
cell transitions to white and, by definition of rule 90,
will remain white.
4.2.3 Rule 60
Rule 60 is similar to rule 90: it implements the
Boolean XOR operator on the left and center cells.
We can also express it with the operator =⇒
1
intro-
duced in Section 4.2.1:
xyz =⇒
1
n
i f x = y
otherwise
We proceed as for rule 90 with the proof, by induction
on k ≥ 1, that:
xC
k
yC
k
C
1
=⇒
2
k
n
i f x = y
otherwise
(2)
To discharge the initial case, k = 1, we observe that:
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
xy =⇒
1
C
1
=⇒
1
These expressions are of the form:
xC
1
yC
1
C
1
=⇒
2
1
n
i f x = y
otherwise
So the inductive hypothesis holds for k = 1.
Let’s assume (2) holds for some k ≥ 1. For the
inductive step, k + 1, we start by establishing the fol-
lowing:
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
Comparing Elementary Cellular Automata Classifications with a Convolutional Neural Network
471
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
C
k
C
k
C
k
xC
k
y =⇒
2
k
C
k
C
k
C
1
=⇒
2
k
These expressions are of the form:
xC
k+1
yC
k+1
C
1
=⇒
2
k+1
n
i f x = y
otherwise
Thus (2) has been proved.
By definition of C
k
, x and y in xC
k
yC
k
C
1
are sep-
arated by 2
k
− 1 cells. So in the specific case of a 2
k
cyclic array the rightmost (x) and the center cell (y)
point to the same cell. From (2), after 2
k
iterations,
each cell transitions to white and, by definition of rule
60, will remain white.
4.3 Results and Analysis
As described in the setup, Section 4.1, once a CNN
classifier is trained for a classification, it is evaluated
on a test set (which counts 51,200 observations, or
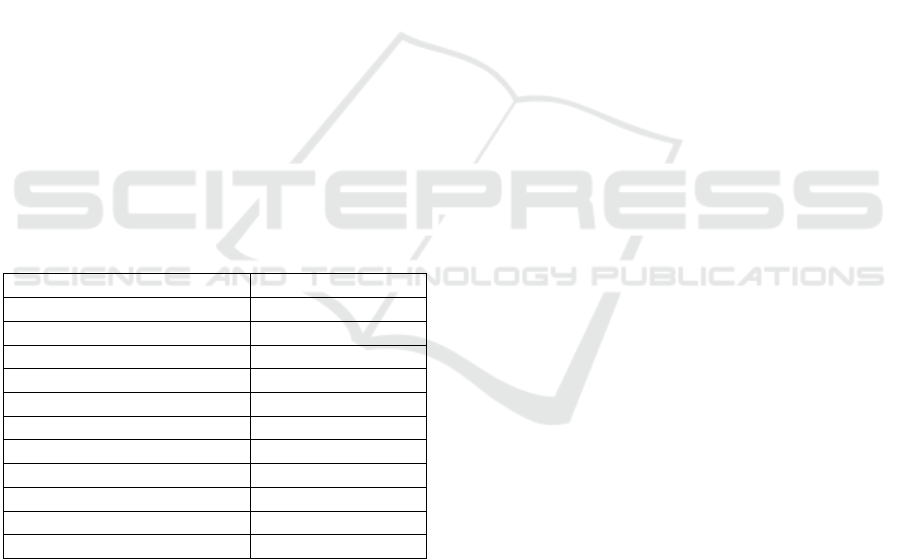
twice the training data size). Table 1 lists the observed
accuracy, for each classification, of the trained CNN
classifier (a classification accuracy greater than 99%
is typeset in bold).
Table 1: Accuracy of the CA rule classifiers (CNN), per
classification (on test set).
Classification CNN accuracy (%)
Wolfram 99.54
Li & Packard 97.58
Wuensche 89.01
ECAM 92.38
Index complexity 87.81
Communication complexity 85.67
Topological 99.08
Topological dynamics 91.99
Normalised compression 99.23
Surface dynamics 99.59
Spectral 96.12
Classifications such as Wolfram’s, Surface dynamics
and Normalised Compression seem to be well learned
by the simple CNN proposed. For reference, they pro-
pose 4, 2 and 3 classes respectively. On the other
hand, classifications such as Wuensche, Index com-
plexity and Communication complexity are less well
learned. They all have 3 classes. Nevertheless, every
classification achieves an accuracy of 85% or greater.
The prediction results on the test set reveal more
than the overall accuracy for each classification, the
results also record the accuracy of each rule, under
each classification. For certain classifications, the im-
ages extracted from the temporal evolution of a par-
ticular ECA are never classified correctly. In those
cases, the CNN classifies most of the 200 unseen ECA
execution images in the same incorrect class. The
CNN seems to have identified a different pattern from
the classification logic. This can depend on our choice
of the image extracted from the execution trace.
Under Wolfram’s classification, 253 of 256 rules
are correctly predicted more than 90% of the time.
The least correctly classified rules are rule 104 (68%)
and 233 (75.5%). They are considered by Wuensche
as equivalent rules, due to their black/white symme-
try. Therefore there is some consistency in the CNN
predictions. In Wolfram’s classification, these rules
are labeled class II (periodic behaviour). When incor-
rectly classified, the predicted class is always class I
(uniform behaviour). These rules display sparse, dou-
ble strip-down lines, while most often the 32 ×32 im-
ages extracted for the 200 test observations do not. A
different, larger, selected image could reduce the in-
correct predictions.
The Normal compression classification (Zenil and
Villarreal-Zapata, 2013) splits the 256 rules in two
classes, C
1,2
and C
3,4
. In summary, the rules as-
signed to class I and II in Wolfram’s classification
are assigned to class C
1,2
, and all rules from Wol-
fram’s class III and IV are assigned to C
3,4
. There
are a few exceptions: rules 62, 73 and 94 belong to
Wolfram’s class II, yet are assigned to C
3,4
. For this
classification, 253 rules of 256 are correctly classi-
fied more than 90% of the time. The rules least cor-
rectly classified are the rule 94 (50.5%) and the rule
133 (55%), which is equivalent to 94. In contrast,
rules 67, 73 and their equivalents are correctly classi-
fied more than 97% of the time. The CNN does not
know how to classify the rule 94. Nevertheless, this
classification accuracy (i.e. the accuracy of the CNN
trained with this classification) is very close to Wol-
fram’s CNN accuracy when it uses only two classes,
with similar split of rules. We could therefore expect
a greater accuracy.
For the Surface Dynamics classification (Seck
Tuoh Mora et al., 2014), 255 rules out of 256 are clas-
sified correctly more than 90% of the time. No rule
stands out in terms of misprediction. Note that this
classification uses three classes, versus four in Wol-
fram’s.
Finally, when inspecting how equivalent rules are
classified, we notice that the less accurate classifiers
(trained for a classification) often incorrectly clas-
sify some equivalent rules, while correctly predict-
ing other equivalent rules. The split between mispre-
dicted and correctly predicted equivalent rules does
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
472

not follow any equivalence logic, such as visual sym-
metries.
The classification accuracy results reported may
also depend on the capacity of the CNN. The chosen
CNN is relatively simple, deeper CNN architectures
might be able to capture the logic in the other, less
well-learned, classifications. This hypothesis could
be tested by performing the same evaluation across a
spectrum of CNNs, of increasing capacity.
5 CONCLUSIONS
Convolutional neural networks have proven their ca-
pability in many applications and in particular for pat-
tern recognition in images. We have used this asset to
compare a long list of elementary cellular automata
classifications. The experimental results demonstrate
the ability of a neural network to learn CA classifica-
tions based on logical or abstract concepts, indirectly,
via their visual representation. Several classifications
(Wolfram, Surface Dynamics, Normalised Compres-
sion, Topological) are extremely well captured by
this approach (and all are well captured), suggesting
that convolutional neural networks could be applied
to other areas of the cellular automata domain. For
example, we could apply the Wolfram CNN classi-
fier presented here on non-CA output, such as part
of the memory of a running program, to observe if
the predicted class matches Wolfram’s class of ECAs
that are thought to be capable of universal computa-
tion (Cook, 2004; Martinez et al., 2013) (such as rule
110).
One uncertainty in this method is the choice of
the extracted image, from the ECA output, which
serves as input data to the neural network. Our ex-
periments show excellent results (prediction accu-
racy) from very small ECA output extracts, using lit-
tle training data (100 instances for each CA rule),
and with a simple CNN architecture (thus quickly
trained). Moreover, the ECA output selection is cho-
sen such that the influence of all 513 cells is accounted
for, in order to capture the complex system behaviour
of an ECA. Different results could be obtained from a
different selection, and more observations.
Also, we provide a sketched proof for a patho-
logical behaviour of two ECA rules, previously un-
reported (to our best knowledge).
The possibility that deeper CNNs could lead to
better accuracy for other classifications is considered
future work. This hypothesis, if true, could reflect the
complexity of a given classification, and thus defines
another comparison method (such as: the size of the
CNN that achieves over 99% accuracy).
Finally, the CNN-based approach and its results
could be used to discover new ECA classifications.
ACKNOWLEDGEMENTS
The authors wish to thank Christian Hundt of the
Nvidia AI Technology Center Luxembourg, and the
ICAART reviewers for their insightful comments.
REFERENCES
Bach, E. (2020). https://commons.wikimedia.org/w/index.
php?curid=15015440. Last accessed 22 July 2020.
Berto, F. and Tagliabue, J. (2017). Cellular automata. In
Zalta, E. N., editor, The Stanford Encyclopedia of Phi-
losophy. Metaphysics Research Lab, Stanford Univer-
sity, fall 2017 edition.
Binder, P. (1993). A phase diagram for elementary cellular
automata. Complex Systems, 7(3):241.
Cook, M. (2004). Universality in elementary cellular au-
tomata. Complex systems, 15(1):1–40.
de Oliveira, G. M. B., de Oliveira, P. P., and Omar, N.
(2000). Guidelines for dynamics-based parameteriza-
tion of one-dimensional cellular automata rule spaces.
Complexity, 6(2):63–71.
He, K., Zhang, X., Ren, S., and Sun, J. (2015). Delv-
ing deep into rectifiers: Surpassing human-level per-
formance on imagenet classification. In Proceedings
of the IEEE international conference on computer vi-
sion, pages 1026–1034.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Kunkle, D. R. (2003). Automatic Classification of One-
Dimensional Cellular Automata. PhD thesis, Citeseer.
Langton, C. (1990). Computation at the edge of chaos:
Phase transition and emergent computation. Techni-
cal report, Los Alamos National Lab., NM (USA).
LeCun, Y., Bengio, Y., et al. (1995). Convolutional net-
works for images, speech, and time series. The
handbook of brain theory and neural networks,
3361(10):1995.
Li, W. and Packard, N. (1990). The structure of the elemen-
tary cellular automata rule space. Complex systems,
4(3):281–297.
Martinez, G. J., Seck-Tuoh-Mora, J. C., and Zenil, H.
(2013). Computation and universality: class iv
versus class iii cellular automata. arXiv preprint
arXiv:1304.1242.
Mart
´
ınez, G. J. (2013). A note on elementary cellular au-
tomata classification. In Adamatzky, A., editor, Jour-
nal of Cellular Automata, volume 8, pages 233–259.
Old City Publishing, Greenville, SC 29616, United
States.
Moore, E. and Burks, A. (1970). Essays on Cellular Au-
tomata. University of Illinois, Urbana.
Comparing Elementary Cellular Automata Classifications with a Convolutional Neural Network
473

Oliveira, G. M., de Oliveira, P. P., and Omar, N. (2001a).
Searching for one-dimensional cellular automata in
the absence of a priori information. In European Con-
ference on Artificial Life, pages 262–271. Springer.
Oliveira, G. M., Oliveira, P. P. d., and Omar, N. (2001b).
Definition and application of a five-parameter charac-
terization of one-dimensional cellular automata rule
space. Artificial life, 7(3):277–301.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-
stein, M., et al. (2015). Imagenet large scale visual
recognition challenge. International journal of com-
puter vision, 115(3):211–252.
Seck Tuoh Mora, J., Medina, J., Martinez, G. J., and
Hern
´
andez Romero, N. (2014). Emergence of density
dynamics by surface interpolation in elementary cel-
lular automata. Communications in Nonlinear Science
and Numerical Simulations, 19:941–966.
Silverman, E. (2019). Convolutional neural networks for
cellular automata classification. In Artificial Life Con-
ference Proceedings, pages 280–281. MIT Press.
Von Neumann, J. et al. (1951). The general and logical
theory of automata. 1951, pages 1–41.
Wolfram, S. (1984). Cellular automata as models of com-
plexity. Nature, 311(5985):419–424.
Wolfram, S. (2002). A new kind of science, volume 5. Wol-
fram media Champaign, IL.
Wuensche, A., Lesser, M., and Lesser, M. J. (1992). Global
Dynamics of Cellular Automata: An Atlas of Basin
of Attraction Fields of One-Dimensional Cellular Au-
tomata, volume 1. Andrew Wuensche.
Zenil, H. and Villarreal-Zapata, E. (2013). Asymptotic
behavior and ratios of complexity in cellular au-
tomata. International Journal of Bifurcation and
Chaos, 23(09):1350159.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
474
