
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias
in Reinforcement Learning for Better Performance
Andreas Pentaliotis and Marco Wiering
Bernoulli Institute, Department of Artificial Intelligence, University of Groningen, Nijenborgh 9, Groningen,
The Netherlands
Keywords:
Reinforcement Learning, Q-learning, Double Q-learning, Estimation Bias, Variation-resistant Q-learning.
Abstract:
Q-learning is a reinforcement learning algorithm that has overestimation bias, because it learns the optimal
action values by using a target that maximizes over uncertain action-value estimates. Although the overestima-
tion bias of Q-learning is generally considered harmful, a recent study suggests that it could be either harmful
or helpful depending on the reinforcement learning problem. In this paper, we propose a new Q-learning
variant, called Variation-resistant Q-learning, to control and utilize estimation bias for better performance.
Firstly, we present the tabular version of the algorithm and mathematically prove its convergence. Secondly,
we combine the algorithm with function approximation. Finally, we present empirical results from three dif-
ferent experiments, in which we compared the performance of Variation-resistant Q-learning, Q-learning, and
Double Q-learning. The empirical results show that Variation-resistant Q-learning can control and utilize
estimation bias for better performance in the experimental tasks.
1 INTRODUCTION
Q-learning (Watkins, 1989) is one of the most widely
used reinforcement learning algorithms. This algo-
rithm tries to compute the optimal action values by
using sampled experiences to update action-value es-
timates. It is model-free, off-policy, relatively easy to
implement, and has a relatively simple update rule.
However, Q-learning has overestimation bias
(Thrun and Schwartz, 1993; Van Hasselt, 2010),
1
and
this has been shown to influence learning (Thrun and
Schwartz, 1993; Van Hasselt, 2010; Van Hasselt et al.,
2016). Moreover, overestimation bias is increased
when Q-learning is combined with function approx-
imation (Gordon, 1995), and this combination can
sometimes cause an agent to fail in learning to solve
a task (Thrun and Schwartz, 1993).
The most successful method to overcome the
problems caused by overestimation bias is Double
Q-learning (Van Hasselt, 2010). This algorithm up-
dates two approximate action-value functions on two
disjoint sets of sampled experiences. When one of
the two action-value functions is updated, it is also
used to determine the action the maximizes the ac-
tion values of the next state, but the maximizing ac-
1
We refer to overestimation bias as an inherent prop-
erty of Q-learning. This does not imply that the algorithm
shows overestimation in every reinforcement learning prob-
lem. The same reasoning applies to the estimation bias of
all the algorithms that we mention in this paper.
tion is evaluated by the other action-value function.
This ensures that the maximum optimal action value
of the next state is not overestimated, although it may
be underestimated. Although Double Q-learning is
an interesting alternative reinforcement learning algo-
rithm, it does not always outperform Q-learning be-
cause overestimation bias can sometimes be prefer-
able to underestimation bias (Lan et al., 2020).
Another reinforcement learning algorithm ad-
dressing the challenge of estimation bias is Bias-
corrected Q-learning (Lee et al., 2013), which sub-
tracts a bias correction term from the update tar-
get to remove overestimation bias. A problem is
that this bias correction term is computed by taking
into account only stochastic transitions and stochas-
tic rewards. Therefore, this algorithm cannot deal
with other sources of approximation error, such as
function approximation and non-stationary environ-
ment. Moreover, overestimation bias can sometimes
be helpful (Lan et al., 2020), and it would be prefer-
able to control it than to remove it.
Weighted Q-learning (D’Eramo et al., 2016) uses
a weighted average of all the action-value estimates
of the next state in the update target. The weight for
each action-value estimate approximates the probabil-
ity that the corresponding action maximizes the opti-
mal action values. This algorithm did not outperform
Double Q-learning in all the tasks it was tested on.
Moreover, it cannot control its estimation bias.
Averaged Q-learning (Anschel et al., 2016) uses
Pentaliotis, A. and Wiering, M.
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance.
DOI: 10.5220/0010168000170028
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 17-28
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

an average of a number of past action-value estimates
in the update target. Consequently, the overestimation
bias and estimation variance of the algorithm is lower
than those of Q-learning. The problem remains that
the overestimation bias is never reduced to zero be-
cause the average operator is applied to a finite num-
ber of approximate action-value functions. Moreover,
this algorithm cannot control its estimation bias.
Weighted Double Q-learning (Zhang et al., 2017)
uses a weighted version of Q-learning and Double Q-
learning to compute the maximum action value of the
next state in the update target. Although this algo-
rithm can control its estimation bias, it cannot un-
derestimate more than Double Q-learning or overesti-
mate more than Q-learning.
A very recent method is Maxmin Q-learning (Lan
et al., 2020), which uses an ensemble of agents to
learn the optimal action values. In this algorithm,
a number of past sampled experiences are stored in
a replay buffer. In each step a minibatch of experi-
ences is randomly sampled from the replay buffer and
is used to update the action-value estimates of one or
more agents. For each experience in the minibatch, all
agents compute an estimate for the maximum action
value of the next state, and the minimum of those es-
timates is used in the update target. The authors pro-
posed this method because they identified that under-
estimation bias may be preferable to overestimation
bias and vice versa depending on the reinforcement
learning problem, and they showed that the estimation
bias of this algorithm can be controlled by tweaking
the number of agents. Although this algorithm can
underestimate more than Double Q-learning, there is
a limit to its underestimation and it cannot overesti-
mate more than Q-learning.
Contributions. In this paper, we propose Variation-
resistant Q-learning to control and utilize estimation
bias for better performance. We present the tabular
version of the algorithm and mathematically prove its
convergence. Furthermore, the proposed algorithm is
combined with a multilayer perceptron as function ap-
proximator and compared to Q-learning and Double
Q-learning. The empirical results on three different
problems with different kinds of stochasticities indi-
cate that the new method behaves as expected in prac-
tice.
Paper Outline. This paper is structured as fol-
lows. In section 2, we present the theoretical back-
ground. In section 3, we explain Variation-resistant
Q-learning. Section 4 describes the experimental
setup and presents the results. Section 5 concludes
this paper and provides suggestions for future work.
2 THEORETICAL BACKGROUND
2.1 Reinforcement Learning
In reinforcement learning, we consider an agent that
interacts with an environment. At each point in time
the environment is in a state that the agent observes.
Every time the agent acts on the environment, the en-
vironment changes its state and provides a reward sig-
nal to the agent. The goal of the agent is to act opti-
mally in order to maximize its total reward.
One large challenge in reinforcement learning is
the exploration-exploitation dilemma. On the one
hand, the agent should exploit known actions in order
to maximize its total reward. On the other hand, the
agent should explore unknown actions in order to dis-
cover actions that are more rewarding than the ones it
already knows. To perform well, the agent must find
a balance between exploration and exploitation.
A widely used method to achieve this balance is
the ε-greedy method. When using this exploration
strategy, the agent takes a random action in a state
with probability ε. Otherwise, it takes the greedy (i.e.
most highly valued) action. The amount of explo-
ration can be adjusted by changing the value of ε.
2.2 Finite Markov Decision Processes
Many reinforcement learning problems can be math-
ematically formalized as finite Markov decision pro-
cesses. Formally, a finite Markov decision process is a
tuple (S,A, R, p, γ,t) where S = {s
1
, s
2
, . . . , s
n
} is a fi-
nite set of states, A = {a
1
, a
2
, . . . , a
m
} is a finite set of
actions, R = {r
1
, r
2
, . . . , r
κ
} is a finite set of rewards,
p : S × R × S × A 7→ [0, 1] is the dynamics function,
γ ∈ [0, 1] is the discount factor, and t = 0, 1, 2, 3, . . . is
the time counter.
At each time step t the environment is in a state
S
t
∈ S. The agent observes S
t
and takes an action A
t
∈
A. The environment reacts to A
t
by transitioning to a
next state S
t+1
∈ S and providing a reward R
t+1
∈ R ⊂
R to the agent. The dynamics function determines
the probability of the next state and reward given the
current state and action.
We consider episodic problems, in which the
agent begins an episode in a starting state S
0
∈ S and
there exists a terminal state S
T
∈ S
+
= S∪{S
T
}. If the
agent reaches S
T
, the episode ends, the environment
is reset to S
0
, and a new episode begins. During an
episode, the agent tries to maximize the total expected
discounted return. The discounted return at time step
t is defined as G
t
=
∑
T
k=t+1
γ
k−t−1
R
k
. The discount
factor determines the importance of future rewards.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
18
A policy π : S × A 7→ [0, 1] determines the proba-
bility of selecting each action given the current state.
In value-function based reinforcement learning, the
agent tries to learn an optimal policy by estimation
value functions. The optimal value of an action a ∈ A
in a state s ∈ S under an optimal policy is determined
by the optimal action-value function, which is defined
as,
q
∗
(s, a) = max
π
E
π
[G
t
|S
t
= s, A
t
= a] (1)
and is always zero for the terminal state. The optimal
action-value function satisfies the Bellman optimality
equation (Bellman, 1958), which is defined as,
q
∗
(s, a) =
∑
s
0
∈S
∑
r∈R
p(s
0
, r | s, a)
r + γ max
a
0
∈A
q
∗
(s
0
, a
0
)
(2)
and is used in the construction of many reinforcement
learning algorithms as it has q
∗
as unique solution.
2.3 Q-learning
In tabular Q-learning, we initialize an approximate
action-value function Q arbitrarily and use a policy
based on Q to sample (S
t
, A
t
, R
t+1
, S
t+1
) tuples. At
each time step t, the Q-function is updated by:
Q(S
t
, A
t
) ←(1 − α)Q(S
t
, A
t
)
+ α(R
t+1
+ γ max
a
0
Q(S
t+1
, a
0
)) (3)
where α is the step size. This version of Q-learning
converges to the optimal action-value function with
probability one (Watkins and Dayan, 1992).
Q-learning can be combined with function ap-
proximation as follows. Assume a differentiable non-
linear function approximator with a weight vector w
w
w
that is used to parametrize Q. The target Y
t
at time
step t is defined as:
Y
t
= R
t+1
+ γ max
a
0
Q(S
t+1
, a
0
;w
w
w) (4)
and the loss function J is defined as:
J(Y
t
, Q(S
t
, A
t
;w
w
w)) = [Y
t
− Q(S
t
, A
t
;w
w
w)]
2
(5)
Although Y
t
depends on w
w
w, we assume that Y
t
is in-
dependent of w
w
w and compute the gradient of J with
respect to w
w
w. We then perform the update,
w
w
w ← w
w
w + α [Y
t
− Q(S
t
, A
t
;w
w
w)]∇
w
w
w
Q(S
t
, A
t
;w
w
w) (6)
where α is the learning rate.
To understand why Q-learning can overestimate,
consider the update rule in equation 3. Assume that
there is some source of random approximation er-
ror, such as stochastic transitions, stochastic rewards,
function approximation, or a non-stationary environ-
ment. Therefore, for all actions a, we have that,
Q(S
t+1
, a) = q
∗
(S
t+1
, a) + e(S
t+1
, a) (7)
where e(S
t+1
, a) is a positive or negative noise term.
Since the max operator is applied over all the actions
in S
t+1
in the update target, the maximum action value
of S
t+1
can be overestimated due to positive noise.
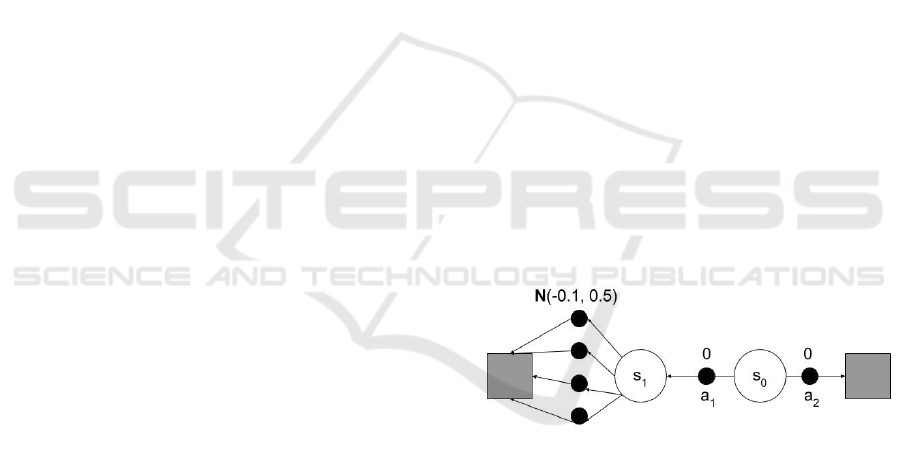
In figure 1, an episodic finite Markov decision
process is shown that was inspired by (Sutton and
Barto, 2018) to examine a case where overestimation
bias could be harmful. In this process, there are two
non-terminal states, s
0
and s
1
, and the terminal state
is depicted by gray squares. The starting state is s
0
and there are two possible actions in s
0
. The action a
2
causes a deterministic transition to the terminal state
with a deterministic reward of zero, whereas the ac-
tion a
1
causes a deterministic transition to s
1
with a
deterministic reward of zero. In s
1
there are four pos-
sible actions that cause a deterministic transition to
the terminal state. The rewards for those actions are
normally distributed with a mean of -0.1 and a stan-
dard deviation of 0.5. If the discount factor is set to
one, the expected return for any possible trajectory
that begins with a
1
is -0.1, whereas the expected re-
turn for taking a
2
is zero. Therefore, the optimal pol-
icy is to choose a
2
in s
0
. However, a Q-learning agent
following an ε-greedy policy could choose a
1
many
times in the beginning of learning, because it overes-
timates the maximum optimal action value of s
1
.
Figure 1: An episodic finite Markov decision process to
highlight the problems caused by overestimation bias. The
starting state is s
0
and the terminal state is depicted by gray
squares. All the transitions are deterministic and the re-
wards are shown above the actions.
2.4 Double Q-learning
In tabular Double Q-learning, we initialize two ap-
proximate action-value functions, Q
1
and Q
2
, arbi-
trarily and use a policy based on both of them to sam-
ple (S
t
, A
t
, R
t+1
, S
t+1
) tuples. At each time step t, we
update Q
1
or Q
2
with equal probability. The update
rule for Q
1
at time step t is defined as:
Q
1
(S
t
, A
t
) ←(1 − α)Q
1
(S
t
, A
t
)
+ α(R
t+1
+ γQ
2
(S
t+1
, A
∗
)) (8)
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance
19

where α is the step size and A
∗
=
argmax
a
0
Q
1
(S
t+1
, a
0
). The update rule for Q
2
at time step t is similar to the one in equation 8 but
with Q
1
and Q
2
swapped. This version of Double
Q-learning converges to the optimal action-value
function with probability one (Van Hasselt, 2010).
Double Q-learning can be combined with func-
tion approximation as follows. Assume two differ-
entiable nonlinear function approximators with two
different weight vectors, w
w
w
1
1
1
and w
w
w
2
2
2
, that are used to
parametrize Q
1
and Q
2
respectively. At each time step
t, we update one of w
w
w
1
1
1
and w
w
w
2
2
2
with equal probability.
The target Y
t
for w
w
w
1
1
1
at time step t is defined as:
Y
t
= R
t+1
+ γQ
2
(S
t+1
, A
∗
;w
w
w
2
2
2
) (9)
where A
∗
= argmax
a
0
Q
1
(S
t+1
, a
0
;w
w
w
1
1
1
). Assuming the
same loss function as in equation 5 and that Y
t
is in-
dependent of w
w
w
1
1
1
, we update w
w
w
1
1
1
as follows:
w
w
w
1
1
1
← w
w
w
1
1
1
+ α [Y
t
− Q
1
(S
t
, A
t
;w
w
w
1
1
1
)]∇
w
w
w
1
1
1
Q
1
(S
t
, A
t
;w
w
w
1
1
1
)
(10)
where α is the learning rate. The target and update
rule for w
w
w
2
2
2
at time step t are similar to the ones in
equations 9 and 10 respectively but with w
w
w
1
1
1
and w
w
w
2
2
2
swapped.
To understand why Double Q-learning can under-
estimate, consider the update rule in equation 8. As-
sume that there is some source of random approxima-
tion error. Therefore, for all actions a, we have that,
Q
1
(S
t+1
, a) = q
∗
(S
t+1
, a) + e
1
(S
t+1
, a) (11)
where e
1
(S
t+1
, a) is a positive or negative noise term.
Since the argmax operator is applied over all the ac-
tions in S
t+1
in the update target, A
∗
may not be the
action that maximizes the action values of Q
2
for S
t+1
due to positive noise. Therefore, the maximum action
value of S
t+1
can be underestimated.
In figure 2, an episodic finite Markov decision
process is shown that was inspired by (Van Hasselt,
2011) to examine a case where underestimation bias
could be harmful. The difference of this process com-
pared to the one shown in figure 1 is that there are now
only two possible actions in state s
1
. The reward for
taking action a
3
is normally distributed with a mean
of +0.2 and a standard deviation of 0.2, whereas the
reward for taking the action a
4
is normally distributed
with a mean of -0.2 and a standard deviation of 0.2.
If the discount factor is set to one, the expected re-
turn for taking a
1
and then a
3
is 0.2. Therefore, the
optimal action in state s
0
is a
1
. However, a Double
Q-learning agent following an ε-greedy policy could
choose a
2
many times in the beginning of learning,
because it could underestimate the maximum opti-
mal action value of s
1
. The reason is that Double Q-
learning could use one of the two approximate action-
value functions to determine that the suboptimal ac-
tion a
4
maximizes the action values of s
1
and then
evaluate a
4
with the other approximate action-value
function. In this process, the overestimation bias of
Q-learning could be helpful, because it could allow
the agent to visit s
1
many times in the beginning of
learning and learn the optimal policy fast.
Figure 2: An episodic finite Markov decision process to
highlight the problems caused by underestimation bias. The
starting state is s
0
and the terminal state is depicted by gray
squares. All the transitions are deterministic and the re-
wards are shown above the actions.
3 VARIATION-RESISTANT
Q-LEARNING
Variation-resistant Q-learning operates similarly to Q-
learning and tries to compute the optimal action-value
function by using sampled experiences to update an
approximate action-value function. However, in this
algorithm a number of past action-value estimates are
stored in memory. The update rule of this algorithm is
similar to the one of Q-learning, but the maximum ac-
tion value of the next state in the update target is trans-
lated by a positive or negative quantity. This quantity
is called the variation quantity and is proportional to
the mean absolute deviation of the stored past esti-
mates of the maximum action value of the next state.
The constant of proportionality in the variation quan-
tity is called the variation resistance parameter. The
variation resistance parameter affects the magnitude
and determines the sign of the variation quantity.
3.1 Tabular Variation-resistant
Q-learning
In tabular Variation-resistant Q-learning, we initial-
ize an approximate action-value function Q arbitrar-
ily, and we also initialize a memory with capacity
n > 1 for each action value. We then use a policy
based on Q to sample (S
t
, A
t
, R
t+1
, S
t+1
) tuples. At
each time step t we first compute the translated maxi-
mum action value of the next state as follows:
e
Q(S
t+1
, A
∗
) = Q(S
t+1
, A
∗
) + λσ
κ
(S
t+1
, A
∗
) (12)
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
20

where A
∗
= argmax
a
0
Q(S
t+1
, a
0
), λ 6= 0 is the vari-
ation resistance parameter, and σ
κ
(S
t+1
, A
∗
) is the
mean absolute deviation of the 0 ≤ κ ≤ n stored past
values of Q(S
t+1
, A
∗
) at time step t. The mean abso-
lute deviation for state s and action a is defined as:
σ
κ
(s, a) =
0, if κ = 0
∑
κ
i=1
Q
i
(s, a) − Q
κ
(s, a)
κ
, otherwise
(13)
where Q
κ
(s, a) is the mean of the κ past values of
Q(s, a). We then perform the update:
Q(S
t
, A
t
) ←(1 − α)Q(S
t
, A
t
)
+ α(R
t+1
+ γ
e
Q(S
t+1
, A
∗
)) (14)
where α is the step size. After the update, the new
value of Q(S
t
, A
t
) is stored in memory. If there are
already n stored past values of Q(S
t
, A
t
), the oldest of
those values is discarded. Note that the action-value
memory capacity should be set to an appropriate value
in order to allow the algorithm to discard information
about outdated past action-value estimates. Note also
that the variation-resistance parameter can be set to a
value greater than one in magnitude if required by the
reinforcement learning problem.
In the appendix we mathematically prove the con-
vergence of this version of the algorithm. In algorithm
1 we show tabular Variation-resistant Q-learning in
pseudocode.
Algorithm 1: Tabular Variation-resistant Q-learning.
Input: step size α ∈ (0, 1], exploration parameter
ε > 0, action-value memory capacity n > 1,
variation resistance parameter λ 6= 0
Initialize Q(s, a) arbitrarily for all s and a
Initialize memory with capacity n for each Q(s, a)
Observe initial state s
while Agent is interacting with the Environment do
Choose action a in s using policy based on Q
Take action a, observe r and s
0
a
∗
← argmax
a
0
Q(s
0
, a
0
)
e
Q(s
0
, a
∗
) ← Q(s
0
, a
∗
) + λσ
κ
(s
0
, a
∗
)
Q(s, a) ← Q(s, a) + α
h
r + γ
e
Q(s
0
, a
∗
) − Q(s, a)
i
Store Q(s, a) in memory
s ← s
0
end
3.2 Variation-resistant Q-learning with
Function Approximation
Variation-resistant Q-learning can be combined with
function approximation as follows. Assume a dif-
ferentiable nonlinear function approximator with a
weight vector w
w
w that is used to parametrize Q and σ.
The target Y
t
at time step t is defined as,
Y
t
= R
t+1
+ γ [Q(S
t+1
, A
∗
;w
w
w) + λσ(S
t+1
, A
∗
;w
w
w)]
(15)
where A
∗
= argmax
a
0
Q(S
t+1
, a
0
;w
w
w) and λ 6= 0 is the
variation resistance parameter. The target Y
t
0
at time
step t is defined as,
Y
t
0
= |Y
t
− Q(S
t
, A
t
;w
w
w)| (16)
and the loss function J is defined as,
J(Y
Y
Y
t
,
ˆ
Y
Y
Y
t
) = [Y
t
− Q(S
t
, A
t
;w
w
w)]
2
+
Y
t
0
− σ(S
t
, A
t
;w
w
w)
2
(17)
with Y
Y
Y
t
=
Y
t
Y
t
0
T
and
ˆ
Y
Y
Y
t
=
Q(S
t
, A
t
;w
w
w) σ(S
t
, A
t
;w
w
w)
T
. To perform an
update at time step t, we assume that Y
Y
Y
t
does not
depend on w
w
w, compute the gradient of J with respect
to w
w
w, and update w
w
w as follows,
w
w
w ← w
w
w − α∇
w
w
w
J(Y
Y
Y
t
,
ˆ
Y
Y
Y
t
) (18)
where α is the learning rate.
Note that this version of Variation-resistant Q-
learning discards information about outdated past
action-value estimates automatically, because the
function approximator adjusts its predictions for the
absolute deviations of the action-value estimates as
new information is provided. From our experience,
this version of the algorithm is more sensitive to the
variation resistance parameter, and selecting
|
λ
|
< 1
may provide better empirical results.
3.3 Discussion
Variation-resistant Q-learning is based on the prin-
ciple that applying the max operator on uncer-
tain action-value estimates can cause overestimation.
Specifically, the probability and amount of overesti-
mation are expected to increase as the number of un-
certain action-value estimates in each state increases
(Van Hasselt, 2011; Van Hasselt et al., 2018). When
there exists any possibility of overestimation, the al-
gorithm increases or decreases the uncertain action-
value estimates in the update targets in order to in-
troduce systematic overestimation or underestimation
respectively. Therefore, the variation resistance pa-
rameter can control the estimation bias of the algo-
rithm by affecting the magnitudes and determining
the signs of the variation quantities.
To understand how the variation resistance pa-
rameter can control the estimation bias of Variation-
resistant Q-learning, consider the translated maxi-
mum action value of the next state in equation 12.
Notice that σ
κ
(S
t+1
, A
∗
) ≥ 0 by definition, and as-
sume that κ > 0, which means that there are past
values of Q(S
t+1
, A
∗
) in memory. If κ is sufficiently
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance
21

large and σ
κ
(S
t+1
, A
∗
) ≈ 0, the algorithm should com-
pute an estimate close to the optimal action value and
its estimation bias should be close to zero. On the
other hand, if the κ past values of Q(S
t+1
, A
∗
) are
noisy, the estimation bias of the algorithm depends
on λ. Specifically, if λ < 0 and σ
κ
(S
t+1
, A
∗
) > 0,
then
e
Q(S
t+1
, A
∗
) < Q(S
t+1
, A
∗
), which means that the
algorithm should overestimate less than Q-learning.
Symmetrically, if λ > 0 and σ
κ
(S
t+1
, A
∗
) > 0, then
e
Q(S
t+1
, A
∗
) > Q(S
t+1
, A
∗
), which means that the al-
gorithm should overestimate more than Q-learning.
Notice that the magnitude and direction of the estima-
tion bias of the algorithm depend on λ. Specifically,
as λ → ∞, Variation-resistant Q-learning can arbitrar-
ily overestimate more than Q-learning. As λ → −∞,
Variation-resistant Q-learning can arbitrarily underes-
timate more than Double Q-learning.
Variation-resistant Q-learning controls estimation
bias in a qualitatively different way than the other
methods discussed in the introduction. The algorithm
does not merely increase the probability of overes-
timation or underestimation, but ensures estimation
bias of a certain magnitude and direction by trans-
lating the uncertain action-value estimates in the up-
date targets. Since overestimation bias encourages ex-
ploration of overestimated actions and underestima-
tion bias discourages exploration of underestimated
actions,
2
the magnitudes and signs of the variation
quantities determine whether the agent is encouraged
or discouraged from exploring states with uncertain
action-value estimates and by how much. Therefore,
the variation resistance parameter can influence the
agent’s exploration behavior in a more direct way than
the other methods.
Variation-resistant Q-learning can deal with any
source of approximation error because it operates di-
rectly on the action-value estimates. However, it
is more difficult to analyze how estimation bias af-
fects performance of the algorithm with sources of
approximation error other than stochastic transitions
and stochastic rewards. For example, when function
approximation is used, updating the weight vector of
the function approximator can change several action-
value estimates simultaneously. This makes the varia-
tion quantity less reliable and the algorithm more sen-
sitive to the variation resistance parameter.
One disadvantage of Variation-resistant Q-
learning is that its tabular version requires sufficient
2
A necessary condition for overestimation bias to en-
courage exploration of overestimated actions and underes-
timation bias to discourage exploration of underestimated
actions is that the algorithm uses a partially greedy policy
for action selection (e.g. ε-greedy). In this paper we assume
that this condition is satisfied.
memory to store a number of past action-value esti-
mates. Moreover, its function approximation version
must allocate part of the capacity of its function
approximator to predict the absolute deviations of
the action-value estimates. Consequently, a function
approximator with more capacity may be needed for
the algorithm to perform well, and this requires more
memory. Therefore, Variation-resistant Q-learning
has higher memory requirements than Q-learning.
We will now motivate the choice of mean absolute
deviation as a measure of statistical dispersion. Note
that the variation quantity is used for a translation op-
eration on the maximum action value of the next state
and depends on the measure of dispersion. Therefore,
variance would not be a suitable choice, because its
magnitude would result in unrealistically high varia-
tion quantities. Standard deviation would also not be a
suitable choice, because it would assign more weight
to past action-value estimates that are statistical out-
liers. This could be a problem when an action-value
estimate is close to the optimal value in general but an
extremely rare transition causes an extreme change in
its value. In this case, standard deviation would be af-
fected by the outlier and the variation quantity would
be higher than desired. Mean absolute deviation is
less sensitive to outliers and therefore makes the vari-
ation quantity more robust.
4 EXPERIMENTS AND RESULTS
We conducted three experiments to compare the per-
formance of Q-learning, Double Q-learning, and
Variation-resistant Q-learning. In each experiment,
we simulated the interaction of three different agents
with an environment.
3
Each agent used one of the
three algorithms. Note that in the result figures of this
section we abbreviate Q-learning to QL, Double Q-
learning to DQL, and Variation-resistant Q-learning
to VRQL.
4.1 Grid World
In figure 3, we show the 3×3 grid world environment
used in our first experiment. In this world each cell is
a different state, and in each state there are four possi-
ble actions that match the agent’s moving directions.
Each of the four actions causes a deterministic tran-
sition to a neighboring cell, and an attempt to move
out of the world results in no movement. The agent
3
Simulation software can be found at:
https://github.com/anpenta/overestimation-bias-reinforcement-
learning-simulation-code
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
22

must move to the goal cell and then take any of the
four actions in order to end the episode.
Figure 3: A 3× 3 grid world. The agent’s starting cell is the
bottom left cell and the goal cell is the top right cell.
Inspired by (Van Hasselt, 2010; D’Eramo et al., 2016;
Zhang et al., 2017), we used the following reward
functions in this experiment:
1. Bernoulli: Reward of +50 or -40 with equal prob-
ability for any action in the goal cell, and reward
of -12 or +10 with equal probability for any action
in any other cell.
2. High-variance Gaussian: Reward of +5 for any
action in the goal cell, and normally distributed
reward with a mean of -1 and a standard deviation
of 5 for any action in any other cell.
3. Low-variance Gaussian: Reward of +5 for any
action in the goal cell, and normally distributed
reward with a mean of -1 and a standard deviation
of 1 for any action in any other cell.
4. Non-terminal Bernoulli: Reward of +5 for any
action in the goal cell, and reward of -12 or +10
with equal probability for any action in any other
cell.
For all reward functions, the expected reward at each
time step is +5 for any action in the goal cell and -1 for
any action in any other cell. Since an optimal policy
ends the episode in five actions, the optimal expected
reward per time step is 0.2. The discount factor was
set to 0.95, and therefore the maximum optimal action
value of the starting state is ≈ 0.36.
In this experiment, we used the tabular versions
of the three algorithms. The step size at time step t
was defined as α
t
(s, a) = n
t
(s, a)
−0.8
where n
t
(s, a) is
the update count for the action-value estimate of the
state-action pair (s, a) at time step t. For action selec-
tion we used an ε-greedy policy, in which the explo-
ration parameter at time step t was defined as ε
t
(s) =
n
t
(s)
−0.5
where n
t
(s) is the state visit count for state s
at time step t. These hyperparameters were used in all
three algorithms and their choice was guided by pre-
vious work (Van Hasselt, 2010; D’Eramo et al., 2016;
Zhang et al., 2017). In Variation-resistant Q-learning
we set the action-value memory capacity to 150 and
the variation resistance parameter to -3, and both hy-
perparameters were determined manually.
In figure 4, we show the reward per time step from
the beginning of learning in the top row, the maximum
action value of the starting state in the middle row,
and the normalized entropy of the state visits in the
bottom row. Each column corresponds to a different
reward function, and the optimal value is marked with
a black horizontal line in the plots of the top and mid-
dle rows. The quantities were averaged over 10,000
simulations.
Q-learning performed poorly when reward func-
tions with highly stochastic rewards for any action in
the non-goal states were used, because it often overes-
timated the optimal values of the suboptimal actions
in the non-goal states. Therefore, the algorithm over-
explored some non-goal states and followed bad poli-
cies for many steps.
Double Q-learning performed better than Q-
learning when reward functions with highly stochas-
tic rewards for any action in the non-goal states were
used, because it often underestimated the optimal val-
ues of the suboptimal actions in the non-goal states.
Therefore, the algorithm visited the goal state more
times and followed good policies for more steps than
Q-learning. When the Bernoulli reward function was
used, this behavior was less extreme because the
highly stochastic rewards for any action in the goal
state confused the algorithm.
Variation-resistant Q-learning achieved superior
performance, because in the beginning of learning it
updated its action-value estimates for the non-goal
states with targets that contained uncertain action-
value estimates. The algorithm translated the uncer-
tain action-value estimates in the update targets us-
ing negative variation quantities that were relatively
high in magnitude. Therefore, the algorithm visited
the goal state more times, learned its optimal action
values in fewer steps, and followed good policies for
more steps than the other two algorithms.
Notice that the Low-variance Gaussian reward
function was the most favorable for all three algo-
rithms. The reason is that the variance of the stochas-
tic rewards for all actions in the non-goal states was
not high enough to confuse the algorithms. Therefore,
all three algorithms followed good policies for many
steps and performed well.
We also conducted experiments with the varia-
tion resistance parameter set to higher values. As
λ increases, the estimates of Variation-resistant Q-
learning for the maximum optimal action value of the
starting state gradually move from underestimation
to overestimation, the performance of the algorithm
gradually becomes worse, and the normalized entropy
of the state visits that corresponds to the algorithm
gradually decreases. This suggests that Variation-
resistant Q-learning computes higher estimates for the
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance
23

Figure 4: Results obtained from the grid world experiment. The reward per time step from the beginning of learning is shown
in the top row, the maximum action value of the starting state is shown in the middle row, and the normalized entropy of
the state visits is shown in the bottom row. Each column corresponds to a different reward function. The optimal values
are marked with black horizontal lines in the plots of the top and middle rows. The quantities were averaged over 10,000
simulations.
optimal action values of the non-goal states and ex-
plores the non-goal states for more steps when λ is
set to higher values.
4.2 Grid World with Function
Approximation
The environment used in our second experiment is a
similar grid world to the one used in our first experi-
ment. The only difference is that the size of this world
is 10 × 10 instead of 3 × 3. The starting state is again
located at the bottom left corner and the goal state at
the top right corner.
In this experiment we used the function approx-
imation versions of the three algorithms with multi-
layer perceptrons as function approximators. At each
time step the current state was represented by a vector
with 200 binary elements that encoded the positions
of the agent and of the goal cell in the grid.
The reward functions used in this experiment are
identical to the ones used in the first experiment.
Since an optimal policy ends the episode in 19 ac-
tions, the optimal expected reward per time step is
≈ −0.68. The discount factor was set to 0.99, and
therefore the maximum optimal action value of all
visited states per time step is ≈ −3.94 and the max-
imum optimal action value of the starting state is
≈ −12.38.
In table 1 we show the hyperparameters used in
this experiment, which were determined manually.
The action selection policy was ε-greedy, and ε was
linearly annealed from the initial exploration value to
the final exploration value based on the exploration
decay steps value. For the multilayer perceptrons, we
used rectified linear units in the hidden layers, and
initialized all the weights with the Glorot uniform ini-
tializer (Glorot and Bengio, 2010). The total number
of steps in an experiment is 100,000 and each experi-
ment is repeated 5 times.
Table 1: Hyperparameters used in the grid world with func-
tion approximation experiment.
Hyperparameter Value
discount factor 0.99
initial exploration 0.5
final exploration 0.01
exploration decay steps 150,000
learning rate 0.0025
number of hidden layers 1
number of hidden layer nodes 512
variation resistance parameter -0.5
Figure 5 shows the reward per time step from the
beginning of learning in the top row, the maximum
action value of all visited states per time step from
the beginning of learning in the middle row, and the
maximum action value of the starting state per time
step from the beginning of learning in the bottom row.
Each column corresponds to a different reward func-
tion, and the optimal value is marked with a black
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
24
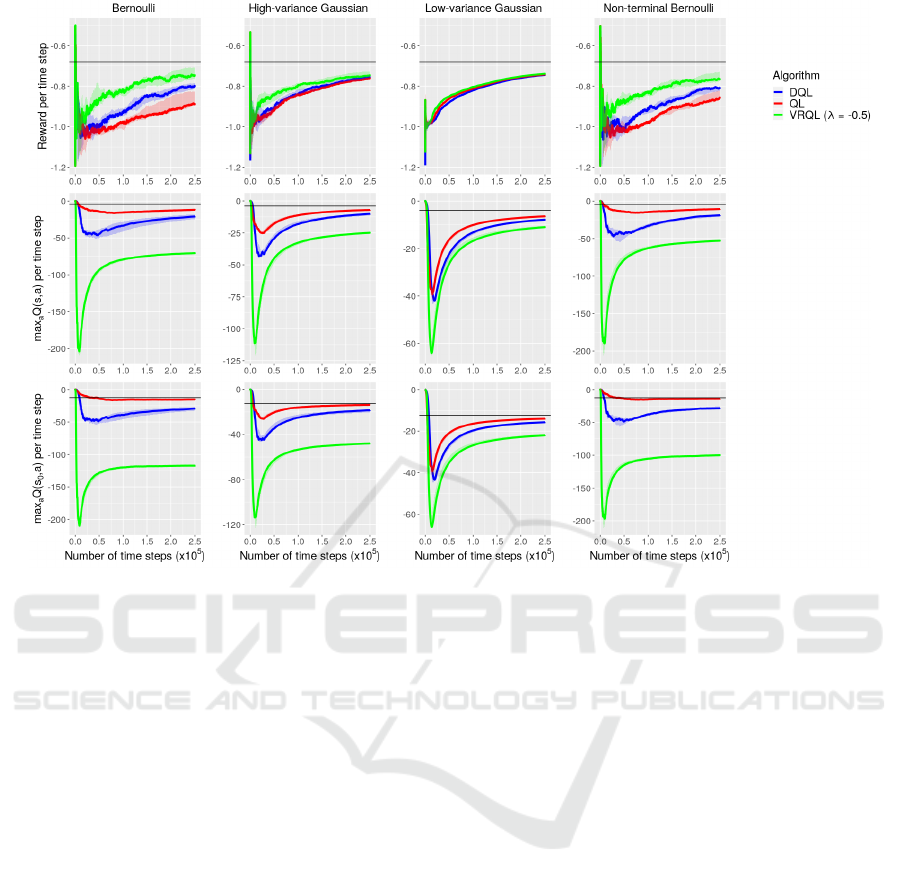
Figure 5: Results obtained from the grid world with function approximation experiment. The reward per time step from the
beginning of learning is shown in the top row, the maximum action value of all visited states per time step from the beginning
of learning is shown in the middle row, and the maximum action value of the starting state per time step from the beginning
of learning is shown in the bottom row. Each column corresponds to a different reward function. The optimal values are
marked with black horizontal lines. The quantities are median values over five simulations, and the shaded areas represent the
intervals between the mean of the two greatest values and the mean of the two least values.
horizontal line in each plot. The quantities are me-
dian values over five simulations with five different
random seeds, and the shaded areas represent the in-
tervals between the mean of the two greatest values
and the mean of the two least values.
Note that in the second experiment Variation-
resistant Q-learning and Double Q-learning were at
a disadvantage compared to Q-learning. In the case
of Variation-resistant Q-learning the reason is that the
algorithm had to allocate part of the capacity of its
multilayer perceptron to predict the absolute devia-
tions of the action-value estimates, whereas in the
case of Double Q-learning the reason is that the algo-
rithm updated the weight vector of only one of its two
multilayer perceptrons in each step. Nevertheless, the
results show that Variation-resistant Q-learning per-
formed better than Double Q-learning, and Double Q-
learning performed better than Q-learning. This hap-
pened for the same reasons as in the first experiment.
Notice that Double Q-learning and Q-learning
performed better than in the first experiment, although
the task of the second experiment was more difficult
than the task of the first experiment. The reason is that
the multilayer perceptrons generalized over the state
space and tried to learn the mean value of the update
targets for each action irrespective of the state.
Because of the behavior of the multilayer percep-
trons in this problem and also because the optimal
policy was not learned, all three algorithms underes-
timated the maximum optimal action values. Never-
theless, Variation-resistant Q-learning underestimated
the optimal values more than Double Q-learning, and
Double Q-learning underestimated the optimal val-
ues more than Q-learning. Underestimation was pos-
itively correlated with performance as expected.
Notice that the performance of all three algorithms
fluctuated greatly in the beginning of learning. The
reasons are that the reward per time step was com-
puted with a limited amount of reward samples in the
beginning of learning and that the median values were
computed over only five simulations.
We also conducted experiments with the varia-
tion resistance parameter set to higher values and
Variation-resistant Q-learning behaved similarly to
the first experiment as expected.
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance
25

4.3 Package Grid World
Figure 6 shows the 10 × 10 package grid world en-
vironment used in our third experiment. The agent’s
starting cell is the bottom left cell, the transitions are
deterministic, an attempt to move out of the world re-
sults in no movement, and there are five cells that con-
tain packages. Moreover, in addition to the four ac-
tions that cause transitions to neighboring cells, there
exists the action “collect”. This action results in no
movement, and if the agent’s cell contains an un-
collected package, the package is removed from the
world. The agent must collect all five packages in or-
der to end the episode.
Figure 6: A 10 × 10 package grid world. The agent’s start-
ing cell is the bottom left cell and there are five cells that
contain packages along the walls of the grid.
In this experiment we used the function approxima-
tion versions of the algorithms with multilayer per-
ceptrons as function approximators. At each time
step the current state was represented by a vector with
200 binary elements that encoded the positions of the
agent and of the uncollected package(s) in the grid.
The deterministic reward function provides a re-
ward of +100 for collecting all the packages, and a
reward of -1 per time step otherwise. Since the opti-
mal policy ends the episode in 32 actions, the optimal
expected reward per time step is ≈ 2.16. The discount
factor was set to 0.95, and therefore the maximum op-
timal action value of all visited states per time step is
≈ 40.47 and the maximum optimal action value of the
starting state is ≈ 4.47.
In table 2 we show the hyperparameters used in
this experiment, which we determined manually. The
action selection policy, the linear annealing procedure
of the exploration parameter, the activation functions
in the hidden layers of the multilayer perceptrons, and
the initialization of the weights of the multilayer per-
ceptrons were identical to the ones used in the second
experiment. Each run lasts for 1,000,000 steps.
In figure 7 we show the reward per time step from
Table 2: Hyperparameters used in the package grid world
experiment.
Hyperparameter Value
discount factor 0.95
initial exploration 1
final exploration 0.05
exploration decay steps 750,000
learning rate 0.005
number of hidden layers 1
number of hidden layer nodes 256
variation resistance parameter +0.6
the beginning of learning in the left plot, the maxi-
mum action value of all visited states per time step
from the beginning of learning in the center plot, and
the maximum action value of the starting state per
time step from the beginning of learning in the right
plot. The optimal value is marked with a black hor-
izontal line in each plot. The quantities are median
values over five simulations with five different ran-
dom seeds, and the shaded areas represent the inter-
vals between the mean of the two greatest values and
the mean of the two least values.
Note that in the third experiment Variation-
resistant Q-learning and Double Q-learning were at
a disadvantage compared to Q-learning for the same
reasons as in the second experiment. This allowed
Q-learning to achieve superior performance in the
task of the third experiment. The reason is that in
this task it is relatively difficult to discover the termi-
nal state, and therefore experiences with the terminal
state are relatively difficult to sample. Q-learning uti-
lized those experiences better and followed good poli-
cies for more steps than the other two algorithms.
Double Q-learning performed worse than the
other two algorithms. The reason is that the task of
the third experiment does not favor underestimation.
As we mentioned above, in this task it is relatively
difficult to sample experiences with the terminal state.
Moreover, the initial states are relatively far from the
terminal state, and therefore the optimal values of the
optimal and suboptimal actions in the initial states do
not differ a lot. Double Q-learning computed lower
estimates for the optimal values of the optimal ac-
tions than the other two algorithms in the beginning
of learning. This suggest that Double Q-learning ex-
plored suboptimal actions and followed bad policies
for more steps and that it needed more experiences
with the terminal state to determine the optimal ac-
tions than the other two algorithms.
We also conducted experiments with the varia-
tion resistance parameter set to lower values. As
λ decreases, the estimates of Variation-resistant Q-
learning for the maximum optimal action values grad-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
26

Figure 7: Results obtained from the package grid world experiment. The reward per time step from the beginning of learning
is shown in the left plot, the maximum action value of all visited states per time step from the beginning of learning is shown in
the center plot, and the maximum action value of the starting state per time step from the beginning of learning is shown in the
right plot. The optimal values are marked with black horizontal lines. The quantities are median values over five simulations
with five different random seeds, and the shaded areas represent the intervals between the mean of the two greatest values and
the mean of the two least values.
ually decrease and the performance of the algorithm
gradually becomes worse. This suggests that the algo-
rithm behaves similarly to Double Q-Learning when
λ is set to lower values as expected.
5 CONCLUSION
In this paper, we proposed Variation-resistant Q-
learning to control and utilize estimation bias for bet-
ter performance and showed empirically that the new
algorithm operates as expected. Although the argu-
ment that reinforcement learning algorithms can im-
prove their performance by controlling and utilizing
their estimation bias is unconventional, we think that
it is worth investigating further and hope that our
work will inspire further research on this topic.
Future Work. One future work direction would be
to provide a better theory for Variation-resistant Q-
learning, such as mathematically proving that the
variation resistance parameter can control the estima-
tion bias of the algorithm. Another future work di-
rection would be to conduct further experiments to
evaluate the algorithm. For example, the performance
of the algorithm could be tested on large-scale tasks
(e.g. in the video game domain) or tasks with non-
stationary environments. An additional future work
direction would be to improve the algorithm. Some
interesting improvements would be to determine the
variation resistance parameter automatically and to
provide functionality for the algorithm to arbitrarily
switch between overestimation and underestimation
during learning.
ACKNOWLEDGEMENTS
We would like to thank the Center for Information
Technology of the University of Groningen for their
support and for providing access to the Peregrine high
performance computing cluster.
REFERENCES
Anschel, O., Baram, N., and Shimkin, N. (2016).
Averaged-dqn: Variance reduction and stabilization
for deep reinforcement learning. arXiv preprint
arXiv:1611.01929.
Bellman, R. (1958). Dynamic programming and stochastic
control processes. Information and control, 1(3):228–
239.
D’Eramo, C., Restelli, M., and Nuara, A. (2016). Esti-
mating maximum expected value through gaussian ap-
proximation. In International Conference on Machine
Learning, pages 1032–1040.
Glorot, X. and Bengio, Y. (2010). Understanding the diffi-
culty of training deep feedforward neural networks.
In Proceedings of the thirteenth international con-
ference on artificial intelligence and statistics, pages
249–256.
Gordon, G. J. (1995). Stable function approximation in dy-
namic programming. In Machine Learning Proceed-
ings 1995, pages 261–268. Elsevier.
Lan, Q., Pan, Y., Fyshe, A., and White, M. (2020). Maxmin
q-learning: Controlling the estimation bias of q-
learning. arXiv preprint arXiv:2002.06487.
Lee, D., Defourny, B., and Powell, W. B. (2013). Bias-
corrected q-learning to control max-operator bias in
q-learning. In 2013 IEEE Symposium on Adaptive
Dynamic Programming and Reinforcement Learning
(ADPRL), pages 93–99. IEEE.
Singh, S., Jaakkola, T., Littman, M. L., and Szepesv
´
ari, C.
(2000). Convergence results for single-step on-policy
reinforcement-learning algorithms. Machine learning,
38(3):287–308.
Variation-resistant Q-learning: Controlling and Utilizing Estimation Bias in Reinforcement Learning for Better Performance
27

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Thrun, S. and Schwartz, A. (1993). Issues in using function
approximation for reinforcement learning. In Pro-
ceedings of the 1993 Connectionist Models Summer
School Hillsdale, NJ. Lawrence Erlbaum.
Van Hasselt, H. (2010). Double q-learning. In Advances in
Neural Information Processing Systems, pages 2613–
2621.
Van Hasselt, H., Doron, Y., Strub, F., Hessel, M., Son-
nerat, N., and Modayil, J. (2018). Deep reinforce-
ment learning and the deadly triad. arXiv preprint
arXiv:1812.02648.
Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep re-
inforcement learning with double q-learning. In Thir-
tieth AAAI conference on artificial intelligence.
Van Hasselt, H. P. (2011). Insights in reinforcement learn-
ing. PhD thesis, Utrecht University.
Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine
learning, 8(3-4):279–292.
Watkins, C. J. C. H. (1989). Learning from delayed rewards.
PhD thesis, King’s College, Cambridge.
Zhang, Z., Pan, Z., and Kochenderfer, M. J. (2017).
Weighted double q-learning. In IJCAI, pages 3455–
3461.
APPENDIX
Definition 1. An ergodic Markov decision process is
a Markov decision process in which each state can
be reached from any other state in a finite number of
steps.
Lemma 1. Let (β
t
, ∆
t
, F
t
) be a stochastic process,
where β
t
, ∆
t
, F
t
: X 7→ R satisfy,
∆
t+1
(x
t
) = (1 − β
t
(x
t
))∆
t
(x
t
) + β
t
(x
t
)F
t
(x
t
)
where x
t
∈ X and t = 0, 1, 2, . . .. Let P
t
be a sequence
of increasing σ-fields such that β
0
and ∆
0
are P
0
-
measurable and β
t
, ∆
t
, and F
t−1
are P
t
-measurable,
with t ≥ 1. Assume that the following conditions are
satisfied:
1. The set X is finite (i.e.
|
X
|
< ∞).
2. β
t
(x
t
) ∈ [0, 1],
∑
t
β
t
(x
t
) = ∞,
∑
t
β
2
t
(x
t
) < ∞ w.p.1,
and ∀x 6= x
t
: β
t
(x) = 0.
3.
k
E{F
t
|
P
t
}
k
≤ κ
k
∆
t
k
+ c
t
, where κ ∈ [0, 1) and
c
t
−→ 0 w.p.1.
4. V{F
t
(x
t
)| P
t
} ≤ C(1 + κ
k
∆
t
k
)
2
, where C is some
constant.
where V{·} denotes the variance and
k
·
k
denotes the
maximum norm. Then ∆
t
converges to zero with prob-
ability one.
Proof. See (Singh et al., 2000).
Theorem 1. In an ergodic Markov decision pro-
cess, the approximate action-value function Q as up-
dated by tabular Variation-resistant Q-learning in al-
gorithm 1 converges to the optimal action-value func-
tion q
∗
with probability one if an infinite number of
experience tuples of the form (S
t
, A
t
, R
t+1
, S
t+1
) are
sampled by a learning policy for each state-action
pair and if the following conditions are satisfied:
1. The Markov decision process is finite (i.e. |S ×
A × R| < ∞).
2. γ ∈ [0, 1).
3. α
t
(s, a) ∈ [0, 1],
∑
t
α
t
(s, a) = ∞,
∑
t
α
2
t
(s, a) < ∞
w.p.1, and ∀s,a 6= S
t
, A
t
: α
t
(s, a) = 0.
Proof. We apply lemma 1 with X = S ×A, ∆
t
= Q
t
−
q
∗
, β
t
= α
t
, P
t
= {Q
0
, σ
0
, S
0
, A
0
, α
0
, R
1
, S
1
, . . . , S
t
, A
t
},
and
F
t
(S
t
, A
t
) = R
t+1
+ γ
e
Q
t
(S
t+1
, A
∗
) − q
∗
(S
t
, A
t
)
where A
∗
= argmax
a
0
Q
t
(S
t+1
, a
0
) and
e
Q
t
(S
t+1
, A
∗
) =
Q
t
(S
t+1
, A
∗
) + λσ
t
(S
t+1
, A
∗
). The first condition of
the lemma is satisfied because |S × A| < ∞. The sec-
ond condition of the lemma is satisfied by the third
condition of the theorem. The fourth condition of
the lemma is satisfied because
|
R
|
< ∞ =⇒ ∀t :
V
{
R
t+1
|
P
t
}
< ∞ =⇒ ∀t : V
{
F
t
(S
t
, A
t
)| P
t
}
< ∞.
For the third condition of the lemma we have that,
F
t
(S
t
, A
t
) = F
t
0
(S
t
, A
t
) + γλσ
t
(S
t+1
, A
∗
)
where F
t
0
(S
t
, A
t
) is the value of F
t
(S
t
, A
t
) in the
case of Q-learning. Since it is well known that ∀t :
k
E{F
t
0
|
P
t
}
k
≤ γ
k
∆
t
k
, it follows that,
k
E{F
t
|
P
t
}
k
=
E{F
t
0
P
t
}
+ γλ
k
E
{
σ
t
|
P
t
}k
≤ γ
k
∆
t
k
+ γλ
k
E
{
σ
t
|
P
t
}k
Therefore, it suffices to show that c
t
=
γλ
k
E
{
σ
t
|
P
t
}k
→ 0 w.p.1.
Since ∀t, s, a : σ
t
(s, a) ∈ [0, ∞), it suffices to show
that, lim
t→∞
σ
t
(S
t
, A
t
) = 0 ⇐⇒ ∀ε > 0 ∃t
0
: ∀t ≥
t
0
=⇒ σ
t
(S
t
, A
t
) < ε. Assume that time step t is such
that the memory for each action value is full. We have
that,
σ
t
(S
t
, A
t
) =
∑
n
i=1
Q
t
i
(S
t
, A
t
) −
Q
t
(S
t
, A
t
)
n
where t
i
< t, ∀i = 1, 2, . . . , n. After the update at time
step t we have that,
σ
t+1
(S
t
, A
t
) =
∑
n+1
i=2
Q
t
i
(S
t
, A
t
) −
Q
t+1
(S
t
, A
t
)
n
where t
(n+1)
= t + 1. Because of the third con-
dition of the theorem, the differences between the
Q
t
i
(S
t
, A
t
) values approach zero as t → ∞. There-
fore, given ε > 0, ∃t
0
: ∀t ≥ t
0
=⇒ σ
t
(S
t
, A
t
) < ε =⇒
lim
t→∞
σ
t
(S
t
, A
t
) = 0.
Since all the conditions of lemma 1 are satisfied,
it holds that, ∀s, a : Q
t
(s, a) → q
∗
(s, a) w.p.1.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
28
