Robust Emergency Medical System Design as a Multi-objective Goal

Programming Problem

Marek Kvet

Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia

Keywords: Location Problems, Emergency Medical Service, Robustness, Multi-objective Problem, Radial Formulation.

Abstract: The main goal of this paper is to introduce and compare three different mathematical modelling approaches

to robust emergency medical service system design. The idea of system robustness follows from the necessity

of making the system resistant to various detrimental events, which may unexpectedly occur in the associated

transportation network and thus negatively affect service. Such viewpoint is important mainly in different

kinds of public service systems including rescue services, in which time necessary for service delivery plays

a very important role. While the standard method of robust system designing takes into account only the worst

possible situation considering the set of detrimental scenarios, suggested modeling approaches compute a

separate objective function value for each scenario and then a special constraint is added to the original

mathematical model. This way, an epsilon-constraint principle to the problem solution is applied. In this paper,

numerical experiments to study the performance characteristics of suggested solving methods accompany the

theoretical explanation of all presented models.

1 INTRODUCTION

This research paper deals with a special class of

discrete network location problems, which are solved

under uncertainty following from randomly and often

unexpectedly occurring failures in the transportation

network (Correia and Saldanha da Gama, 2015, Pan

et al., 2014, Scaparra and Church, 2015). The main

focus is on the application of suggested optimization

approaches to the emergency medical system (EMS)

designing. The rescue system performance efficiency

is directly influenced by locations of service centers,

which send the emergency vehicles to satisfy the

requests raised at system users’ locations. Obviously,

the number of service providing centers is limited due

to economic and technological restrictions. It is not

possible to locate a separate service center to each

served geographical area or to each system users’

community.

The most commonly used objective function in

the mathematical models for EMS designing takes

into account the service accessibility of an average

user. This way, the emergency service system design

problem can be described as the weighted p-median

problem broadly studied by many researchers (Avella

et al., 2007, Current et al., 2002, Ingolfsson et al.,

2008, Jánošíková, 2007, Snyder and Daskin, 2005)

mainly from the points of developing effective exact

and approximate solving techniques. It is worth

mentioning, for example, the radial formulation of the

problem, successfulness of which is based on the fact

that there is only finite set of radii, which need to be

taken into account (Elloumi et al., 2004, García et al.,

2011, Janáček, 2008). Such model reformulation

makes the problem easier, smaller and thus better

solvable.

Simultaneously, several approximate approaches

have been developed to get a good solution of the

problem in acceptably short time (Doerner et al. 2005,

Gendreau and Potvin, 2010).

It is often assumed that service center has enough

capacity to serve all assigned users and thus, each

system user can be serviced from the nearest located

service center. Otherwise, the concept of so-called

generalized disutility can be applied to incorporate

stochastic behavior of real system into the

mathematical model (Kvet and Janáček, 2018). This

model extension enables to consider more service

centers, which can provide the associated service to

the same user. In the research reported in this paper,

only the nearest located service centers for each

system user are considered.

Kvet, M.

Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem.

DOI: 10.5220/0010179600210028

In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 21-28

ISBN: 978-989-758-485-5

When the emergency service system is designed,

the designer must take into account that the transfer

time from a service center to the affected user might

be negatively impacted by various random events

caused by weather or traffic. Furthermore, possible

failure of a part of critical infrastructure should be

taken into account because of congestion, disruptions

or blockages. In other words, the system resistance to

such critical events should be included into the

decision-making process.

Most of available approaches to increasing the

system robustness (Correia and Saldanha da Gama,

2015, Kvet and Janáček, 2017b, Pan et al., 2014,

Scaparra and Church, 2015) are based on making the

system resistant to possible failure scenarios, which

can appear in the associated transportation network as

a consequence of random failures due to congestion,

disruptions or blockages. Thus, a finite set of failure

scenarios is considered and each individual scenario

is characterized by particular time distances between

the users’ locations and possible center locations.

The most commonly used objective function in

the above-mentioned weighted p-median problem

consists in minimizing the time accessibility of the

service for an average user, i.e. a min-sum objective

function is minimized subject to associated solution

feasibility constraints. On the other hand, the most

frequently used objective function of the robust

design focuses on minimizing the maximal objective

function of the individual instances corresponding

with particular scenarios. It means that the worst

possible impact of individual scenarios is minimized.

It follows that the original min-sum objective

function used in the weighted p-median problem is

replaced by the min-max criterion. The min-max

model uses the link-up constraints to limit the

individual scenario min-sum objectives by their upper

bound corresponding to the objective function of the

resulting min-max model. In addition, incorporating

the scenarios into the model causes the model soize to

increase proportionally to the cardinality of the

scenario set. Both the model structure and the

increase in model size represent a burden to the

computational process of most available IP-solvers.

Thus, complementary approximate approaches to the

robustness constitute a big challenge to operational

researchers and professionals in the field of Applied

Informatics (Janáček and Kvet, 2016, Janáček and

Kvet, 2017, Kvet and Janáček, 2017a, Kvet and

Janáček, 2017b).

This paper focuses on the main disadvantage of

the min-max approach to robust EMS design; only the

worst impact of individual scenarios is minimized.

The set of scenarios may contain a bad scenario with

very low probability of occurring, yet this scenario

may seriously affect the optimal robust system

design. This paper discusses three approaches to the

problem based on multi-objective optimization

(Antunes and Henriques, 2016). These techniques

consider each scenario to form a separate objective

function and they apply epsilon-constraint principle

to the problem solution.

The remainder of this paper is organized as

follows: Section 2 is devoted to the description of the

original min-max robust design of emergency

systems, in which all scenarios are taken into account.

Section 3 explains two coefficients for robustness

evaluation. The core of this contribution is reported in

Section 4, in which all suggested multi-objective

approaches are introduced and explained. The fifth

Section discusses numerical experiments and yields a

brief comparative analysis of the resulting designs.

The results and findings are summarized in Section 6.

2 STANDARD APPROACH TO

ROBUST EMS DESIGN

The standard approach to emergency medical service

system design usually leads to formulation of a min-

sum problem (Current et al., 2002, Ingolfsson et al.,

2008, Jánošíková, 2007), in which the average system

accessibility for users (average response time) is

minimized. The robust system design is formulated as

a min-max model bringing some difficulties into the

computational process (Kvet and Janáček, 2017b).

To formulate the mathematical model for robust

EMS design, we introduce the following notations..

Let symbol J denote the set of users’ locations and

let symbol I denote the set of possible service center

locations. Furthermore, let b

denote the number of

users sharing the location j. To solve the problem, p

locations from I must be chosen so that the maximal

scenario objective function value is to be minimized.

The objective function value of an individual scenario

is defined as a sum of users’ distances from the

location of the service center providing them with

service multiplied by b

. To incorporate system

robustness into the mathematical model, a set U of

possible failure scenarios is needed to be introduced.

This set contains also one specific scenario called

basic scenario, which represents standard conditions

in the associated transportation network. For the

purpose of conciseness, let U

denote the set of

scenarios without the basic one, i.e. U

= U – {basic

scenario}. The integer distance between locations i

and j under a specific scenario u∈U is denoted by d

iju

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

Even if the radial model is originally suggested for

integer distance or time values only, the used

principle enables us to adjust the model also for real

values without any big problems.

The decisions, which determine the structure of

the rescue service system, are modeled by decision

variables y

∈{0,1} modeling the decision on service

center location at the place i∈I by the value of 1 if a

service center is located at i and by the value of 0

otherwise. In the robust problem formulation, the

variable h denotes the upper bound of the objective

functions over the set U of scenarios. To formulate

the radial model, the integer range [0, v] of all

possible distances of the matrices {d

iju

} is partitioned

into zones according to (García et al., 2011, Janáček,

2008). The value of v is computed according to the

expression (1).

{

}

max : , , 1

iju

vdiIjJuU=∈∈∈− (1)

The radial formulation of the problem is based on

the idea of making a system of zones. The zone s

corresponds to the interval (s, s+1]. To complete the

radial model, auxiliary zero-one variables x

jus

for j∈J,

u∈U and s = 0 … v need to be introduced. The

variable x

jus

takes the value of 1, if the distance of the

user at j∈J under the scenario u∈U from the nearest

located center is greater than s and it takes the value

of 0 otherwise. Based on these assumptions, the

expression x

ju0

+ x

ju1

+ x

ju2

+ … + x

juv

constitutes the

distance d

ju*

from user location j to the nearest located

service center under scenario u∈U. Similarly to the

set covering problem, let us introduce a zero-one

constant a

iju

under scenario u∈U for each i∈I , j∈J,

s∈[0..v]. The constant a

iju

is equal to 1, if the

disutility d

iju

between the user location j and the

possible center location i is less than or equal to s,

otherwise a

iju

is equal to 0. Then the model of the

robust system design problem can be formulated as

follows.

inimize h

(2)

,0,1 ,

jsu iju i

Subject to x a y

or j J s , , v u U

∈

+≥

∈= ∈





(3)

∈



(4)

jjsu

jJ s

bx hforuU

∈=

≤∈



(5)

{0, 1}

for i I∈∈

(6)

{0, 1} , 0, 1 ,

jsu

for j J s , ,v u U∈∈=∈

( 7 )

0h ≥

(8)

The objective function (2) gives an upper bound

of all objective function values corresponding to the

scenarios. The constraints (3) ensure that the

variables

jus

are allowed to take the value of 0, if

there is at least one center located in radius

s from the

user location

j and constraint (4) limits the number of

located service centers by

p. The link-up constraints

(5) ensure that each perceived disutility (time or

distance) is less than or equal to the upper bound

The obligatory constraints (6), (7) and (8) are

included to ensure the domain of the decision

variables

, x

jus

and h.

3 SERVICE SYSTEM

ROBUSTNESS EVALUATION

The main goal of robust service system design is to

make the system resistant to randomly occurring

failures on the associated transportation network. To

evaluate the gauges of robustness, we introduce the

following additional notations. As before, let

denote the set of all considered failure scenarios,

which contains also the

basic scenario. Let y denote

the vector of location variables

; i∈I. Let y

correspond to the basic system design, i.e. the

solution of a simple weighted

p-median problem, in

which only the

basic scenario is taken into account.

Let

(y) denote the associated objective function

value. Similarly, let

denote the solution of the

model (2)-(8), which brings the robust system design.

Finally, the objective function (2) will be denoted by

(y). The price of robustness (POR) expresses the

relative increment (additional cost) of the basic

scenario objective function, when

is applied instead

of the optimal solution

obtained for the basic

scenario. Its value is defined by (9).

() ()

()

100*

br bb

POR

−

(9)

Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem

The price of robustness expresses the percentage

increase in cost in the basic scenario when the robust

system design is chosen, but it does not express what

we gain by applying the robust solution. Therefore,

we introduce also a coefficient called

gain of

robustness

(GOR) expressed by (10).

() ()

()

100*

rb rr

GOR

−

(10)

This coefficient evaluates the profit following

from applying the robust solution instead of the

standard one in the worst case ignoring detrimental

scenarios.

4 MULTI-OBJECTIVE

APPROACHES

The main disadvantage of the standard approach to

robust service system design described by the model

(2)-(8) consists in minimizing only the worst possible

impact of detrimental scenarios on the resulting

system performance measured by average service

accessibility for system users (average response

time). It must be noted that the partial objective

functions corresponding to individual scenarios may

take different values and it is assumed that not only

the highest one should be considered. Therefore, three

different multi-objective-based approaches will be

introduced in the following subsections.

4.1 Function GetGoalMinMax

The first approach is based on minimization of the

objective function for the

basic scenario under the

condition that the objective functions corresponding

to the detrimental scenarios do not increase too much.

To achieve this goal, the following denotation must

be introduced and it will be used in the remaining

parts of this paper. If the index

u is set to the value of

zero, it means that the

basic scenario is concerned. In

other words, the matrix {

ij0

} corresponds to the basic

scenario

If all the scenario objective functions are to be

taken into account in the form of separate constraints,

the goal value

G(u) for each scenario u∈U

should be

computed. The expression (11) shows the weighted

p-median problem solved for each failure scenario.

Remember, that the symbol

denotes the set of

detrimental scenarios without the

basic scenario.

()

min min

iju

diI

Gu b

II p

∈



∈ 











⊆=









(11)

Based on these preliminaries, a non-negative

parameter

ε can be introduced to limit the maximal

increase of the objective function

G(u) for scenario

u∈U

. The parameter ε can either take a given exact

value or it can be expressed as some percentage of the

objective function

G(u). Then, the model for robust

EMS design can be formulated by the expressions

(12)-(17).

jJ s

inimize b x

∈=



(12)

,0,1 ,

jsu iju i

Subject to x a y

or j J s , , v u U

∈

+≥

∈= ∈





(13)

∈



(14)

()

jjsu

jJ s

bx Gu foruU

∈=

≤+ ∈



(15)

{0, 1}

for i I∈∈

(16)

{0, 1} , 0, 1 ,

jsu

for j J s , ,v u U∈∈=∈

( 1 7 )

Since the mathematical model (12)-(17) has very

similar structure as the original model (2)-(8), it is not

necessary to explain each constraint separately. There

are only two differences to be noted.

The first one is the objective function, which now

corresponds to the service accessibility of all users

under the

basic scenario.

The second difference consists in the link-up

constraints (15), in which the objective functions of

all scenarios are limited by their goal values instead

of their upper bound.

4.2 Function AdjGetGoalMinMax

The second suggested approach to robust EMS design

follows from the previous

GetGoalMinMax function

described by the model (12)-(17) and goal values

G(u) for all scenarios from the set U

The adjustment consists in replacing the link-up

constraints (15) of the former model by their adjusted

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

version (18), in which only the maximal goal is taken

into account.

jjsu

jJ s

bx MG foruU

∈=

≤+ ∈



(18)

The maximal goal value

MG can be obtained by

the following expression (19). The individual goals

G(u) are defined by (11).

()

{

}

max :

GGuuU=∈ (19)

This way, the

AdjGetGoalMinMax strategy can be

described by minimizing the objective function (12)

under the constraints (13), (14), (16), (17) and (18).

4.3 Function GetGoalMinH

The last modeling strategy GetGoalMinH is based on

a different principle. Here, the robust service system

design is obtained in such a way that the goal

objective function value

G(0) for the basic scenario

is computed first. Then, the value of parameter

ε must

be given to limit the maximal possible increase of

mentioned goal value

G(0). The objective function

used in this approach minimizes possible increase

of the maximal goal

MG over the set of scenarios. The

associated mathematical model can be formulated in

the following way.

inimize h

(20)

,0,1 ,

jsu iju i

Subject to x a y

or j J s , , v u U

∈

+≥

∈= ∈





(21)

∈



(22)

jjsu

jJ s

bx MGhforuU

∈=

≤+ ∈



(23)

()

jjs

jJ s

bx G

∈=

≤+



(24)

{0, 1}

for i I∈∈

(25)

{0, 1} , 0, 1 ,

jsu

for j J s , ,v u U∈∈=∈

( 2 6 )

0h ≥

(27)

The minimized objective function (20) expresses

the increase of the maximal goal value

MG over the

objective functions corresponding to individual

scenarios. The constraints (21) ensure that the

variables

jus

are allowed to take the value of 0, if

there is at least one center located in radius

s from the

user location

j and constraint (22) limits the number

of located centers by

p. The link-up constraints (23)

ensure that each perceived disutility (time or distance)

is less than or equal to the maximal goal value

increased by

h. The constraint (24) does not allow to

exceed given value of the objective function for the

basic scenario G(0) by more than ε. Finally, the

obligatory constraints (25), (26) and (27) are included

to ensure the domain of the decision variables.

5 CASE STUDY

The main goal of the computational study reported in

this section was to study:

• robustness coefficients,

• computational time demands.

The first aspect consists in robustness coefficients

POR and GOR introduced in Section 3. Since each

approach minimizes different objective function, for

each resulting vector

y of location variables y

the

robust objective functions

and f

were computed in

order to evaluate

POR and GOR. The values of f

and

are defined by (28) and (29) respectively.

{

}

() min : 1

jiji

fbdy

∈



(28)

{

}

min : 1 :

() max

j iju i

bdy

∈













∈





y (29)

The second studied characteristic of all suggested

modeling approaches consists in computational time.

All numerical experiments were performed using

the optimization software FICO Xpress 7.3. They

were run on a PC equipped with the Intel® Core™ i7

5500U processor with 2.4 GHz and 16 GB RAM.

The benchmarks were derived from the real

emergency health care system, which was originally

implemented in eight regions of Slovak Republic. For

each region (Bratislava (BA), Banská Bystrica (BB),

Košice (KE), Nitra (NR), Prešov (PO), Trenčín (TN),

Trnava (TT) and Žilina (ZA)), all cities and villages

with corresponding population

were taken into

account. The coefficients

were rounded to

hundreds. In the benchmarks, the set of communities

represents both the set

J of users’ locations and the set

Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem

I of possible center locations as well. The cardinalities

of these sets are reported in the tables together with

the number

p of located centers. The network time -

distances from a user to the nearest located center

were derived from the real transportation network.

Due to the lack of scenario benchmarks for the

experiments, the problem instances used in the

computational study were created in the way used in

(Janáček and Kvet, 2016). There were selected one

quarter of matrix rows so that these rows

corresponded to the biggest cities concerning the

number of system users. Then same of them were

chosen randomly and the associated time distance

values were multiplied by the randomly chosen

constant from the numbers 2, 3 and 4. The rows,

which were not chosen by this random process, stay

unchanged. This way, 10 different scenarios were

generated for each self-governing region. These

benchmarks and generated scenarios were used also

in the research reported in (Janáček and Kvet, 2016,

Janáček and Kvet, 2017, Kvet and Janáček, 2017a,

Kvet and Janáček, 2017b).

The experiments were organized so that each of

suggested multi-objective-based approaches was

used to get the resulting robust EMS design for two

different values of parameter

ε. The obtained results

are reported in the following six tables. The left part

of all tables contains the sizes of used benchmarks.

The right part contains the obtained results reported

by four values:

• Let the symbol ObjF denote the particular

model objective function.

• Computational time in seconds is reported in

columns denoted by

CT.

• Finally, the coefficients POR and GOR are

reported in percentage.

The expressions (9) and (10) define their values.

In this short computational study, the values of

parameter

ε were set directly, i.e. they were not set to

any percentage of the scenario goals.

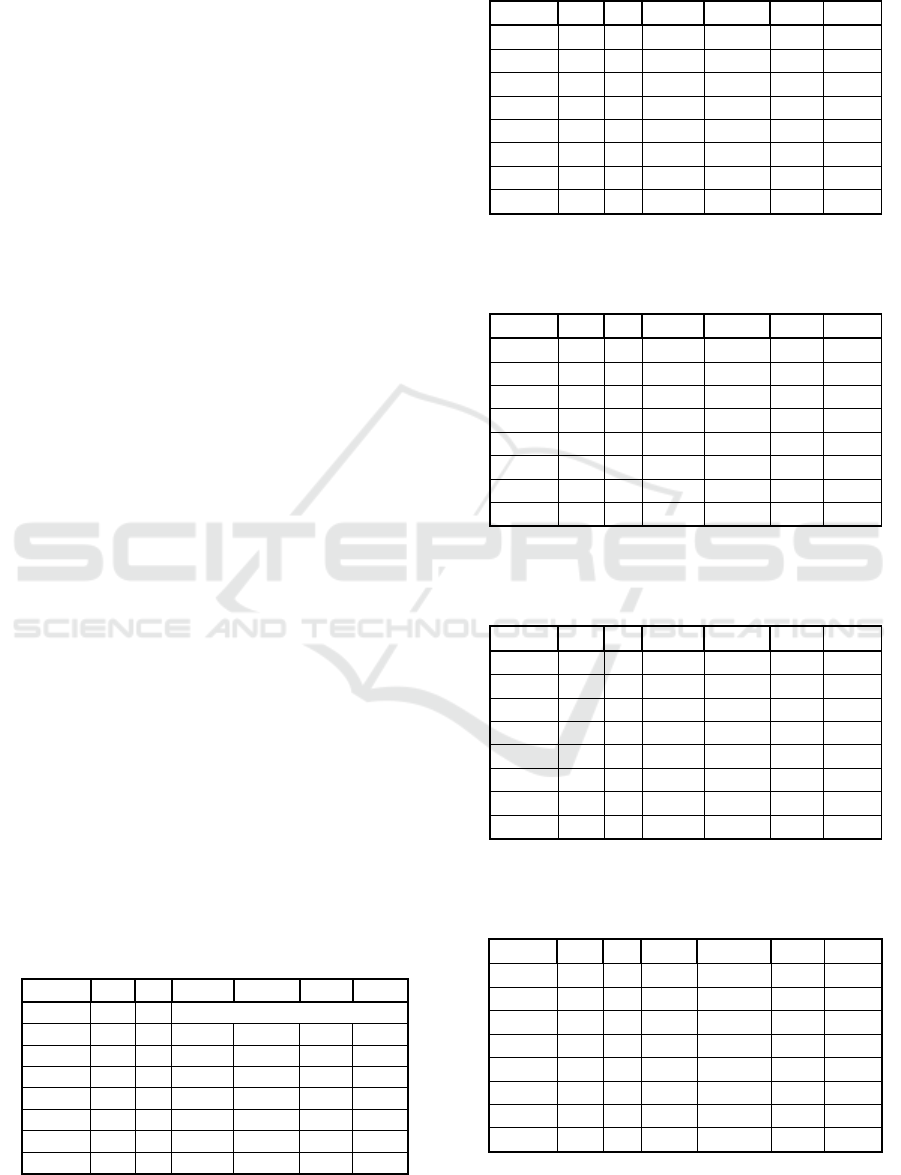
Table 1: Results of the GetGoalMinMax approach applied

on benchmarks derived from the self-governing regions of

Slovakia. The parameter ε was set to 1600.

Region |I| p ObjF CT POR GOR

BA 87 14 Problem infeasible

BB 515 52 17289 705.0 0.00 0.00

KE 460 46 20063 929.1 0.10 3.55

NR 350 35 22728 1299.7 0.34 2.24

PO 664 67 20025 1203.7 0.00 0.00

TN 276 28 15739 478.4 0.34 3.19

TT 249 25 18966 1422.9 0.49 3.55

ZA 315 32 21320 4593.6 1.55 8.53

Table 2: Results of the GetGoalMinMax approach applied

on benchmarks derived from the self-governing regions of

Slovakia. The parameter ε was set to 3000.

Region |I| p ObjF CT POR GOR

BA 87 14 21999 126.0 8.15 32.18

BB 515 52 17289 492.3 0.00 0.00

KE 460 46 20042 392.4 0.00 0.00

NR 350 35 22651 268.9 0.00 0.00

PO 664 67 20025 1111.3 0.00 0.00

TN 276 28 15686 75.9 0.00 0.00

TT 249 25 18873 133.7 0.00 0.00

ZA 315 32 21119 779.4 0.59 4.99

Table 3: Results of the AdjGetGoalMinMax approach

applied on benchmarks derived from the self-governing

regions of Slovakia. The parameter ε was set to 1600.

Region |I| p ObjF CT POR GOR

BA 87 14 22050 138.2 8.40 36.24

BB 515 52 17289 710.1 0.00 0.00

KE 460 46 20055 841.1 0.06 1.46

NR 350 35 22756 1132.7 0.46 3.76

PO 664 67 20025 1165.5 0.00 0.00

TN 276 28 15706 473.0 0.13 3.26

TT 249 25 18939 1011.5 0.35 1.72

ZA 315 32 21320 539.4 1.55 8.53

Table 4: Results of the AdjGetGoalMinMax approach

applied on benchmarks derived from the self-governing

regions of Slovakia. The parameter ε was set to 3000.

Region |I| p ObjF CT POR GOR

BA 87 14 21999 75.7 8.15 32.18

BB 515 52 17289 788.4 0.00 0.00

KE 460 46 20042 434.3 0.00 0.00

NR 350 35 22651 250.0 0.00 0.00

PO 664 67 20025 1284.7 0.00 0.00

TN 276 28 15686 188.8 0.00 0.00

TT 249 25 18873 134.2 0.00 0.00

ZA 315 32 21119 559.2 0.59 4.99

Table 5: Results of the GetGoalMinH approach applied on

benchmarks derived from the self-governing regions of

Slovakia. The parameter ε was set to 500.

Region |I| p ObjF CT POR GOR

BA 87 14 6871 83.7 1.70 10.98

BB 515 52 386 18380.0 2.61 2.73

KE 460 46 548 15768.5 2.16 6.29

NR 350 35 710 15775.4 2.14 6.84

PO 664 67 286 18419.1 2.00 5.48

TN 276 28 328 1522.6 3.16 9.85

TT 249 25 998 2226.6 2.08 4.61

ZA 315 32 601 2957.5 2.33 12.93

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

Table 6: Results of the GetGoalMinH approach applied on

benchmarks derived from the self-governing regions of

Slovakia. The parameter ε was set to 1500.

Region |I| p ObjF CT POR GOR

BA 87 14 3217 104.4 6.88 25.70

BB 515 52 386 18054.0 2.61 2.73

KE 460 46 548 23663.2 2.16 6.29

NR 350 35 657 13426.0 2.47 7.07

PO 664 67 286 19660.5 2.00 5.48

TN 276 28 284 2378.1 4.05 10.13

TT 249 25 788 2267.6 3.87 5.68

ZA 315 32 525 4196.0 3.75 13.31

Analyzing the results reported in Tables 1 - 6, the

expectations have been confirmed. As can be

observed, the quality of obtained resulting system

designs measured by the values of coefficients

POR

and

GOR depend on the parameter settings. As far as

the service system robustness is concerned, presented

approaches represent suitable contribution to the

state-of-the-art methods for robust system designing.

Focusing on computational time requirements, the

big difference between the first two approaches and

the third one can be explained by the model structure.

While the mathematical model used in the functions

GetGoalMinMax and AdjGetGoalMinMax uses a

min-sum optimization criterion, the model used in the

GetGoalMinH approach takes the form of a min-max

problem, which is generally harder to solve, leading

to longer computation times.

6 CONCLUSIONS

This paper was focused on robust emergency medical

service system design. The robustness follows the

idea, which aims to make the system resistant to

various randomly occurring detrimental events,

which may negatively affect system performance and

quality of the service provided. The main focus was

on the set of detrimental scenarios, which allows

forming an additional constraint to the model for each

element of the scenario set. In this paper, three

approaches were introduced and experimentally

compared.

It can be observed that the computational time

demands depend on the model structure. If we replace

a min-sum objective by a min-max optimization

criterion, then the model gets more complicated so it

requires a longer computation time.. Besides that,

quality of obtained results is very satisfactory.

The future research in this field could be aimed at

other approximate techniques, which will enable to

reach shorter computational time with acceptable

solution accuracy. Another future research goal could

be focused on mastering the presented problem with

a larger set of detrimental scenarios.

ACKNOWLEDGEMENT

This paper was supported by the research grant

VEGA 1/0689/19 “Optimal design and economically

efficient charging infrastructure deployment for

electric buses in public transportation of smart cities”.

This work was also supported by the Slovak Research

and Development Agency under the Contract no.

APVV-19-0441.

REFERENCES

Antunes, C., H. and Henriques, C. O. 2016 Multi-objective

optimization and multi-criteria analysis models and

methods for problems in the energy sector. Multiple

criteria decision analysis, Springer, 1071-1169.

Avella, P., Sassano, A., Vasil’ev, I., 2007. Computational

study of large scale p-median problems. In Mathematical

Programming, Vol. 109, No 1, pp. 89-114.

Correia, I. and Saldanha da Gama, F. 2015 Facility

locations under uncertainty. In Laporte, G. Nikel, S. and

Saldanha da Gama, F. (Eds). Location Science,

Heidelberg: Springer Verlag, pp. 177-203.

Current, J., Daskin, M., Schilling, D., 2002. Discrete

network location models. In Drezner Z. (ed) et al.

Facility location. Applications and theory, Berlin,

Springer, pp. 81-118.

Doerner, K. F. et al., 2005. Heuristic solution of an

extended double-coverage ambulance location problem

for Austria. In Central European Journal of Operations

Research, Vol. 13, No 4, pp. 325-340.

Elloumi, S., Labbé, M., Pochet, Y., 2004. A new

formulation and resolution method for the p-center

problem. INFORMS Journal on Computing 16, pp. 84-

94.

García, S., Labbé, M., Marín, A., 2011. Solving large p-

median problems with a radius formulation. INFORMS

Journal on Computing, Vol. 23, No 4, pp. 546-556.

Gendreau, M., Potvin, J. 2010. Handbook of

Metaheuristics, Springer Science & Business Media,

648 p.

Ingolfsson, A., Budge, S., Erkut, E., 2008. Optimal

ambulance location with random delays and travel

times, In Health Care Management Science, Vol. 11,

No 3, pp. 262-274.

Janáček, J., 2008. Approximate Covering Models of

Location Problems. In Lecture Notes in Management

Science: Proceedings of the 1st International

Conference ICAOR, Yerevan, Armenia, pp. 53-61.

Janáček, J. and Kvet, M. 2016. Designing a Robust

Emergency Service System by Lagrangean Relaxation.

Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem

In Proceedings of the conference Mathematical

Methods in Economics, September 6th-9th 2016,

Liberec, Czech Republic, pp. 349-353.

Janáček, J. and Kvet, M. 2017. An Approach to Uncertainty

via Scenarios and Fuzzy Values. Croatian Operational

Research Review 8 (1), pp. 237-248.

Jánošíková, Ľ. 2007. Emergency Medical Service Planning.

Communications Scientific Letters of the University of

Žilina, 9(2), pp. 64-68.

Kvet, M. and Janáček, J. 2017a. Hill-Climbing Algorithm

for Robust Emergency System Design with Return

Preventing Constraints. In 9th International Conference

on Applied Economics: Contemporary Issues in

Economy, 2017, Toruń, Poland, pp. 156-165.

Kvet, M. and Janáček, J. 2017b. Struggle with curse of

dimensionality in robust emergency system design. In

Proceedings of the 35th international conference

Mathematical Methods in Economics MME 2017,

September 13th -15th 2017, Hradec Králové, Czech

Republic, pp. 396-401.

Kvet, M. and Janáček, J. 2018. Reengineering of the

Emergency Service System under Generalized

Disutility. In the7th International Conference on

Operations Research and Enterprise Systems ICORES

2018, Madeira, Portugal, pp. 85-93.

Pan, Y., Du, Y. and Wei, Z. 2014. Reliable facility system

design subject to edge failures. American Journal of

Operations Research 4, pp. 164-172.

Scaparra, M.P., Church, R.L. 2015. Location Problems

under Disaster Events. Location Science, eds. Laporte,

Nikel, Saldanha da Gama, pp. 623-642.

Snyder, L. V., Daskin, M. S., 2005. Reliability models for

facility location; The expected failure cost case. In

Transport Science, Vol. 39, No 3, pp. 400-416.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems