Indextron

Alexei Mikhailov

and Mikhail Karavay

Institute of Control Problems, Russian Acad. of Sciences, Profsoyuznaya Street, 65, Moscow, Russia

Keywords: Pattern Recognition, Machine Learning, Neural Networks, Inverse Sets, Inverse Patterns, Multidimensional

Indexing.

Abstract: How to do pattern recognition without artificial neural networks, Bayesian classifiers, vector support

machines and other mechanisms that are widely used for machine learning? The problem with pattern

recognition machines is time and energy demanding training because lots of coefficients need to be worked

out. The paper introduces an indexing model that performs training by memorizing inverse patterns mostly

avoiding any calculations. The computational experiments indicate the potential of the indexing model for

artificial intelligence applications and, possibly, its relevance to neurobiological studies as well.

https://orcid.org/0000-0001-8601-4101

https://orcid.org/0000-0002-9343-366X

1 INTRODUCTION

Typically, pattern classification amounts to

assigning a given pattern

x to a class

out of K

available classes. For this,

K class probabilities

( ), ( ),..., ( )

pp pxx x

need to be calculated, after

which the pattern

x is assigned to the class

with a

maximum probability

()

p x

(Theodoridis, S. and

Koutroumbas, K. , 2006). This paper avoids a

discussion of classification devices, directly

proceeding to finding class probabilities by a pattern

inversion. Not only such approach cuts down on

training costs, it might also be useful in studying

biological networks, where details of intricate

connectivity of neuronal patterns may not need to be

unraveled. Then, for a given set of patterns, results

of computational experiments can be compared to

that of physical experiments.

For example, Tsunoda et al. (2001) demonstrated

that “objects are represented in macaque

inferotemporal (IT) cortex by combinations of

feature columns”. Figure 1 shows the images that

were taken by Tsunoda et al. (2001) with a camera

attached above a monkey’s IT-region, where a piece

of skull was removed. The anaesthetized monkey’s

IT-region responded to three cat-doll pictures, which

were shown, in turn, with active spots marked by

red, blue and green circles, correspondingly. The

active spots appear on the IT-cortical map because

the neurons under these spots exert increased blood

flow, which is registered by an infrared camera. A

clear set-theoretical inclusion pattern was observed,

in which blue circles make a subset of red circles

and green circles make a subset of blue circles.

This paper describes an experiment, where

similar real cat pictures were shown to an indexing

model referred to as the indextron. The outcomes are

presented in (Figure1, IM) and annotated in the

section Results, points 1.

Also, a comparative performance of the

indextron versus artificial neural networks and

decision functions was tested against benchmark

datasets (see the section Results, points 2 - 3).

Comments are provided in the section 3. The

indextron is considered in details in the Section 4.

2 RESULTS

1) A set-theoretical inclusion pattern, which is

similar to that in Figure 1, IT, was observed in the

memory of the indextron (Figure 1, IM). For that,

this model was shown, in turn, complete and partial

real cat images D, E, F retrieved from (Les Chats,

2010).

Mikhailov, A. and Karavay, M.

Indextron.

DOI: 10.5220/0010180301430149

In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 143-149

ISBN: 978-989-758-486-2

143

Figure 1: Activity in IT-region of a monkey and in the indextron memory (IM): (IT) The encircled areas were activated in

IT-region of a monkey by cat-doll pictures. (A) Full cat-doll picture activated read areas. (B) Head cat-doll picture activated

blue areas. (C) Head contour cat-doll picture activated green areas. (IM) Activity elicited in the model (a part of indextron

memory is shown). (D) Full real cat picture activated read circles in IM. (E) Head picture activated blue areas in IM.

(F) Ears activated green areas in IM. A clear set-theoretical inclusion pattern, where green circles are subsets of blue circles

that are, in turn, subsets of red circles, is observed in both the IT-region and the model.

Table 1: Neural network versus indexing classifier.

Classifier Accuracy (%) Training (sec) Hardware & Libraries

4 layer neural network *)

Layers: Flatten, Dropout,

Dense (256 neurons, ReLu activation function),

Dense (10 neurons, softmax)

85.3 900 AMD Ryzen 5 3600, Python,

Nvidia GeForce GTX 1660 Super,

TensorFlow, Keras, cuDNN

Indextron 82.87 16 AMD Ryzen 5 3600, Python

*) For feature extraction, the convolutional neural network VGG16 from the web-site KERAS (2019) had been pre-trained

on the ImageNet database (2016). Next, VGG16 was trained on 50000 grey level 32x32 images (10 categories) from the

CIFAR-10 dataset providing 512 features per image. Finally, 512 x 50000 features were used for training both a 4-layer

neural network and the indextron. For testing, 10000 images (512 x 10000 features) from the above dataset were classified

using both the 4- layer neural network and the indextron.

2) CIFAR – 10 dataset (Krizhevsky et al, 2009) was

used for testing the indextron against artificial neural

networks. It was shown that the indextron reduced

the training time by the factor of 50 in comparison to

a 4-layer neural network (ref. to Table 1).

3) The indextron’s performance against decision

functions was tested with the CoverType dataset

(Chang D., Canny J., 2014). It was shown that the

indextron algorithm running on a 1.6 MHz CPU

outperformed by a factor of 2 a much more powerful

4-GPU NVidia platform (ref. to Table 2).

3 DISCUSSION

1) The structure of the indextron algorithm

resembles that of a back-of-the-book index. If the

observed similarity of responses between the

indextron and a biological cortical region is not a

coincidence, then it might be possible to suggest that

cortical regions work similar to indexing systems,

where input features serve as keywords activating

outcomes with little or no arithmetic.

2) The fact that at a competitive 85% accuracy, a

mundane 2-core CPU outperforms in terms of

throughput a much more powerful 4-GPU, 8-core

CPU

platform can be explained by the simplicity of

the indextron algorithm, which does not involve any

floating-point operation, multiplications and

adjustable coefficients.

3) Figure 1, IT, shows only a 10% sub-area of active

model area, - the sub-area, which fits the image.

Nonetheless, the inclusion relationship holds

throughout the entire area.

ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods

144

Table 2: Time and accuracy of classifiers at train / test samples 290506 / 290506 Cover Type dataset division.

Platform Method Training Time (sec) Accuracy %

4GPU (NVidia GT X-690 64GB RAM

8-core CPU at 2.2 GHz

SkiKit 138.17 87.7

CudaTree 30.47 96.0

BiDMachRF 67.27 71.0

Dual-core CPU at 1.6MHz 3GB RAM Indextron 16* 90

4) Experiments with the indextron suggest that two

monkeys looking at the same pictures may elicit

different active spot arrangements in their IT-region

as they most probably learnt their visual experiences

in different circumstances.

4 MATERIALS AND METHODS

4.1 Feature Extraction

Sets of local features were used to represent real

cat’s images from (Les Chats, 2010) (see Figure 1,

(D, E, F)). Each color image was converted to a grey

level image that was subject to edge detection

followed by thinning out a list of edge points. For

each remaining edge point, a histogram of distances

from a current point to its 20 nearest neighbors was

created to represent this point’s vicinity by a feature

vector

( , ,..., )

xx=x

Next, this vicinity was

classified in an unsupervised fashion by the

indextron model, where each active vicinity was

represented by a cell on a two-dimensional memory

plane. Since there does not exist a one-to-one

mapping between an

N -dimensional ( 2N > )

space and a two-dimensional plane, the active cells

were randomly placed on the plane on a first-come-

first-occupy basis (shown by circles on Figure. 1,

(IT)). Colors of the circles represent 2

level classes

(body, head, and ears), where a 2

level class was

assigned a red, blue or green color, respectively.

level classifier takes as its input a histograms of

level classes, i.e., a histograms of vicinity classes.

4.2 Pattern Classification

This paper introduces an indexing classifier referred

to as the indextron. The indextron comprises a

number of identical levels. Each level takes in as its

input either a feature vector or a feature set and

returns an index that represents the input’s class.

Once a set of indexes has been accumulated, a

histogram of indexes can be used as an input for the

next level, which returns its output index that

represents a meta-class of first level inputs. And so

on “up to infinity”. A single level classification

problem can be summarized in strict mathematical

terms as follows.

Let all variables be integers and

K pattern

classes be represented by a collection of

K vectors

,1 , ,

,..., ,..., , 1,2,...,

kknkN

xxxk=

(1)

in N-dimensional space, such that all vector

components are restricted as

X£<

. It is

also assumed that the Chebyshev distance between

any two vectors

,kj

is greater than R, that is, any

two vectors differ in at least one component

, : | |

kn jn

kj n x x R"$ - >

Problem: Given an unknown vector

( ), 1,2,...,

nn N=

, find its class, that is, find

the vector k from the given collection, such that the

Chebyshev distance between these two vectors is

less than R

| ( ) |

nxn x R"-£

Solution: Consider the indexed sets

{}

defined

{} { : | () | }

0 , 1,2,...,

xn kn

kkxnxR

xXn N

=-£

£< =

(2)

The solution can be found as the class index

from

the intersection

Indextron

145

() ,

{}

nrn

nr R

==-

(3)

Note 1: The intersection (3) is empty if

max ( )

kN<

, where the histogram

()

calculated as follows

() ,

calculate

,: || , {}

() ()1

nrn

nr r R k k

Hk Hk

"" £ "Î

Note 2: If the intersection (3) is not empty then there

always exists a single solution. This statement is a

consequence of the following properties of the

pattern transform. Each dimension

- contains exactly K distinct class indexes

|{ } |

- does not have intersecting sets:

, ,

{} {}

xm yn

kk=ÆI

Note 3: If the intersection (3) is empty then, on

learning, the original collection (1) is to be expanded

by the vector

( ), 1,2,...,

nn N=

, that is

assigned to a new class

1KK

. However, the

collection (1) does not physically exist in the

memory. Instead, the memory is populated with sets

(2).

Note 4: Whereas elements

,kn

of vectors (1)

constitute the pattern features, the elements of sets

{}

represent pattern classes. The sets (2) are

referred to as the inverse patterns or columns. If the

intersection (3) is empty then, on learning, the

columns are updated as

, ,

{ } { } , 1,2,...,

xn xn

kkKn N

==U

For an example, refer to Figure 2.

Figure 2: Three iterations involving growing columns that

graphically represent inverse patterns.

For this example, the indexes 1, 2, 3 of the patterns

123

(1,1,2) , (2,1,3) , (1,3,2)

are stored in

respective columns. For instance,

3, 2

{} {3}

1, 1

{} {3,1}

1, 3

{}

=Æ

A notion of inverse patterns was introduced in

(Mikhailov, A. et al., 2017) and further discussed in

(Mikhailov, A. and Karavay, M., 2019). This notion

is related to inverse files technology used in Google

search engine (Brin, S. and Page, L., 1998) and in

the bag-of-words approach (Sivic, J. and Zisserman,

A., 2009). Whereas the latter approach recasts visual

object retrieval as text retrieval, the indextron

evaluates class probabilities of visual objects and

other objects such as sets, etc. by analyzing inverse

patterns of numeric features. For example, the

features a, b, c from indexed sets

{, }, {, }ab bc

are associated with the inverse sets

{1} , {1, 2} , {2}

abc

, which indicate that the feature

a belongs only to the set 1, the feature b belongs to

both the set 1 and the set 2, whereas the feature c

belongs only to the set 2.

For patterns, inverse pattern of a feature

is a set

{}

of classes

associated with this feature. So,

for two classes А,

А, А and Т, Т, the feature

“horizontal line” takes part in both A- and T-classes

whereas the feature “vertical line” takes part only in

class T:

{,}

{}T

The value of

in the transform (2) controls a

generalization capability of the classifier. Although

the total number

K of classes grows as new patterns

arrive, the rate of growth is inverse proportional to

generalization radius

ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods

146

Figure 3: Image segmentation.

4.3 Generalization Radius

In accordance with the definition (1), any feature

change

112 2

, ,...,

xx x+D +D +D

, such that

a variation

|| , 1,2,..,

Rn ND£ =

, does not

affect a pattern’s class. An influence of the radius

is shown on Figure 3. For this application, the pixels

of the left-hand side image are to be classified into 3

classes (water, vegetation, urban development).

Each pixel of the left-hand-side is represented by a

4-dimensional vector comprising components in the

256-level range in red, green, blue and infrared

spectra (only one component is shown). For original

images, refer to Gonzalez, R. and Woods, R. (2008).

The image at the center shows the segmentation

result at

0R =

, where most pixels remain

unclassified. The right-hand side image shows a

high quality image segmentation at

10%R = of

256-brightness range.

4.4 Indextron Architecture

The main parameters of the indextron are: the

pattern dimensionality

, the feature range

and

the maximum number

K of classes that can be

created by the classifier. In other words, the

indextron comprises

N groups of addresses, where

each group

contains

addresses ranging from

0 to 1

- . Typically, the normalized integer

feature range

[0,1, 2,..., 255]

. Each address

(, )

n is a gateway to the inverse pattern

{}

referred to as column (Figure 4).

Figure 4: N groups of indextron columns presenting a

cardinality distribution of inverse patterns.

Each column holds class indexes

, so that a column

height is equal to the cardinality of the

corresponding inverse pattern. A macro-column is

defined by the generalization radius

and contains

the neighboring columns with addresses from the

interval

[-, ]

Rx R+ .

In Figure 4, inverse patterns are shown as

groups of columns, each group containing

columns. The average column height

does not

account for 0-height columns. With classification

computational complexity of

()OhN , a flat

cardinality distribution of the inverse patterns is

preferable to a delta-like distribution.

A parallel processing of

column groups can

be implemented in a FPGA-chip, which leads to a

practically instantaneous learning. A memory that

needs to be allocated to column groups can be

arrange in three ways, that is, (a) static columns, (b)

dynamically allocated columns, (c) iterated one-

dimensional maps (Dmitriev A. et al., 1991;

Andreev et al., 1992). These methods would require

XN , 2

N and

N memory cells, respectively.

The method (c) makes possible an FPGA-

implementation of the

(, , )

= (512, 256,

1024) indextron with a 1,44 MB chip (Figure 5).

Indextron

147

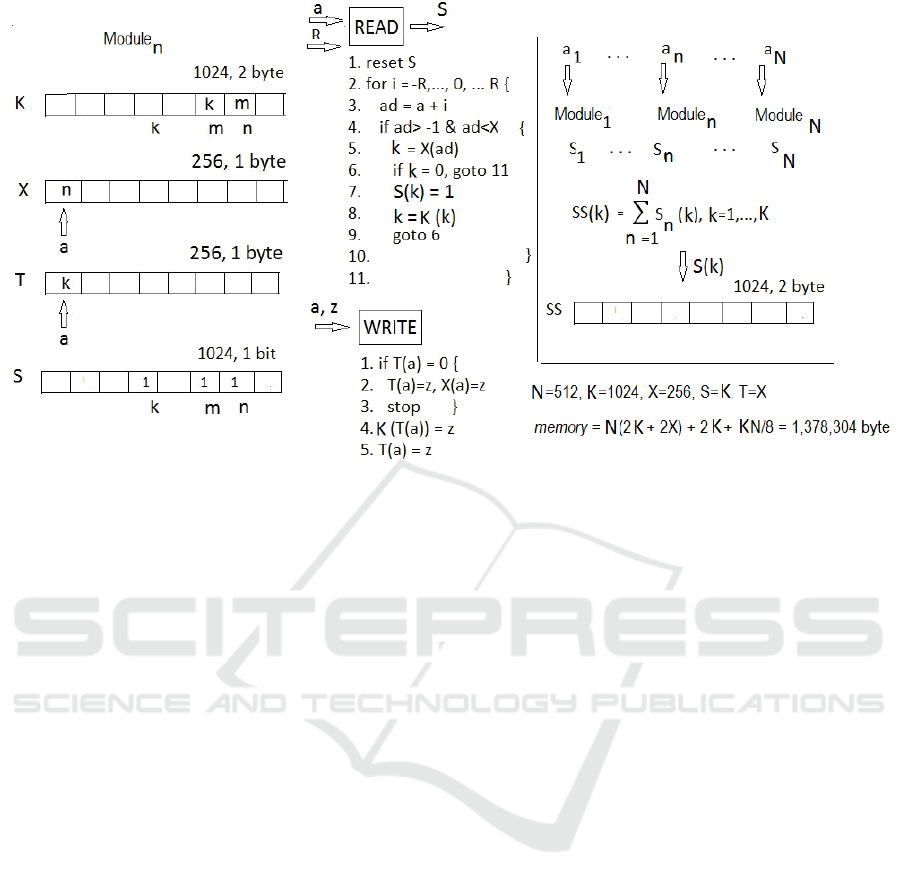
Figure 5: Indextron conceptual diagram.

In this case the total memory can be divided into

N groups of four arrays (N, X, T, S) plus the

common array SS. The total memory

amounts to

(2 /8) 2 (byte) MKNXTN N=++++

A normalized discrete feature range of X = 256 has

been found to be sufficient for most pattern

recognition applications meaning that

both float

point features and integer features can be converted

to 256 discrete levels without sacrificing an overall

accuracy.

In such implementation scheme

N identical

modules work in parallel. The component

of the

feature vector

,..., ,...,

aaa

serves as the address

to the 256-byte array

of the

-th module.

On inference, the READ-code is executed (see

Figure. 5). The module’s output is a 1024-bit

word

. Next,

outputs are to be summed up

producing the 1024-element array

, whose

elements are represented by 2-byte words

( ) ( ), 1, 2,...,

SS k S n k K

This array contains a conditional class distribution.

On learning, the WRITE-code is executed.

Again, the component

of the feature vector

,..., ,...,

aaa

serves as the address to the 256-byte

array

of the

-th module, where the class index

z will be stored.

ACKNOWLEDGEMENTS

We thank Prof. Tanifuji, Riken Brain Science

Institute, for the permission to reproduce the image

of the IT-cortical region of a monkey (Figure 1, IT).

REFERENCES

Theodoridis S. & Koutroumbas K. (2006). Pattern

Recognition, Academic Press (3

edition).

Tsunoda K., Yamane Y., Nishizaki M., Tanifuji M.,

(2001). Complex objects are represented in macaque

inferotemporal cortex by the combination of feature

columns. In Nat. Neurosci. 4 (8).pp.832-838.

doi:10.1038/90547. PMID 11477430

Les Chats. (2010). Retrieved from http://chatset

chiens3005.kazeo.com/les-chats-a122215626

Krizhevsky A., Nair V., Hinton G., (2009). CIFAR-10.

Retrieved from https://www.cs.toronto.edu/~kriz/

cifar.html

Chang D,. Canny J,. (2014). Optimizing Random Forests

on GPU. Tech. Report No. UCB/EECS-2014-2095.

Retrieved from http://www.eecs.berckeley.edu/Pubs/Tech

Rprts/2014/Eecs-2014-205.html

ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods

148

Keras (2019). Retrieved from https://keras.io

Imagenet (2016). Retrieved from http://image-net.org

Mikhailov A., Karavay M., Farkhadov M. ( 2017). Inverse

Sets in Big Data Processing. In Proceedings of the

11th IEEE International Conference on Application of

Information and Communication Technologies

(AICT2017, Moscow). М.: IEEE, Vol. 1

https://www.researchgate.net/publication/321309177_

Inverse_Sets_in_Big_Data_Processing

Mikhailov A.and Karavay M. (2019). Pattern Recognition

by Pattern Inversion. In Proceedings of the 2nd

International conference on Image, Video

Processing and Artificial Intelligence, Shanghai, China.

SPIE Digital Library V.11321.

Brin S.and Page L. (1998). The Anatomy of a large-scale

hypotextual web search engine. In Computer Networks

and ISDN Systems Volume 30, Issues 1–7. Stanford

University, Stanford, CA, 94305, USA. Retrieved

from https://doi.org/10.1016/S0169-7552(98)00110-X

Sivic J., Zisserman A. (2009). Efﬁcient visual search of

videos cast as text retrieval. In IEEE Transactions on

Pattern Analysis and Machine Intelligence Volume:

31, Issue: 4. doi: 10.1109/TPAMI.2008.111

Gonzales R. & Woods R., (2008). Digital Image

Processing. Pearson Prentice Hall (3rd edition).

http://www.imageprocessingplace.com/root_files_V3/i

mage_databases.htm

Dmitriev A., Panas A., Starkov S. (1991). Storing and

recognizing information based on stable cycles of one-

dimentional maps. In Phys. Lett. .

Andreev Y., Dmitriev A., Chua L, Wu C. (1992).

Associative and random access memory using one-

dimensional maps. In International Journal of

Bifurcation and Chaos vol.2, No 3. World Scientific

Publishing Company.

Indextron

149