
SAT-MARL: Specification Aware Training in Multi-Agent
Reinforcement Learning
Fabian Ritz
1
, Thomy Phan
1
, Robert M
¨
uller
1
, Thomas Gabor
1
, Andreas Sedlmeier
1
, Marc Zeller
2
,
Jan Wieghardt
2
, Reiner Schmid
2
, Horst Sauer
2
, Cornel Klein
2
and Claudia Linnhoff-Popien
1
1
Mobile and Distributed Systems Group, LMU Munich, Germany
2
Corporate Technology (CT), Siemens AG, Germany
Keywords:
Multi-Agent, Reinforcement Learning, Specification Compliance, AI Safety.
Abstract:
A characteristic of reinforcement learning is the ability to develop unforeseen strategies when solving prob-
lems. While such strategies sometimes yield superior performance, they may also result in undesired or even
dangerous behavior. In industrial scenarios, a system’s behavior also needs to be predictable and lie within
defined ranges. To enable the agents to learn (how) to align with a given specification, this paper proposes to
explicitly transfer functional and non-functional requirements into shaped rewards. Experiments are carried
out on the smart factory, a multi-agent environment modeling an industrial lot-size-one production facility,
with up to eight agents and different multi-agent reinforcement learning algorithms. Results indicate that
compliance with functional and non-functional constraints can be achieved by the proposed approach.
1 INTRODUCTION
Reinforcement Learning (RL) enables an autonomous
agent to optimize its behavior even when its hu-
man programmers do not know what optimal be-
havior looks like in a specific situation (Sutton and
Barto, 2018). Recent breakthroughs have shown
that RL even allows agents to surpass human perfor-
mance (Silver et al., 2017). Yet, RL systems are typ-
ically given a well-defined target, e.g. “win the game
of chess”. But when applying RL to real-world prob-
lems such as industrial applications, the ideal target
itself is often less clear. In this paper, we consider an
adaptive production line as it is supposed to be part of
the factory of the near future (Wang et al., 2016).
Typically, a smart factory is given a clear func-
tional requirement in the form of an order of items
that can be translated into a series of tasks for the
present machines (Phan et al., 2018). Its goal is to
produce all ordered items within a certain time frame.
However, there often exist a lot of non-functional re-
quirements as well: the system should not exhaust all
of its time if faster production is possible; it should
avoid operations that could damage or wear down the
machines; it should be robust to unexpected events
and human intervention (Cheng et al., 2009; Belzner
et al., 2016; Bures et al., 2017). The full set of func-
tional and non-functional requirements is the specifi-
cation of a system.
The fulfillment of a given specification could be
regarded as a clear target for an RL agent. How-
ever, it involves an intricate balance of achieving the
convoluted requirements at the same time, resulting
in a sparse reward signal that prohibits any learning
progress. Still, weighing various requirements while
neither introducing erratic nor unsafe behavior was
also discovered to be difficult challenge in the litera-
ture (see Sec. 3). E.g., if multiple agents need to leave
through the same exit, approaches such as restricting
single actions might prevent collisions but would not
incentivize the agents to learn coordinated behavior,
thus resulting in a deadlock. In Sec. 4, we introduce
a new domain based on a smart factory populated by
multiple agents acting independently. For this setting,
we show how a full specification of functional and
non-functional requirements can be transferred into
reward functions for RL (see Sec. 5). Evaluating the
different reward schemes in Sec. 6, we observe that
some non-functional requirements are (partially) sub-
sumed by overarching functional requirements, i.e.
they are learned easily, while others significantly af-
fect convergence and performance. Our main contri-
butions are:
• A novel multi-agent domain based on the indus-
trial requirements of a smart factory
28
Ritz, F., Phan, T., Müller, R., Gabor, T., Sedlmeier, A., Zeller, M., Wieghardt, J., Schmid, R., Sauer, H., Klein, C. and Linnhoff-Popien, C.
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning.
DOI: 10.5220/0010189500280037
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 28-37
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

• The application of specification-driven reward en-
gineering to a multi-agent setting
• A thorough evaluation of the impact of typical
secondary reward terms on different multi-agent
reinforcement learning algorithms
2 FOUNDATIONS
2.1 Problem Formulation
We formulate our problem as Markov game M
SG
=
hD, S , A, P , R , Z, Ωi, where D = {1, ..., N} is a set of
agents, S is a set of states s
t
, A = A
1
× ... × A
N
is the
set of joint actions a
t
= ha
t,1
, ..., a
t,N
i, P (s
t+1
|s
t
, a
t
)
is the transition probability, r
t,i
= R
i
(s
t
, a
t
) is the re-
ward of agent i ∈ D, Z is a set of local observa-
tions z
t,i
for each agent i, and Ω(s
t
, a
t
) = z
t+1
=
hz
t+1,1
, ..., z
t+1,N
i ∈ Z
N
is the joint observation func-
tion. For cooperative MAS, we assume a common
reward function r
t
= R (s
t
, a
t
) for all agents.
The behavior of a MAS is defined
by the (stochastic) joint policy π(a
t
|z
t
) =
hπ
1
(a
t,1
|z
t,1
), ..., π
N
(a
t,N
|z
t,N
)i, where π
i
(a
t,i
|z
t,i
)
is the local policy of agent i.
The goal of each agent i is to find a
local policy π
i
(a
t,i
|z
t,i
) as probability distribu-
tion over A
i
which maximizes the expected dis-
counted local return or local action value function
Q
i
(s
t
, a
t
) = E
π
[
∑
∞
k=0
γ
k
R
i
(s
t+k
, a
t+k
) | s
t
, a
t
], where
π = hπ
1
, ..., π
N
i is the joint policy of all agents and
γ ∈ [0, 1] is the discount factor. The optimal local pol-
icy π
∗
i
of agent i depends on the local policies π
j
of
all other agents j 6= i.
2.2 Multi-Agent Reinforcement
Learning
In Multi-Agent Reinforcement Learning (MARL),
each agent i searches for an (near-)optimal local pol-
icy π
∗
i
(a
t,i
|z
t,i
), given the policy π
j
of all other agents
j 6= i. In this paper, we focus on value-based RL. Lo-
cal action value functions are commonly represented
by deep neural networks like DQN to solve high-
dimensional problems (Mnih et al., 2015; Silver et al.,
2017).
DQN has already been applied to MARL, where
each agent is controlled by an individual DQN and
trained independently (Leibo et al., 2017; Tampuu
et al., 2017). While independent learning offers scala-
bility w.r.t. the number of agents, it lacks convergence
guarantees, since the adaptive behavior of each agent
renders the system non-stationary, which is a require-
ment for single-agent RL to converge (Laurent et al.,
2011).
Recent approaches to MARL adopt the paradigm
of centralized training and decentralized execution
(CTDE) to alleviate the non-stationarity problem
(Rashid et al., 2018; Sunehag et al., 2018; Son et al.,
2019). During centralized training, global informa-
tion about the state and the actions of all other agents
are integrated into the learning process in order to sta-
bly learn local policies. The global information is
assumed to be available, since training usually takes
place in a laboratory or in a simulated environment.
Value decomposition or factorization is a com-
mon approach to CTDE for value-based MARL in
cooperative MAS. Value Decomposition Networks
(VDN) are the most simple approach, where a lin-
ear decomposition of the global Q
∗
(s
t
, a
t
)-function
is learned to derive individual value functions for
each agent (Sunehag et al., 2018). Alternatively,
the individual value functions of each agent can be
mixed with a non-linear function approximator to
learn the Q
∗
(s
t
, a
t
)-function (Rashid et al., 2018; Son
et al., 2019). QMIX is an example for learning
non-linear decompositions which uses a monotonic-
ity constraint, where the maximization of the global
Q
∗
(s
t
, a
t
)-function is equivalent to the maximization
of each individual value function (Rashid et al., 2018).
2.3 Reward Shaping in RL
Reward shaping is an evident approach to influence
an RL agent’s behavior. Specifically, potential based
reward shaping (PBRS) (Ng et al., 1999) was proven
not to alter the optimal policy in single-agent systems
and not introducing additional side-effects that would
allow reward hacking. In PBRS, the actual reward
applied for a time step is the difference between the
prior and the posterior state’s potential:
F(s, s
0
) = γ · Φ(s
0
) − Φ(s) (1)
Initially requiring a static potential function, the prop-
erties of PRBS were later shown to hold for dy-
namic potential functions as well (Devlin and Ku-
denko, 2012). Subsequently, PBRS has also been the-
oretically analyzed in and practically applied to MAS
and episodic RL (Devlin et al., 2014; Grze
´
s, 2017).
The fundamental insight is that PBRS does not alter
the Nash equilibria of MAS, but may affect perfor-
mance in any direction, depending on scenario and
applied heuristics. This paper’s reward shaping dif-
fers from PBRS in one detail: It uses γ = 1.0 dur-
ing reward shaping while the learning algorithms use
γ = 0.95 in most experiments. For the theoretic guar-
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning
29

antees of PBRS to hold, learning algorithm and re-
ward shaping must use the same value of γ. Note
that, however, the results of the fourth evaluation sce-
nario (see Sec. 6) indicate that the practical impact
is negligible (at least in our case) and there is cur-
rently no proven optimality guarantee for DQN-based
algorithms using deep neural networks for function
approximation anyway.
3 RELATED WORK
Regarding safety in RL, prior work compiled a list
of challenges for learning to respect safety require-
ments in RL (Amodei et al., 2016) and provided a
set of gridworld domains allowing to test a single RL
agent for safety (Leike et al., 2017). Yet, the funda-
mental issues remain unsolved. Further, a compre-
hensive overview of safe RL approaches subdivides
the field into modeling either safety or risk (Garc
´
ıa
et al., 2015). While some approaches use these con-
cepts to constrain the MDP to prevent certain actions,
this paper does not model risk or safety explicitly. In-
stead, it aims for agents learning (how) to align to a
given specification as constraining the MDP may be-
come infeasable in complex multi-agent systems.
Regarding learned safety in RL, one recent ap-
proach extends the MDP by a function mapping state
and action to a binary feedback signal indicating the
validity of the taken action (Seurin et al., 2019). A
second neural network is trained to predict this va-
lidity in addition to training a DQN. The DQN’s
training objective is augmented by an auxiliary loss
pushing Q-values of forbidden actions below those of
valid actions. Similarly, another approach accompa-
nies the Q-Network with an Action Elimination Net-
work (AEN) that is trained to predict the feedback sig-
nal (Zahavy et al., 2018). A linear contextual bandit
facilitates the features of the penultimate layer of the
AEN and eliminates irrelevant actions with high prob-
ability, therefore directly altering the action set. Both
approaches reduced certain actions and improved per-
formance, but were evaluated in single agent domains
only and not compared with reward shaping.
Regarding the training of MARL system,
population-based approaches such as FTW enable
individuals to learn from internal, dense reward
signals complementing the sparse, delayed global
reward (Jaderberg et al., 2019). Distinct environ-
ment signals are used in handcrafted rewards and
a process during that agents learn to optimize the
internal rewards in accordance with maximizing
the global reward. Similrly, separate discounts
can be used to individually adjusts dense, internal
rewards to optimize the top level goal (Liu et al.,
2019). While these approaches demonstrated the
capabilities of shaped, dense rewards in MARL and
how automatically evolved rewards can outperform
hand-crafted rewards, they only aim on boosting the
system’s performance and do not consider additional
specification constraints. While in (video) games,
MARL lead to innovative strategies of which humans
were unaware before (Silver et al., 2017), the goal
of specification compliance is to avoid unintended
side-effects which is especially important for indus-
trial and safety-critical domains (Belzner et al., 2016;
Bures et al., 2017).
Reward shaping has also been applied to improve
cooperation in MAS by addressing the credit assign-
ment problem, where all agents observe the same re-
ward signal. For example, Kalman filtering can be
used to extract individual reward signals from the
common reward (Chang et al., 2004). Moreover, the
difference between the original reward and an alterna-
tive reward where the agent would have chosen a de-
fault action can be used to derive an individual train-
ing signal for each agent (Wolpert and Tumer, 2002).
Also, counterfactual baselines can be used to improve
credit-assignment in policy gradient algorithms (Fo-
erster et al., 2018). While these approaches address
the problem of improving cooperation, they do not ex-
plicitly address non-functional requirements to avoid
side-effects.
4 SMART FACTORY DOMAIN
This paper’s smart factory is inspired by a domain
proposed in the literature (Phan et al., 2018) with
respect to modeling the components and production
processes of a highly adaptive facility in a virtual sim-
ulation. It consists of a 5 × 5 grid of machines with
different machine types as shown in Fig. 1. Each item
is carried by one agent i and needs to be processed at
various machines according to its randomly assigned
processing tasks tasks
i
= [{a
i,1
, b
i,1
}, {a
i,2
, b
i,2
}, ...],
where each task a
i, j
,b
i, j
is contained in a bucket.
Fig. 1b shows an example for an agent i, rendered
as a green cylinder, with tasks
i
= [{5, 6}], rendered
as green boxes. While tasks in the same bucket can
be processed in any order, buckets themselves have
to be processed in a specific order. Consequently, i
can choose between different machines to process the
tasks a
i,1
= 5 and b
i,2
= 6. The agent’s initial posi-
tion is fixed (Fig. 1a). The agent can move along the
machine grid (left, right, up, down), enqueue at the
current position or stay put (no-op). The domain is
discrete in all aspects including agent motion. Each
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
30

(a) Smart Factory Overview (b) Zoom-in on Bottom Left
Figure 1: 3d visualization of the discrete domain used in this paper. Contrary to a fully connected grid world, the agents can
only move to adjacent cells via a connecting path and can only doge each other via on one of the 4 capacitive cells (rendered
with transparent boxes). Agents spawn on the entry position on the left and finish on the exit position on the right (both
rendered with blue boxes).
machine can process exactly one item per time step.
Enqueued agents are unable to perform any actions.
If a task is processed, it is removed from its bucket. If
a bucket is empty, it is removed from the item’s tasks
list. An item is complete if its tasks list is empty.
Contrary to fully-connected grid worlds, every
grid cell in the present smart factory has an agent
capacity limit and defined connections (paths) to the
surrounding grid cells. An agent may only move to
another grid cell if a connecting paths exists and the
target grid cell’s maximum capacity is not exceeded.
Entry and exit can hold all agents simultaneously, the
four grid cells fully connected to their neighbors can
hold half the agents. Fig. 1b shows such a grid cell, lo-
cated south to example agent i, rendered with a trans-
parent box. All other grid cells can only hold one
agent. In presence of multiple agents, coordination is
required to avoid conflicts when choosing appropriate
paths and machines.
5 TRANSFERRING
SPECIFICATION
CONSTRAINTS
Inspired by PBRS, this paper proposes to omit pri-
mary rewards, transfer both functional and non-
functional requirements into a potential function and
use potential differences as rewards. Setting the func-
tional domain goal to complete items as fast as possi-
ble, a first approach is to increase the potential by α
once an agent completes its item and decrease it by δ
per step. This is implemented by reward scheme r0.
As positive feedback in r0 is sparse and delayed, a de-
composition into more dense, positive terms β, added
whenever a single task is finished, may improve learn-
ability. This is implemented by reward scheme r1.
Given an industrial background, the system may
need to comply with a certain non-functional spec-
ification, resulting in behavioral constraints. In this
domain, the evaluated soft constraints are to only use
the machine type needed by the task, to stay on the
defined paths and not to collide with other agents. In
the simulation, items processed by wrong machines
remain unaltered and any agent trying to move to a
grid cell without sufficient capacity or path connec-
tion stays put. Therefore, soft constraints do not op-
pose the goal of completing items (fast) as agents
would not benefit from violations anyway. Moreover,
agents shall freeze if the emergency signal is active as
a hard constraint. In the simulation, the agents can
ignore the emergency signal in order to finish their
tasks faster. Therefore, the hard constraint introduces
a target conflict. As constraint violations shall be min-
imized, they are transferred into negative terms ζ (ma-
chine operation cost), η (path violation penalty), θ
(agent collision penalty) and ι (emergency violation
penalty) of different quantity, considered in the re-
ward schemes r2, r3, r4 and r5.
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning
31

Table 1: Reward overview.
(a) reward components: variables and signs
reward component variable sign
item completion rew. α +
single task reward β +
step cost δ -
machine operation cost ζ -
path violation penalty η -
agent collision penalty θ -
emergency violat. pen. ι -
(b) reward schemes: variable values
scheme α β δ ζ η θ ι
r0 5.0 0.1
r1 1.0 0.1
r2 1.0 0.1 0.2
r3 1.0 0.1 0.1
r4 1.0 0.1 0.4
r5 1.0 0.1 0.2 0.1 0.4 1.0
rx 1.0 0.1 0 − 0.2 0.1 0 − 0.4 0 − 1.0
Inspired by curriculum learning (Bengio et al.,
2009), reward scheme rx only contains β, δ and η in
the first part of the training process in order to learn
the basic task. ζ, θ and ι are added later during train-
ing, so that some constraints are introduced to the
agents gradually. A summary of all reward schemes,
their components and values is given in Tab. 1. To ac-
tually employ the reward schemes, the smart factory
provides a corresponding interface for each compo-
nent, e.g. the number of completed items, at any time
step. Depending on the learning algorithm, the poten-
tial function is evaluated either per agent or globally.
Bringing all together:
Φ(s) = α · itemCompleted(s) + β · tasksFinished(s)
+ δ · stepCount(s) + ζ · machinesUsed(s)
+ η · pathViolations(s) + θ · agentCollisions(s)
+ ι · emergencyViolations(s)
6 EVALUATION
6.1 Experimental Setup
The reward schemes listed in Table 1b were evaluated
on different layouts of the smart factory domain. The
reported layout (see Fig. 1a) turned out to be most
challenging. Agents always spawn on an entry (on
the left), should then process two buckets of each two
random tasks and finally move to the exit (the mirror
position to the entry). Machines are not grouped by
type as one might expect in a real world setting but
distributed equally to maintain solvability in presence
of up to 8 agents. Episode-wise training is carried out
for 5000 episodes, each limited to 50 steps. While the
components of reward schemes r0 to r5 remain fixed
during training, rx alters ζ, θ and ι during training.
After adding or altering values, the exploration rate is
set back to 0.25 and the optimizer momentum is reset.
As a white-box test, independent DQN is trained
in each scenario: due to the individual rewards, agents
are able to directly associate the shaped feedback sig-
nals with their actions. The DQN consists of two
dense layers of 64 and 32 neurons, using ELU acti-
vation. The output dense layer consists of |A
i
| = 6
neurons with linear activation. ADAM is used for op-
timization. Except evaluation scenario 4, Q-values are
discounted with γ = 0.95. ε−greedy exploration with
linear decay lasts for approx. 1000 steps. The expe-
rience buffer holds up to 20000 elements. The target
network is updated after each 4000 training steps. Per
training step, a batch of 64 elements is sampled via
prioritized experience replay.
As a black-box test, VDN and QMIX agents were
trained: due to the global reward, agents cannot di-
rectly associate the shaped feedback signal with their
individual actions (at least in the beginning of the
training). Both VDN and QMIX use the same hy-
perparameters as DQN and the same architecture for
their local Q-networks. In addition, QMIX uses a
mixing network with one hidden, dense layer of 64
neurons using ELU activation and an output dense
layer with a single neuron using linear activation.
Performance is captured through steps until
solved, representing the episode step in which all
agents have finished their tasks. By this paper’s def-
inition, a lower value indicates better performance.
Compliance is measured in soft and hard constraint
violations. These are summed over all agents and all
steps of an episode. Again, by definition, lower val-
ues indicate higher compliance. Depending on po-
tential function and learning algorithm, these metrics
may not always be fully visible to the agents. For all
values, mean and 95% confidence interval of 10 inde-
pendently trained networks are reported. Experiments
are structured in four scenarios:
1. To analyze the impact of isolated reward com-
ponents on compliance and performance during
training, reward schemes r2, r3 and r4 are ap-
plied on 4 DQN agents. For comparison, reward
scheme r1 is always evaluated. The sparse reward
scheme r0 and the combined reward scheme r5
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
32

are evaluated in an additional overview.
2. To quantify the impact of combined reward com-
ponents on scalability, reward scheme r5 is ap-
plied on 8 agents with DQN, VDN and QMIX and
compared with reward scheme r1.
3. To examine whether scalability can be improved,
reward scheme rx is gradually applied on 8 agents
with DQN, VDN and QMIX and compared to the
static reward schemes r1 and r5.
4. To outline whether the proposed approach could
be used in safety-critical domains, reward scheme
rx is compared to r5 during the training of 6 DQN
agents in a scenario with emergency signals that
introduce target conflicts. To not break with the
theoretical guarantees of PBRS in this particular
scenario, DQN discounts with γ = 1.0 and agents
are moved to an absorbing state with zero poten-
tial at the end of each episode as proposed in the
literature (Devlin et al., 2014), thus the number of
steps peaks at 51.
6.2 Results
The results of the first scenario are depicted in Fig. 2.
Excluding the sparse reward scheme r0 (see Fig. 2g,
2h), convergence can be observed for all other reward
schemes in all subfigures. Regarding compliance,
wrong enqueueing and path violations can be mini-
mized with small negative terms (see Fig. 2a, 2c). In
contrast, minimizing agent collisions requires greater
negative potentials (see Fig. 2e). Regarding perfor-
mance, punishing path violations makes no differ-
ence at all (see Fig. 2d) and punishing agent collisions
slows down convergence only in case of big penalties
(see Fig. 2f). However, punishing wrong enqueueing
results in more steps until all tasks are finished. This
effect becomes more significant with higher penalties
(see Fig. 2b). Summing up the first scenario, reward
scheme r5 notable decreases the overall constraint vi-
olations while the number of steps until all tasks are
finished remains the same.
The results of the second scenario are shown in
Fig. 3. When scaled to 8 agents, r5 also lowers the
number of constraint violations with the impact dif-
fering per learning algorithm. Compared to DQN,
VDN causes less violations with r1 and more viola-
tions with r5 (see Fig. 3a). Independent of the reward
function, QMIX always causes more violations than
DQN and VDN. Regarding performance, r5 causes
an increased number of steps with compared to r1
with DQN, VDN and QMIX (see Fig. 3b). Overall in
the second scenario, reward scheme r5 decreases the
overall constraint violations but increases the number
of steps until all tasks are finished.
The results of the third scenario are depicted in
Fig. 4. Note that in all subfigures, characteristic
spikes at episode 2000 and 3000 are present in the
data series of rx. In terms of compliance, DQN and
VDN show a reduced number of constraint violations
with rx compared to r1, nearly as low as with r5 at the
end of the training (see Fig. 4a). The same applies to
QMIX, even though it converges slower (see Fig. 4c).
Regarding performance, DQN with rx approaches the
level of r1 step-wish which is significantly lower than
that of r5 (see Fig. 4b). Contrarily, rx disrupts VDN’s
convergence, resulting in more steps than r1 and only
sightly less than r5. QMIX with rx shows the same
phenomenon (see Fig. 4d), although the final number
of steps is between r1 and r5. Summing up the third
scenario, reward scheme rx leads to a step-wise de-
crease of constraint violations nearly to the level of
r5. However, agents with rx solve the scenario faster
than with r5, sometimes as fast as with r1.
The results of the fourth scenario are depicted in
Fig. 5. Due to a single reward adjustment, only one
characteristic spike can be seen around episode 2500.
While DQN with r5 succeeds to prevent hard con-
straint violations and minimizes soft constraint vio-
lations with 6 agents (see Fig. 5b), it fails to solve
the environment in less than 50 steps (see Fig. 5b).
Contrary, rx resolves the target conflict introduced by
the emergency signals after the reward adjustment by
maintaining adequate performance while minimizing
all constraint violations.
6.3 Discussion
First of all, results indicate that the presented domain
is suitable to benchmark practically relevant proper-
ties of a MAS. While this smart factory can be solved
straightforwardly with up to 4 agents, deploying 6
and 8 agents resulted in more constraint violations.
Also, notably more steps were required and naive
approaches struggled to finish their tasks. In such
settings, we suppose agents to effectively compete
for machines (to process items) and path segments
(to navigate to the machines), leading to conflicts.
Such scenarios require cooperative behavior between
agents to perform well. Techniques restricting the ac-
tion space cannot solve such scenarios alone as dead-
locks would not necessarily be resolved.
Also, we observed sparse reward schemes such as
r0 do not lead to convergence, which is not surpris-
ing. However, its decomposed counterpart r1 lead to
solid performance throughout all scenarios. Although
soft specification violations in the smart factory are
actions not solving the environment, r1 fails to com-
pletely minimize them in limited training time. In-
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning
33
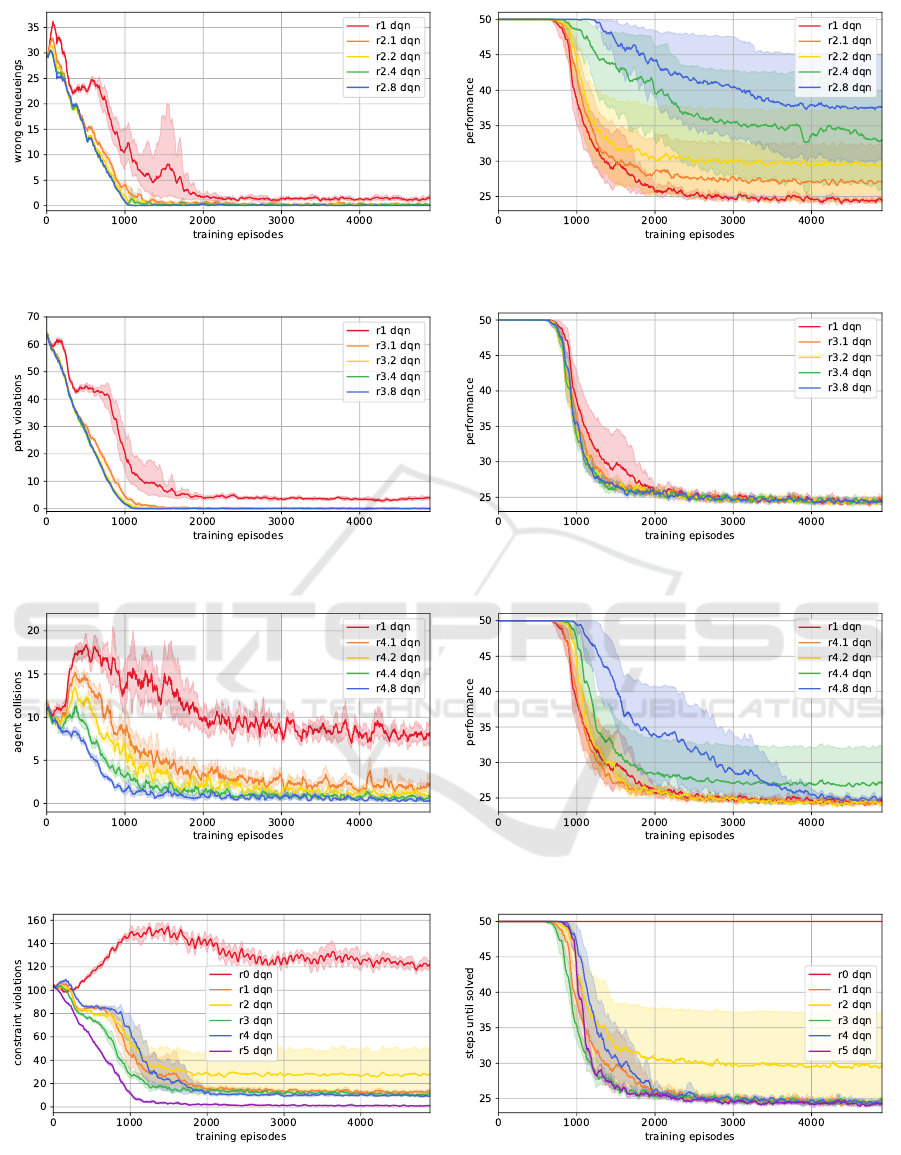
(a) Compliance when punishing wrong enqueueing (b) Performance when punishing wrong enqueueing
(c) Compliance when punishing path violations (d) Performance when punishing path violations
(e) Compliance when punishing agent collisions (f) Performance when punishing agent collisions
(g) Compliance comparison of static reward schemes (h) Performance comparison all static reward schemes
Figure 2: Impact of isolated reward components (schemes r2, r3 and r4) on compliance and performance during training of 4
DQN agents. r0 is sparse with only functional components, r1 its dense counterpart. r5 contains all components of r1-r4.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
34

(a) Compliance of 8 agents (b) Performance of 8 agents
Figure 3: Impact of combined reward components (scheme r5) on compliance and performance during training of DQN, VDN
and QMIX. r1 has only functional components.
(a) Compliance: DQN, VDN (b) Performance: DQN, VDN
(c) Compliance: DQN, QMIX (d) Performance: DQN, QMIX
Figure 4: Impact of gradually adding components at steps 2000 and 3000 via rx on compliance and performance during
training. r5 is a static scheme with all components, r1 is a static scheme with only functional components. 8 agents were
trained with DQN, VDN and QMIX.
(a) Compliance of 6 agents (b) Performance of 6 agents
Figure 5: Impact of gradually adding components at step 2500 via rx during training of 6 DQN agents. Agents shall freeze
in steps with active emergency signal (hard constraint). All prior constraints are considered soft constraints. r5 is a static
scheme with the same components as rx but weights them fully during the whole training.
stead, reward schemes containing more specification
components such as r5 turned out to increase compli-
ance throughout all scenarios, which is considered a
major insight.
Yet, depending on the learning algorithm and the
number of agents, r5 partially increase the time until
the environment was solved, especially when scaled
to 8 agents. Moreover, r5 failed to resolve the target
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning
35

conflict introduced with the hard constraints in Fig. 5.
Obviously, providing the whole specification to the
agents from the beginning on does not necessarily
lead to optimal behavior. Results of adaptive reward
schemes such as rx further show that starting with a
basic reward scheme and gradually adding more com-
ponents once the learner started to converge is capable
of increasing specification compliance while main-
taining performance. Conversely, some reward com-
ponents may simply be unsuitable to begin the train-
ing with as they negatively affect exploration. As the
learning algorithms also reacted differently to rx, tim-
ing when to add components and the correct value is
assumed to be substantial. Such side-effects of reward
shaping have also been reported in the literature (De-
vlin et al., 2014).
7 CONCLUSION AND FUTURE
WORK
In this work, we considered the problem of specifica-
tion compliance in MARL.
We introduced an involved multi-agent domain
based on a smart factory setting. We translated the
system’s goal specification into a shaped reward func-
tion and analyzed how the system’s non-functional re-
quirements can be modeled by adding more terms to
that reward function. Besides the raw performance,
we also evaluated specification compliance in RL on
a multi-agent setting.
While simple shaped rewards, which weight only
functional requirements like the task rewards or the
step cost, can lead to agents that are able to achieve
the basic goal, our results show that they still have
a high tendency to violate the non-functional re-
quirements, which could be harmful for industrial or
safety-critical domains.
Our approach to explicitly translating these re-
quirements into a shaped reward function was shown
to still enable agents to solve the global goal, while
being able to consider these additional requirements,
making them specification-aware. In accordance with
other results (Bengio et al., 2009; Gupta et al., 2017),
we found an inherent benefit due to gradually applied
rewards where reward function and scenario become
increasingly more complicated.
An immediate generalization of our experiments
would be to replace the hand crafted shaping and
scheduling with some kind of auto-curriculum mech-
anism. This would allow the reward functions to ad-
just themselves in direct response to the agents’ learn-
ing progress (Jaderberg et al., 2019; Liu et al., 2019)
but focusing on non-functional objectives. Such tech-
niques have also been employed for adversarial learn-
ing (Lowd and Meek, 2005), but our results sketch a
path on how to implement reward engineering as an
adversary given a fixed specification.
As we now only considered a cooperative setting,
it seems natural to expand our study to groups of self-
interested agents with (partially) opposing goals. As
these all have their own reward signal, deriving re-
ward functions from a shared specification for the
whole systems becomes dramatically more difficult
(at least doing so manually). However, especially in
industrial applications, ensuring safety between par-
ties with different interests is all the more crucial and
formulating the right secondary reward terms to en-
sure “fair play” might allow for even greater improve-
ment in the whole system’s performance than it does
for the cooperative setting.
Eventually, we would suspect that results from our
evaluation can be applied back to the formulation of
the original specification. Requirements that are not
needed within the reward function might not right-
fully belong in the specification. This way, the usu-
ally human-made specification can be improved via
the translation to a reward function and the execution
of test runs of RL.
REFERENCES
Amodei, D., Olah, C., Steinhardt, J., Christiano, P. F.,
Schulman, J., and Man
´
e, D. (2016). Concrete prob-
lems in AI safety. CoRR, abs/1606.06565.
Belzner, L., Beck, M. T., Gabor, T., Roelle, H., and Sauer,
H. (2016). Software engineering for distributed au-
tonomous real-time systems. In 2016 IEEE/ACM 2nd
International Workshop on Software Engineering for
Smart Cyber-Physical Systems (SEsCPS), pages 54–
57. IEEE.
Bengio, Y., Louradour, J., Collobert, R., and Weston, J.
(2009). Curriculum learning. In Proceedings of the
26th Annual International Conference on Machine
Learning, ICML ’09, pages 41–48. ACM.
Bures, T., Weyns, D., Schmer, B., Tovar, E., Boden, E.,
Gabor, T., Gerostathopoulos, I., Gupta, P., Kang,
E., Knauss, A., et al. (2017). Software engineer-
ing for smart cyber-physical systems: Challenges and
promising solutions. ACM SIGSOFT Software Engi-
neering Notes, 42(2):19–24.
Chang, Y.-H., Ho, T., and Kaelbling, L. P. (2004). All learn-
ing is local: Multi-agent learning in global reward
games. In Advances in neural information processing
systems, pages 807–814.
Cheng, B. H., de Lemos, R., Giese, H., Inverardi, P., Magee,
J., Andersson, J., Becker, B., Bencomo, N., Brun, Y.,
Cukic, B., et al. (2009). Software engineering for
self-adaptive systems: A research roadmap. In Soft-
ware engineering for self-adaptive systems, pages 1–
26. Springer.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
36

Devlin, S. and Kudenko, D. (2012). Dynamic potential-
based reward shaping. In Proceedings of the 11th
International Conference on Autonomous Agents and
Multiagent Systems - Volume 1, AAMAS ’12, pages
433–440. International Foundation for Autonomous
Agents and Multiagent Systems.
Devlin, S., Yliniemi, L., Kudenko, D., and Tumer, K.
(2014). Potential-based difference rewards for mul-
tiagent reinforcement learning. In Proceedings of
the 2014 International Conference on Autonomous
Agents and Multi-agent Systems, AAMAS ’14, pages
165–172. International Foundation for Autonomous
Agents and Multiagent Systems.
Foerster, J. N., Farquhar, G., Afouras, T., Nardelli, N., and
Whiteson, S. (2018). Counterfactual multi-agent pol-
icy gradients. In Thirty-Second AAAI Conference on
Artificial Intelligence.
Garc
´
ıa, J., Fern, and o Fern
´
andez (2015). A comprehen-
sive survey on safe reinforcement learning. Journal of
Machine Learning Research, 16(42):1437–1480.
Grze
´
s, M. (2017). Reward shaping in episodic reinforce-
ment learning. In Proceedings of the 16th Conference
on Autonomous Agents and MultiAgent Systems, AA-
MAS ’17, pages 565–573. International Foundation
for Autonomous Agents and Multiagent Systems.
Gupta, J. K., Egorov, M., and Kochenderfer, M. (2017).
Cooperative multi-agent control using deep reinforce-
ment learning. In International Conference on Au-
tonomous Agents and Multiagent Systems, pages 66–
83. Springer.
Jaderberg, M., Czarnecki, W. M., Dunning, I., Marris, L.,
Lever, G., Casta
˜
neda, A. G., Beattie, C., Rabinowitz,
N. C., Morcos, A. S., Ruderman, A., Sonnerat, N.,
Green, T., Deason, L., Leibo, J. Z., Silver, D., Has-
sabis, D., Kavukcuoglu, K., and Graepel, T. (2019).
Human-level performance in 3d multiplayer games
with population-based reinforcement learning. Sci-
ence, 364(6443):859–865.
Laurent, G. J., Matignon, L., Fort-Piat, L., et al. (2011).
The world of Independent Learners is not Marko-
vian. Journal of Knowledge-based and Intelligent En-
gineering Systems.
Leibo, J. Z., Zambaldi, V., Lanctot, M., Marecki, J.,
and Graepel, T. (2017). Multi-Agent Reinforcement
Learning in Sequential Social Dilemmas. In Proceed-
ings of the 16th Conference on Autonomous Agents
and Multiagent Systems, pages 464–473. IFAAMAS.
Leike, J., Martic, M., Krakovna, V., Ortega, P. A., Everitt,
T., Lefrancq, A., Orseau, L., and Legg, S. (2017). AI
safety gridworlds. CoRR, abs/1711.09883.
Liu, S., Lever, G., Merel, J., Tunyasuvunakool, S., Heess,
N., and Graepel, T. (2019). Emergent coordination
through competition. In 7th International Conference
on Learning Representations, ICLR 2019, New Or-
leans, LA, USA.
Lowd, D. and Meek, C. (2005). Adversarial learning. In
Proceedings of the eleventh ACM SIGKDD interna-
tional conference on Knowledge discovery in data
mining, pages 641–647. ACM.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
Level Control through Deep Reinforcement Learning.
Nature.
Ng, A. Y., Harada, D., and Russell, S. J. (1999). Pol-
icy invariance under reward transformations: Theory
and application to reward shaping. In Proceedings
of the Sixteenth International Conference on Machine
Learning, ICML ’99, pages 278–287. Morgan Kauf-
mann Publishers Inc.
Phan, T., Belzner, L., Gabor, T., and Schmid, K. (2018).
Leveraging statistical multi-agent online planning
with emergent value function approximation. In Pro-
ceedings of the 17th International Conference on Au-
tonomous Agents and MultiAgent Systems, AAMAS,
pages 730–738.
Rashid, T., Samvelyan, M., de Witt, C. S., Farquhar, G., Fo-
erster, J., and Whiteson, S. (2018). QMIX: Monotonic
Value Function Factorisation for Deep Multi-Agent
Reinforcement Learning. In International Conference
on Machine Learning, pages 4292–4301.
Seurin, M., Preux, P., and Pietquin, O. (2019). ”i’m sorry
dave, i’m afraid i can’t do that” deep q-learning from
forbidden action. CoRR, abs/1910.02078.
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I.,
Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M.,
Bolton, A., et al. (2017). Mastering the Game of Go
without Human Knowledge. Nature, 550(7676):354.
Son, K., Kim, D., Kang, W. J., Hostallero, D. E., and Yi, Y.
(2019). QTRAN: Learning to Factorize with Transfor-
mation for Cooperative Multi-Agent Reinforcement
Learning. In International Conference on Machine
Learning, pages 5887–5896.
Sunehag, P., Lever, G., Gruslys, A., Czarnecki, W. M.,
Zambaldi, V., Jaderberg, M., Lanctot, M., Sonnerat,
N., Leibo, J. Z., Tuyls, K., et al. (2018). Value-
decomposition networks for cooperative multi-agent
learning based on team reward. In Proceedings of the
17th International Conference on Autonomous Agents
and Multiagent Systems (Extended Abstract), pages
2085–2087. IFAAMAS.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. A Bradford Book, Cambridge,
MA, USA.
Tampuu, A., Matiisen, T., Kodelja, D., Kuzovkin, I., Korjus,
K., Aru, J., Aru, J., and Vicente, R. (2017). Multia-
gent Cooperation and Competition with Deep Rein-
forcement Learning. PloS one, 12(4):e0172395.
Wang, S., Wan, J., Zhang, D., Li, D., and Zhang, C.
(2016). Towards smart factory for industry 4.0: a
self-organized multi-agent system with big data based
feedback and coordination. Computer Networks,
101:158–168.
Wolpert, D. H. and Tumer, K. (2002). Optimal payoff func-
tions for members of collectives. In Modeling com-
plexity in economic and social systems, pages 355–
369. World Scientific.
Zahavy, T., Haroush, M., Merlis, N., Mankowitz, D. J.,
and Mannor, S. (2018). Learn what not to learn: Ac-
tion elimination with deep reinforcement learning. In
Bengio, S., Wallach, H., Larochelle, H., Grauman, K.,
Cesa-Bianchi, N., and Garnett, R., editors, Advances
in Neural Information Processing Systems 31, pages
3562–3573. Curran Associates, Inc.
SAT-MARL: Specification Aware Training in Multi-Agent Reinforcement Learning
37
