
FLIC: Fast Lidar Image Clustering
Frederik Hasecke
1,2 a
, Lukas Hahn
1,2,∗ b
and Anton Kummert
1 c
1
University of Wuppertal, Faculty of Electrical Engineering, Wuppertal, Germany
2
Aptiv, Wuppertal, Germany
Keywords:
Clustering, Dimensionality Reduction, LiDAR.
Abstract:
In this work, we propose an algorithmic approach for real-time instance segmentation of Lidar sensor data. We
show how our method uses the underlying way of data acquisition to retain three-dimensional measurement
information, while being narrowed down to a two-dimensional binary representation for fast computation.
Doing so, we reframe the three-dimensional clustering problem to a two-dimensional connected-component
labelling task. We further introduce what we call Map Connections, to make our approach robust against over-
segmenting instances and improve assignment in cases of partial occlusions. Through detailed evaluation on
public data and comparison with established methods, we show that these aspects improve the segmentation
quality beyond the results offered by other three-dimensional cluster mechanisms. Our algorithm can run at
up to 165 Hz on a 64 channel Velodyne Lidar dataset on a single CPU core.
1 INTRODUCTION
Lidar sensors have been introduced in an ever grow-
ing number of different driver assistance systems to
automotive series production in recent years and are
considered an important building block for the prac-
tical realisation of autonomous driving. Precise seg-
mentation of object instances is an important infor-
mation for a variety of applications ranging from on-
line object detection to offline computer-aided data la-
belling. Lidar sensor data is usually represented as
a three-dimensional point cloud in Cartesian coordi-
nates. Hence it makes sense to consider clustering al-
gorithms to fulfil the task of object segmentation for
this type of sensor. This work presents a Lidar point
cloud segmentation approach, which provides a high
level of accuracy in point cloud segmentation, while
being able to run in real time, faster than the sensor
recording frequencies at a constant rate with very lit-
tle fluctuation independent of the scene’s context. We
a
https://orcid.org/0000-0002-6724-5649
b
https://orcid.org/0000-0003-0290-0371
c
https://orcid.org/0000-0002-0282-5087
∗
This work is a result of the research project @CITY
Automated Cars and Intelligent Traffic in the City. The
project is supported by the Federal Ministry for Economic
Affairs and Energy (BMWi), based on a decision taken by
the German Bundestag. The author is solely responsible for
the content of this publication.
Figure 1: Three-dimensional point cloud with clustered
points. Every Instance is assigned a random colour.
do so by avoiding the creation of a three-dimensional
point cloud from the range measurements provided by
the Lidar scanner and work directly on the laser range
values of the sensor. If not available, the computations
can be applied to a spherical range image projection
of the three-dimensional point cloud and projected
back to the point cloud as demonstrated in Figure 1.
This approach circumvents the problem of sparsity in
the point cloud by forcing a two-dimensional neigh-
bourhood on each measurement and thus offers the
advantage of working with dense, two-dimensional
data with clearly defined neighbourhood relationships
between adjacent measurements. A Python imple-
mentation of our approach runs in real time on a single
Intel
R
Core
TM
i7-6820HQ CPU @ 2.70 GHz core at
a frame rate of up to 165 Hz.
Hasecke, F., Hahn, L. and Kummer t, A.
FLIC: Fast Lidar Image Clustering.
DOI: 10.5220/0010193700250035
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 25-35
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
25

2 RELATED WORK
There is a large number of previous works on Lidar
instance segmentation especially of, but not limited
to, automotive applications. The main focus of most
clustering approaches is on improving segmentation
accuracy and execution time. Most of these separate
objects in the three-dimensional space, result in high
accuracy but comparatively long runtime. Notable ex-
amples are the DBSCAN (Ester et al., 1996), Mean
Shift (Fukunaga and Hostetler, 1975) (Comaniciu and
Meer, 2002) and OPTICS (Ankerst et al., 1999) algo-
rithm.
Other approaches use voxelization to reduce the
complexity of the point cloud and find clusters in the
representation (Himmelsbach et al., 2010) or apply
bird’s eye view projection coupled with the height in-
formation to separate overlapping objects (Korchev
et al., 2013).
(Moosmann et al., 2009) proposed the use of a
local convexity criterion on the spanned surface of
three-dimensional Lidar points in a graph-based ap-
proach. Based on this metric, (Bogoslavskyi and
Stachniss, 2016) used a similar criterion - the spanned
angle between adjacent Lidar measurements in rela-
tion to the Lidar sensor origin - to define the convex-
ity of the range image surface as a measure to seg-
ment objects. They further utilise the neighbourhood
conditions in the range image to achieve the fastest
execution time to date. (Zermas et al., 2017) exploit
the same relationship in scan lines of Lidar sensors to
find break points in each line and merge the separate
lines of channels into three-dimensional objects in a
subsequent step.
Other current methods use machine learning di-
rectly on three-dimensional point clouds (Lahoud
et al., 2019) (Zhang et al., 2020) (Yang et al., 2019),
projections into a camera image (Wang et al., 2019a),
or on spherical projections of Lidar points in the range
image space (Wang et al., 2019b), to segment object
instances in point clouds. These results look very
promising in some cases, but suffer from a longer run-
time, which currently prevents application on embed-
ded automotive hardware.
Related research areas that need to be mentioned
at this point are the semantic segmentation and even
more so the panoptic segmentation of Lidar data. The
dataset “SemanticKITTI”(Behley et al., 2019), which
we use to evaluate our method in 4.2, has advanced
a number of new algorithms in the area of seman-
tic segmentation (Kochanov et al., 2020) (Zhou et al.,
2020) (Zhang et al., a). The task is concerned with the
classification of each Lidar point. Leading algorithms
have achieved great performance on assigning a class
label and some are even real-time capable on a sin-
gle GPU (Tang et al., 2020) (Gerdzhev et al., 2020)
(Cortinhal et al., 2020). The difference to instance
segmentation is the separation of instances. The se-
mantic segmentation does not differentiate between
multiple objects, but assigns the same label to each in-
stance of the same class. The panoptic segmentation
is the combination of the semantic and the instance
segmentation. (Milioto et al., 2020) even manage to
reach real-time capability on a single GPU with a run-
time of 85 ms by jointly segmenting the instances and
the class.
Our method is concerned with the separation of in-
stances independently of the class labels. We base our
approach on the works of Bogoslavskyi and Stachniss
(Bogoslavskyi and Stachniss, 2016) as well as general
three-dimensional Euclidean algorithms (Ester et al.,
1996) (Fukunaga and Hostetler, 1975) (Comaniciu
and Meer, 2002) (Ankerst et al., 1999). We com-
bine the fast execution time of range image clustering
with the precise segmentation of distance thresholds
to connect and separate Lidar points.
3 METHODS
The raw data from Lidar sensors is usually provided
as a list of range measurements, each coupled with
a number relating to the channel and the lateral po-
sition. The two values correspond to the y- and x-
position of the measurements in the range image.
This can also be used to create a three-dimensional
representation of the measurements, but doing so
will increase the computation time for the proposed
method. Therefore, we work directly on the raw two-
dimensional representation.
3.1 Ground Extraction
For object segmentation, we assume that the Lidar is
a part of a ground-based vehicle. Based on this as-
sumption, we want to extract and ignore the points
belonging to the ground plane from the segmentation.
This will prevent the algorithm from connecting two
instances via this plane. Here, a simple height based
threshold is not sufficient, as the road surface itself
can be uneven. Pitching and rolling of the ego vehicle
can also influence the way the ground is perceived in
the sensor data. Since we have detailed information
about the Lidar sensor itself, we can use the angle po-
sition of each given channel to determine the angle in
which the laser beam would hit the surface. We use
this information to exclude all range image values be-
longing to a horizontal plane below a certain height.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
26

Figure 2: Top: Ground segmentation; Blue points represent ground points, red points are not part of the ground.
Bottom: Angle image used to find horizontal surfaces for the ground segmentation.
To do so, we compare each cell of the range image
with the neighbouring one above using the equation
β = arctan (
d
2
· sin α
d
1
− d
2
· cos α
), (1)
in which the selected cell value is d
2
, the one above
the cell is d
1
corresponding to the respective depth
measurement and α is the angle between the two mea-
surements.
As a result, we obtain the image shown in Figure
2 representing the angle values of the Lidar beam in
relation to the point cloud surface spanned between
the current Lidar measurement and the measurement
of the Lidar channel below, (see Figure 3). Using a
lookup table of the channel angles δ
r
with respect to
the channel r, we exclude all range image cells that
span a horizontal surface up to a certain threshold an-
gle θ of ±10
◦
to a full horizontal surface.
To speed up the computation we change the θ
threshold to the tangent of θ to directly compare the
tangent of β. We therefore remove the arctan from the
equation for β, as it is computationally expensive and
can not easily be provided as a lookup table due to
the two float variables d
1
and d
2
. We also provide
the sine and cosine of α as constant pre-calculated
values. The proper handling of the quadrants of the
Euclidean plane usually requires the atan2 function
as opposed to the arctan (and therefore the tangent)
(Bogoslavskyi and Stachniss, 2016). We circumvent
this restriction as the provided depth measurements
are always positive or zero, any zero value is automat-
ically removed as ground/invalid value. These pre-
calculations change the equation for the horizontal
plane estimation to a set of multiplications and each
one division and subtraction:
tan(β) =
d
2
·
Constant
z
}|{
sinα
d
1
− d
2
· cosα
|{z}
Constant
. (2)
This method rejects all horizontal surfaces. To pre-
vent excessive removal of valid measurements from
elevated horizontal surfaces such as car roofs or
hoods, we use a height image, in which the range val-
ues are replaced by the Cartesian z-coordinate in re-
lation to the ego vehicle. We use this image to keep
all horizontal surfaces above a certain height, in the
above case, the line from the wheel position of the ego
vehicle to the maximum possible elevation spanned
by the 10
◦
slope threshold. A comparable metric has
been described by Chu et al. (Chu et al., 2017) al-
though with relative height thresholds, we have de-
cided to use absolute values to reduce the computa-
tion time. Figure 3, top, depicts the relationship of
the channel angles δ
r
(angle in relation to the hori-
zontal 0
◦
line) to the surface angles β
r
(angle of the
tangent of two neighbouring measurements and the
sensor origin).
FLIC: Fast Lidar Image Clustering
27
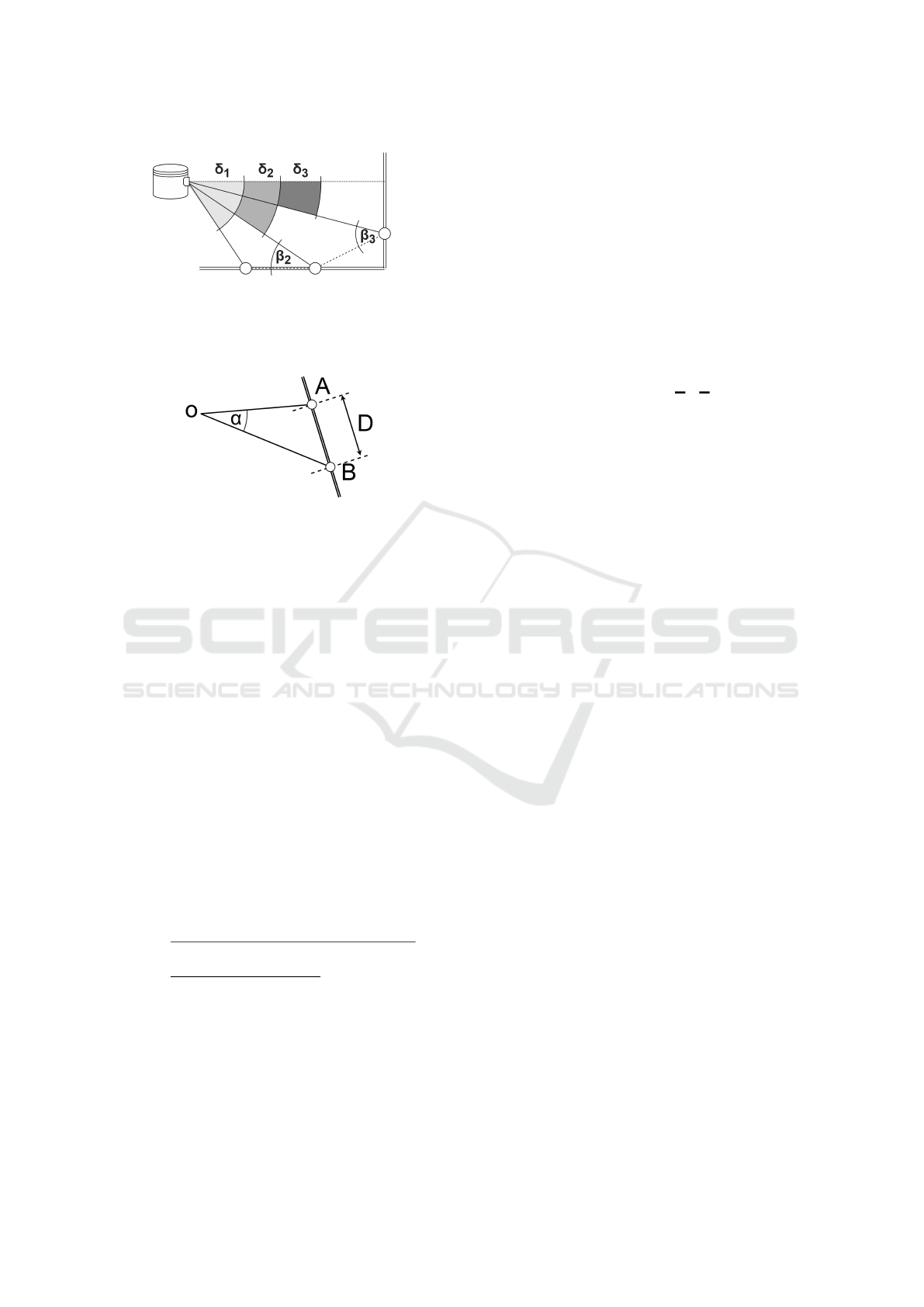
(a) The angle measurement of Lidar points in the
vertical direction is used to define a horizontal ori-
entation for the ground plane extraction. (Note
that there is not β
1
, as the first Lidar channel has
no previous channel, we therefore extend β
2
to the
first channel.)
(b) With the Lidar Sensor in O, the lines OA
and OB show two neighbouring distance measure-
ments. The distance between the two measure-
ments is calculated using the spanned angle α be-
tween the points.
Figure 3: Trigonometric relationships used in the ground
segmentation (a) and the cluster separation (b).
3.2 Clustering
We use a systematic approach to create an object
instance segmentation for Lidar sensor data through
clustering in the image space of the range image. This
approach relies on the removal of the Lidar measure-
ments belonging to the ground plane from the range
image. Inspired by the work of Bogoslavskyi and
Stachniss (Bogoslavskyi and Stachniss, 2016), we ex-
ploit the neighbourhood relationship of adjacent mea-
surements in the range image. As visualised in the
bottom illustration of Figure 3, we compare the given
range values ||OA|| and ||OB|| for each pair of Li-
dar measurements. We apply the cosine law to calcu-
late the Euclidean distance D in the three-dimensional
space using the two-dimensional range image:
D =
q
||OA||
2
+ ||OB||
2
− 2||OA|| · ||OB||cosα
=
q
d
2
1
+ d
2
2
− 2 · d
1
· d
2
cosα.
(3)
The α angle between adjacent Lidar measurements is
required for the calculation and is usually provided
by the manufacturer of the Lidar sensor for both the
horizontal and vertical direction. Using the physi-
cal distance between two measured points, we de-
fine a threshold value between those, which are close
enough together to belong to the same object, or too
far apart to be considered neighbours on the same ob-
ject. The distance of neighbouring points on a given
object is in general relatively close. The distances
of those points in the range image from two sepa-
rate objects are substantially larger. By exclusively
using variables which are given by the range measure-
ments and reducing the computational effort by pre-
calculating the cosine of the given angles, we reduce
the calculation of the squared Euclidean distance to a
total of four scalar multiplications, an addition and a
subtraction:
D
2
= d
1
· d
1
+ d
2
· d
2
− 2 · cos α
| {z }
Constant
·d
1
· d
2
. (4)
These efficient operations are decreasing the runtime
on embedded hardware.
With the calculated threshold between each mea-
surement, we are able to connect all Lidar points in
the range image into separate clusters and background
points. With the use of the Euclidean distance as a
threshold value, we provide a single parameter im-
plementation with a clear physical meaning, which is
adaptable to different sensors.
We reached a good performance with a threshold
of 0.8 metres as the limit for the connections between
two points. This threshold theoretically enables the
clustering of three-dimensional objects with e.g. a
Velodyne HDL-64E up to 114.59 metres before the
measured points are too far apart on a vertical surface.
Horizontally connected components can, in theory, be
detected up to a distance of 509.3 metres which is
more than four times the reliable range for vehicles
of 120 metres, defined by the manufacturer.
3.2.1 Connected-component Labelling
Our approach exploits the vectorised nature of the
range image to apply operations used in image pro-
cessing for different purposes. Specifically, we
redefine the three-dimensional Euclidean clustering
to a two-dimensional connected-component labelling
(CCL) problem. To do so, we create two virtual
copies of the range image and shift one copy over
the x axis and the other one over the y axis. These
shifted images enable us to stack all three images on
a third axis and compare every value with its vertical
and horizontal neighbour over the whole multidimen-
sional array. Thus by using Equation 4 on this image
we calculate the three-dimensional distance between
each point and his vertical and horizontal neighbour-
ing measurement. After applying the threshold on the
resulting distance values calculated for each measure-
ment and its direct neighbourhood, we end up with
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
28
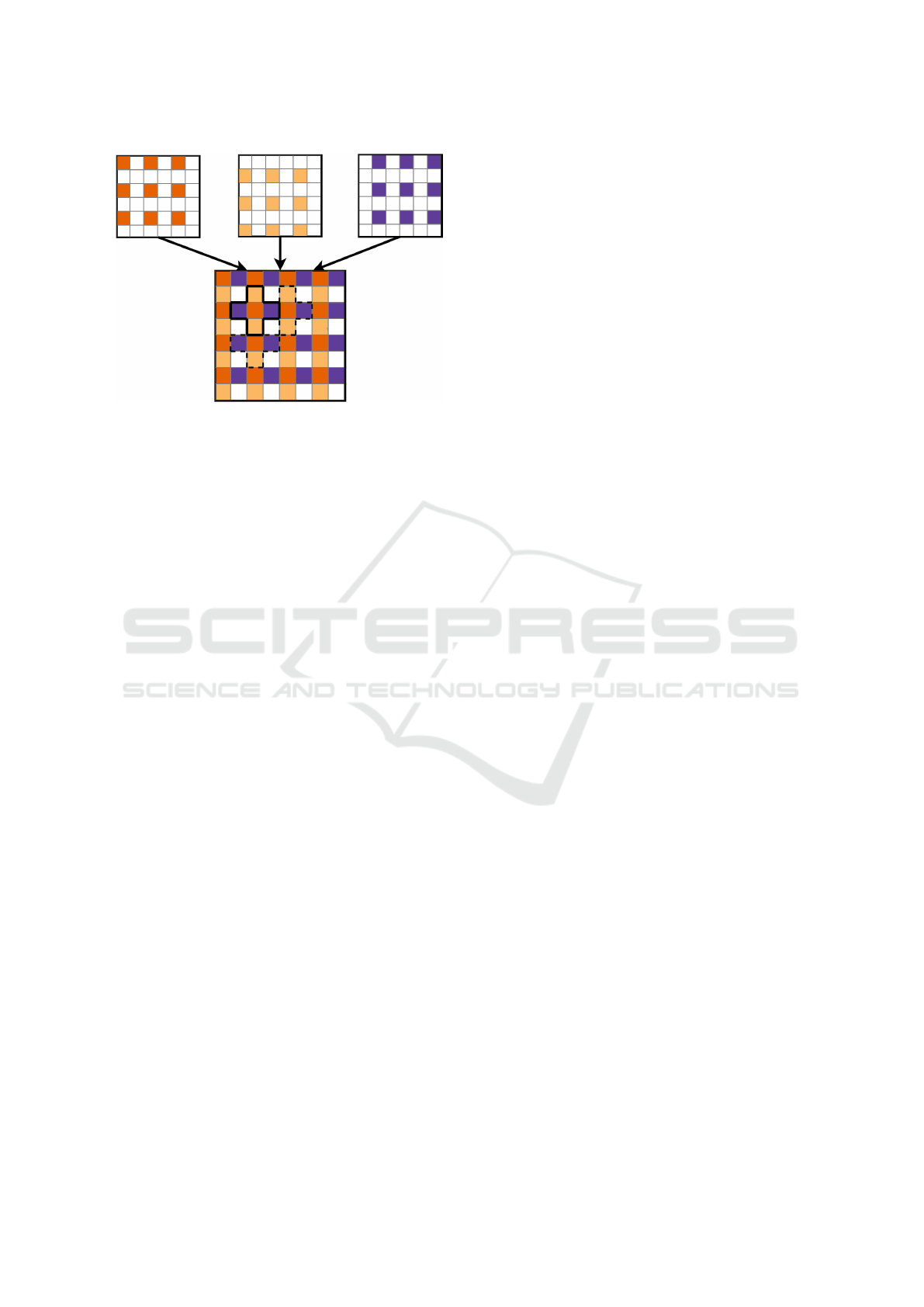
Figure 4: Combination of defined image representations for
instance segmentation. The red squares represent the binary
value of present Lidar measurements, the yellow and blue
squares represent the horizontal and vertical connections of
these measurements respectively.
the original range image and two binary images rep-
resenting the connection or separation between two
points in the range image. The range image is now re-
duced to a binary image representing the presence and
absence of Lidar measurements for the corresponding
pixels in the image.
The three created binary images contain all the
required information to segment the Lidar measure-
ments of the whole frame into clusters and back-
ground points. For this, we utilise a simple and
efficient image processing algorithm; connected-
component labelling. The 4-connected pixel connec-
tivity, also known as von Neumann neighbourhood
(Toffoli and Margolus, 1987), is defined as a two-
dimensional square lattice composed of a central cell
and its four adjacent cells. To apply the pixel connec-
tivity to our data, we combine the binary Lidar mea-
surements with the binary threshold images of the dis-
tances between Lidar points. By arranging these three
images as shown in Figure 4, we are able to apply
CCL algorithms with a 4-connectivity on the resulting
image to label each island of interconnected measure-
ments as a different cluster. The resulting segmented
image is now subsampled to the original range im-
age. Thus we provide the three-dimensional cluster
labels directly from the connected-component image,
as each pixel corresponds to a given Lidar point in the
three-dimensional point cloud.
There is a multitude of CPU-based implemen-
tations for CCL problems most common are the
”one component at a time” (AbuBaker et al., 2007)
and the Two-pass algorithm (Hoshen and Kopelman,
1976). We have decided to use the first method
in the straight-forward implementation of the scipy
library ”label” for n-dimensional images (Virtanen
et al., 2020), as it provides a fast cython based func-
tion. More recent CCL algorithms make use of GPUs
by applying the labels in parallel (Hennequin et al.,
2018) (Allegretti et al., 2019). This can be a very
promising approach, as all previous processing steps
in this work are applied to rasterised images and can
be directly computed in parallel on a GPU. We have
not attempted this approach, as our goal is a real-time
application for CPU-based automotive hardware.
In a subsequent step we apply a threshold on the
labelled clusters for objects below a certain number of
Lidar measurements to reduce false clusters resulting
from noise in the sensor, in our case we decided on
a minimum of 100 points to be considered a cluster
candidate, as our objects of interest are cars, pedestri-
ans and other road users. Lower thresholds are rec-
ommended to include static objects such as poles and
debris on the road.
We have thus segmented the measurements into
connected components of separate objects and non-
segmented points, which correspond to the ground
plane and background noise.
3.2.2 Map Connections
Segmentation algorithms are prone to under- and
over-segmentation, due to the characteristics of Lidar
sensors; namely the sparsity (especially in vertical di-
rection) and missing measurements resulting from de-
flected laser beams, which have no remission value
back to the sensor. Missing values result in missing
connections between areas of the same object, due to
which the direct neighbourhood approach described
above will over-segment a single object into multiple
clusters. Examples of such challenging instances are
shown in Figure 5.
To overcome the limitations of the direct neigh-
bourhood approach and to ensure a more robust seg-
mentation, we have extended the two-dimensional
Euclidean clustering by what we call Map Connec-
tions (MC). For this, we reduce the combined image
shown in Figure 4 to a sparse matrix, connecting only
every n
th
point in the vertical and horizontal direc-
tion, thus connecting a subset of original points. The
schematic visualisation in Figure 6 displays a con-
nection of each measurement with its second neigh-
bour. Due to the known α angle between all measure-
ments, we can extend the Euclidean distance calcu-
lation from each measurement to any other using the
cosine law described in Equation 4, by adjusting the
angle to the given offset. This allows us to robustly
connect segments of the same object, which have no
direct connection due to missing measurements or ob-
struction by other objects in the range image.
FLIC: Fast Lidar Image Clustering
29
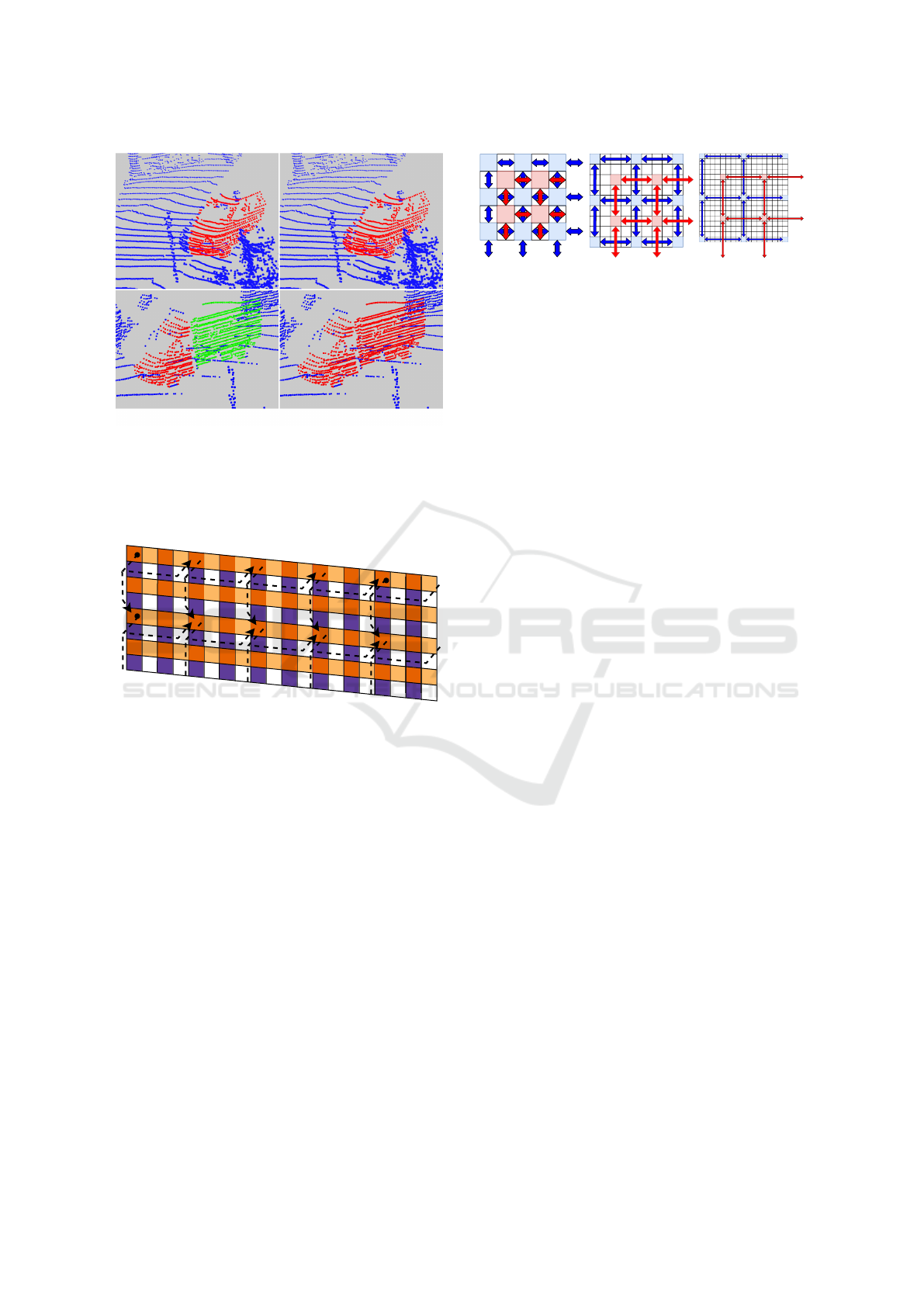
Figure 5: Left: Results using only the direct connectivity
between neighbouring Lidar points. Right: A single addi-
tional MC between every second Lidar measurement. The
proposed MCs enable a more accurate segmentation of the
car (top) and reduce the over-segmentation of partially oc-
cluded objects, as the truck in the bottom images shows.
Figure 6: Additional Map Connections (dotted lines) be-
tween non-neighbouring Lidar points on top of the di-
rect connections to neighbouring points (yellow and blue
squares).
An example of this improved segmentation can be
seen in Figure 5. In the results shown in Section 4
we have added one MC between every second mea-
surement as sketched in Figure 6, 6 MCs as shown
in Figure 7 and 14 MCs along the main diagonal of
the range image. The Maps of reduced point-sets
are smaller than the original point-set and thus re-
quire only a fraction of the computation time on top of
the directly connected clusters. The additional map-
ping of the cluster-ids of the original clusters with
the MCs, results in a slightly increased runtime as
shown in Section 4.1. The combined use of the direct
connectivity of neighbouring measurements and the
MCs enables a pseudo three-dimensional Euclidean
clustering while exploiting the fast runtime of two-
dimensional pixel connectivity. Thus, we are able to
improve the quality of the segmentation without sac-
rificing our real-time ability.
Figure 7: Visualisation of the 6 Map Connection structure
for increasing the connection area with the least amount of
maps.
4 EXPERIMENTAL EVALUATION
The first experimental evaluation measures our meth-
ods ability to run in real time at usual sensor recording
frequencies, while offering a constant processing rate
with very little fluctuation independent of the scene’s
context. The second experiment is mainly concerned
with a quantitative metric of the segmentation quality.
4.1 Runtime
Following the experimental setup of (Bogoslavskyi
and Stachniss, 2016), we designed our first exper-
iment on the provided data by Moosmann et al.
(Moosmann, 2013) to support the claim, that the pro-
posed approach can be used for online segmentation.
All listed methods have been evaluated on the same
Intel
R
Core
TM
i7-6820HQ CPU @ 2.70 GHz.
Figure 8 shows the execution time of the 5 meth-
ods over the 2500 Frames dataset (Moosmann, 2013).
The proposed method runs at an average of 165 Hz
and is therefore faster than the previously fastest al-
gorithm of (Bogoslavskyi and Stachniss, 2016) at 152
Hz, while exhibiting less fluctuation due to the bi-
nary image implementation when used without any
additional MCs. A box-plot of the average runtime
of (Bogoslavskyi and Stachniss, 2016) and the pro-
posed method can be seen in Figure 9, which shows
the fluctuating nature of methods depending on the
scene context, as opposed to ours. As can be seen in
Figure 8, when adding MCs to the proposed methods,
the execution suffers from a slightly longer runtime,
while still running at a frequency of 26 to 105 Hz de-
pending on the number of additional MCs. This is
still between 2.6 to ten times faster than the record-
ing frequency of the used sensor. Please note that we
only used up to 14 MC in this timing. More MCs in-
crease the execution time accordingly and endanger
the real time capability of the proposed method. Im-
plementations of the Map Connection assignment in
an efficient programming language like C++ might
enable the use of more MCs with less influence on
the execution time.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
30
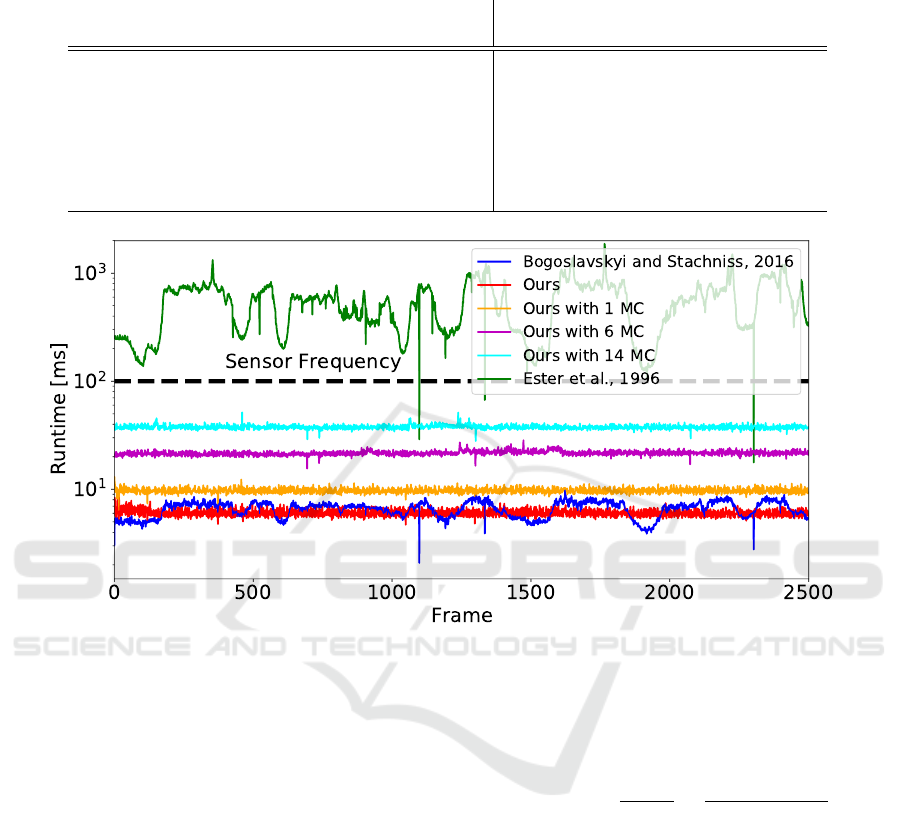
Table 1: Comparison of the segmentation quality using the Intersection over Union and the precision average for the algorithms
of (Bogoslavskyi and Stachniss, 2016), (Ester et al., 1996), and variations of the proposed method.
Method IoU
µ
IoU
µ
P
µ
P
0.5
P
0.75
P
0.95
(No Ground) (Ground)
Bogoslavskyi et al. 73.93 73.93 59.31 83.75 63.52 13.18
Ours 76.20 72.31 63.73 84.30 67.51 22.03
Ours (1 MC) 77.97 73.65 66.68 85.60 70.21 27.19
Ours (6 MC) 81.14 75.48 71.92 88.25 74.99 36.05
Ours (14 MC) 84.25 76.39 74.68 89.75 77.61 40.63
DBSCAN 76.21 72.77 76.50 81.54 76.45 69.25
Figure 8: Frame-wise execution timings on a 64-beam Velodyne dataset (Moosmann, 2013). Please note the logarithmic scale
for the runtime.
4.2 Segmentation Results
For our evaluation, we use the dataset “Se-
manticKITTI” by Behley et al. (Behley et al.,
2019) as object instance segmentation ground truth.
This dataset enriches the KITTI dataset’s (Geiger
et al., 2012) odometry challenge with semantic and
instance-wise labels for every Lidar measurement.
To reduce the influence of the proposed ground
plane extraction in Section 3.1 and focus on the results
of the clustering mechanisms, we have conducted the
evaluation once without the Lidar points of the classes
road, parking, sidewalk, other-ground, lane-marking
and terrain. And a second time without any usage of
the semantic labels by applying the ground extraction
proposed in 3.1 on all methods.
For each ground truth object with at least 100 Li-
dar point measurements, we select each algorithm’s
object cluster output with the most ground truth over-
lap. Using these two lists of points, we calculate
the Intersection over Union (IoU). By averaging these
IoU values of every single instance over all 10 se-
quences, we get the averaged mean IoU
µ
of each algo-
rithm. The IoU or Jaccard Index for a single ground-
truth instance with a single cluster is defined as
J(A, B) =
|A ∩ B|
|A ∪ B|
b=
T P
T P + FP + FN
. (5)
The connection and separation of instances solely
through the distance harbours the risk of under-
segmentation in the case of objects that are in con-
tact or are close by. For this reason, we measure
our results in the subsequent evaluation instance-wise.
If two instances are represented by only one clus-
ter, we count only the object with the higher IoU,
while the second object is marked as not found. We
compute this metric for each algorithm listed below,
over all ten sequences with Lidar instance ground
truth in the dataset. We compare the quality of
our algorithm to the currently fastest algorithm (Bo-
goslavskyi and Stachniss, 2016) as well as a very pre-
cise three-dimensional euclidean clustering algorithm
(Ester et al., 1996). We use scikit-learn’s implemen-
tation of DBSCAN (Pedregosa et al., 2011). If you
FLIC: Fast Lidar Image Clustering
31
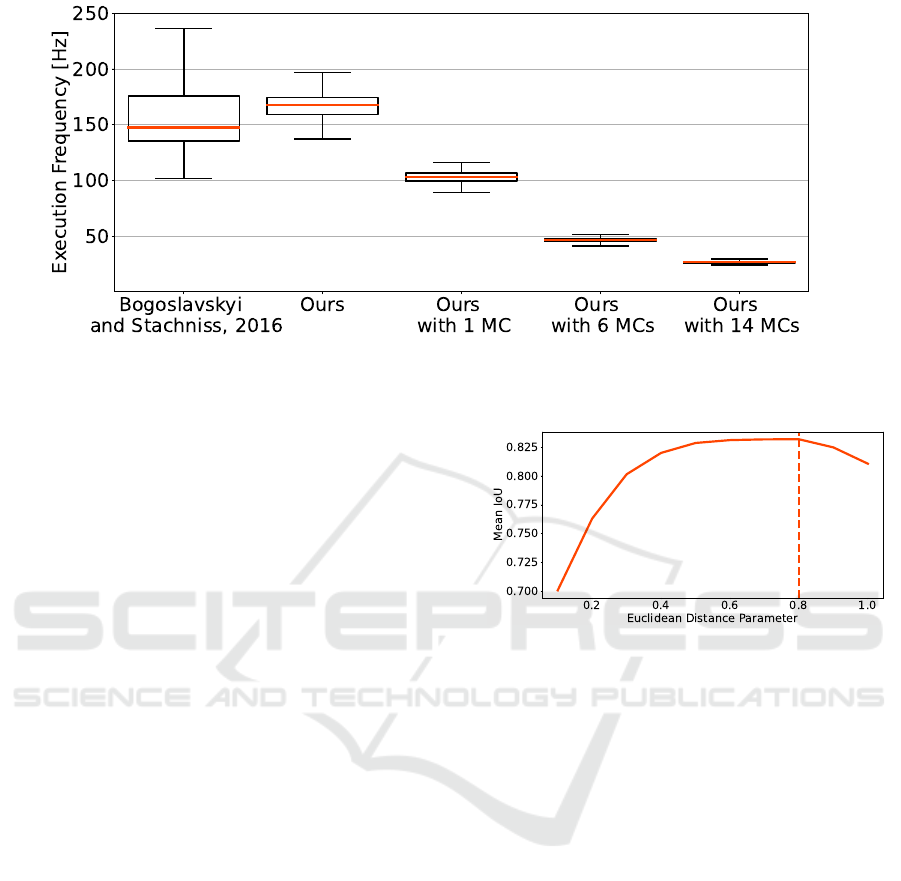
Figure 9: Averaged runtime in Hz for segmenting approximately 2,500 scans from a 64-beam Velodyne dataset (Moosmann,
2013) with our approach and up to 14 Map Connections compared to the method by Bogoslavskyi and Stachniss (Bogoslavskyi
and Stachniss, 2016).
consider the age of this algorithm, it might be sur-
prising to see that it is still used in modern cluster-
ing applications (Zhang et al., b) (Mao et al., 2020)
(Cheng et al., 2019). This long-term relevance was
also confirmed by the ”Test of Time” Award from
ACM SIGKDD (SIGKDD, 2014). The algorithm was
also revisited by the original authors in a follow-up
paper (Schubert et al., 2017) fairly recently to show
the continued relevance in many clustering applica-
tions. Therefore we use the DBSCAN to compare
our pseudo three-dimensional approach to a well per-
forming three-dimensional algorithm.
We present the mean of the IoUs with the best-
performing parameters of each method. With our
threshold parameter set as 0.8m, we outperform (Bo-
goslavskyi and Stachniss, 2016) with the direct neigh-
bourhood implementation without any MCs while ex-
hibiting a faster run-time. This parameter has been set
with an additional experiment on a single log of the
dataset as can be seen in Figure 10. Other Lidar sen-
sors perform better with a higher or lower threshold
depending on the horizontal and vertical resolution of
the Lidar sensor. We recommend to evaluate the eu-
clidean distance parameter for the use of different sen-
sors. On average our method is 8% faster, while the
difference in the respectively longest execution time
of a given frame is 15%. Together with the proposed
MCs between all odd measurements, we manage to
perform higher on the average IoU than the more gen-
eral three-dimensional Euclidean distance clustering
algorithm DBSCAN (Ester et al., 1996), as shown in
Table 1.
Using 6 MCs, we surpass the performance of DB-
SCAN with a larger margin and manage to reach a
noticeably higher mean IoU. A total of 14 MCs out-
performs the three-dimensional DBSCAN algorithm
Figure 10: Parameter study of the maximum distance be-
tween two points, to be considered part of the same cluster.
The dashed line shows the maximum IoU for the evalua-
tion log. The plateau between 0.5m and 0.8m shows a very
broad and robust sweet spot for the proposed method.
on 4 of the 6 shown metrics in Table 1, with an av-
erage execution frequency of 26 Hz it still runs at 2.6
times the sensor frequency. We suspect that the re-
striction to the immediate surroundings of the mea-
surements prevents under-segmentation of separate,
close objects, but still enables the skipping of gaps
on the same object.
Without any MCs we are on average 120 times
faster. With an increasing number of additional MCs
we are 67, 25 and 14 times faster than the DBSCAN
Algorithm. Even if we drastically increase the num-
ber of MCs, our proposed method is at least 14 times
faster than the DBSCAN and remains clearly above
the sensor recording frequency.The run-time increase
does not scale logarithmically as one would expect
with additional MCs (since they apply the same func-
tion to a smaller subset of the original point cloud).
This issue might result from the mapping overhead
caused by our python implementation. We did not
re-implement the method in a different programming
language, as the computation time was still far below
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
32

the sensor frequency and does not bring any further
benefits to do so.
The second column of Table 1 shows, that the pro-
posed ground extraction method of Section 3.1 de-
grades the performance of all listed algorithms, ex-
cept for (Bogoslavskyi and Stachniss, 2016) as the
used metric for the ground segmentation is very sim-
ilar to the cluster separation metric used by Bo-
goslavskyi et al. A better ground separation will
lead to a much better performance for the proposed
method as the IoU values with the ground truth (GT)
ground segmentation show. Improving the ground
separation is therefore critical to improve the instance
segmentation.
For further evaluation of the instance-level per-
formance, we compute the precision similar to (Bo-
goslavskyi and Stachniss, 2016) in a more refined
fashion on the GT ground removed point clouds. We
define 10 bins of point-wise overlap of the GT and
proposed clusters ranging from an IoU of 0.5 to 0.95
in steps of 0.05. We average the precision of all bins
into one single metric score (P
µ
) which is shown in
Table 1 for each method. We additionally list the Pre-
cision for the overlap values of 0.5, 0.75 and 0.95, in
which the definition of a correctly segmented object
is defined as above the denoted IoU. The precision,
which shows how many instances are matched with
an IoU of at least x is therefore defined as
P
x
=
1
N
N
∑
n=0
M
∑
m=0
a
n,m
with a
n,m
=
(
1, if J(n, m) >= x,
0, else.
(6)
for N instances and M clusters in which each in-
stance and cluster are matched via the Jaccard Index
(IoU). Please note, that due to the definition of the
Jaccard Index only one cluster can match a ground
truth instance with an IoU > 0.5.
We show in Table 1, that we match on average
more GT instances than (Bogoslavskyi and Stachniss,
2016) and are close to the mean segmentation preci-
sion of the DBSCAN algorithm. With a higher num-
ber of MCs, we achieve better precision values for
overlap values of 0.5 and 0.75, while the DBSCAN
algorithm matches more instances with higher over-
lap values due to the full three-dimensional clustering
on all points of the dataset.
We only compare up to 14 MCs in order to not
endanger our real-time capability. However, with just
these 14 MCs, we achieve a clustering segmentation
which performs comparable to, and in some regards
better, than the full three-dimensional algorithm. The
high precision values for the lower overlap regions of
0.5 and 0.75 are particularly important in the context
of driver assistance systems, since a missed instance
can lead to dramatic outcomes, as opposed to a not
perfectly matched instance. We further proved, that
the proposed MCs improve the results of our algo-
rithm immensely and help to find otherwise missed
objects.
Attentive readers will notice the performance of
both our method and the method by (Bogoslavskyi
and Stachniss, 2016) drop noticeably in the 0.95 IoU
bracket. We see this issue to be due to the under-
lying data. The “SemanticKITTI” dataset (Behley
et al., 2019) has a pre-applied ego-motion compensa-
tion, due to which the three-dimensional point cloud
is slightly shifted and rotated away from the origi-
nal sensor configuration to compensate the movement
in the 0.1s recording time of a single frame. This
compensation has already been applied to the original
odometry dataset of Geiger et al. (Geiger et al., 2012)
to provide better Lidar odometry for static inter-frame
point cloud matching.
Our method builds on this three-dimensional point
cloud and expects an unaltered version of the Lidar
sensor to enable a one-to-one matching of the three di-
mensional points to the two-dimensional range image
representation. This can not be fully achieved with
this ego-motion compensated data and results in miss-
ing and wrongly assigned points and in turn hurts our
performance in the 0.95 IoU bracket, which requires
a precise projection. We see the same drop amplified
in the range-image based algorithm of (Bogoslavskyi
and Stachniss, 2016), while the DBSCAN algorithm
runs directly on the manipulated three-dimensional
data and does not suffer from this restriction.
5 CONCLUSION
We have presented an algorithm for real-time instance
segmentation of Lidar sensor data using raw range
images to connect points by their three-dimensional
distance. To make this approach more robust against
over-segmentation, we introduced what we call Map
Connections, which use the larger neighbouring con-
text for a more precise assignment of measured points
to an instance, especially in cases of partial occlusion.
These properties of our method facilitate the preserva-
tion of three-dimensional information in the measure-
ments when reduced to a two-dimensional represen-
tation for fast computation.
In a detailed evaluation, we have shown, that our
approach is faster than comparable state-of-the-art
methods, while being more stable in its runtime, and
more importantly, providing an overall better perfor-
FLIC: Fast Lidar Image Clustering
33

mance in instance segmentation. The experiments
show, that not only our accuracy in separating ob-
jects is higher than comparable fast approaches, but
we are able to match most ground truth instances
with a significant overlap of the ground truth. This
is particularly important in the context of driver as-
sistance systems, since a missed instance is a bigger
problem than an object that was not matched with all
Lidar points. We have also illustrated, that the pro-
posed MCs improve the results of our algorithm and
help to find otherwise missed objects. The further
use of segmented point clouds for classification and
to remove false positives, is outside the scope of this
work. However, this application has previously been
researched by (Hahn et al., 2020) and shows promis-
ing results.
REFERENCES
AbuBaker, A., Qahwaji, R., Ipson, S., and Saleh, M. (2007).
One scan connected component labeling technique.
In 2007 IEEE International Conference on Signal
Processing and Communications, pages 1283–1286.
IEEE.
Allegretti, S., Bolelli, F., Cancilla, M., and Grana, C.
(2019). A block-based union-find algorithm to la-
bel connected components on gpus. In International
Conference on Image Analysis and Processing, pages
271–281. Springer.
Ankerst, M., Breunig, M. M., Kriegel, H.-P., and Sander, J.
(1999). Optics: ordering points to identify the cluster-
ing structure. ACM Sigmod record, 28(2):49–60.
Behley, J., Garbade, M., Milioto, A., Quenzel, J., Behnke,
S., Stachniss, C., and Gall, J. (2019). Semantickitti:
A dataset for semantic scene understanding of lidar
sequences. In Proceedings of the IEEE International
Conference on Computer Vision, pages 9297–9307.
Bogoslavskyi, I. and Stachniss, C. (2016). Fast range
image-based segmentation of sparse 3d laser scans
for online operation. In 2016 IEEE/RSJ International
Conference on Intelligent Robots and Systems (IROS),
pages 163–169. IEEE.
Cheng, H., Li, Y., and Sester, M. (2019). Pedestrian group
detection in shared space. In 2019 IEEE Intelligent
Vehicles Symposium (IV), pages 1707–1714. IEEE.
Chu, P., Cho, S., Sim, S., Kwak, K., and Cho, K. (2017). A
fast ground segmentation method for 3d point cloud.
Journal of information processing systems, 13(3).
Comaniciu, D. and Meer, P. (2002). Mean shift: A robust
approach toward feature space analysis. IEEE Trans-
actions on pattern analysis and machine intelligence,
24(5):603–619.
Cortinhal, T., Tzelepis, G., and Aksoy, E. E. (2020). Sal-
sanext: Fast semantic segmentation of lidar point
clouds for autonomous driving. arXiv preprint
arXiv:2003.03653.
Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).
A density-based algorithm for discovering clusters in
large spatial databases with noise. In Kdd, volume 96,
pages 226–231.
Fukunaga, K. and Hostetler, L. (1975). The estimation of
the gradient of a density function, with applications in
pattern recognition. IEEE Transactions on informa-
tion theory, 21(1):32–40.
Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready
for autonomous driving? the kitti vision benchmark
suite. In 2012 IEEE Conference on Computer Vision
and Pattern Recognition, pages 3354–3361. IEEE.
Gerdzhev, M., Razani, R., Taghavi, E., and Liu, B. (2020).
Tornado-net: multiview total variation semantic seg-
mentation with diamond inception module. arXiv
preprint arXiv:2008.10544.
Hahn, L., Hasecke, F., and Kummert, A. (2020). Fast ob-
ject classification and meaningful data representation
of segmented lidar instances. 23rd IEEE Interna-
tional Conference on Intelligent Transportation Sys-
tems (ITSC).
Hennequin, A., Lacassagne, L., Cabaret, L., and Meunier,
Q. (2018). A new direct connected component label-
ing and analysis algorithms for gpus. In 2018 Con-
ference on Design and Architectures for Signal and
Image Processing (DASIP), pages 76–81. IEEE.
Himmelsbach, M., Hundelshausen, F. V., and Wuensche,
H.-J. (2010). Fast segmentation of 3d point clouds for
ground vehicles. In 2010 IEEE Intelligent Vehicles
Symposium, pages 560–565. IEEE.
Hoshen, J. and Kopelman, R. (1976). Percolation and clus-
ter distribution. i. cluster multiple labeling technique
and critical concentration algorithm. Physical Review
B, 14(8):3438.
Kochanov, D., Nejadasl, F. K., and Booij, O. (2020). Kpr-
net: Improving projection-based lidar semantic seg-
mentation. arXiv preprint arXiv:2007.12668.
Korchev, D., Cheng, S., Owechko, Y., et al. (2013). On
real-time lidar data segmentation and classification. In
Proceedings of the International Conference on Im-
age Processing, Computer Vision, and Pattern Recog-
nition (IPCV), page 1. The Steering Committee of The
World Congress in Computer Science, Computer . . . .
Lahoud, J., Ghanem, B., Pollefeys, M., and Oswald, M. R.
(2019). 3d instance segmentation via multi-task met-
ric learning. In Proceedings of the IEEE International
Conference on Computer Vision, pages 9256–9266.
Mao, J., Xu, G., Li, W., Fan, X., and Luo, J. (2020).
Pedestrian detection and recognition using lidar for
autonomous driving. In 2019 International Confer-
ence on Optical Instruments and Technology: Opti-
cal Sensors and Applications, volume 11436, page
114360R. International Society for Optics and Pho-
tonics.
Milioto, A., Behley, J., McCool, C., and Stachniss, C.
(2020). LiDAR Panoptic Segmentation for Au-
tonomous Driving.
Moosmann, F. (2013). Interlacing self-localization, mov-
ing object tracking and mapping for 3d range sensors,
volume 24. KIT Scientific Publishing.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
34

Moosmann, F., Pink, O., and Stiller, C. (2009). Segmen-
tation of 3d lidar data in non-flat urban environments
using a local convexity criterion. In 2009 IEEE Intel-
ligent Vehicles Symposium, pages 215–220. IEEE.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Schubert, E., Sander, J., Ester, M., Kriegel, H. P., and Xu,
X. (2017). Dbscan revisited, revisited: why and how
you should (still) use dbscan. ACM Transactions on
Database Systems (TODS), 42(3):1–21.
SIGKDD, A. (2014). 2014 sigkdd test of time
award. https://www.kdd.org/News/view/2014-sigkdd-
test-of-time-award.
Tang, H., Liu, Z., Zhao, S., Lin, Y., Lin, J., Wang, H., and
Han, S. (2020). Searching efficient 3d architectures
with sparse point-voxel convolution. arXiv preprint
arXiv:2007.16100.
Toffoli, T. and Margolus, N. (1987). Cellular automata ma-
chines: a new environment for modeling. MIT press.
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.,
Reddy, T., Cournapeau, D., Burovski, E., Peterson,
P., Weckesser, W., Bright, J., et al. (2020). Scipy
1.0: fundamental algorithms for scientific computing
in python. Nature methods, 17(3):261–272.
Wang, B. H., Chao, W.-L., Wang, Y., Hariharan, B., Wein-
berger, K. Q., and Campbell, M. (2019a). Ldls: 3-d
object segmentation through label diffusion from 2-
d images. IEEE Robotics and Automation Letters,
4(3):2902–2909.
Wang, Y., Yu, Y., and Liu, M. (2019b). Pointit: A fast
tracking framework based on 3d instance segmenta-
tion. arXiv preprint arXiv:1902.06379.
Yang, B., Wang, J., Clark, R., Hu, Q., Wang, S., Markham,
A., and Trigoni, N. (2019). Learning object bounding
boxes for 3d instance segmentation on point clouds. In
Advances in Neural Information Processing Systems,
pages 6740–6749.
Zermas, D., Izzat, I., and Papanikolopoulos, N. (2017). Fast
segmentation of 3d point clouds: A paradigm on li-
dar data for autonomous vehicle applications. In 2017
IEEE International Conference on Robotics and Au-
tomation (ICRA), pages 5067–5073. IEEE.
Zhang, F., Fang, J., Wah, B., and Torr, P. Deep fusionnet for
point cloud semantic segmentation.
Zhang, F., Guan, C., Fang, J., Bai, S., Yang, R., Torr, P., and
Prisacariu, V. (2020). Instance segmentation of lidar
point clouds. ICRA, 4(1).
Zhang, S., Di Wang, F. M., Qin, C., Chen, Z., and Liu, M.
Robust pedestrian tracking in crowd scenarios using
an adaptive gmm-based framework.
Zhou, H., Zhu, X., Song, X., Ma, Y., Wang, Z., Li, H., and
Lin, D. (2020). Cylinder3d: An effective 3d frame-
work for driving-scene lidar semantic segmentation.
arXiv preprint arXiv:2008.01550.
FLIC: Fast Lidar Image Clustering
35
