
Imperfect Oracles: The Effect of Strategic Information on Stock Markets
Miklos Borsi
a
Department of Computer Science, University of Bristol, Bristol, U.K.
Keywords:
Economic Agent Models, Multi-Agent Systems, Stock Markets.
Abstract:
Modern financial market dynamics warrant detailed analysis due to their significant impact on the world. This,
however, often proves intractable; massive numbers of agents, strategies and their change over time in reaction
to each other leads to difficulties in both theoretical and simulational approaches. Notable work has been done
on strategy dominance in stock markets with respect to the ratios of agents with certain strategies. Perfect
knowledge of the strategies employed could then put an individual agent at a consistent trading advantage.
This research reports the effects of imperfect oracles on the system - dispensing noisy information about
strategies - information which would normally be hidden from market participants. The effect and achievable
profits of a singular trader with access to an oracle were tested exhaustively with previously unexplored factors
such as changing order schedules. Additionally, the effect of noise on strategic information was traced through
its effect on trader efficiency.
1 INTRODUCTION
A line of research was started by Vernon Smith’s ex-
periments in a paper (Smith, 1962) studying the trad-
ing behaviour of humans and allocative efficiency of
the market as a whole in a Continuous Double Auc-
tion, the style of market mechanism used in almost all
financial exchanges around the world. This work was
groundbreaking for its experimental approach to eco-
nomic theory which previously often held unclear or
inaccurate prior beliefs about its claims. For example,
the number of participating agents in a double auction
that achieves a good equilibrium was defined as “nu-
merous” or with the common mathematical approx-
imation “close to infinite”. In the real, reproducible
situation however, the “invisible hand” of the market
was shown to be in effect from as little as 8 agents, 4
buyers and 4 sellers, who were also untrained for the
situation.
Initial work by Gode and Sunder (Gode and Sun-
der, 1993) indicated that traders with practically zero
intelligence - but some constraints - can produce the
invisible hand effect as well. This was later proven by
Cliff to be a mere byproduct of the underlying proba-
bility distribution and the supply-demand curves used
(Cliff and Bruten, 1997).
Cliff proposed an algorithm called Zero Intel-
ligence Plus that emulated the previous attempt to
a
https://orcid.org/0000-0002-2185-7404
make a minimally intelligent trading algorithm. In
IBM’s 2001 experiments (Das et al., 2001) algo-
rithmic traders were able to outperform humans and
made 7% more profit on average. The algorithms in-
cluded ZIP, Kaplan’s Sniper and Gjerstad-Dickhaut
(Gjerstad and Dickhaut, 1998) (Tesauro and Bredin,
2002) (Rust et al., 1992) (Rust et al., 1994).
The next addition to the algorithmic roster came in
2008 with Vytelingum’s paper on the Adaptive Ag-
gressive trading strategy (Vytelingum, 2006), which
has been shown to be dominant over human traders in
every scenario.
The introductory study claimed that it is dominant
over the other algorithms previously mentioned but
that claim has not fully held up in subsequent research
by other authors. Different ratios of trading agents
in the market lead to different strategies being dom-
inant. It is not enough to pit two algorithms against
each other in varying ratios and declare a winner if
all pairwise scenarios are one-sided. One must con-
sider the entire trading environment with other traders
and strategies in the background, as well as different
market conditions - changes in supply or demand over
time or a shift in price. See (Snashall and Cliff, 2019)
for a more detailed discussion of when and why AA
does not always dominate.
The simulations discussed in this paper are
based on (Cliff, 2018), available on GitHub at
https://github.com/davecliff/BristolStockExchange.
Borsi, M.
Imperfect Oracles: The Effect of Strategic Information on Stock Markets.
DOI: 10.5220/0010198201970204
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 197-204
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
197

1.1 An Argument for Strategic Analysis
There is a constant stream of research aimed at dis-
cerning market trends and the effects of various real-
world phenomena on them. While this is a useful pur-
suit in general, there is an argument for taking a dif-
ferent approach to market dynamics.
An intuitive approach to the research hypothe-
sis would be as such: imagine a rock-paper-scissors
game played by thousands. If one particular player
were to know that 60% of the other players always
show rock, said knowledgeable player would adapt
their strategy to show more papers and such on aver-
age win more matches.
Of course, this is an extremely simplified view.
Stock markets have many more variables, informa-
tion and more complex strategies. These strategies
often adapt to market conditions every second. Yet
still, past research has shown that in certain condi-
tions, certain algorithms are dominant over other al-
gorithms. If one agent was given information about
what algorithms the others were following - but not
their internal variables - could they reliably pick a
dominant algorithm for themselves? And would the
addition of another agent into the trader pool lessen
this dominant algorithm advantage?
The research hypothesis was that if traders were
in possession of perfect strategic information, then
they would be able to significantly outperform other
traders not in possession of said information, in a ma-
jority of cases. In addition, this advantage was ex-
pected to decrease once noise is added to the infor-
mation.
The high-level objective of this research project
was to establish an upper bound for profit gained from
strategic information in a market and analyse the loss
in profit from noise in the information. Specifically,
the aims were:
1. Establish an upper bound for advantage gain-able
from perfect knowledge of the strategies used by
other traders in a stock market.
2. Introduce noise to the strategic information
through a prediction simulation with a distorted
trader strategy ratio.
3. Map the severity of the noise to the loss in advan-
tage.
4. Examine the underlying trader ratio dynamics.
5. Check the effect of different order schedules on
occurring phenomena.
2 EXPERIMENTS
This section will explain the approach taken
to experiment design, focusing on what factors
were accurately measured and what other factors
may influence the results. All parameters af-
fecting the simulation are shown and discussed,
and the code is available online on GitHub at
https://github.com/borsim/imperfect oracles for easy
reproducibility. As previously mentioned, all possible
combinations of traders have been tried, with some
constraints. Combinations included at least 1 of each
trader type and had an equal number of buyers and
sellers for each strategy. These experiments are novel
in the way that they focus on two previously unex-
plored factors in stock market dynamics: dynamic and
varied supply/demand schedules; and strategic infor-
mation. Neither of these factors was previously indi-
vidually tested in depth and their combination brings
additional interactions to be discussed as well.
2.1 Strategic Information
Strategic information is at the core of the research hy-
pothesis; it was tested exhaustively. Every single pos-
sible combination of the discussed four trading algo-
rithms was simulated for every order schedule. This
ensured a good coverage of all possible scenarios of
strategies in the market. Trader ratios of higher granu-
larity that are not directly mapped out by these experi-
ments may be approximated by interpolating from the
closest ratio points.
2.2 Supply/Demand Schedules
Supply/demand schedules cannot be exhaustively
tested: the number of possibilities is dependent on
multiple potentially infinite variables. To produce
a good coverage of scenarios a randomization ap-
proach was taken. Order schedules were crafted from
a multi-dimensional space. They were composed of
a number of sub-schedules, each with its own set of
parameters. The only constraint was that supply and
demand schedules do not change independently; sub-
schedules on the supply and demand side were re-
spectively equally long in duration. The number of
dimensions in this space varied based on the first ran-
domized parameter, the number of sub-schedules.
Simulations were run for a number of timesteps.
Each timestep allowed each trader to act and react
once, issue orders and update internal values. The full
duration was divided into intervals - this controlled
the frequency of customer order replenishment and
change cycles.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
198

• Drawn once per order schedule:
– Number of sub-schedules (integer)
– Duration of sub-schedules (integer)
– Time mode (set of possible values)
• Drawn once per sub-schedule:
– Volatility (integer)
– Midprice change (integer)
– Step mode (set of possible values)
The full order schedules were crafted with the se-
quence of steps shown in Algorithm 1.
2.2.1 General Experiment Parameters
Simulations were ran for 240 timesteps, split into at
most 8 intervals of 30 steps. These intervals each con-
tained orders arriving to the traders. Orders prices in
this interval averaged 100 ± 40, with each individual
order being at most 60 away from the midprice. The
timing of the orders is set by the deployment function.
The market contained a total of 32, 16 buy-only and
16 sell-only agents. Every possible combination of
traders was tried for 100 random schedules.
• Time Parameters: duration: 240, interval: 30,
maximum number of sub-schedules: 8
• Order Schedule Parameters: midprice: 100,
maximum volatility: 60, maximum midprice
change: 40
• Order Deployment Parameters: stepmode:
fixed/jittered/random, timemode: periodic/drip-
poisson/drip-jittered/drip-fixed
• Trader Parameters: number of buyers: 16, num-
ber of sellers: 16
• Simulation Parameters: number of order sched-
ules: 100, trials for a given trader combination and
given schedule: 1
2.3 Establishing the Baseline
The first experiment established a baseline, a clear
limit for the maximum possible efficiency/profit
achievable by a trader with access to a perfect ora-
cle providing information about the strategies of other
market participants. See Figure 1 for an overview of
the experiment design.
A “control group” market simulation was per-
formed for a given order schedule and a given com-
bination of traders. The simulation returns the aver-
age profit achieved by traders of particular types. This
serves as the oracle. The trader type with the highest
average profit was deemed “dominant”. There was
Algorithm 1: Creating series of random order sched-
ules.
Draw timemode with even probability from
{periodic, drip − poisson, drip −
jittered, drip − f ixed}
Draw # of sub-schedules with even
probability from {1, 2, ..., max schedules}
for (num intervals -
max schedules) do
Extend an evenly drawn random
sub-schedule’s duration by
interval length
end
supply schedules = {}
demand schedules = {}
for num schedules do
for {supply-side, demand-side} do
Draw volatility with even probability
from {0, 1, ..., max volatility}
Draw midprice change with even
probability from {mid price −
max change, ..., mid price +
max
c
hange}
Draw stepmode with even probability
from { f ixed, random, jittered}
Set price range lower bound to
mid price + mid price change −
volatility
Set price range upper bound to
mid price + mid price change +
volatility
Set schedule step mode to the
random step mode Set sub-schedule
duration to value calculated before
the loop
end
Append sub-schedule to respective list
end
return order schedule = {timemode,
supply schedules, demand schedules}
no distinction between buyers and sellers for the pur-
poses of strategy dominance, their account balances
were pooled to obtain the average. An additional
trader of this dominant type was added to the buyer
and the seller pool - this was to take into account the
effect of an intelligent agent on the market. Simulat-
ing a market then counting the best outcome will be,
simply put, the best. Simulating a market and slightly
changing the conditions this way will show if the ob-
servations have actionable value and whether some-
thing optimal in one setting could remain close to op-
timal in another.
The second simulation was performed with the
Imperfect Oracles: The Effect of Strategic Information on Stock Markets
199

Figure 1: Design of Experiment 1.
thusly expanded pool, this time to obtain the real data.
Between the two simulations trader strategy ratios
and overall supply/demand patterns were shared. Par-
ticular orders may be different if the stepmode con-
tained randomness - i.e. it was not fixed. The se-
quence of order arrivals may also differ.
The expected result of the experiment was that
traders following the optimal strategy determined in
the control simulation would usually dominate in the
repeated simulation. The concrete amount of profit
earned of course depended on the supply/demand
schedule the simulation was performed with. For this
reason the target end result of the experiment was a
ratio; a multiplier on the average trader’s profit.
2.3.1 Results of Experiment 1
The results of Experiment 1 can be viewed in this rep-
resentation on Figure 2. It shows a comparison of how
the strategy predicted as dominant fared in the sec-
ond simulation with the expanded trader pool. The
axes mark the gross average profit per trader of the
predicted dominant type and the colour of points in-
dicates which strategy it is. For added visibility the
“breakeven line” is also plotted - on this line the pre-
dicted best type trader earned exactly as much as the
market average.
The data confirmed the abovementioned expecta-
tions. A number of points fell below the breakeven
line but the majority are above and the data could be
reasonably fit on a line. Predicting the best strategy
would, indeed, on average keep a trader above market
average.
2.4 Experiment 2
Experiment 2 attempted to measure the effect of the
noise described in the experiment design section. A
similar overall design was adopted for Experiment 2.
The significant difference was the presence of a dis-
tortion between the prediction and the actual test ra-
Figure 2: Overall results of Experiment 1.
tios. Additionally, the number of order schedules and
trader combinations varied; this was only a numerical
difference and does not have an effect on methodol-
ogy.
Experiment 2 was not immediately conclusive.
Smaller scale trials were run first to confirm the pres-
ence (or lack thereof) of correlation before com-
mitting a large amount of computational resources.
Methodology was then adapted to reduce the noise in
the resulting data. Finally a large trial was performed
to provide more accurate numerical output showcas-
ing the merit of the previous changes. All components
of Experiment 2 had the market session duration ex-
tended from 240 to 330 timesteps.
2.4.1 Definition of Noise Used in this Experiment
One could have selected a different definition of noise
and it would not influence the validity of the results
derived here. It is possible to conduct analysis on
different noise patterns by looking purely at the data
points and connecting any two as a prediction and re-
sult into a different noise definition. The particular
noise function for this research was chosen for sim-
plicity and intuitive ease. It is parametrized by a sin-
gle parameter p. Each trader in the “real” point has p
probability of being viewed as one following a strat-
egy that is not the same as their true strategy. The
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
200

“mistaken” strategy is chosen with an even probabil-
ity from the strategies present in the market, exclud-
ing the “true” strategy. As such p scales the expected
distance of the prediction point from the real point
and the direction was chosen uniformly from the set
of available points. By this definition maximum noise
was achieved when all traders have an equal probabil-
ity of being seen as any strategy.
p
max
= 1 − (
1
|S|
)
where S is the set of possible strategies and |S| denotes
the number of elements in S.
2.4.2 Inconclusive Trial
The first trial closely followed Experiment 1. It also
involved 100 random order schedules. Each order
schedule was assigned a noise p with the first hav-
ing 0%, the second 0.75% following to the 100th hav-
ing (75 − 0.75)% and each of these schedules had all
trader combinations trialed once. The line fit coeffi-
cient was less than 0.0003 away from horizontal and
visual observation did not reveal strong trends that
were covered with noise or outliers. This means that
there was no evidence that in this case the prediction
conferred a valuable piece of information.
The number of incorrect predictions - cases where
the predicted best type did not earn the highest aver-
age profit - was expected to have an upwards slope as
noise in the prediction ratios increased. While it did
have an upwards slope, the data surrounding it was
very noisy and the change itself was fairly small com-
pared to the full set. With a coefficient of 0.01, at the
highest noise level (where on average each trader is
assigned a type through a roll of a 4 sided die) on av-
erage 7.5 more incorrect predictions were made. This
was a change of 1.5% when in the context of a full
set of 455 prediction-result pairs, the change being a
result of going from zero noise to the maximum possi-
ble noise. Combined with the previous result on prof-
its this suggested that these predictions are just not
particularly good. Over half of them were incorrect
from the outset.
2.4.3 Reduced Randomness in Order Schedules
A followup mini-experiment aimed to check whether
the randomisation of order schedules had too much of
an effect on the outcomes of the previous, inconclu-
sive trial. For this experiment the order schedule was
set to a very simple base case reminiscent of those of
Vernon Smith. The supply and demand ranges had
equal limits, prices were allocated at even steps in
these ranges and resupplied to all traders periodically.
Save for the order-trader allocations and the order of
incoming orders from the set everything else was de-
terministic. This schedule was similarly sampled at
10 distinct noise probabilities.
The line’s slope coefficient was −0.001 (per 1%
of probability). While this was an order of magnitude
greater than that of the previous experiment it was still
lacking the expected, slightly more marked decrease.
While the overall number of incorrect predictions was
lower in the very simple and deterministic schedule,
the environment was still noisy and the smaller num-
ber of points in this mini-experiment even produced a
downward trend. Considering how poor the fit was it
should just be regarded as no evidence for a correla-
tion.
2.4.4 Averaged Samples
The next mini-experiment focused on the low predic-
tion accuracy shown so far. It sampled the simple
order schedule at 10 evenly spaced probabilities and
introduced a large change in how predictions were
made. More than one prediction was made each time -
in this case, 10. The predicted best trader was the one
that has the highest average profit in the sum of the 10
predictions combined. The real data trials were done
in a similar fashion; the final value for a prediction-
real pair was the average profit in the 10 trials. Note
that each prediction used the same (noisy) trader ratio
combination. Trader ratios were not re-randomized
in-between predictions.
As a result of these changes the range of profits
was much narrower. Because multiple trials were av-
eraged with a simple mean calculation that is linear
in its treatment of outliers, the averaged values were
lower as well when contrasted to the least-squares fit
of the previous dataset. The data was far more com-
pact with a range of just 0.5 − 3 instead of 0 − 10,
indicating significantly improved prediction accuracy.
Instead of profit multiplier values of 5 and beyond, no
single averaged-trial went above 2.5. However, the
slope of the profit line was still very close to hori-
zontal with a coefficient of 0.001. Despite that, this
coefficient was objectively a more useful value due to
how the narrower and more regular data range led to a
stronger implication of a cause and effect rather than
random noise.
Prediction accuracy further supports the above ar-
gument. The previous prediction accuracy line fit is
of very poor quality and as such exact metrics like
the residuals of the fit were meaningless in context.
The line fit of this experiment, however, was far bet-
ter. It shows the expected clear upward trend - more
noise in the prediction resulted in more wrong pre-
dictions. This trend was also significantly higher in
Imperfect Oracles: The Effect of Strategic Information on Stock Markets
201

impact than the previous existing trends. Going from
277 wrong predictions at no noise to 297 at maximum
noise it nearly tripled the previous prediction error
change with a better fit.
For the large scale simulation repeated predictions
and real trials appeared to be a must.
2.4.5 Large-scale Experiment: Repeated
Predictions & Randomized Schedules
One additional change was made in addition to the
previously discussed ones. Due to its low perfor-
mance and unlikeliness of being the best on its own
merit, SNPR traders were taken out of the pool of pos-
sibilities. This resulted in a number of changes to the
starting parameters of the simulation:
• The total number of participating traders de-
creased with the number of available strategies to
4 ∗ 3 = 12 for the prediction trials and 12 + 2 for
the real trials
• The total number of possible trader combinations
dropped from 455 to 55
• The maximum possible noise probability lowered
to 66.6%
Due to how passive and nonadaptive SNPR traders
have proven to be, this change had an additional bene-
ficial effect. The three advanced algorithms were now
in closer contest with fewer bystanders, meaning that
the profit ratio being measured is closer to 1. Previ-
ously all of them had a fair amount of extra profit just
by taking advantage of bad SNPR trades.
This large trial was done on 10 different and ran-
domized order schedules. In one of the schedules
the randomizer produced an unfavourable schedule,
resulting in few to none trades in most of the trials
and as such the data from that was discarded. The
other schedules were tested at 14 distinct noise prob-
abilities in the range of 0% − 65% with increments
of 5%. Each probability point was tested for all 55
trader combinations and each trader combination had
a set of 50 prediction subtrials and 50 real subtrials.
Before the summaries relating to the main hypoth-
esis of this research are presented, a slight correction
in evaluation methods must be made. Previous, less
exhaustive experiments did not show the phenomena
presented below in an impactful way when plotting
profit so the credibility of using least squares line fits
for them has not changed. For this subsection how-
ever, the least squares fit on its own was no longer
an accurate enough tool. The market average profit
should, under every condition, stay constant. In cases
where a line fit would indicate this not being the case,
the line fit is wrong. The market average does not
change with noise and it was taken from all trader
combinations equally for each probability. The target
of analysis is the difference in slopes between the two
lines of market average and enhanced trader average.
Analysis of cases where the market average was not
flat was problematic - though less so than it appears
due to the comparison being point-wise rather than
line-wise. Still, the least-squares fit in some complex
schedules should be taken with a grain of salt.
The observed phenomena still hinted at being the
closest to fitting on a line. Fits of higher degree poly-
nomials were attempted but the higher-rank coeffi-
cients were close to 0. Even after increasing pre-
diction accuracy some outlier removal steps still had
to be taken, especially with the re-inclusion of more
complex order schedules. The data range has a com-
plex structure with traders sometimes earning extraor-
dinarily high profits - outliers on the upper end were
far more common than those on the lower end. Out-
liers were removed with a method common in statis-
tics but with slightly different parameters. Generally,
points outside 1.5 times the inter-quartile range are
considered outliers. For the purposes of not losing
too much important data - it should be noted that even
these outliers awerere a result of 50 + 50 individual
data points - this interquartile range requirement was
loosened. The central range was the interdecile range
(between 10% and 90%). The multiplier for accept-
able points was 1 times this range from the edges.
Figure 3 shows the line fits on all schedules. The
colour of the line indicates how good the line fit is; a
darker colour has closer to 0 residuals. The lightest
colour was set as the maximum residuals out of the 9
line fits.
The majority of trends displayed a clear down-
wards slope, among which were the three closest fits.
One third of the studied order schedules displayed an
upwards slope of moderate uncertainty. These trends
are closely paired with the prediction accuracy graphs
in Figure 4, which shows four lines with a downwards
slope where upwards was the expected direction -
more noise meaning more prediction errors. Three of
those coincided with the upwards profit schedules and
one poor line fit of prediction accuracy had a down-
ward slope on the profit graph.
The overall result of the large-scale experiment
supported the research hypothesis. The majority of
order schedules tested show an above-average profit
earned from good predictions that steadily decreased
over increasing prediction noise in strategic informa-
tion. Figure 5 is a visualization of distribution dif-
ferences in the trial profits. It presents comparisons
through nonparametric Wilcoxon tests of the distribu-
tions involved in the nine order schedules.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
202
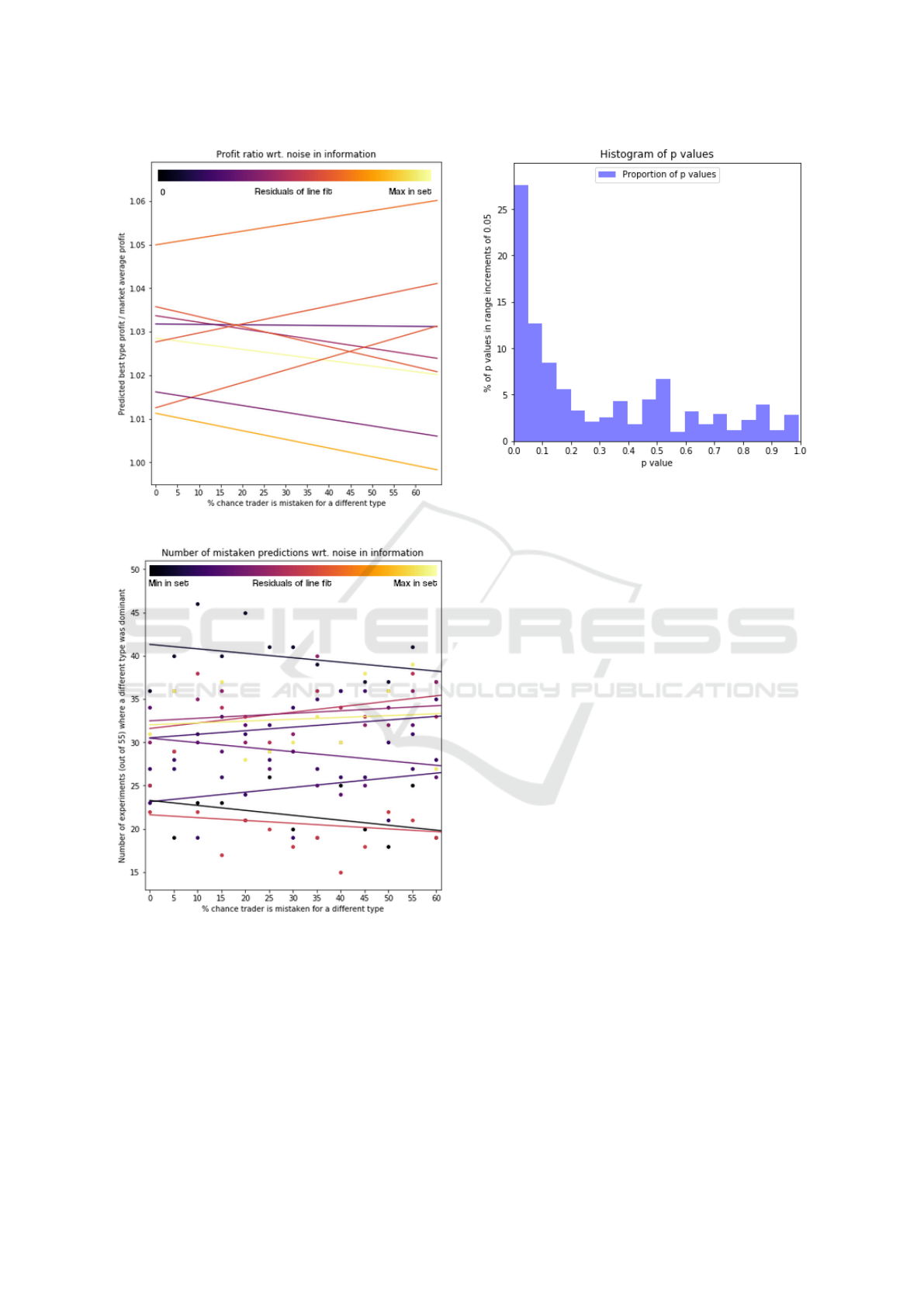
Figure 3: Profit trends for 9 order schedules.
Figure 4: Prediction accuracy for 9 order schedules.
Individual data points are a pairwise comparison be-
tween the noiseless prediction-result distribution and
a noisy prediction-result distribution. Small p values
indicate strong certainty that the samples were drawn
from different distributions. A large portion of these
tests indicate that the samples with noise involved can
usually be distinguished from samples without pre-
diction noise. A possible explanation for the uncer-
tain predictions and upwards profit trends could be
Figure 5: P values of Wilcoxon tests.
that certain order schedules spawned more compli-
cated strategic dynamics. For the majority of sched-
ules the addition of two extra traders of a kind did
not nullify the advantage of having had access to pre-
dictions. However, for the schedules that show nega-
tive correlations, this alteration in trader ratios might
have ended up working against the traders with access
to an oracle, pushing them over the boundary where
the predicted strategy was no longer the optimal one.
Such a scenario could have arisen when most of the
strategic landscape was dominated by a single trader
with very small pockets of other types. Figure 6 and
Figure 7 show a comparison between Schedule 3 -
where predictions performed well - and Schedule 7
where they did not.
3 CONCLUSIONS
The fairness and regulatory tools of financial mar-
kets draw notable attention, especially after reces-
sions like the 2008 housing crash or the fallout of the
2020 COVID pandemic. It is vital to have scientifi-
cally estimated bounds for what advantage is reason-
able as a function of access to information. This ex-
ploratory study suggests an approximate 10% profit
advantage difference between perfect and no informa-
tion in most cases. Excessive advantage could prove
to be a strong hint towards requiring further, manual
investigation of a market participant.
As well as confirming the initial hypothesis, this
research explored the most significant factors influ-
encing market predictions in a simulated environ-
ment. Future research now has a proven process to use
Imperfect Oracles: The Effect of Strategic Information on Stock Markets
203

Figure 6: Well-predictable order schedule.
Figure 7: Badly-predictable order schedule.
as a basis, with knowledge of the primary obstacles in
assessing predictions, such as the need for an aver-
age prediction set, as opposed to perfect knowledge
of the current market state. Some failure cases of the
proposed prediction system were also unveiled, where
a counter-intuitive correlation was present. The fail-
ure cases were supported in evidence of their differing
nature from two independent sources of experiment
data, profit ratio and prediction accuracy. Follow-
ing work can either avoid said failure cases or delve
deeper into why they produce the results in question.
This project extended the Bristol Stock Exchange
simulator with more functionality. These extensions
are open for anyone to copy, use or modify. The data
pipeline of the analysis is also published online and
may be used directly on any experiment data file with
no additional steps.
All data points in the data files may be reinter-
preted in their relation to each other. The data ob-
tained remains useful as one may perform an analysis
of a different noise phenomenon without the need to
re-generate hundreds of thousands of lines of data.
REFERENCES
Cliff, D. (2018). Bse: A minimal simulation of a limit-
order-book stock exchange. In Affenzeller, M., Bruz-
zone, A., Jimenez, E., Longo, F., Merkuryev, Y., and
Piera, M., editors, 30th European Modeling and Simu-
lation Symposium (EMSS 2018), pages 194–203, Italy.
DIME University of Genoa.
Cliff, D. and Bruten, J. (1997). Zero is not enough: On the
lower limit of agent intelligence for continuous double
auction markets.
Das, R., Hanson, J. E., Kephart, J. O., and Tesauro, G.
(2001). Agent-human interactions in the continuous
double auction. In International joint conference on
artificial intelligence, volume 17, pages 1169–1178.
Lawrence Erlbaum Associates Ltd.
Gjerstad, S. and Dickhaut, J. (1998). Price formation in
double auctions. Games and Economic Behavior,
22(1):1 – 29.
Gode, D. K. and Sunder, S. (1993). Allocative efficiency
of markets with zero-intelligence traders: Market as a
partial substitute for individual rationality. Journal of
Political Economy, 101(1):119–137.
Rust, J., Miller, J., and Palmer, R. (1992). The Double
Auction Market: Institutions, Theories, and Evidence,
chapter Behavior of trading automata in a computer-
ized double auction market. Addison-Wesley, Red-
wood City, CA.
Rust, J., Miller, J. H., and Palmer, R. (1994). Characterizing
effective trading strategies: Insights from a computer-
ized double auction tournament. Journal of Economic
Dynamics and Control, 18(1):61 – 96. Special Issue
on Computer Science and Economics.
Smith, V. L. (1962). An experimental study of competi-
tive market behavior. Journal of political economy,
70(2):111–137.
Snashall, D. and Cliff, D. (2019). Adaptive-aggressive
traders don’t dominate. In ICAART.
Tesauro, G. and Bredin, J. L. (2002). Strategic sequential
bidding in auctions using dynamic programming. In
Proceedings of the First International Joint Confer-
ence on Autonomous Agents and Multiagent Systems:
Part 2, AAMAS ’02, page 591–598, New York, NY,
USA. Association for Computing Machinery.
Vytelingum, P. (2006). The Structure and Behaviour of the
Continuous Double Auction. PhD thesis, University
of Southampton.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
204
