
A History-based Framework for Online Continuous Action Ensembles
in Deep Reinforcement Learning
Renata Garcia Oliveira
a
and Wouter Caarls
b
Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro RJ 38097, Brazil
Keywords:
Reinforcement Learning, Deep Reinforcement Learning, Continuous Ensemble Action, Ensemble
Algorithms, Hyperparameter Optimization.
Abstract:
This work seeks optimized techniques of action ensemble deep reinforcement learning to decrease the hyper-
parameter tuning effort as well as improve performance and robustness, while avoiding parallel environments
to make the system applicable to real-world robotic applications. The approach is a history-based frame-
work where different DDPG policies are trained online. The framework’s contributions lie in maintaining a
temporal moving average of policy scores, and selecting the actions of the best scoring policies using a single
environment. To measure the sensitivity of the ensemble algorithm to the hyperparameter settings, groups were
created that mix different amounts of good and bad DDPG parameterizations. The bipedal robot half cheetah
environment validated the framework’s best strategy surpassing the baseline by 45%, even with not all good
hyperparameters. It presented overall lower variance and superior results with mostly bad parameterization.
1 INTRODUCTION
Reinforcement learning (RL) (Sutton and Barto,
2018) is based on a mathematical framework known
as a Markov Decision Process (MDP). It is widely
used for controlling environments, maximizing a re-
ward signal for trial and error in order to achieve a
goal. Deep Deterministic Policy Gradient (DDPG) is
a model-free algorithm that can learn policies in high-
dimensional state space and continuous action space
(Lillicrap et al., 2016; Silver et al., 2014).
RL algorithms such as DDPG need fine-tuning of
their hyperparameters to converge. The search for
best parameters can be performed by grid search. This
procedure is computationally expensive, hence there
are several hyperparameters optimization methods;
recent studies use bayesian optimization (Bertrand,
2019), bandit-based approach (Li et al., 2018), ge-
netic algorithm (Fernandez and Caarls, 2018) and se-
quential decision (Wistuba et al., 2015). Another
method for learning optimal parameters is population-
based training (PBT) (Jaderberg et al., 2017) and
CERL (Khadka et al., 2019), it uses multiple learn-
ers as a population to train neural networks inspired
by genetic algorithm, copying the best hyperparame-
a
https://orcid.org/0000-0001-8226-3178
b
https://orcid.org/0000-0001-9069-2378
ters across the population. Unlike these, population-
guided parallel policy search (Jung et al., 2020) opti-
mizes by using a soft manner to guide a better search.
The population based approaches consider multiple
environments.
As opposed to hyperparameter tuning for super-
vised learning, where the same data set can be re-used
over and over, RL demands new environment data ac-
quisition for each configuration, since it is necessary
to run the control policy being optimized in the en-
vironment, which takes time. In addition, applying
this process in the real world takes much longer, and
risks damage to the robot (Tan et al., 2018). The goal
is to learn from a single environment combining an
ensemble of continuous actors while improving per-
formance and robustness.
Action ensembles in literature use pre-learned al-
gorithms. In discrete actions, ensemble algorithms
(Wiering and Van Hasselt, 2008) are combined in
a single agent using action probability aggregations,
among them the majority voting ensemble signifi-
cantly outperforms others methods in final perfor-
mance running in maze environments. For continuous
action, ensembles of neural networks (Hans and Ud-
luft, 2010) use Neural Fitted Q-Iteration and presents
advantages in majority voting action aggregation over
Q-averages aggregation in the pole balancing environ-
ment, being advisable to use different network topolo-
580
Oliveira, R. and Caarls, W.
A History-based Framework for Online Continuous Action Ensembles in Deep Reinforcement Learning.
DOI: 10.5220/0010199005800588
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 580-588
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

gies. Another study presents the data center and the
density based aggregations (Duell and Udluft, 2013),
the latter results in reliable policies in most experi-
ments with neural network-based RL in a gas turbine
simulation A recent study uses mean aggregation of
continuous action in a deep ensemble reinforcement
learning with multiple DDPG (Wu and Li, 2020) to
train autonomous vehicles in multiple environments.
As opposed to cited literature, we specifically tar-
get online learning policies in a single environment, to
make it possible the use in real system, in addition to
reducing the hyperparameter tuning effort. A History-
Based Framework is proposed to aggregate the con-
tinuous actions leading to a good result even if some
algorithms do not converge separately. The main con-
tribution resides in the use of a temporal moving av-
erage of policy scores and also in the online selection
of the best scoring policies.
This article is organized in 6 sections. Section 2
presents the background of DDPG and Ensemble Ac-
tions. Section 3 presents the History-Based Frame-
work to continuous action ensembles in DDPG. Sec-
tion 4 explains the planning and execution of the ex-
periments. Finally, sections 5 and 6 present the dis-
cussion and conclusion of the work.
2 BACKGROUND
DDPG. It is an actor-critic algorithm applicable in
continuous-action tasks with high dimensional state
spaces (Lillicrap et al., 2016). It is an approach based
on the Deterministic Policy Gradient (DPG) algo-
rithm (Silver et al., 2014). The critic Q(s, a) learns to
approximate a value function satisfying the Bellman
equation as in deep Q-learning (Mnih et al., 2014).
DDPG optimizes the critic by minimizing the loss
(Equation (1) and (2)), where the function approxi-
mator is parameterized by θ
Q
and θ
Q
0
, the former be-
longing to the training network and the latter referring
to the target network. s and a are the state and action
in a certain time step, r is the reward and s
0
represents
the next state. The loss function is
L(θ
Q
) = E
(s,a,r,s
0
)
h
y
t
− Q(s, µ(s)|θ
Q
)
2
i
(1)
where
y
t
= r
t
+ γQ(s
0
, µ(s
0
)|θ
Q
0
) (2)
The Bellman error of the value function of the tar-
get policy is the performance objective, averaged over
the state distribution of the behaviour policy. The
policy is learned from a parameterized actor function
µ(s|θ
µ
), which deterministically maps states to a spe-
cific action. Equation (3) presents the actor update,
which takes a step in the positive gradient criteria of
the critic with respect to the actor parameters. Ap-
plying the chain rule, J represents the expected return
over the start distribution and ρ
β
a different (stochas-
tic) behavior policy.
∇
θ
µ
J =
E
s
t
∼ρ
β
∇
a
Q(s, a|θ
Q
)|
s=s
t
,a=µ(s
t
)
∇
θ
µ
µ(s|θ
µ
|
s=s
t
)
(3)
Taking advantage of off-policy data, experiments are
stored for use as a Replay Memory, inducing sam-
ple independence. The samples s, a, r, s
0
are generated
by exploring sequentially the environment and storing
them in the replay memory (R ). Every time step, a
minibatch is sampled uniformly from the replay mem-
ory, updating the actor and critic. This memory size is
chosen big enough to avoid overfitting (Liu and Zou,
2018).
Note that y
t
in Eq (2) depends on θ
Q
0
, a target
network used to stabilize the network learning with
a time delay. This “soft” target update considers the
exponentially decaying average for actor and critic
networks parameters as in Equation (4). This tech-
nique stabilizes the problem of learning the action-
value function and brings the problem closer to the
case of supervised learning (Lillicrap et al., 2016).
θ
0(t)
= τθ
(t−1)
+ (1 − τ)θ
0(t−1)
with τ ∈ [0, 1] (4)
The exploration in continuous action spaces is a chal-
lenge in RL. A noise N is added to sample the pol-
icy π = µ(s
t
|θ
µ
t
) + N . The N uses the Ornstein-
Uhlenbeck process (Uhlenbeck and Ornstein, 1930)
to generate temporally correlated exploration for ex-
ploration efficiency in physical environments that
have momentum (N θ = 0.15 and N σ = 1). The
Ornstein-Uhlenbeck process models the velocity of a
Brownian particle with friction, which results in tem-
porally correlated values centered around zero (Lilli-
crap et al., 2016).
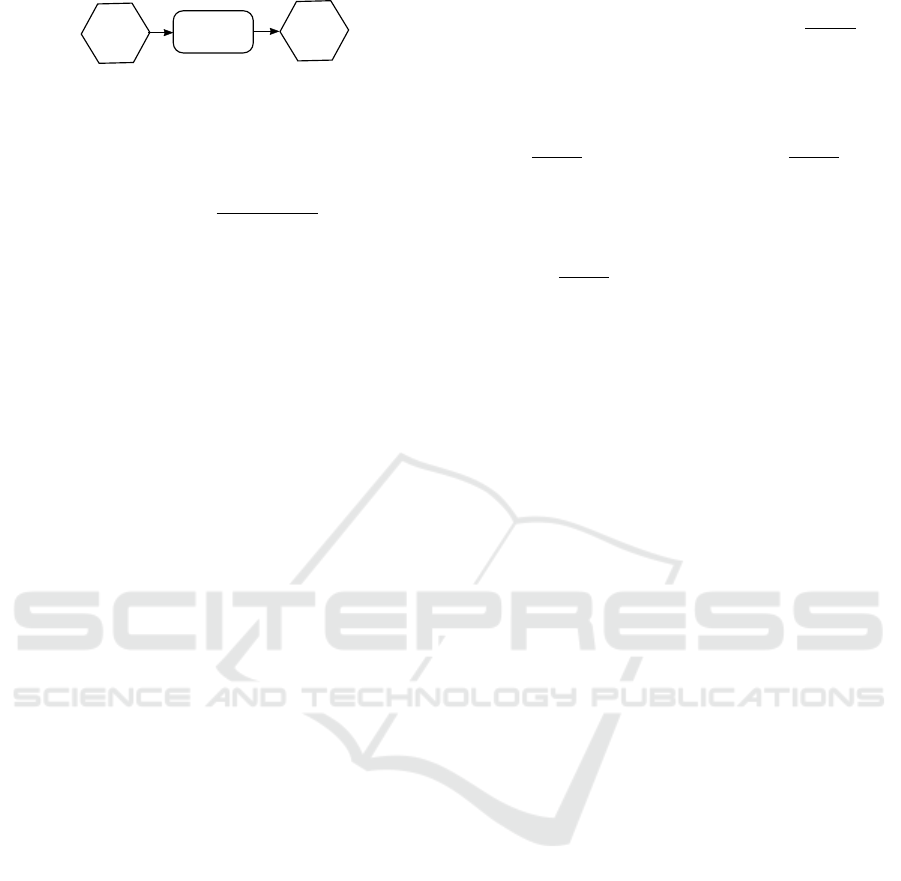
Ensemble Aggregation. These techniques below
form a base case in experiments. Figure 1 illustrates
the interaction.
• Density Based: is a way to extend majority voting
to continuous action spaces. It seeks the action
with the highest density (d
i
) in the space of actions
(Duell and Udluft, 2013).
The density d
i
is calculated for each action a
i
in the action ensemble of cardinality N using an
isotropic Gaussian density over its k dimensions,
where each action dimension is normalized to
[−1;1]. The distance parameter r is using value
A History-based Framework for Online Continuous Action Ensembles in Deep Reinforcement Learning
581
(1)
Ensemble
Aggregation
(A)
Action
Ensemble
(B)
Center
Action
Figure 1: Conventional Ensemble Aggregation Strategy.
0.025. After calculating all actions’ densities, the
action with the highest density value is chosen.
d
i
=
N
∑
j=1
e
−
∑
k
l=1
(
a
il
−a
jl
)
2
r
2
(5)
• Data Center: in the first step, the Euclidean dis-
tance is calculated for each action with respect
to the mean of the action ensemble. The action
with the longest distance is removed and the pro-
cedure is repeated until only two actions remain
(Duell and Udluft, 2013). Finally, the average of
the last two actions is the chosen action. This is a
parameter-free algorithm.
• Mean: this function returns the arithmetic mean of
the ensemble actions, or sum of all values divided
by the total number of values. If we are dealing
primarily with well-tuned hyperparameters algo-
rithms and up to 3 learners agent, this should lead
to a good ensemble action (Wu and Li, 2020).
3 HISTORY-BASED
FRAMEWORK
Ordinarily, ensemble aggregations consider pre-
learned policies, while this study aims to perform on-
line action aggregation. Assuming that policy perfor-
mance is time-correlated, the framework uses histor-
ical performance to make decisions. As such, poli-
cies with bad performance in the past can be dis-
carded from the aggregation. The Ensemble Frame-
work, presented in Figure 2, was created to select the
best ensemble action. In order to explore the best way
to define historical performance, the framework al-
lows different scoring functions. Before explaining
the framework step by step, it is important to high-
light its mechanisms.
Performance History Parameter. Although con-
sidering that the ensemble can make a better trade-off
between exploration and exploitation (Wiering and
Van Hasselt, 2008), it has been found empirically that
it can be difficult for the ensemble aggregations to
maintain consistency when simply selecting the ac-
tion of the highest scoring algorithm in the ensem-
ble. Therefore, an exponentially weighted moving
average filter is applied, reducing the action chatter-
ing between the algorithms. For this, the scores vari-
able accumulates performance at each time step using
the historical learning rate α
h
= 0.01 (chosen empiri-
cally) as shown in Equation (6).
scores = α
h
· scores + (1 − α
h
) · scores (6)
Active Set Aggregation. It was created to take ad-
vantage of action filtering that becomes possible due
to the performance history. The group is ranked ac-
cording to scores which allows filtering the actions of
the best performing parametrizations. Thus, the best
actions compose a new action ensemble and a new ag-
gregation is performed to select the best action from
the active set.
3.1 Framework
This section presents the framework as a structure of
functions and intermediate data that allow applying
the exponential moving average filter, using various
techniques and evaluatons in order to find the most ef-
ficient among the environments. At the beginning of
Figure 2, the Framework seeks to score the ensemble
of actions — (A) Action Ensemble — by an aggrega-
tion strategy, thus the (1) Ensemble Aggregation uses
methods described in Section 2 to find (B) Center Ac-
tion. This step is only necessary when the Squared
Euclidean Distance is used in the next function —
(2) Scoring. Otherwise, another scoring function that
does not require a center action is used.
The (A) and (B) data serve as input to (2) Scoring
which calculates a weighting of values, a score, for
each action — (C) Scores. The following methods
are specifically used or adapted for this scoring step:
Data Center Ranking, Density Raking and Squared
Euclidean Distance.
Data Center Ranking. The data center ranking
uses the concept of data center (Section 2). During the
process of selecting the center element, the one far-
thest from the center is selected to be removed. Data
Center Ranking returns the step at which the partic-
ular policy’s action was removed, where the smallest
value is the center itself.
Density Scores. The density of each action (d
i
) is
presented in Section 2. In Density Based Aggrega-
tion, the density information d
i
assigned to each ac-
tion is returned.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
582
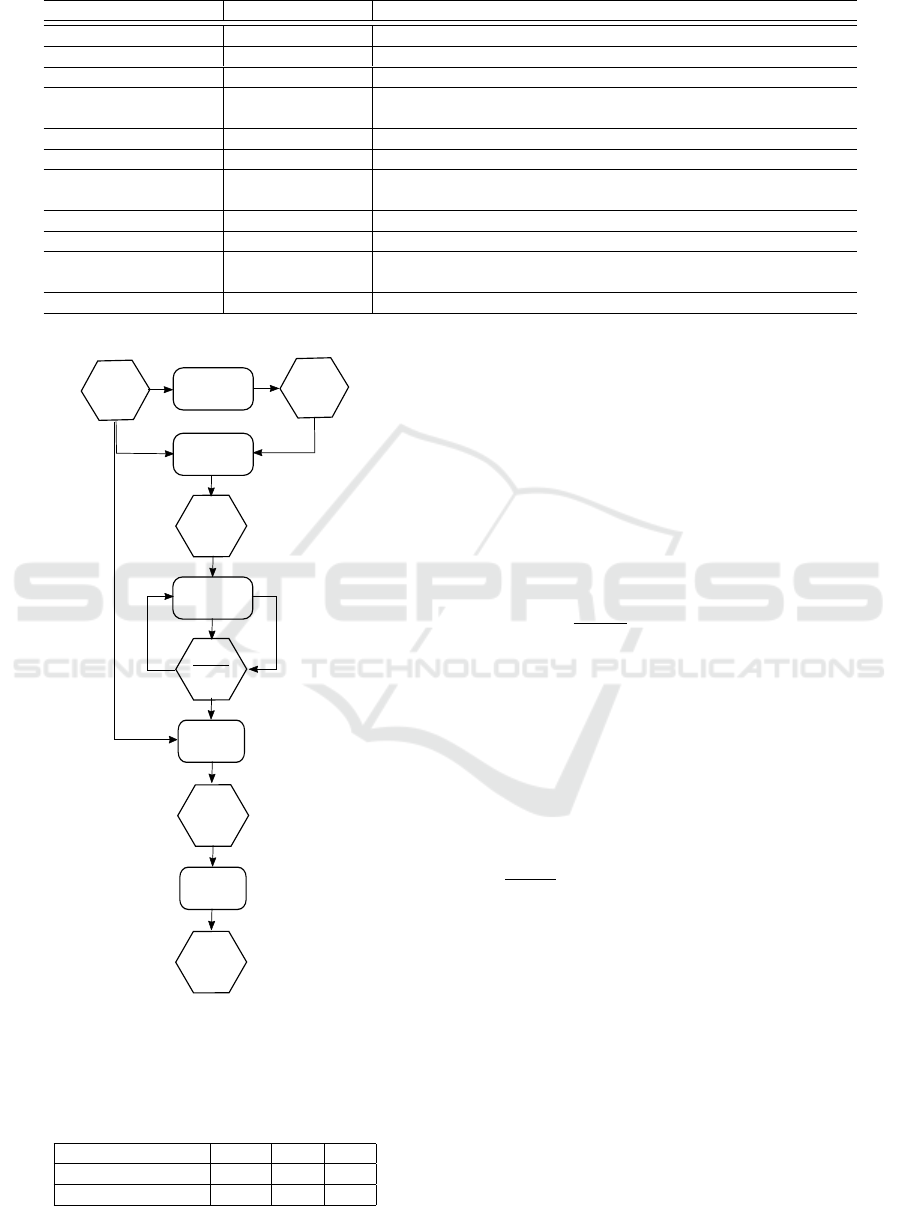
Table 1: Table with the hyperparameters’ description used to build each algorithm of the ensemble.
Hyperparameters Value Description
discount factor 0.98 or 0.99 Discount factor used in the Q-learning update.
reward scale 0.001, 0.1 or 1 Scaling factor applied to the environment’s rewards.
soft target update rate 0.01 Update rate of the target network weights.
target network 10 or 100 Steps number, or frequency, with which the target
update interval network parameters are updated.
learning rate 0.001 and 0.0001 Update rate used by AdamOptimizer.
replay steps 32 to 512 Number of minibatches used in a single step.
minibatch size 32 to 512 Number of transitions from the environment used in batch to
update the network.
layer size 50 to 400 Number of neurons in regular densely-connected NN layers
activation layer relu or softmax Output function of the hidden layers.
replay memory size 1000000 Size of the replay memory array that stores the agent’s
experiences in the environment.
observation steps 1000 Observation period to start replay memory using random policy.
(1)
Ensemble
Aggregation
(A)
Action
Ensemble
(2)
Scoring
(F)
Final
Action
(3)
Moving
Average
(4)
Percentile
Filtering
(D)
Scores
(5)
Active Set
Aggregation
(E)
Active Set
Actions
(C)
Scores
(B)
Center
Action
Figure 2: History-Based Framework for Ensemble Aggre-
gation.
Table 2: Composition of test configurations. The values
indicate how many parameterizations of each category were
included resulting in a group of 16 algorithms.
parametrizations good mid bad
best 12 8 4
worst 4 8 12
Squared Euclidean Distance. This is a well know
approach, very effective and widely used in the liter-
ature (Krislock and Wolkowicz, 2012). Equation (7)
presents the square of the difference between a policy
action and some aggregate action ¯a. ¯a can be cal-
culated using any of the ensemble aggregation tech-
niques described in Section 2.
ed
i
=
N
∑
j=1
(a
i j
− ¯a)
2
(7)
The (3) Moving Average uses the (C) Scores to up-
date the (D) Scores, history based variable, presented
in Equation (6). The function of the framework is the
(4) Percentile Filtering, where the specified percent-
age of the (A) Action Ensemble is selected based on
the order of scores to form the (E) Active Set Actions.
The idea is to use the scores’ history to filter the best
actions, safeguarding those policies that perform well
over time. Finally, the (F) Final Action is selected by
the (5) Active Set Aggregation. The aggregation used
here is Best, Data Center, Density Based and Mean.
The best aggregation selects the best action based on
the scores; in this configuration flow , the (4) Per-
centile Filtering function is not relevant.
The code used in the framework is available in
GRL (https://github.com/renata-garcia/grl).
4 EXPERIMENTS
In order to verify the efficiency of actor ensembles,
we used an approach testing three groups of good and
bad parametrizations with different algorithms. For
this, 32 DDPG agents with different hyperparame-
ters were individually tested. Table 1 presents the
hyperparameters values which were derived from the
DDPG presented in literature (Lillicrap et al., 2016).
A History-based Framework for Online Continuous Action Ensembles in Deep Reinforcement Learning
583

Note that, not necessarily good hyperparameters in
one environment will be good in the other. As such,
the classification of a parameterization as either good
or bad depends on the environment.
Three groups were created and called good, mid
and bad. The groups were created to measure the
interference of bad hyperparameters on the methods.
The average end performance of 31 (10 in case of Half
Cheetah) learning runs was used to order the individ-
ual parameterizations. The 12 best were classified as
good, and the 12 worst as bad. The good, mid and bad
groups contain different amounts of good and bad pa-
rameterizations, as defined in Table 2.
Since ensemble strategies for continuous rein-
forcement learning use pre-learned algorithms (Duell
and Udluft, 2013), such simulations were performed
for comparison purposes. The base case considers
just the data center, density based and mean strate-
gies.
Table 3 introduces the history-based framework
instances (Section 3). The first set of algorithms cho-
sen are the base case strategies highlighted at the top
of the table. A composition of acronyms was created
to enable the identification of the configuration used
in the History-Based Framework.
• DC: Data Center;
• DB: Density Based;
• M: Mean;
• DCR: Data Center Ranking;
• DS: Density Scores;
• ED: Euclidean Distance Squared.
Initially a class of instances was chosen considering
performing only history-based score filtering while
choosing the best scoring policy at the end of the pro-
cess. These three strategies are indicated in the table
by: DCR-B, DS-B and M-ED-B.
Another experiment was to perform active set ag-
gregation. For this, after history-based filtering 25%
of the actions with the best moving average scores are
selected and used to calculate the final action. These
three strategies are indicated in the table by: DCR-
DC, DS-DB, and M-ED-M.
Finally, other experiments were performed based
on the observed performance of the previous strate-
gies. These three strategies are presented at the end
of table: M-ED-DC, M-ED-DB and DC-ED-DC.
In the comparative result, we always show the
mean and the 95% confidence interval over 31 runs
(10 in case of Half Cheetah), considering that ran-
domly observed samples larger than 30 may be sup-
posed normally distributed (Triola, 2015, p.280). The
strategies presented in bold numbers are those whose
mean is within 95% confidence interval of best en-
semble result. Strategies with a mean within or above
the 95% confidence interval of the best single policy
are marked with an asterisk.
In order to measure the overall performance of the
framework setups to select the strategy used for vali-
dation in the Half Cheetah v2 environment, the aver-
age relative regret is calculated as in Equation 8. For
such a performance test, m represents the set of all
strategies for the group and the environment selected,
so the n strategies are compared with the best strategy
in that set. The result is normalized by the maximum
value and added up, summarizing the error according
to the best result obtained in each set of strategies.
The strategy with the least error is the one chosen for
testing with the new environment.
argmin
m
∑
i
n
∑
j
max(x
i
) − x
i j
max(x
i
)
(8)
4.1 Ensemble of Pre-trained Algorithms
In ensemble research, it is common to use previ-
ously trained algorithms. The tables presented below
are simulations with pre-learned algorithms. Table 4
presents the inverted pendulum environment, Tables 5
and 6 present cart pole and cart double pole environ-
ments. All tables show that many ensemble strategies
presented have performance equal to or better than the
best base case.
In the good group, almost all the strategies per-
form better than the best single policy. The exception
is the cart double pole environment, that in this case
only DC-ED-DC stands out. Analyzing the tables, the
best results are found predominantly in the new strate-
gies created by the history based framework.
Looking at the mid group, it is interesting to note
that some strategies maintain performance, although
half of the algorithms participating in the ensemble do
not learn. For the bad group, only the cart double pole
maintains convergence, probably because, in this test
case, it already begins learning near the equilibrium
end point.
4.2 Ensemble Online Training
In ensemble online training, the individual DDPG
policies are trained from scratch during execution,
learning together. The Table 4 presents the inverted
pendulum environment, the Table 5 and 6 present cart
pole and cart double pole environment. All tables
show that many ensemble strategies presented have
performance equal to or better than the best base case,
mainly for the good group.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
584
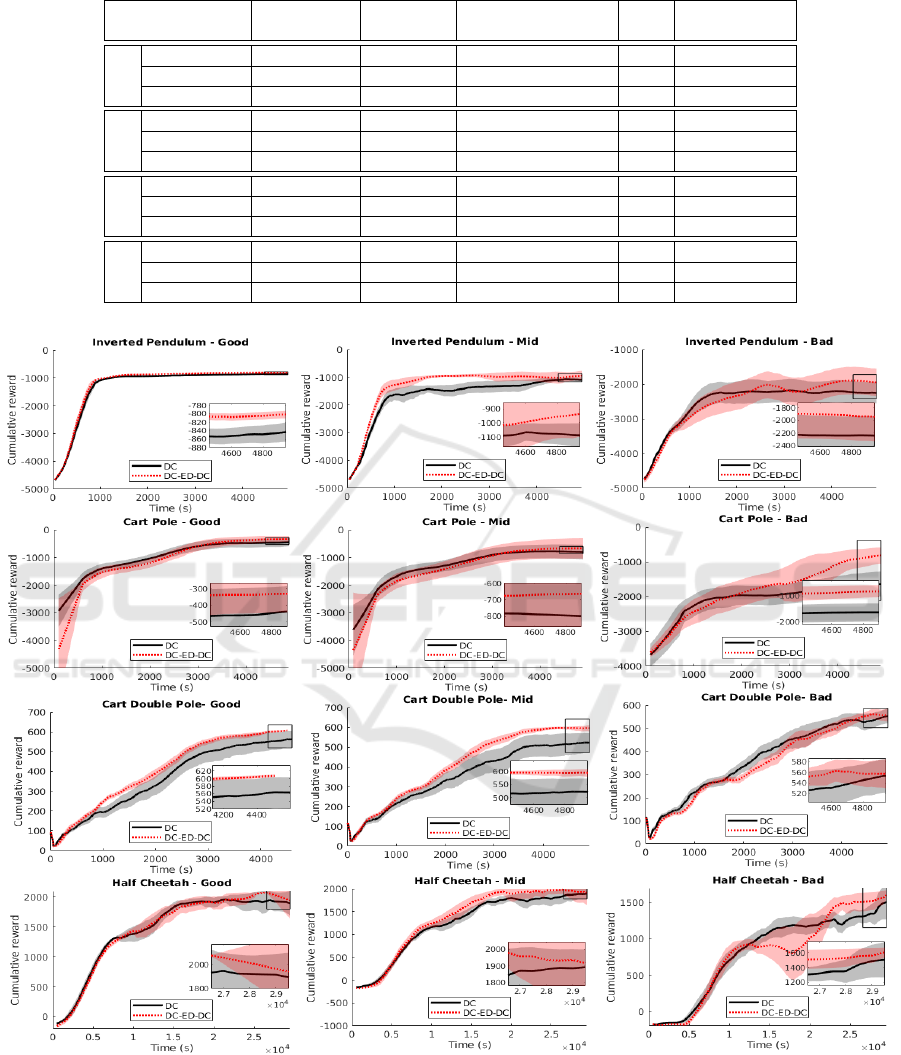
Table 3: Ensemble Strategies Configuration.
strategy
ensemble
aggregation
percentile
filtering
scoring
a
h
active set
aggregation
BASE
DC — — — 1.0 data center
DB — — — 1.0 density based
M — — — 1.0 mean
DCR-B — — data center ranking 0.01 best
DS-B — — density scores 0.01 best
M-ED-B mean — euclidean distance 0.01 best
DCR-DC — 25% data center ranking 0.01 data center
DS-DB — 25% density scores 0.01 density based
M-ED-M mean 25% euclidean distance 0.01 mean
M-ED-DC mean 25% euclidean distance 0.01 data center
M-ED-DB mean 25% euclidean distance 0.01 density based
DC-ED-DC data center 25% euclidean distance 0.01 data center
Figure 3: Illustration of DC and DC-ED-DC Learning curves.
In the mid group, cart pole does not present good con-
vergence. The bad group of cart pole presents perfor-
mance compared to mid for the DC-ED-DC strategy.
This environment performs better when policies are
more consistent. The DC-ED-DC strategy presented
the lowest error, Equation (8), having 2.3% average
relative regret. Figure 3 shows an illustration of the
learning curves with strategy DC and DC-ED-DC.
A History-based Framework for Online Continuous Action Ensembles in Deep Reinforcement Learning
585

4.3 Half Cheetah Test
Half cheetah (Todorov et al., 2012) is a complex en-
vironment chosen to validate the strategy of online
continuous action ensembles. It seeks the goal of
a bipedal walk. The half cheetah v2 environment
is tested with DC (best base case strategy) and DC-
ED-DC (best strategy with the lowest error method
as described in the Section 4) for comparison of re-
sults. Table 7 presents the pre-learned and online
learning ensemble strategies’ performance in the half
cheetah environment respectively. The noteworthy re-
sult is that half cheetah learns consistently better for
online learning when compared to the best individ-
ual simulations. Considering the best single parame-
terization in our set, the DC-ED-DC online learning
strategy shows 45% improvement in the good group
(2057±72 vs. 1419±73). Overall, the DC-ED-DC is
consistently better than, or equal (mid group), to the
base case DC. Besides that, training policies online
presents much better results than using pre-learned
policies.
Finally, to test the decreased hyperparameter tun-
ing effort in our approach, random continuous values
of the hyperparameters’ intervals described in Sec-
tion 3 were generated. Note that, due to the random
choice, the chosen parameters naturally tend to fall
more in the middle of the range than at the extremes,
generating more acceptable average values (Table 1).
For a random test, 30 ensembles with 16 parameteri-
zations were generated and run once. In the previous
experiments, the formation for groups always ensured
that at least 4 algorithms (good group) were not able
to converge. In contrast, for the random generation no
such control was made. The random Half Cheetah v2
hyperparameter ensemble using the DC-ED-DC strat-
egy resulted in mean performance of 3684±626.
5 DISCUSSION
In literature, the density-based aggregation strategy
showed better results in the experiments performed
(Wiering and Van Hasselt, 2008; Hans and Udluft,
2010; Duell and Udluft, 2013), although the case
studies analyzed in this article have shown more con-
sistent data center results. One reason may be the
need to parameterize density, which may have nega-
tively influenced performance. Another consideration
is that both the off-policy algorithm and the environ-
ments are different. Still, there are good results in the
combined strategies of the framework that include the
density algorithm.
Regarding the separation of the tests into groups,
the good group presented better results as expected.
Another point is that the best ensemble strategies in
the good group perform considerably better than the
best individual algorithm, while the density based
strategy performs less consistently. That is, the best
ensemble results improve robustness and accuracy as
expected (Zhang and Ma, 2012). Although the best
strategy varies with group and environment, DC-ED-
DC showed more consistent overall performance.
Looking at the other groups, the mid group for
some cases was able to keep up with the expected
good performance allowing significant leeway in
choosing hyperparameter realizations. In the bad
group, the cart double pole and half cheetah environ-
ments surprisingly presented performance compara-
ble to the best tuned run. The former environment
already started in the final position equilibrium. The
latter showed the ability to maintain excellent perfor-
mance over the best individual algorithm, mainly be-
cause of the 45% improvement demonstrated in the
good group.
The final fully randomized validation test demon-
strated the performance of hyperparameters found
randomly within the composition expected in a real-
istic DDPG implementation. In the half cheetah envi-
ronment, it can be seen that the strategies performed
surprisingly well compared to the single run.
6 CONCLUSION
This article proposed the use of continuous action en-
sembles while learning control policies from scratch.
It demonstrated a reduction in the need for hyperpa-
rameter tuning in DDPG algorithms when testing in
the half cheetah environment. To achieve this we in-
troduced a history-based framework that considers the
ensemble’s historical performance.
The framework proposed is capable of capturing
different compositions of ensemble strategies, pre-
senting a combined ensemble strategy as the one that
performed the best. The best strategy DC-ED-DC,
takes the squared euclidean distance of each action
from the average found by the data center, performs
the moving average by updating the scores, selects
25% of the actions with best scores and applies the
data center algorithm again. This paper made compar-
isons with ensemble strategies presented in the state
of the art and demonstrated that the chosen strategy
outperforms the baseline algorithms. It also demon-
strated the advantage in simulation of using an ensem-
ble algorithm over individual algorithms.
In the benchmark environments, pre-learned
strategies mostly showed better results than online
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
586

Table 4: Pendulum results for different ensemble strategies (31 runs).
strategy
pre-learned learning online learning
good mid bad good mid bad
BASE
DC -779±11* -894±89 -2327±367 -850±25 -1075±80 -2244±321
DB -846±75 -1406±189 -2553±279 -1594±264 -2633±342 -2810±254
M -1416±115 -2851±116 -4043±62 -2835±286 -3574±172 -4234±108
DCR-B -775±10* -874±176 -2388±428 -804±17* -841±59 -2477±413
DS-B -794±22* -1188±325 -3339±206 -1783±343 -2233±376 -3468±79
M-ED-B -1067±353 -1490±509 -3359±518 -810±18 -1358±442 -2343±584
DCR-DC -770±10* -876±180 -2386±430 -791±13* -1008±176 -2341±375
DS-DB -796±33* -1471±398 -3433±135 -846±24 -1105±94 -2346±379
M-ED-M -793±20* -884±63 -2174±486 -894±159 -1139±251 -2369±374
M-ED-DC -778±13* -786±12* -1765±489 -790±11* -783±12* -1677±444
M-ED-DB -782±11* -799±13* -1713±486 -793±10* -861±77 -1448±306
DC-ED-DC -775±11* -864±182 -2066±471 -806±14 -974±201 -1913±400
Table 5: Cart Pole results for different ensemble strategies (31 runs).
strategy
pre-learned learning online learning
good mid bad good mid bad
BASE
DC -392±51* -507±162 -1062±247 -463±170 -783±261 -1684±364
DB -931±138 -1189±144 -1582±183 -1077±206 -1317±279 -1322±214
M -516±109 -878±222 -1637±233 -2153±254 -2805±249 -3411±294
DCR-B -306±54* -571±230 -1180±326 -434±143 -831±319 -1895±435
DS-B -860±148 -1373±173 -2190±240 -920±272 -2020±379 -2316±365
M-ED-B -379±115* -985±326 -2349±542 -379±99* -1382±410 -2483±392
DCR-DC -275±54* -550±220 -1141±313 -727±351 -812±303 -1450±440
DS-DB -380±54* -510±157 -1062±249 -462±164 -735±288 -1338±289
M-ED-M -268±27* -363±160* -924±247 -632±158 -1851±431 -2624±504
M-ED-DC -244±20* -315±144* -1083±418 -296±94* -913±441 -2474±604
M-ED-DB -263±24* -352±157* -953±269 -236±24* -766±377 -1659±531
DC-ED-DC -228±15* -362±170* -837±291 -340±121* -677±367 -912±291
Table 6: Cart Double Pole results for different ensemble strategies (31 runs).
strategy
pre-learned learning online learning
good mid bad good mid bad
BASE
DC 609±10 554±27 485±32 565±42 392±60 551±33
DB 222±62 225±65 183±57 278±61 234±49 296±65
M 535±42 435±45 317±35 88±12 89±11 84±11
DCR-B 603±18 502±42 436±43 612±2 598±12 577±26
DS-B 292±64 258±58 218±53 523±51 368±52 477±48
M-ED-B 577±27 477±51 406±47 552±41 419±52 287±48
DCR-DC 613±3 509±39 435±39 611±2 595±12 560±27
DS-DB 610±7 555±26 499±33 247±31 530±48 462±57
M-ED-M 603±10 546±38 479±40 485±36 292±40 258±29
M-ED-DC 611±3 557±33 494±40 606±7 571±25 467±45
M-ED-DB 606±8 561±29 488±39 606±6 599±10 534±31
DC-ED-DC 614±3* 587±24 500±41 606±5 600±10 560±27
Table 7: Half Cheetah v2 validation results (10 runs).
strategy
pre-learned learning online learning
good mid bad good mid bad
DC 1324±144 1043±249 1002±146 1945±222* 1870±201* 1325±322
DC-ED-DC 1501±39* 817±459 1166±83 2057±72* 1962±229* 1515±174*
A History-based Framework for Online Continuous Action Ensembles in Deep Reinforcement Learning
587

learning. However, evaluating the half cheetah en-
vironment, the approach to online learning policies
made a very significant difference. Improving per-
formance for both the base case strategy and the best
strategy, DC-ED-DC. Online learning and the use of
a single environment have advantages in the applica-
bility of the system in real-world robotic applications.
For future work, we would like to test with other
environments. A limitation of this work is that it only
uses the policies’ actions. It would be interesting to
also consider other variables, such as their value func-
tion, as ensemble or incorporating the value functions
into the framework.
REFERENCES
Bertrand, H. (2019). Hyper-parameter optimization in deep
learning and transfer learning: applications to medi-
cal imaging. PhD thesis, Universit
´
e Paris-Saclay.
Duell, S. and Udluft, S. (2013). Ensembles for continu-
ous actions in reinforcement learning. In ESANN 2013
proceedings, pages 24–26, Bruges, Belgium.
Fernandez, F. C. and Caarls, W. (2018). Parameters tun-
ing and optimization for reinforcement learning al-
gorithms using evolutionary computing. In Interna-
tional Conference on Information Systems and Com-
puter Science (INCISCOS), pages 301––305, Quito,
Equador. IEEE.
Hans, A. and Udluft, S. (2010). Ensembles of neural net-
works for robust reinforcement learning. In 2010
Ninth International Conference on Machine Learning
and Applications, pages 401–406, Washington, USA.
IEEE.
Jaderberg, M., Dalibard, V., Osindero, S., Czarnecki,
W. M., Donahue, J., Razavi, A., Vinyals, O., Green,
T., Dunning, I., Simonyan, K., et al. (2017). Pop-
ulation based training of neural networks. CoRR,
abs/1711.09846.
Jung, W., Park, G., and Sung, Y. (2020). Population-
guided parallel policy search for reinforcement learn-
ing. arXiv preprint arXiv:2001.02907.
Khadka, S., Majumdar, S., Nassar, T., Dwiel, Z., Tumer,
E., Miret, S., Liu, Y., and Tumer, K. (2019). Collab-
orative evolutionary reinforcement learning. In Pro-
ceedings of the 36th International Conference on Ma-
chine Learning, volume 97 of Proceedings of Machine
Learning Research, pages 3341–3350, Long Beach,
California, USA. PMLR.
Krislock, N. and Wolkowicz, H. (2012). Euclidean distance
matrices and applications. In Handbook on Semidefi-
nite, Conic and Polynomial Optimization, pages 879–
914. Springer, Boston, MA.
Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A., and
Talwalkar, A. (2018). Hyperband: A novel bandit-
based approach to hyperparameter optimization. Jour-
nal of Machine Learning Research, 18(1):6765–6816.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2016). Con-
tinuous control with deep reinforcement learning. In
Proceedings of International Conference on Learning
Representations, San Juan, Puerto Rico.
Liu, R. and Zou, J. (2018). The effects of memory replay in
reinforcement learning. In 56th Annual Allerton Con-
ference on Communication, Control, and Comput-
ing (Allerton), pages 478–485, Monticello, IL, USA.
IEEE.
Mnih, V., Heess, N., Graves, A., et al. (2014). Recurrent
models of visual attention. In Advances in neural in-
formation processing systems.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and
Riedmiller, M. (2014). Deterministic policy gradient
algorithms. In Proceedings of the 31st International
Conference on International Conference on Machine
Learning, volume 32, pages 387–395, Bejing, China.
JMLR.org.
Sutton, R. S. and Barto, A. G. (2018). Introduction to Re-
inforcement Learning. MIT Press, Cambridge, MA,
USA.
Tan, J., Zhang, T., Coumans, E., Iscen, A., Bai, Y., Hafner,
D., Bohez, S., and Vanhoucke, V. (2018). Sim-to-
real: Learning agile locomotion for quadruped robots.
arXiv preprint arXiv:1804.10332.
Todorov, E., Erez, T., and Tassa, Y. (2012). Mujoco:
A physics engine for model-based control. In 2012
IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 5026–5033. IEEE.
Triola, M. F. (2015). Elementary Statistics Technology Up-
date. Pearson Education, Rio de Janeiro, Reprint
(Translated), 11th edition.
Uhlenbeck, G. E. and Ornstein, L. S. (1930). On the theory
of the brownian motion. Physical review, 36(5):823.
Wiering, M. A. and Van Hasselt, H. (2008). Ensemble algo-
rithms in reinforcement learning. IEEE Transactions
on Systems, Man, and Cybernetics, Part B (Cybernet-
ics), 38(4):930–936.
Wistuba, M., Schilling, N., and Schmidt-Thieme, L. (2015).
Sequential model-free hyperparameter tuning. In
2015 IEEE International Conference on Data Mining,
pages 1033–1038.
Wu, J. and Li, H. (2020). Deep ensemble reinforcement
learning with multiple deep deterministic policy gra-
dient algorithm. Mathematical Problems in Engineer-
ing, 6:1–12.
Zhang, C. and Ma, Y. (2012). Ensemble machine learning:
methods and applications. Springer Science & Busi-
ness Media.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
588
