
Markov Logic Network for Metaphor Set Expansion
Jaya Pathak
a
and Pratik Shah
b
Indian Institute of Information Technology Vadodara, Gandhinagar, India
Keywords:
Metaphor Identification, Markov Logic Network (MLN), Information Completion.
Abstract:
Metaphor is a figure of speech, that allow us to understand a concept of a domain in terms of the other. One
of the sub-problems related to the metaphor recognition is of metaphor set expansion. This in turn is an
instance of information completion problem. We, in this work, propose an MLN based approach to address
the problem of metaphor set expansion. The rules for metaphor set expansion are represented in the first order
logic formulas. The rules are either soft or hard depending on the nature of the rules according to which
corresponding logic formulas are then assigned weights. Many a times new metaphors are created based on
usages of Is-A pair knowledge base. We, in this work model this phenomena by introducing appropriate
predicates and formulas in clausal form. For experiments, we have used dataset from Microsoft concept
graph consisting Is-A patterns. The experiments show that the weights for the formulas can be learnt using
the training dataset. Moreover the formulas and their weights are easy to interpret and in-turn explains the
inference results adequately. We believe that this is a first effort reported which uses MLN for metaphor set
expansion.
1 INTRODUCTION
Metaphor plays a vital role in expressing and com-
municating human emotions, ideas and concepts. Ex-
pressing unknown in terms of known is a key to learn-
ing. We use metaphors in our daily lives for effec-
tive communication. For example, “John is a Shining
Star”, tells us about John’s personality and achieve-
ments by comparing the properties of a star with John.
Metaphor is a mapping of concepts from a source do-
main to a target domain (Lakoff and Johnson, 1980).
The source concepts are mapped to target when they
share some common traits. In, ‘John is a Shining
Star’, the source concept is Shining Star and target
concept is John.
To understand metaphoric figures, the knowledge
of various concepts (a person, animal, etc) is useful.
Psychologist Gregory Murphy stated that “Concepts
are the glue that holds our mental world together”.
So for a metaphor to make sense, any of the two
concepts should be explicitly defined, i.e. either the
source or the target. In the above example, both the
source (Shining Star) and target the (John) are clearly
defined.
a
https://orcid.org/0000-0001-9368-8753
b
https://orcid.org/0000-0002-4558-6071
Before identifying a source-target pair, we should
recognize a metaphoric sentence. There are several
existing work for recognizing metaphors. For a Type-
I metaphor, an ideal way is to use the concept of Is-
A relation. The sentence having Is-A pattern can be
a potential metaphoric sentence. The first noun in
a Is-A sentence is the target, while the second noun
is source. After pairing them as (Target, Source),
check whether there is any knowledge about that pair.
To differentiate metaphoric and literal sentences, two
sets symbolized as Γ
m
(Metaphor set) and Γ
H
(Hearst
pair set) respectively are used.
We in our work, model the metaphor set expan-
sion as an information completion problem. We pro-
pose to solve the same using Markov logic Network.
The two key challenges of machine learning concepts
are uncertainty and complexity of the rule base. MLN
merges the logical and statistical models into a sin-
gle representation. One of the reasons to use MLN
for information completion problem of metaphor set
expansion is to infer about a complex and uncertain
problem in an explainable manner. We use MLN for
metaphor set expansion by formulating the formulas
of the rule base in the first order logic. We work with
Type-I metaphors, where source and target concepts
are derived from Is-A pattern. The proposed MLN
based approach is validated based on the experiments
Pathak, J. and Shah, P.
Markov Logic Network for Metaphor Set Expansion.
DOI: 10.5220/0010205606210628
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 621-628
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
621

conducted. For experiments, we have used Tuffy (Niu
et al., 2011). It is an efficient Markov logic network
inference engine. For experiments, we have used
dataset from Microsoft concept graph for short text
understanding (Wu et al., 2012). It provides the core
version of Is-A data mined from billions of web pages
(Cheng et al., 2015). With the available Is-A relations
we derive the set Γ
H
of Hearst pairs. Hearst pairs are
instances and concepts pairs i.e. (Instance,Concept).
Assuming that a small set of metaphors Γ
m
is avail-
able, the task of identifying new metaphors and in-
clude them in Γ
m
is called metaphor set expansion.
2 EXISTING WORK
A metaphor connects two concepts based on the con-
tent the resemblance between the concept domains.
Resemblance describes the nature of the idea they
share in common. A metaphor has two domains:
the target (the one which is being targeted) and the
source (the one whose characteristics are being used).
The initial work on metaphor recognition known as
met, was introduced by Fass in 1991 (Fass, 1991).
It proposes a method for differentiating literals and
metaphors. The problem with the approach is its hard
decision rule base. Without a probabilistic frame-
work, reasoning about metaphor explanation is not
meaningful. Even when the probability assignment is
done by one or the other approach, it is difficult to ex-
plain the inference drawn about given pair. The other
approach use hand-coded knowledge which are still
implausible and need technology boost. The previous
works on recognizing and identifying metaphors uses
contextual preferences, like the matching of similar-
ity between predicate-object, object-object, etc which
are difficult to recognize sometimes.
At present, there is a need for statistical meth-
ods to recognize and identify metaphors. The au-
thors in (Shutova, 2010) put forward the need of cre-
ating a publicly available metaphor corpus consisting
of known metaphoric sentences with the help of the
existing dataset using statistical pattern matching.
Recently, in computational linguistics approach
based on statistical inference have been applied to
metaphor recognition. The authors in (Schulder and
Hovy, 2014) use term relevance measure based on fre-
quency of occurrence in target domains for metaphor
detection. In (Tsvetkov et al., 2014), the authors
uses lexical semantic features to distinguish between
a metaphor and literal sentence by building a cross-
lingual model.
In our work, we first identify the source-target
mapping in sentences. The source domain is usually
explicitly defined while the target is mostly unclear.
Following are some of the existing methods for iden-
tification of metaphor set (Li et al., 2013).
2.1 Metaphor Identification
Detecting Is-A relation : There is a likelihood that
sentences having Is-A pair are metaphors. But this
is not true in general. For example, “Apple is a fuel”
can be designated as a metaphor but “Apple is a fruit”
has literal meaning and cannot be considered as a
metaphor. Every Is-A relation need not always be a
metaphor. Is-A pattern can be categorized in : the
literal Is-A relation and metaphoric Is-A relation.
Figure 1: Relation between Γ
H
, Γ
m
and Is-A pairs (Li et al.,
2013).
Γ
m
set of metaphors, consists of metaphors in
(Source,Target) pair form. For example, in “Apple is
a Fuel”, (Fuel, Apple) is the source-target pair, such
that
(Apple, f uel) ∈ Γ
m
Hearst pattern data set Γ
H
, is discussed in (Wu
et al., 2012). This consists of literal Is-A relations in
the form (x , h
x
), a pair of (hyponym,hypernym) such
that x be an instance of h
x
. For example, “Apple is a
fruit”, the Hearst pair
(x, h
x
) ≡ (Apple, Fruit) ∈ Γ
H
2.2 Metaphor Set and Hearst Pair Set
Both the above sets do not overlap as the metaphors
do not provide literal meaning in a sentence (Li et al.,
2013). So, if any pair of Γ
m
is also present in Γ
H
then
it is to be removed from Γ
m
.
From the available data set from Microsoft con-
cept graph of (Cheng et al., 2015; Wu et al., 2012)
Is-A relations, we build the Hearst pairs Γ
H
using
pairs of concepts and instance as (Instance, Concept).
Given a sample data, “Apple is a Food” where Apple
is an instance and Food is a concept, we get the pair
(Apple, Food).
The goal is to use the existing Γ
H
and Γ
m
pairs to
expand Γ
m
. Any pair is more likely to be a metaphor if
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
622

it does not appear in the set extracted from the Hearst
pattern.
To expand the set Γ
m
set we use transitive proper-
ties on Is-A relations (Li et al., 2013). If (x, y) ∈ Γ
m
and (x, h
x
) ∈ Γ
H
, then by transitivity we can add
(h
x
, y) to Γ
m
. For example, let (Apple, Fuel) ∈ Γ
m
and (Apple, Food) ∈ Γ
H
then, (Food, Fuel) ∈ Γ
m
.
In (Li et al., 2013), the authors propose a proba-
bility assignment to a pair (x,y) as :
P(x, y) =
occurrences o f (x, y) in Is − A pattern
occurrences o f Is − A pattern
(1)
We, use the transitivity as suggested above and in-
clude the same in the form of a first order formula rep-
resenting the knowledge (rule base) about metaphor
set expansion in MLN.
2.3 Probabilistic Model for Metaphor
Set Expansion
Metaphor expansion problem is same as that of a in-
formation completion. We propose to use Markov
logic network (MLN) for the same. MLN inte-
grates of the logical and statistical models into a sin-
gle representation. The knowledge representation is
done using first order logic and probabilistic graphi-
cal model. Logic handles the casual relationship be-
tween rule base and probability deals with the uncer-
tainty (Richardson and Domingos, 2006). We work
with Type-I metaphors, and try to expand the exist-
ing metaphor set. With the closed world assumption,
it is possible to extract metaphors from the existing
knowledge base (Γ
m
and Γ
H
).
In the next section we give an introduction to
Markov Logic Network and the notation that will be
used for the subsequent sections. We will present the
MLN with the help of a set of examples which will
help formulate the metaphor set expansion problem
in MLN framework.
3 MARKOV LOGIC NETWORK
Markov logic network is considered as a possibility
for unified learning mechanism. It is a probabilistic
graphical approach (Richardson and Domingos,
2006). MLN comprises of formulas in first-order
logic form and to each of the formula a real valued
weight is assigned. The nodes of the network graph
are the terms from the ground formulas and the edges
are the logical connectives among them. The nodes
represents atomic variables and edges describe the
probabilistic interaction between them. Consider a
Markov network for formula h:
h : Instance(u) → Concept(u)
constant set C
1
= {apple, orange, f ruit, company}.
Concept( f ruit)
Instance(apple)Instance(orange)
Concept(company)
h
1
h
2
h
3
h
4
Figure 2: A formulated ground Markov logic Network.
Relation between variables are represented using
First order logic in a Markov Network. First or-
der logic makes representation easy as compared to
other logical representations and are constructed us-
ing variables, constants, functions and predicates.
From Figure 2, the variables {u, v} range over the ob-
ject domain and takes any value from the constant.
Constants represent the objects in the domain of in-
terest. A function maps from one object set to an-
other e.g. Instance(), Concept(). Predicate represents
the relationship between objects e.g. metaphor(x,y).
Predicate value can be either true or false. Using the
above representations with logical connectives and
quantifiers, formulas (clauses) are modeled.
A ground atom is a term taking a constant value
from set and is the smallest unit of a formula. In figure
2, Instance(apple) is a ground atom with ‘Instance’ as
a function taking ‘apple’ as input from the constant
set C
1
. An atomic formula is defined as a predicate
term used with a constant set, Instance(apple) →
Concept( f ruit). Grounding refers to the method of
removing variables with constant value. A ground
formula is defined as set of predicates accompanied
by connectives using constant values as inputs. In
Figure 2, h
1
, h
2
, h
3
, h
4
are the ground formulas for for-
mula h. A possible world is described as the truth
values (0, 1) assigned to each ground atom in a net-
work. A world is defined as the set of truth values
which can be assigned to all ground atoms (Domin-
gos et al., 2008).
Together, Markov Network with First order logic
are combined as Markov logic Network (MLN)
(Richardson and Domingos, 2006).
3.1 Markov Logic Network
A Markov logic network (MLN) (Richardson and
Domingos, 2006) is a set of weighted first order logic
formulas (F, w), where F is the set of formulas in first
order logic form and w ∈ R
|F|
. A ground network is
formed w.r.t to the grounding of the formulas using a
Markov Logic Network for Metaphor Set Expansion
623

set of constants C = {c
1
, c
2
, ..., c
|C|
}. With the con-
stant set, the ground Markov network is built which
contains sub-graph for each ground formula in the
network. There are nodes for each ground predicate
or clause in the network, if any ground predicate is
TRUE, the value of the corresponding node will be 1.
For a set of constants, it can produce different net-
works. The probability distribution over a possible
world ω stated by ground Markov network is given as
P(W = ω) =
1
Z
exp
F
∑
i=1
w
i
n
i
(ω)
=
1
Z
exp
w
i
∗n
i
(2)
where n
i
(ω) is number of true groundings of F
i
in
ω, true grounding refers to the number of grounded
formulas satisfied in specific world (Richardson and
Domingos, 2006). The ω
i
s are the truth values of the
atoms in a specific world and Z is the partition func-
tion.
In the next section, we formulate the metaphor set
expansion in the framework of MLN.
4 PROBLEM FORMULATION
4.1 Metaphor Set Expansion as
Information Completion
We use MLN for metaphor set expansion by formu-
lating the rules of expansion as formulas in first or-
der logic. In this work we discuss Type-I metaphors
only. We use this knowledge represented in the form
of FOL formulas, to expand the existing metaphor
set. By using the closed world assumption, we show
how to extract metaphors from the existing knowl-
edge base.
FOL formulas are derived below:
• If a pair (x, y) belongs in Γ
m
, it is a metaphor. If
the pair is in Is-A knowledge base Γ
H
then that
means it has literal meaning and is not a metaphor.
If pair (x, y) belongs to Γ
m
as well as in Γ
H
, then
it has to removed from Γ
m
, because a metaphor
does not have a literal meaning.
∞ H(x, y) =⇒ ∼ m(x, y) (3)
where H(x, y) denotes (x,y) is a Hearst pair and
m(x, y) indicates (x,y) is a metaphor.
• If a new pair doesn’t belong to any of the sets,
there is a possibility that it is a new metaphor.
We expand the Γ
m
by obtaining metaphors de-
rived from Γ
m
and Γ
H
. We use a known metaphor
m(x, y) and a compatible Hearst pattern H(x, h
x
)
for deriving a new metaphor.
Let (x, y) ∈ Γ
m
and (x, h
x
) ∈ Γ
H
, using transitive
property we add this derived metaphor (h
x
, y) to
Γ
m
.
w
1
m(x, y) ∧ H(x, h
x
) =⇒ m(h
x
, y) (4)
• Next, we use the new metaphor for further expan-
sion.
w
2
m(x, y) ∧ H(h
x
, x) =⇒ m(h
x
, y) (5)
For each grounding of formula the weights are same.
A formula with infinity (∞) as a weight indicates a
hard rule.
4.2 MLN Constructed for Metaphor Set
Expansion Problem
We present an example to illustrate the working of
Markov logic network. Let H be the set of Hearst
pairs and m be the metaphoric pairs, the two formulas
(3 and 4) are re-written as
g
1
: H(x, y) =⇒ ∼ m(x, y)
g
2
: m(x, y) ∧ H(x, z) =⇒ m(z, y)
Given a knowledge base with x, y and z as vari-
ables and constant set C = {apple, f uel, f ruit}.The
formula g
1
will have 9 instances, as shown in Table 1.
Similarly, formula g
2
will have 27 instances shown in
Table 2.
Combining all the ground predicates obtained
from formula g
1
and g
2
together, we get the ground
Markov network with 18 ground predicates. Figure 5
shows a section of the ground Markov network.
Table 1: Ground formulas for g
1
with all possible predicates
N
indicates a ground predicate.
• g
1,1
:
1
H(apple, f ruit) ⇒∼ m(apple, f ruit)
2
• g
1,2
:
3
H(apple, f uel) ⇒∼ m(apple, f uel)
4
• g
1,3
:
5
H( f ruit, f uel) ⇒∼ m( f ruit, f uel)
6
• g
1,4
:
7
H( f ruit, apple) ⇒∼ m( f ruit, apple)
8
• g
1,5
:
9
H( f uel, apple) ⇒∼ m( f uel, apple)
10
• g
1,6
:
11
H( f uel, f ruit) ⇒∼ m( f uel, f ruit)
12
• g
1,7
:
13
H(apple, apple) ⇒∼ m(apple, apple)
14
• g
1,8
:
15
H( f ruit, f ruit) ⇒∼ m( f ruit, f ruit)
16
• g
1,9
:
17
H( f uel, f uel) ⇒∼ m( f uel, f uel)
18
H(apple, f ruit) m(apple, f ruit)
g
1,1
Figure 3: Predicates with factor nodes for formula g
1
.
We represent the ground predicates in the form of
graph as shown in Figure 3 and 4. Each ground pred-
icate is represented as a node, if two nodes are related
there is an edge between them and this relation among
nodes is given by a factor node.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
624

Using constant set C, we get 9 sub-graphs
g
1,1
...g
1,9
shown in Figure 3, each with 2 nodes using
formula g
1
and 27 sub-graph g
2,1
...g
2,27
each with 3
nodes using formula g
2
as shown in Figure 4.
4.3 Inference using MLN
The constructed MLN can now be used for inference.
For the given evidence it can compute probability of
the desired query. For the above example, we have
m(apple, f uel) and H(apple, f ruit) in the evidence
set. And we wish to compute how likely the predi-
cate m( f ruit, f uel) is. The corresponding conditional
probability is,
P[m( f ruit, f uel)| m(apple, f uel), H(apple, f ruit)] =
P[m( f ruit, f uel)=1,m(apple, f uel)=1,H(apple, f ruit)=1]
P[m(apple, f uel)=1,H(apple, f ruit)=1]
(6)
To solve a network with 18 predicates (specified
in Table I) there will be 2
18
possible worlds. If
a predicate is present in a specific world its value
will be 1 else 0. Lets denote each predicate with a
number as follows, H(apple, f ruit) numbered as
1
,
m(apple, f uel) as
4
,m( f ruit, f uel) as
6
and so on.
If presence of predicate is unknown it is denoted as
* (value as 0 or 1). In equation 6 numerator, value
of
1
,
4
,
6
= 1 and rest unknown *. Similarly, for
denominator
1
and
4
have value as 1. Substituting
values for predicates in equation 6, we get
P[m( f ruit, f uel)| m(apple, f uel), H(apple, f ruit)] =
{1,∗,∗,1,∗,1,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗}
{1,∗,∗,1,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗,∗}
m( f ruit, f uel)
m(apple, f uel) H(apple, f ruit)
g
2,1
Figure 4: Factor node among related nodes.
Table 2: Ground formulas of g
2
.
• g
2,1
: m(apple, f uel) ∧ H(apple, f ruit) ⇒ m( f ruit, f uel)
• g
2,2
: m(apple, f ruit) ∧ H(apple, f uel) ⇒ m( f ruit, f uel)
. .
. .
• g
2,26
: m( f uel, f ruit) ∧ H( f uel, apple) ⇒ m(apple, f ruit)
• g
2,27
: m(f ruit, Apple) ∧ H( f ruit, f uel) ⇒ m( f uel, apple)
m( f ruit, f uel)
m(apple, f uel) H(apple, f ruit)
H( f ruit, apple)
m(apple, apple)
m( f ruit, apple)
H(apple, apple)
g
2,1
g
2,6
g
2,3
g
1,7
Figure 5: A section of ground Markov network.
5 EXPERIMENTAL RESULTS
5.1 Dataset and Tool
We have used dataset from Microsoft concept graph
for short text understanding (Wu et al., 2012),
that provides the core version of Is-A data mined
from billions of web pages. This data contains
5,376,526 unique concepts, 12,501,527 unique in-
stances, and 85,101,174 Is-A relations (Cheng et al.,
2015). From these Is-A relations, we build the Hearst
pairs Γ
H
using pairs of concepts and instance as
(Instance, Concepts) and include related metaphor
pairs in Γ
m
to expand the existing metaphor set Γ
m
.
Experiments are carried in ‘Tuffy’ (Niu et al., 2011).
It takes 3 input files: (1) program.mln stores pred-
icates with their definitions and formulas with their
respective weights. (2)evidence.db consisting avail-
able ground terms and (3) a query.db. The output to
the inference result is test.txt.
5.2 Expansion of Metaphor Set in Case
of Unique Hearst Pairs in the
Evidence Set
To know the confidence of the outcome, we calcu-
late the marginal probabilities for derived metaphor.
These results may vary as Tuffy takes different sam-
ples each time. An example of a program for
metaphor expansion given in section 4.2, probabil-
ity values of the resultant marginal probability of
Markov Logic Network for Metaphor Set Expansion
625

Table 3: A program for metaphor set expansion with unique Hearst pairs.
Program.mln Evidence.db Query Output.txt
∗ob j(ob ject) ob j(apple) m(x, y)
∗H(ob j, ob j) ob j( f ruit)
m(ob j, ob j) ob j( f uel)
!H(a1, a2)∨!m(a1, a2). H(apple, f ruit)
1 !m(a1, a2)∨!H(a1, a3) ∨ m(a3, a2)
m(apple, f uel)
1 !m(a1, a2)∨!H(a3, a1) ∨ m(a3, a2) 0.7110 m(“ f ruit, f uel”)
10 !m(a1, a2)∨!H(a1, a3) ∨ m(a3, a2)
5 !m(a1, a2)∨!H(a3, a1) ∨ m(a3, a2) 0.9960 m(“ f ruit, f uel”)
A MLN program with different evidence set.
∗ob j(ob ject) ob j(apple) m(x, y) 0.994 m(“brand, money”)
∗H(ob j, ob j) ob j(brand) 0.783 m(“business, money”)
∗HighH(ob j, ob j) ob j(money) 0.684 m(“gadget, money”)
m(ob j, ob j) ob j(business)
!HighH(a1, a2)∨!m(a1, a2). HighH(apple, brand)
10 !m(a1, a2)∨!HighH(a1, a3) ∨ m(a3, a2) H(apple, business)
1 !m(a1, a2)∨!H(a1, a3) ∨ m(a3, a2) m(apple, money)
Table 4: A program for Metaphor set expansion with Multiple Hearst pairs.
Program.mln Evidence.db Query.db Average marginal
probabilities
∗ob j(ob ject) ob j(apple) m(x, y) 0.9960 m(“ f ruit, f uel”)
∗H(ob j, ob j) ob j( f uel) 0.6730 m(“gadget, f uel”)
∗HighH(ob j, ob j) ob j( f ruit)
m(ob j, ob j) ob j(gadget)
!HighH(a1, a2)∨!m(a1, a2). HighH(apple, f ruit)
10 !m(a1, a2)∨!HighH(a1, a3) ∨ m(a3, a2) H(apple, gadget)
1 !m(a1, a2)∨!H(a1, a3) ∨ m(a3, a2) m(apple, f uel)
(a) Marginal probability val-
ues with unique Hearst pairs.
(b) Marginal probability
value with multiple Hearst
pairs.
Figure 6: Average marginal probabilities of pairs to be in-
cluded in the expanded metaphor set.
m(Fruit, Fuel) = 0.7110 shown in Table 3.
Additionally, variation in weights of the formulas
provides a way to control the contribution of formulas
in computation of the probability value of the query.
For instance, in Table 3, with higher weights, w
1
= 10
and w
2
= 5 results in higher probability values com-
pared with the previous.
Figure 7: Knowledge base used in weight learning for
metaphor expansion.
5.3 Expansion of Metaphor in Case of
Multiple Occurrences of Hearst
Pairs in Evidence Set
If a particular pair is occurring more than once in
the dataset, it means the usage of that Is-A pair is
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
626

Figure 8: Weights learned using evidence given in Figure 6
as knowledge base.
Table 5: A small dataset for comparing both existing and
proposed method for metaphor set expansion.
x = {Apple, Orange} h
x
= { f ruit, company}
Hearst pairs Metaphor pairs
H(Apple, f ruit) m(Apple, f uel)
H(Apple, company)
H(Orange, f ruit)
m(“orange, f uel”) =?
high. We indicate this by introducing a predicate
HighH(a, b) as shown in Table 4, depicting Hearst
pair H(a, b) has high occurrence in evidence data set.
5.4 An Experiment on Larger Dataset
We next perform experiments on a relative larger data
set. We use 344 Is-A pairs out of which 56 belongs to
Γ
m
and the rest in Γ
H
. We experimented using single
occurrence of Hearst pairs as well as multiple occur-
rences. The results are shown in Figure 6(a) and 6(b).
We conclude that the average weight for the derived
metaphors (h
x
, y) are greater than that of the other ex-
tracted candidate metaphor pairs.
5.5 An Experiment on Weight Learning
from Training Dataset
Weight learning in MLN is similar to inference pro-
gram. MLN tries to learn the weights using the given
evidence dataset as input and computes the weights of
the formula by maximizing likelihood of given dataset
(Doan et al., 2011).
We tried weight learning of metaphor expansion
problem, with same MLN program and an instance
of the larger dataset shown in figure 7. A specimen
of the knowledge base used is given in Figure 6. We
learn the weights by running the program for 50 iter-
ations with 20 samples in each iteration. The average
weights learnt are shown in Figure 8.
In Table 7, we compare the results using both
unique as well as multiple occurrence of Hearst pairs
in knowledge base Γ
H
for fixed and learnt weights.
5.6 Comparison with the Existing
Data-driven Approach
We compare our experimental results with previous
data driven approach (Li et al., 2013) for metaphor
set expansion. We performed our experiments us-
ing Type-I metaphor, where the source and target
pairs are explicitly defined. The odds of a pair be-
ing a metaphor, probability values are considered. We
can argue that MLN does a meaningful job in cal-
culating the odds of pair being a metaphor, as MLN
helps soften the constraints, we can get higher prob-
ability values, hence more number of new extracted
metaphor pairs.
As shown in Table 6 with (x, y) ≡ (Orange, f uel),
if we compare the respective probability values for
pair (x, y) by existing and MLN methods, it is ob-
served from Table 8, that the proposed MLN based
approach gives better probability values by softening
the constraints.
6 CONCLUSION
In this work, we have shown a possibility of using
MLN for metaphor set expansion. We have used a
set of Is-A patterns divided into a metaphor set and a
literal set, for identifying potential metaphors.
A single rule base was formulated and converted
to the first order logic formulas. Further, based on the
importance of rules the weights were assigned appro-
priately. From results of the experiments carried out it
is evident that the proposed approach is able to draw a
meaningful inference by assigning appropriate prob-
ability values, even in case of multiplicity of Hearst
pairs.
It follows from our formulation that the estimated
marginal probability values of resultant metaphors
due to multiple occurrence of Hearst pairs in the
knowledge base will differ from unique occurrence
case. It also shows that information completion with
MLN provides explainable and meaningful results in
comparison with the existing completion methods.
We would like to work on a domain specific
dataset and explore the possibility of automated
metaphor generation. In addition, we also would like
to extend the existing work to incorporate Type-II and
Type-III metaphors.
Markov Logic Network for Metaphor Set Expansion
627
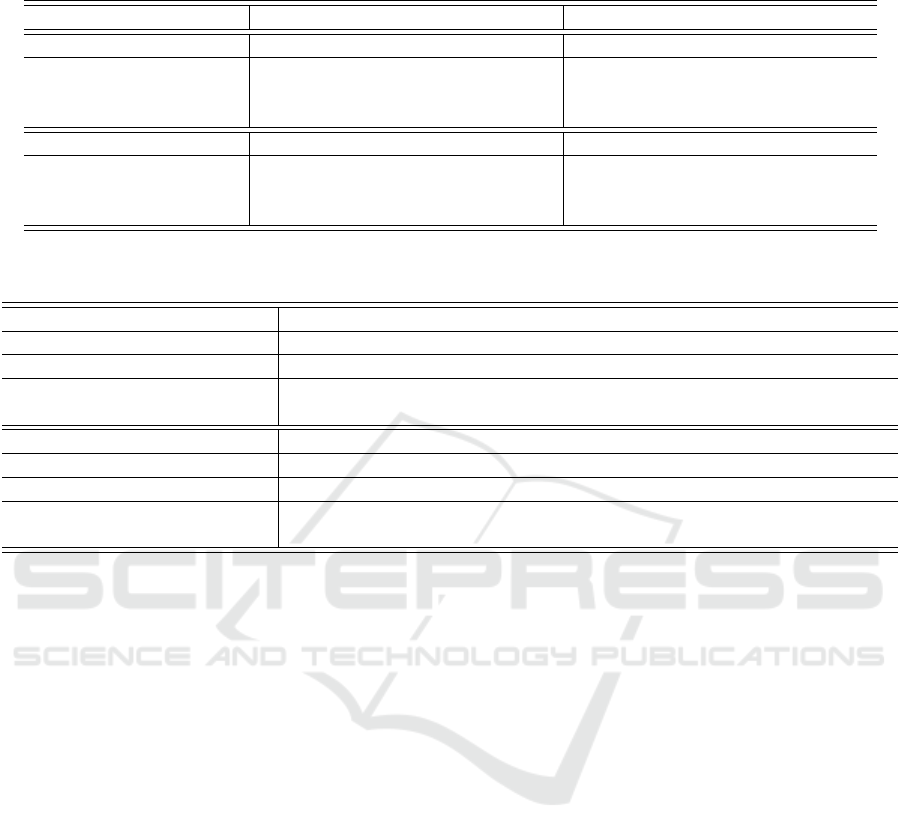
Table 6: Weight learning of formulas with unique occurrence of Hearst pairs vs multiple occurrence of Hearst pairs.
Unique occurrence Multiple occurrence
Initial weights w
1
= 1, w
2
= 1 w
1
= 10, w
2
= 1
Prob. using initial weights m(“ f ruit, f uel”) = 0.6600 m(“ f ruit, f uel”) = 0.9990
m(“orange, f uel”) = 0.7600 m(“orange, f uel”) = 0.7460
m(“company, f uel”) = 0.7600 m(“company, f uel”) = 0.8970
Learned weights w
1
= 4.3, w
2
= 13.1 w
1
= 2.2, w
2
= 8.1
Prob. using actual weights m(“ f ruit, f uel”) = 0.9400 m(“ f ruit, f uel”) = 0.7900
m(“orange, f uel”) = 0.9400 m(“orange, f uel”) = 0.8300
m(“company, f uel”) = 0.9900 m(“company, f uel”) = 0.8100
Table 7: Inference results using the data driven approach(Li et al., 2013) vs the proposed approach for a MLN method using
small example dataset.
Single occurrence Existing Method (Li et al., 2013) Proposed Method
Modern decision parameters δ = 0.5714 w
1
= 10, w
2
= 1
Marginal prob. of (x, y) m(“Orange, f uel”) = 0.1428 m(“Orange,fuel”) = 0.5800
Prob. of derived metaphor (h
x
, y) m(“ f ruit, f uel”) = 0.2857 m(“fruit,fuel”)= 0.6600
m(“company, f uel”) = 0.1428 m(“company,fuel”)= 0.7600
Multiple occurrence
Modern decision parameters δ = 0.5849 w
1
= 10, w
2
= 1
Marginal prob. of (x, y) m(“Orange, f uel”) = 0.2830 m(“Orange,fuel”) = 0.7460
Prob. of derived metaphor (h
x
, y) m(“ f ruit, f uel”) = 0.5660 m(“fruit,fuel”) = 0.9990
m(“company, f uel”) = 0.2325 m(“company,fuel”) = 0.8970
REFERENCES
Cheng, J., Wang, Z., Wen, J.-R., Yan, J., and Chen, Z.
(2015). Contextual text understanding in distribu-
tional semantic space. In ACM International Con-
ference on Information and Knowledge Management
(CIKM). ACM - Association for Computing Machin-
ery.
Doan, A., Niu, F., R
´
e, C., Shavlik, J., and Zhang, C. (2011).
User manual of tuffy 0.3. Technical report.
Domingos, P., Kok, S., Lowd, D., Poon, H., Richardson, M.,
and Singla, P. (2008). Markov Logic, pages 92–117.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Fass, D. (1991). met*: A method for discriminating
metonymy and metaphor by computer. Computational
Linguistics, 17(1):49–90.
Lakoff, G. and Johnson, M. (1980). Metaphors we Live by.
University of Chicago Press, Chicago.
Li, H., Zhu, K. Q., and Wang, H. (2013). Data-driven
metaphor recognition and explanation. Transac-
tions of the Association for Computational Linguis-
tics, 1:379–390.
Niu, F., R
´
e, C., Doan, A., and Shavlik, J. W. (2011). Tuffy:
Scaling up statistical inference in markov logic net-
works using an RDBMS. CoRR, abs/1104.3216.
Richardson, M. and Domingos, P. (2006). Markov logic
networks. Machine learning, 62(1-2):107–136.
Schulder, M. and Hovy, E. (2014). Metaphor detection
through term relevance. In Proceedings of the Second
Workshop on Metaphor in NLP, pages 18–26, Balti-
more, MD. Association for Computational Linguis-
tics.
Shutova, E. (2010). Models of metaphor in NLP. In Pro-
ceedings of the 48th Annual Meeting of the Associ-
ation for Computational Linguistics, pages 688–697,
Uppsala, Sweden. Association for Computational Lin-
guistics.
Tsvetkov, Y., Boytsov, L., Gershman, A., Nyberg, E., and
Dyer, C. (2014). Metaphor detection with cross-
lingual model transfer. In Proceedings of the 52nd
Annual Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers), pages 248–258,
Baltimore, Maryland. Association for Computational
Linguistics.
Wu, W., Li, H., Wang, H., and Zhu, K. Q. (2012). Probase:
A probabilistic taxonomy for text understanding. In
ACM International Conference on Management of
Data (SIGMOD).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
628
