
CAMP-IRL Agents: Extracting Multiple Behavior Profiles
for Pedestrian Simulation
Nahum Alvarez
1 a
and Itsuki Noda
2 b
1
Airbus Central Research & Technology, Munich, Germany
2
National Institute of Advanced Industrial Science and Technology, Japan
Keywords:
Pedestrian Simulators, Agent Behavior, Inverse Reinforcement Learning.
Abstract:
Crowd simulation has been subject of study due to its applications in the fields of evacuation management,
smart town planning and business strategic placing. Simulations of human behavior have many useful ap-
plications but are limited in their flexibility. A possible solution to that issue is to use semi-supervised ma-
chine learning techniques to extract action patterns for the simulation. In this paper, we present a model for
agent-based crowd simulation that generates agents capable of navigating efficiently across a map attending
to different goal driven behaviors. We designed an agent model capable of using the different behavior pat-
terns obtained from training data, imitating the behavior of the real pedestrians and we compared it with other
models attending to behavioral metrics.
1 INTRODUCTION
Crowd behavior simulation has a large number of ap-
plications in diverse domains. However, experiment-
ing with real crowd presents a number of logistic dif-
ficulties and it is usually not practical, or even infea-
sible in certain instances. Therefore, a way to solve
this issue is to use a simulator in order to replicate
the desired scenario. Agent based models are com-
monly used to perform those simulations, due to their
flexibility and scalability, and allow to produce com-
plex crowd interactions using models composed of
simple actions, given that we understand its behavior
rules. However, modeling human behavior is a com-
plex problem due to be subject to hidden rules; the re-
sulting behavior appears to follow sub-optimal plans
that are difficult to understand. A way to approach
this problem is to use machine learning techniques on
available data in order to give the agents a way to react
to new but similar situations.
In this paper, we present an agent model that
works with a novel variant of Inverse Reinforcement
Learning (IRL from here on), able to capture hidden
pedestrian behavior rules training with observed data.
The model then applies those rules to agents simu-
lating pedestrians, giving them decision making ca-
a
https://orcid.org/0000-0003-1717-2506
b
https://orcid.org/0000-0003-1987-5336
pabilities. Our technique allows to evaluate different
sets of actions depending on the location of the agent,
extracting different behavior patterns, called policies,
from the data. Hence, we called this method ”Con-
textual Action Multiple Policy Inverse Reinforcement
Learning”, or CAMP-IRL. Our objective is to repro-
duce more realistic pedestrian behavior, and by ana-
lyzing how this behavior is influenced by the features
in the environment, we would be able to decide which
spot is best for certain type of feature and how would
change pedestrian affluence if we add new features or
modify the existent ones.
The rest of the present document is organized as
follows: Section 2 consists on a survey of related
work about IRL in agent behavior and pedestrian sim-
ulators. Our crowd simulator and its architecture are
described in Section 3, and the CAMP-IRL technique
and the behavioral model of the agents are detailed
in Section 4. Section 5 contains our behavior com-
parison experiment and its results. Finally section 6
presents our conclusions.
2 IRL IN CROWD SIMULATORS
Pedestrian and traffic simulations have been the object
of interest because it can deal with a number of real-
life problems in our society. For example, it can be
216
Alvarez, N. and Noda, I.
CAMP-IRL Agents: Extracting Multiple Behavior Profiles for Pedestrian Simulation.
DOI: 10.5220/0010209602160223
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 216-223
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

used to improve transportation systems and networks
and in obtaining solutions to lower car pollution (Fac-
cin et al., 2017), or to assist in the design of evac-
uation strategies in concrete scenarios like natural or
disasters (Yamashita et al., 2009) or terrorist incidents
(L
¨
ammel et al., 2010).
There is a wide spectrum of works in pedestrian
simulation with agents, using different techniques.
Systems based in video analysis give good results,
like the one found in (Zhong et al., 2016), but in
order to remain practical they narrow their domain,
using tile location and pre-generated trajectories for
the agents. Another common strategy is to model the
agents with a dual behavior system controlling two
types of movement: micro and macro movement. The
first deals with collision avoiding in the near space
and adjusting the agent’s velocity in the crowd’s flow,
and the second is the one in charge of driving the
agent towards its goal, creating and updating its route
and taking care of the decision making process (Tor-
rens et al., 2012). Our pedestrian simulator, uses as
well a multi-agent approach to represent pedestrians.
Instead of scripting the agents by hand, having
low flexibility and escalating badly, we can take ad-
vantage of machine learning techniques to learn their
behavior. Concretely, apprenticeship learning meth-
ods have been widely used in intelligent agents’ sys-
tems to train them to perform tasks in dynamic envi-
ronments like (Svetlik et al., 2016) or observe strate-
gies to emulate predefined driving behaviors in (Fac-
cin et al., 2017). There are also works where agents
are given a behavior cognitive model for pedestrians
like in (Luo et al., 2008), (Martinez-Gil et al., 2017)
or (Crociani et al., 2016). However, we see that in all
of those works the behavior model (i.e. the policies
ruling the agents) is predefined by a designer, but in
the case of pedestrians, the rules and goals directing
their actions are not visible, so learning those behav-
ior patterns is a difficult problem.
To overcome this problem, an useful technique is
Inverse Reinforcement Learning, being appropriate to
model behavior because it tackles the problem of not
knowing the reward function that drives the behav-
ior, needing a set of expert demonstrations (Ng et al.,
2000). IRL techniques work on domains that can be
modeled by a Markov Decision Process (MDP, from
here on after) and are used to learn its hidden reward
function. Works using IRL to control agent behav-
ior are sparse but effective (Herman et al., 2016), as
it is shown in (Abbeel and Ng, 2004) where driving
styles are learned by an agent, or (Natarajan et al.,
2010) where different agents work together for rout-
ing traffic. Other IRL methods perform even better,
like (Dvijotham and Todorov, 2010), which works on
a subset of MDPs, but it does not match well with our
domain, or (Levine et al., 2011) which works with
non-linear reward functions.
As different pedestrians have different goals that
drive different types of behavior, we should learn each
one separately instead of merging all of them in one.
Obtaining multiple policies from observed behavior
has already been tackled by a number of works. We
can consider plan recognition techniques, like the one
contained in (Ram
´
ırez and Geffner, 2009), used to
identify the objective of the agent in an observed state,
selecting it from a list of defined goals. These kinds
of techniques work well and have good performance
when compared with IRL basic approaches, like max-
imum entropy IRL, as seen in (Lelerre et al., 2017)
or (Le Guillarme et al., 2016). However, our pedes-
trian behavior domain has a number of desired re-
quirements that would be very limited if we use these
techniques: they assume that the agent’s decisions
should be optimal, with deterministic state transitions,
but real pedestrians do not have those characteristics.
Also, they select the goals from a predefined set, but
we may not have that information in the training data.
Finally, they consider the goals as mutually exclusive,
whilst actual pedestrians behavior is a product of the
combination of goals.
With this requirements in mind, we preferred to
explore unsupervised learning techniques to segment
the data into different behavior profiles, and looked
to approaches that mix well with our IRL behavior
model. In (Surana and Srivastava, 2014), we can find
a method to switch between different MDPs to ob-
tain their related policy functions that works reason-
ably well extracting different behaviors. (Michini and
How, 2012) show how to divide the data in smaller
sub-goals in order to obtain simple reward functions,
and (Krishnan et al., 2016) describe a hierarchical
method for selecting MDP partitions with different
policies for each sub-MDP, which can be interest-
ing for domains where the agent has a number of se-
quential small sub-goals. In our case, we decided to
based our method on the one found in (Choi and Kim,
2012), which is able to infer different policies from
the data by clustering the trajectories in the training.
3 PEDESTRIAN SIMULATOR
Our simulator, called CrowdWalk (Alvarez and Noda,
2018), is a pedestrian simulator designed for generic
uses, where each pedestrian is represented by an
agent. CrowdWalk allows the generation of complex
behavior and escalates well, being suitable for large
scenarios with high numbers of agents; it can simulate
CAMP-IRL Agents: Extracting Multiple Behavior Profiles for Pedestrian Simulation
217

movements of more than 1 million agents in a diverse
array of locations, like multi-storied buildings or large
city areas. Maps can be created by hand or obtained
from open source formats, and pedestrian behaviors
are configurable so that we can conduct simulations
with various situations. Internally, CrowdWalk uses
a Network-based model; the map is described in the
form of a network where nodes represent intersections
and links represent paths. A link has length and width
attributes, influencing how long the agents need to
walk from an end to another and how many agents
can walk in parallel, and can be two-way or one-way.
Nodes and links can contain features, usually describ-
ing what facilities are on that location.
CrowdWalk contains an agent factory that gen-
erates one agent per pedestrian. Each agent has its
own decision model, composed by the micro and
macro behavior modules. The micro behavior mod-
ule in each agent takes care of micro movements au-
tomatically, calculating when an agent has to stop,
walk slower or deciding when it is unable to continue
through the current path. The speed of an agent is
given in relation with the density of the link it is cur-
rently in, being slower as the link is more crowded,
until a maximum capacity limit where it is not possi-
ble to continue advancing. The macro behavior mod-
ule is the one in charge of planning the agent’s route
to its goal, and updating it if necessary. Our CAMP-
IRL module controls directly this module when it is
used.
4 AGENT MODEL
Our CAMP-IRL module contains two separated parts:
one part is executed before the simulation, which con-
tains the CAMP-IRL method itself, and the other con-
trols the agents’ macro behavior during the simula-
tion, being the CAMP-IRL agents’ controller. The
next subsections describe in depth each one of those.
4.1 The CAMP-IRL Learning Process
The CAMP-IRL method consists in a non-parametric
Bayesian approach to IRL, that works with an adap-
tation of the MDP to our domain.
We define Contextual Action Multiple Policy
MDP(CAMP-MDP) as an MDP {S,A,T ,γ,R } us-
ing the definition of S as the set of states, the transi-
tion function T (s, a, s’ ) from one state to another by
executing an action, and γ as the discount factor.
We also define the super set A(s) of actions as a
function of a state s, and a set of Reward functions R .
Each reward function can be defined as R(s) where s ∈
S and can be used to generate a policy π that contains
a list of consecutive pairs of states and actions in the
form s,a where a ∈ A(s). This allows for each state
to have a different set of actions.
In our domain, where each map node has a dif-
ferent number of possible links to take, we can iden-
tify each node with a state and the links available to
them to their set of actions. To reduce the size of
the solution space, those actions are contextual, so
they have different meaning depending on the current
state, keeping the total number of actions small. Also,
the map features contained on each node, are assigned
to the correspondent states, and will be used in the
training process
The CAMP-IRL algorithm is based on the Dirich-
let process mixture model Bayesian IRL, adapting it
to be able to work with a CAMP-MDP, considering
that each state will have a different action set. The
Dirichlet process (Neal, 2000) is used to classify the
trajectories into different clusters, and then the reward
is calculated for each cluster using a Bayesian ap-
proach to the IRL method using the next algorithm
and formulas:
1. Initialize the cluster set C containing K elements
and the reward set {r}
K
k=1
.
(i) The initial clusters and their reward function
are randomized. The reward function consists
in a weight vector containing the weights of all
the map features.
(ii) An initial policy is generated randomly from
each reward. This policy consists in a vector
containing the optimal action to perform for
each node, and it is obtained by calculating the
value of performing the most optimal action a
from the available actions in the state s follow-
ing the next function:
V
∗
(s) = max
a∈A(s)
R (s,a) + γ
∑
s
0
∈S
T (s,a,s
0
)V
∗
(s
0
)
2. For each element m in the trajectory set, select
a new cluster candidate c
∗
m
using the following
rules:
(i) If the trajectory has no assigned cluster, gener-
ate a new one and a reward function for it
(ii) If it has one, obtain the most populated cluster
(iii) Assign the trajectory to the new cluster with
probability:
P(X
m
|c
∗
m
)
P(X
m
|c
m
)
3. For each cluster k:
(i) Create a weight vector candidate
r
∗
k
= r
k
+
τ
2
2
∇log(P(X
k
|r
k
)P(r
k
)) +τα
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
218

where τ is a scaling factor and α is a random
number sampled from a multinomial distribu-
tion (0,1).
(ii) Update the weight vectors with probability
P(X
k
|r
∗
k
)P(r
∗
k
)g(r
∗
k
,r
k
)
P(X
k
|r
k
)P(r
k
)g(r
k
,r
∗
k
)
being the function g() the gradient from the
Langevin algorithm calculated as follows:
g(x,y) =
exp
−1
2 τ
2
x − y −
τ
2
2
∇log(P(X
k
|x)P(x))
(2πτ
2
)
D/2
where τ is a scaling factor.
4. Repeat the process from (2) until convergence.
Once finished, it is possible to use the obtained
set of optimal policies for each cluster to calcu-
late the value vector as follows:
V
π
(s) = R (s,π) + γ
∑
s
0
∈S
T (s,π,s
0
)V
π
(s
0
)
This value represents the expected reward of exe-
cuting the policy π on a node s.
The inputs of the CAMP-IRL method are the map
used by CrowdWalk, which is converted into a
CAMP-MDP, and a file containing the trajectories we
want to train. Once the training process finishes, we
obtain two files: one containing the weight vectors of
the features of each discovered cluster, and another
containing the value of each map node (as defined in
the step 4 of the algorithm) for each cluster. We group
both weight vector and node’s values by the cluster
they belong to, defining these groups as ”behavior
profiles” and storing them in a file format. Thus, those
files will be used in the simulation by the CAMP-IRL
agents to select the behavior profile they should have
and which path to take.
Finally, this process can be iterated by simulating
agents with the obtained behavior profiles and train-
ing the system again with their resulting trajectories,
generating a new set of behavior profiles. We con-
sider this new set as a refinement of the original pro-
files, and in our experimental observations the new
ones performed always better than the originals; we
will extend more on this topic in the experiments sec-
tion.
4.2 The CAMP-IRL Agents
Once the simulation starts, CrowdWalk’s Agent Han-
dler creates the agents using our CAMP-IRL Agent
Controller. The CAMP-IRL agents use three input
files directing their behavior; the first two files are the
Weight and value files from the CAMP-IRL process,
and the third one consists in a database containing
their goals. Those can be generic features, like “visit-
ing a restaurant”, or concrete nodes from the map, like
“visiting the node labeled as nd00465”. Also, this file
contains an evacuation point to go after completing
the goals.
The decision making process of the CAMP-IRL
agent is shown in Figure 1. First, the agent selects the
profile that has the highest weight for the features as-
sociated to its goals. As the agent may have multiple
goals and also the weights may be similar, the agent
selects a set composed of the profiles that are within a
threshold from the one with the highest weight. From
the experience of our tests, we concluded that a 10%
of threshold gives the best results. The set of selected
profiles from the agent’s profile list. Once completed
this step, the agent chooses from this list the profile
with the highest value in its current node according to
the value file.
Whenever an agent enters in a node, it checks if
that is a goal in its list or not. In case it is not a
goal, the agent compares the value of the nodes con-
nected to the current one and selects randomly one
node within the set of best valued ones. This set is
created also using a threshold range from the highest
valued node, and again a threshold of a 10% gave us
the best results. The selection of the best valued nodes
ignores the node the agent is coming from, under the
rationale of the agent coming from a node with an al-
ready high value and having to conform with lower
values after that. Once the best node to go is selected,
the agent moves to it.
If the agent entered in a node containing a goal,
then the agent enters in an state of waiting, represent-
ing the agent satisfying its goal. The goal satisfaction
time is given by the training process, which in paral-
lel with the CAMP-IRL algorithm, performed a linear
regression to learn from the waiting times present in
the trajectories, using the node features to estimate
such time. When the goal is satisfied, the agent ver-
ifies if it has remaining goals. If all the goals have
been satisfied, the agent evacuates by going directly
to the evacuation point (this movement is no more be-
havioral, and is performed by calculating the shortest
route to the evacuation node).
If there are still goals unsatisfied, the agent pro-
ceeds to select a new profile. However, before select-
ing one it updates its profile’s list, as it has fewer goals
now, so some profiles are not useful anymore. After
deleting those profiles related with the satisfied goals,
the agent chooses a profile from its list in the same
way that it did initially.
Finally, the agent has a timeout in case it spends
too much time wandering across the map without
CAMP-IRL Agents: Extracting Multiple Behavior Profiles for Pedestrian Simulation
219
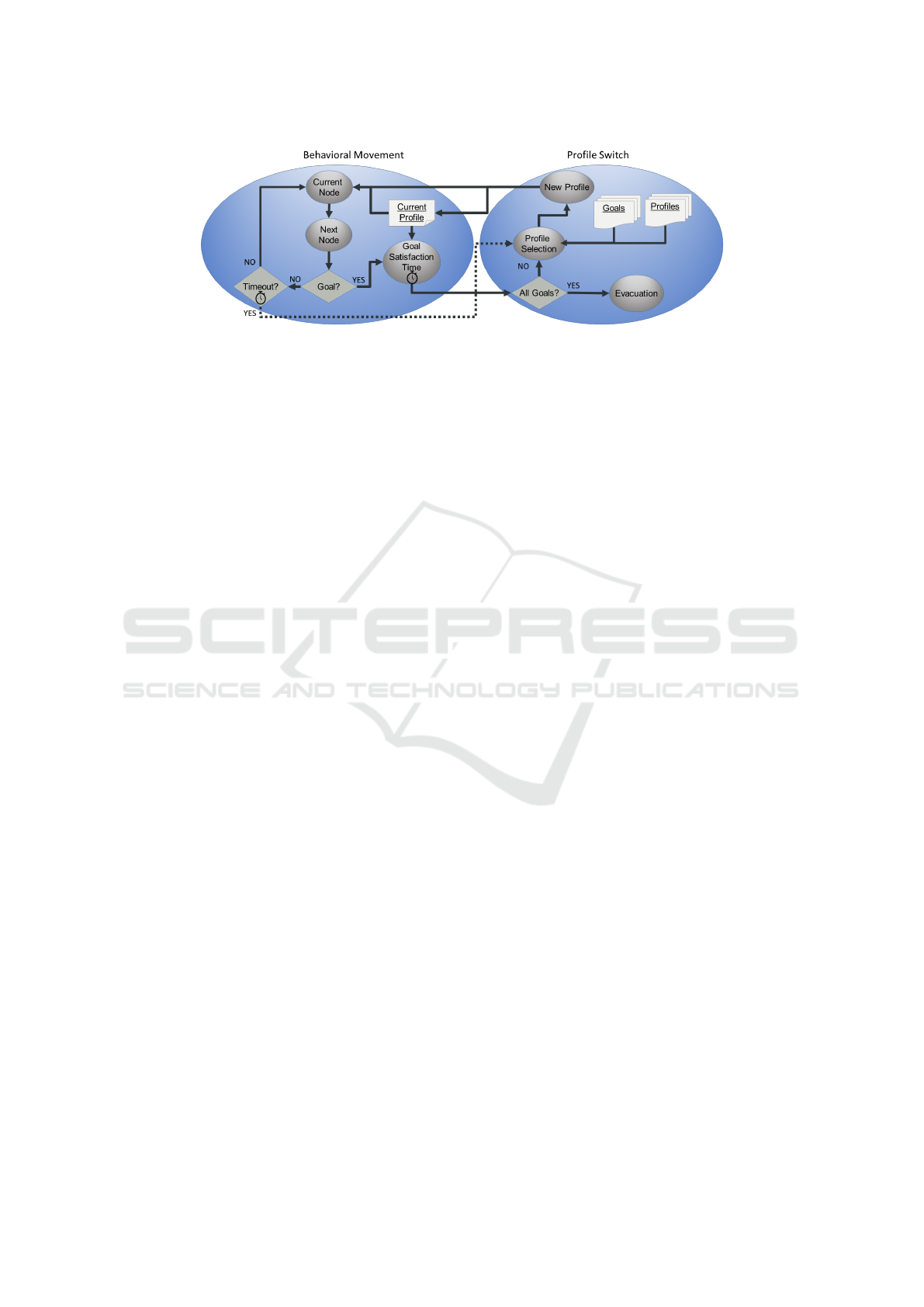
Figure 1: The CAMP-IRL agents’ algorithm. Once they reach a map node, they use the profile correspondent to its current
goal to choose the next one. If they satisfy a goal, they search for another one selecting the profile that suits it best.
reaching any goal. If the timeout finishes, the agent
will select a new profile, but this time the method it
uses is different. Instead of selecting a profile from
its profile’s list, the agent selects randomly another
profile from the whole set, with the only condition
that it has to be different than the previous one. This
represents the agent deciding that its previous actions
where not advancing it to the goal, and it has to “ex-
plore” the map.
5 EXPERIMENTAL RESULTS
We performed an experiment in order to evaluate two
aspects: first, the performance of the CAMP-IRL
agents, and second, their behavior similarity with the
trained data. For the first aspect, we measured the
time the agents took in satisfying goals belonging to
different pedestrian profiles whose trajectories were
previously trained. We compared our agents with
other types of agents: one agent using a different IRL
method that extracts only a unique policy and reward
function from the whole set of trajectories and does
not use contextual actions (this means it has a fix set
of actions and only one profile) called “Single IRL
Agent” and finally one agent that extracts multiple
profiles but with no contextual actions called “Multi
IRL Agent”. The Single IRL Agent used the max-
imum entropy algorithm from (Ziebart et al., 2008),
chosen because it works well when the agents do not
have much information about the layout of the map,
and the Multi IRL agent used the method shown in
(Choi and Kim, 2012). We also compared each type’s
coverage of the map.
The training set consisted in 150 trajectories that
could be divided into five hypothetical behavior pro-
files: “restaurant” for pedestrians that are going look-
ing for a place to eat; “books” for pedestrians that are
going to buy books, magazines or other paper ware;
“cinema” for pedestrians going to the cinema or simi-
lar entertainment places (theater, games, etc.); “shop-
ping” for pedestrians that want to buy clothes; and
finally “supermarket” that covers pedestrians going
to supermarkets or convenience stores. The trajecto-
ries were created by artificial methods due to the lack
of real data in this domain, but they were designed
to be as realistic as possible. The trajectories were
slightly noisy, with the pedestrians making small de-
tours and wandering a bit while they were going to
their goals. The map we used was a portion of Tokyo
from the Toshima ward area, containing commercial
areas, entertainment spots, a train station, and resi-
dential zones.
After we trained the system with the original train-
ing set, we obtained a total of 7 profiles for feeding
the agents, which will be called “CAMP-IRL A” from
here on. We observed that from these 7 profiles, three
of them were strongly related one-to-one to three of
the original behavior profiles we intended to train, and
the other four were a combination of some of the orig-
inal profiles. Then, after we trained again the system
with the trajectories obtained from a simulation using
these agents, we obtained a set of eight profiles for
a second agent, which we will call “CAMP-IRL B”.
Each training process took between 6 and 7 hours to
complete.
We observed that CAMP-IRL agents A and B had
three identical profiles, and other two profiles that
were moderately similar. Our explanation for this is
that some profiles are strongly tied to certain features,
like restaurants, or cinemas, but other are the prod-
uct of a combination of profiles, that represent more
generic activities like shopping. In the case of those
profiles moderately similar to others, it is because the
combination is similar with slight variations of the
features’ weight.
In the future will be interesting to isolate the pro-
file extraction from the IRL method, and comparing
it with other methods like the inverse planning tech-
niques we described in Section 2. Even with the re-
striction of having a predefined set of exclusive goals,
we could use it as a trade-off comparison. Also, inter-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
220

esting improvements to those methods have been pro-
posed, like in (Ram
´
ırez and Geffner, 2011), allowing
them to work with POMDP models, so we could use
them to work with no deterministic environments.
We prepared simulations for all the agent types.
The simulator was set under the same configuration
for each type: 150 agents, each one with five goals,
one for each one of the original profiles. Each simu-
lation was executed 20 times in order to average the
results; we considered this number enough to have
confidence in our validation as we did not observe a
significant deviation in the final results. Also, in or-
der to avoid adding noise to the results, we set all the
agents to not taking any time in satisfying the goals
and keep walking immediately; the training trajecto-
ries were also created without such delays.
Table 1: Average clear times by agent type.
Agents Individual Whole set
CAMP-IRL A 53:09 5:24:05
CAMP-IRL B 41:43 3:00:42
Multi IRL 1:30:13 10:16:31
Single IRL 2:22:06 12:33:04
Table1 shows the average times for an individual
agent to satisfy the goals and the average clear time
for the whole set of 150 agents of each simulation.
By seeing the results, we confirmed that CAMP-IRL
B agents obtain substantially better times than the oth-
ers, taking only three hours to complete the simula-
tion.
Table 2: Average trajectory length in number of nodes.
Agents Trajectory Length
Trained routes 41
CAMP-IRL A 75
CAMP-IRL B 56
Multi IRL 142
Single IRL 206
Table 2 shows the average trajectory length of each
type of agent, including training trajectories infor-
mation for reference reasons; CAMP-IRL agents not
only beat the others in the time to clear all the goals
but also their paths are more efficient, wandering less
than the others. The trajectories of CAMP-IRL B
agents were the closest to the trained routes.
Evaluating the second aspect, behavior, is more
difficult; we decided to compare agent’s behavior us-
ing as our metric the popularity of the map features
and goals, i.e. how often the agents traverse those
spots or go directly to there. It is important to note
that we do not want to replicate the trajectories, so us-
ing path comparison is not enough to give insight to
how similar the behavior is, and also images of the
trajectories generated by the different agents are ap-
parently similar. However, we can compare the most
popular nodes in the map for each feature and how the
agents distribute across them.
The rationale of this idea is the following: we can
identify popular nodes in the original training routes,
and future pedestrians should also consider them pop-
ular; however, as the training routes did not cover all
the possible routes and goal combinations, if we want
to imitate behavior instead of trajectory planning, the
pedestrian distribution on the test map should be dif-
ferent compared to the trained ones, but also the popu-
lar nodes should be still consistent. In sort, we search
for high similarity in the list of top ten popular nodes
and low similarity in the distribution of the agents
over that list. This effect also would allow to obtain
the expected popularity of areas with little or no data
by simulating the agents on them.
Table 3 shows the similarity degree between the
agents and the trained routes on node popularity and
on distribution of the agents when looking actively
for a goal node. We can see that in general all the
agents have high similarity in top node popularity,
with CAMP-IRL B agents having slightly higher val-
ues. This is due to IRL being a good method in gen-
eral to extract hidden rewards assigned to the nodes,
identifying which ones are the best to get goals. How-
ever, when we observe the distribution of the agents
across the map, we see that CAMP-IRL agents have
the lowest values, meaning that these agents choose
more diverse options while maintaining knowledge of
the rewards; on the other hand, agents with high val-
ues in the similarity of the distribution are inclined to
just imitate the trained routes. This follows the line
of our hypothesis: having high values in the top node
similarity, but low values in the distribution. We ob-
served a particular case with the cinema goal features;
as there are only 4 in the map, the top ten only con-
tained 4 nodes, and all the agents have maximum sim-
ilarity in that aspect. However, the distribution still
gets its lowest value with CAMP-IRL B agents.
A potential use of this analysis is to obtain the
list of nodes that are popular because they are sought
actively to satisfy a goal, or which ones are popular
because a high number of pedestrians are passing by
them. This information can be very useful to get busi-
ness insight of future facilities by simulating them on
the map with the CAMP-IRL agents. Also, by seeing
the results we can affirm that popular locations are
different if we use pedestrian affluence or goal driven
behavior as the metric to obtain, being both useful for
CAMP-IRL Agents: Extracting Multiple Behavior Profiles for Pedestrian Simulation
221

Table 3: Similarity with the training routes in goal popularity and similarity of the agent distribution across the top nodes.
Feature CAMP-IRL A CAMP-IRL B Multi IRL Single IRL
Distrib. Top Nodes Distrib. Top Nodes Distrib. Top Nodes Distrib. Top Nodes
Shop 63.47% 60% 59.36% 70% 82.01% 70% 71.96% 70%
Supermarket 51.72% 70% 48.16% 70% 60.91% 70% 71.81% 70%
Books 74.08% 90% 57.7% 90% 52.15% 80% 67.08% 90%
Cinema 74.68% 100% 60.73% 100% 65.85% 100% 87.42% 100%
Restaurant 47.46% 70% 53.01% 80% 68.72% 80% 63.08% 70%
Total 62.28% 78% 55.79% 82% 65.92% 80% 72.27% 80%
management reasons as we may be just looking for a
spot with high affluence in order to sell to casual cus-
tomers, or aim for more specialized customers that go
on purpose to certain locations.
We also noted space to improvement, as we ob-
served that some useful information from the map and
the routes is not being reflected in the learning pro-
cess: in the experiments, cinemas were a scarce fea-
ture that only was present in four nodes of the map;
the agents were able to find it, but the wandered exces-
sively before doing it. After analyzing why this was
happening, we found this situation was due to the co-
incidence of two factors: scarcity of the goal feature
and few and indirect ways to reach it. In our example
to reach one of those features, the agents had to cross
a large avenue which could only be crossed on cer-
tain points of the map, but those points were not very
remarkable in terms of value for the profile selected
to reach that feature. Thus, agents near that feature
were conducted by their profiles to go towards it, but
when reaching the large avenue they could not find the
crossing point which was far away. We plan to solve
this issue by enriching the map information, estab-
lishing semantic relations between nodes like those
crossing points and the featured nodes.
Finally, we observed consistently in our exper-
iments that the act of retraining the system with
CAMP-IRL agents as the source of data improved
greatly its performance, and after analyzing their be-
havior profiles, we noted that some of the profiles are
kept across the training steps, but other are combi-
nations of some sort. That may be the reason of the
improvement in the results, as those combined pro-
files are refined in subsequent training stages. Hence,
we want to analyze more in depth how this effect is
produced.
6 CONCLUSIONS
This paper presents a behavioral model for pedes-
trian agents using a technique called CAMP-IRL. The
CAMP-IRL method works with contextual actions,
different depending on the location of the agent, and
generates multiple policy functions for them, creat-
ing a profile per policy. Our model converts a city
map into a CAMP-MDP and trains with the trajec-
tories database, generating a set of behavior profiles.
These profiles are used to navigate across the map by
the agents, choosing the profile that fits best to their
goal. The generated agent behavior can be analyzed
then in order to obtain insight on what are the most
popular features in the map, and predict how would
be the performance of new ones.
We performed an experiment in order evaluate our
agents’ performance and how much similar are their
generated behaviors to the trained data. Our CAMP-
IRL agents perform better than others trained using
different methods and get the best clear times in the
simulator. They also have more optimal routes, with
results similar to the trained ones with the difference
of having no knowledge of the map. When looking
at behavior similarity, we observed that our agents
consider similar nodes for goal seeking as the train-
ing data, but their actual decisions are based on the
current surroundings and behavior profile, resulting
in a more different agent distribution. We also noted
in our experiments that re-training the system using
data obtained from a previously trained agents yielded
even better results, with CAMP-IRL B agents obtain-
ing consistently the best results in our tests.
We think the results of our experiment opened in-
teresting research paths, and we plan to add a pre-
processing step to the CAMP-IRL process to enrich
the map information, in order to improve more the
agents’ navigation around difficult areas. Also, we
observed that it is possible to extract knowledge of
the popularity of the map locations, either due to be-
ing an actively sought goal or due to be in spots very
transited or complementary to other goals, and pre-
dict the popularity of other areas, not only analyz-
ing pedestrian affluence but also goal driven behav-
ior, giving different results depending on which one
of those metrics is used. We plan to analyze how
re-training affects the profiles and how they are com-
bined in subsequent training cycles as the improve-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
222

ment in performance was very evident but still the
concrete reason being unclear.
ACKNOWLEDGEMENTS
This work was partially supported by JSPS KAK-
ENHI Grant Number 18H03301.
REFERENCES
Abbeel, P. and Ng, A. Y. (2004). Apprenticeship learning
via inverse reinforcement learning. In Proceedings of
the twenty-first international conference on Machine
learning, page 1. ACM.
Alvarez, N. and Noda, I. (2018). Inverse reinforcement
learning for agents behavior in a crowd simulator. In
International Workshop on Massively Multiagent Sys-
tems, pages 81–95. Springer.
Choi, J. and Kim, K.-E. (2012). Nonparametric bayesian in-
verse reinforcement learning for multiple reward func-
tions. In Advances in Neural Information Processing
Systems, pages 305–313.
Crociani, L., Vizzari, G., Yanagisawa, D., Nishinari, K., and
Bandini, S. (2016). Route choice in pedestrian sim-
ulation: Design and evaluation of a model based on
empirical observations. Intelligenza Artificiale, 10(2).
Dvijotham, K. and Todorov, E. (2010). Inverse optimal con-
trol with linearly-solvable mdps. In Proceedings of the
27th International Conference on Machine Learning.
Faccin, J., Nunes, I., and Bazzan, A. (2017). Understand-
ing the Behaviour of Learning-Based BDI Agents in
the Braess’ Paradox, pages 187–204. Springer Inter-
national Publishing.
Herman, M., Gindele, T., Wagner, J., Schmitt, F., Quignon,
C., and Burgard, W. (2016). Learning high-level nav-
igation strategies via inverse reinforcement learning:
A comparative analysis. In Australasian Joint Confer-
ence on Artificial Intelligence. Springer.
Krishnan, S., Garg, A., Liaw, R., Miller, L., Pokorny, F. T.,
and Goldberg, K. (2016). Hirl: Hierarchical inverse
reinforcement learning for long-horizon tasks with de-
layed rewards. arXiv preprint arXiv:1604.06508.
L
¨
ammel, G., Grether, D., and Nagel, K. (2010). The rep-
resentation and implementation of time-dependent in-
undation in large-scale microscopic evacuation simu-
lations. Transportation Research Part C: Emerging
Technologies, 18(1):84–98.
Le Guillarme, N., Mouaddib, A.-i., Gatepaille, S., and Bel-
lenger, A. (2016). Adversarial intention recognition as
inverse game-theoretic planning for threat assessment.
Lelerre, M., Mouaddib, A.-i., and Jeanpierre, L. (2017). Ro-
bust inverse planning approaches for policy estimation
of semi-autonomous agents. pages 951–958.
Levine, S., Popovic, Z., and Koltun, V. (2011). Nonlin-
ear inverse reinforcement learning with gaussian pro-
cesses. In Advances in Neural Information Processing
Systems, pages 19–27.
Luo, L., Zhou, S., Cai, W., Low, M. Y. H., Tian, F., Wang,
Y., Xiao, X., and Chen, D. (2008). Agent-based hu-
man behavior modeling for crowd simulation. Com-
puter Animation and Virtual Worlds, 19(3-4).
Martinez-Gil, F., Lozano, M., and Fern
´
andez, F. (2017).
Emergent behaviors and scalability for multi-agent re-
inforcement learning-based pedestrian models. Simu-
lation Modelling Practice and Theory, 74:117–133.
Michini, B. and How, J. P. (2012). Bayesian nonparamet-
ric inverse reinforcement learning. In Joint European
Conference on Machine Learning and Knowledge
Discovery in Databases, pages 148–163. Springer.
Natarajan, S., Kunapuli, G., Judah, K., Tadepalli, P., Ker-
sting, K., and Shavlik, J. (2010). Multi-agent inverse
reinforcement learning. In Ninth International Con-
ference on Machine Learning and Applications. IEEE.
Neal, R. M. (2000). Markov chain sampling methods for
dirichlet process mixture models. Journal of compu-
tational and graphical statistics, 9(2):249–265.
Ng, A. Y., Russell, S. J., et al. (2000). Algorithms for in-
verse reinforcement learning. In Icml, pages 663–670.
Ram
´
ırez, M. and Geffner, H. (2009). Plan recognition as
planning. In Proceedings of the 21st International
Joint Conference on Artifical Intelligence, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Ram
´
ırez, M. and Geffner, H. (2011). Goal recognition over
pomdps: Inferring the intention of a pomdp agent. In
Proceedings of the 22nd International Joint Confer-
ence on Artificial Intelligence, IJCAI’11. AAAI Press.
Surana, A. and Srivastava, K. (2014). Bayesian nonpara-
metric inverse reinforcement learning for switched
markov decision processes. In Machine Learning and
Applications (ICMLA), 2014 13th International Con-
ference on, pages 47–54. IEEE.
Svetlik, M., Leonetti, M., Sinapov, J., Shah, R., Walker,
N., and Stone, P. (2016). Automatic curriculum graph
generation for reinforcement learning agents.
Torrens, P. M., Nara, A., Li, X., Zhu, H., Griffin, W. A., and
Brown, S. B. (2012). An extensible simulation en-
vironment and movement metrics for testing walking
behavior in agent-based models. Computers, Environ-
ment and Urban Systems, 36(1):1–17.
Yamashita, T., Soeda, S., and Noda, I. (2009). Evacua-
tion planning assist system with network model-based
pedestrian simulator. In PRIMA. Springer.
Zhong, J., Cai, W., Luo, L., and Zhao, M. (2016). Learning
behavior patterns from video for agent-based crowd
modeling and simulation. Autonomous Agents and
Multi-Agent Systems, 30(5):990–1019.
Ziebart, B. D., Maas, A. L., Bagnell, J. A., and Dey,
A. K. (2008). Maximum entropy inverse reinforce-
ment learning. In AAAI, volume 8, pages 1433–1438.
Chicago, IL, USA.
CAMP-IRL Agents: Extracting Multiple Behavior Profiles for Pedestrian Simulation
223
