Online Learning of non-Markovian Reward Models

Gavin Rens

1 a

, Jean-Franc¸ois Raskin

, Rapha

el Reynouard

and Giuseppe Marra

1 b

DTAI Group, KU Leuven, Belgium

Universit

e Libre de Bruxelles, Belgium

Keywords:

non-Markovian Rewards, Learning Mealy Machines, Angluin’s Algorithm.

Abstract:

There are situations in which an agent should receive rewards only after having accomplished a series of

previous tasks, that is, rewards are non-Markovian. One natural and quite general way to represent history-

dependent rewards is via a Mealy machine. In our formal setting, we consider a Markov decision process

(MDP) that models the dynamics of the environment in which the agent evolves and a Mealy machine syn-

chronized with this MDP to formalize the non-Markovian reward function. While the MDP is known by the

agent, the reward function is unknown to the agent and must be learned. Our approach to overcome this chal-

lenge is to use Angluin’s L

∗

active learning algorithm to learn a Mealy machine representing the underlying

non-Markovian reward machine (MRM). Formal methods are used to determine the optimal strategy for an-

swering so-called membership queries posed by L

∗

. Moreover, we prove that the expected reward achieved

will eventually be at least as much as a given, reasonable value provided by a domain expert. We evaluate our

framework on two problems. The results show that using L

∗

to learn an MRM in a non-Markovian reward

decision process is effective.

1 INTRODUCTION

Traditionally, a Markov Decision Process (MDP)

models the probability of going to a state s

from the

current state s while taking a given action a together

with an immediate reward that is received while per-

forming a from s. This immediate reward is deﬁned

regardless of the history of states traversed in the past.

Such immediate rewards thus have the Markovian

property. But many situations require the reward to

depend on the history of states visited so far. A reward

may depend on the particular sequence of (sub)tasks

that has been completed. For instance, when a nu-

clear power plant is shut down in an emergency, there

is a speciﬁc sequence of operations to follow to avoid

a disaster; or in legal matters, there are procedures

to follow which require documents to be submitted

in a particular order. So, many tasks agents could

face need us to reason about rewards that depend on

some history, not only the immediate situation (non-

Markovian).

Learning and maintaining non-Markovian reward

functions is useful for several reasons: (i) Many tasks

are described intuitively as a sequence of sub-tasks or

https://orcid.org/0000-0003-2950-9962

https://orcid.org/0000-0001-5940-9562

mile-stones, each with their own reward (cf. the re-

lated work below) (ii) Possibly, not all relevant fea-

tures are available in state descriptions, or states are

partially observable, making it necessary to visit sev-

eral states before (more) accurate rewards can be dis-

pensed (Amato et al., 2010; Icarte et al., 2019). (iii)

Automata (reward machines) are useful for model-

ing desirable and undesirable situations facilitating

tracking and predicting beneﬁcial or detrimental sit-

uations (Alshiekh et al., 2018; K

ret

ınsk

y et al., 2018;

Giacomo et al., 2019). Actually, in practice, it can be

argued that non-Markovian tasks are more the norm

than Markovian ones.

In this work, we assume that the states and the

transition function are known, but the reward func-

tion is unknown. It is also assumed that the reward be-

havior of the environment is possibly non-Markovian.

The aim is to learn a model of the non-Markovian re-

ward function and use it whenever possible, even if it

is not yet known to be a complete model. We describe

an active learning algorithm to automatically learn

non-Markovian reward models by executing ‘exper-

iments’ on the system. In our case, a non-Markovian

reward model is represented as a Mealy machine; a

deterministic ﬁnite automaton (DFA) that produces

output sequences that are rewards, from input se-

quences that are hstate, actioni observations. We refer

Rens, G., Raskin, J., Reynouard, R. and Marra, G.

Online Learning of non-Markovian Reward Models.

DOI: 10.5220/0010212000740086

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 74-86

ISBN: 978-989-758-484-8

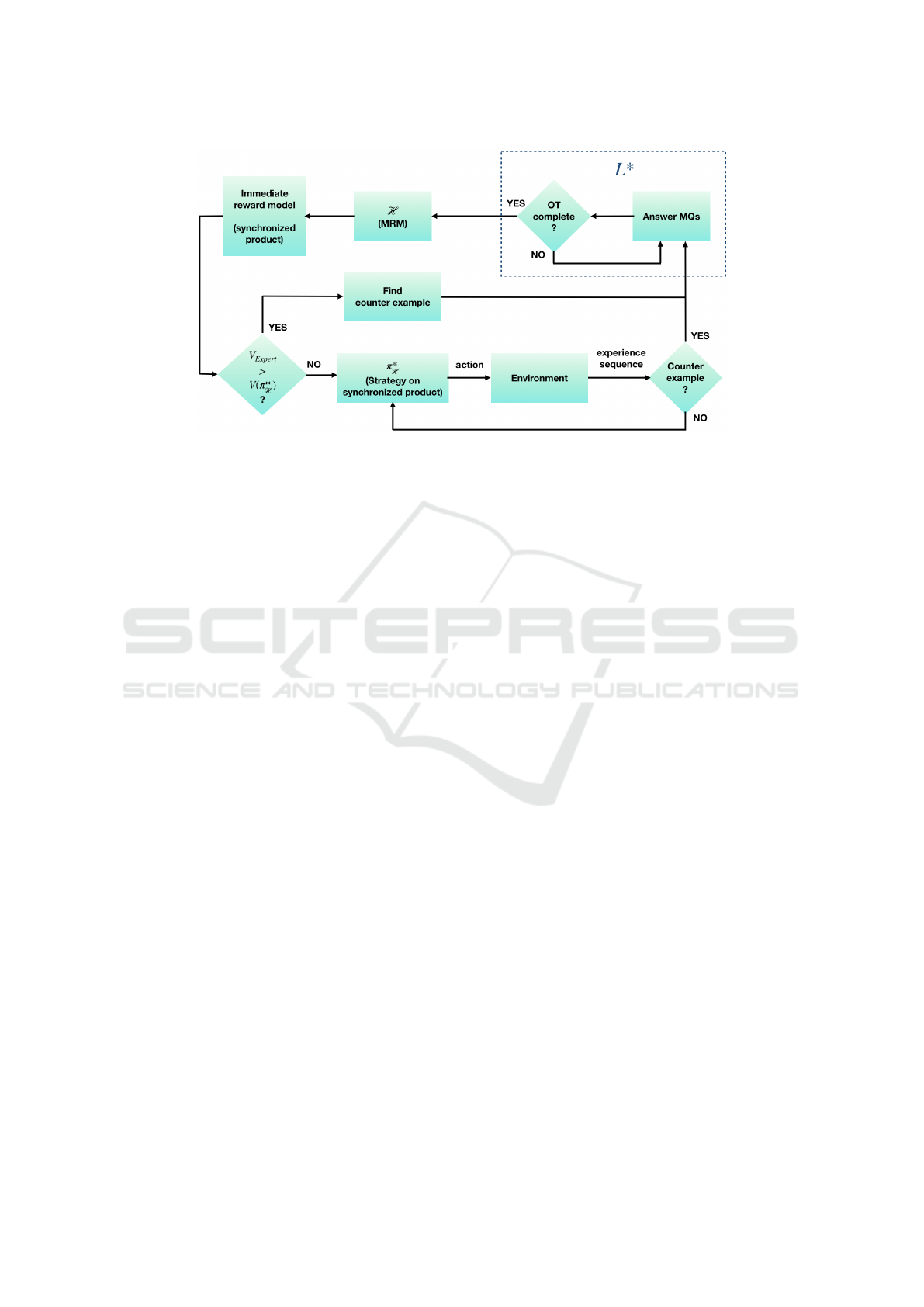
Figure 1: Flow diagram of the proposed framework for learning and exploiting Mealy reward machines (MRMs).

to such ﬁnite state reward models as Mealy Reward

Machines (MRM). Our framework (Fig. 1) is consid-

ered to be for online systems, alternating between a

learning phase and an exploitation phase. The learn-

ing phase is based on Angluin’s L

∗

active learning al-

gorithm (Angluin, 1987) to learn ﬁnite automata. It

is an active learning algorithm because it poses a se-

ries of queries to a teacher who must provide answers

to an agent performing experiments on/in the system

being learnt. In our case, the learner is an agent in an

MDP and the teacher is the environment. The queries

consist of sequences of observations and the answers

are the corresponding sequences of rewards that the

agent experiences. In this setting, answering mem-

bership queries is already a challenge. An observa-

tion is a function of an action and the successor state.

Encountering a particular observation sequence when

actions are stochastic and observations have the func-

tional dependencies just mentioned is non-trivial.

When L

∗

has enough input/output data, it can

build a corresponding MRM as an hypothesis of the

true underlying MRM. In our framework, whenever

an hypothesis is inferred, the agent enters the ex-

ploitation phase. The agent then acts to maximize re-

wards until it encounters a sequence of observations

and rewards which contradicts the current hypothesis.

The agent then goes back to learning with L

∗

Due to the stochasticity of actions in MDPs, a

challenge is for the agent to experience exactly the

observation sequence posed by L

∗

as a query, and to

do so efﬁciently. We rely on known formal methods to

compute the sequence of actions the agent should exe-

cute to encounter the observation sequence with high-

est probability or least expected number of actions.

Another important aspect of the framework is that,

given an (hypothesized) MRM, a synchronized prod-

uct of the MRM and the MDP is induced so that an im-

mediate reward function is available from the induced

product MDP. This means that existing (Markovian)

MDP planning or reinforcement learning techniques

can be employed in the exploitation phase. We use

model-based optimization methods as developed by

(Baier and Katoen, 2008).

Furthermore, in our framework, a special reset ac-

tion is introduced at the time the synchronized prod-

uct is formed. This action is available at every state of

the product MDP such that it takes the system to its

initial state. In this way, the product MDP is strongly

connected and we can then prove some useful prop-

erties of our framework. The engineer needs not be

concerned with the reset action when modeling the

system, that is, the MDP of the system does not have

to mention this action. However, the engineer should

keep in mind that the framework is best used for sys-

tems which can actually be reset at any time. Another

useful feature of our framework is that it allows a do-

main expert to provide a value that the system should

be able to achieve in the long-run if it follows the op-

timal strategy. This ‘expert value’ needs not be the

optimal expected value, but some smaller value that

the system owner wants a guarantee for.

Our contribution is to show how a non-Markovian

reward function for a MDP can be actively learnt

and exploited to play optimally according to this non-

Markovian reward function in the MDP. We provide

a framework for completely and correctly learning

the underlying reward function with guarantees under

mild assumptions. To the best of our knowledge, this

is the ﬁrst work which employs traditional automata

inference for learning a non-Markovian reward model

in an MDP setting.

Online Learning of non-Markovian Reward Models

Related Work. There has been a surge of interest in

non-Markovian reward functions recently, with most

papers on the topic being publications since 2017.

But unlike our paper, most of those papers are not

concerned with learning non-Markovian reward func-

tions.

An early publication that deserves to be men-

tioned is (Bacchus et al., 1996). In this paper, the

authors propose to encode non-Markovian rewards by

assigning values using temporal logic formulae. The

reward for being in a state is then the value associated

with a formula that is true in that state. They were

the ﬁrst to abbreviate the class of MDP with non-

Markovian reward as decision processes with non-

Markovian reward or NMRDP for short. A decade

later, (Thi

ebaux et al., 2006) presented the Non-

Markovian Reward Decision Process Planner: a soft-

ware platform for the development and experimenta-

tion of methods for decision-theoretic planning with

non-Markovian rewards. In both the cases above, the

non-Markovian reward functions is given and does

not need to be learned.

A closely related and possibly overlapping re-

search area is the use of temporal logic (especially

linear temporal logic (LTL)), for specifying tasks in

Reinforcement Learning (RL) (Alshiekh et al., 2018;

Icarte et al., 2018a; Icarte et al., 2018b; Camacho

et al., 2019; Giacomo et al., 2019; Hasanbeig et al.,

2019a).

Building on recent progress in temporal logics

over ﬁnite traces (LTL

), (Brafman et al., 2018) adopt

linear dynamic logic on ﬁnite traces (LDL

; an ex-

tension of LTL

) for specifying non-Markovian re-

wards, and provide an automaton construction al-

gorithm for building a Markovian model. The ap-

proach is claimed to offer strong minimality and com-

positionality guarantees. In those works, the non-

Markovian reward function is given and does not have

to be learned as in our setting.

In another paper (Camacho et al., 2018), the au-

thors are concerned with both the speciﬁcation and

effective exploitation of non-Markovian rewards in

the context of MDPs. They specify non-Markovian

reward-worthy behavior in LTL. These behaviors are

then translated to corresponding deterministic ﬁnite

state automata whose accepting conditions signify

satisfaction of the reward-worthy behavior. These au-

tomata accepting conditions form the basis of Marko-

vian rewards by taking the product of the MDP and

the automaton (as we do).

None of the research mentioned above is con-

cerned with learning non-Markovian reward func-

tions. However, in the work of (Icarte et al., 2019), an

agent incrementally learns a reward machine (RM) in

a partially observable MDP (POMDP). They use a set

of traces as data to solve an optimization problem. “If

at some point [the RM] is found to make incorrect pre-

dictions, additional traces are added to the training set

and a new RM is learned.” Their approach is also ac-

tive learning: If on any step, there is evidence that the

current RM might not be the best one, their approach

will attempt to ﬁnd a new one. One strength of their

method is that the the reward machine is constructed

over a set of propositions, where propositions can

be combined to represent transition/rewarding condi-

tions in the machine. Currently, our approach can take

only single observations as transition/rewarding con-

ditions. However, they do not consider the possibility

to compute optimal strategies using model-checking

techniques.

Moreover, our approach is different to that of

(Icarte et al., 2019) in that our agents are guided by the

∗

algorithm to answer exactly the queries required to

ﬁnd the underlying reward machine. The approach

of (Icarte et al., 2019) does not have this guidance

and interaction with the learning algorithm; traces for

learning are collected by random exploration in their

approach.

Next, we cover the necessary formal concepts and

notations. In Section 3, we deﬁne our Mealy Reward

Machine (MRM). Section 4 explains how an agent

can infer/learn an underlying MRM and present one

method for exploiting a learnt MRM. We discuss the

guarantees offered by the framework in Section 5.

Section 6 reports on experiments involving learning

and exploiting MRMs; we consider two scenarios.

The last section concludes this paper and points to fu-

ture research directions.

2 FORMAL PRELIMINARIES

We review Markov Decision Processes (MDPs) and

Angluin-style learning of Mealy machines.

An (immediate-reward) MDP is a tuple

hS,A,T, R,s

i, where S is a ﬁnite set of states;

A is a ﬁnite set of actions; T : S × A × S 7→ [0,1] is

the state transition function such that T (s,a,s

) is the

probability that action a causes a system transition

from state s to s

; R : A × S 7→ R is the reward

function such that R(a,s) is the immediate reward for

performing action a in state s; and s

the initial state

the system is in. A non-rewarding MDP (nrMDP) is

a tuple hS,A, T, s

i without a reward function.

The following description is from (Vaandrager,

2017). (Angluin, 1987) showed that ﬁnite automata

can be learned using the so-called membership and

equivalence queries. Her approach views the learn-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

ing process as a game between a minimally adequate

teacher (MAT) and a learner who wants to discover

the automaton. In this framework, the learner has to

infer the input/output behavior of an unknown Mealy

machine by asking queries to a teacher. The MAT

knows the Mealy machine M . Initially, the learner

only knows the inputs I and outputs O of M . The

task of the learner is to learn M through two types

of queries: (1) With a membership query (MQ), the

learner asks what the output is in response to an input

sequence σ ∈ I

∗

. The teacher answers with output se-

quence M (σ). (2) With an equivalence query (EQ),

the learner asks whether a hypothesized Mealy ma-

chine H with inputs I and outputs O is correct, that is,

whether H and M are equivalent (∀σ ∈ I

∗

,M (σ) =

H (σ)). The teacher answers yes if this is the case.

Otherwise she answers no and supplies a counter-

example σ

∈ I

∗

that distinguishes H and M (i.e.,

such that M (σ

) 6= H (σ

)).

The L

∗

algorithm incrementally constructs an ob-

servation table with entries being elements from O.

Two crucial properties of the observation table allow

for the construction of a Mealy machine (Vaandrager,

2017): closedness and consistency. We call a closed

and consistent observation table complete.

(Angluin, 1987) proved that her L

∗

algorithm is

able to learn a ﬁnite state machine (incl. a Mealy ma-

chine) by asking a polynomial number of membership

and equivalence queries (polynomial in the size of the

corresponding minimal Mealy machine equivalent to

M ). Let |I | be the size of the input alphabet (obser-

vations), n be the total number of states in the target

Mealy machine, and m be the maximum length of the

counter-example provided by the MAT for learning

the machine. Then the correct machine can be pro-

duced by asking maximum O(|I |

+ |I |mn

) queries

(using, e.g., the L

algorithm) (Shahbaz and Groz,

2009).

In an ideal (theoretical) setting, the agent (learner)

would ask a teacher whether H is correct (equiva-

lence query), but in practice, this is typically not pos-

sible (Vaandrager, 2017). “Equivalence query can be

approximated using a conformance testing (CT) tool

(Lee and Yannakakis, 1996) via a ﬁnite number of

test queries (TQs). A test query asks for the response

of the [system under learning] to an input sequence,

similar to a membership query. If one of the test

queries exhibits a counter-example then the answer to

the equivalence query is no, otherwise the answer is

yes” (Vaandrager, 2017). A ﬁnite and complete con-

formance test suite does exist if we assume a bound

on the number of states of a Mealy machine (Lee and

Yannakakis, 1996).

Our present framework, however, does not rely on

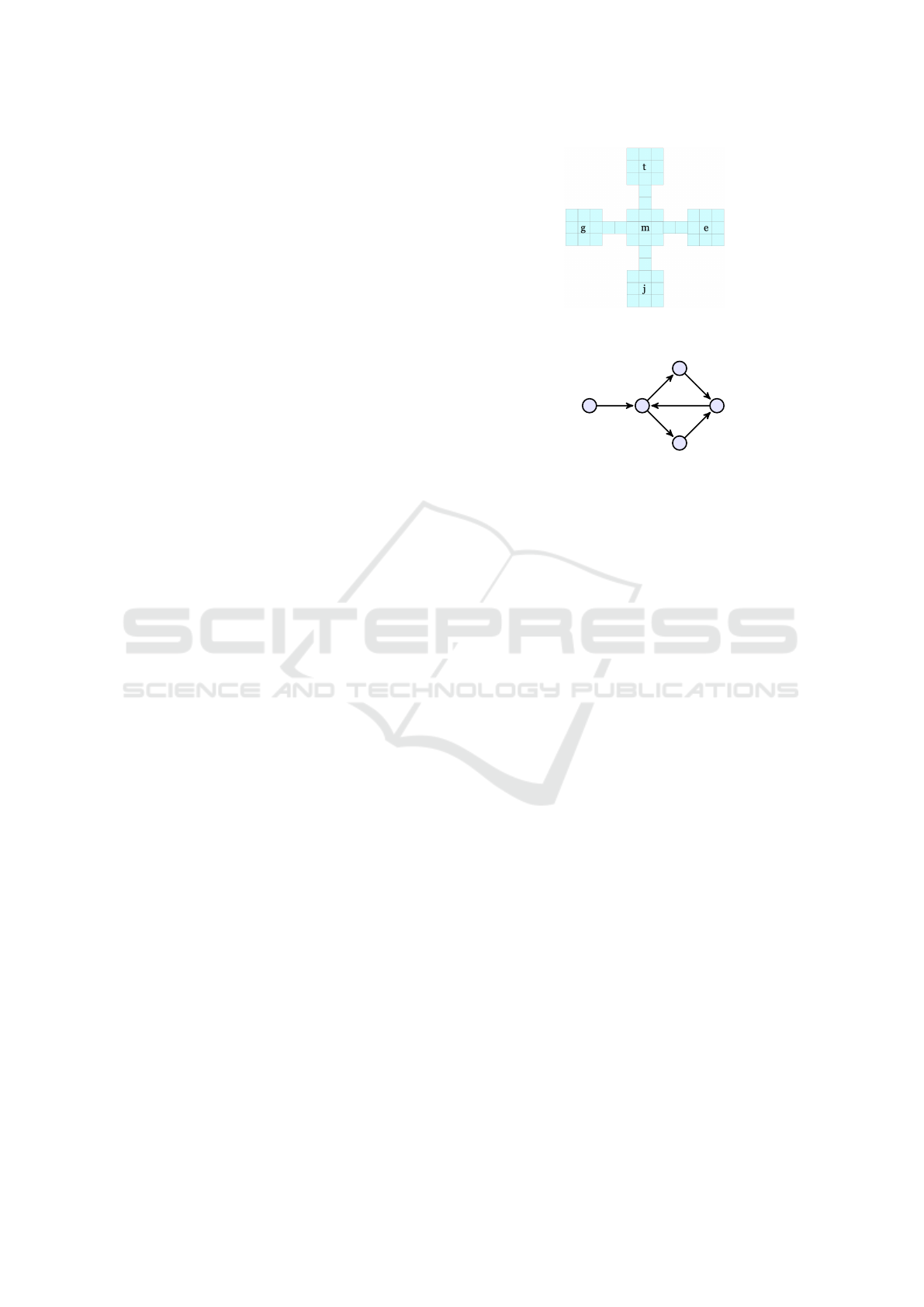
(a) The treasure-map world. Blank cells

contain observation null by default.

m | 10

e | 80

g | 70

t | 80

t | 95

j | 180

(b) A Mealy reward machine. Self-loops are not shown.

Figure 2: The treasure-map scenario.

conformance testing by performing a particular suite

of TQs. Rather, if it is found that the current hypothe-

sis would under-perform compared to what a domain

expert expects, the framework executes a weaker kind

of conformance testing: the agent performs actions

uniformly at random until a counter-example is found.

3 MODELING NON-MARKOVIAN

REWARDS

3.1 Running Example

Consider, as a running example (Fig. 2), an agent who

might stumble upon a person with a map (m) for a

hidden treasure (t) and some instruction on how to re-

trieve the treasure. The instructions imply that the

agent purchase some specialized equipment (e) be-

fore going to the cave marked on the treasure map.

Alternatively, the agent may hire a guide (g) who al-

ready has the necessary equipment. If the agent is

lucky enough to ﬁnd some treasure, the agent must

sell it at the local jewelry trader (j). The agent can

then restock its equipment or re-hire a guide, get some

more treasure, sell it and so on. Unfortunately, the in-

structions are written in a coded language which the

agent cannot read. However, the agent recognizes that

the map is about a hidden treasure, and thus spurs

the agent on to start treasure hunting to experience

rewards and learn the missing information.

Besides the four movement actions, the agent can

also buy, sell and collect. In the next subsection, we

deﬁne a labeling function which takes an action and a

Online Learning of non-Markovian Reward Models

state, and maps to an observation. For this example,

the labeling function has the following effect. If the

agent is in the state containing m, e or g and the does

the buy action, then the agent observes m, e respec-

tively g. If the agent is in the state containing t, and

does the collect action, then the agent observes t. If

the agent is in the state containing j, and does the sell

action, then the agent observes j. In all other cases,

the agent observes null.

After receiving the treasure map, the agent might

not ﬁnd a guide or equipment. In general, an agent

might not ﬁnish a task or ﬁnish only one version of a

task or subtask. In this world, the agent can reset its

situation at any time; it can receive a map again and

explore various trajectories in order to learn the entire

task with all its variations.

The reward behavior in this scenario is naturally

modeled as an automaton where the agent receives

a particular reward given a particular sequence of

observations. There is presumably higher value in

purchasing equipment for treasure hunting only af-

ter coming across a treasure map and thus deciding

to look for a treasure. There is more value in being

at the treasure with the right equipment than with no

equipment, etc.

We shall interpret features of interest as obser-

vations: (obtaining) a map, (purchasing) equipment,

(being at) a treasure, (being at) a jewelry trader, for

example. Hence, for a particular sequence of in-

put observations, the Mealy machine outputs a cor-

responding sequence of rewards. If the agent tracks

its observation history, and if the agent has a correct

automaton model, then it knows which reward to ex-

pect (the last symbol in the output) for its observation

history as input. Figure 2a depicts the scenario in two

dimensions. The underlying Mealy machine could be

represented graphically as in Figure 2b. It takes obser-

vations as inputs and supplies the relevant outputs as

rewards. For instance, if the agent sees m, (map), then

j, then t, then the agent will receive rewards 10, then 0

and then 0. And if it sees the sequence m · g · t · j, then

it will receive the reward sequence 10 ·70 ·95 · 180.

We deﬁne intermediate states as states that do not

signify a signiﬁcant progress towards completion of

a task. In Figure 2a, all blank cells represent in-

termediate states. We assume that there is a default

reward/cost an agent gets for entering intermediate

states. This default reward/cost is ﬁxed and denoted

c in general discussions. Similarly, the special null

observation (null) is observed in intermediate states.

An agent might or might not be designed to recognize

intermediate states. If the agent could not distinguish

intermediate states from ‘signiﬁcant’ states, then null

would be treated exactly like all other observations

and it would have to learn transitions for null obser-

vations (or worse, for all observations associated with

intermediate states). If the agent can distinguish inter-

mediate states from ‘signiﬁcant’ states (as assumed in

this work), then we can design methods to take advan-

tage of this background knowledge.

3.2 Mealy Reward Machines

We introduce the Mealy reward machine to model

non-Markovian rewards. These machines take a set Z

of observations representing high-level features that

the agent can detect (equivalent to the set of input

symbols for L

∗

). A labeling function λ : A × S 7→

Z ] {null} maps action-state pairs onto observations;

S is the set of nrMDP states and Z is a set of observa-

tions. The meaning of λ(a,s) = z is that z is observed

in state s reached via action a. The null observation

always causes the trivial transition in the machine (i.e.

self-loop) and produced a default reward denoted c.

For Mealy reward machines, the output symbols for

∗

are equated with rewards in R.

Deﬁnition 3.1 (Mealy Reward Machine). Given a set

of states S, a set of actions A and a labeling func-

tion λ, a Mealy Reward Machine (MRM) is a tuple

hU, u

,Z,δ

,δ

,ci, where

• U is a ﬁnite set of MRM nodes,

• u

∈ U is the start node,

• Z ] {null} is a set of observations,

• δ

: U ×Z 7→U is the transition function, such that

,λ(a, s)) = u

for a ∈ A and s ∈ S, speciﬁ-

cally, δ

,null) = u

• δ

: U ×Z 7→ R is the reward-output function, such

that δ

,λ(a, s)) = r

for r

∈ R, a ∈ A and s ∈ S,

speciﬁcally, δ

,null) = c.

We may write δ

and δ

to emphasize that the func-

tions are associated with MRM R .

A Markov Decision Process with a Mealy reward

machine is thus a non-Markovian reward decision

process (NMRDP). In the diagrams of MRMs, an

edge from node u

to node u

labeled z | r denotes that

,z) = u

and δ

,z) = r.

In the following deﬁnitions, let s

∈ S, a

∈ A,

∈ Z, and r

∈ R. • An interaction trace of

length k in an MDP represents an agent’s (recent)

interactions with the environment. It has the form

·· ·s

k−1

and is denoted σ

inter

. That

is, if an agent performs an action at time t in a state

at time t, then it reaches the next state at time t + 1

where/when it receives a reward. • An observation

trace is extracted from an interaction trace (employ-

ing a labeling function) and is taken as input to an

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

MRM. It has the form z

·· ·z

and is denoted σ

. •

A reward trace is either extracted from an interaction

trace or is given as output from an MRM. It has the

form r

·· ·r

and is denoted σ

. • A history has the

form s

·· ·s

and is denoted σ

Given a history σ

, we extend δ

to take histories

by deﬁning δ

∗

,σ

) inductively as

,λ(a

)) · δ

∗

(δ

,λ(a

)),a

·· ·s

Finally, we extend δ

to take histories by deﬁning

∗

,σ

) inductively as

,λ(a

)) · δ

∗

(δ

,λ(a

)),a

·· ·s

∗

explains how an MRM assigns rewards to a history

in an MDP.

3.3 Expected Value of a Strategy under

an MRM

A (deterministic) strategy to play in a nrMDP M =

hS,A, T, s

i is a function π : S

∗

7→ A that associates to

all sequences of states σ ∈ S

∗

of M the action π(σ)

to play. In this version of the framework, the agent

tries to maximize mean payoff, deﬁned as M P (σ

) =

∑

i=1

, where r

is the reward received at step i.

Let M P (R ) be the mean payoff of an inﬁnite reward

trace generated by reward model R . Then the ex-

pected mean payoff under strategy π played in MDP

M from state s is denoted as E

M,π

(M P (R )).

Being able to produce a traditional, immediate re-

ward MDP from a non-Markovian rewards decision

process is clearly beneﬁcial: One can then apply all

the methods developed for MDPs to the underlying

NMRDP, whether to ﬁnd optimal or approximate so-

lutions. The following deﬁnition is the standard way

to produce an MDP from a non-reward MDP (nr-

MDP) and a deterministic ﬁnite automaton.

Deﬁnition 3.2 (Synchronized Product). Given an nr-

MDP M = hS,A, T,s

i, a labeling function λ : A×S 7→

Z ] {null} and an MRM R = hU,u

,Z,δ

,δ

i, the

synchronized product of M and R under λ is de-

ﬁned as an (immediate reward) MDP P = M ⊗

R =

⊗

i, where

• S

⊗

= S ×U,

• A

⊗

= A,

• T

⊗

((s,u),a,(s

)) =



T (s,a,s

) if u

= δ

(u,λ(a,s

))

0 otherwise.

• R

⊗

(a,(s,u)) = δ

(u,λ(a,s)),

• s

⊗

= (s

)

Due to MRMs having deterministic transitions (δ

and δ

∗

are functions), we have that the histories in M

and P are in bijection. This is stated formally in the

following proposition. Let H(M) and H(P) denote all

histories that can be generated from M, resp. P.

Proposition 3.1. Let B : H(M) 7→ H(P) be deﬁned for

= s

·· ·s

B(σ

) = (s

)

,δ

,λ(a

))

,δ

(δ

,λ(a

)),λ(a

)))

·· ·

k−1

,last(δ

∗

,σ

))),

As a consequence, given a strategy π for M, we

can deﬁne a strategy π

⊗

for P as follows. For all σ

∈

H(M), π

⊗

(B(σ

)) = π(σ

Corollary 3.1. The strategies in M and P are in bi-

jection.

The following proposition states that the expected

value of an nrMDP with an MRM is equal to the ex-

pected value of their product under the same strategy.

Proposition 3.2. Given an nrMDP M = hS,A, T,s

a labeling function λ : A × S 7→ Z ] {null}, an MRM

R = hU, u

,Z,δ

,δ

i, P = M ⊗

R , for all strategies

π for M and π

⊗

in bijection, we have that

M,π

(M P (R )) = E

P,π

⊗

)

(M P (R

⊗

)).

3.4 Adding a Reset Action

We make the important assumption that the environ-

ment and the agent’s state can be reset. Resetting also

sets the underlying and hypothesized MRMs to their

start nodes. Having a reset action available means

that the underlying domain need not be strongly con-

nected, that is, there needs not exists a path between

all pairs of states. Having the option to reset at any

time allows one to learn in terms of episodes: ei-

ther an episode ends naturally (when the maximum

episode length is reached or when the task is achieved

to satisfaction) or the episode is cut short by reset-

ting the system due to lack of progress. Of course,

the agent retains the hypothesized MRM learnt so far.

Resetting a system is not always feasible. We are,

however, interested in domains where an agent can be

placed in a position to continue learning or repeat its

task.

The results discussed in the next section rely on

the implicit presence of a special reset action x.

Instead of modifying the learning procedure, this

amounts to adding x when deﬁning sybchronized

products ( ⊗

). Formally, this is done as follows.

Let s

and u

be the unique starting state of MDP

M and the unique starting node of MRM R , respec-

tively. Then M ⊗

R is deﬁned as before, and with

Online Learning of non-Markovian Reward Models

x available at every product state (s,u) such that

T ((s,u),x,(s

)) = 1. By adding x in this way,

the products become strongly connected.

Deﬁnition 3.3 (Synchronized Product with Homing).

Given an nrMDP M = hS,A,T, s

i, a labeling func-

tion λ : A × S 7→ Z ] {null}, a reset cost c

and

an MRM R = hU,u

,Z,δ

,δ

i, we deﬁne the hom-

ing/‘resetable’ synchronized product of M and R un-

der λ as an (immediate reward) MDP P = M ⊗

R =

⊗

i, where

• S

⊗

= S ×U

• A

⊗

= A ] {x}

• T

⊗

((s,u),a,(s

)) =







T (s,a,s

) if a 6=x ∧u

= δ

(u,λ(a,s

))

0 if a 6=x ∧u

6= δ

(u,λ(a,s

))

1 if a =x ∧(s

) = (s

)

• R

⊗

(a,(s,u)) =



(u,λ(a,s)) if a 6=x

otherwise

• s

⊗

= (s

)

Note that adding the reset action does not change the

result of Proposition 3.2.

The following proposition states that the expected

value of an nrMDP with an MRM is equal to the ex-

pected value of their product under the same strategy.

Corollary 3.2. Given an nrMDP M = hS, A,T,s

i, a

labeling function λ : A × S 7→ Z ] {null}, an MRM

R = hU,u

,Z,δ

,δ

i, P = M ⊗

R , for all strategies

π for M and π

⊗

in bijection, we have that

M,π

(M P (R )) = E

P,π

⊗

)

(M P (R

⊗

)).

A strategy π : S

∗

7→ A is memoryless if ∀σ

,σ

∈ S

∗

such that last(σ

) = last(σ

), then π(σ

) = π(σ

that is, if the action played by π for sequence σ de-

pends only on the last state in σ. Because memoryless

strategies are sufﬁcient to play optimally in order to

maximize E

P,π

⊗

)

(M P (R

⊗

)) in immediate reward

MDPs, and together with Corollary 3.2, we conclude

that we can play optimally in M under R in a ﬁnite

memory strategy π

∗

(ﬁnite in the memory required

for R ; but memoryless if viewed as P = M ⊗

R ).

Strategy π

∗

can be computed with, for instance, the

STORM probabilistic model checking software pack-

age.

In this work, we use STORM to compute π

∗

for

M ⊗

H (product of the nrMDP and the hypothesis

MRM).

STORM can be found at http://www.stormchecker.org

4 THE FRAMEWORK

4.1 Flow of Operation

A high-level description of the process follows (recall

Fig. 1).

1. Play a ﬁnite number of episodes to answer mem-

bership queries by extracting reward traces from

the appropriate interaction traces until the obser-

vation table (OT) is complete;

2. As soon as OT becomes complete, construct new

hypothesized MRM H from OT and compute

the optimal strategy π

∗

for M ⊗

H with value

V (π

∗

) employing STORM;

3. If V(π

∗

) is less than the value provided by a do-

main expert, then we know that H must be wrong,

in which case, we seek an interaction trace which

is a counter example to H by playing actions uni-

formly at random (strategy π

);

4. Else, if V(π

∗

) is greater than or equals the value

provided by the domain expert, then repeatedly

execute actions using π

∗

;

5. Whenever a counter-example to H is discovered

(experienced), stop exploitation and go to step 1

(the learning phase).

4.2 Answering Membership Queries

Efﬁciently

Execution of L

∗

requires answers to membership

queries: given a sequence of observations σ

, we need

to discover what the associated reward σ

= H (σ

)

is. Because the transitions in the MDP are stochas-

tic, there is in general no sequence of actions ¯a that

is guaranteed to force the occurrence of σ

. Forc-

ing the sequence σ

is a planning problem. Proce-

dure getExperience(σ

) implements this in the al-

gorithm formalizing the framework. Here we distin-

guish two natural variants of this planning problem.

The ﬁrst variant, called MAX asks to synthesize

the strategy π

MAX

that produces (from the initial state

of the MDP) the sequence σ

with the highest proba-

bility α. Let π

MAX

be the optimal strategy for MAX.

Then we can play π

MAX

repeatedly, and reset the sys-

tem as soon as the preﬁx of observations is not com-

patible with σ

. Each such try will succeed with prob-

ability α, and so by repeating trials, we are guaranteed

to observe σ

with probability 1− (1 −α)

after n tri-

als, and so with probability one in the long run. To

synthesize the strategy π

MAX

, we construct a MDP M

from M and σ

in which states are pairs (s,i) where s

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

is a state of M and i is an index that tracks the preﬁx of

the sequence σ

that has been observed so far. MDP

is reset as soon as the observed preﬁx is not com-

patible with σ

. The goal is to reach any state (s,k)

where k is the length of the sequence of observations

. The model-checking tool STORM can then be

used to synthesized, in polynomial time, the strategy

that maximizes the probability α of reaching this set

of states.

The second variant, called MIN is more reﬁned

and asks to synthesize the strategy π

MIN

that mini-

mize the expected number of steps N that are needed

(including resets of M) in order to observe σ

. This

strategy π

MIN

is played and the sequence of observa-

tions σ

is observed after an expected number of N

steps. Again, we use STORM to compute this strat-

egy in polynomial time. It can be computed as the

strategy that minimizes the expected cost (each step

costs 1) to reach a state of the form (s, k) where k is

the length of the sequence of observations σ

in the

MDP M

described in the previous paragraph.

5 FORMAL GUARANTEES OF

THE LEARNING FRAMEWORK

Our framework provably offers two guarantees that

can be stated as follows: (1) When playing π

∗

on-

line, with probability 1: either we obtain V (π

∗

) in the

long-run or we observe a counter-example to H , (2)

If the expert’s value, V

expert

is less than the long-run

value of playing the optimal strategy (of the underly-

ing reward machine R ), then with probability 1, we

learn hypothesis H such that V (π

∗

) ≥ V

expert

. In the

rest of this section, we prove these two claims.

5.1 Consequence of Playing π

∗

M ⊗

We introduce a special counter-example state CE

for the theory in this section. CE is entered when

a counter-example is encountered. To describe the

effect of playing π

∗

online, we need to work in

the state-space (S × U

× U

) ∪ {CE} of process

M ⊗

R ,H (deﬁned below) and to study the asso-

ciated Markov chain when π

∗

is used. Intuitively, we

use s and u

in hs, u

i to determine what action

is played by π

∗

. The reward observed online from

R and predicted by H are compared: either the re-

wards for u

and u

in the two RMs agree and the

RMs are updated accordingly, or we go to a special

counter-example state CE.

Formally, the transition probabilities between

states in this space are deﬁned as follows. Let a ∈

A \ {x} and z = λ(a, s

) then:

T (hs,u

i,a, hs

i) =











T (s,a,s

) if











,z) = δ

,z)∧

,z) = u

∧

,z) = u

0 otherwise.

T (hs,u

i,a, CE) =

∑

|δ

,z)6=δ

,z)

T (s,a,s

)

T (hs,u

i,x, hs

i) =



1 if hs

i = hs

R 0

H 0

0 otherwise.

Additionally, CE is a sink (never left when entered).

Reaching CE occurs when a counter-example to the

equivalence between R and H has been discovered

online. If h is the history that reaches CE, then h can

be used to restart L

∗

and compute a new hypothesis

as it contains a sequence of observations on which

R and H disagree.

Deﬁnition 5.1 (BSCC (Baier and Katoen, 2008)). Let

M = hS,A, T,s

i be an nrMDP and C ⊆ S. Let P(s,s

)

be the probability of reaching state s

from state s (via

a sequence of actions). C is strongly connected if for

every pair of states v,w ∈ C, the states v and w are mu-

tually reachable, i.e., P(v,w) > 0 and P(w, v) > 0. A

strongly connected component (SCC) of M is a maxi-

mally strongly connected set of states. That is, C is an

SCC if C is strongly connected and C is not contained

in another strongly connected set of states D ⊆ S with

C 6= D. A bottom SCC (BSCC) of M is an SCC B from

which no state outside B is reachable, i.e., for each

state b ∈ B it holds that

∑

∈B

P(b,b

) = 1.

Theorem 5.1. When playing π

∗

online, with prob-

ability 1: either V (π

∗

) is obtained or a counter-

example to H is found.

Proof. To prove this theorem, we show that if no

counter-example is found when playing π

∗

online

(playing on M ⊗

R ,H ), then the long run mean-

payoff of the observed outcome is V(π

∗

) with prob-

ability one.

First, we note that the MDP M ⊗

H on which

we compute π

∗

is strongly connected. As a conse-

quence, all the states of the MDP have the same opti-

mal mean-payoff value which is V (π

∗

). It also means

that all the states in the associated Markov chain,

Online Learning of non-Markovian Reward Models

noted M ⊗

H (π

∗

), have the same value V (π

∗

In turn this implies that all the BSCC of this Markov

chain have the same value V (π

∗

). From that, we de-

duce that the mean-payoff obtained by a random walk

in those BSCCs has a value equal to V (π

∗

) with prob-

ability one (see e.g. (Puterman, 1994)).

Next, we are interested in the expected value ob-

tained when playing π

∗

on M ⊗

R ,H conditional

to the fact that no counter-example is encountered,

that is, while CE is not reached. We claim that the

behavior of π

∗

on M ⊗

R ,H is then exactly the

same as in M ⊗

H . This is a consequence of the fol-

lowing property: there are only two kinds of BSCCs

in M ⊗

R ,H (π

∗

): (i) {CE} and (ii) BSCCs B not

containing CE. When in B, R and H fully agree in

the sense that, for all hs,u

i ∈ B, as CE cannot be

reached (otherwise B would not be a BSCC), the ac-

tion chosen by π

∗

triggers the same reward from R

and H . So we conclude that the expected reward in B

is as predicted by H and is equal to V (π

∗

). Hence,

again the value observed will be V (π

∗

) with proba-

bility 1 and the theorem follows. 

5.2 Leveraging off Expert Knowledge

Now we show how one can take advantage of the

knowledge a domain expert has about what value can

be expected when playing optimally in the domain.

This idea is exploited in Step 3 of the description of

the ﬂow of our algorithm (Sect. 4.1).

To this end, we ﬁrst establish how we can ﬁnd

counter-examples systematically using random explo-

ration. For that, we deﬁne the strategy π

which plays

uniformly at random all actions in A ∪ {x}, that is,

: S ×U

×U

7→ ∆(A ∪ {x})

such that π

(hs,u

i)(a) = 1/(|A| + 1).

and

prove the following result.

Lemma 5.1. While playing π

online, a counter-

example is found (with probability one) if and only

if R and H are not equivalent.

Proof. First, we note that the Markov chain M ⊗

R ,H (π

) is composed of two strongly connected

components: C

= {CE} and C

that contains all the

other states. We also note that C

= {CE} is reach-

able in this Markov chain iff R and H are not equiv-

alent. So, when playing π

on M ⊗

R ,H , two mu-

tually exclusive scenarios are possible. First, R and

H are not equivalent. Then, there are transitions from

to C

, and C

is the only BSCC of the Markov

chain. As a consequence, the execution of π

ends in

∆(X) is all probability distributions over set X.

with probability 1. Second, R and H are equiva-

lent. Then, there are no transitions from C

to C

, and

is the only reachable BSCC of the Markov chain

and no counter-examples exist. 

Suppose that a domain expert can provide us with

a value V

expert

which is realistic in the following sense:

expert

is below the true optimal value achievable on

M ⊗

R . Then the following theorem holds.

Theorem 5.2. If V

expert

is less than or equal to the

optimal value V (π

∗

) of M ⊗

R , then with prob-

ability 1, a hypothesis H will be learned such that

V (π

∗

) ≥ V

expert

Proof. Note that if V (π

∗

) < V

expert

, then it must

be the case that the hypothesized MRM H does not

model the underlying MRM R (i.e., they are not

equivalent). Furthermore, if V (π

∗

) < V

expert

, then

our algorithm plays the uniform random strategy π

and by Lemma 5.1, a counter-example is found with

probability 1 which triggers L

∗

to be restarted in or-

der to obtain a new hypothesis H

. Now, we note

that the scenario above can happen only a number

of times bounded by the number of states in R , be-

cause the L

∗

algorithm is guaranteed to learn R af-

ter a number of equivalence queries that is at most

equal to the number of states in R (Angluin, 1987).

So, either we ﬁnd a hypothesis that predicts a better

value than V

expert

, or we end up with an hypothesis H

which is correct and so equivalent to R , implying that

V (π

∗

) = V (π

∗

) ≥ V

expert

. We conclude that our al-

gorithm is guaranteed to obtain online a mean-payoff

value which is at least V

expert

with probability 1. 

6 EXPERIMENTAL EVALUATION

Our online active-learning algorithm was imple-

mented, and evaluated on two small problem do-

mains.

The two problems are also evaluated w.r.t.

a baseline based on neural networks. In this section,

we describe the baseline, and then in the following

two subsections, we describe the problem domain,

describe in more detail the experiment setup for the

particular problem and present the results. However,

some aspects of the experiments are common to all

our cases and discussed immediately:

For convenience, we refer to our framework as

ARM (for Angluin Reward Machine) and the base-

line as DQN (for Deep Q-function Network). When

using ARM, the number of actions allowed per trial

includes actions required for answering membership

For the L

∗

algorithm, we used a Python

implementation provided by Georges Bossert

(https://github.com/gbossert/pylstar).

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

queries and for searching for counter-examples. Re-

wards received during exploration, learning, exploita-

tion are all considered. In all domains, the agent can

move north, east, west and south, one cell per ac-

tion. To add stochasticity to the transition function,

the agent is made to get stuck 5% of the time when

executing an action. We measure the cumulative re-

wards gained (Return) per episode. Procedure getEx-

perience is set to use mode MIN (cf. Sect. 4.2) in all

experiments. Episode length, total number of steps

(actions) and number of trials performed are domain

dependent; they will be mentioned for each domain.

To achieve similar total experiment times (per prob-

lem), episode lengths of DQN were increased.

6.1 Deep Q-learning Baseline

We implemented a Deep Q-learning network agent

(DQN) (Mnih et al., 2015). To improve the stability

and the convergence speed of the learning, we aug-

mented the agent with two standard techniques: expe-

rience replay (Mnih et al., 2015) and double-q func-

tion (Hasselt, 2010).

Let f

S → R

|A|

be a standard deep Q function,

receiving as input a state representation and return-

ing as output the real vector of Q-values for each sin-

gle action. The state representation space

S depends

on the particular domain. For the domains used in

this paper, it is the set of (x, y) coordinates of the

grid. Since ‘regular’ deep Q-learning algorithms as-

sume a Markovian setting, a naive application of deep

reinforcement learning techniques does not provide

us with a fair competitor. Therefore, we enhanced

our DQN baseline with the ability to make decisions

based on observation history: In particular, we ex-

tended the standard deep Q network in three ways.

First, we added a one-hot representation of the

current observation to the input space. Let i be the

index of the current observation, its one-hot represen-

tation is a zero-vector with a single 1 in position i. For

example if the observation map is indexed as i = 2 out

of 4 possible observations, its one-hot representation

is v = [0,1,0,0]. Let

O be the space of one-hot repre-

sentations of the current observation.

Second, we added a bag-of-words (BoW) repre-

sentation of the past observations. Given a sequence

of past observations, its BoW representation is a vec-

tor v representing the multiset of the observations, i.e.

is equal to the number of times observation indexed

by i is encountered in the history. For example, if the

past observations were hmap,treasure,mapi (in that

order), indexed by I = [2,4,2], then their BoW repre-

sentation is h = [0, 2,0,1]. Note that if the agent sees

htreasure,map,mapi (in that order), then the repre-

Figure 3: Results for the Treasure-Map world (averaged

over ten trials for ARM and twenty trials for DQN).

Episodes were 507 steps long for ARM and 1014 steps

for DQN. Average running-times per episode: ARM 24.9s;

DQN: 10.4s.

sentation of the history is still h = [0, 2,0,1]. Hence,

a Q-learning agent can distinguish bags of observa-

tions, but not the order in which they were perceived.

Sometimes BoW is a sufﬁcient statistic for discrimi-

nating between cases, like in document classiﬁcation

(McTear et al., 2016).Let

H be the set of BoW repre-

sentations of the past observations.

Third, we extended the action set A with a reset

action that mimics the behavior of x in our ARM

framework. This is resembling the way our algorithm

interacts with the environment. The reset action is a

special one, because the agent is forced to reset its

past observation representation (i.e. set to the zero-

vector) each time this action is selected.

Finally, we can deﬁne the history-augmented deep

Q function as the function f

S ×

O ×

H → R

|A|+1

We implemented the deep network and the Q-

learning algorithm in Tensorﬂow (Abadi et al., 2016).

Once the input space of the network is augmented

with the history-based information, standard RL

frameworks can be exploited. In particular, we se-

lected KerasRL (Plappert, 2016). The neural network

architecture is a feed-forward neural network, with

three hidden layers with ﬁfty ReLU units each and

a linear output layer. The Adam algorithm (Kingma

and Ba, 2014) with a learning rate of 10

−3

is selected

as weight-update rule. The epsilon-greedy policy is

used, with ε = 0.1.

6.2 Treasure-Map World

The agent starts in one of the four corners of one of the

ﬁve areas; one of these twenty locations is randomly

chosen. The default cost c was set to -0.1 and the cost

for resetting was set to -10. The optimal value for this

domain is 9.884 (computed by STORM for the cor-

rect reward machine). We set V

expert

= 9. The perfor-

mance of our framework applied to the Treasure-Map

Online Learning of non-Markovian Reward Models

a | 0

b | 2

a | 0

b | 1

b | 0

(a) The underlying reward

machine.

a | 0

b | 2

a | 0

b | 1

b | 0

(b) The minimal reward ma-

chine.

Figure 4: The cube reward machine.

Figure 5: Results for the Cube problem (averaged over ﬁve

trials). Episodes were 75 steps long for ARM and 600 steps

for DQN. Average running-times per episode: ARM: 1.1s;

DQN: 45s.

world can be seen in Figure 3. On average, for ARM,

there were 835 membership-queries, and 509 counter-

examples found during exploitation. The huge vari-

ance in the return for DQN is most likely due to its

dependence on seeing the ‘right’ sequence of obser-

vations, which is inﬂuenced by the stochasticity of the

underlying MDP. ARM relies on an optimal strategy

based on a well-deﬁned model (the current MRM),

which makes variance of return minimal.

6.3 The Cube Problem

The environment is a 5-by-5 grid without obstacles,

and with two cells where a is perceived and two cells

where b is perceived. The underlying reward model

is the one shown in Figure 4 (top). The agent always

starts in the bottom right-hand corner. The default

cost c is 0 and the cost for resetting is -1.

The optimal value for this problem is 0.1624

(computed by STORM for the correct reward ma-

chine). We set V

expert

= 0.15. If V

expert

is set too high,

then the agent will keep on seeking counter-examples.

Initially (for the ﬁrst hypothesis RM), STORM com-

putes an optimal value below 0.15. Random explo-

ration commences, a counter-example is soon found

and a correct reward machine is learnt.

The performance of our framework applied to the

Cube problem can be seen in Figure 5. On average,

for ARM, there were 850 membership-queries, and

248 counter-examples found during exploitation. In

this example (and in the Ofﬁce-Bot domain), another

beneﬁt of the L

∗

algorithm can be seen: it produces

the minimal machine (Figure 4, bottom), which usu-

ally makes its meaning clearer, and produces expo-

nentially smaller synchronized product MDPs.

7 CONCLUSION

We proposed a framework for learning and exploiting

non-Markovian reward models, represented as Mealy

machines. Angluin’s L

∗

algorithm is employed to

learn Mealy Reward Machines within a Markov De-

cision Process setting. The framework was imple-

mented and used for evaluation as a proof-of-concept.

Some useful theorems were proven, relying on ex-

isting theory of probabilistic model-checking and au-

tomata learning theory. The main result is that, under

reasonable assumptions, we can guarantee that a sys-

tem will eventually achieve a performance level pro-

vided by a domain expert if that performance level is

realistic/achievable for that domain.

We found that in empirical evaluation, the frame-

work learns the underlying MRM of the applicable

domain correctly, that is, after answering a ﬁnite num-

ber of membership queries as posed by the L

∗

algo-

rithm, within a ﬁnite time. And it signiﬁcantly outper-

forms a Deep Q-Network augmented to take history-

based observations as input. Moreover, the learnt

MRM is minimal; least possible number of nodes.

As investigated in some of the related literature

mentioned in the introduction, an agent with a non-

Markovian (reward) model is better equipped to avoid

dangerous or undesirable situation in some domains.

A challenge is, how to safely learn non-Markovian

(reward) models in unsafe domains? Some work

has been done on safe learning/exploration (Turchetta

et al., 2016; Hasanbeig et al., 2019b; Cheng et al.,

2019)

We expect that more complex non-Markovian

reward environments will require intelligent explo-

ration strategies. It will be interesting to investi-

gate the exploration-exploitation trade-off in the non-

Markovian setting. And if an expert value is not

available, one could employ an ε-greedy (or similar)

strategy to allow for the agent to observe counter-

examples if they exist. This will be investigated in

future work.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

ACKNOWLEDGEMENTS

This work is partially supported by the ARC project

Non-Zero Sum Game Graphs: Applications to Re-

active Synthesis and Beyond (F

eration Wallonie-

Bruxelles), the EOS project (No. 30992574) Verify-

ing Learning Artiﬁcial Intelligence Systems (F.R.S.-

FNRS & FWO), and the COST Action 16228

GAMENET (European Cooperation in Science and

Technology).

REFERENCES

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,

J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,

et al. (2016). Tensorﬂow: A system for large-scale

machine learning. In Twelfth USENIX symposium on

operating systems design and implementation (OSDI

16), pages 265–283.

Alshiekh, M., Bloem, R., Ehlers, R., K

onighofer, B.,

Niekum, S., and Topcu, U. (2018). Safe reinforce-

ment learning via shielding. In Proc. of Thirty-Second

AAAI Conf. on Artif. Intell. (AAAI-18), pages 2669–

2678. AAAI Press.

Amato, C., Bonet, B., and Zilberstein, S. (2010). Finite-

state controllers based on Mealy machines for central-

ized and decentralized POMDPs. In Proc. of Twenty-

Fourth AAAI Conf. on Artif. Intell. (AAAI-10), pages

1052–1058. AAAI Press.

Angluin, D. (1987). Learning regular sets from queries

and counterexamples. Information and Computation,

75(2):87–106.

Bacchus, F., Boutilier, C., and Grove, A. (1996). Rewarding

behaviors. In Proc. of Thirteenth Natl. Conf. on Artif.

Intell., pages 1160–1167. AAAI Press.

Baier, C. and Katoen, J. (2008). Principles of Model Check-

ing. MIT Press.

Brafman, R., Giacomo, G. D., and Patrizi, F. (2018).

LTL

/LDL

non-Markovian rewards. In Proc. of

Thirty-Second AAAI Conf. on Artiﬁcial Intelligence

(AAAI-18), pages 1771–1778. AAAI Press.

Camacho, A., Chen, O., Sanner, S., and McIlraith, S.

(2018). Non-Markovian rewards expressed in LTL:

Guiding search via reward shaping (extended version).

In Proc. of First Workshop on Goal Speciﬁcations for

Reinforcement Learning, FAIM 2018.

Camacho, A., Icarte, R. T., Klassen, T., Valenzano, R.,

and McIlraith, S. (2019). LTL and beyond: Formal

languages for reward function speciﬁcation in rein-

forcement learning. In Proc. of Twenty-Eighth Intl.

Joint Conf. on Artiﬁcial Intelligence, IJCAI-19, pages

6065–6073.

Cheng, R., Orosz, G., Murray, R., and Burdick, J. (2019).

End-to-end safe reinforcement learning through bar-

rier functions for safety-critical continuous control

tasks. In The Thirty-third AAAI Conf. on Artiﬁcial In-

telligence, pages 3387–3395. AAAI Press.

Giacomo, G. D., Favorito, M., Iocchi, L., and Patrizi, F.

(2019). Foundations for restraining bolts: Reinforce-

ment learning with LTL

/LDL

restraining speciﬁca-

tions. In Proc. of Twenty-Ninth Intl. Conf. on Auto-

mated Planning and Scheduling (ICAPS-19), pages

128–136. AAAI Press.

Hasanbeig, M., Abate, A., and Kroening, D. (2019a).

Logically-constrained neural ﬁtted q-iteration. In Ag-

mon, N., Taylor, M. E., Elkind, E., and Veloso, M.,

editors, Proc. of Eighteenth Intl. Conf. on Autonomous

Agents and Multiagent Systems, AAMAS-2019, pages

2012–2014. Intl. Foundation for AAMAS.

Hasanbeig, M., Kroening, D., and Abate, A. (2019b). To-

wards veriﬁable and safe model-free reinforcement

learning. In Proc. of First Workshop on Artiﬁcial In-

telligence and Formal Veriﬁcation, Logics, Automata

and Synthesis (OVERLAY).

Hasselt, H. (2010). Double q-learning. In Advances in neu-

ral information processing systems 23, pages 2613–

2621.

Icarte, R. T., Klassen, T., Valenzano, R., and McIlraith, S.

(2018a). Teaching multiple tasks to an RL agent us-

ing LTL. In Proc. of Seventeenth Intl. Conf. on Au-

tonomous Agents and Multiagent Systems, AAMAS-

2018, pages 452–461. Intl. Foundation for AAMAS.

Icarte, R. T., Klassen, T., Valenzano, R., and McIlraith,

S. (2018b). Using reward machines for high-level

task speciﬁcation and decomposition in reinforcement

learning. In Proc. of Thirty-Fifth Intl. Conf. on Ma-

chine Learning, volume 80 of ICML-18, pages 2107–

2116. Proceedings of Machine Learning Research.

Icarte, R. T., Waldie, E., Klassen, T., Valenzano, R., Castro,

M., and McIlraith, S. (2019). Learning reward ma-

chines for partially observable reinforcement learning.

In Proc. of Thirty-third Conf. on Neural Information

Processing Systems, NeurIPS 2019.

Kingma, D. and Ba, J. (2014). Adam: A method

for stochastic optimization. arXiv preprint

arXiv:1412.6980.

ret

ınsk

y, J., P

erez, G., and Raskin, J.-F. (2018). Learning-

based mean-payoff optimization in an unknown MDP

under omega-regular constraints. In Proc. of Twenty-

Ninth Intl. Conf. on Concurrency Theory (CONCUR-

18), pages 1–8, Schloss Dagstuhl, Germany. Dagstuhl.

Lee, D. and Yannakakis, M. (1996). Principles and methods

of testing ﬁnite state machines - a survey. Proc. of

IEEE, 84(8):1090–1123.

McTear, M., Callejas, Z., and Griol, D. (2016). The conver-

sational interface. Springer Verlag, Heidelberg, New

York, Dortrecht, London.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A., Veness,

J., Bellemare, M., Graves, A., Riedmiller, M., Fidje-

land, A., Ostrovski, G., et al. (2015). Human-level

control through deep reinforcement learning. nature,

518(7540):529–533.

Plappert, M. (2016). keras-rl. https://github.com/keras-rl/

keras-rl.

Puterman, M. (1994). Markov Decision Processes: Discrete

Dynamic Programming. Wiley, New York, NY.

Shahbaz, M. and Groz, R. (2009). Inferring Mealy ma-

chines. In Cavalcanti, A. and Dams, D., editors, Proc.

Online Learning of non-Markovian Reward Models

of Intl. Symposium on Formal Methods (FM-09), num-

ber 5850 in LNCS, pages 207–222. Springer-Verlag,

Berlin Heidelberg.

Thi

ebaux, S., Gretton, C., Slaney, J., Price, D., and

Kabanza, F. (2006). Decision-theoretic planning

with non-Markovian rewards. Artif. Intell. Research,

25:17–74.

Turchetta, M., Berkenkamp, F., and Krause, A. (2016). Safe

exploration in ﬁnite markov decision processes with

gaussian processes. In Proc. of Thirtieth Conf. on Neu-

ral Information Processing Systems, NeurIPS 2016.

Vaandrager, F. (2017). Model Learning. Communications

of the ACM, 60(2):86–96.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence