A Hierarchical Decomposition Approach for the Optimal Design of a

District Cooling System

Bingqian Liu

1 a

, C

ome Bissuel

1 b

, Franc¸ois Courtot

, C

eline Gicquel

3 c

and Dominique Quadri

EDF R&D, Chatou, France

EDF R&D China, China

Universit

e Paris Saclay, LRI, France

Keywords:

Local Energy System Design, Mixed-integer Linear Programming, Branch & Bound, Hierarchical

Decomposition.

Abstract:

A district cooling system is a centralized cooling supply system providing air conditioning to a set of buildings

located in the same district. Designing and sizing such a system is very complex, as both the initial construction

cost and the operation cost of the cooling system during its entire life must be considered. We ﬁrst propose a

modeling approach aiming at formulating this combinatorial optimization problem as a mixed-integer linear

program of tractable size. We then extend a previously published hierarchical decomposition technique in

order to ﬁnd the optimal solution in an efﬁcient way. Finally, we provide preliminary computational results

based on a real-life case study located in China.

1 INTRODUCTION

A district cooling system (DCS) is a centralized cool-

ing supply system. It consumes electricity to cool

down water and distributes it through an underground

pipe network to the buildings in the district to provide

them with air conditioning. DCSs usually are highly

energy-efﬁcient cooling systems. Thus, according to

the Electrical and Mechanical Services Department

of Hong Kong EMSD (2020), using DCSs instead

of traditional air-cooled air-conditioning systems re-

sults in energy savings of 35%. DCSs also compare

well with individual water-cooled air-conditioning

systems using cooling towers as the energy savings

may be up to 20%. Furthermore, this lower energy

consumption leads to lower greenhouse gas emis-

sions, which helps reduce the environmental impact

of the system.

Designing a DCS involves choosing the type and

number of chillers to be installed as well as the ice

storage capacity. These decisions should take into

account not only the construction costs, but also the

operation costs of the system during its whole life-

time. Computing these operation costs is a chal-

https://orcid.org/0000-0001-7493-4277

https://orcid.org/0000-0002-5430-3168

https://orcid.org/0000-0002-2719-7443

lenging problem. Namely, the demand for cooling

power is highly variable and features a daily, weekly

and yearly seasonality together with random varia-

tions. Moreover, due to technical reasons owing to

the chillers, these operations costs are not at all pro-

portional to the produced cooling power. Thus, in or-

der to accurately estimate them, a detailed schedule

describing, on a hourly basis, the on/off status and the

load allocation of each chiller should be built for an

horizon spanning a whole year. Furthermore, the de-

ployment of a district cooling system is usually not

a one-shot decision but rather a process in which in-

vestment decisions are made step by step, following

the development of the district and the upward trend

of the average demand over the years. This implies

that a multi-phase strategic deployment plan should

be built.

This optimization problem can be formulated as a

mixed-integer program. However, its resolution poses

several difﬁculties. The ﬁrst one comes from the non-

linearity of the chillers’ performance curves. These

performance curves give, for each chiller, the amount

of electricity consumed as a function of the amount

of produced cooling power and thus play a key role

in the estimation of the system operation costs. Sec-

ond, the need to simultaneously build a multi-year

phasing plan and a detailed operational schedule for

each day of the planning horizon leads to the formu-

Liu, B., Bissuel, C., Courtot, F., Gicquel, C. and Quadri, D.

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System.

DOI: 10.5220/0010220403170328

In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 317-328

ISBN: 978-989-758-485-5

317

lation of a huge mathematical program, which can-

not be solved directly by current mathematical pro-

gramming solvers. Finally, the use of classical de-

composition methods, such as the Benders’ decom-

position approach, is not straightforward as it would

imply sub-problems involving binary and/or integer

decision variables. The mixed-integer program mod-

eling the problem is thus computationally intractable

as such.

However, solution approaches exploiting the nat-

ural hierarchy between decisions relative to the sys-

tem design and decisions relative to the daily op-

eration schedules have been investigated in several

works. Weber et al. (2007) thus studied the optimal

design of a multi-energy system. A two-level opti-

mization method is implemented. The master opti-

mization level explores the set of possible system de-

signs with the use of an evolutionary algorithm. For

each considered system design, the slave optimiza-

tion level calculates the optimal cost by linear pro-

gramming. This approach does not provide a guaran-

teed optimal solution and the formulation of the slave

sub-problems as linear programs does not allow to ac-

curately model the way the system operates in prac-

tice. Iyer and Grossmann (1998) also use a bi-level

method to optimize the choice and sizes of equipment

for utility systems. At the design optimization level,

the problem aims at ﬁxing the system infrastructure.

All binary decision variables relative to the opera-

tion schedules are removed from this master problem.

Each time a potential infrastructure is found, the op-

eration optimization level solves a set of single-period

scheduling sub-problems taking the current system

infrastructure as input data. Design cuts are used to

tighten the gap between the solutions found at both

levels. Yokoyama et al. (2015) consider local energy

supply systems and propose a customized Branch &

Cut algorithm exploiting the hierarchical relationship

between the design and operation decision variables

of the mathematical program. The upper level prob-

lem corresponds to the initial optimization problem

in which all operational integer and binary variables

are kept but relaxed to be continuous. Each time an

integer feasible solution is found at the upper level,

a sequence of single-period independent operation

sub-problems is solved to check the feasibility and

value of the current design solution. Note that Iyer

and Grossmann (1998) and Yokoyama et al. (2015)

both consider a single-phase variant of the problem,

i.e. a variant in which all design decisions are one-

shot decisions. Moreover, their design infrastruc-

ture did not allow short-term intra-day energy stor-

age. This allows them to consider single-period (i.e.

one-hour) scheduling sub-problems rather than multi-

period (i.e. 24-hour) scheduling sub-problems, which

signiﬁcantly decreases the size of these sub-problems.

In the present work, we propose a solution ap-

proach for the optimal design, over a multi-phase in-

vestment horizon, of a local district cooling system

in which intra-day ice storage is allowed. This ap-

proach relies on three key elements. First, we seek

to reduce the size of the initial optimization problem.

We thus consider a deployment plan involving a lim-

ited number of phases, some of which spanning sev-

eral years. Moreover, we use the clustering approach

described in Zatti et al. (2019) to select a small set

of typical days to represent with the smallest pos-

sible loss of accuracy the various conditions under

which the system will be operated. Second, we build

a piecewise linear approximation of the performance

curves of each chiller and propose a way to exploit

their convexity to reduce the size of the formulation

of the operation scheduling sub-problems. This re-

sults in the formulation of a large-size mixed-integer

linear program (MILP). Thirdly, we develop an ex-

act solution algorithm based on the hierarchical de-

composition method recently proposed by Yokoyama

et al. (2015) to solve this MILP.

The remaining of the paper is organized as fol-

lows. Section 2 gives a detailed description of the

problem under study. In Section 3, the approximation

of the nonlinear performance curves and the cluster-

ing method used to identify typical days are ﬁrst pre-

sented. The formulation of the optimization problem

as an MILP is then provided. Section 4 introduces the

hierarchical decomposition algorithm used to solve

this MILP. In Section 5, the results of our preliminary

computational experiments based on a real-life case

study in China are reported.

2 PROBLEM PRESENTATION

Before the actual construction of a cooling system,

a thorough and reliable system design is necessary.

The system design consists in selecting the appropri-

ate chillers and in sizing the ice storage capacity to

be installed. The main objective is to design a sys-

tem which will be able to meet the clients’ cooling

demand at all time while leading to the lowest long-

term investments and operation costs.

2.1 Resources

A chiller is a machine that removes heat from a liq-

uid by using a variety of techniques such as vapor-

compression. We consider here electric-powered

chillers which are used to cool water. These chillers

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

318

can be classiﬁed into two main categories depend-

ing on their functionality. Standard chillers (de-

noted by STDC) only produce cooling power to sat-

isfy the instantaneous demand of the customers. Ice

chillers (denoted by ICEC) have two distinct operat-

ing modes: they either produce cooling power, but

usually with a lower efﬁciency than the one of a

STDC, or they produce ice. This ice can be stored

for a few hours in an ice storage tank and be melted

afterwards to provide cooling power.

Within each category of chillers (STDC or ICEC),

there are chillers with different production capacity

levels. Each level corresponds to a predeﬁned produc-

tion range, i.e. to a minimum and maximum cooling

power (or ice) it can provide per hour when turned

on, and to a set of performance curves. Namely, the

energy consumption of a chiller is a function of the

produced cooling power and the ambient tempera-

ture. We thus have performance curves representing

the relation between the electric power consumed by a

chiller and the cooling power (or ice) produced under

different ambient temperatures. Note that these per-

formance curves are usually not linear. In the present

paper, we will focus on the case of non-linear convex

performance curves. The more general non-convex

case is left for future work.

Another key resource in the system is the ice stor-

age tank. This tank is linked to all the ice chillers of

the system, can store the produced ice for a few hours

and release it afterwards to produce cooling power. It

has a maximal storage capacity, which can be chosen

within a predeﬁned range.

See Figure 1 for a schematic representation of the

studied DCS.

Figure 1: Overview of a DCS.

2.2 Cooling Demand

As highlighted in the introduction, the cooling de-

mand to be satisﬁed by the local cooling system is

highly variable. First, the demand for cooling power

varies throughout the day and is usually much higher

at daytime than at night. There are also weekly and

yearly variations: the demand pattern of a weekday

thus signiﬁcantly differs from the one observed dur-

ing the week-end and the total daily demand varies

during the year, in particular with the summer and

winter seasons. Finally, during the ﬁrst operating

years of the system, the demand displays a general

upward trend as new clients join the district cooling

system. After this initial period, the demand usually

gets more or less stable for the rest of the system life-

time.

Parts of these demand variations display a sea-

sonal pattern and are thus to some extent predictable.

However, the demand is also subject to the presence

of extreme weather conditions which are difﬁcult to

anticipate. Days with such effects should be consid-

ered separately from others. This translates in partic-

ular into the existence of extreme days, i.e. days in

which the total daily or hourly demand is exception-

ally low or high as compared to its usual value.

A key requirement is that the system should be

able to satisfy the demand for cooling power at all

time, whatever the hour of the day, the day in week or

the season. In particular, it should be able to satisfy

all the demand, even if it is exceptionally low or high.

2.3 Electricity Supply

The chillers are powered by electricity bought from

an external utility provider.

Similar to the cooling power demand, the elec-

tricity price displays daily, weekly and yearly varia-

tions. In particular, within a day, three types of peri-

ods, termed peak, ﬂat and valley periods, can be dis-

tinguished. They correspond respectively to the high-

est, intermediate or lowest prices. Peak periods are

usually at noon and in the evening, the valley peri-

ods at night and early in the morning and the rest of

the day corresponds to ﬂat periods. These price varia-

tions can be exploited to reduce the total energy cost,

e.g. by producing ice at night when the demand for

cooling power is low and the electricity rather cheap,

storing it for a few hours and releasing ice to produce

cooling power at daytime when the demand is high

and the electricity more expensive.

Moreover, in many cases, the contract with the

electricity provider includes a maximum allowed in-

stantaneous power consumption from the grid. This

upper limit is set contractually at the beginning of

each year. The corresponding cost, called the con-

tract fee, is proportional to the subscribed maximum

power. This contract fee differs from the electricity

consumption cost. It namely buys the permission of

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System

319

consuming electric power and sets an upper limit (ex-

pressed in kW) to this instantaneous consumption. In

contrast, the electricity consumption cost depends on

the total amount of consumed electric energy which

is expressed in kWh.

2.4 Costs

The total cost of the system comprises two main parts:

the design cost and the operation cost.

The design cost is the sum of the purchase, instal-

lation and maintenance costs of the chillers and ice

storage tank, and of the annual contract fee. Once the

cooling system design is chosen, this cost will be de-

termined.

The operation cost corresponds to the cost of the

electricity consumed when the system operates to sat-

isfy the customers’ cooling demand. Due to the non-

linearity of the chillers’ performance curves, this cost

is not proportional to the amount of produced cooling

power. In order to accurately estimate it, we need to

build a detailed production schedule for each day of

the planning horizon using a ﬁne time discretization.

The objective of this optimization problem is to

ﬁnd a system design which can minimize the sum of

the design and operation costs. Therefore, the best

system design as well as the most cost-efﬁcient daily

optimal operation strategy corresponding to the cho-

sen system should be searched.

3 PROBLEM MODELING

3.1 Selection of Typical Days

The huge size of the optimization problem, which

combines both long-term design and detailed (usually

with an hourly timestep) production scheduling deci-

sions, makes it computationally intractable. A pos-

sible way of getting over this difﬁculty consists in

selecting, within the available data, a subset of typ-

ical days and extreme days which will represent the

various conditions under which the system will be

operated. These days should be carefully chosen as

they will have a strong impact on the selection of the

chillers and sizing of the ice storage tank.

This can be done by solving a clustering problem

such as the k-medoid problem. In our case, this prob-

lem consists in partitioning the set of days belonging

to the available historical time series into groups or

clusters and in choosing one member (i.e. one day)

in each cluster to represent it so as to minimize the

total Euclidian distance between each day in the time

series and its representative. In this work, we use the

extension of the k-medoid problem proposed by Zatti

et al. (2019) to select typical days for optimizing the

design of our system.

3.2 Piecewise Linear Approximation of

the Performance Curves

The performance curves of a given type of chiller are

supplied by its manufacturer. They give, for a dis-

crete set of values of the ambient temperature, the

amount of electric energy consumed as a function of

the output cooling power. Their non-linearity is a ma-

jor source of difﬁculty for the resolution of our opti-

mization problem. We thus propose to build a piece-

wise linear approximation of each curve.

This approximation is built using the following

procedure. We ﬁrst ﬁx a predeﬁned number of break-

points in the piecewise linear approximation to be

built. We then determine the coordinates of these

breakpoints by heuristically solving a small non-

linear optimization problem aiming at minimizing the

distance between the approximate performance curve

and the actual one.

Then, for each hour of each selected day, we use

historical data about the average ambient temperature

to determine the approximate performance curve that

should be used to compute the energy consumption of

each type of chiller during each time period.

3.3 Notation

The problem modeling relies on a three-level time dis-

cretization. The forecast lifetime of the system is ﬁrst

divided into a set of phases or investment periods,

each one typically spanning one or several years: we

assume that design decisions such as the installation

of a new chiller can be only made at the beginning

of a new phase. Let Φ be the number of considered

phases. Within each considered phase, the various

conditions under which the system will be operated

will be represented by a number of preselected typ-

ical days and extreme days. We denote by D

the

set of typical days and extreme days used to repre-

sent the various daily demand patterns during phase

φ ∈ {1, ...,Φ}. Each selected day d of phase φ has a

weight w

φ,d

corresponding to the number of days it

represents, i.e. to the number of days of the original

historical time series which were assigned to the clus-

ter it belongs to. Finally, in order to describe the intra-

day variations of the cooling demand and electricity

price, each selected day is divided into 24 one-hour

periods. For the sake of readability, in what follows,

we use the letter t to represent the time period (φ,d,h)

corresponding to phase φ, selected day d and hour h.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

320

Let Dem

(resp. EP

) represent the cooling power de-

mand (resp. the electricity price) at time period t.

There are different types of chillers that may be

installed in the system. Each type of chiller m = (p, l)

can be described by its category p ∈ {ST DC, ICEC}

(i.e. standard or ice chiller), which deﬁnes the list of

commodities C

⊂ {COLD, ICE} it can produce, and

its production capacity level l ∈ {1, ..., L

}. Let M =

{(p, l)|p ∈ {ST DC, ICEC}, l ∈ {1,...,L

}} be the set

of all chiller types. We denote by P

min

m,c

and P

max

m,c

the

minimum and maximum output power of a chiller of

type m = (p, l) producing commodity c ∈ C

. As ex-

plained above, the performance curve of a chiller of

type m producing commodity c at time period t is ap-

proximately represented by a piecewise linear func-

tion comprising B

t,m,c

breakpoints. Let a

t,m,c,b

and

t,m,c,b

be the abscissa and ordinate of breakpoint b

of this piecewise linear function.

With respect to the design of the system, some

restrictions have to be taken into account. There is

namely an upper bound SD

max

to the total number of

chillers of type m that may be installed in the sys-

tem. The total ice storage capacity built in the system

should also stay below a maximum allowed capacity

StoC

max

. Moreover, in terms of design costs, we de-

note by FC

φ,m

the ﬁxed cost of investing in a chiller

of type m at phase φ. This ﬁxed cost comprises the

construction or capital expenditure cost at phase φ and

the total maintenance cost of the chiller over its whole

lifetime (from phase φ to phase Φ ). Regarding the

ice storage capacity, the installation cost is broadly

proportional to the installed capacity. We denote by

the cost of building one unit of ice storage ca-

pacity at phase φ. Finally, the unit subscription cost

for the maximum instantaneous power is assumed de-

noted by SC

. Note that all the design costs FC

φ,m

and SC

are assumed uniform along each deploy-

ment phase.

3.4 Variables

In order to model the problem as a mixed-integer lin-

ear program, we introduce two sets of decision vari-

ables.

The ﬁrst set of decision variables corresponds to

long-term design decisions which will determine the

general structure of the system, together with the

multi-year phasing plan. Thus, SD

φ,m

represents the

integer number of chillers of type m to be installed at

the beginning of phase φ, StoC

is a continuous vari-

able representing the ice storage capacity built at the

beginning of phase φ and C

is the maximum allowed

electric power consumption contracted with the elec-

tricity provider for phase φ. These variables will be

referred to as design decision variables in what fol-

lows.

The second set of decision variables are used to

build the operational schedule for each selected day

d ∈ D

of each phase φ. In the present work, we will

focus on the special case in which all performance

curves of the chillers are convex. This assumption

allows us to use aggregate performance curves (see

Appendix for more detail about this) and to build the

schedule while considering, in each period t, aggre-

gate scheduling variables, i.e. variables pertaining

to the set of chillers of identical type producing the

same commodity c during t, instead of disaggregate

scheduling variables, i.e. variables pertaining to the

status and output of each individual chiller installed

in the system in period t.

We thus introduce S

t,m,c

the integer number of

chillers of type m producing commodity c during pe-

riod t, P

t,m,c

the total amount of commodity c pro-

duced by the chillers of type m during period t and

t,m,c

the total electric consumption of the chillers of

type m producing commodity c in period t. More-

over, in order to monitor the ice storage and release,

we deﬁne STO

the amount of ice stored in the tank

at the beginning of period t and R

the amount of ice

released during t. These decisions will be referred to

as operation decision variables in what follows.

3.5 Objective Function

We seek to minimize the sum of the design and op-

eration costs of the system over its whole lifetime.

The objective function of the mathematical program

is thus given by:

min

∑

φ=1

∑

m∈M

φ,m

+ LC

StoC

+SC

∑

d∈D

φ,d

∑

h=0

∑

m∈M

∑

c∈C

φ,d,h

φ,d,h,m,c

(1)

where α

is the actualization rate for the costs in-

curred in phase φ.

3.6 Constraints

Similar to the decision variables, the constraints of the

mathematical model can be classiﬁed into two groups:

design constraints and operation constraints.

3.6.1 Design Constraints

Design constraints are constraints involving only de-

sign decision variables. In the present case, for each

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System

321

type of chiller m ∈ M , we have the following con-

straint which states that the total number of chillers of

type m included in the DCS should be less than the

maximum number of chillers of this type allowed.

∑

ϕ=1

ϕ,m

≤ SD

max

(2)

Similarly, Constraint (3) makes sure that the to-

tal ice storage capacity of the system stays below the

maximum allowed value.

∑

ϕ=1

StoC

≤ StoC

max

(3)

3.6.2 Operation Constraints

Operations constraints are constraints involving op-

eration decision variables, together with design vari-

ables in some cases. For each time period t, we have

the following set of constraints.

Demand Satisfaction. The demand for cooling

power must be satisﬁed at all time. This can be done

either by directly using the cooling power produced

by the currently turned on chillers and by releasing

some ice from the ice storage tank.

∑

m∈M

t, m,COLD

+ R

= Dem

(4)

Chillers. Regarding the chillers, two sets of con-

straints should be introduced in the formulation.

First, for each type of chiller m ∈ M , the total

number of operating (i.e. turned on) chillers should

be less than the number of chillers currently installed

in the DCS:

∑

c∈C

t,m,c

≤

∑

ϕ=1

ϕ,m

(5)

Second, for each type of chiller m ∈ M and each

commodity c ∈ C

it can produce, the total amount

produced by the turned on chillers should stay within

the allowed production range:

t,m,c

≤ P

max

m,c

t,m,c

(6)

t,m,c

≥ P

min

m,c

t,m,c

(7)

Electric Consumption. As shown in Appendix,

when the chillers’ performance curve are convex, the

aggregate electric consumption of the set of chillers

corresponding to a given type m = (p,l) ∈ M and pro-

ducing commodity c ∈ C

in t belongs to the epigraph

of a piecewise linear function deﬁned by breakpoints

b = 1...B

t,m,c

. We thus have, for each m = (p,l) ∈ M ,

each c ∈ C

and each b ∈ {1...B

t,m,c

− 1}, the follow-

ing inequality:

t,m,c

≥ s

t,m,c,b

t, m, c

+ c

t,m,c,b

t,m,c

(8)

where s

t,m,c,b

t,m,c,b+1

−o

t,m,c,b

t,m,c,b+1

−a

t,m,c,b

is the slope of the

line segment between breakpoints b and b + 1 and

t,m,c,b

= o

t,m,c,b

− s

t,m,c,b

the corresponding

constant value. Note that Constraints (8) accurately

compute the electric consumption of a set of chillers

only if the corresponding performance curve is con-

vex. The more general case of non-convex perfor-

mance curve is left for future work.

Moreover, the total amount of electric energy con-

sumed in period t is limited by an upper bound, C

1hour, which represents the maximum instantaneous

power C

contracted with the electricity provider

times the duration of the period (one hour):

∑

m∈M

∑

c∈C

t,m,c

≤ C

(9)

Ice Storage. Regarding the ice storage, three con-

straints should be considered in each time period.

First, the amount of ice stored in the tank should

not exceed the current storage capacity.

STO

≤

∑

ϕ=1

StoC

(10)

Second, the amount of ice released during the pe-

riod should be less than the amount stored in the tank

at the beginning of the period.

≤ STO

(11)

Third, the evolution of the ice inventory stored in

the tank should comply with inventory balance equa-

tions. We ﬁrst consider time periods (φ, d,h) corre-

sponding to h ∈ {0...22} as the last hour of the day

h = 23 requires a special treatment. For each period

(φ,d, h) such that h ∈ {0...22}, we have:

STO

φ,d,h

ICEC

∑

l=1

φ,d,h,ICEC,l,ICE

− R

φ,d,h

= STO

φ,d,h+1

(12)

Constraints (12) state that the amount of ice stored

at the beginning of hour h +1, STO

φ,d,h+1

, is equal to

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

322

the amount of ice already stored at the beginning of

hour h, STO

φ,d,h

, plus the total amount of ice pro-

duced by the ice chillers of various capacity levels

during h minus the ice melted during h. Note that the

loss of ice stored in the tank during a day is assumed

to be negligible.

Moreover, for each time period (φ, d, h) corre-

sponding to h = 23, i.e. to the last hour of the se-

lected day, we have the following inventory balance

equation:

STO

φ,d,23

ICEC

∑

l=1

φ,d,23,ICEC,l,ICE

− R

φ,d,23

= STO

φ,d,0

(13)

Namely, in practice, the entering inventory of a

given day in the scheduling horizon is imposed by

the leaving inventory of the previous day. In our

case, we do not consider each individual day of the

scheduling horizon but rather a number of represen-

tative days which will not necessarily occur succes-

sively in practice. We thus impose that the leav-

ing ice inventory of a selected day d, computed as

STO

φ,d,23

∑

ICEC

l=1

φ,d,23,ICEC,l,ICE

− R

φ,d,23

should

be equal to the entering inventory of the same selected

day d, STO

φ,d,0

. This might be understood as the fact

that the selected day d will be cyclically repeated w

φ,d

times in the simpliﬁed scheduling horizon used in our

optimization problem for phase φ.

4 SOLUTION APPROACH

The mathematical program (1)-(13) formulated in

Section 3 displays a particular structure. We namely

have a set of independent sub-problems. Each of them

corresponds to optimizing the detailed schedule for a

single selected day d of a single phase φ and involves

operation variables and operation constraints relative

only to the corresponding day (φ, d). These indepen-

dent sub-problems are linked together by the design

variables.

A Benders decomposition approach might seem

appropriate for a problem displaying such a structure

in which coupling variables link together a set of inde-

pendent sub-problems. However, its application is not

straightforward here as each sub-problem involves in-

teger variables (namely variables S

t,m,c

) and Benders

decomposition algorithms rely on the strong duality

theory to generate Benders cuts. We thus investigate

another hierarchical decomposition approach recently

proposed by Yokoyama et al. (2015).

4.1 Hierarchical Structure of the

Problem

To better highlight the hierarchical structure of the

problem and more easily explain the decomposition

approach, we will use a compact formulation of the

problem.

Vector x represents in a synthetic way the de-

sign variables relative to all phases, i.e. x =

(SD

,StoC

,...,SD

,StoC

). Vector y

rep-

resents all the continuous operation variables relative

to a given selected day k = (φ, d) whereas z

stands

for all the binary or integer variables relative to day k.

With this notation, Problem (1)-(13) can be for-

mulated as follows.

minZ = f

(x) +

∑

k∈K

) (14)

h(x) ≤ 0 (15)

(x,y

) ≤ 0 ∀k ∈ K (16)

x ∈ Z

(17)

∈ R

∀k ∈ K (18)

∈ Z

∀k ∈ K (19)

In the objective function (14), the term f

(x)

corresponds to the design cost whereas the term

) computes the operation cost for each se-

lected day k in the set K = {(φ,d), φ = 1...Φ,d ∈

}. Constraints (15) correspond to the design con-

straints. Constraints (16) represent in a concise man-

ner all the operations constraints relative to day k ∈

K . Constraints (17)-(19) give the deﬁnition domain

of each variable vector. Problem (14)-(19) will be re-

ferred to as the Complete Model (CM) in what fol-

lows.

Note how all design variables are deﬁned as in-

teger variables in (17). This restriction is added to

the problem as it is a necessary condition for the use

of the hierarchical decomposition algorithm proposed

by Yokoyama et al. (2015).

This hierarchical decomposition algorithm uses as

a starting point a relaxation of (CM) in which the de-

sign variables x are kept integer or binary whereas

the binary or integer operation variables z are relaxed.

This gives the following semi-relaxed or upper level

problem denoted by (SRM).

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System

323

minZ

SRM

= f

(x) +

∑

k∈K

) (20)

h(x) ≤ 0 (21)

(x,y

) ≤ 0 ∀k ∈ K (22)

x ∈ Z

(23)

∈ R

∀k ∈ K (24)

∈ R

∀k ∈ K (25)

Problem (SRM) thus involves the same number of

variables and constraints as the initial problem (14)-

(19). However, the number of binary and integer vari-

ables is drastically reduced, which should ease its res-

olution.

Furthermore, the hierarchical decomposition algo-

rithm relies on the key observation that in Problem

(CM), when the design of the system is determined,

the problem can be decomposed into a set of small

independent operation sub-problems. Let Problem

]

) be the Operation Model relative to the op-

timization of the schedule of day k ∈ K , given a ﬁxed

design of the system described by vector x

]

. It is for-

mulated as:

minZ

]

) = f

) (26)

]

) ≤ 0 (27)

∈ R

(28)

∈ Z

(29)

4.2 Decomposition Algorithm

The decomposition algorithm proposed by

Yokoyama et al. (2015) exploits the hierarchical

structure described above. Thus, at the upper level,

a relaxed version of the initial problem, i.e. problem

SRM, is solved by a Branch & Cut algorithm. Each

time a potential incumbent solution (x

]

z) is found

during this tree search, the corresponding values of

the design variables x

]

are used as input data to solve

a series of independent scheduling sub-problems,

namely problems OM

]

),k ∈ K . This gives an

accurate estimation of the feasibility and value of the

potential design solution x

]

at the operation level.

If x

]

is found to be feasible and less expensive than

the current incumbent solution, it is accepted as the

new incumbent solution. Otherwise, it is rejected.

When all the branches are searched in the upper level

Branch & Bound search tree, the current incumbent

solution gives the optimal solution of the original

problem. This hierarchical decomposition approach,

provided it converges within the allotted computation

time, thus guarantees the optimality of the found

solution.

More precisely, the algorithm comprises the fol-

lowing main steps. See also Figure 2 for a ﬂow chart

of the decomposition algorithm.

Step 1. A Branch & Bound search tree is carried out

within the feasible space of problem SRM: see

 on

the ﬂow chart. The branching is done on the design

variables x until there is no open node left, in which

case we end the calculation, or an integer feasible

solution of SRM, denoted by (x

]

z), is obtained,

in which case we go to Step 2. The value

Z(x

]

) =

]

) +

∑

k∈K

(

) provides a lower bound of

the actual cost of the design solution x

]

Step 2. Before accepting x

]

as a new incumbent so-

lution for the upper level problem, we check its feasi-

bility and compute its actual cost Z(x

]

- We ﬁrst initialize the value of Z(x

]

) as Z(x

]

) ←−

Z(x

]

Then, for each k ∈ K :

- We solve Sub-problem OM

]

) using a standard

Branch & Cut algorithm: see

 on the ﬂow chart.

- If OM

]

) is unfeasible, x

]

cannot be feasible for

Problem (CM). We stop and go to Step 4.

- Otherwise, we record the optimal integer solution of

]

), (y

), and its optimal cost f

- We update the current estimation of the actual cost

of the design solution x

]

by computing Z(x

]

) ←−

Z(x

]

) + f

) − f

(

- If Z(x

]

) is larger than the incumbent value, x

]

cannot

be an optimal solution of Problem (CM). We stop and

go to Step 4: see

 on the ﬂow chart.

- If all days in K have been considered, we go to Step

3. Otherwise, we go on with the next day in K .

Step 3. We replace the incumbent solution by (x

]

,y,z)

and the incumbent value by Z(x

]

) and go to Step 4:

see

 on the ﬂow chart.

Step 4. We reject the current node in Problem SRM to

prevent the solver from taking the semi-relaxed objec-

tive value of the design solution x

]

Z(x

]

), as a valid

upper bound to be used for the rest of the Branch &

Bound search at the upper level. This allows us to

guarantee that the cutoff value taken into account to

close nodes in the branching process is the actual cost

Z(x

]

) of the current incumbent design solution x

]

, see

Yokoyama et al. (2015). Then go back to Step 1: see

 on the ﬂow chart.

Finally, we noted in our preliminary experiments,

that while running the hierarchical algorithm de-

scribed above, we often had to solve multiple times

the same operations problem OM

(.). Namely, two

different design solutions x

and x

may e.g. be sim-

ilar for the ﬁrst phases and differ only for the last

phases. It may also happen that two different design

solutions x

and x

differ with respect to the decisions

relative to the ﬁrst phases of the horizon but give the

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

324

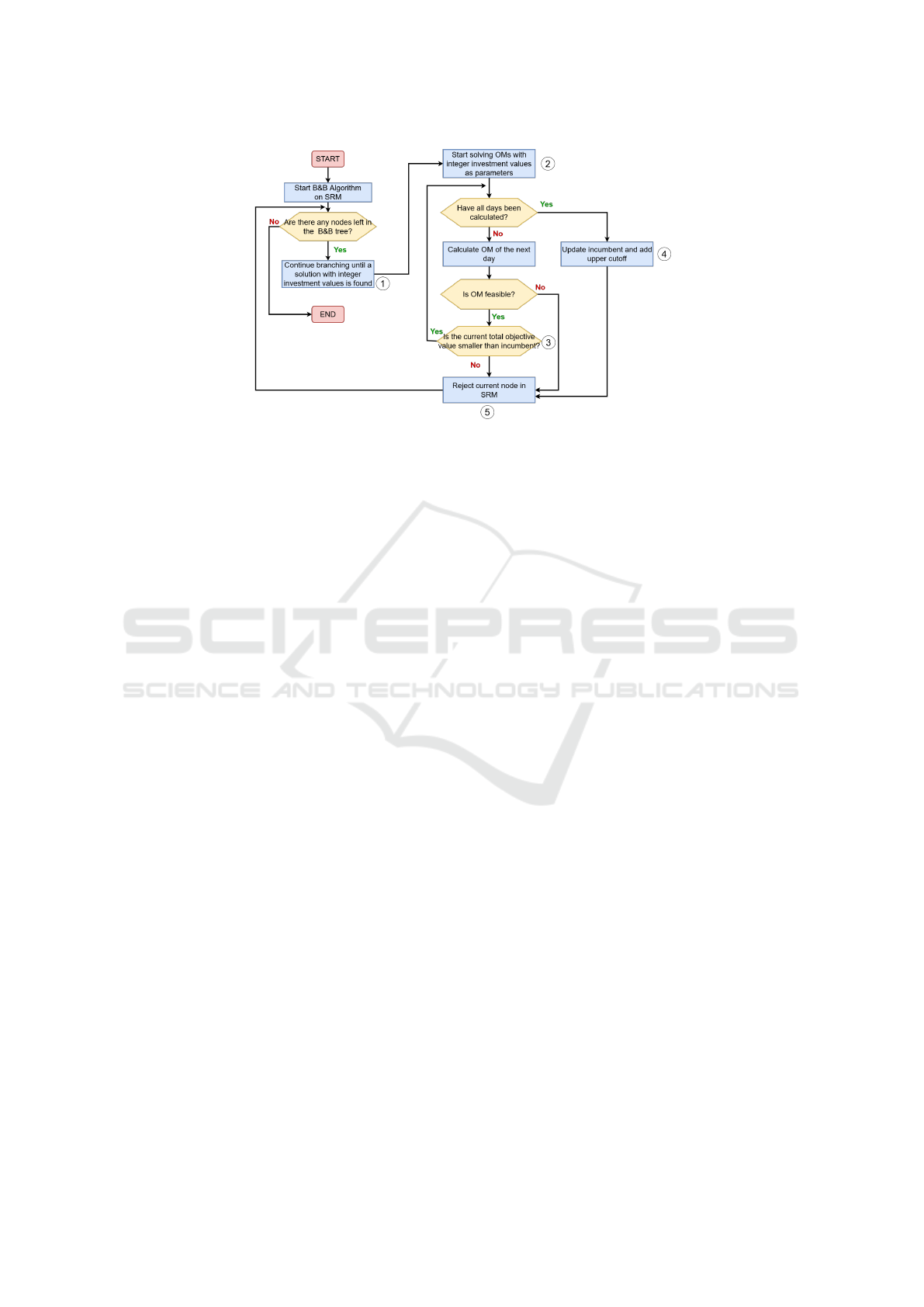
Figure 2: Flow chart of hierarchical decomposition algorithm.

same system infrastructure for the last phases. In both

cases, operations problems OM

) and OM

)

will be equivalent for all the selected days k corre-

sponding to the phases in which x

and x

provide the

same system infrastructure.

In order to avoid this useless computational ef-

fort, we thus modify the implementation of the hi-

erarchical decomposition algorithm. When the op-

eration cost of a newly encountered system infras-

tructure needs to be evaluated for a given phase,

the operation sub-problems relative to this phase are

solved and the corresponding optimal operation cost

∑

k st. d∈D

) is recorded in memory. Then,

over the course of the algorithm, each time the op-

eration cost of a design solution corresponding to the

same system infrastructure in the same phase needs to

be evaluated, we simply use the recorded value with-

out recomputing it from scratch.

5 PRELIMINARY NUMERICAL

RESULTS

In order to assess the performance of the proposed

solution approach, we consider a real-life case study

corresponding to a DCS under construction in China.

The expected lifetime of the cooling system is

30 years. The total annual cooling demand is an-

ticipated to increase in the ﬁrst three years and stay

stable afterwards. We thus consider Φ = 3 invest-

ment phases. Phases 1 and 2 correspond to the ﬁrst

two years whereas Phase 3 corresponds to the last 28

years. To show the increase in demand, we compare

in Table 1 the total yearly demand, which is the sum

of demand of one year, and the maximum hourly de-

mand for each phase. New chillers and storage ca-

pacity should be installed at the beginning of the ﬁrst

three years to guarantee that the cooling supply will

meet the increasing demand. The hourly cooling de-

mand value is predicted by combining historical data

on the cooling consumption in the area and forecasts

on the future number of clients which will connect to

the DCS.

There are L

ST DC

= 3 types of standard chillers and

ICEC

= 2 types of ice chillers available. Their maxi-

mum output capacity P

max

p,l,c

and installation cost FC

φ,m

(in millions of CNY) are shown in Table 3. Note that

chillers of type (ST DC,1) and (ST DC, 2) have the

same maximum output capacity P

max

p,l,COLD

but chillers

of type (ST DC, 2) are less efﬁcient and less expen-

sive than the ones of type (ST DC,1). For each type of

chiller and each corresponding commodity, the min-

imum output power P

min

p,l,c

is equal to 0.10P

max

p,l,c

. Fig-

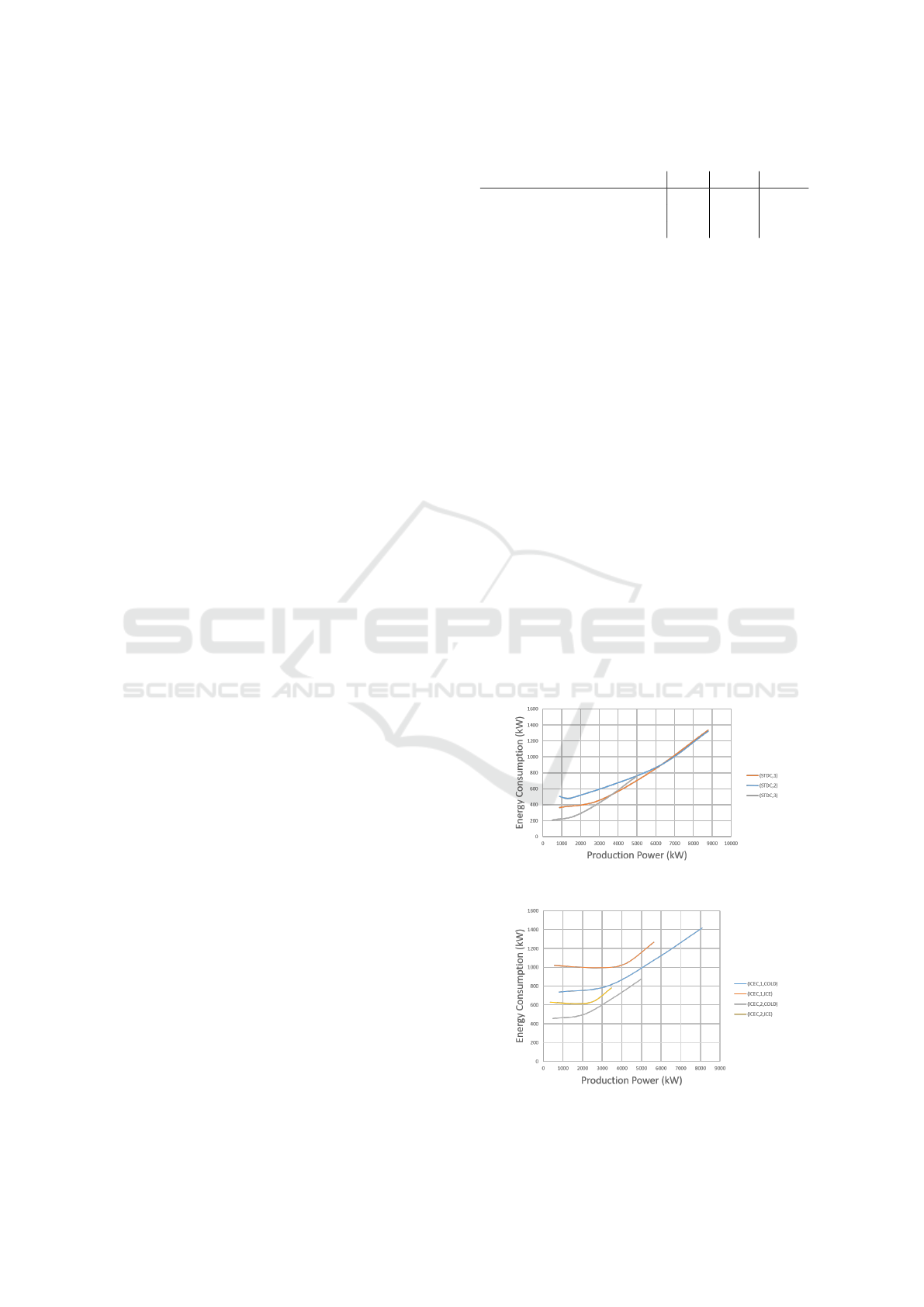
ures 3 and 4 display the performance curves of the

available standard and ice chillers at an ambient tem-

perature of 30

◦

C. We use B

t,m,c

= 4 breakpoints to

build the piecewise linear approximation of the per-

formance curve of the chillers of type m producing

commodity c at time period t. The coordinates are

determined by solving a small non-linear optimiza-

tion problem thanks to a heuristic method belonging

to the numpy package in Python. Finally, for each

type of chiller m, the maximum number of chillers

that can be installed, SD

max

is set to 10.

The unit cost of installing ice storage capacity LC

is 222.16CNY per kWh and the unit subscription cost

for the maximum instantaneous power allowed, SC

is 276CNY per kW. Since the installed storage capac-

ity and the subscribed contract power are discretized,

a unit of storage capacity is 6000kWh and a unit of

contract power is 3000kW. The installed storage ca-

pacity should be lower than StoC

max

= 200GWh and

the contract power should be no more than 30GW.

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System

325

The discount rate α

is 8%.

The electricity price features a daily seasonality

but no weekly nor yearly variations. Figure 5 shows

the unit price of electricity as a function of the hour

of the day. As the electricity price does not change

with the day in the week or the season, the typical

days and extreme days are selected so as to represent

as best as possible the variations in the cooling power

demand. For each phase, 30 typical days are selected

using the approach proposed by Zatti et al. (2019) and

4 extreme days are identiﬁed: the day with the highest

hourly demand, the one with the highest total demand,

the one with the lowest non-zero hourly demand and

the one with the lowest non-zero total demand. There-

fore, there are a total of 34 × 3 = 102 operation sub-

problems.

This results in the formulation of a large-size

MILP. The model involves 64381 variables, among

which 22053 are integer and 600 are binary, as well as

101422 constraints. This MILP is solved using the hi-

erarchical decomposition algorithm presented in Sec-

tion 4. This algorithm is implemented in Python using

the mathematical programming solver CPLEX12.8.

All the problems are solved using a machine with a

Intel Xeon 2.90GHz processor and 16GB RAM.

Table 4 describes the optimal solution in terms of

the number of chillers and the storage capacity built

in each phase, together with the contract power. Fig-

ure 6 shows the operation of chillers and storage in

one of the typical days. The periods in which the ice

production of (ICEC,2) seems to take negative value

correspond to periods in which ice is produced and

stored in the tank.

Furthermore, we carried out additional experi-

ments in order to get a preliminary assessment of the

computational efﬁciency of the hierarchical decom-

position algorithm and to evaluate the impact of the

selection of representative days on the infrastructure

design. We thus created 4 additional instances based

on our case study by varying the number of selected

days per phase from 6 to 34. The corresponding re-

sults are provided in Table 2. The ﬁrst line in the table

indicates the number of selected days for each phase.

Lines 2 to 5 provide indications on the size of the

MILP to be solved: we note that the number of vari-

ables and constraints in the problem increases linearly

with the number of selected days. Lines 6 to 9 corre-

spond to the results obtained while directly solving

Problem (CM) with CPLEX12.8 whereas Lines 10 to

13 correspond to the results obtained with the hierar-

chical decomposition algorithm. For each algorithm,

we report the computation time (which was limited

to a maximum of 2 hours), the total and design cost

of the best solution found within the available time

Table 1: Phases and Demand.

Phase 1 2 3

Length (yr) 1 1 28

Total Yearly Demand (GWh) 54.7 250.0 276.8

Max Hourly Demand (MWh) 13.6 62.2 93.8

limit and the remaining gap (i.e. the relative differ-

ence between the values of the best solution and the

best lower found after 2 hours of calculation).

These results ﬁrst show that the hierarchical de-

composition algorithm is signiﬁcantly more efﬁcient

than the standard Branch & Cut algorithm embedded

in CPLEX12.8. Namely, with this algorithm, we were

able to solve to optimality the 5 considered instances,

and this with a computation time divided by a factor

of at least 2.25.

Moreover, results from Table 2 also show that the

system infrastructure found by solving the MILP de-

pends on the number of selected days. This can be

seen among others by the fact that the investment cost

varies with the number of selected days, which indi-

cates that the structure of the system and the deploy-

ment plan vary with this number. We note however

that, when using the hierarchical decomposition ap-

proach, both the total cost and the investment cost

become stable when more than 26 selected days are

considered for each phase. Additional computational

experiments are needed to determine the exact value

of the minimum number of selected days per phase

above which the system design does not change any

more.

Figure 3: Performance curves of STDC at 30

◦

Figure 4: Performance curves of ICEC at 30

◦

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

326

Table 2: Comparison between complete model and hierarchical decomposition.

Instance Number of Days 6 10 18 26 34

Size Number of Variables 11461 19021 34141 49216 64381

Number of Integer Variables 3909 6501 11685 16869 22053

Number of Binary Variables 180 240 360 480 600

Number of Constraints 17938 29854 53710 77566 101422

CPLEX Computation time 1726s >7200s >7200s >7200s >7200s

Objective Value 5.50 × 10

5.70 × 10

5.75 × 10

Investment Cost 2.45 × 10

2.35 × 10

2.36 × 10

2.37 × 10

Relative Gap 0.00% 0.02% 0.15% 0.34% 0.42%

Hier. Dec. Computation time 220s 922s 942s 1435s 1831s

Objective Value 5.50 × 10

5.70 × 10

5.74 × 10

5.75 × 10

Investment Cost 2.45 × 10

2.35 × 10

Relative Gap 0.00% 0.00% 0.00% 0.00% 0.00%

Table 3: Available chillers.

Type P

max

p,l,COLD

max

p,l,ICE

(STDC,1) 8791 - 13

(STDC,2) 8791 - 12

(STDC,3) 5000 - 7.7

(ICEC,1) 8087 5626 13

(ICEC,2) 5000 3478 8.3

Table 4: Optimal system design and phasing obtained with

30 typical days and 4 extreme days at the operation level.

Phase 1 2 3

(STDC,1) 0 0 0

(STDC,2) 1 5 3

(STDC,3) 0 1 0

(ICEC,1) 0 0 0

(ICEC,2) 1 0 0

Storage Capacity (MWh) 24 0 0

Contract Power (MW) 3 9 15

Figure 5: Electricity Price of a Day.

6 CONCLUSION

We presented a modeling and solving approach for

the optimal design of a district cooling system involv-

ing intra-day energy storage over a multi-phase hori-

zon. The modeling approach relies on a clustering

algorithm to identify a subset of typical days and on a

Figure 6: Operation Result of a Typical Day in Phase 3.

piecewise linear approximation of the chillers’ perfor-

mance curves. It results in the formulation of a large-

size mixed-integer linear program. An improved hier-

archical decomposition method is then implemented

to optimally solve this MILP. This decomposition

method exploits the hierarchy between upper-level in-

frastructure design decision and lower-level operation

scheduling decisions. Our preliminary computational

results carried out on a real-life case study located

in China show that the proposed hierarchical decom-

position algorithm signiﬁcantly outperforms a mathe-

matical programming solver at providing optimal so-

lutions of the MILP. Moreover, our results also show

that, provided a minimum number of typical days are

taken into account to estimate the operation costs, the

ﬁnal system infrastructure and the deployment phas-

ing do not change with the subset of selected typical

days, which is an important point to gain the trust of

the decision makers.

There are several possible directions for future re-

search suggested by the present work. First, addi-

tional computational experiments are needed to evalu-

ate the impact of the use of a limited number of repre-

sentative days and of the piecewise linear approxima-

tion of the chillers’ performance curves on the solu-

tion provided by the proposed approach. Second, on

a longer term perspective, it would be interesting to

extend the proposed approach to consider non-convex

A Hierarchical Decomposition Approach for the Optimal Design of a District Cooling System

327

performance curves for the chillers and to study more

general local energy systems, in particular systems si-

multaneously providing a district with several sources

of energy (electricity, heat, cold, ...).

REFERENCES

EMSD (2020). Beneﬁts of dcs. http:

//aiweb.techfak.uni-bielefeld.de/content/

bworld-robot-control-software/. [September 9,

2020].

Iyer, R. and Grossmann, I. E. (1998). Synthesis and op-

erational planning of utility systems for multiperiod

operation. Computers & Chemical Engineering, 22(7-

8):979–993.

Weber, C., Mar

echal, F., and Favrat, D. (2007). Design and

optimization of district energy systems. In Computer

aided chemical engineering, volume 24, pages 1127–

1132. Elsevier.

Yokoyama, R., Shinano, Y., Taniguchi, S., Ohkura, M.,

and Wakui, T. (2015). Optimization of energy supply

systems by MILP branch and bound method in con-

sideration of hierarchical relationship between design

and operation. Energy conversion and management,

92:92–104.

Zatti, M., Gabba, M., Freschini, M., Rossi, M., Gambarotta,

A., Morini, M., and Martelli, E. (2019). k-milp: A

novel clustering approach to select typical and ex-

treme days for multi-energy systems design optimiza-

tion. Energy, 181:1051–1063.

APPENDIX

Convex Performance Curves

When the performance curves of the chillers are con-

vex, we have the following property.

Lemma 1. For a set of identical chillers producing

the same commodity, the optimal load allocation con-

sists in equally distributing the total output power be-

tween the chillers.

Proof. The proof is done by contradiction. Suppose

we have two identical chillers, producing a total cool-

ing power of P with chiller 1 producing P

and chiller

2 producing P

> P

. Let π : P 7→ Q = π(P) be

the convex performance curve of these two chillers.

The total amount of electricity consumed by the two

chillers producing P is Q = π(P

) +π(P

We show that this load allocation is not optimal,

i.e. that it is possible to reduce the total amount of

consumed electricity. Namely, let δP be a small varia-

tion in the output. By decreasing the output of chiller

2 by δP, we can obtain a decrease in the electricity

consumed by this chiller of π

)δP, where π

is the

derivative function of π. In order to still be able to

provide a total output of P, we increase the output of

chiller 1 by δP, which leads to an increase in its elec-

tricity consumption of π

)δP.

By convexity of function f , π

) < π

Hence the total amount of electricity consumed with

the load allocation (P

+ δP, P

− δP) is smaller than

the one consumed with the load allocation (P

The result follows.

Let us now focus on the case in which the perfor-

mance curve π is convex and piecewise linear. When

multiple identical chillers are simultaneously produc-

ing the same commodity, the relation providing the

total amount of consumed electricity as a function of

the total amount of output power can be plotted as an

aggregate performance curve. We have the following

property:

Lemma 2. Let π be the piecewise linear and convex

performance curve of a given type of chiller. π in-

volves B breakpoints. Let (a

) be the abscissa and

ordinate of breakpoint b.

The aggregate performance curve Π

of S identi-

cal chillers of this type is also piecewise linear and

convex. It involves B breakpoints whose coordinates

are given by (Sa

,So

Proof. Let us consider the case where the total out-

put of the S chillers is P ∈ [SP

min

;SP

max

] where

min

max

] is the production range of a single chiller.

By Lemma 1, the optimal load allocation consists

in requiring each chiller γ = 1...S to produce the same

output P

. Let b be the index of the breakpoint

of function f such that P

∈ [a

b+1

]. The energy

consumed by each chiller γ is thus given by: Q

+ c

where s

and c

are the slope and constant

value of the b

line segment of π. The total energy

consumed by the S chillers is thus equal to Q = s

P +

S. This equality holds for any value of P such that

∈ [a

b+1

], i.e. any value of P ∈ [Sa

,Sa

b+1

]. This

means that Π

is linear over the segment [Sa

,Sa

b+1

with a slope equal to s

and a constant value of c

By generalizing this result to all possible values

of the total output P, we have that Π

is a piecewise

linear function involving B breakpoints of coordinates

(Sa

,So

). Moreover the slope of Π

on its b

seg-

ment is s

. As π is convex, we have s

≤ s

b+1

,b =

1...B. Π

is thus convex.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

328