
Decision Support for Bundle Shipment Choices: Orthogonal
Two-dimensional Bin Packing with Practical Constraints
Yizi Zhou
1a
, Jiyin Liu
2b
, Rupal Mandania
2c
, Shuyang Li
1
, Kai Chen
1
and Rongjun Xu
1
1
Huawei Technologies Co Ltd, Bantian Huawei Base, Shenzhen, China
2
School of Business and Economics, Loughborough University, Loughborough, U.K.
Keywords: Orthogonal 2D-BPP, LTL Shipping, FTL Shipping, Mixed-integer Linear Programming.
Abstract: In this paper, we study a real life application of an orthogonal two dimensional bin packing problem (2D-
BPP) with a small assortment of different shapes of bins and items. A telecommunication equipment company
ships its products to customers several times daily by trucks and it currently uses the less-than-truckload
(LTL) shipping option which is priced as unit price per volume times the total volume of products. However,
depending on scale of products to be shipped, full-truckload (FTL) shipping which is priced as a single price
per truck may be cheaper. In this paper we aim to help the company to decide on the delivery choice as well
as on how to pack the truck optimally when FTL shipping is selected. We model the problem as a variant of
an orthogonal 2D-BPP using mixed-integer linear programming (MIP) with the objective to minimise the
total cost of delivery. Practical conditions influencing the feasibility of packing patterns are also considered.
Practical guidance such as those on some modelling techniques and the application of the model, are applied
to enhance the solving efficiency. The problems are solved by commercial solver CPLEX to optimality up to
34 pallets within an acceptable time. For lager problems, we adopt an approach to combine same items into
larger rectangles and then pack them. This increases the solvability to 154 pallets. On average, our method
help the company save 26% shipping cost.
1 INTRODUCTION
We study a problem where a telecommunication
equipment company sends products from warehouses
to customer sites in mainland China once a day by
truck. There are two types of truck delivery service:
less-than-truckload (LTL) shipping and full-
truckload (FTL) shipping, as illustrated in Figure 1.
LTL is priced as unit price multiplied by total volume
of products shipped and normally the products are
packed with products of other companies. FTL is
priced as a single price per truck. When there is a
small amount of products, it is cheaper to use LTL
shipping. However, when there is a large amount of
products, the company should choose FTL shipping.
The service level agreement (SLA) of FTL is also
faster than FTL. For FTL shipping, the company need
to load the products themselves. This part of cost is
internal and negligible. The decisions to make are on
a
https://orcid.org/0000-0003-2140-9801
b
https://orcid.org/0000-0002-2752-5398
c
https://orcid.org/0000-0002-9025-0569
the type of shipping to choose, the number of trucks
needed for FTL and the loading sequence and
positions of products onto each truck. We modelled
the problem as a variant of an orthogonal 2D-BPP
using mixed-integer linear programming (MIP) with
the objective to minimise the total cost of delivery. It
combines two discrete optimization problems: Bin
packing and optimal bundle shipment decisions. It is
therefore modelled as an integrated mixed integer
programing model (MIP) with two sets of constraints:
one for bin packing and the other for bundle shipment
cost computation. The products to be packed are
fragile and cannot be stacked, which means there is
only one layer of products inside a truck. Practical
constraints are also needed, for example, no more
than two customers can be loaded onto the same
truck, some customers must be delivered later on the
route as the unloading time could be long for those
customers due to warehouse service capability, and
Zhou, Y., Liu, J., Mandania, R., Li, S., Chen, K. and Xu, R.
Decision Support for Bundle Shipment Choices: Orthogonal Two-dimensional Bin Packing with Practical Constraints.
DOI: 10.5220/0010221201610168
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 161-168
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
161

products for the same customers must be placed
together for unloading convenience. We solve the
problems using CPLEX solver. Experiments are
carried out to demonstrate the performance of the new
model. A 26% of reduction in delivery cost is
achieved by applying this model in real life cases.
Also, we provide some practical guidance on how to
reformulate the problem with care to improve the
solving efficiency. We solve the reformulated model
on the same numerical examples and reduced the
computational time to 1/100% of before which helps
the model to be implemented in real life business.
The paper is organized as follows. In section 2,
literature on the 2D-BPP formulation, typology,
practical applications, and related solution algorithms
are reviewed. Section 3 presents the mathematical
models for our problem and discusses how to pick up
an appropriate value for the number of trucks to be
used in the model when infinitely many are available.
In section 4, the proposed mathematical model is
tested through numerical experiments using general
purpose MIP solver. A 26% saving in delivery cost is
achieved on real life instances with this model. In
section 5, we discuss how to improve the solving
efficiency by choosing fixed charges in the MIP
formulation, reducing symmetry and carefully
implementing the MIP model for large cases. We
show how careful formulation for a mixed integer
program (MIP) can lead to a solution of the
mathematical model in a reasonable amount of time,
while some formulations of the same problem can
make the model practically unsolvable. The reduction
in computational time is critical for practical
implementation. Finally, conclusions and future
research directions are provided in section 6.
Figure 1: Illustration of FTL Shipping vs. LTL Shipping.
2 LITERATURE REVIEW
The basic BPP involves two sets, one set of bins, with
same size or different sizes, and one set of items to be
packed normally with different sizes. All items and
bins have fixed rectangular shapes. The problem is to
place the items within the bins in order to optimize
some functions, such as minimise the bins used,
minimise cost, or maximise the items packed, subject
to some physical or business constraints. Commonly
considered physical constraints are: items cannot
overlap (share the same region in the truck) if they are
assigned to the same truck and any item must be
completely located within a bin. The number of
dimensions involved define the problem into 2D and
3D BPP referring to two-dimensional and three-
dimensional problems. As the pallets contains
valuable objects that cannot be stacked so we simplify
the problem into 2D-BPP and are only interested in
the arrangement of the pallets on a plane (the floor of
the truck). Pallets can be rotated by 90
, but cannot
be flipped over and their sides must be parallel to the
sides of the truck (orthogonal packing). Allowing
rotation can improve the number of pallets packed
into a single bin by two times (Martins, 2003).
According to Dyckhoff (1990)’s typology
classification of this problem, our problem’s typology
is:
Kind of Assignment: a selection of trucks and all
pallets
Assortment: the number of different shapes of
pallets and truck. We considered a small
assortment of different shapes for both pallets
and trucks. Many pallets of relatively few
different shapes and sizes.
Availability: the constraints on the available
quantities for pallets and bins. We consider no
restrictions on availability of trucks.
Pattern restrictions: no pattern restrictions
accepting non-guillotine cut patterns vs
connectivity of pallets of the same type.
Status of knowledge: Full knowledge off-line
algorithm.
Scheithauer and Sommerweiß (1998) listed some
practical conditions influencing the feasibility of
packing, these are the maximum load constraint,
which is the maximum weigh of items that a truck can
carry; the placement constraint restrict that some
items, because of their density, weight, or contents
may not be placed on top of other items. The splitting
constraints mean that some items cannot be split onto
different trucks. Some items of the same type must be
placed side by side (connectivity) and finally for
stability purpose, large and heavy item must be placed
below small and light item. As the products shipped
in our problem are lightweight cargo but cannot be
stacked, the maximum load and placement constraints
need not considered.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
162

A 2D-BPP instance consists of a list N of
rectangular items with dimensions
,
for all ∈
and a list of bins with dimensions
,
for
all ∈ and cost
for all ∈. It is known as a
strongly NP-hard problem and is also in practice very
difficult to solve (Garey and Johnson, 1979; Martello
and Vigo, 1998). Solution algorithms for 2D-BPP can
be classified into three types, exact algorithms,
heuristics and metaheuristics, with many literatures
devoted to the improvement on lower bounds
provided by heuristics (Lodi, 2002). Lodi (2017)
proposed a heuristic algorithm for 2D-BPP with no
rotation allowed based on enumeration tree. Each
level of the tree represents the current content for the
pth bin in the solution. In particular, each bin is filled
by applying a packing strategy that packs one item at
a time according to a given selection rule and
guillotine split rule. The selection rule determines the
next item to pack (and its position in the bin), whereas
the guillotine split rule is used to ensure the produced
pattern being guillotinable. The tree is pruned using a
depth-first strategy. This heuristic can solve many
benchmark problems to optimality and yield near
optimal solution for other cases. Cui (2017) presented
a construction heuristic to solve the 2D-BPP problem
in three phases. The first phase generates triple-block
patterns, the second phase uses some of the patterns
to construct solutions, and the third phase solves an
ILP problem to improve the solutions. The gap to LB
is reduced by 30% compared to some best known
algorithms on some test instances. In this paper, we
also implement n-block patterns to speed up the
solution for our MIP model. Buljubašić and Vasquez
(2016) proposed a tabu search algorithm with a
consistent neighborhood search approach to solve the
1D-BPP and 2D-VPP problems and yield best-known
solutions for all benchmark test instances they used.
The bins available are infinite, they start with
1 bins, where UB is an upper bound obtained
by using a variant of the classical First Fit heuristic.
LB and UB will be input for our implementation of
the mathematical model presented in this paper.
Pisinger and Sigurd (2007) studied an exact algorithm
branch-and-price-and-cut for 2D-BPP. The master
problem is formulated as a set covering problem
where each set represents a feasible packing. All
feasible packings (sets) could be large and the model
will have much more columns than rows (variables
than constraints), so column generation is applied to
gradually add sets. Each restricted master problem is
solved using dual simplex method. In each iteration
of column generation, a pricing problem is solved by
finding the set with smallest reduced cost to be added.
Problems with pp to n=100 items are solved to
optimality through this algorithm. Polyakovskiy and
M’Hallah (2020) combined two difficult discrete
optimisation problems: BPP and machine scheduling
and model the problem as an integrated constraint
program with two sets of constraints, bin packing
feasibility and single machine scheduling constraints
respectively. They also proposed two decompositions
approaches, a master problem is a relaxation of BPP
and then validate the solutions by row generations.
Their results show that an integrated model
outperforms the decomposition approaches. We will
study an integrated model in this paper.
To the best of our knowledge, this paper is the first
to consider the combined problem of bundle shipment
or shipment selections and 2D-BPP with rotations.
We introduce a new mathematical formulation for the
integrated problem with practical constraints and
discuss how to improve the solving efficiency from a
model formulation point of view. The model is
currently being used by a large telecommunication
service company and it has helped the company to
save shipment cost.
3 MATHEMATICAL MODEL
There are normally three different problem
representations for BPP: coordinates (Christofides
and Whitlock, 1977), sequence pairs (Murata et al.,
1995) and graphs (Lins et al., 2002). We use the first
one as different graph representations can lead to the
same arrangement adding complexity for search
algorithms. We need to decide on: partition (
),
order position
,
, orientation
and relative
position
,
,
,
. The detailed definition of
notation is shown in section 3.1. Although we assume
the number of trucks is unlimited, the mathematical
model needs an initial value of the number of each
types of trucks. We could use a sufficiently large
number of trucks but it will lead to much larger model
than necessary and longer computational times. So
we will use the lower bound generated from literature
of heuristics as the starting point for the number of
trucks available for the math model.
There is an obvious lower bound on the number
of trucks, which is the sum of area of squares divided
by the area of truck floor:
∑
∈
/
. In
many cases,
can be inadequate for an effective
use for the exact algorithm. Several better bounds are
provided by Martello and Vigo (1998). In this paper,
we will use
for simplicity reason.
Decision Support for Bundle Shipment Choices: Orthogonal Two-dimensional Bin Packing with Practical Constraints
163

2.1 Problem Representation
A problem solution is represented by coordinates of a
pallet left bottom corner, relative positions and
rotations. As only one layer of pallets can be packed
into the truck, the truck loading result can be shown
on a two dimensional graph (top view) as shown in
Figure 2. We can build a Cartesian coordinate system
around the truck container where the origin is set to
be the bottom left corner of the truck. The position of
each pallet packed is also represented by the position
of its bottom left corner
,
. As rotation is
allowed, the two rectangular shown in Figure 2 are
identical, and the right one is the rotated version of
the original pallet (only 90
is allowed). To make
sure any two pallets do not overlap, they must not
overlap in x axis (one on the left of another in the
graph), or not overlap in y axis (one below another in
the graph), or not overlap in both axis.
Figure 2: Graph representation of a truck loading result.
Index:
N: index set of pallets to be packed;
K: index set of trucks;
,:index of pallet, ∀, ∈ ;
: index of truck, ∀ ∈ .
M: a big number
Parameters:
: delivery price for FTL delivery of truck;
: unit price for LTL delivery per volume of pallet
;
: volume of pallet ;
: width of pallet ;
: length of pallet ;
: the customer that pallet belongs to;
: width of truck;
: length of truck;
Ns: the set of pallets of telecommunication customers
Nn: the set of pallets of other customers
Variables:
: the x coordinate of pallet i in a truck;
: the y coordinate of pallet i in a truck;
1,
0,
;
;
1,
0,
;
;
1,
0,
;
;
1,
0,
;
;
1,
0,
;
;
Objective:
Min:
∑
∈
∑
∈
1
∑
∈
s.t.
,∀∈,∈
(1)
1
1
,∀,
∈,
(2)
1
1
,∀,
∈,
(3)
∈
1,∀∈
(4)
1
1
,∀
∈,∈
(5)
1
1
,∀
∈,∈
(6)
2
1,∀,
∈,
,∀
∈
(7)
2
1, ∀,
,∈
,
,
,∀∈
(8)
2
,∀∈,
∈,∀∈
(9)
2,∀,
,∈,
,∀∈
(10)
∈
∈
,∀,
∈,
(11)
0,
0,∀,
∈
(12)
Variables
,
,
,
,
and are all binary
variables.
The objective of the model is to minimise the total
delivery cost of shipping all the pallets, with
∑
∈
indicating the total cost of FTL and
∑
∈
1
∑
∈
representing the cost of
LTL. Constraints (1) show that once a pallet is
assigned to a truck (
1) then this truck is in use
(
1). Constraints (2) and (3) mean that any two
pallets cannot overlap (share the same region in the
truck) if they are assigned to the same truck.
Constraints (4) demonstrate that all pallets must be
assigned to at most one truck or to LTL shipping.
Constraints (5) and (6) indicate that any pallet must
be completely located within a truck when it is
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
164
assigned to that truck. Constraints (7) avoid
overlapping between pallets. Constraints (8)
implement the non-splitting conditions, meaning if
the pallets of one customer can fit into one truck, we
should not split the loading into two trucks.
Constraints (9) show the placement requirement of
the real life situation, the pallets of
telecommunication customers must be unloaded after
other customers and other customers’ pallets will be
placed near the door of the truck for mixed load.
Constraints (10) indicates that a truck can only be
loaded with pallets of up to two different customers
as a truck can only ship to two different places in a
single day. Constraints (11) show that pallets of the
same customer can only select one shipping options
either LTL or FTL.
4 NUMERICAL EXPERIMENTS
Ten test instances are selected from real life shipping
data to verify the mathematical model and comparing
the results with historical shipping (LTL). We solved
the ten test cases using a general purpose commercial
solver CPLEX, which implements a powerful branch
and bound algorithm. The numerical experiments are
carried out on a PC with 64-bit Windows operating
system, eight GigaBytes of RAM and an Intel i7
processor with quad-cores. The computational results
are shown in Table 1, where ID is the instance id, N
is the number of customers involved, Pallets are the
number of pallets to be shipped and before, after
indicate the shipping cost.
Table 1: CPLEX results of the original model.
ID N Pallets Before After Time(s)
1 7 22 10156 7361 17.47
2 5 23 7934 5593 MLR
3 5 18 7166 6072 3.05
4 2 22 7890 5398 MLR
5 2 32 11090 9805 MLR
6 7 23 8295 6065 MLR
7 7 33 10012 9898 18.25
8 2 14 4638 3100 MLR
9 2 8 3054 2600 0.18
10 3 4 1461 1461 0.16
SUM
71703 57355
103.91
For the current model formulation, we solved 5
out of 10 instances to optimality within 200s time
limit. The average computation time is 103.91s. The
reduction in delivery cost is 20%. The reduction in
cost is promising for the business, but the
computational time is a bit long for daily business, as
we need to save enough time for the operations and
actual loading. The row in the table labelled ‘MLR’
means those instances haven’t been solved to
optimality within the time limit and the after cost for
those cost are the current best feasible solution found.
4.1 Example
There are three different trucks available with
different costs. The truck information is shown in
Table 2.
Table 2: Trucks Information.
ID Length Width Price
10T 9.6 2.4 2600
18T 13.5 2.5 4100
20T 16.5 2.5 4300
We have 22 pallets to be packed and 7 different
customers. Three customers are special customers
that needed to be drop off later on route. The packing
results are shown in Table 3. CID is the customer ID,
PID is the pallet ID, l, w, vol are the length, width and
volume of the pallets, TP is the indicator of whether
the customer is telecommunication customer and the
Sol column is the solution.
Table 3: Example One Input Data.
CID PID l w vol TP Sol
1 0 1.65 1.15 4.07 YES LTL
2 1 1.91 1.11 2.79 NO 10T-1
2 2 1.91 1.11 5.29 NO 10T-1
2 3 1.91 1.11 5.29 NO 10T-1
2 4 1.91 1.11 5.29 NO 10T-1
3 5 1.91 1.11 5.29 NO 10T-2
3 6 1.91 1.11 5.29 NO 10T-2
3 7 1.91 1.11 5.29 NO 10T-2
3 8 1.91 1.11 5.29 NO 10T-2
3 9 1.91 1.11 5.29 NO 10T-2
3 10 1.91 1.11 5.29 NO 10T-2
4 11 1.91 1.11 5.29 YES LTL
5 12 1.91 1.11 1.42 NO 10T-1
5 13 1.91 1.11 5.29 NO 10T-1
5 14 1.91 1.11 5.29 NO 10T-1
5 15 1.91 1.11 5.29 NO 10T-1
6 16 1.91 1.11 5.29 NO 10T-2
6 17 1.91 1.11 5.29 NO 10T-2
6 18 1.91 1.11 5.29 NO 10T-2
6 19 1.91 1.11 5.29 NO 10T-2
7 20 1.41 1.15 3.04 YES LTL
7 21 1.41 1.15 3.04 YES LTL
The visualizations of the packing results are
shown in Figure 3 and Figure 4. We can see that the
optimal solution is a mix of LTL and FTL shipping.
Decision Support for Bundle Shipment Choices: Orthogonal Two-dimensional Bin Packing with Practical Constraints
165

The optimal cost is 7361.64 while the original
shipping with all pallets shipped LTL is 10156.95. A
28% reduction in delivery cost is achieved in this
instance within 7.2 seconds.
Figure 3: Packing Result of Example (10T Truck No.1).
Figure 4: Packing Result of Example (10T Truck No.2).
5 ENHANCE SOLVING
EFFICIENCY
A careful formulation for a mixed integer program
(MIP) can lead to a solution of the mathematical
model in a reasonable amount of time, while some
formulations of the same problem can make the
model practically unsolvable. The key principle of a
better formulation of a MIP model is to make the
feasible region of LP relaxation model as tight as
possible even if this will make the LP model harder
to solve. This topic is covered in various text books
(Nemhauser and Wolsey, 1988; Williams, 1990). In
this paper, we consider improving the solving
efficiency by tailored fixed charges in the MIP,
reducing symmetry and a careful implementation of
the MIP model for large cases.
5.1 Tailored Big M
To model a fixed charge—a cost that is incurred once
when a process is used, but is not proportional to the
level of the process—a "Big M" formulation is
usually used. We could choose a sufficiently large
value for M, but there are some drawbacks when
solve the LP relaxation of the MIP problem. If the
relaxation objective value is too far from the integer
objective value; the branching algorithm will try to
force
to 0 first, because the LP solution value of
is already close to 0. So we need to choose M
carefully; big enough for the bounding purpose but
not too large. The values of M in constraints (2), (3),
(5), (6), (8) and (9) are max
, max
,
max
, max
, 2 and max
respectively.
5.2 Symmetry in Trucks
,∀12
(13)
If k1 and k2 are the same type (same dimension) of
trucks, we would select k1 first to break the
symmetry/tie in trucks. Because select k1 and k2 will
yield the same objective value and create ties in the
candidate solutions.
5.3 Symmetry in Pallets
2
1,∀
,
(14)
If pallet i and pallet j are identical, we would place
pallet j either below pallet i or to the left of pallet i to
break the symmetry. Also, the routing sequence
conditions constraints (9) also help to reduce
symmetry in pallets.
5.4 Sequence Pairs Restriction
To make sure any two pallets do not overlap, they
must not overlap in x axis (one on the left of another
in the graph), or not overlap in y axis (one below
another in the graph), or not overlap in both axis.
Based on this information, we can add two other
constraints to obtain a tighter LP relaxation of the
MIP and make the feasible region described by the
linear programming relaxation as close as possible to
the feasible region that contains only feasible integer
solutions.
21,∀
(15)
21,∀
(16)
Constraints (15) and (16) void the other eight
infeasible sequence pairs, meaning the relative
position of two pallets cannot be left and right (top
and bottom) at the same time.
5.5 Pre-grouped Pallets
In this problem, we only consider a small assortment
of pallets size. Pallets of the same type can be
prepacked into a lager item and significantly reduce
the problem sizes. An example was shown in Table 4.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
166
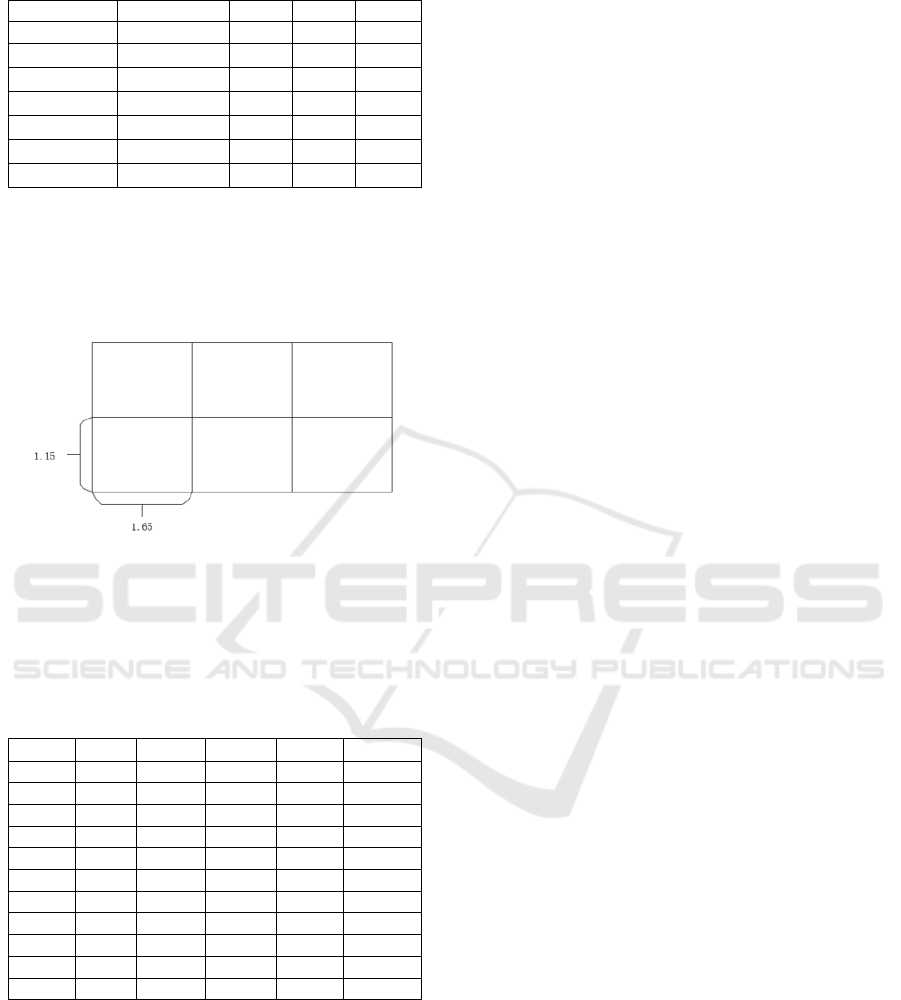
Table 4: A data example after pallets combination.
CID PID l w vol
1 c0 4.95 2.3 24.36
1 c1 4.95 2.3 24.36
2 c2 4.95 2.3 24.36
2 c3 4.95 2.3 24.36
2 c4 4.95 2.3 24.36
2 7 1.65 0.4 0.75
2 11 1.65 0.4 0.75
c0-c4 are prepacked pallets set as shown in Figure
5. The original problem is unsolvable within 200s,
and the modified problem is solved in 0.34s. The
objective value is 7200, which is a 35.13% saving in
delivery cost than before.
Figure 5: 6-blocks Pattern (Pre-combined Pallets).
We rerun the modified model with all techniques
proposed in section 5.1 – section 5.5 for the ten test
cases in Table 1 and the new results are shown in
Table 5.
Table 5: CPLEX results of the modified model.
ID
Pallets Before After Time(s)
1 7 22 10156 7361 3.57
2 5 23 7934 5593 0.84
3 5 18 7166 6072 4.05
4 2 22 7890 5898 0.9
5 2 32 11090 7200 0.34
6 7 23 8295 5707 0.91
7 7 33 10012 9898 1.69
8 2 14 4638 3100 0.58
9 2 8 3054 2600 0.18
10 3 4 1461 1461 0.16
SUM
71703 54892
1.32
With the new formulated mathematical model and
the 6-blocks patterns generation, we can solve all ten
instances to optimality within 200s time limit. The
average computation time is now only 1.322s. The
reduction in delivery cost is 23.45%. We reduce the
computational time significantly and it could be
applied in the real life business. We also did stress test
of this model with CPLEX. The original problems are
solved by commercial solver CPLEX to optimality up
to 34 pallets within 200s. For the modified version of
the model, the solvability is increased to 154 pallets.
6 CONCLUSIONS
In this paper, we study a problem where a
telecommunication equipment company sends
products from warehouses to customer sites in
mainland China once a day by truck. There are two
types of truck delivery service: less-than-truckload
(LTL) shipping and full-truckload (FTL) shipping.
We help the company to make the decisions on the
type of shipping to choose, number of trucks needed
for FTL as well as the loading sequence and positions
of products onto each truck. We modelled the
problem as a variant of an orthogonal 2D-BPP using
mixed-integer linear programing (MIP) with the
objective to minimise the total cost of delivery. It
combines two discrete optimization problems: Bin
packing and optimal bundle shipment decisions.
Hence we model this as an integrated mixed integer
programing model (MIP) with two sets of constraints,
one for bin packing the other for bundle shipment cost
computation. The problem is solved using the
CPLEX solver. Experiment results are carried out to
demonstrate the performance of the new model.
A 26% of reduction in delivery cost is achieved
by applying this model in real life cases. Also, we
provided some practical guidance on how to
reformulate the problem with care to improve the
solving efficiency. We solved the reformulated model
on the same numerical examples and reduced
computational time to 1.3 seconds on average and
help the model to be implemented for a real life
business.
REFERENCES
Buljubašić, M. and Vasquez, M., 2016. Consistent
neighborhood search for one-dimensional bin packing
and two-dimensional vector packing. Computers &
Operations Research, 76, pp.12-21.
Christofides, N. and Whitlock, C., 1977. An algorithm for
two-dimensional cutting problems. Operations
Research, 25(1), pp.30-44.
Cui, Y. P., Yao, Y. and Zhang, D., 2017. Applying triple-
block patterns in solving the two-dimensional bin
packing problem. Journal of the operational research
society, pp.1-14.
Dyckhoff, H. and Wäscher, G., 1990. Cutting and packing
(special issue). European Journal of Operational
Research, 44(2).
Decision Support for Bundle Shipment Choices: Orthogonal Two-dimensional Bin Packing with Practical Constraints
167

Garey, M. R. and Johnson, D.S., 1979. Computers and
intractability (Vol. 174). San Francisco: freeman.
Lins, L., Lins, S. and Morabito, R., 2002. An n-tet graph
approach for non-guillotine packings of n-dimensional
boxes into an n-container. European Journal of
Operational Research, 141(2), pp.421-439.
Lodi, A., Martello, S. and Monaci, M., 2002. Two-
dimensional packing problems: A survey. European
journal of operational research, 141(2), pp.241-252.
Lodi, A., Monaci, M. and Pietrobuoni, E., 2017. Partial
enumeration algorithms for two-dimensional bin
packing problem with guillotine constraints. Discrete
Applied Mathematics, 217, pp.40-47.
Martello, S. and Vigo, D., 1998. Exact solution of the two-
dimensional finite bin packing problem. Management
science, 44(3), pp.388-399.
Martins, G. H., 2003. Packing in two and three dimensions.
Naval Postgraduate School Monterey CA Dept of
Operations Research.
Murata, H., Fujiyoshi, K., Nakatake, S. and Kajitani, Y.,
2003. Rectangle-packing-based module placement. In
The Best of ICCAD (pp. 535-548). Springer, Boston,
MA.
Pisinger, D. and Sigurd, M., 2007. Using decomposition
techniques and constraint programming for solving the
two-dimensional bin-packing problem. INFORMS
Journal on Computing, 19(1), pp.36-51.
Polyakovskiy, S. and M’Hallah, R., 2020. Just-in-time two-
dimensional bin packing. Omega, p.102311.
Scheithauer, G. and Sommerweiß, U., 1998. 4-block
heuristic for the rectangle packing problem. European
Journal of Operational Research, 108(3), pp.509-526.
Williams, H. P., 1990. Integer and combinatorial
optimization. Journal of the Operational Research
Society, 41(2), pp.177-178.
Wolsey, L. A. and Nemhauser, G. L., 1999. Integer and
combinatorial optimization (Vol. 55). John Wiley &
Sons.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
168
