A City-aware Car Parks Marketplace for Smart Parking
Claudia Di Napoli
1 a
and Silvia Rossi
2 b
1
Istituto Di Calcolo e Reti Ad Alte Prestazioni, C.N.R., Naples, Italy
2
Department of Electrical Engineering and Information Technologies, University of Naples Federico II, Naples, Italy
Keywords:
Automated Negotiation, Multi-Agent Systems, Smart Parking, Resource Allocation, Social Welfare.
Abstract:
Searching for a parking space in high populated urban areas is one of the major sources of traffic congestion,
increased carbon emission, and wasted time for drivers. In this work, a multi-agent smart parking system is
proposed to reserve parking spaces in response to parking requests. It is based on a distributed negotiation
mechanism simulating a car park marketplace composed of parking space buyers and sellers. Negotiation is
used to obtain parking allocations by taking into account different needs regarding parking location and price,
an efficient distribution of parking spaces, and car circulation restrictions. In order to simulate a realistic mar-
ketplace, the distributed negotiation mechanism occurs among a set of drivers requesting parking spaces, and
a set of parking vendors. The aim of the experimental evaluation is to determine the scalability of a distributed
marketplace with respect to parking space re-sellers that share common city policy regulations, to allow for
a smart distribution of allocations. The negotiation outcome is experimentally evaluated by considering the
resulting social welfare of all the involved negotiators.
1 INTRODUCTION
Several studies highlighted how the problem of
searching for a parking space in high populated urban
areas is one of the major sources of traffic conges-
tion, increased carbon emission and, not least, a very
frustrating and time-consuming experience for drivers
(Polycarpou et al., 2013). Commercial products have
already been developed to equip urban areas with ve-
hicle sensors, wireless communications, and data an-
alytics systems in order to collect parking availability
and location (Nakamura et al., 2000), so increasing
the probability for drivers to find park spaces.
Nevertheless, these solutions leave the burden of
making the parking decision on the drivers according
to the available information on the destination area,
but without limiting the competition for the available
parking spaces. This forces to re-plan the search with
consequences on the city life, and sometimes causing
even more congestion in the monitored areas. More-
over, these solutions often do not support drivers in
finding parking spaces that can be satisfying, since
drivers unfamiliar with the location may not be aware
of available alternatives that are not in the destina-
a
https://orcid.org/0000-0002-8626-5805
b
https://orcid.org/0000-0002-3379-1756
tion area, but are easily connected with it, for example
by using public transportation (Di Martino and Rossi,
2016). In addition, the fragmentation of public and
private parking owners, each one adopting their own
technology to collect occupancy data and to advertise
their availability, does not allow for a better utilisation
of the parking spaces offered by a city as a whole. In-
deed, smart parking applications should include bene-
fits and revenues for the city itself. They should make
it easier for drivers to find parking spaces, but also to
take into account specific city needs that may change
in time according to volatile events affecting car cir-
culation at a specific time.
In this context, centralised agent negotiation
mechanisms are proposed in our previous works to
manage parking supply and demand. In (Barile et al.,
2015; Di Napoli et al., 2014), negotiation occurs
among software agents representing drivers searching
for parking spaces, and one software agent represent-
ing a city authority in charge of administrating a set
of parking spaces belonging to different car parks lo-
cated in different city zones. The city authority is
in charge of taking into account drivers preferences,
parking vendors requirements, and social benefits for
the city, so simulating a car parks marketplace where
different and sometimes conflicting interests have to
converge to a common solution, if any. Nevertheless,
242
Di Napoli, C. and Rossi, S.
A City-aware Car Parks Marketplace for Smart Parking.
DOI: 10.5220/0010227102420249
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 242-249
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

centralised negotiation models based on a single agent
acting as parking re-seller are not suitable when the
number of parking requests, and the number of man-
aged parking spaces increases.
In the present work, differently from the previ-
ous centralised negotiation, a distributed negotiation
mechanism is proposed occurring among a set of
agents representing drivers, and a set of agents rep-
resenting parking re-sellers, each one responsible for
managing car park belonging to a specific city area.
The car parks managed by the set of parking re-sellers
are distributed in different city location, so covering
wide city areas. Parking re-sellers negotiate in their
own economic interests trying on the one hand to
fill the less occupied car parks to increase their in-
come, and on the other hand to meet user require-
ments regarding parking spaces. At the same time,
they try to avoid the circulation and occupancy of city
zones that are subject to certain limitations for cir-
cumstances that can occur in an unexpected and dy-
namic way (e.g., a strike, a protest, road works, and
so on), or for specific city planning (e.g., pedestrian
zones, resident-only zones, and so on), so preserving
also city interested. To evaluate the benefits of the
proposed mechanism, the outcomes of the negotiation
are measured in terms of social welfare accounting for
the different needs considered during negotiation.
The evaluation of the distributed negotiation
mechanism shows that when more parking re-sellers
are involved sharing the same city policies other than
to their own profit, the global social welfare has the
same trend. Furthermore, the proposed approach has
the benefit to manage, and hence allocate, more park-
ing spaces with respect to the centralised negotiation.
2 A CAR PARK MARKETPLACE
From an open market point of view, the problem of
finding and booking a vacant parking space in densely
populated urban areas involves drivers (i.e., buyers)
who want to find a vacant parking space that meets
their requirements, but also parking spaces suppliers
(i.e., vendors) who want to maximize their economic
incomes by selling as many parking spaces as possi-
ble. Their interaction can be modeled as a demand
and supply market mechanism regulating the parking
space allocation. Nevertheless, in a smart city, in or-
der to limit the negative impact on the city caused
by looking for a parking space, also the city needs
concerning car circulation should be taken into ac-
count. This is to avoid car circulation in specific ar-
eas of the city, to have a fair distribution of parking
spaces among drivers, and to limit traffic congestion
in the proximity of car parks. In this context, finding
a parking space is not merely a selection problem in
a sequence of alternatives, but rather the possibility
to find an agreement accommodating different needs
coming from drivers, parking owners, and city man-
agers aware of city needs regarding car circulation.
In this context, the proposed Car Park Market-
place is an infrastructure aimed at helping drivers
to reserve parking spaces by serving their requests
through negotiation. Negotiation takes place among a
set of Driver Agents (DAs), each one acting on behalf
of a driver that wants to reserve a parking space for a
required time in order to reach a specific destination,
and a set of Parking Managers (PMs) that supply/re-
sell parking spaces. Utility functions, mapping the
DAs and PMs evaluation criteria on the negotiation
outcome, lead to a partial ordering of outcomes, so
providing a measure of the satisfaction level of that
outcome for the respective agents (Barbuceanu and
Lo, 2001). The allocation of a parking space occurs
if an agreement can be found as the result of the auto-
mated negotiation process.
In order to consider both the PMs incomes and
city needs when allocating parking spaces distributed
among the available car parks, a business model is as-
sociated to PMs modelling the economic needs of car
parks suppliers/re-sellers. The model is based on the
assumption that PMs try to fill their car parks as much
as possible to improve their profit, and, at the same
time, they act to meet the same city needs consisting
in limiting traffic congestion due to the concentration
of cars in specific and/or more requested city areas.
The DA model is based on the assumptions that
drivers have preferences on the cost and the location
of a parking space, and that they are unaware of park-
ing spaces that could be available for their needs, so
they do not have enough information to make counter-
proposals. For this reason, each DA decides whether
to accept or not a parking space allocation by consid-
ering only its own utility value. The utility is com-
pared with a value, called threshold value, associated
to each DA, that characterizes its attitude to reach a
compromise determining the acceptance of an offered
parking space.
2.1 Negotiating for Parking Allocations
For each DA’s request, a negotiation process consists
in m one-to-many iterative sub-negotiations, each one
occurring between a DA and one of the m PMs that
received the request. Only PMs make an offer by
proposing a parking space, at each negotiation iter-
ation. On the contrary, a DA does not issue a counter-
proposal, and it can only accept or reject a received
A City-aware Car Parks Marketplace for Smart Parking
243

offer. A single sub-negotiation with a PM can pro-
ceed until there are available parking spaces (corre-
sponding to different off-street parking places with
different attribute values) to offer, so the maximum
number of iterations, known as the negotiation dead-
line, is different for each sub-negotiation and it is set
by each PM as the number of available car parks it is
in charge of. The deadline is not known to the DA
that can keep on negotiating until at least one PM has
an available parking proposal. The negotiation occurs
in an incomplete information configuration from the
DA side, since the information on all the available car
parks is known only to the PMs, even though each PM
only knows the car parks it is responsible for. The in-
complete information setting leads to the possibility
of accepting a sub-optimal agreement.
A negotiation starts with a DA that sends a park-
ing request, cfp, to all the available PMs. If there are
not available offers, the negotiation ends with a fail-
ure. Otherwise, the DA collects the offers received
by each PM (within a fixed deadline), it evaluates
them according to its utility function, and it selects
the one with the greater utility (best bid B). In case
the selected parking space satisfies the driver’s re-
quirements to some extent (i.e., the utility values for
the DA is greater that the threshold value v
DA
(B) >
DA
att
), it accepts the offer, otherwise a new negotia-
tion iteration is started with all available PMs. Once
an offer is accepted, the corresponding DA waits for a
booking confirmation by the PM that issued the offer.
The DA requests are processed concurrently by
the PMs hence, from the PM point of view, a ne-
gotiation process consists of multiple single negoti-
ations taking place between the PM and each DA that
sent a request. Once a cfp is received, each PM
retrieves a set of possible alternatives to be offered
to the DA with respect to the received query loca-
tion, and it evaluates the corresponding utility accord-
ing to its utility function, ranking the parking spaces
in descendant order. Offers are sent one by one to
the DA at each iteration according to this order. If
an agreement is reached with the offer sent at itera-
tion t, the PM checks the status of the corresponding
car park, and it updates the utility value of the ac-
cepted offer, since it may have changed during nego-
tiation because of parking space allocations occurred
in other negotiations. If such value did not change
or it changed within an acceptable range for the PM,
then the parking space is allocated, and the park space
occupancy is updated. Otherwise, the offer is dis-
charged, an inform of failure is sent, and the nego-
tiation proceeds. A parking space offered at round t
is not considered available at round t + 1 for the same
DA to model the possibility to assign a rejected park-
ing space to another driver. In case there are not pro-
posals available satisfying the DA request, a failure
message is sent to the DA and the negotiation ends.
2.2 Agents Utility Functions
Both the PM and the DA have their own private multi–
dimensional utility functions (Barbuceanu and Lo,
2001), allowing them to evaluate the offers in terms
of their own preferences, where each dimension re-
lates to an attribute of a parking space. These utility
functions are based on static attributes of a parking
space, such as its default hourly price, its location in
the city, the capacity of the car park it belongs to, and
on dynamic attributes, such as its distance from a re-
quired location, the current occupancy, or its current
price, whose values are calculated at the time a park-
ing request is processed. The agreement on the out-
come is reached if the values of parameters, used by
the PMs and the DAs to evaluate their utility values,
are in their respective agreement spaces (Di Napoli
et al., 2013). Even though the object of negotiation
is a parking space, the attributes, used by the PM and
the DA to evaluate it, are different because they have
different preferences regarding a parking solution. Of
course, an agreement between them is possible if their
respective acceptable regions have a non-empty inter-
section, i.e. a parking space with attribute values ac-
ceptable for both of them.
Upon receiving a DA request for parking a PM se-
lects the set of car parks located in the city sectors it
is responsible for, within a given radius (named tol-
erance) from the user request. In order to incentivize
a DA to park outside a red zone and in less occupied
car parks, the PM adopts a dynamic parking pricing
scheme that applies a discount to the default parking
hourly price depending on the car park occupancy and
location, i.e., the farther away the parking space is
from a red zone, the higher the discount factor is, and
the higher the occupancy percentage is, the lower the
discount factor is. The PM evaluates each selected
car park according to its private utility function, and
it orders them in a descending order of their utility
values. The strategy adopted by the PM to issue a
counter-proposal, i.e. a new offer, is to concede in
its utility by offering one parking space at a time in
the same descending evaluation order, so applying a
monotonic concession strategy. The utility function
is the weighted sum, normalised in [0,1], of the car
park availability (q
1, j
), i.e., the number of free park-
ing spaces at the time the request is processed, and the
car park distance from the nearest red area (q
2, j
).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
244

U
PM
(p
j
) =
2
∑
k=1
(α
k
∗
q
k, j
− min(q
k, j
)
max(q
k, j
) − min(q
k, j
)
) (1)
j ∈ {1, . .. , n}
where, α
k
are weights associated with each parame-
ter (with
∑
α
k
= 1), and n is the number of car parks
selected for the request. Both terms of the summa-
tion are normalized w.r.t. the minimum (min(q
k, j
)),
and the maximum (max(q
k, j
)) values of each param-
eter among all the selected car parks. Weights model
the possibility for the PM to privilege one parameter
or the other, according to the specific city needs at the
moment the request is processed, i.e., by increasing
parking occupancy or pushing drivers towards more
distant car park.
The DA evaluates each offer according to its util-
ity function given by the weighted sum of the parking
space hourly cost (p
1, j
), and its travel distance from
the required destination (p
2, j
):
U
DA
(x
j
) = 1 −
2
∑
k=1
β
k
∗
p
k, j
− c
k
h
k
− c
k
(2)
where, β
k
are weights associated to each parameter
(with
∑
β
k
= 1), c
k
is the DA preferred value over
the k-th parameter, h
k
are constant values introduced
for normalising each term of the formula into the set
[0,1]. Such weights can be used to model different
decision models of drivers.
The DA strategy is to accept an offer if its util-
ity value is above a threshold value (DA
att
) repre-
senting a measure of its attitude to be flexible on its
preferred values for the considered parking space at-
tributes. Since the utility function is normalised, its
values may range in the interval [0,1]. It should be
noted that the DA utility varies according to the re-
ceived offer, so it is not monotonic as the PM one.
This means that keeping on negotiating does not guar-
antee the DA to find a better parking space in terms
of its utility. Moreover, as already discussed, the DA
can evaluate an offer only with respect to its own util-
ity since previously proposed parking spaces are not
available anymore. In addition, the DA is not aware
of the available car parks, so it could end up without
reserving any parking space if it keeps on negotiating.
3 EVALUATING THE BENEFITS
OF PARKING ALLOCATIONS
In order to evaluate the social welfare of the interac-
tion (one DA and multiple PMs), we considered only
the utility of the DA and the PM pair whose negotia-
tion reached an agreement on a parking space assign-
ment (x
agr
). Note that, it cannot be the case that more
than one PM has a positive utility value as a result
of a single request. A set of parking space requests
are considered as a request block, each one processed
through a negotiation process. The problem can be
assimilated to a distributed indivisible resource allo-
cation case, where the selection of resources to be al-
located for a specific request is carried out through
a bilateral negotiation without considering the other
requests. In our case, given a set of available re-
sources R (i.e., parking spaces), and a set of driver
agents D A , the overall process is to assign a single
resource to each request (if available), in order to best
match the DA request and, at the same time, to fulfill
as many requests as possible. In resource allocation
problems the social welfare is also used as a metric to
evaluate the efficient allocation of resources (Endriss
et al., 2006). Hence, social welfare, computed for all
requests, including the not fulfilled ones, can be used
also as a metric to evaluate an efficient allocation of
parking spaces.
Given a set DA of agents requesting a parking
space, an optimal allocation of available spaces is the
one that maximizes the social welfare. Here, we con-
sider a social welfare (SW
+
) obtained as the sum of
DA and PM utilities.
SW
+
= [
∑
i∈D A
((U
i
(x
agr
) +U
PM
(x
agr
))/2)]/|DA| (3)
This definition does not account for imbalanced dis-
tribution of utilities among agents, so the Nash So-
cial Welfare definition (SW
∗
) (Ramezani and Endriss,
2010), is also used.
SW
∗
= [
∑
i∈D A
(U
i
(x
agr
) ·U
PM
(x
agr
))]/|DA| (4)
The prototype for the experimental evaluation is im-
plemented as a client/server application within the
JADE framework (Bellifemine et al., 2008). A nego-
tiation session occurring among a set of DAs and a set
of PMs is a multi-threaded process, where each thread
manages a negotiation of one PM and one DA. A
storage module is responsible for maintaining infor-
mation on the available car parks, their capacity and
their occupancy that is updated every time a parking
request is fulfilled. In addition, PMs collect informa-
tion from external services: Google Maps (Pan et al.,
2007) to compute the arrival time from a car park to
the destination specified by a driver, OpenStreetMap
(Haklay and Weber, 2008) to collect information on
car park locations, a city planning service to collect
information regarding the red zones.
Our reference scenario consists of a large number
of drivers all choosing a destination in the red zone
A City-aware Car Parks Marketplace for Smart Parking
245

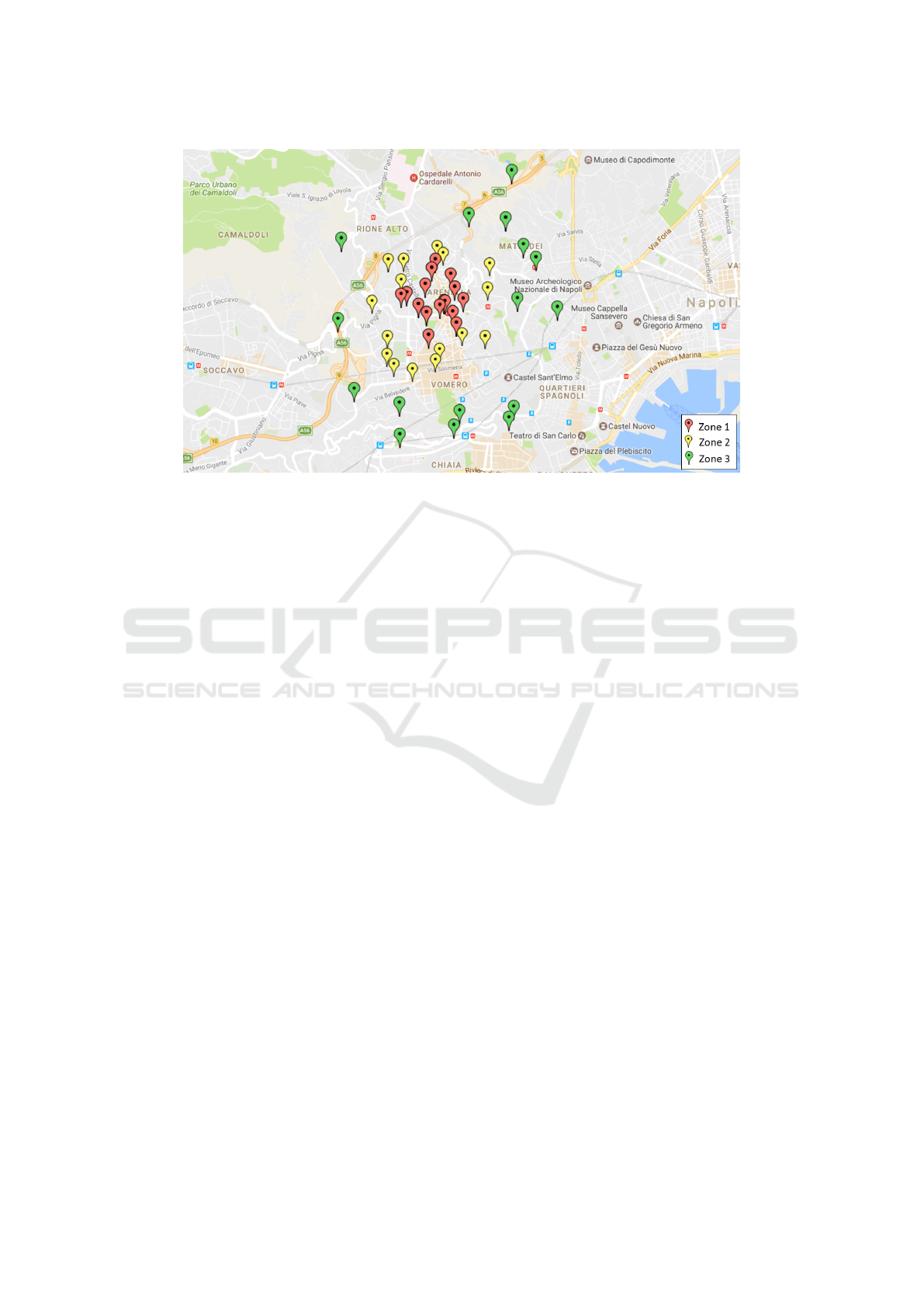
Figure 1: Parking distribution w.r.t the nearness of city zones to the red zone.
and for the same time window to evaluate both the al-
location of parking spaces in terms of the social wel-
fare of the whole multi-agent system, and the distribu-
tion of allocated parking spaces among the considered
zones. In this set of experiments, we also evaluated
the impact of having more than one PM on the so-
cial welfare of the system. Hence, we considered four
different settings, respectively with 1, 2, 4 or 8 PMs.
Our hypothesis is that the case of only one PM would
result in a better application of the smart city policy
(and so a greater PM utility). For each setting, we
considered the cases of 50, 100, 400, 1200 simultane-
ous requests in the red zone. Each test is repeated 50
times. The total number of available parking spaces
was set to 960 and equally distributed among the con-
sidered 48 car parks. Moreover, each PM will have
the same distribution of parking spaces among the ar-
eas. In Figure 1, the parking distribution for the con-
sidered zones in the city of Naples is shown, with each
zone identified by a different colour. The considered
drivers have the same preferences regarding the park-
ing space attributes and the same attitute to come to
an agreement β
1
= 0.4, β
2
= 0.6, and DA
att
= 0.5.
In Figure 2, the average utilities of the DAs and
the PMs are plotted for each setting. As we expected,
by increasing the number of available PMs, the aver-
age utility of the PMs decreases (see Figure 2 (right)).
However, this trend is shown only for the cases of 50
and 100 requests. Indeed, by increasing the number
of requests, the average utility of the PMs is constant.
In these two cases (50 and 100 requests), the num-
ber of parking requests is smaller than the number of
available places. This, in the case of more available
PMs, will produce a competition among PMs and so
a smaller average utility (see Figure 2 (right)). Rea-
sonably, in the case of few requests and more PMs,
there are more available and better choices for the DA,
so the average DAs utility increases in the case of 50
and 100 requests and an increased number of PMs. A
greater number of requests, on the contrary, will al-
low each PM to allocate more parking spaces, leading
to an average PMs and DAs constant utilities for all
considered cases.
Finally, by increasing the number of requests, the
average utility of the PMs decreases. Of course, with
few requests, only the parking spaces with the high-
est PMs utilities are allocated, while by increasing the
number of requests also spaces with lower PMs utility
values are selected by the DAs. Notice that a constant
PMs utility is obtained also in the case of 400 requests
(with respect to 960 available parking spaces). The
lower line reports the 1200 requests case. The op-
posite trend happens in the case of DAs utilities. By
increasing the number of simultaneous requests leads
to longer negotiations (see Figure 4 (left)), so, poten-
tially, parking spaces that are better for the DAs and
worse for the PMs are gradually disclosed. However,
also for the DAs, the case of 1200 requests is the one
with the lowest value since the number of requests is
greater than the number of available parking spaces,
so the average utility considering all the requests (in-
cluding failures) decreases.
In Fig. 3, the average values for SW
+
and SW
∗
are
plotted for the cases of 100 and 400 requests. Follow-
ing the trend in Figure 2, the social welfare average
values SW
+
, that is obtained by considering the sum
of the PMs utilities (with positive values) and the DAs
utilities, does not change varying the number of PMs.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
246

Figure 2: DAs (left) and PMs (right) average utilities varying the number of PMs.
Figure 3: SW
+
and SW
∗
average values varying PMs for 100 and 400 requests.
This is because the slight decrease in the PMs utility
is compensated by an increase in the DAs one. How-
ever, the calculation of the social welfare takes into
account also the total number of requests (thus includ-
ing also the unsuccessful negotiations). The average
social welfare is slightly smaller in the case of 8 PMs
and 100 requests, but such difference is not signifi-
cant. Trends of 50 and 1200 requests are similar, and
so they are not reported here. The trends of SW
∗
also
show a constant behavior by varying the number of
PMs and the number of requests. Contrarily to what
expected, including more than one PM does not pro-
duce a negative impact on the global social welfare.
In Figure 4 (left), the trend of the average num-
ber of negotiation rounds with respect to the number
of queries and the number of available PMs is plot-
ted. The plots show that, by increasing the number of
available PMs, and so the number of possible park-
ing choices at each iteration, the average number of
rounds, considering only the cases of successful ne-
gotiations, decreases. This is to say that, while from
one hand having more than one PM will produce an
increase in the communication (since more messages
are needed), from the other hand this is compensated
by a decrease in the number of required rounds. As
we expected, increasing the number of considered re-
quests produces an increase in the average number of
rounds. However, while in the case of a single PM,
there is a variation of 8 rounds between the cases
of 1200 and 50 considered requests, the increase of
the number of PMs reduces this variation only to 2
rounds. So, a market with more PMs leads to a more
stable negotiation behavior.
In Figure 4 (right), a plot reporting the ratio bene-
fit/cost of the negotiation is shown, and it is evaluated
as the obtained average social welfare (SW
+
) with re-
spect to the number of rounds. This plot shows that,
when considering a fixed set of requests, the case with
more PMs will always produce a better benefit/cost
value. Moreover, the reported values for the case of
50 and 100 queries are very similar, while they de-
crease when considering a larger set of queries.
To conclude, in Figure 5, the percentage of the dis-
tribution of the parking allocations in each zone for
100 and 400 queries, by varying the number of PMs
is plotted. Remember that, Zone 1 is the destination
zone of the considered set of requests (that is indeed
a red zone). As we already discussed, the increase
in the number of considered requests has an impact
on the zones selected for the allocations, since also
parking spaces with lower PMs values are disclosed,
and so selected by the DAs. In particular, in the case
of few requests (50 or 100), most of the selected car
parks were mainly in Zone 3 or eventually in Zone 2.
A City-aware Car Parks Marketplace for Smart Parking
247

Figure 4: Average number of rounds varying the number of PMs (left), and benefit/cost plot w.r.t. different requests sets.
Figure 5: Distribution of the parking allocations in each zone in percentage.
Only a low percentage of selections were made in the
Zone 1, for the case of 8 PMs (and also 4 PMs for 100
DAs). Cases with 400 and 1200 requests showed a
uniform distribution of allocations among the consid-
ered zones, leading to the case of 1200 queries where
the percentage of allocations in the Zone 1 is the same
as the allocation in Zone 2 (with lesser allocations in
Zone 3). Note that the case of 1200 requests does not
correspond to a complete allocation of the 960 park-
ing spaces (namely 646 in the average), since there are
still failures, and so there is not an equal distribution
of allocations among zones.
4 CONCLUSIONS
Reservation-based parking systems have been pro-
posed in the literature developing optimal park al-
location strategies. For example, (Geng and Cas-
sandras, 2013) proposed an efficient and optimal al-
location strategy obtained by solving a sequence of
Mixed-Integer Linear Programming problems, which
are guaranteed to have a feasible solution and to sat-
isfy some fairness constraints. Optimality is obtained
by making allocations for all the considered users, and
users who have already reserved a resource may be
assigned to a different one in a successive decision
point until they physically reach the resource and oc-
cupy it. Here, we do not consider the possibility to
modify the resource allocation after an assignment, so
all requests are independent from each other. The op-
timal allocation of car parking spaces was also stud-
ied in (Mejri et al., 2013), where a semi-centralised
approach for optimising the parking space allocation
is proposed, improving the fairness among parking
zones by balancing their occupancy-load. This ap-
proach considers all the drivers’ requests over a time
window and it assigns a free parking space to each
one simultaneously. Parking coordinators are used for
distributing the optimisation allocation problem that
is not manageable in a centralised way. Here we do
not consider collaboration among parking sellers be-
cause in a marketplace sellers negotiate for their own
interests, but sharing a common city policy.
Multi-agent negotiation has already been used for
parking allocations in Intelligent Transportation Sys-
tem applications. In (Chou et al., 2008), negotiation
on parking price is used to find better and cheaper
parking spaces from the driver point of view. Each
parking manager announces the parking spaces and
waits for bids from drivers, so parking price changes
according to the level of drivers competition. In
(Adler and Blue, 2002), cooperative agent negotia-
tion is used to optimise traffic management relying on
shared knowledge between drivers and network oper-
ators about routing preferences. Here, the negotia-
tion items are the parking spaces to be assigned with
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
248

dynamical characteristics (i.e.; the price) that may
change from one request to another, but they are fixed
during a single negotiation process.
In this work, a multi-agent smart parking mar-
ketplace is proposed relying on a distributed negoti-
ation mechanism. Negotiation allows parking man-
agers and drivers to evaluate parking spaces accord-
ing to their own private preferences, and to come to
a solution that can be acceptable by both parties. A
dynamic pricing scheme is used to incentivize drivers
to select parking spaces that lead to both a better car
park utilisation, and to limit traffic circulation in spe-
cific city areas. Differently from a centralised ne-
gotiation approach previously proposed, a distributed
solution is more realistic and more suitable to deal
with the complexity of modern transportation sys-
tems. The benefit of the negotiation was evaluated
in terms of a Social Welfare metrics measuring the
degree of satisfaction of all involved parties. Results
showed that, in the case of the number of parking re-
quests smaller than the number of available parking
spaces, the increasing number of Parking Managers
leads to a competition among them, and consequently
to a smaller average utility for the Parking Managers.
Of course, since there are more and better choices for
the Driver Agents, their average utility increases. On
the contrary, a greater number of requests allows each
Parking Manager to allocate more parking spaces, so
leading to an average Parking Managers and Driver
Agents constant utilities. In addition, by increasing
the number of Parking Managers and the number of
queries, the social welfare remain constant, so a de-
centralised negotiation approach does not have a neg-
ative impact on the overall level of satisfaction of the
involved negotiators. Finally, by increasing the num-
ber of available Parking Managers, and so the num-
ber of possible parking choices, the average number
of rounds necessary for successful negotiations de-
creases. So, while from one hand having more than
one PM causes an increased communication cost due
to an increased number of exchanged messages, it
is compensated by a decreased number of rounds to
reach an agreement.
REFERENCES
Adler, J. L. and Blue, V. J. (2002). A cooperative multi-
agent transportation management and route guidance
system. Transportation Research Part C: Emerging
Technologies, 10(5–6):433 – 454.
Barbuceanu, M. and Lo, W.-K. (2001). Multi-attribute util-
ity theoretic negotiation for electronic commerce. In
Agent-Mediated Electronic Commerce III, Current Is-
sues in Agent-Based Electronic Commerce Systems,
pages 15–30. Springer-Verlag.
Barile, F., Di Napoli, C., Di Nocera, D., and Rossi, S.
(2015). Evaluating the social benefit of a negotia-
tion–based parking allocation. In Advances in Practi-
cal Applications of Agents, Multi-Agent Systems, and
Sustainability: The PAAMS Collection, volume 9086
of LNCS, pages 15–26.
Bellifemine, F., Caire, G., Poggi, A., and Rimassa, G.
(2008). Jade: A software framework for developing
multi-agent applications. lessons learned. Inf. Softw.
Technol., 50(1-2):10–21.
Chou, S.-Y., Lin, S.-W., and Li, C.-C. (2008). Dynamic
parking negotiation and guidance using an agent-
based platform. Expert Systems with Applications,
35(3):805–817.
Di Martino, S. and Rossi, S. (2016). An architecture for a
mobility recommender system in smart cities. Proce-
dia Computer Science, 98:425 – 430.
Di Napoli, C., Di Nocera, D., and Rossi, S. (2014). Agent
negotiation for different needs in smart parking alloca-
tion. In Advances in Practical Applications of Hetero-
geneous Multi-Agent Systems. The PAAMS Collection,
volume 8473 of LNCS, pages 98–109.
Di Napoli, C., Pisa, P., and Rossi, S. (2013). Towards a dy-
namic negotiation mechanism for qos-aware service
markets. In Trends in Practical Applications of Agents
and Multiagent Systems, volume 221 of AISC, pages
9–16. Springer.
Endriss, U., Maudet, N., Sadri, F., and Toni, F. (2006). Ne-
gotiating socially optimal allocations of resources. J.
Artif. Intell. Res. (JAIR), 25:315–348.
Geng, Y. and Cassandras, C. (2013). New smart parking
system based on resource allocation and reservations.
IEEE Transactions on Intelligent Transportation Sys-
tems, 14(3):1129–1139.
Haklay, M. and Weber, P. (2008). Openstreetmap: User-
generated street maps. Pervasive Computing, IEEE,
7(4):12–18.
Mejri, N., Ayari, M., and Kamoun, F. (2013). An efficient
cooperative parking slot assignment solution. In The
Seventh International Conference on Mobile Ubiqui-
tous Computing, Systems, Services and Technologies,
pages 119–125. IARIA.
Nakamura, K., Hondo, I., Hataoka, N., and Horii, S. (2000).
Car information systems for its. Hitachi Review,
49(3):102–106.
Pan, B., Crotts, J. C., and Muller, B. (2007). Develop-
ing web-based tourist information tools using google
map. In Sigala, M., Mich, L., and Murphy, J., edi-
tors, Information and Communication Technologies in
Tourism 2007, pages 503–512. Springer Vienna.
Polycarpou, E., Lambrinos, L., and Protopapadakis, E.
(2013). Smart parking solutions for urban areas. In
IEEE 14th International Symposium on World of Wire-
less, Mobile and Multimedia Networks (WoWMoM),
pages 1–6. IEEE.
Ramezani, S. and Endriss, U. (2010). Nash social welfare
in multiagent resource allocation. In Agent-Mediated
Electronic Commerce. Designing Trading Strategies
and Mechanisms for Electronic Markets, volume 59
of LNBIP, pages 117–131. Springer.
A City-aware Car Parks Marketplace for Smart Parking
249