Blockchain-based Task-centric Team Building

Alexander Jahl, Stefan Jakob, Harun Baraki, Yasin Alhamwy and Kurt Geihs

Distributed Systems Department, University of Kassel, Wilhelmsh

oher Allee, Kassel, Germany

Keywords:

Multi-Agent Systems, Cooperation and Coordination, Self Organizing Systems, Agent Models and

Architectures, Task Planning and Execution.

Abstract:

Large-scale dynamic environments like Industry 4.0, Smart Cities, and Search & Rescue missions require

a distributed and effective management of participating autonomous units. Usually, these units and their

capabilities are heterogeneous and partially unknown at design time. Thus, the management has to adapt

dynamically to the current situation. Several units have to collaborate to solve common tasks, and thus have to

share their knowledge. However, complex tasks typically require the splitting of a team of units into subteams

that solve smaller subtasks. A common approach to tackle this problem is to employ a decentralised, self-

organising system. Traditionally, such systems are modelled either agent-centric or organisation-centric. In

contrast, in this paper we shift the focus to a task-centric view. Tasks are enabled to search and bind suitable

execution units based on their capabilities. These units can be either single agents, teams of agents, or teams

of teams. A blockchain-based allocation model supports the task-centric view and controls the distributed

task assignment. We present a proof-of-concept implementation that shows the viability of our presented

approach.

1 INTRODUCTION

Teamwork is essential in large-scale dynamic do-

mains, such as Search & Rescue operations in dis-

aster scenarios, Industry 4.0 applications, Smart City,

and warehouse logistics. In these areas, devices of

different parties are applied, which vary in their capa-

bilities and knowledge representation. In smart ware-

house logistics, for example, applications run in the

Cloud, on local edge servers, and on robots equipped

with various sensors and actuators. The collaboration

requires efﬁcient and effective management. One op-

tion to realise such collaborative behaviour is the co-

ordination management by a central instance. This

leads to some disadvantages, such as bottlenecks, sin-

gle point of failures, constant communication, and

limited scalability. Applications in such dynamic do-

mains would beneﬁt from features provided by decen-

tralised and self-organising systems that do not in-

troduce the aforementioned shortcomings. Further-

more, self-organising systems allow applications to

adapt to changes in their structure and their environ-

ment. However, team coordination and teamwork ex-

ecution lead to several non-trivial problems that need

to be solved. These include, for example, distributed

coordination, heterogeneous knowledge representa-

tion, and decentralised decision making. The re-

search ﬁelds of self-organisation (Martin-Flatin et al.,

2006; De Wolf and Holvoet, 2004) and swarm tech-

nology (Brambilla et al., 2013) focus on these prob-

lems which are addressed especially by multi-agent

systems and their distributed design. Applications in

this area can be considered from the agent-centric and

the organisation-centric view (Picard et al., 2009).

On the one hand, these views focus on local agent

behaviour and apply techniques in the ﬁeld of swarm

intelligent algorithms to assign tasks. On the other

hand, they focus on system organisation and use tech-

niques to solve the task allocation problem of type-

based approaches and market-based algorithms.

In contrast, we present an architecture that is

based on a task-centric view. It applies the Unit-Skill-

Task model presented in (Jahl et al., 2021) that allows

task instances to actively search for suitable execu-

tion units and bind them to themselves. This approach

offers beneﬁts such as scalability, robustness and dy-

namic adaptations depending on the current situation

and in the case of environment changes. A short in-

troduction to this model can be found in Section 2.

This paper extends the concept, focusing in particular

on the key challenges of self-organised team building

and allocation of execution units to tasks.

The main contribution of this paper is the new dy-

namic self-organised system for teams and teams-in-

250

Jahl, A., Jakob, S., Baraki, H., Alhamwy, Y. and Geihs, K.

Blockchain-based Task-centric Team Building.

DOI: 10.5220/0010227402500257

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 1, pages 250-257

ISBN: 978-989-758-484-8

teams using the novel task-centric view. The system

addresses speciﬁc requirements that are essential for

critical systems in the area of Industry 4.0, Smart City

etc. Here, the key challenges are robustness, reliabil-

ity, transparency, security and access control. Hence,

our system integrates a distributed blockchain ap-

proach that supports grouping of execution units and

active unit-task allocation. The distributed blockchain

fulﬁls in particular the mentioned requirements. Fur-

thermore, it ensures the correct distribution of the cur-

rent state of the token in the blockchain network, man-

ages the allocation of execution units to active tasks

by tokens in a coordinated manner, and organises the

teams and teams in teams that have been created.

The structure of the paper is organised as follows.

In Section 2, we provide an overview of the underly-

ing foundational concepts and frameworks. Section 3

presents the unit-task allocation concept and addi-

tional implementation details. Section 4 shows the

experiments and analyses the results. Related work is

discussed in Section 5, and Section 6 concludes the

paper.

2 FOUNDATIONS

In this section, we introduce the foundations of our

work. This includes a brief introduction of task allo-

cation, distributed blockchain, and Answer Set Pro-

gramming. Additionally, we present a short overview

of our previous work (Jahl et al., 2021), a task-centric

Unit-Skill-Task model for hierarchical team manage-

ment, which is continued in this work.

2.1 Task Allocation

In a multi-agent system, agents cooperate or collabo-

rate to solve different kinds of tasks. The challenge

of task assignment is to decide which agent should

perform which task. Task assignment with multi-

ple agents increases the complexity since, in the sim-

plest case, the best possible mapping from agents to

tasks still requires polynomial time. Hence, com-

mon methods approximate the exact solution but do

not guarantee it. Furthermore, the complexity of the

task affects the number of agents that are required to

perform the task. Properties such as agent budgets,

task costs, time, capacity limitations, etc., may have

a great inﬂuence on the complexity, but vary depend-

ing on the agent-task assignment. A task allocation

without any additional properties commonly refers to

a balanced assignment problem where the number of

agents matches the number of tasks. (Gerkey and

Matari

c, 2004) deﬁne a common classiﬁcation for dif-

ferent task allocation categories. The classiﬁcation

distinguishes different combinations of single or mul-

tiple agents, single or multiple tasks, as well as instan-

taneous assignment and time-extended assignment.

These correspond to the different complexity classes.

While most works consider the combinations of sin-

gle agents and single tasks, several works use combi-

nations of a single task and multiple agents to realise

architectures that provide coalition formation. Differ-

ent methods, such as market-based, threshold-based,

swarm intelligent, utility-based, and consensus-based

algorithms, have already been evaluated in various

studies which solve the problem of task allocation.

They are distinguished by two categories: centralised

and decentralised task allocation (Ye et al., 2016;

Turner, 2018). In centralised task assignment sys-

tems, a central entity calculates the task allocations

for all agents. It collects all information about the

agents and thus can optimise the overall target. Con-

sequently, the central entity is the bottleneck of the

system. It has to communicate with each agent and

must not fail. The decentralised task allocation al-

lows the simultaneous execution of the task assign-

ment on each agent. By communicating the partial

solutions of the agents among themselves, a common

solution is found. This requires a consensus process,

since different agents may have different information

about the current situation, which may result in differ-

ent solutions. Assigning and exchanging roles allows

agents to compute a consistent solution and to execute

a task more efﬁciently.

2.2 Blockchain Technology

A blockchain is a distributed ledger, i. e. recorded

set of transactions. It represents a decentralised,

shared database. No central authority or intermedi-

ary is needed for processing, validating and authen-

ticating transactions, events, and other kinds of data

exchange. Such information can only be stored in

the ledger if all involved parties agree using some

kind of consensus algorithm. Once information is

entered into the ledger it can never be deleted. A

distributed blockchain enables a distributed peer-to-

peer network. Untrustworthy participants can inter-

act in a veriﬁable manner without a trusted interme-

diary (Crosby et al., 2016). Various kinds of scripting

languages allow the blockchain users to deﬁne smart

contracts. These contract scripts correspond to proce-

dures or methods that are stored in the blockchain.

One distributed ledger platform for running smart

contracts in a permissioned blockchain network is

the Hyperledger Sawtooth framework (Olson et al.,

2018). This framework is designed with a focus on

Blockchain-based Task-centric Team Building

251

modularity, extensibility, and larger networks. It pro-

vides basic features such as the communication be-

tween the nodes of a network, the storage manage-

ment of data in the blockchain, and the architecture

to connect smart contract and consensus algorithms.

Each node in the network includes a validator and a

set of transaction processors (see Figure 1).

Client

 Blockchain Node

Validator

Transaction

Processor

Transaction

Processor

Transaction

Processor

P2P

Network

Figure 1: Hyperledger Sawtooth architecture.

The validator manages transactions, consensus, the

blockchain, connections to other nodes, and the in-

ternal state. Hyperledger Sawtooth identiﬁes entities

based on their public key and thus manages transac-

tion and validator permissions. Instead of handling

lists of public keys, Hyperledger Sawtooth utilises a

dedicated family of transactions. Each transaction

is processed by a transaction processor which han-

dles the predeﬁned transaction family. Hyperledger

Sawtooth allows network authorisation directly at the

peer-to-peer level. Each individual Sawtooth node

can be managed by controlling the connection access

to the Hyperledger Sawtooth network, the synchroni-

sation with the current ledger state, sending of con-

sensus messages, participation on the consensus pro-

cess, and transmission of transactions to the network.

2.3 Answer Set Programming

Answer Set Programming (ASP) (Gelfond and Kahl,

2014) is a declarative problem solving paradigm. It

roots in logic programming, allows non-monotonic

reasoning, and provides defaults for expressing stan-

dard representations. ASP can be applied in domains

like planning, optimization, and decision making for

solving NP and NP

problems. Instead of providing

an algorithm to solve a problem, an ASP program de-

scribes the problem itself. An answer set solver then

takes the ASP program as input and returns all solu-

tions (answer sets) for that program. An ASP program

includes a set of rules, where a rule is formalised as

shown in (1).

a ← b

,...,b

, not c

,...,not c

where {a,b

,...,b

,...,c

} ⊆ A

(1)

a represents the head of the rule. b

,...,b

specify the

positive body and not c

,...,not c

the negative body.

The complete body is the conjunction of the positive

and negative body. A is the set of all available atoms.

The head a is true if all positive literals (b

,...,b

)

in the body are true and no negative literal (c

,...,c

)

holds. A rule without a body is a fact since it is uncon-

ditionally true. A rule without a head is a constraint .

In the case that a constraint holds, false is derived and,

thus, the respective answer set is discarded. Further-

more, ASP distinguishes between two kinds of nega-

tion.

innocent ← not guilty (2)

innocent ← ¬guilty (3)

The rule (2) is a negation as failure. It deﬁnes that

someone is innocent until proven guilty. In contrast,

rule (3) represents the strong respectively classical

negation. With these speciﬁcations, it is feasible to

model a knowledge representation. The rules (4-7)

illustrate a simple example.

bird(X) ← eagle(X) (4)

bird(X) ← penguin(X) (5)

¬ f ly(X) ← penguin(X) (6)

f ly(X) ← bird(X), not ¬ f ly(X) (7)

Rule (4) and (5) deﬁne that eagle and penguin are

birds, while rule (6) speciﬁes that a penguin cannot

f ly. Finally, rule (7) describes that if ¬ f ly(X) can-

not be derived for a bird, it can f ly. The key advan-

tage of ASP is that knowledge or given defaults can

be changed and extended at runtime by new informa-

tion without causing inconsistencies. This is essential

in dynamic and heterogeneous environments.

2.4 Task-centric Unit-Skill-Task Model

In our task-centric Unit-Skill-Task concept, presented

in (Jahl et al., 2021), the task-centric view deﬁnes a

task as a separate active element that is independent

of agents.

 Complex Skills Primitive Skills

Characteristic

Behaviour

Action

Perception

Capability

Skill

Figure 2: Skill classiﬁcation.

Moreover, the concept abstracts each agent or team

into a SKILL-Unit that has speciﬁc skills and serves

as an execution unit. Figure 2 presents two types of

skills. While Primitive Skills represent characteristics

and capabilities, Complex Skills describe behaviours,

actions, and sensory perceptions. Complex Skills can

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

252

depend on certain Primitive Skills. SKILL-Units can

contain other SKILL-Units. All enclosed SKILL-Units

pass on their set of Skills to the aggregated SKILL-

Unit. A pool of units provides idle SKILL-Units

where each unit can contain units via a hierarchical

model. Tasks actively search for suitable SKILL-Units

and bind them.

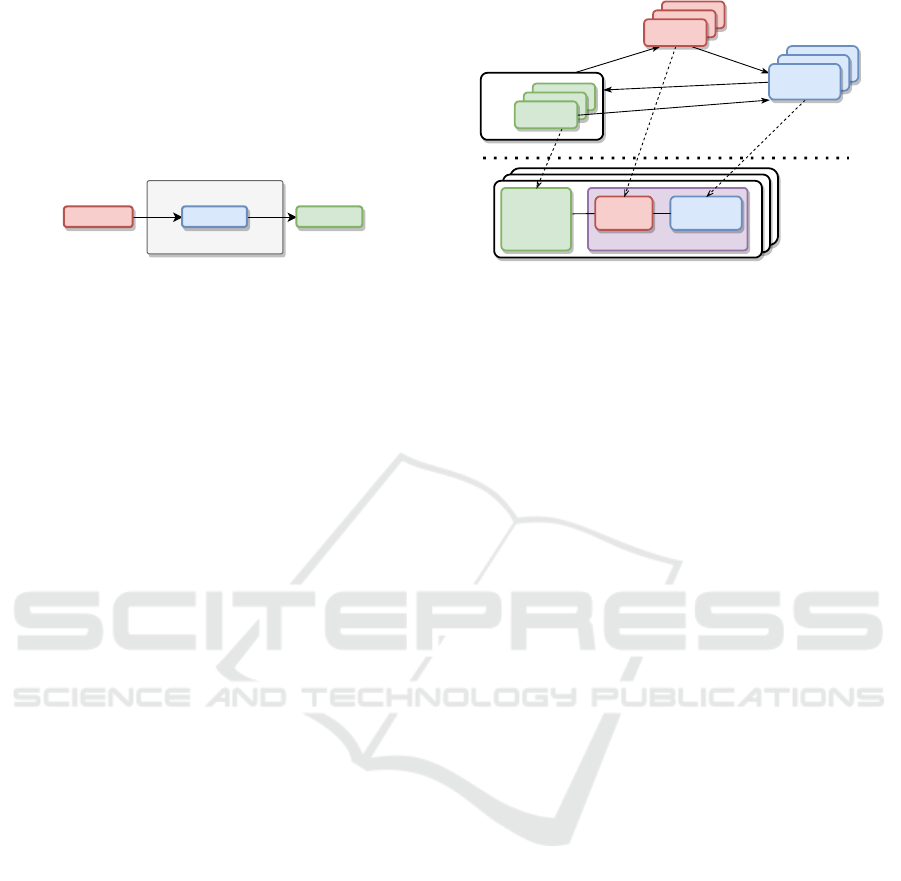
Task Skill Unit

Task Requirements

Provided by Unit

Figure 3: Unit-Skill-Task concept.

The Unit-Skill-Task concept, shown in Figure 3, con-

siders the allocation of SKILL-Units to tasks from the

task-centric view. It is formalised as a tuple

c = (t, u) where ∀s ∈ S

: s ∈ S

(8)

For the concept c, a SKILL-Unit u with the Skill set S

that can perform a task t has to fulﬁl the Skill require-

ments S

of the task t. The allocation matrix A for all

units is then

(

1 if c

is fulﬁlled

0 otherwise

(9)

Tasks can be assigned to several SKILL-Units. This

means that they are executed multiple times in paral-

lel. Finally, plans contain one or several tasks and

subplans, which in turn can contain subplans with

subtasks, resulting in a plan tree. Each plan represents

a team. Thus, all units bound by the tasks contained

in the plan are team members.

3 UNIT-TASK MANAGEMENT

This section presents our dynamic team and teams-

in-teams organisation management of execution units.

The task-centric Unit-Skill-Task model (Section 2.4)

results in several requirements for the unit-task man-

agement. A separation of tasks and execution units is

necessary. Tasks must be able to actively search for

suitable execution units and bind them to themselves.

Furthermore, unbound execution units should be ac-

cessible via a pool. Figure 4 shows the blockchain-

based SKILL-Unit task model.

The basic concept of the unit-task management at

the top illustrates the conceptual separation and inter-

action of SKILL-Units, tasks, and blockchain nodes.

The resulting P2P architecture at the bottom virtu-

alises the tasks as part of the blockchain component

and combines them with the SKILL-Unit to form a

P2P node. The blockchain component is based on

 Blockchain Node Component

Blockchain

Node

Atomic

SKILL-Unit

Component

Task

Manager

Unit Pool

Task

SKILL-Unit

Blockchain

Node

Blockchain

Node

Blockchain

Node

search &

update

SKILL-Units

Manage Grouping

allocated

Basic Concept

P2P

 Architecture

Figure 4: Blockchain-based SKILL-Unit task model.

nodes of a permissioned blockchain network, as de-

scribed in Section 2.2 and extended by a unit-task

management. In the implementation, Hyperledger

Sawtooth is used to realise blockchain node compo-

nents. This allows it to use the database and consis-

tency mechanisms provided by the blockchain. As

shown in Figure 4, the P2P architecture thus in-

cludes pairwise combinations of SKILL-Units and

blockchain nodes as peers.

The initial step towards creating a network of

blockchain-based SKILL-Unit task nodes is the join-

ing process. This process is controlled by the

TaskManager. The ﬁrst node that is started initialises

the main group, which corresponds to the unit pool

described in the task-centric Unit-Skill-Task model.

In general, a group refers to all SKILL-Units that share

a symmetric secret key to encrypt messages. En-

crypted group messages are communicated via broad-

cast. Only members have the secret key and can de-

crypt the messages. Therefore, the starting node de-

ﬁnes a secret key and creates a transaction to store

all group information in the blockchain. Additionally,

the node registers for all events of this group and sets

itself as maintainer for the group voting. Subgroups

can be created in the same way through initial nodes.

A new node that wants to join the network has to

send a join request to the network via a speciﬁc ad-

dress. The group voting maintainer gets the request

and then starts the voting process. If the result of the

votes are positive, the secret key is sent to the new

node. Subsequently, it will become a member of the

group, and thus part of the network. The mechanism

of the voting process is shown as pseudo code in Al-

gorithm 1.

The algorithm requires a voting strategy (Line 2)

and the number of group members (Line 3) which

are involved in the voting. The voting strategy can

be deﬁned individually for each group but is then the

same for all members of the group. A voting strat-

egy can be, for example, a majority decision. The

strategy may be chosen according to the desired se-

Blockchain-based Task-centric Team Building

253

Algorithm 1: Voting Mechanism.

1 GroupVotingMaintainer M

2 VotingStrategy S

3 NumberOfParticipants P

Input : Candidate C, Group G

Output: Voting Result

4 broadcast VotingRequest for C in G

5 while no timeout and responses.size < P do

wait for responses

6 if new response then

7 add response to listO f Results

8 S validates the listO f Results and stores

results in votingResult

9 if votingResult is access granted then

10 set C as new M of G

11 return votingResult

curity. The number of group members participating

in the vote is also determined individually when the

group is created. A selection strategy is used to se-

lect the involved members by themselves. To avoid

unnecessary communication, the selection strategy al-

lows members to know without additional communi-

cation, whether they are involved in the current voting

or not. Therefore, the selection is only dependent on

the total number of group members and the deﬁned

number of involved voters. An example is shown in

Algorithm 2. This algorithm allows the group mem-

ber to know whether it is a voter or not by means of

simple modulo calculation and, if necessary, to trig-

ger the calculation of the votes afterwards. The group

and the candidate are required as input for the voting

algorithm. The group voting maintainer who received

the request sends a broadcast to the group (Line 4 in

Algorithm 1). Subsequently, the maintainer waits for

the answers until the number of responses reaches the

number of voters or a deﬁned timeout occurs (Line 5-

7 in Algorithm 1). The answers are collected in a list.

Finally, the voting strategy processes the list, e. g. to

check whether a majority has voted for it. In case the

result is positive, the candidate is assigned as the new

group voting maintainer, and the result is published in

the blockchain (Line 8-11 in Algorithm 1).

The network is now able to create groups and sub-

groups dynamically. Due to the described group ad-

ministration, only members are allowed to grant ac-

cess to candidates. Furthermore, only members can

read encrypted messages that are distributed inside

the group. Nodes in the network can create not only

new subgroups and invite other nodes, but also are

able to remove themselves from a subgroup. Further-

Algorithm 2: Selection Strategy.

Input : MemberList M,

NumberOfParticipants P

1 p ← get own position in M

2 i ← M/P

3 m ← (p+1) mod i

4 if m = 0 then voting participant

5 calculate votes

6 send votes to the group

more, the last node in a subgroup can delete the group.

If one member in the group no longer meets the Skill

requirements of the task or is unavailable, the task can

not be executed anymore. The group is released and

dissolved and the contained members are returned to

the main group (unit pool group). This mechanism

provides the basis for the unit-task assignment. Since

an individual unit is not able to assess the needs of all

tasks in the whole system, it is reasonable to delegate

the allocation process to the individual tasks, as de-

scribed in (Jahl et al., 2021). An appropriate solution

to deal with the unit-task allocation in a decentralised

way is to apply a token-based approach. The token

communication allows minimising computational and

communication efforts. To realise the blockchain-

based SKILL-Unit task approach, the token contains

information about available tasks, their Skill require-

ments, and their already allocated units as well as a

list of not yet visited units. The token is stored in

and communicated over the blockchain. Only nodes

whose unit are in the unit pool group have access to

the token. Tasks that need units are listed in the to-

ken and thus can be checked by the TaskManager of

the current token owner node. Not every unit in the

network needs to know the current formation and the

current Skill set of the group members.

Algorithm 3 illustrates the process of token han-

dling in the TaskManager. All non-executed tasks

stored in the token are called consecutively (Line 1).

The plan which is associated with the current task

needs a subgroup in the unit pool group in the

blockchain (Lines 4-5). Skills required to perform the

task are then compared with the Skills provided by the

unit (Line 6). The comparison is based on a shared

ontology described in a logic programming language.

For the experimental implementation, ASP (see Sec-

tion 2.3) is used, since it allows simple and read-

able deﬁnitions and offers several high-performance

solvers. To compute the Skill set S

in Algorithm 3 in

Line 6, a matching rule (see Listing 1) speciﬁes that

a SKILL is missing in case a task requires a SKILL

which is not given by the UNIT. This rule remains the

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

254

Algorithm 3: Token Mechanism.

Input : Received Token

1 get non-executed tasks from token

2 forall task t in non-executed tasks do

3 get plan p

that is associated with t

4 if p

has no sub group then

5 create sub group for p

6 compute Skills S

= S

\ S

7 if S

is ∅ then

8 allocate unit u to task t

9 remove t from token

10 if all tasks in p

have units then

11 create new unit u

with all Skills

of all tasks in p

12 break

13 remove visited unit u from unit pool in the

token

14 if there are still non-executed tasks then

15 send the token to a not yet visited unit in

the unit pool group

same for each execution, since TASK, SKILL, and UNIT

are assigned to the current representatives.

1 mis s i ng ( SKILL ) :- ta s k ( TASK ) ,

re q u ire ( TASK , SKIL L ) , unit ( UN I T )

, n o t has ( UNIT , S K I LL ) .

Listing 1: Matching rule.

The required rules which represent all facts for the

considered unit and currently active task are gener-

ated individually. Therefore several generating tem-

plates (see Listing 2) are deﬁned which need both as

input. TASK , UNIT , and SKILL are placeholders

and will be replaced by the current identiﬁers of the

task and the unit and their Skills. Lines 1 and 3 gen-

erate the two facts for the task and unit identiﬁer as

an ASP program. While Line 2 is executed as often

as Skills are available in the task, the same occurs for

the unit in Line 4. A corresponding number of Skill

facts are generated. Afterwards, the missing rule (see

Listing 1) and the generated facts are combined to one

ASP program.

1 task ( _TA S K_ ) .

2 re q ui re ( _TASK_ , _SK I LL _ ).

3 unit ( _UN I T_ ) .

4 has ( _UNIT_ , _S K IL L_ ).

Listing 2: Rule templates.

The run time that a task needs to calculate all map-

pings is the sum of all run times of comparing its re-

quired Skills with the Skills of each unit in the unit

pool. In case, there is a matching between both Skill

sets, the current task allocates the current unit, stores

the matching result in the blockchain, and removes

itself from the task list in the token (Lines 8-9 in Al-

gorithm 3). Subsequently, all tasks of the current plan

are checked whether they are in the unit list of the

token. If no task can be found in the list, a new unit

will be created that represents the subgroup of the cur-

rent plan and includes all Skills of the included units

(Lines 10-12 in Algorithm 3). Finally, the visited unit

is removed from the unit pool, and the token is sent to

the next unvisited unit (Lines 13-15 in Algorithm 3).

A self-developing network of individual teams

and teams within teams is created. Since the tasks ac-

tively search for units with suitable Skills and decide

themselves to bind them, no optimisation of the task

allocation is necessary. All restrictions for the alloca-

tion process are modelled in the Skill requirements of

the tasks. Communication to coordinate the coopera-

tion of units in individual teams is not explicitly part

of the blockchain network. Therefore, the resulting

network includes two communication channels, one

for communication across the distributed blockchain

nodes and one for communication between the units

within the task subgroups.

4 EXPERIMENTAL RESULTS

We have implemented our framework based on our

modiﬁed version of Hyperledger Sawtooth. Our

framework is optimised for the communication of

agent-based systems. It allows simpliﬁed access to

encrypted sockets, the blockchain, and its event sub-

system. To evaluate the allocation of units to tasks

and the building process of teams and the teams in

teams, a smart warehouse example as presented in

(Jahl et al., 2021).

The scenario has a plan tree (see Section 2.4)

which includes all tasks. The tasks can only be suc-

cessfully executed through teamwork. The root plan

of the tree is the Warehouse Plan. It includes the Main

Task and two sub plans, Service Sub Plan and Robots

Sub Plan. The Service Sub Plan contains two tasks,

Edge Service Task and Cloud Service Task. While

the Edge Service Task needs the Skill workAsNaviga-

tor, the Cloud Service Task requires the Skill workAs-

KnowledgeBase. The Robots Sub Plan in turn in-

cludes two tasks, Transport Robot Task and UAV Task.

The Transport Robot Task needs the Skill canTrans-

port and the UAV Task requires the Skill canFly. The

Blockchain-based Task-centric Team Building

255

Main Task contains all requirements of all tasks of the

sub plans. Hence, it needs the Skills workAsNaviga-

tor, workAsKnowledgeBase, canTransport, and can-

Fly. Furthermore, the ASP program mentioned in

Section 3 is necessary for the correct functionality

of the framework. Therefore, the program needs the

matching rule in Listing 1 and additional individual

rules generated at runtime (see Listing 2 in Section 3).

1 task ( ua v T ask ) .

2 re q ui re ( ua v T a s k , c anT r ans p ort ) .

3 unit ( ua v ) .

4 has ( uav , c anT r ans p or t ).

Listing 3: Generated rules.

As an example for these generated rules, the UAV

Task and the execution unit UAV are considered. List-

ing 3 shows the rules (facts) for the UAV Task (Line 1)

and the required Skill canTransport (Line 2) on the

one hand. On the other hand, it includes the facts

for the unit UAV (Line 3) and the available Skill

canTransport (Line 4). The complete ASP program

consists of the missing rule and all generated facts.

The ﬁlter query subsequently extracts any missing

facts from the resulting answer set, consisting of the

missing facts and generated facts. For the presented

example rules, the answer set is then empty, since the

uavTask requires the canTransport Skill which is

provided by the uav unit. For the smart warehouse

example, calculating a mapping of the Skill sets for

one task and one unit takes on average 3 ms.

5 RELATED WORK

Teamwork, especially in the ﬁeld of multi-agent sys-

tems is a well-studied area of research (Geihs, 2020).

In this context, coalition forming and team organi-

sation are essential to establish cooperation between

agents. Researchers in this area address, in particular,

the task allocation problem. As already mentioned in

the introduction, centralised solutions are not suitable

for the task allocation problem addressed in this pa-

per due to the disadvantages of a central entity such

as bottlenecks, single-point-of-failures, and commu-

nication and participant limitations.

Threshold-based task allocation methods are ad-

dressed by many works. These methods combine

each agent with an activation threshold for each task

that needs to be performed. They observe signals of

tasks or role allocation processes and react to these

if it surpasses an internal threshold. While sim-

ple approaches use ﬁxed thresholds, most approaches

focus on adaptive threshold methods. The authors

in (Ferreira et al., 2010) solve task allocation with

Swarm-GAP. Agents in this probabilistic approach se-

lect tasks using a model that adapts the distribution of

tasks among social insects. If an agent perceives an

incomplete task in the current environment, it can ini-

tiate the creation of a token that is only applied to this

task. This token is then generated by a central entity

whereas in our approach the token is generated and

managed by the distributed blockchain. However, in

contrast to our approach, agents only perceive tasks

in their local environment. This assumption can limit

the amount of tasks recognised by the agents.

Besides threshold-based solutions, market-based

approaches are widely used to solve task allocation

problems. These approaches apply an auctioneer that

publishes tasks inside the multi-agent system. Agents

then submit bids, indicating their costs or beneﬁts to

perform the tasks. The auctioneer decides by means

of the various bids which agent is entrusted with

which task. (Chen et al., 2018) applies such a task

allocation method based on multi-objective optimi-

sation. The approach utilises two indicators, time

and energy, in a utility function for its optimisation.

The method provides the deﬁnition of the energy util-

ity function. The task allocation in (Iijima et al.,

2017) is based on the preferences declared by sin-

gle agents. During the task allocation process, that

maximises the utility for the shared and required per-

formance, agents can give weight to individual pref-

erences based on their own speciﬁcations and capa-

bilities. That leads to collaborative agents that can

autonomously decide their preference adaptively in

dynamic environments. This approach follows the

agent-centric view that focuses on designing local be-

haviour and peer-to-peer interactions. Instead, our so-

lution enables the task-centric view that deﬁnes a task

as a separate active element which is independent of

agents. It is tailored for environments with a dynamic

number of heterogeneous agents, but concrete tasks.

There is further work in the area of swarm in-

telligence. The approach formalised in (Dahl et al.,

2009) presents a concept of a vacancy chain schedul-

ing model for the task allocation problem in spatially

classiﬁable domains. The concept takes into account

variations in the performance of individual agents.

However, using a learning methods for task alloca-

tion requires additional resources and time. Another

concept is proposed in (Brutschy et al., 2014). The

authors apply tasks that are sequentially interdepen-

dent. The mechanism neither needs global knowledge

nor centralised entities. Since the approach does not

require communication between agents, it is suitable

for use in swarms of simple agents.

Other works propose methods which apply ge-

netic algorithms, for example, (Padmanabhan Panchu

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

256

et al., 2018). The approach deals with the task allo-

cation of multiple agents to multiple tasks in a decen-

tralised way. The drawback is that genetic algorithms

are not optimal for time critical solutions since no pre-

diction about the duration of the respective problem-

solving is possible. Even with simple genotypes, such

algorithms rapidly reach limits due to memory con-

sumption and computing speed.

However, the fact that the agents in the related

work receive the tasks is different from the approach

presented in this paper. Here, agents, or the respec-

tive units have no inﬂuence on the assignment. Fur-

thermore, the allocation process inside a task does not

require an optimisation algorithm to assign units to

tasks. It should be as simple as possible; ﬁrst come,

ﬁrst serve.

6 CONCLUSIONS

This paper presents a self-organised, task-centric sys-

tem for teams and teams-in-teams. It allows tasks

to independently search for suitable execution units

and to bind them. For this purpose, the task-centric

Unit-Skill-Task model is integrated into a distributed-

blockchain-based approach. Since the individual

tasks themselves are responsible for the allocation,

optimisation methods are not necessary to assign

them. Units do not need to have global knowledge.

Without optimisation and by the distribution of data

on the blockchain, the overall resource consumption

is reduced.

Our on-going research focusses primarily on the

following aspects: (1) The development of an auto-

mated Skill management powered by behaviour mod-

els and logic-program-based decision making; (2) the

separation of the knowledge into Reﬂection Layers;

(3) the implementation of Transferable Behaviours;

and (4) the integration of the Skill management, the

Reﬂection Layers, and the Transferable Behaviours

in our blockchain-based framework and a subsequent

evaluation in a real, automated warehouse scenario.

REFERENCES

Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M.

(2013). Swarm Robotics: A Review from the Swarm

Engineering Perspective. Swarm Intelligence, 7(1):1–

41.

Brutschy, A., Pini, G., Pinciroli, C., Birattari, M., and

Dorigo, M. (2014). Self-organized Task Alloca-

tion to Sequentially Interdependent Tasks in Swarm

Robotics. Autonomous agents and multi-agent sys-

tems, 28(1):101–125.

Chen, J., Wang, J., Xiao, Q., and Chen, C. (2018). A

Multi-Robot Task Allocation Method Based on Multi-

Objective Optimization. In 15th ICARCV 2018, pages

1868–1873. IEEE.

Crosby, M., Pattanayak, P., Verma, S., Kalyanaraman, V.,

et al. (2016). Blockchain Technology: Beyond Bit-

coin. Applied Innovation, 2(6-10):71.

Dahl, T. S., Matari

c, M., and Sukhatme, G. S. (2009).

Multi-robot Task Allocation through Vacancy Chain

Scheduling. Robotics and Autonomous Systems, 57(6-

7):674–687.

De Wolf, T. and Holvoet, T. (2004). Emergence versus Self-

organisation: Different Concepts but Promising when

Combined. In International workshop on engineering

self-organising applications, pages 1–15. Springer.

Ferreira, P. R., Dos Santos, F., Bazzan, A. L., Epstein, D.,

and Waskow, S. J. (2010). RoboCup Rescue as Mul-

tiagent Task Allocation among Teams: Experiments

with Task Interdependencies. Autonomous Agents and

Multi-Agent Systems, 20(3):421–443.

Geihs, K. (2020). Engineering Challenges Ahead for Robot

Teamwork in Dynamic Environments. Applied Sci-

ences, 10(4):1368.

Gelfond, M. and Kahl, Y. (2014). Knowledge Representa-

tion, Reasoning, and the Design of Intelligent Agents:

The Answer-Set Programming Approach. Cambridge

University Press.

Gerkey, B. P. and Matari

c, M. J. (2004). A Formal Analysis

and Taxonomy of Task Allocation in Multi-robot Sys-

tems. The International journal of robotics research,

23(9):939–954.

Iijima, N., Sugiyama, A., Hayano, M., and Sugawara, T.

(2017). Adaptive Task Allocation based on Social

Utility and Individual Preference in Distributed En-

vironments. Procedia computer science, 112:91–98.

Jahl, A., Jakob, S., Baraki, H., and Geihs, K. (2021). Task-

centric Hierarchical Team Management. Submitted at

SAC 2021 DADS.

Martin-Flatin, J.-P., Sventek, J., and Geihs, K. (2006). Self-

managed Systems and Services. Communications of

the ACM, 49(3).

Olson, K., Bowman, M., Mitchell, J., Amundson, S., Mid-

dleton, D., and Montgomery, C. (2018). Sawtooth: An

Introduction. The Linux Foundation.

Padmanabhan Panchu, K., Rajmohan, M., Sundar, R., and

Baskaran, R. (2018). Multi-objective Optimisation

of Multi-robot Task Allocation with Precedence Con-

straints. Defence Science Journal, 68(2).

Picard, G., H

ubner, J. F., Boissier, O., and Gleizes, M.-

P. (2009). Reorganisation and Self-Organisation in

Multi-Agent Systems. In 1st International Workshop

on Organizational Modeling, pages 66–80.

Turner, J. (2018). Distributed Task Allocation Optimisation

Techniques. In Proceedings of the 17th international

conference on autonomous agents and multiagent sys-

tems, pages 1786–1787.

Ye, D., Zhang, M., and Vasilakos, A. V. (2016). A Sur-

vey of Self-Organization Mechanisms in Multiagent

Systems. IEEE Transactions on Systems, Man, and

Cybernetics: Systems, 47(3):441–461.

Blockchain-based Task-centric Team Building

257