
Using Agents and Unsupervised Learning for Counting Objects in
Images with Spatial Organization
Eliott Jacopin
a
, Naomie Berda, L
´
ea Courteille, William Grison, Lucas Mathieu,
Antoine Cornu
´
ejols
b
and Christine Martin
c
UMR MIA-Paris, AgroParisTech, INRA, Universit
´
e Paris-Saclay, 75005, Paris, France
Keywords:
Image Processing, Computer Vision, Counting Objects, Multi-Agent Systems, Unsupervised Learning.
Abstract:
This paper addresses the problem of counting objects from aerial images. Classical approaches either consider
the task as a regression problem or view it as a recognition problem of the objects in a sliding window over the
images, with, in each case, the need of a lot of labeled images and careful adjustments of the parameters of the
learning algorithm. Instead of using a supervised learning approach, the proposed method uses unsupervised
learning and an agent-based technique which relies on prior detection of the relationships among objects. The
method is demonstrated on the problem of counting plants where it achieves state of the art performance when
the objects are well separated and tops the best known performances when the objects overlap. The description
of the method underlines its generic nature as it could also be used to count objects organized in a geometric
pattern, such as spectators in a performance hall.
1 INTRODUCTION
Object counting is an important task in computer vi-
sion motivated by a wide variety of applications such
as crowd counting, traffic monitoring, ecological sur-
veys, inventorying products in stores and cell count-
ing. In agriculture, for instance, Unmanned aerial
vehicles (UAVs) allow for cheaper image recording,
enabling flexible and immediate image processing
(Gn
¨
adinger and Schmidhalter, 2017). One critical
challenge lies in the automatic counting of plants in
fields, if possible at various stages of development.
However, counting objects is difficult as objects
are often variable in terms of shape, size, pose and
appearance and may be partially occluded. In agri-
culture, the presence of weeds and blurry effects as
well as varying growth stages affect performance.
Existing methods can be categorized mainly into
two classes: detection-based and regression-based
(Zou et al., 2019).
In the detection-based approach, a classifier is
learned to recognize the presence of the object(s) of
interest in a sub-image or window, and then this win-
dow is scrolled through the image in order to count
a
https://orcid.org/0000-0002-4568-283X
b
https://orcid.org/0000-0002-2979-3521
c
https://orcid.org/0000-0003-3956-4789
the number of recognized objects. There are however
difficulties associated with this approach. First, it re-
quires (very) numerous labeled training examples, of-
ten in the form of manually drawn bounding boxes
or pixel annotations, which are notoriously costly to
acquire. Second, classification of objects is itself a
challenging task because of the variability of their ap-
pearance, the presence of noise and possible partial
occlusions. Besides the selection of relevant descrip-
tors, such as wavelets, shapeless, edgeless, and so on,
it requires also the fine-tuning of the parameters of the
algorithm. Finally, the choice of the size of a sliding
window and of the scrolling process can be tricky.
In contrast, regression-based methods attempt to
directly estimate the number of objects of interest
from an overall characterization of the image. This
overcomes most of the difficulties of detection-based
methods and, in recent years, these methods have
defined the state-of-the-art performances, specially
through the use of convolutional neural networks.
However, lots of training images as well as advanced
expertise to train deep neural networks are still re-
quired. In addition, retraining is needed when the ob-
jects of interest change.
In this paper, we introduce a novel approach, valid
when the objects of interest have regular spatial rela-
tionships, like spectators in a performance hall, goods
on the shelves of a retail store or plants in fields. It
688
Jacopin, E., Berda, N., Courteille, L., Grison, W., Mathieu, L., Cornuéjols, A. and Martin, C.
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization.
DOI: 10.5220/0010228706880697
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 688-697
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

works in two phases. First, the approximate spatial
relationships between objects are estimated. Second,
based on the structure thus found, a multi-agent based
approach is used where the structure determines the
initial positions of the agents as well as a hierarchy of
control agents and therefore a set of communication
channels between the agents. Each agent is a weak
classifier which guesses if it is positioned over an ob-
ject of interest in the image and can confirm or deny
its guess through exchanges with other agents. The
second phase is iterative until the agents are no longer
undergoing any changes. The number of final agents
gives the number of detected objects.
The advantages of the approach are that:
1. it does not require numerous training images since
the determination of the structure is unsupervised
and the agents themselves are simple detectors.
2. it easily adapts to various conditions on the struc-
ture, nature of the objects, their size and appear-
ance
3. it achieves high performances over the variety of
experimental conditions tested.
These good properties come from the assumption that
a regular structure exists among objects. The ap-
proach should therefore not work on crowd counting,
or on cells counting for instance. But when a regular
structure exists, this knowledge brings a power that
should not be wasted.
Figure 1 provides an example of an aerial image of
a sunflower field. One can see rows of plants, here in a
rather late stage with overlap between plants, shadows
of various sizes and patches of weeds, especially on
the left side of the image.
Cependant, cette méthode ne permet pas de différencier les adventices des plants de tournesols car ce sont
deux objets de couleur verte. Nous avons donc cherché une autre méthode de segmentation de manière à éviter
que les adventices soient retenus (c’est à dire affichés en blanc) à l’issue de cette étape.
2.1.2 Deuxième niveau par la méthode d’Otsu
On voit nettement sur les images que les tournesols apparaissent plus clairs que la plupart des adventices
(Figure 4). Nous avons alors exploité cette différence de teinte pour effectuer une deuxième é tape d e segmen-
tation et essayer de s é p are r les pixels des tournesols des pixels des adventices.
Figure 4–ImagedelaparcelledeNiort.Aucentre,lesadventicesapparaissentplusfoncés.
Une méthode de segmentation automatique présentée par Otsu [12] permet de trouver automatiquement
une valeur de seuil optimale qui sépare deux groupes de pixels. Cette méthode est très employée pour l’analyse
d’images de champs et permet d’effectuer une séparation automatique de pixels de deux teintes de vert différentes
(voir article [15] par exemple). Cette sép aration est réalisée grâce à un seuil qui se place au tomatiquement afin
de former deux groupes de valeurs. Ces deux groupes sont trouvés de sorte que la variance intra-groupe soit
minimale, et la variance inter-groupe maximale (minimisation du rapport
intra
inter
). Nous avons appliqué cette
méthode de segmentation sur des images ExG (section 2.1.1)afindeséparerlesvaleursd’indicesExGpropres
aux tournesols de celles propres aux adventices. L’algorithme de séparation d’Otsu ne différencie que deux
groupes. Or dans notre cas nous en avons 3 : le sol, les adventices et les tournesols. C’est pourquoi il faut
au préalable régler u n seuil minimal de départ de recherche qui exclut d’office le premier groupe de pixels
correspondant au sol, du reste. La séparation ne se fait alors qu’entre les pixels du groupe adventices et du
groupe tournesol. (Figure 5)
Figure 5–Agauche,l’imageoriginale.Au milieu l’image en indice ExG. Adroite,unprofilschématique
de l’histogramme des valeurs d’ExG sur lequel est appliqué l’algorithme de séparation d’Otsu. Encadré en
orange,lesvaleursd’ExGnontraitéesparl’algorithme(bornesupérieurefixéeparl’utilisateur).La ligne
verticale rouge correspond à une illustration d’un seuil de séparation possiblement trouvé par l’algorithme
d’Otsu
Cet algorithme permet de bien séparer les adventices des tournesols comme le montre la figure 6.En
revanche, la qualité de la séparation ad ventice-tournesol dépend de la valeur seuil de départ de recherche de
l’algorithme (fixée par l’utilisateur).
4
Figure 1: Example of an aerial image from a sunflower field.
The paper is structured as follows. Section 2 presents
the proposed approach. Information about the gen-
eration of synthetic datasets used in the experiments
is provided in Section 3 and the results of the experi-
ments are reported in Section 4. Section 5 concludes
and gives perspectives on future works.
2 THE METHOD
2.1 Analyzing the Spatial Relationships
Crop fields usually exhibit a geometrical design. The
rows of a crop field are indeed usually parallel to
each other and evenly spaced. In addition, crops are
planted on the basis of a target density which induces
an even distance between two consecutive plants.
One main theme of this paper is to underline the
interest of researching and exploiting information on
the geometry of the objects in the images to be an-
alyzed. For crop fields images, in order to estimate
the inter-rows and inter-plants distances, the method
presented begins with (i) isolating the green areas of
the images; then (ii) rotating the images enough for
the rows to be collinear with the Y axis; and, finally,
(iii) applies a Fourier Transform (FT) analysis on the
signal produced by projecting the coordinates of the
green pixels on the X and Y axis.
2.1.1 Image Segmentation
Before estimating the inter-rows and inter-plants dis-
tances, it is necessary to identify the areas of the im-
ages corresponding to plants. To that end, we used
the vegetation index Excess Green (ExG) in associa-
tion with Otsu’s automatic segmenting method (Otsu,
1979; Guerrero et al., 2012; Guijarro et al., 2011;
P
´
erez-Ortiz et al., 2016). At the end of the segmen-
tation process, the RGB crop fields images are trans-
formed into black and white images, referred as Otsu
images, where the white pixels are expected to corre-
spond to a plant (crop or weed).
2.1.2 Vertically Adjusting the Images
To ease the estimation of the inter-rows and inter-
plants distances, the rotation of all the images of the
datasets was computed in order for the crop rows to
be oriented along the Y axis. This method succeeds
as long as two consecutive rows do not overlap with
each other or weed do not cover all the inter-rows
space. Should this happen, one can apply a filter to
the Otsu images in order to only keep the skeleton
of the crop rows in white. This can be implemented
with, for example, the midpoint encoding suggested
in (Han et al., 2004).
2.1.3 Estimating the Inter-rows and Inter-Plants
Distances
Items 1 and 3 on Fig. 2 illustrate how a periodic
signals is detected out of a vertically adjusted Otsu
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization
689

Figure 2: Fourier Analysis on the X and Y axis. The signal processed by the Fourier Transform is made from the projection
of the white pixels of the Otsu images on the X and Y axis.
image. Since the rows are assumed to have been re-
aligned with the Y axis, the periodicity of the posi-
tions of the rows appears on the X axis: the peaks
of the density distribution of the white pixels on the
X axis mirror the positions of the rows on the im-
age (item 1). The inter-rows distance is computed us-
ing a Fourier analysis on the density distribution and
keeping the maximal frequency thus found. The inter-
plants distance is then estimated using the projections
on the Y axis of the white pixels attributed to each row
(items 3 and 4).
2.2 A Multi-Agent Approach
Just like (Hofmann., 2019) in the case of remote im-
age sensing, we advocate the use of a multi-agent sys-
tem (MAS) which takes advantage of the knowledge
gathered on the geometry in the image. In the context
of the plant counting task, we identified four types of
agents that are organized hierarchically as shown in
Fig. 3. The agent at the top of the system is called
the Director Agent (DA), then come the Row Agents
(RAs), the Plant Agents (PAs) and finally the Pixel
Agents (PXAs). Each agent of one layer either acts on
its own or receive orders from an agent of the upper
layer: there is no communication between agents of
the same layer. The environments in which the agents
act are the vertically adjusted Otsu images.
2.2.1 The Director Agent
The DA can initialize or destroy RAs according to
the predictions made using the Fourier analysis (see
2.1.3) and decide when to stop the simulation. (see
2.1.3). It is also the one that computes the inter-plants
critical distance (IPCD) (see below).
Managing the Row Agents. At the beginning of
the simulation, the DA analyses the rows detected us-
ing the Fourier analysis in an attempt to exclude the
false positives: rows that are only made out of weeds.
A special procedure is devised to do so based on the
fact that these will be positioned in between real RAs
(rows consisting in plants).
Computing the Inter-Plants Critical Distance
(IPCD). Most of the decisions of the agents depend
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
690
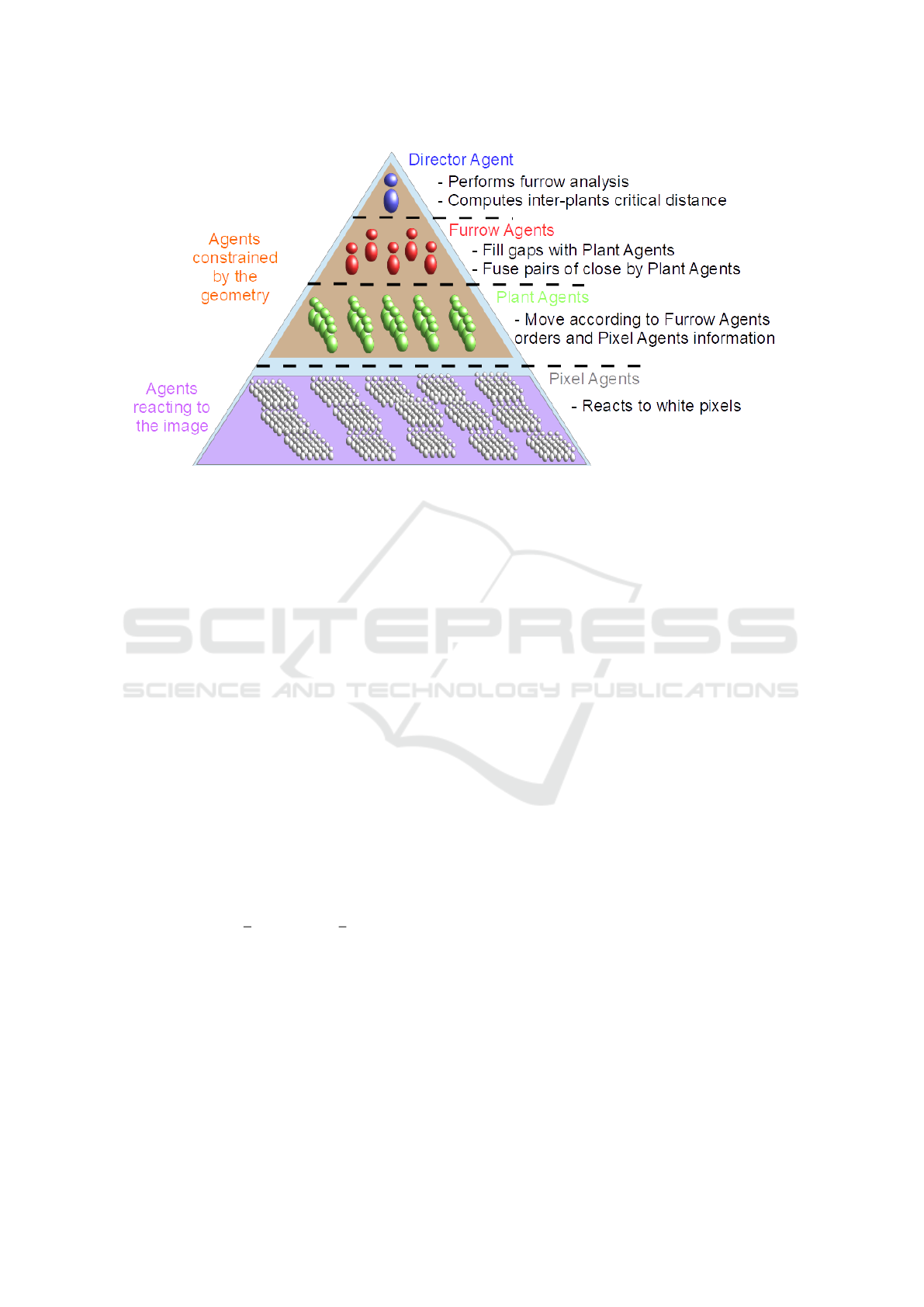
Figure 3: Hierarchical architecture of the multi-agent system.
on the IPCD. It is set equal to the maximum of the
density distribution of the inter-plant distances.
2.2.2 The Pixel Agents
The PXAs sense the Otsu images and are instantiated
by a PA. They become activated if they are positioned
on a white pixel and their position is determined by
the PA they are dependent upon.
2.2.3 The Plant Agents
The PAs are ultimately the most important agents for
the plant counting task. The number of PAs at the
end of the simulation determines the number of plants
detected in the frame of the image. Each PA has under
its supervision a group of PXAs that is centered on the
position of the PA. The role of the group of PXAs is to
guide the PA toward the most white parts of an Otsu
image (i.e. guiding them toward plants). Therefore, at
step i + 1 of the simulation, a PA moves on the mean
point of all its activated PXAs at step i:
(PA
i+1
x
,PA
i+1
y
) = (
1
n
∑
PXA∈A
PXA
i
x
,
1
n
∑
PXA∈A
PXA
i
y
)
(1)
with A the set of activated PXAs. The x and y are
the positions of the agents. Finally, a PA can decide
to decrease or increase its sensing area by eliminating
PXAs or by initializing new PXAs. In our simula-
tions, we set the goal of the PA to have between 20%
and 80% of its PXAs activated.
2.2.4 The Row Agents
RAs are instantiated by the DA according to the rows
detected by the Fourier Analysis (Fig. 2, item 2). In
turn, each RA first initializes as many PAs as were
detected using the Fourier analysis (Fig. 2, item 4).
Because the Fourier analysis may miss plants at the
edges of the rows detected, additional PAs are evenly
spaced at 1.1ν times the IPCD, ν being the PAs fusing
factor (see next paragraph). At each simulation’s step,
RAs eliminate the PAs that are located in black areas
of the Otsu image: PAs with less than a proportion δ
of activated PXAs .
Filling and Fusing PAs. A RA may consider that
the distance between two consecutive PAs is either too
large or too small. It then decides to either fill in the
gaps with new PAs of fuse the two involved PAs:
Decision =
Fill if |PA
i+1
y
− PA
i
y
| > µ IPCD
Fuse if |PA
i+1
y
− PA
i
y
| < ν IPCD
(2)
with µ and ν the filling and fusing factor respectively.
Constraining PAs Movements. In a crop field, the
rows usually exhibit a linear shape, aligned with the Y
axis when adjusting the images (Section 2.1.2). The
plants that are part of the same row are thus expected
to be aligned. As a consequence, a RA can constrain
the moves of the PAs that it supervises in order to keep
them as aligned as possible.
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization
691

2.2.5 Running the Simulation
The simulation consists in a sequence of actions that
the agents carry out in a deterministic order (Algo. 1).
The final count of the plants occurs when the number
of PAs remains constant.
Algorithm 1: Simulation.
Input: max nb steps, µ, ν, δ, π
1 initialize DA, RAs, PAs, PXAs
/* Sec. 2.2.1 */
2 AnalyseRows(π)
3 ComputeIPCD()
4 AnalyseRowsEdges(ν, IPCD)
5 StopSimu ←− False
6 RE Eval ←− False
7 i ←− 1
8 while
i ≤ max nb steps & StopSimu = False do
/* Sec. 2.2.3 */
9 MoveToMeanPoint()
/* Sec. 2.2.4 */
10 ConstrainPAsXMovement()
11 FillOrFusePAs(µ, ν, IPCD)
/* Sec. 2.2.3 */
12 AdaptSize()
/* Sec. 2.2.4 */
13 DestroyLowActivityPAs(δ)
14 if Nb PAs
i
− Nb PAs
i−1
= 0 then
15 if RE Eval = False then
16 DA ComputeIPCD()
17 RE Eval ←− True
18 else
19 StopSimu ←− True
20 end
21 else
22 RE Eval ←− False
23 end
24 i←− i+1
25 end
3 SYNTHETIC DATASETS
Training an automatic counting algorithms requires
large data sets with at the very least hundreds of im-
ages, with thousands of objects, each of them to be
labeled. In the case of plant counting, there are no
publicly available data sets. This entails a lack of la-
beled training data and a problem of reproducibility
Figure 4: Parameters involved in the placement of crops
along rows. The red labels are parameters undergoing ran-
domization.
of experiments.
The solution we adopted is to use a virtual envi-
ronment engine to generate artificial crop fields. They
are indeed nowadays able to generate very realistic
images, and the labelling of the objects is automatic.
We chose to use the game engine Unity (Technolo-
gies, 2020).
3.1 The Field Generator
The parameters mainly manage the surface of the
field, the virtual crop, the weed, the sun and the sim-
ulated drone. Figure 5 describes the UAV flight plan.
Crops position in the field are based on several pa-
rameters shown in red on Figure 4. All parameters
except the growth probability are drawn randomly.
Weeds cannot be expected to follow any geometry at
the scale of the field but they can regularly be found
clustered together. This is why we used the Perlin
Noise (Perlin, 1985) to generate spaces on the crop
field where the weeds would be present.
3.2 Content of the Datasets
Plants may overlap as the plants grow. It is assumed
that the overlap interferes with the signal used by the
counting method, and previous studies on automatic
counting of plants from UAV images have raised that
the difficulty of the task increases with the proportion
of crop overlap (Garc
´
ıa-Mart
´
ınez et al., 2020). In or-
der to assess this effect, we generated three datasets
with three different levels of overlap between crops.
The plants are separated (S) from each other in the
first dataset; they overlap for some leaves and do not
overlap for others (B) in the second datase; and fi-
nally, the third dataset exhibits overlap (O) between
neighbouring plants. The dataset (S) is considered
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
692
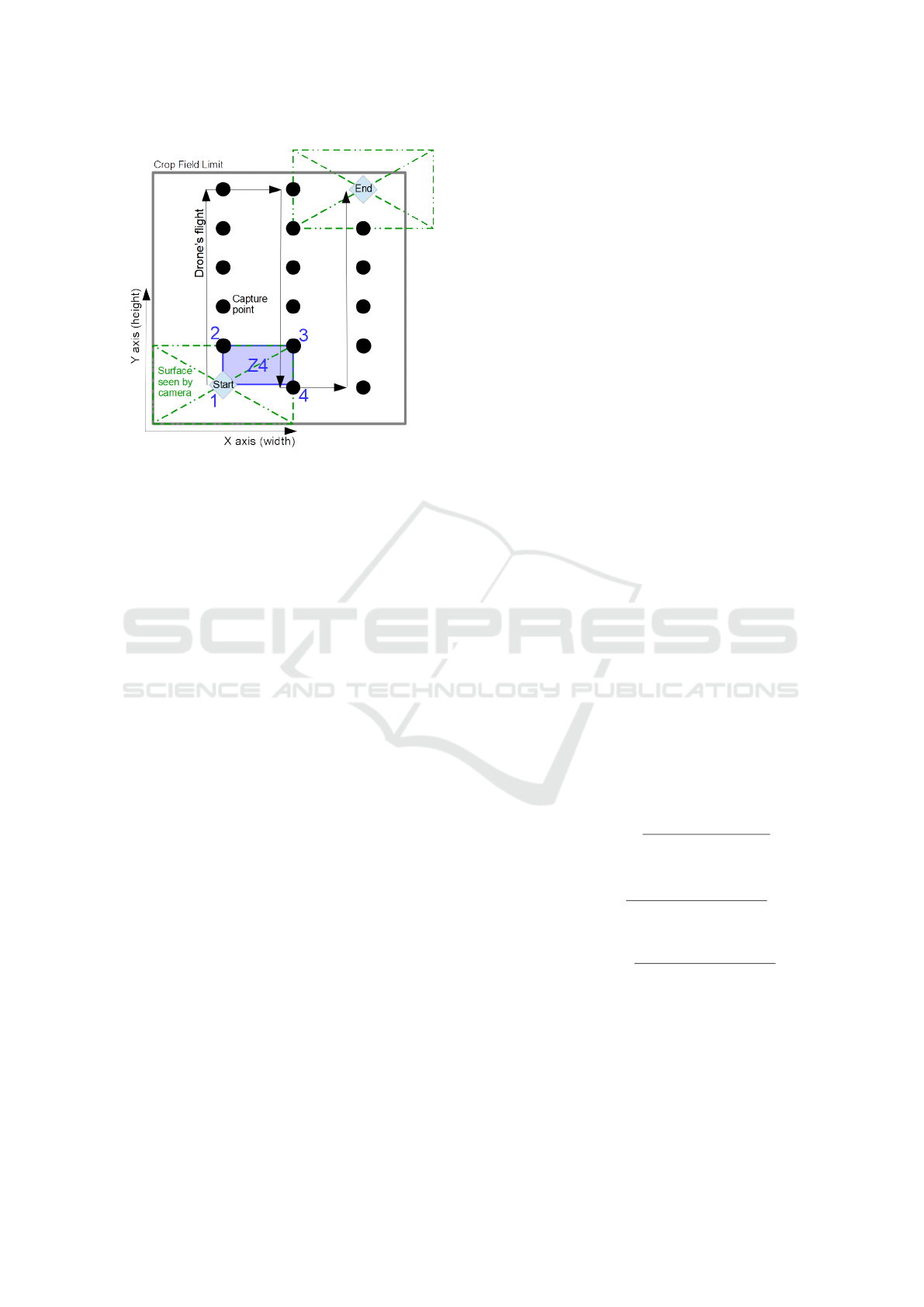
Figure 5: Scheme of a UAV flight plan above the virtual
crop field. The start position is calibrated to capture the
bottom left corner of the field. The other capture points
are calculated depending on the image overlap configured
on the X and Y axis (here, 50% on both). As a result, the
images of the upper and right limit of the field may go over
these. The area named Z4 is subsequently captured four
times, one by each of the four captured points numbered in
blue.
easy, (B) is intermediate and (O) is difficult. Aside
from varying the scale of the plant 3D model to sim-
ulate its growth, the parameters used to generate the
fields are similar for all three datasets. Each crop field
was generated with an inter-rows distance of 70 cm
and an inter-plants distance of 20 cm with 5% vari-
ability. This yields a target average of 7 plants/m
2
which matches typical sunflower crop fields. The
plant growth probability was set to 0.8. The Perlin
noise threshold used to generate the surfaces where
weed grows was set to 0.75 while the weed growth
probability was set to 0.6. In each of these datasets,
100 crop fields were generated, and from each of them
four images were taken. So, each dataset contains
400 images which amounts to 1200 images in total.
To take pictures of the virtual fields, we simulated a
short drone flight plan that covers the lower left cor-
ner of the field as it moves once along the height and
width of the field (see the blue numbers on Fig. 5).
We have configured the motion of the simulated drone
to overlap the image by 50% along both their height
and width, as is usual with images from UAVs.
Fig. 6 gives an example of an image of a virtual
crop field. Fig. 6b is the same image after an Otsu
filter has been applied and the image has been reori-
ented so that the rows are aligned with the Y axis. (see
sections 2.1.1 and 2.1.2).
4 EXPERIMENTS AND RESULTS
The method we propose is a two steps method with
the first phase that detects and estimates the spatial
structure, and the second phase which, starting from
this structure identifies the objects.
The goal of the experiments carried out is three-
fold. First, to assess the performance of the first
phase alone in counting plants, second, to measure
the added value of the second phase based on a multi-
agent approach, and, third, to look at the gain of per-
formance, if any, when parts of a field are covered
by multiple passes of the UAV and a redundancy of
information follows (see area Z4 in Figure 5 for an
example).
First, we present the rules under which we consid-
ered that the method had successfully detected a plant
and how the counting performance was measured.
4.1 Assessing the Results
In order to measure the performance of the Fourier
analysis alone, the rule is that if the plant position,
which is known in synthetic data sets, falls within a
40 square pixel area of a predicted position, then this
is counted as a true positive (TP).
For the MAS, we considered that a PA detected a
plant if that plant was located within the sensing area
defined by the PXAs of the PA. If two PA happen to
detect the same plant, then only one PA is counted as
TP and the other is counted as a false positive (FP).
Additionally, a PA or a prediction from the Fourier
analysis that does not contain a plant in their sensing
area are also considered as FP. Finally, a plant that has
not been detected is counted as a false negative (FN).
In addition to these three indicators, three scores are
computed:
Detection Accuracy =
T P
Total number of PAs
(3)
Detection Recall =
T P
Total number of Plants
(4)
Counting Accuracy =
Total number of PAs
Total number of Plants
(5)
These scores are later referenced as DAc, DR and CA
respectively.
In the following, we compare the performances of
the Fourier analysis alone (Section 4.2), of the multi-
agent approach from a single image of the area (Sec-
tion 4.3), and of a technique that takes into account
that several images (up to four) can cover a given area
(Section 4.4).
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization
693

(a) An image of a virtual field (b) Otsu image vertically adjusted
Figure 6: Example of a an synthetic image and its vertically adjusted Otsu image.
Figure 7: Example of row detection thanks to Fourier anal-
ysis. The histogram in yellow results from the projection of
the white pixels of an Otsu Image on the X axis. The blue
parts of the histogram are the detected rows.
4.2 Detecting the Spatial Structure and
Counting
As explained in Section 2.1.3, we use Fourier analysis
to approximate the spatial structure in an image. We
first try to discover the rows and then to locate plants
within the presumed rows. This relies on the analy-
sis of the density distribution of the projection of the
white pixels from an Otsu image on the X or Y axis
(Fig. 7 shows such a density distribution (in yellow)
as well as the detected peaks (in blue)). Notice that
the largest peaks indeed correspond to rows, but that
weeds can also produce peaks, albeit smaller ones.
The results obtained for the three scores are sum-
marized in Table 1 in the line Fourier while Fig. 8
provides details on the distribution of the counting ac-
curacies (CAs) (violet boxes indicate the results of the
Fourier analysis).
It is apparent that the Fourier analysis alone tends
to underestimate the number of plants on dataset (S),
(the well separated plants) (12% on average) while
over estimating this number on datasets (B) (between
separated and overlapping) (by 3%) and (O) (overlap-
ping plants) (by 7% on average). Why is it so?
For dataset (S), the plants are well separated, but
this also entails that the peaks of the histogram used
by the Fourier analysis are rather narrow, and one con-
sequence is that if a peak is slightly off a predicted
position by the analysis, it may be entirely missed by
it. This may result in ignoring existing rows or plants
within a row.
For datasets (B) and (O), the overlapping leaves
between plants induces noise that leads the Fourier
analysis dedicated to the plants identification to find a
slightly higher frequency than the actual target. This
results in overestimating the number of plants. Over-
all, still, taking into account that the Fourier analysis
is in fact used only to estimate the spatial relationships
between plants on crop fields, the counting results are
surprisingly good.
4.3 Effect of the Multi-Agents Analysis
The multi-agent stage initializes the PAs using the
predictions made by the detector of spatial relation-
ships, and then let the PAs evolve and converge to-
wards presumed plants. The question is: how much
this can improve the counting performance? In which
way can it correct false positives and false negatives?
In our experiments on plant counting, we ran
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
694

Figure 8: Results on Counting Accuracy (CA). The colors of the whisker boxes indicate the method used to count the number
of plants. With Fourier Img. 1 we counted the plants with the Fourier analysis on one imagefor each of the 100 fields of
the dataset. The same images were used with MAS Img. 1 that counts the plants using the MAS. MAS Img. All and MAS
Img. All Aligned are methods that exploit the redundancy when several images cover the same area in a field. The black dots
represent outliers. The boxes’ lower and upper limits indicate the 0.25-th and 0.75-th percentile respectively. The median is
represented on each box by a white line mark while the mean is represented as a black line mark. The grey diamond represents
the interval of confidence. Non-overlapping diamond between pairs of boxes are equivalent to rejecting the null hypothesis of
equal means of a two-sample t-Test.
the simulations with the following parameters values:
max nb steps = 50, µ = 1.5, ν = 0.5, δ = 0.01 and
π = 0.0001. max nb steps was set as an upper limit of
the number of steps of the simulation which has never
been reached in our experiments. The values µ and
ν were chosen for geometric reasons. ν is the PAs’
fusion factor; a value of 0.5 means that two PAs per-
fectly positioned on consecutive plants will absorb a
wrongly positioned PA in-between them which is de-
sirable. µ is the PAs’ filling factor; if two PAs are per-
fectly positioned on plants but another plant has been
missed in-between them, then a value of 2 should al-
low its detection. However a value of 1.5 proved to
be better during tests. Lowering the values of δ and
π will lead the simulation to overestimate the number
of plants while raising them will lead to underesti-
mation. These values were optimized by repeatedly
testing the system on training synthetic datasets. The
reported results have been obtained on test datasets,
different from the training ones.
As can be seen in Fig. 8 and in Table 1, the re-
sults show that the multi-agent phase significantly im-
proves the counting performance. For the (S) and (B)
datasets, the mean value is closer to the value 1 (ap-
proximately 0.98 instead of 0.87 for the Fourrier anal-
ysis alone), which means that the estimated number
of plants is close to the correct one, and the confi-
dence interval is much narrowed (standard deviation
of 0.04 instead of 0.11). The gain is less pronounced
on the (O) dataset. Even if the distribution of the re-
sults are very similar between the Fourier analysis and
the multi-agent one (violet and orange boxes on Fig.
8), the average for the multi-agent analysis is signif-
icantly lower than the average of the Fourier analy-
sis as indicated by the fact that the grey diamonds on
the boxes do not overlap (non-overlapping diamonds
mean that the null hypothesis of equal means can be
rejected using a 2-sample t-Test).
It is thus apparent that the proposed two step
method: first detecting a structure, then using a MAS
to refine the counting, gives very promising results.
But, most of the areas of a crop field are covered by
several different images from UAVs (up to four times
in the example of Figure 5). Is it possible then that
even these good results can be improved by resorting
to the redundancy thus offered?
4.4 Exploiting Image Overlapping
A common practice when acquiring images of crop
fields is to let consecutive images overlap each other.
One of the main motivation for this is to avoid that
plants located at the edges of an image are only par-
tially visible, and thus ignored. Another motivation is
the hope that the mistakes made on an image can be
compensated on another image that partially covers
the same area. In our case, the synthetic datasets were
built with 50% overlap on the height and width of the
images. As an illustration, in our example, it exists
an area (e.g. Z4) that is covered by all four images.
The results when combining the informations coming
from the four images are presented under the name
MAS Img. All in Table 1 and Fig. 8. Another vari-
ant of this algorithm (called MAS Img. All Aligned)
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization
695

Table 1: Average scores results on the three datasets. Standard deviation is in parenthesis. Values were rounded to the second
digit.
Datasets Separate (S) Border (B) Overlap (O)
Scores DAc DR CA DAc DR CA DAc DR CA
Fourier
Img. 1
0.93
(0.04)
0.82
(0.11)
0.88
(0.12)
0.87
(0.06)
0.89
(0.05)
1.03
(0.04)
0.81
(0.05)
0.86
(0.05)
1.07
(0.05)
MAS Img.
1
0.99
(0.01)
0.97
(0.07)
0.97
(0.07)
0.98
(0.02)
0.98
(0.04)
1.00
(0.04)
0.83
(0.05)
0.86
(0.06)
1.03
(0.07)
MAS Img.
All
0.99
(0.01)
0.99
(0.01)
1.00
(0.01)
0.99
(0.02)
1.00
(0.01)
1.01
(0.02)
0.88
(0.04)
0.96
(0.02)
1.10
(0.05)
MAS Img.
All Aligned
0.99
(0.01)
0.98
(0.01)
0.99
(0.02)
0.99
(0.02)
0.98
(0.02)
1.00
(0.02)
0.90
(0.04)
0.94
(0.03)
1.05
(0.05)
was introduced with the motivation that aligning the
N images covering a given area could help the clus-
tering procedure to gather relevant PAs.
The results reported in Table 1 and in Figure 8
show that combining information from the analysis
of several images brings improvement in the count-
ing accuracy for the (S) and (B) datasets. For the (O)
dataset, the variant MAS Img. All Aligned is to be pre-
ferred to the MAS Img. All method, while MAS Img.
All is better than MAS Img. All Aligned on the (S)
and (B) datasets. If the counting accuracy of the com-
bined method is slightly lower than for the method
analyzing only one image for the (O) datasets (1.05
instead of 1.03), on the other hand the detection accu-
racy (DA) is significantly improved from 0.83 to 0.90
which means that the plants are better recognized.
Overall, combining information from several im-
ages seems to be a good strategy.
4.5 Application to Real Images
We also applied the method to a subset of the dataset
of real crop fields provided by Christophe Sausse
from Terres Inovia.
In total, the dataset contains 2111 non-labelled
images from which we randomly extracted 50 that
were manually labeled and used to test our method.
The images mix areas where the plants are well sepa-
rated and areas where the leaves of one plant overlap
with those of its neighbors in the same row. In ad-
dition, the drone captured the original images at an
altitude of 30m (compared to 10m for the synthetic
data) and the sunflowers overlap with many weeds in
some images, making it sometimes difficult, even for
a human, to visually identify the sunflowers. It is thus
fair to say that the chosen subset of data contains im-
ages comparable to the ones of the (S), (B) and (O)
synthetic datasets.
Our method yielded an average counting accuracy
of 1.03 for a standard deviation of 0.12 on the 50 im-
ages subset. The detection accuracy and detection re-
call fared at 0.87 and 0.90 respectively for a standard
deviation of 0.14 for both. These scores are at least as
good as the ones reported in the state of the art (see
Section 4.6). Furthermore, they are quite close to the
results obtained on the synthetic dataset even if the
standard deviation is larger.
This confirms that using synthetic datasets for tun-
ing the method we propose is a promising procedure,
effectively leading to good results on real data.
4.6 The State of the Art
Counting objects can be done through the detection of
the objects, or it can be done from a density estimate,
usually directly from an analysis at the pixel level of
the image. In the first case, object detection relies
either on some prior knowledge of the shape of the
objects to be counted or on machine learning to rec-
ognize objects. Deciding which templates are useful
is generally difficult, while using supervised learning
requires (very) many labeled images and large com-
puting resources, for example using deep neural net-
works. On the other hand, density estimation seems
simpler but it still requires large training sets and
yields coarser estimates of the number of objects in
an image. Both approaches, object-based and density-
based, are subject to large errors when objects are oc-
cluded or overlapping.
For plant counting, (Garc
´
ıa-Mart
´
ınez et al., 2020)
is an example of the template approach. In their maize
plant counting experiments, they selected 4 to 12 tem-
plates and used a Normalized Cross-Correlation tech-
nique to estimate the number of plants. The method
requires that representative plants in the images be
chosen, and no recipe is given for this. They obtain a
percentage or error of 2.2% when using 12 templates,
but acknowledge that the performance drops to 25.7%
when the plants overlap.
In their paper, (Ribera et al., 2017) use deep neural
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
696

networks to learn how to recognize sorghum plants.
They describe the rather involved preprocessing and
formatting steps that are necessary before learning
can take place. They also had to develop a technique
to increase the number of labelled training images.
Learning itself took between 50,000 and 500,000 it-
erations which entails a very heavy computing load.
They obtained a Mean Absolute Percentage Error of
6,7%. It is not possible to know if the data sets used
included overlapping plants or not.
The density-based approach is illustrated in
(Gn
¨
adinger and Schmidhalter, 2017). They first elim-
inate what can be presumed to be weeds and para-
sitic signals using a clustering method. Then they set
thresholds on different wavelengths in order to clas-
sify pixels as belonging to plants or not. This requires
some fine tuning. They obtain error rates around 5%
with fairly large standard deviations. Here too, plant
overlapping leads to a deterioration in performance.
5 CONCLUSIONS
With the generalization of devices for taking images,
it is increasingly critical to develop reliable and trans-
parent image vision systems (Olszewska, 2019). This
paper has introduced a new method to count objects
while satisfying these constraints. It is applicable
when objects are spatially organized according to a
regular pattern. The method first detects the pattern
and then uses it to seed agents in a MAS. The method
is simple, requiring no complex fine tuning of param-
eters, the tricky definition of templates or costly learn-
ing. In fact, it requires very modest computing re-
sources. In a series of extensive experiments on con-
trolled data sets and real aerial images of crop fields,
the method yielded state of the art or better perfor-
mance when the objects are well-separated and ex-
ceeded the best known performances when the objects
overlap. For future work, we plan to test the method
on other other object counting problems with differ-
ent geometries such as counting people in stadiums
or performance halls or vehicles in parking lots.
ACKNOWLEDGEMENTS
We thank Terres Inovia for sharing their dataset of
crop fields images captured with a UAV.
REFERENCES
Garc
´
ıa-Mart
´
ınez, H., Flores-Magdaleno, H., Khalil-
Gardezi, A., Ascencio-Hern
´
andez, R., Tijerina-
Ch
´
avez, L., V
´
azquez-Pe
˜
na, M. A., and Mancilla-Villa,
O. R. (2020). Digital count of corn plants using im-
ages taken by unmanned aerial vehicles and cross cor-
relation of templates. Agronomy, 10(4):469.
Gn
¨
adinger, F. and Schmidhalter, U. (2017). Digital counts
of maize plants by unmanned aerial vehicles (uavs).
Remote sensing, 9(6):544.
Guerrero, J. M., Pajares, G., Montalvo, M., Romeo, J., and
Guijarro, M. (2012). Support vector machines for
crop/weeds identification in maize fields. Expert Sys-
tems with Applications, 39(12):11149–11155.
Guijarro, M., Pajares, G., Riomoros, I., Herrera, P., Burgos-
Artizzu, X., and Ribeiro, A. (2011). Automatic seg-
mentation of relevant textures in agricultural images.
Computers and Electronics in Agriculture, 75(1):75–
83.
Han, S., Zhang, Q., Ni, B., and Reid, J. (2004). A guid-
ance directrix approach to vision-based vehicle guid-
ance systems. Computers and Electronics in Agricul-
ture, 43(3):179–195.
Hofmann., P. (2019). Multi-agent systems in remote sens-
ing image analysis. In Proceedings of the 11th In-
ternational Conference on Agents and Artificial Intel-
ligence - Volume 1: ICAART 2019, pages 178–185.
INSTICC, SciTePress.
Olszewska, J. (2019). Designing transparent and au-
tonomous intelligent vision systems. In Proceed-
ings of the 11th International Conference on Agents
and Artificial Intelligence - Volume 2: ICAART 2019,
pages 850–856. INSTICC, SciTePress.
Otsu, N. (1979). A Threshold Selection Method from
Gray-Level Histograms. IEEE Transactions on Sys-
tems, Man, and Cybernetics, 9(1):62–66. Conference
Name: IEEE Transactions on Systems, Man, and Cy-
bernetics.
P
´
erez-Ortiz, M., Pe
˜
na, J. M., Guti
´
errez, P. A., Torres-
S
´
anchez, J., Herv
´
as-Mart
´
ınez, C., and L
´
opez-
Granados, F. (2016). Selecting patterns and features
for between-and within-crop-row weed mapping us-
ing uav-imagery. Expert Systems with Applications,
47:85–94.
Perlin, K. (1985). An image synthesizer. ACM SIG-
GRAPH Computer Graphics, 19(3):287–296.
Ribera, J., Chen, Y., Boomsma, C., and Delp, E. J. (2017).
Counting plants using deep learning. In 2017 IEEE
global conference on signal and information process-
ing (GlobalSIP), pages 1344–1348. IEEE.
Technologies, U. (2020). Unity 2019.4.1.
Zou, Z., Shi, Z., Guo, Y., and Ye, J. (2019). Object Detec-
tion in 20 Years: A Survey. arXiv:1905.05055 [cs].
arXiv: 1905.05055.
Using Agents and Unsupervised Learning for Counting Objects in Images with Spatial Organization
697
