
Generating Reactive Robots’ Behaviors using Genetic Algorithms
Jesus Savage
1
, Stalin Mu
˜
noz
2
, Luis Contreras
3
, Mauricio Matamoros
1
, Marco Negrete
1
,
Carlos Rivera
1
, Gerald Steinbabuer
2
, Oscar Fuentes
1
and Hiroyuki Okada
3
1
Bio-Robotics Laboratory, School of Engineering, National Autonomous University of Mexico (UNAM), Mexico
2
Graz University of Technology, Austria
3
Advance Intelligence and Robotics Research Center, Tamagawa University, Japan
Keywords:
Evolutionary Algorithms, Robot Behaviors, Finite State Machines, Hidden Markov Models.
Abstract:
In this paper, we analize and benchmark three genetically-evolved reactive obstacle-avoidance behaviors for
mobile robots. We buit these behaviors with an optimization process using genetic algorithms to find the one
allowing a mobile robot to best reactively avoid obstacles while moving towards its destination. We compare
three approaches, the first one is a standard method based on potential fields, the second one uses on finite
state machines (FSM), and the last one relies on HMM-based probabilistic finite state machines (PFSM). We
trained the behaviors in simulated environments to obtain the optimizated behaviors and compared them to
show that the evolved FSM approach outperforms the other two techniques.
1 INTRODUCTION
In the many years of research on robot navigation sev-
eral algorithms for robot exploration in unknown en-
vironments have been proposed, many of them based
on Finite State Machines (FSM) (Fraundorfer and
Scaramuzza, 2012). In these algorithms, a robot with
negligible errors in both, the sensor readings and its
motion, under the same initial conditions, should be-
have always in the same way due to the deterministic
nature of its control algorithm.
While this behavior fits most applications, the ex-
ploration of new environments makes desirable for
the robot to behave differently every time under simi-
lar conditions (for example, to construct a complete
map of a scene by aggregating unexplored areas).
Therefore a probabilistic finite state machine is used.
Consequently, we built these state machines using a
modified version of Hidden Markov Models (HMM)
and we proposed an optimization process to find the
best HMM model using Genetic Algorithms (GA).
The paper is organized as follows: in Section 2
we present the related work in this area. Section 3
presents the standard robot behavior of potential fields
to be compared with the behaviors proposed in this
paper. Meanwhile, in Section 4 we detail how to cre-
ate navigation behaviors using FSM. Then, in Sec-
tion 5 we present the Probabilistic Finite State Ma-
chines (PFSM) using HMM. Further, in Section 6 we
explain how we got the fittest behaviors for the po-
tential fields approach, the FSM and the PFSM using
Genetic Algorithms. Finally, in Section 7 we detail
the experiments and results, and close in Section 8
with the conclusions of this work.
2 RELATED WORK
Brooks proposed a new robotics paradigm to con-
trol robots in which their behaviors are built using
Augmented Finite State Machines (AFSM) (Brooks,
1986). To Brooks, by connecting together the AFSM,
each one containing a behavior, emergent intelligence
can be achieved by a robot.
Simulated emergent patterns from a collection of
artificial agents refers back to Barricelli (1954). In
this work, as refereed by Fogel (2006), Barricelli sim-
ulates an early version of cellular automaton in which
numbers, that live in one and two dimensional worlds,
interact following simple rules. His computer simula-
tions showed that such simple rules are sufficient to
give rise to regular patterns which he called “organ-
isms”.
Meanwhile, starting in 1962, Lawrence J. Fogel
and colleagues successfully applied artificial evolu-
tion algorithms to the problem of finding predictions
in sequences of symbols in finite alphabets (Fogel,
698
Savage, J., Muñoz, S., Contreras, L., Matamoros, M., Negrete, M., Rivera, C., Steinbabuer, G., Fuentes, O. and Okada, H.
Generating Reactive Robots’ Behaviors using Genetic Algorithms.
DOI: 10.5220/0010229306980707
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 698-707
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

2006). In their work, they used finite state machines
to represent the behavior of the agent (Fogel, 2006).
This early evolutionary algorithm uses a population
of states machines and exploits several kinds of mu-
tations to generate the offspring. The task to solve
was to predict whether the next number in a sequence
will be a prime number or not. The algorithm quickly
learned to discriminate even numbers and numbers di-
visible by three as non-prime and achieved a 78% of
prediction accuracy.
In (Negrete et al., 2018), from a red, green, blue
and distance (RGBD) sensor, as the Kinect, a differ-
ent map representation is used where the free space is
divided into regions using vector quantization where
each centroid represents a node in a topological map
useful for robot navigation, where quantization has
been proven to be the state-of-the-art for scaling the
search space (Guo et al., 2020). A probabilistic map
representation has been proposed in (Savage et al.,
2018) where we represent the current pose with a Hid-
den Markov Model and determine the next navigation
node by incorporating new laser readings and the all
trajectory information into the model; therefore, al-
though reactive, this approach produces smooth tra-
jectories. Probabilistic representation given by a Hid-
den Markov Model from a number of sensor read-
ings and robot displacements have been proven use-
ful for robot localization and navigation (Shahriar and
Zelinsky, 1999), (Shahriar and Zelinsky, 2014), and
(Mohanan and Salgaonkar, 2020). Furthermore, path
planning in mobile robots is a very well known prob-
lem and Genetic Algorihms have been widely applied
to solve this problem (Yakoubi and Laskri, 2016) and
(Yakoubi and Laskri, 2018).
3 ROBOT BEHAVIORS USING
POTENTIAL FIELDS
In this type of behavior, the robot is modeled as a
particle that is under the influence of two potential
fields, one attracts it towards the destination, while an-
other takes him away from obstacles (Latombe et al.,
1991). Obstacles exert repulsive forces, while the
goal destination generates and attraction force. The
robot moves through a potential field on the steepest
slope until it brings it to the destination.
The robot position in the environment is
q
n
= [x
n
,y
n
], and the potential field exerted on the
robot at that point is:
U(q) = U
atr
(q) +U
rep
(q)
the gradient of the potential field:
F(q) = ∇U(q) =
∂U
∂x
ˆ
i +
∂U
∂y
ˆ
j
using the “steepest descent” technique the next posi-
tion of the robot is given by:
q
n
= q
n−1
− δ
i
f
q
n−1
where δ
i
are constants that determine the size of the
robot advance, sometimes it remains fixed.
f
q
n−1
is a unit force vector in the direction of
the gradient:
f (q
n−1
) =
F(q
n−1
)
F(q
n−1
)
The robot moves following the steepest slope of the
potential field, given by the forces of attraction and
repulsion:
F(q
n−1
) =F
atr
(q
n−1
) + F
rep
(q
n−1
)
q
n
=q
n−1
− δ
i
f
q
n−1
3.1 Attraction Field
The destination that the robot needs to reach is:
q
dest
= (x
dest
,y
dest
)
We define the attractive field of parabolic type as:
U
atr
(q) =
1
2
ε
1
|q − q
dest
|
2
where ε
1
it is a constant that modulates the field and
is found empirically. The attractive force in q is:
∇U
atr
(q) = ε
1
[q − q
dest
] = F
atr
(q)
3.2 Repulsive Fields
We define the repulsive field as:
U
rep
(q) =
1
2
η
1
|q − q
obs
|
−
1
d
0
2
where q
obs
= (x
obs
,y
obs
) is the obstacle centroid
position. This repulsion field applies when
|q − q
obs
| ≤ d
0
. Otherwise, it is considered that the
obstacle does not generate any repulsive force be-
cause it is too far away. Where η is a constant that
modulates the field and is found empirically. Then
the potential field is:
Generating Reactive Robots’ Behaviors using Genetic Algorithms
699

∇U
rep
(q) = −η
1
|
q − q
obs
|
−
1
d
0
q − q
obs
|
q − q
obs
|
3
!
= F
rep
(q)
The repulsion force generated by the obstacle k
F
rep
k
(q) = 0 if
q − q
obs
k
> d
0
the total force exerted on the robot in the position q
is:
F(q) = F
atr
(q) +
N
∑
k=1
F
rep
k
(q)
where N is the number of obstacles in the environment
where the robot navigates.
The new position of the robot is given by the fol-
lowing equation:
q
n
= q
n−1
− δ
i
f
q
n−1
For the potential field approach it is necessary to find
the constants that control this behavior, namely η,ε
1
and d
0
.
4 DETERMINISTIC FINITE
STATE MACHINES
In mobile robots, behaviors are often used for navi-
gation (Arkin, 1998). These methods can be imple-
mented using finite state machines FSM.
Figure 1 shows a simple behavior for a robot
whose goal is to avoid obstacles on its path. The robot
has two proximity sensors, one on its left (LS) and one
on its right side (RS), allowing it to detect obstacles.
The sensors are binary and return 1 when an obstacle
is detected within their range. The robot has two mo-
tors for propulsion in differential pair configuration.
Figure 1 shows the algorithm state machine
(ASM) for the obstacle avoidance behavior shown in
the same figure.
There are many ways to physically implement the
obstacle avoidance behavior using of state machines.
One option is to use standard memories. Figure 2
shows an architecture of a state machine that uses a
memory. In it, the ASM is encoded in a look-up ta-
ble that contains the next state and the outputs of each
state. The inputs of the state machine, sensors, and
the next state are linked together to form the address
of the memory that contains the next state and outputs
for the present state.
This type of architecture can be implemented in a
FPGA for robots with small computational resources,
but also can be implemented using a look-up table in
Figure 1: Robot avoiding an obstacle.
Figure 2: Implementation of an State Machine Using Mem-
ories.
high level languages as C/C++, Python, etc. Using
this method, depending of the number of states N
s
,
each state is represented by N
b
= dlog
2
(N
s
)e bits. The
number of memory locations used is 2
(N
s
+N
i
)
, where
N
i
is the number of inputs. Figure 1 shows the ASM
with 12 states and with two inputs.
Table 1 shows the coding of the actions the mobile
robot can perform:
Using this method, each state is represented by
N
b
= dlog
2
(N
s
)e bits where N
s
is the number of states.
The number of memory locations used is 2
(N
s
+N
i
)
,
where N
i
is the number of inputs.
Table 1 below shows the coding of the actions the
mobile robot can perform:
The number of bits to encode the outputs is N
o
=
dlog
2
(Num.Actions)e Thus each memory location re-
quires N
b
+ N
o
bits to indicate the next state and the
robot’s actions. The obstacle avoidance algorithm
shown in Figure 1, requires four memory locations
to represent each state, to select the memory location
the 4 bits that represent the states and the 2 bits for the
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
700

Table 1: Robot Action Coding.
Robot Action Binary Code
Stop 000
Forward 001
Backward 010
Turn Left (45
◦
) 011
Turn Right (−45
◦
) 100
Turn Left (45
◦
) and Forward 101
Turn Right (45
◦
) and Forward 110
Turn Right Twice (90
◦
) and For-
ward
111
inputs are concatenated to form the memory address,
then the total number of memory locations necessary
is 64, with a width of each location of 7 bits.
For the ASM shown in Figure 1, the state 0 has
one conditional output (Forward) shown inside the
oval. This output is generated when both inputs LS
and RS are zero. For any the other cases the robot
will Stop. The inputs LS and RS represent the digital
value from the sensors. Table 2 shows the encoding
of this state 0.
Table 2: AFSM MEMORY.
Pr. State S
t
Inputs Next State S
t+1
Outputs
A B C D LS RS ABCD b
2
b
1
b
0
0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 0 1 0 0 0 1 1 0 0 0
0 0 0 0 1 1 0 1 0 1 0 0 0
As we can see in Table 2 changing one of the bits of
the memory will change the algorithm hance also the
robot’s behavior. For instance, in the third row of Ta-
ble 2, if two bits of the memory contents are randomly
changed as in Table 3, the state machine will jump to
est
11
instead of state est
3
given the same conditions,
generating therefore a Turn Right output instead of a
Stop one.
Thus, one of the goals is to find the best configura-
tion of the memory content to get a robot’s behavior.
Table 3: Third raw State 0 AFSM MEMORY.
Pr. State S
t
Inputs Next State S
t+1
Outputs
A B C D LS RS ABCD b
2
b
1
b
0
0 0 0 0 1 0 1 0 1 1 1 0 0
Without or small errors in the sensing and in the
movements the robot, under the same conditions, that
is, with the same initial pose, x
o
,y
o
,θ
o
and same des-
tination x
d
,y
d
, the robot should behave always in the
same way, because the algorithm that control it it
is deterministic. While this type of behavior is de-
sired for some robotics applications, in others it would
be desired that the robot behaves in a different way
each time under similar conditions, thus a probabilis-
tic FSM is used. This kind of state machines are build
using HMM, as it is explained in the next section.
5 PROBABILISTIC FINITE STATE
MACHINES
The algorithm of a Probabilistic Finite State Ma-
chines (PFSM) depends on random variables (Vidal
and Thollard, 2005) and therefore it can be model us-
ing Hidden Markov Models (HMM). In this section,
we explain our approach to this problem, referred as
the Behavior HMM, and later it is explained how
we optimize this model through Genetic Algorithms
(GA).
5.1 Hidden Markov Models
A HMM is a doubly stochastic process, in which the
set of states S is hidden and the set of symbols O are
observable (Rabiner and Juang, 1986). The stochas-
tic process exhibits the Markov property, that is, the
probability of reaching a particular next-state depends
only on the current state and not in the whole history
of the process. States are not directly observable and
can only be inferred by their probabilistic emission of
observable symbols.
The observation symbols are V = (V
0
,V
1
,...,V
L
).
And the probability of emitting symbol k being in
state i, b
i
(k) = p(O
t
= k|S
t
= i), where S
t
= i means
the Markov chain was in state i at time t, and O
t
= k
means the observed symbol at time t was k.
The transition probability defines the probability
of taking the transition from a particular state to an-
other state or itself. Where a
i j
is the probability of
taking a transition from state i to state j:
a
i j
= p(S
t+1
= j|S
t
= i).
Also included is the initial state distribution probabil-
ity:
π
i
= P[s
1
= S
i
], 1 <= i <= N
A standard Markov model is formed by a structure
called λ = (A,B,π), where A and B are two matrices
with components: A = (a
i j
), B = (b
ik
) for all i, j and
k, with N states and L observation symbols; and π.
Generating Reactive Robots’ Behaviors using Genetic Algorithms
701

5.2 Discrete Hidden Markov Models for
Robots Behaviors
In this work, we propose a probabilistic representa-
tion of the algorithm’s FSM by a HMM, in this, the
states are part of a probabilistic state machine, that
have the similar characteristics as the states in the
deterministic ones, but taking into consideration the
stochastic behavior of the system. There is a direct
matching between the inputs of the FSM, becoming
observations in a HMM, and also for the transitions
from one state to another. The inputs in the determin-
istic FSM become the observation in the HMM. That
is, the observation symbols are formed by quantized
version of the input sensors as is explained in Sec-
tion 5.5.
The decision to change to another state depends on
the present state S
t
, the observed symbol O
t
at time t
and the λ model of the HMM.
Given a HHM model λ = (A, B, π) with N states
and L observation symbols, and with the system been
in states {S
1
...S
t−2
,S
t−1
}, past observation sequence
{O = O
1
,O
2
,...,O
t−1
} and a new observation O
t
, to
find which will be the next state s
j
at time t, it is nec-
essary to calculate the maximum transition probabil-
ity of going from any state i to j:
δ
t
( j) = max
1<i<N
P[S
1
...S
t−1
= i, O
1
,...,O
t
|λ] (1)
where
1 < j < N
that is, δ
t
( j) keeps the highest probability of reaching
state j, and this calculation is done with all states 1 <
i < N. This is similar to the calculations used by the
Viterbi algorithm (Viterbi, 1967; Rabiner and Juang,
1986) to find the best sequence of states that reaches
a particular state, the difference with our approach is
that we want to predict which is the most probable
next state. Then the most probable next one is:
S
t
= j = arg max
1<i<N
[δ
t
(i)]
This equation can be calculated recursively, with the
following procedure:
Initialization:
δ
1
(i) = π
i
b
i
(O
1
), 1 < i < N, (2)
S
1
= j = arg max
1<i<N
[δ
1
(i)] (3)
Recursion:
δ
t
( j) = max
1<i<N
[δ
t−1
(i)a
i j
]b
j
(O
t
), 1 < j < N (4)
S
t
= j = arg max
1<i<N
[δ
t
(i)] (5)
Figure 3 shows each state having a δ
t−1
at time t − 1
and at time t, for each state j, δ
t
( j) needs to be calcu-
lated again, by taking into consideration the transition
probabilities a
i j
and the symbols probabilities b
j
(O
t
).
Figure 3: Best next state j given by δ
t
( j).
Thus, matrix B needs to be created taking into con-
sideration equation Equation (4).
5.3 Action Symbols
In our approach, we incorporate the outputs of the
FSM as action symbols attached to the states of the
HMM. The action symbols are:
U = { Stop, Forward, Backward, Turn Left (45
◦
),
Turn Right (−45
◦
), Turn Left and Forward, Turn
Right and Forward, Turn Right twice (−90
◦
) and For-
ward} = {U
0
,U
1
,U
2
,U
3
,U
4
,U
5
,U
6
,U
7
}.
Figure 4 shows the structure of the HMM taking into
consideration the sensor symbols (FSM inputs) and
the action symbols (FSM outputs).
Figure 4: Extended version of an HMM, the sensor inputs
and the robot’s actions are incorporated in the HMM.
Thus, we needed to incorporate matrix C, into the
robot’s behavior model HMM λ = (A,B,C,π), that
contains the probability of generate an action AC
t
=
U
k
given that we are on state S
t
= j and with observa-
tion O
t
= Vi:
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
702

Let C = c
l,k
such as l = concat ( j,i) where concat
is a bit concatenation operation, j is the index of the
state S
t
and i is the index of observation O
t
c
l,k
= p(U
t
= k|S
t
= j,O
t
= i).
To form the C matrix’s rows indices is a concatenation
of the state’s index j together with the observation in-
dex i.
We call this new type HMM model λ = (A,B,C,π)
an extended HMM (EHMM).
5.4 Execution of the Behavior HMM
To start the execution of the probabilistic state ma-
chine, given the robot’s behavior model EHMM, λ =
(A,B,C,π), first the robot needs to make an observa-
tion at time t = 1, O
1
, and then to calculate the fol-
lowing equations to find the first state:
δ
1
(i) = π
i
b
i
(O
1
), 1 < i < N, (6)
S
1
= j = arg max
1<i<N
[δ
1
(i)] (7)
Once the first state is calculated then the output ac-
tion needs to be found, due to the stochastic nature of
the probabilistic state machine, the output is not just
generated using the action symbol with the highest
probability in that state, but by generating a random
number and comparing in which region it is of all pos-
sible outputs in a particular case. In our approach, the
row of matrix C to be used in the calculation of the
probabilities of the output is by a concatenation of the
state’s index j together with the observation index i.
With this row, a range of the outputs symbol proba-
bilities is created, as it is shown in Table 4.
Table 4: Symbol output range table.
Output i Range r
0 [0,c
ji,1
) r
1
1 [c
ji,1
,c
ji,1
+ c
ji,2
) r
2
... ... ...
k [
k−1
∑
m=1
c
ji,m
,
k
∑
m=1
c
ji,m
) r
i
... ... ...
K-1 [
K−1
∑
m=1
c
ji,m
,1] r
K
A random number x with uniform density between 0
and 1 is generated and using Table 4 it is checked in
which range this number is, if r
i
≤ x < r
i+1
then the
first state output is AC
1
= U
i
.
i f 0 ≤ x < r
1
the output 0 is generated, that is Stop
i f r
k
≤ x < r
k+1
the output k is generated
This procedure continues for t > 1 with:
δ
t
( j) = max
1<i<N
[δ
t−1
(i)a
i j
]b
j
(O
t
), 1 < j < N (8)
S
t
= j = arg max
1<i<N
[δ
t
(i)]
And generating AC
t
in the same way as it was de-
scribed before.
Summarizing for execution of robots’ behaviors
using EHMMs:
INPUTS:
EHMM λ = (A,B,C,π)
Robot’s initial pose: X
1
= (x
1
,y
1
)
Robot’s final pose: X
d
= (x
d
,y
d
)
OUTPUTS:
Robot’s actions: AC = { stop, forward,
backward, turn left (45
◦
), turn right (−45
◦
), turn left
and go forward, turn right and go forward and turn
right twice (−90
◦
) and go forward}
t = 1
O
1
= quantized sensor data in X
1
δ
1
(i) = π
i
b
i
(O
1
), 1 < i < N,
S
1
= j = arg max
1<i<N
[δ
1
(i)]
AC
1
= Action(S
1
,C)
WHILE {X
t
6= X
d
}
t = t + 1
X
t
= Movement(X
t−1
,AC
t−1
)
O
t
= quantized sensor data in X
t
δ
t
( j) = max
1<i<N
P[S
1
...S
t−1
= i, O
1
,...,O
t
|λ],
1 < j < N
S
t
= j = arg max
1<i<N
[δ
t
(i)]
AC
t
= Action(S
t
,C)
ENDWHILE
The robot’s behavior with a PFSM using a model
EHMM λ = (A, B,C,π) can be optimized by several
methods: Waum-Welch, Genetic Algorithms, etc. In
our research, we optimized the model using GA.
Generating Reactive Robots’ Behaviors using Genetic Algorithms
703

5.5 Range Quantizer
In our research a range vector quantizer is used, which
has N range centroids vectors that best represent the
majority of the sensor readings. To create the range
quantizer first the robot collects range vectors.
S
t
= (r
t
1
,r
t
2
,...,r
t
i
,...,r
t
M
)
Each r
t
i
represents distance from the range sensor to
the objects in line of sight at time t.
The robot navigates in the environment to collect
range vectors by taking readings with its range sen-
sors:
S
1
= (r
1
1
,r
1
2
,...,r
t
i
,...,r
1
M
)
S
2
= (r
2
1
,r
2
2
,...,r
t
i
,...,r
2
M
)
...
S
J
= (r
J
1
,r
J
2
,...,r
J
i
,...,r
J
M
)
Given a set of N
J
vectors of range readings, a set
of centroids C = (C
1
,C
2
,...,C
N
) that best represent
them, is found using the vector quantization Lloyd’s
algorithm called LBG (Linde-Buzo-Gray).
The robot gets a reading with the range sensor, ob-
taining a range vector S
t
and to quantize it, it is com-
pared with each of the centroids of the range quantizer
C. And it is choose the centroid vector C
i
, that is the
closest vector to it.
The centroid C
i
is chosen if:
d(S
t
,C
i
) < d(S
t
,C
j
) ∀ j
d(S
t
,C
t
)
is a function that measures the similitude of the vec-
tors S
t
and the C vectors of the quantizer.
In this case the similitude function uses the Eu-
clidean distance. For our experiments we use 8 range
centroids.
The orientation of the light source relative to the
robot is quantized with 8 quadrants.
Also the intensity of the light source is quantized
in 4 values.
6 EVOLUTIONARY ROBOTICS
Evolutionary Robotics (ER) refers to the field of in-
quiry comprising methods for automatically generat-
ing artificial brains and morphologies for autonomous
robots that are inspired by Darwinian evolutionary
theory (Floreano et al., 2008). Some applications
of ER include (Konig, 2015): (i) obstacle avoid-
ance (Banzhaf et al., 1997; Seok et al., 2000; Nelson
et al., 2009), (ii) wall following (Banzhaf et al., 1997),
(iii) object seeking (Banzhaf et al., 1997), (iv) active
vision (Marocco and Floreano, 2002), and (v) object
detection.
Our research is concentrated on how to evolve
robots algorithms for object seeking and obstacle
avoidance using the concept of deterministic and
probabilistic state machines. To achieve this goal
FSM and Extended Hidden Markov Models (EHMM)
robot’s behavior model, λ = (A,B,C,π), are evolved
to find individuals that are able to look for light source
beacon while avoiding obstacles using Genetic Algo-
rithms.
A GA performs operations over populations of so-
lutions that resemble sexual reproduction, mutation
and artificial selection of apt individuals in a given en-
vironment. Often classified within the realm of search
and optimization algorithms, it has been argued they
are robust techniques that trade off efficacy and effi-
ciency when dealing with different environments by
exploiting intrinsic parallelism. The population dy-
namics allows for the emergent convergence to spe-
cific regions of the search space as well as implicit
clustering of solutions. Genetic algorithms have been
successfully applied to a variety of engineering and
scientific problems. In particular to the evolution of
robot controllers and behaviors.
1. First a population is generated randomly, with L
individuals B
1
,B
2
,...,B
L
, in which each individual’s
chromosome is a string of binary numbers that repre-
sents the behaviors B
i
= {011011...0101}.
The string is separated into small segments that
represent the parameters that define the behavior, B
i
=
{bh
i
0
bh
i
1
... bh
i
j
... bh
i
k
}.
2. Each individual (chromosome) is evaluated giv-
ing a fitness value according to the individual’s per-
formance. The fitness function evaluates how well the
robot’s behavior performed his operation, and it takes
into consideration several aspects of its performance.
Some of them are: the distance between the last
position reached and the goal, the number of times
the robot hits an obstacle, the number of steps used to
reach the goal and also the number of times the robot
went backward, etc.
The Fitness function used in our experiments is:
Fitness = K1 ∗ N ∗ D
o
+ K2 ∗ N/D
d
+ K3 ∗ S
d
The mobile robots have N
k
discrete times to go from
an origin to a destination. N
s
is the number of steps of
that the robot used to reach a destination. If the robot
did not reach the destination N
s
= N
k
.
For the first term of the Fitness function, N =
(N
k
− N
s
+ 1)
D
o
is the distance between the last position of the
robot X and the robot’s original position X
o
: D
o
=
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
704

kX − X
o
k, that means that a robot that uses few steps
to reach the destination and it gets faraway from its
original position will be well evaluated.
For the second term D
d
is the distance between the
last position of the robot and the destination goal, plus
distance of to the destination using the shortest path
found by the Dijkstra algorithm in a topological map
of the environment. This is to make the robot to learn
that even that is closed to an obstacle, but if there is an
obstacle in front of it, it needs to surround the obsta-
cle. The Dijkstra algorithm is only used for training,
when the final behavior is obtained, is no longer used
by the robot navigation system.
D
d
= kX − X
d
k + DistDi jkstra(X ,X
d
)
DistDijkstra (X, X
d
) is a function that measures the
distance of the nodes of a topological that joins the
last position of the robot X and the destination posi-
tion X
d
using the Dijkstra algorithm. Dividing N by
D
d
makes this function to reward individuals that get
closed to the destination.
The third term of the Fitness function is the stan-
dard deviation σ, S
d
, of the robot’s positions X
i
be-
tween the robot’s original position X
o
and its final po-
sition X. This term is to measure if the robot went
into a local minimum.
Constants K
1
,K
2
and K
3
are used to tone the per-
formance of the robot according to its specifications.
The value of the constants Ks where found empiri-
cally: K
1
= 10, K
2
= 20 and K
3
= 11.
3. Select the best individuals according to their fit-
ness function and create a new population with indi-
viduals generated trough evolutionary’s operators (se-
lection, crossover and mutation).
4. The offspring and their selected parents form
the new population.
5. Iteration from 2 to 4 is repeated for M genera-
tions or until the overall fitness criteria between two
generation is less than a given ε, or total number of
generations N
g
is achieved.
• Evolving Robot Behaviors using Potential Fields.
For the potential field approach we evolved some of
the constants of this behavior: η, ε
1
and d
0
.
Each of these constants where represented by 16
bits, 1 bit for the sign, 7 bits for the integer part and
8 bits for the fraction one. Thus, each individual was
represented by 48 bits, and the population consist of
100 individuals. This requires 48 bits per individual’s
chromosome.
• Evolving FSM Behaviors.
The algorithm of the FSM was implemented using the
concept described before of building state machines
using memories or look-up tables, as is shown in Fig-
ure 2. Each Evolved Finite State Machines (EFSM)
had 16 states (4 bits). The inputs of the sensors are
structurated in the following way: 16 range values are
introduced in a range vector quantizer with eight cen-
troids, with the index of the closest centroid, the quan-
tized quadrant index and the quantized light source,
they are concatenated to form the input. This input
is concatenated with the next state to form the next
state index for the look-up table. Thus this index is
formed by concatenating 2 bits of the quantized light
source, 3 bits of the quantized orientation, 3 bits of
the index of the range VQ and 4 bits that represent
the next state, in total giving 12 bits. Then the size of
the look-up table is 4096 rows of a size of 7 bits each,
4 bits that represent next state and 3 bits to indicate
the output. This requires 28672 bits per individual’s
chromosome.
• Evolving EHMM Behaviors.
The extended HMM requires to find each of the com-
ponents of its model λ = (A,B,C, π). For the EHMM
behaviors we defined each individual chromosome as
follows: number of states N
s
= 16, number of obser-
vation symbols N
l
= 256, number of outputs N
o
= 8,
and the number of bits per variable N
b
= 8.
Then, there are N
s
probabilities variables for vec-
tor π, N
s
N
s
for matrix A, N
s
N
l
for matrix B and
(N
s
N
l
)N
o
for matrix C. In total the number of bits per
individual is
N
t
= N
b
(N
s
+ N
s
N
s
+ N
s
N
l
+ N
s
N
l
N
o
).
N
t
= 8x(16 + 16x16 + 16x256 + (16x256)x8) =
297,088
7 EXPERIMENTS AND RESULTS
We tested the behaviors using our simulation module,
in which range readings to obstacles can be simulated,
as well as, the robot’s movements. The simulated mo-
bile robot had a 240 degree simulated range readings,
as the laser Hokuyo URG
04LXUG01, selecting the
readings with a separation of 15 degrees each, making
16 range readings in each sensing.
The destination goal is described by a yellow cir-
cle; the free space is green; the obstacles are described
by polygons in red; the robot is a black circle and the
proximity sensor readings are represented by blue col-
ors.
For the genetic algorithm, we had a population of
100 individuals and the evolution lasted 900 gener-
ations. The robot’s radio was r = 3cm. During the
Generating Reactive Robots’ Behaviors using Genetic Algorithms
705
execution of the GA, noise was added to the move-
ments of the robot, as well as, to the sensors: for the
linear movement it was added a random variable with
a uniform density function of [−0.004,0.004] meters,
for rotation movement a uniform density function of
[−0.03927,0.03927] radians and for the range sen-
sor a Gaussian random variable with mean µ = .004
and standard deviation σ = .0004. The behaviors,
to avoid obstacles, were tested in 13 simulated envi-
ronments, with different sizes, configurations, robot’s
starting positions and goal destinations. There were
two types of environments: one with random gener-
ated polygons; and office type environments, similar
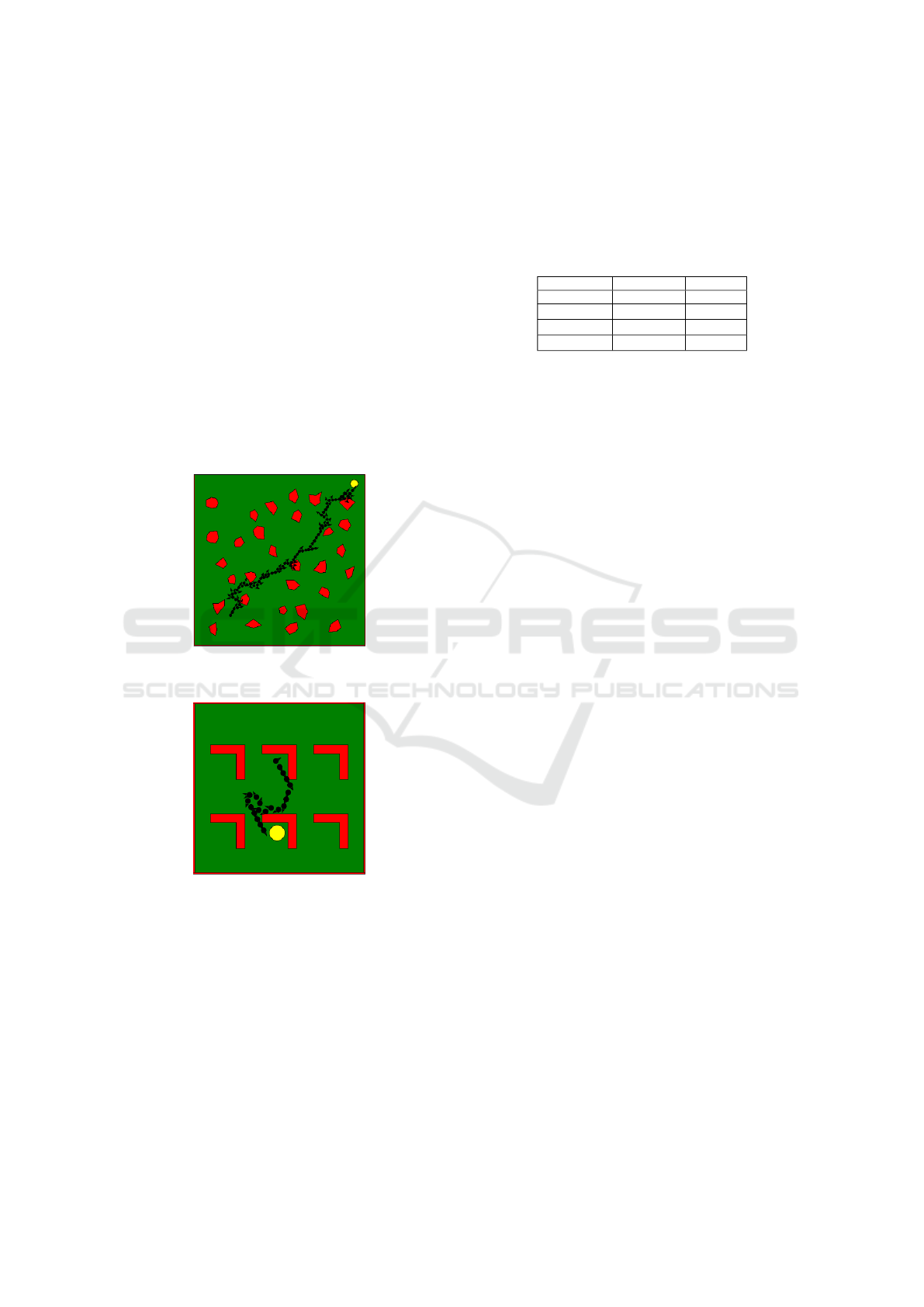
to the shown in figures 5 and 6
The Figures 5 and 6 show evolved behaviors with
a robot starting in a initial position and reaching a des-
tination, a light source, in two types of environments.
Figure 5: The path found by an evolved robot’s behavior in
a polygon type environment.
Figure 6: The path found by an evolved robot’s behavior in
a office type environment.
Table 5 shows the average performance of the best
individuals for each of the behaviors in polygon and
office type environments, during 1000 trials. As we
can see in both cases the best performance is done by
the FSM behavior.
Despite the fact that all the behaviors performed
worst in the office type environments, we can see
that in this type of environments the performance
of the behaviors with memory, the FSM and PFSM
are much better than the potential field behavior ap-
proach, that does not have any memory. In polygonal
type environments the FSM is better than the potential
field approach by 14.8 % and for office type environ-
ments is by 21.94 %.
Table 5: Best average fitness of the behaviors in two differ-
ent type environments: Polygons and Office.
Env. Polygons Env. Office
Behavior Fitness Fitness
FSM 4267 2541
PFSM 4243 2153
POTENTIALS 3635 1983
8 CONCLUSIONS
We proposed the optimization of the methods for po-
tential fields and state machines to achieve mobile
robot behaviors, the state machines were built us-
ing deterministic and probabilistic methods. For the
deterministic FSM we proposed an architecture of a
state machine that uses a look-up table that encodes
the algorithm, that is, the robot behavior. This look-
up table contains the next state and the outputs of each
state. The inputs of the state machine, sensors, and
the next state are linked together to form the index
of the look-up table that contains the next state and
outputs for the present state. For the PFSM a modi-
fied version of Hidden Markov Models, that we called
EHMM, was used to encode the mobile robot behav-
ior. We also proposed how to find the optimum be-
haviors for potential field approach, the FSM and the
PFSM using Genetic Algorithms. Our experiments
proved that the obtained robots’ behaviors, when they
are used for robot navigation, that the deterministic
FSM outperforms the potential field approach and the
PFSM.
The robot’s behaviors using FSMs and the PFSMs
outperforms the ones using potential fields, mainly
because they are more complex machines and they are
able to stay out of local minima and can retain some
memory and learn how to get out of these. Meanwhile
the FSM outperforms the PFSMs behaviors due to
the type of environments where the experiments were
tested and the type of noise that was added to the sen-
sory data, as well as, to the robot’s movements. For
future work it is necessary to test with more strong
noise and more complex HMMs, with more states and
observation symbols to see if their performance im-
proves.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
706

REFERENCES
Arkin, R. (1998). Behavior-Based Robotics. MIT Press.
Cambridge. MA 1998.
Banzhaf, W., Nordin, P., and Olmer, M. (1997). Generating
adaptive behavior using function regression within ge-
netic programming and a real robot. In Proceedings of
the Second International Conference on Genetic Pro-
gramming, San Francisco, pages 35–43.
Barricelli, N. A. (1954). Esempi numerici di processi di
evoluzione. volume 6, pages 45–68. Methods.
Brooks, R. (1986). A robust layered control system for a
mobile robot. In IEEE Journal of Robotics and Au-
tomation, volume 2, pages 14–23. IEEE.
Floreano, D., Husbands, P., and Nolfi, S. (2008). Evolution-
ary robotics. In Springer handbook of robotics, pages
1423–1451. Springer.
Fogel, D. B. (2006). Nils barricelli-artificial life, coevolu-
tion, self-adaptation. In Computational Intelligence
Magazine, volume 1, pages 41–45. IEEE.
Fraundorfer, F. and Scaramuzza, D. (2012). Visual odome-
try [tutorial]. In IEEE Robotics and Automation Mag-
azine, volume 19, pages 78–90. IEEE.
Guo, R., Sun, P., Lindgren, E., Geng, Q., Simcha, D.,
Chern, F., and Kumar, S. (2020). Accelerating large-
scale inference with anisotropic vector quantization.
Konig, L. (2015). In Complex Behavior in Evolutionary
Robotics. Walter de Gruyter GmbH & Co KG, 2015.
Latombe, J.-C., Lazanas, A., and Shekhar, S. (1991). Robot
motion planning with uncertainty in control and sens-
ing. Artificial Intelligence, 52(1):1 – 47.
Marocco, D. and Floreano, D. (2002). Active vision and
feature selection in evolutionary behavioral systems.
In From animals to animats, volume 7, pages 247–
255.
Mohanan, M. G. and Salgaonkar, A. (2020). Probabilistic
Approach to Robot Motion Planning in Dynamic En-
vironments. SN Computer Science, 1(181).
Negrete, M., Savage, J., and Contreras, L. (2018). A
Motion-Planning System for a Domestic Service
Robot. SPIIRAS Proceedings, 60(5):5–38.
Nelson, A. L., Barlow, G. J., and Doitsidis, L. (2009). Fit-
ness functions in evolutionary robotics: A survey and
analysis. volume 57, pages 345–370. Elsevier.
Rabiner, L. and Juang, B. (1986). An introduction to hidden
markov models. volume 3, pages 4–16. Assp maga-
zine, IEEE.
Savage, J., Fuentes, O., Contreras, L., and Negrete, M.
(2018). Map representation using hidden markov
models for mobile robot localization. In 13th Interna-
tional Scientific-Technical Conference on Electrome-
chanics and Robotics.
Seok, H.-S., Lee, K.-J., and Zhang, B.-T. (2000). An on-
line learning method for objectlocating robots using
genetic programming on evolvable hardware. In Pro-
ceedings of the Fifth International Symposium on Ar-
tificial Life and Robotics, volume 1, pages 321–324.
Citeseer.
Shahriar, S. and Zelinsky, A. (1999). Mobile robot naviga-
tion based on localisation using hidden markov mod-
els. In Australasian Conference on Robotics.
Shahriar, S. and Zelinsky, A. (2014). Robot localization
from minimalist inertial data using a hidden markov
model. In IEEE International Conference on Au-
tonomous Robot Systems and Competitions.
Vidal, E. and Thollard, F. (2005). Probabilistic finite-state
machines. In IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, volume 27, pages 1013–
1025.
Viterbi, A. (1967). Error bounds for convolutional codes
and an asymptotically optimum decoding algorithm.
In IEEE Transactions on Information Theory, vol-
ume 13, pages 260–269.
Yakoubi, M. A. and Laskri, M. T. (2016). The path planning
of cleaner robot for coverage region using genetic al-
gorithms. In Journal of Innovation in Digital Ecosys-
tems, volume 3.
Yakoubi, M. A. and Laskri, M. T. (2018). Genetic algo-
rithm based approach for autonomous mobile robot
path plannings, procedia computer science. 127:180–
189.
Generating Reactive Robots’ Behaviors using Genetic Algorithms
707
