
Moving Solitons in Coupled Bragg Gratings with a Uniform
and a Nonuniform Bragg Gratings
Md. Bellal Hossain and Javid Atai
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
Keywords:
Soliton, Kerr Nonlinearity, Dispersive Reflectivity.
Abstract:
We consider the dynamics of moving solitons in a dual-core nonlinear system which consists of a uniform
Bragg grating coupled with a nonuniform Bragg grating where nonuniformity is provided by dispersive re-
flectivity. It is found that moving solitons fill the entire bandgap. We also consider the effect of the dispersive
reflectivity on the stability of the moving solitons.
1 INTRODUCTION
Fiber Bragg grating (FBG) is a periodic optical
medium which offers a strong dispersion that can
be counterbalanced by the Kerr nonlinearity of op-
tical fiber results a gap soliton (GS). Theoretically,
it has been shown that GSs can travel at any veloc-
ity in the range of zero to the speed of light within
the medium (Aceves and Wabnitz, 1989; De Sterke
and Sipe, 1994; Christodoulides and Joseph, 1989).
The existence of moving GSs have been confirmed
experimentally (Eggleton et al., 1999; Mok et al.,
2006; De Sterke et al., 1997; Taverner et al., 1998).
So far, the moving GSswith the velocity of 23% of
the speed of light speed in the medium have been
observed (Mok et al., 2006). The existence and
stability of GS have also been considered in other
systems such as dual-core systems (Atai and Mal-
omed, 2000; Mak et al., 1998a; Mak et al., 2004;
Chowdhury and Atai, 2014), waveguide arrays (Dong
et al., 2011; Mandelik et al., 2004), photonic crystals
(Monat et al., 2010), nonuniform gratings (Atai and
Malomed, 2005; Baratali and Atai, 2012; Neill et al.,
2008), quadratic nonlinearity (Conti et al., 1997; Mak
et al., 1998b), and cubic-quintic nonlinearity (Atai
and Malomed, 2001; Dasanayaka and Atai, 2013).
Slow moving Bragg solitons may be used to develop
several optical devices such as optical delay lines, op-
tical switches and logic gates (Krauss, 2008; Fraga
et al., 2006).
The interest in dual-core and dual-mode nonlin-
ear systems arises from their rich dynamical char-
acteristics (Atai and Chen, 1992; Mak et al., 2004;
Chen and Atai, 1998; Chen and Atai, 1995). Addi-
tionally, the nonlinear dual-core systems with non-
identical cores are known to offer better switching
characteristics than the ones with identical cores (Atai
and Chen, 1992; Bertolotti et al., 1995). Also, it has
been found that dispersive reflectivity in FBGs may
significantly influence on the solitons’ stability (Atai
and Malomed, 2005; Neill et al., 2008; Baratali and
Atai, 2012; Chowdhury and Atai, 2014). Hence, in
this work, we consider the existence and stability of
moving solitons in a dual-core system with the Kerr
nonlinearitywhere one core has a uniform Bragg grat-
ing and the other one is equipped with a Bragg grating
with dispersive reflectivity.
2 THE MODEL
Propagation of light in a dual-core system in the pres-
ence of Kerr nonlinearity where one core has a uni-
form Bragg grating and the other one has a Bragg
grating with dispersive reflectivity is described by the
following system of differential equations (Hossain
and Atai., 2020):
i(u
1t
+ u
1x
) + u
1
1
2
|u
1
|
2
+ |v
1
|
2
+λu
2
+ v
1
+ mv
1xx
= 0,
i(v
1t
− v
1x
) + v
1
1
2
|v
1
|
2
+ |u
1
|
2
+λv
2
+ u
1
+ mu
1xx
= 0,
i(u
2t
+ u
2x
) + u
2
1
2
|u
2
|
2
+ |v
2
|
2
+λu
1
+ v
2
= 0,
i(v
2t
− v
2x
) + v
2
1
2
|v
2
|
2
+ |u
2
|
2
+λv
1
+ u
2
= 0.
(1)
32
Hossain, M. and Atai, J.
Moving Solitons in Coupled Bragg Gratings with a Uniform and a Nonuniform Bragg Gratings.
DOI: 10.5220/0010229700320035
In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 32-35
ISBN: 978-989-758-492-3
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
In Eqs. (1), u
1,2
(x,t) and v
1,2
(x,t) represent the
forward- and backward-propagating waves in core 1
and core 2, respectively. λ represents the coupling
coefficient between two cores and m denotes the co-
efficient of dispersive reflectivity which accounts for
nonuniformity in the Bragg grating. m varies from 0
to 0.5, since m > 0.5 doesn’t have any physical im-
portance (Atai and Malomed, 2005).
To obtain the dispersion relation for moving soli-
tons, the system of Eqs. (1) are first transformed into
the moving frame using the transformation {X, T} =
{x− st, t} where s stands for the moving solitons’ ve-
locity. After some straiaghtforward algebraicmanipu-
lations, the following dispersion relation for the mov-
ing solitons is obtained:
Ω = ±
1+ k
2
+ λ
2
∓
1
2
m
4
k
8
− 4m
3
k
6
+4m
2
λ
2
k
4
+ 4m
2
k
4
− 16mλ
2
k
2
+ 16λ
2
k
2
+16λ
2
1
2
−mk
2
+
1
2
m
2
k
4
1
2
− sk.
(2)
Here, Ω denotes the frequency in the moving frame.
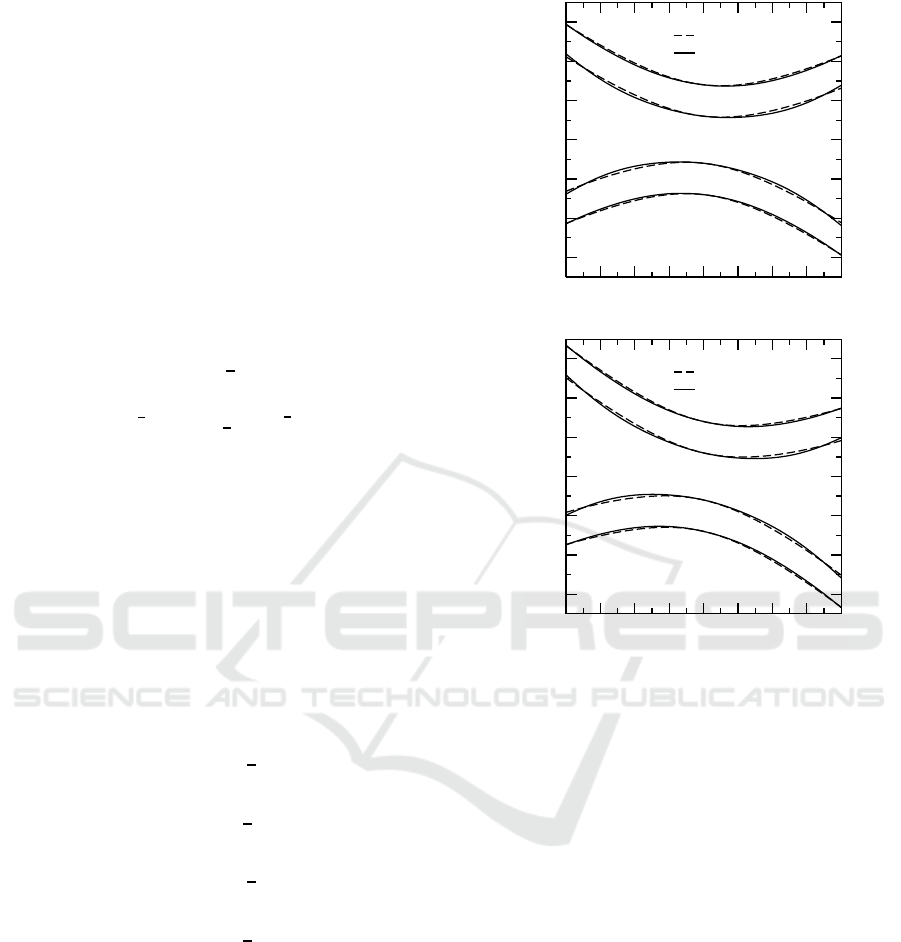
Figure 1 shows the linear spectrum in (k, Ω) plane for
different values of m.
3 SOLITON SOLUTIONS
To find the solutions for moving solitons, we sub-
stitute U(X, t) = U(X)exp(−iΩt) and V(X,t) =
V(X)exp(−iΩt) into the system of Eqs. (1) which
leads to the following system of equations:
ΩU
1
+ i(1− s)U
1X
+U
1
1
2
|U
1
|
2
+ |V
1
|
2
+λU
2
+V
1
+ mV
1XX
= 0,
ΩV
1
− i(1+ s)V
1X
+V
1
1
2
|V
1
|
2
+ |U
1
|
2
+λV
2
+U
1
+ mU
1XX
= 0,
ΩU
2
+ i(1− s)U
2X
+U
2
1
2
|U
2
|
2
+ |V
2
|
2
+λU
1
+V
2
= 0,
ΩV
2
− i(1+ s)V
2X
+V
2
1
2
|V
2
|
2
+ |U
2
|
2
+λV
1
+U
2
= 0.
(3)
Since there is no exact analytical solution for Eqs.
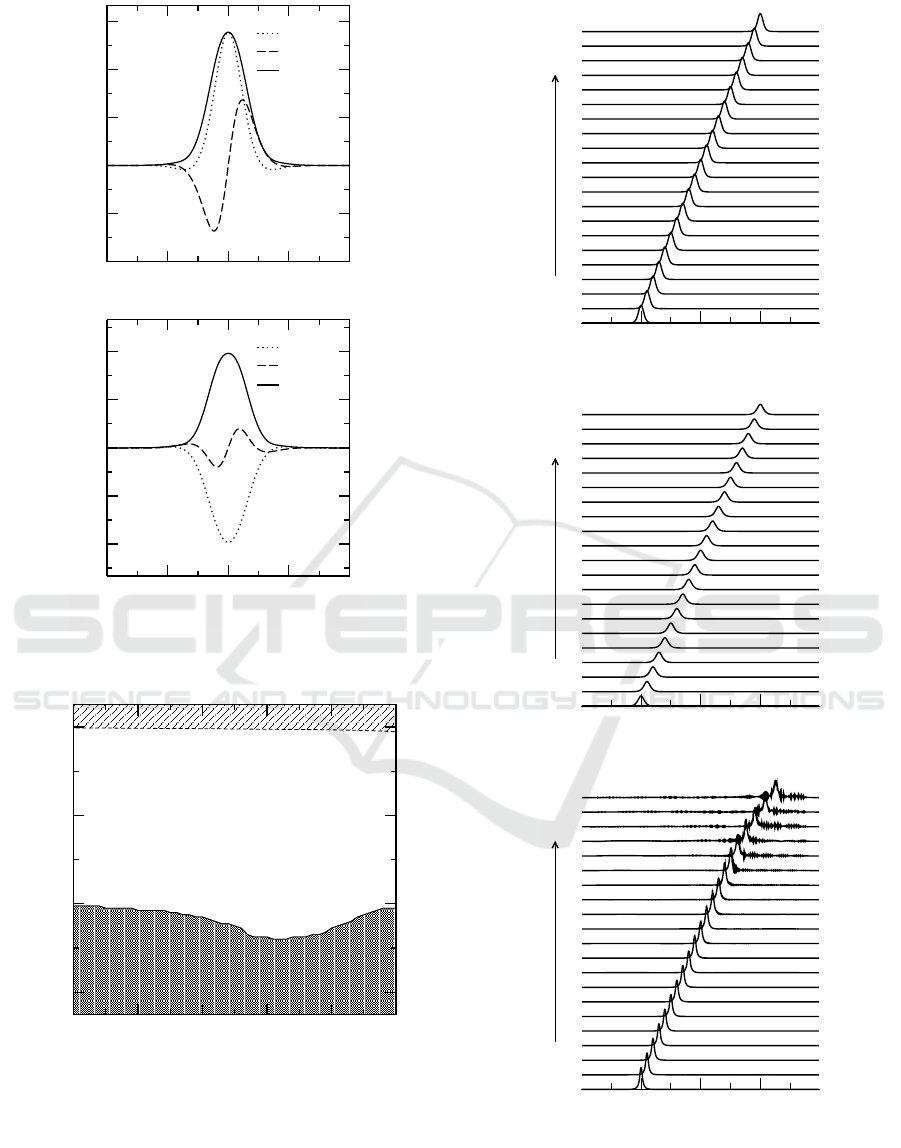
(3), the equations need to be solved numerically. Fig-
ure 2 shows examples of the moving solitons’ profile
(the real component, imaginary component, and am-
plitude of u
1
and v
1
).
4 STABILITY ANALYSIS
We have investigated the stability of solitons by nu-
merically simulating their propagation. We have
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
k
-3
-2
-1
0
1
2
3
Ω
m = 0.20
m = 0.40
(a)
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
k
-3
-2
-1
0
1
2
3
Ω
m = 0.20
m = 0.40
(b)
Figure 1: Examples of dispersion diagrams for moving
solitons for different values of dispersive reflectivity at λ =
0.40. (a) s = 0.20 and (b) s = 0.40.
found both stable and unstable solitons in the
bandgap. Fig. 3 shows some examples of the sta-
ble and unstable moving solitons. As is shown in Fig.
3(c), unstable solitons radiate some energy after some
period of time and subsequently are destroyed. Fig.
4 shows the stability diagram which summarizes the
stability of solitons in (m, Ω) plane for λ = 0.2 and
s = 0.1. A notable feature shown in this figure is that
for moderate values of dispersive reflectivity (i.e. be-
tween 0.25 and 0.35), the stable region is enlarged.
The effect and interplay of λ and the velcoity of soli-
tons on the stability of solitons are very complex and
are currently being investigated.
5 CONCLUSION
We have studied the existence and stability of moving
solitons in a dual-core system with Kerr nonlinear-
ity where one core possesses a uniform Bragg grat-
ing and another core possesses a nonuniform Bragg
Moving Solitons in Coupled Bragg Gratings with a Uniform and a Nonuniform Bragg Gratings
33
-10
-5
0
5
10
x
-0.6
-0.3
0
0.3
0.6
0.9
Re(u )
Im(u )
|u |
(a)
1
1
1
-10
-5
0
5
10
x
-0.6
-0.3
0
0.3
0.6
Re(v )
Im(v )
|v |
(b)
1
1
1
Figure 2: Moving solitons’ profiles for s = 0.20, λ = 0.20,
m = 0.40, and Ω = 0.40. (a) u
1
and (b) v
1
.
0 0.1 0.2 0.3 0.4
0.5
m
-0.4
0
0.4
0.8
Ω
Stable
Unstable
No Solution
Figure 4: Stability diagram for λ = 0.20 and s = 0.10.
grating. The analysis shows that moving solitons ex-
ist throughout the bandgap. The stability character-
istics of moving solitons have been investigated nu-
merically. It is found that both stable and unstable
solitons exist in the bandgap. We have determined
nontrivial stability borders in the plane of dispersive
-80 -40 0 40 80
x
t
400
t
(a)
0
-80 -40 0 40 80
x
t
400
t
(b)
0
-80 -40 0 40 80
x
t
400
t
(c)
0
Figure 3: Examples of moving solitons’ propagation of (a)
stable u
1
, (b) stable u
2
for m = 0.32, Ω = 0.64, and (c)
unstable u
1
for m = 0.12, Ω = −0.64 while s = 0.20, λ =
0.20.
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
34

reflectivity and frequency. Another finding is that the
presence of dispersive reflectivity in one core can lead
to enhancement of the stability of solitons in certain
parameter ranges.
REFERENCES
Aceves, A. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Physics Letters A, 141(1-2):37–42.
Atai, J. and Chen, Y. (1992). Nonlinear couplers com-
posed of different nonlinear cores. Journal of applied
physics, 72(1):24–27.
Atai, J. and Malomed, B. A. (2000). Bragg-grating solitons
in a semilinear dual-core system. Physical Review E,
62(6):8713.
Atai, J. and Malomed, B. A. (2001). Families of bragg-
grating solitons in a cubic–quintic medium. Physics
Letters A, 284(6):247–252.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Physics Letters A,
342(5-6):404–412.
Baratali, B. and Atai, J. (2012). Gap solitons in dual-core
bragg gratings with dispersive reflectivity. Journal of
Optics, 14(6):065202.
Bertolotti, M., Monaco, M., and Sibilia, C. (1995). Role of
the asymmetry in a third-order nonlinear directional
coupler. Optics communications, 116(4-6):405–410.
Chen, Y. and Atai, J. (1995). Polarization instabilities in
birefringent fibers: A comparison between continuous
waves and solitons. Phys. Rev. E, 52:3102–3105.
Chen, Y. and Atai, J. (1998). Stability of fundamental soli-
tons of coupled nonlinear schr¨odinger equations. Opt.
Commun., 150(1):381 – 389.
Chowdhury, S. S. and Atai, J. (2014). Stability of bragg
grating solitons in a semilinear dual core system with
dispersive reflectivity. IEEE Journal of Quantum
Electronics, 50(6):458–465.
Christodoulides, D. and Joseph, R. (1989). Slow bragg soli-
tons in nonlinear periodic structures. Physical review
letters, 62(15):1746.
Conti, C., Trillo, S., and Assanto, G. (1997). Doubly reso-
nant bragg simultons via second-harmonic generation.
Physical review letters, 78(12):2341.
Dasanayaka, S. and Atai, J. (2013). Stability and collisions
of moving bragg grating solitons in a cubic-quintic
nonlinear medium. JOSA B, 30(2):396–404.
De Sterke, C. and Sipe, J. (1994). Gap solitons progress in
optics. North-Holland, 33:203–260.
De Sterke, C. M., Eggleton, B. J., and Krug, P. A. (1997).
High-intensity pulse propagation in uniform gratings
and grating superstructures. Journal of lightwave
technology, 15(8):1494–1502.
Dong, R., R¨uter, C. E., Kip, D., Cuevas, J., Kevrekidis,
P. G., Song, D., and Xu, J. (2011). Dark-bright gap
solitons in coupled-mode one-dimensional saturable
waveguide arrays. Physical Review A, 83(6):063816.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. (1999).
Bragg solitons in the nonlinear schr¨odinger limit: ex-
periment and theory. JOSA B, 16(4):587–599.
Fraga, W., Menezes, J., Da Silva, M., Sobrinho, C., and
Sombra, A. (2006). All optical logic gates based on
an asymmetric nonlinear directional coupler. Optics
communications, 262(1):32–37.
Hossain, B. and Atai., J. (2020). Solitons in a dual-core sys-
tem with a uniform bragg grating and a bragg grating
with dispersive reflectivity. In Proceedings of the 8th
International Conference on Photonics, Optics and
Laser Technology - Volume 1: PHOTOPTICS,, pages
76–79. INSTICC, SciTePress.
Krauss, T. F. (2008). Why do we need slow light? Nature
Photonics, 2(8):448.
Mak, W. C., Chu, P., and Malomed, B. A. (1998a). Solitary
waves in coupled nonlinear waveguides with bragg
gratings. JOSA B, 15(6):1685–1692.
Mak, W. C., Malomed, B. A., and Chu, P. (1998b). Three-
wave gap solitons in waveguides with quadratic non-
linearity. Physical Review E, 58(5):6708.
Mak, W. C., Malomed, B. A., and Chu, P. L. (2004). Sym-
metric and asymmetric solitons in linearly coupled
bragg gratings. Physical Review E, 69(6):066610.
Mandelik, D., Morandotti, R., Aitchison, J., and Silberberg,
Y. (2004). Gap solitons in waveguide arrays. Physical
review letters, 92(9):093904.
Mok, J. T., De Sterke, C. M., Littler, I. C., and Eggleton,
B. J. (2006). Dispersionless slow light using gap soli-
tons. Nature Physics, 2(11):775–780.
Monat, C., De Sterke, M., and Eggleton, B. (2010). Slow
light enhanced nonlinear optics in periodic structures.
Journal of Optics, 12(10):104003.
Neill, D. R., Atai, J., and Malomed, B. A. (2008). Dynam-
ics and collisions of moving solitons in bragg gratings
with dispersive reflectivity. Journal of Optics A: Pure
and Applied Optics, 10(8):085105.
Taverner, D., Broderick, N., Richardson, D., Laming, R.,
and Ibsen, M. (1998). Nonlinear self-switching and
multiple gap-soliton formation in a fiber bragg grat-
ing. Optics letters, 23(5):328–330.
Moving Solitons in Coupled Bragg Gratings with a Uniform and a Nonuniform Bragg Gratings
35
