Decision Guidance Framework for a Hybrid Renewable Energy

System Investment Model

Roberto Levy and Alexander Brodsky

Computer Science Department, George Mason University, Fairfax, VA, 22030, U.S.A.

Keywords: Hybrid Renewable Energy System, Mixed Integer Linear Programming, Optimization, Power Networks,

Investment Decision Guidance.

Abstract: This paper focuses on making optimal investment and operational recommendations for a Hybrid Renewable

Energy System (HRES). For this purpose we develop a modular composite analytic performance model for

HRES investment, which is based on an extensible library of atomic component models, including renewable

sources such as solar and wind, power storage, power contracts, and programmable customer loads’ switches.

The performance model formally expresses feasibility constraints and key performance indicators, including

total tost of ownership, environment impact, and infrastructure resilience, as a function of investment and

operational decision variables. Based on the performance model, we design and develop a decision guidance

system to enable actionable investment recommendations that optimize key performance indicators subject

to the operational constraints associated with the network. Finally, we demonstrate the model in a case study

based on a real world example for a municipal electric utility.

1 INTRODUCTION

1.1 Drivers for Renewable Energy

Networks and Key Trends

The focus of this paper is to provide a flexible

framework that allows for modelling and optimizing

the investment in resources for a Hybrid Renewable

Energy System (HRES).

The planning and management of power had

undergone a significant transformation in the past few

years. Developments in the technological and

political-economic landscape have been driving

significant changes and complexity to electric power

networks, transforming the existing mechanisms for

supplying energy to satisfy electricity demand. At the

forefront, environmental concerns are causing a surge

in motivation to integrate renewable energy sources

into the power grid. Political factors intensify this

trend, as there is a significant push for reducing

dependency on imported fossil fuels (understanding

that these considerations will vary between countries,

as the sources of energy may be more or less abundant

within a particular geography). Economic aspects

take into account the financial viability of operating

those solutions, as well as the need to maintain a

reliable source of supply. Concerns with long-term

resilience of the infrastructure reflect the incidence of

natural disasters as well as potential terrorist threats.

Finally, the technology allows the expansion of

alternative sources of energy (such as solar and wind)

at a lower cost (in some cases even cheaper than

traditional generation methods), even operated by the

end consumers, combined with more efficient energy

storage mechanisms. Control of power networks

becomes more sophisticated through the development

of smart grids.

The combined effect of environmental concerns

with geo-political factors regarding the dependency

on fossil fuels, is driving the establishment of power

networks that are resilient, reliable, and economically

efficient, and that have a reduced impact on the

environment. In this context, several complementary

developments come in place to address these needs.

First, the establishment of smart grids, which expand

the more traditional power grids, by using two-way

flows of electricity and information to create an

automated and distributed advanced energy delivery

network. Figure 1 (U.S. Energy Information

Administration, 2014), depicts a typical network

configuration for a power grid, which we will expand

later on, with a more detailed explanation of the

different components’ role.

Second, as a specialization of these smart grids,

we see the development of Hybrid Renewable Energy

338

Levy, R. and Brodsky, A.

Decision Guidance Framework for a Hybrid Renewable Energy System Investment Model.

DOI: 10.5220/0010231203380346

In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 338-346

ISBN: 978-989-758-485-5

System (HRES) (sometimes also called Integrated

Renewable Energy Systems). HRES denotes an

elaborate energy grid that relies on multiple sources –

most prevalent of which are renewable sources such

as solar, wind, and hydro, combined with more

traditional sources such as fossil-fired power

generators, as well as with storage technology at key

locations of the grid, to establish a reliable, cleaner

and stable flow of supply. In this context, the role of

electricity storage is particularly important in order to

address multiple needs: balancing power supply

(uncertain due to potential fuel shortages and the

stochastic nature of renewable sources), deferring

costly upgrades of the transmission/distribution

infrastructure, allowing frequency regulation, and

creating opportunity for revenue generation through

secondary markets.

1.2 The Problem and Technical

Challenges

There are key decisions to be made by stakeholders

in the public and private sector, who need to

determine the policies, investment and operations of

an HRES for the energy and power sector, as is the

focus of this paper. One involves determining the

optimal investment in a balanced portfolio amongst a

growing set of energy resources and providers with

varying capital investment costs and constraints.

Another key decision is finding the most efficient

way to operate the different HRES resources. In this

paper, we focus on the investment and operations

decisions associated with an HRES described as a

pool of electric power, fed by a variety of components

to satisfy distributed sources of demand (although our

work will not focus on the distribution/transmission

question, functioning instead as a centralized model).

Analyzing and making actionable recommendations

on investment in the grid is challenging due to a

number of factors:

● Highly complex interaction among

different components of a power network

● Trade-offs between multiple goals and

objectives, including the total cost of ownership, CO2

emissions and environmental impacts, service

reliability, grid resilience and socio-economic impacts.

● Uncertain patterns of energy demand, as

well as supply, especially when relying on renewable

sources.

There has been extensive research to support

modelling of hybrid energy systems (Chauhan and

Saini, 2014) and (Erdinc, and Uzunoglu, 2012).

Typically, however, the models are hard-wired for

specific energy technologies and scenarios, and do

Figure 1: Distributed power system with storage

technologies (Source: U.S. Energy Information

Administration).

not provide a flexible framework to allow easy

composition of designs of networks or microgrids for

a variable combination of components such as

generators, batteries, etc. There has been some work

that allows a more flexible modelling framework and

software implementation (see for example HOMER

(Gilman et al., 2006)). Most of the research, however,

is less reliant on mathematical programming (MP)

and formal optimization methods, and more on

heuristics or on simulation based engines. Among

those works that effectively use MP, it is common to

see the application of Mixed Integer Linear

Programming (MILP) to investment and operations

problems in power networks. For a good overview of

MILP and other related integer optimization

problems and approaches, see (Hoffman and Ralphs,

2012). There is a body of research that uses MILP

Optimization models for power generation

investment and operations decision (see (Omu et al.,

2013), (Wouters et al., 2015), (Tenfen and Finardi,

2015), (Yang et al., 2015)), while others focus on

Demand-Side Management (DSM) optimization (see

(Barbata and Capone, 2014) for a survey). These

papers, however, do not provide a way to model the

network with components that can unify aspects of

power supply and demand optimization in one

integrated framework. Additionally, these works do

not attempt to build the investment decision model

from the optimal operation of the underlying day-to-

day model; instead, they make simplifying

assumptions regarding the operation to derive the

rough-cut impact of the investment decisions. An

alternative approach is the one provided by

(Papavisiliou and Oren, 2013). They define the Unit

Commitment Problem as a set of interconnected

nodes/buses with stochastic elements reflecting

supply and demand uncertainty. The proposed

solution approach is based on a two-stage mixed

Decision Guidance Framework for a Hybrid Renewable Energy System Investment Model

339

stochastic programming, to commit generation to

demand source. This approach is robust and well

suited to address stochastic problems on dispatching

energy. However, it is directed towards operational

decisions, and does not attempt to address the

investment decisions, which are key to our research.

When addressing an MILP approach for the types

of applications described, it is common to recur to

modelling languages that are specialized in

mathematical programming and optimization

problems (Hoffman and Ralphs, 2012). Powerful

languages such as OPL and AMPL are in place to

address those needs (Martin, 2002) and (Fourer et al.,

1990). OPL and AMPL provide many advantages to

make the optimization modelling easier and less

error-prone. Some good examples of Power Network

optimization models utilizing OPL are found in (Levy

et al., 2016). However, they still require a

considerable knowledge of optimization methods to

properly program with them. Furthermore, they are

not built for the use of reusable components between

models; instead, each new model has to be created

from scratch.

1.3 Key Contributions

Bridging these gaps is exactly the focus of this paper.

More specifically, the contributions of the paper are

as follows: First, we develop a modular composite

analytic performance model (PM) for investment

decisions in the HRES, which is based on an

extensible library of atomic models for HRES

components, such as diesel generators, renewable

sources such as solar and wind, power storage,

contractual agreements with third parties, and

programmable switches. The performance model

expresses metrics of interest and feasibility

constraints as a function of investment and operation

decision variables. Decision variables include all

investment choices and system operational controls

over the time horizon, such as (1) power flows in the

network as a whole, (2) specific controls for each

physical network component, and (3) financial

instruments such as contracts with external power

providers. Feasibility constraints include capacity

limitation of physical resources, power flow

equilibrium, contractual terms, and satisfying power

demand over the planning horizon. Metrics of interest

include net present value of investment and operation

over the planning horizon, or the amount of carbon

dioxide emissions, or a combined measure of

financial and environmental impact. Second, we

develop an HRES Decision Guidance System (DGS)

based on the performance model. The HRES DGS is

unique in that it allows extensibility of a model

component library similar to simulation systems, yet

achieves the quality of optimization results and

computational time of mathematical programming

solvers. This is achieved by using the Decision

Guidance Analytics Language (DGAL) and

Management System (Brodsky and Wang, 2008),

(Brodsky and Luo, 2015), (Nachawati et al., 2017).

The HRES DGS performs simulation, optimization,

and trade-off analysis to support investment

decisions, based on an extensible Knowledge Base

(KB) of reusable component models. Finally, we

provide a case study based on a real world example

for a microgrid application, utilizing real data

documented for a municipal electric utility, to

demonstrate the applicability of the model and to

derive actionable recommendations on investments

on selected technologies, and the operations of the

same technologies.

The remainder of this paper is organized as

follows: Section 2 describes an application example

for an electric utility, to be used as a basis for the

formalization; Section 3 presents the design of the

formal mathematical model to be used for

optimization; Section 4 discusses the implementation

of the model through the use of the DGS; Section 5

examines a microgrid case study, using a combination

of real data and realistic assumptions applicable to a

municipal utility. Section 6 provides our conclusions

and directions for further development of this

research.

2 MUNICIPAL ELECTRIC

UTILITY EXAMPLE

2.1 Overview

To better visualize the application of the formal

model, we will refer to a case study that constitutes a

practical implementation of the approach. This case

study was developed as part of a joint initiative

between the Department of Computer Science and the

School of Public Policy of George Mason University.

The effort was driven towards identifying relevant

planning problems of a municipal utility, and

developing a solution model to address them. We

believe this to be a good initial ground for developing

our framework, which could be further expanded to

allow variability and complexity, and better illustrate

the flexibility of the model.

Different municipalities in Virginia are associated

in a central organization, which has a contract with a

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

340

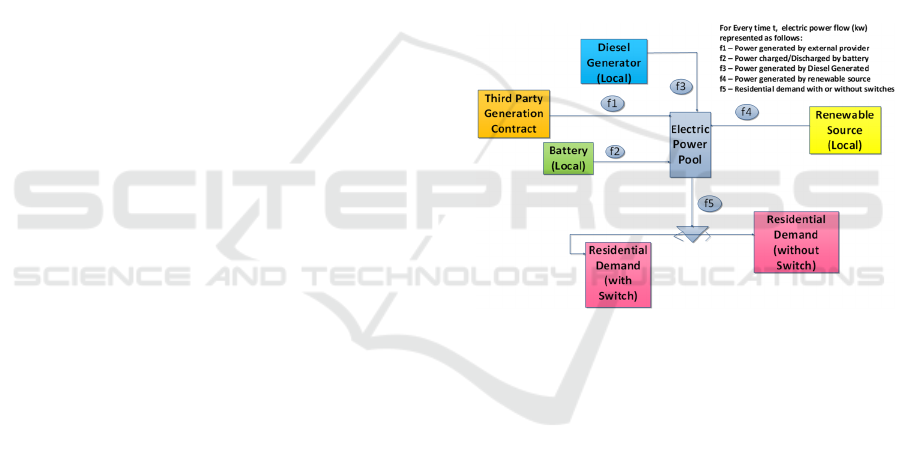
third party power generation company, to purchase

electric power. This contract is based on separate

metering for each municipality, and drives charges on

different elements, mainly peak power demand and

actual energy consumption. A typical electric supply

for a municipality is composed of a number of

substations for its residential customers, and separate

substations serving industrial customers. The

municipality may own diesel generators located in

these substations that are bid into the capacity pool. If

the generation provider needs additional generation to

meet their peak demand, it may dispatch the

additional generation capacity, for a cost (if a unit is

not available when dispatched, a penalty may be

incurred). The generator capacity will not affect the

peak demand for billing calculation.

The peak demand charge is based on coincidental

demand, i.e. the demand at the municipality level

occurring at the time the generation provider

identifies and communicates an overall peak that

occurs for the month. Other peak demand times (non-

coincidental) are also observed, so if a non-

coincidental peak demand is above a certain ratio to

the coincidental peak demand, the charge is adjusted

to account for the non-coincidental peak demand.

This way the municipal utility is not incentivized to

shift the demand artificially to reduce the coincidental

peak, and therefore reduce the overall cost.

In addition, each municipality operates a program

involving switches for water heaters and HVAC,

which can control the consumers’ demand and

therefore affect peak billing. When water heater

switches are activated they delay the corresponding

demand for a different time period. HVAC demand

locks a certain temperature for a period of time. The

municipality provides a monetary incentive (or a

corresponding free service) for customers that agree

to install the switches in their households.

Some municipalities are examining different

problems related to the investment and operation of

some of the technologies. Regarding the generation,

they have to decide whether to invest in additional

diesel generators, to replace any of the existing ones

either with new generators, or possibly to consider

other technologies such as batteries or solar power

instead, and determine the best schedule for

dispatching those sources (above and beyond the

requirements from the external generation provider).

Regarding the switches, decisions are to be made

as to the number of additional switches to install at its

customers’ locations, and how best to operate them.

We use some of these problems as a basis for our

case study, and to provide a starting point for the

development of our formal model.

Our initial problem formulation is to recommend

an optimal portfolio of investments between diesel

generators, batteries, solar and household switches, as

well as optimal operations within a given time

horizon to minimize total costs of ownership (TCO)

at present value.

2.2 Problem Statement and Illustration

We present here the problem statement and an

intuitive description of a simple instantiation based on

the formal model. The problem is stated as

recommending an optimal portfolio of investments

between different local technologies (e.g. diesel

generators, batteries, and renewable sources) and

household switches, as well as optimal operations to

satisfy demand within a given time horizon to

minimize total costs of ownership (TCO) at present

value.

Figure 2: Simplified HRES Problem Schematic.

Based on this model, we developed an initial

framework and component library to reflect the

performance model for each of the components:

generator, battery, households, and power generation

contract. Each component generates metrics

including the daily cash flows corresponding to

operations and investment costs, and the power

generated/consumed by time interval. A separate

performance model consolidates the cash flows and

the power for the microgrid across the individual

components. The investment decision variables

include buying/installing a diesel generator,

buying/installing a battery, buying/installing a solar

generation unit, and the number of new switches to be

installed at the households. The operations decision

variables include, for each time interval, the amount

of energy generated by the diesel generator, the

amount of charge/discharge of the battery, and the

state of activation of the switches. The objective

function is the minimization of the net present value

Decision Guidance Framework for a Hybrid Renewable Energy System Investment Model

341

of the investment and operational costs for all

components for the time horizon.

3 FORMAL MODEL

3.1 Notation for Optimization Problem

Formulation

We consider HRES investment optimization

problems of the form:

𝑚𝑖𝑛𝑖𝑚𝑖𝑧𝑒/𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝐼𝑂𝑃,𝑉

subject to: IC(P,V) (1)

where:

● P is a vector of parameters to the problem that

range over a domain Dp

● 𝑉 is a vector of investment and operation

decision variables that range over a domain Dv

● 𝐼𝑂:𝐷𝑝  𝐷𝑣 → 𝑅 is the investment objective

function (such as net present cost) that gives a

value in R for for any instance of (P,V) in the

domain 𝐷𝑝  𝐷𝑣

● 𝐼𝐶: 𝐷𝑝  𝐷𝑣 →



𝑇,𝐹



is the investment

constraint, expressed as a Boolean function, that

gives, for any instance of (P,V) in the domain

𝐷𝑝  𝐷𝑣, T (true) if the constraint is met, or F

(false) otherwise

To support a range of HRES optimization problem

for different objective functions IO and reusability of

model components, we define an HRES analytic

performance model as a tuple

P, V, Cmp, M, C

where:

 P, V are defined above

 Cmp is a computation procedure that computes,

given an input (P,V):

 a vector of metrics M = 𝑀



,...,𝑀



) that

contains the investment objective IO(P,V), i.e.,

IO(P,V) = 𝑀



for 1  i  k.

 the investment constraint C, i.e., IC(P,V) = C

the HRES optimization problem is defined by the

HRES analytic performance model

P, V, Cmp, M, C

and a metric 𝑀



in M designated as the optimization

objective.

3.2 HRES Analytic Performance

Model

We now define the elements of (P, V, Cmp, M, C) for

the HRES formalization.

3.2.1 Parameters P

P includes generic parameters, as well as the

parameters specific to each HRES component, i.e.,

we define P as the tuple:

𝑃: 𝑇,𝑇𝑜𝑡𝑀𝑜𝑛𝑡ℎ𝑠,𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝐿𝑒𝑛𝑔𝑡ℎ,𝑀𝑜𝑛𝑡ℎ,𝐼𝑅,



𝑃











where:

● T = is the length of the time horizon in days. We

use the term time horizon TH = {1,…,T} to

denote the set of days within the considered

investment time horizon.

● TotMonths = {1,..,endmonth} is the set of

calendar months corresponding to the contractual

billing cycles, as well as other operational and

leasing costs, where endmonth is the last

calendar month within the time horizon.

● IntervalLength is the duration of each time

interval in hours (assume a fixed number of time

intervals during a day)

● Month is the set of time intervals {t

,…, t

}

where time t

is the first interval of the calendar

month, and t

is the last interval of the calendar

month

● We compute

numIntervals =





(2)

● as the number of intervals in T

● 𝐼𝑅 ∈ 0,1 is the market annual rate of return for

investment

● 𝑃



,𝑖1,…𝑘, is the set of parameters specific to

component i (see example of initial library of

components in the Appendix)

3.2.2 Variables V

V includes decision variables specific to each

component defined as:

𝑉:



𝑉











where:

● 𝑉



,𝑖1,…𝑘,is the set of decision variables

specific to component i (see example in

Appendix)

3.2.3 Computations Cmp

Cmp includes computations specific to each

component, and general ones as defined below.

 For every component i = 1,…,k, perform

computations 𝐶𝑚𝑝



𝑃



,𝑉



. Each computation

𝐶𝑚𝑝



𝑃



,𝑉



 returns (𝐶𝐹



,𝑘𝑤



,𝐼𝐶





where:

 𝐶𝐹



:𝑇𝐻 →𝑅 is the cash flow of component i

𝐶𝐹



(d), d∈𝐻𝑇 gives the dollar amount spent by

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

342

component I on day d (note that 𝐶𝐹



(d) 

0 represents net revenue)

 𝑘𝑤



:𝑇𝐻 →𝑅, where 𝑘𝑤





𝑖𝑛𝑡



,𝑖𝑛𝑡

1,…,𝑛𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠, is the amount of power

that component i produces at time interval int

(note 𝑘𝑤





𝑖𝑛𝑡



0 represents power

consumption)

 𝐼𝐶



∈𝑇,𝐹 is the Boolean value representing

satisfaction of feasibility constraints of

component i

 Compute:𝐻𝑇 →𝑅 , which is the integrated cash

flow across all components. i.e.

𝐶𝐹𝑑  





𝐶𝐹



𝑑 ∀ 𝑑 𝜖 𝑇𝐻

(3)

 Compute 𝑁𝑃𝑉 (Net Present Value) for the

HRES:

𝑁𝑃𝑉  





𝐶𝐹𝑑



1𝐷𝑎𝑖𝑙𝑦𝐼𝑅





(4)

Where

𝐷𝑎𝑖𝑙𝑦𝐼𝑅 



1𝐼𝑅



/

- 1

(5)

 Compute balance flow constraint BalFlow:

𝐵𝑎𝑙𝐹𝑙𝑜𝑤  ⋀











𝑘𝑤





𝑖𝑛𝑡



0

(6)

 Compute overall feasibility constraint:

𝐼𝐶  𝐵𝑎𝑙𝐹𝑙𝑜𝑤 ⋀ ⋀





𝐼𝐶



 (7)

3.2.4 Metrics M

M are the metrics computed for each component, that

are defined generically as the following tuple:

𝑀:



𝐶𝐹











𝑘𝑤









,𝑁𝑃𝑉,𝐶𝐹

where:

𝐶𝐹



, 𝑘𝑤



,𝑁𝑃𝑉,𝐶𝐹 are obtained as computed by Cmp

as in section 3.2.3

3.2.5 Investment Constraints IC

IC includes general constraints, as well as the

constraints specific to each component defined as the

tuple:

𝐼𝐶:



𝐼𝐶









,𝐼𝐶,𝐵𝑎𝑙𝐹𝑙𝑜𝑤

where

● 𝐼𝐶



, 𝐼𝐶,𝐵𝑎𝑙𝐹𝑙𝑜𝑤 are obtained as computed by Cmp

as in section 3.2.3

3.2.6 Component Model

In the appendix, we demonstrate how we apply our

general model to our initial library of components,

constituted with initial object that supports the

example described in the prior section.

4 DGS IMPLEMENTATION

USING DGAL

An initial version of this model was developed using

the language JSoniq, a data manipulation language

over the JSON data format. To perform optimization,

we use Unity DGMS and DGAL, which machine-

generate an MILP optimization problem formulation

in the AMPL equational language and invoke the

Bonmin solver. For this version, we utilized our

initial library of components, as described in the

appendix, to develop the applicable routines. Figure

3 illustrates the high-level DGMS/ DGAL

framework.

A separate module was designed for each

component: diesel generator, battery, solar,

household demand (with or without water heater

switches), and generation contract for energy

provision. Each module is independent of the others,

and includes the calculation of the relevant metrics

for each component for the planning time horizon (i.e.

power consumed/produced by time interval, and cash

flows for operations costs, investment amount), and

the binary variable of constraint, indicating if the

constraints for the component were met. An

investment/integration model consolidates the

metrics, validating for example that all power

supplies and demands match for each time interval,

and calculating the aggregated cash flows, the

aggregated investment values, and the net present

value for the overall network.

The code is designed so that the future addition of

new components (e.g. solar panels to be installed at

the households, different generator models, wind

farms, etc.) will not affect the individual components

already defined.

Figure 3: DGAL Framework.

Decision Guidance Framework for a Hybrid Renewable Energy System Investment Model

343

5 CASE STUDY APPLICATION

For the initial, simplified scenario in our case study,

we follow the example described in Section 2,

utilizing a combination of real data from a

municipality in Virginia (for example daily energy

consumption during a calendar year and peak demand

events), and realistic synthetic data (for elements not

currently in place such as investment and

maintenance costs for batteries and renewable

sources) for twelve months of operation to

recommend optimal combination of investments and

operations of a diesel generator, a battery, a solar

source, and water heater switches. Our initial test

focuses on daily demand data for an entire year in one

particular area, based on the billing and historical

consumption data gathered.

The investment and operational costs associated

with each technology were based on studies by third

party companies as evaluation of possible

replacement of current generators in place. Other data

such as fuel costs and efficiency were based on

available market data. Information for generation

prices were obtained from billing and contractual

data.

The core methodology for this application

consisted in collecting the data for each of the

parameters over the time horizon, based on the time

interval being used, and transforming the data in a

spreadsheet to the format required by the model. The

data is then consolidated in a JSON format that is

used as the input file for the model.

The model had a total of 1100 decision variables,

including the purchase decisions of each component,

the power per day generated or consumed by

component for the twelve months, the status of the

switches, and the upper bounds of peak power and

transmission. For this size, it took a little over 8

minutes to achieve the optimal values for each

variable for minimizing the Total Cost of Ownership

(TCO) including investment and operations for the

whole system, when running on a Toshiba Satellite

S55 Laptop, with an Intel i7 2.40 GHz processor and

12 GB RAM.

As expected, the recommendations for purchase

and daily operations for each component were

directly affected by the comparative parameters

between the components, e.g. the

purchase/installation cost for each component, the

maintenance costs, fuel costs (for diesel generator),

billing rates for the external utility, demand patterns

per month and peaks, etc. Consequently any changes

in the variables associated to one of the components

potentially affected the operations and the purchase

decisions of all the other components as well.

Although we did not establish a direct comparison

of our results to a more traditional investment model

that doesn’t account for the short term operations,

note that, from the sensitivity analysis, the impact of

short term parameters and variables have an

accumulated effect on the investment decision.

Therefore, this indicates (pending future detailed

comparisons of results) that the integration of the

short term operational decisions represent a more

accurate method for investment decisions.

We also note that the solution is modular, in that

we can at any point remove or add individual

components/resources, without any need to modify

the remainder of the model, therefore providing

scalability to increase the model to address more

complex scenarios with higher variability of

resources. Likewise, in our simplified example we

treated each component as an individual resource, not

accounting for the combined value of, for example,

batteries and solar/renewable sources. The model can

accommodate this factor by either defining joint

constraints applying to the solar generation and the

battery, or alternatively creating a composite element

defined by the two individual components with their

combined performance characteristics.

Finally, the model can account to changes in our

objective function to include different metrics such as

the total emissions of the system as a whole (driven

as a function of the total power generated by

source/component), or a balanced combination of

TCO and emission. In such a scenario, the model

would favor clean energy solutions such as batteries

and solar at the expense of diesel generators.

6 CONCLUSIONS AND FUTURE

DIRECTIONS

In this work, we developed a formal mathematical

formulation for a modular, extensible analytic

performance model for investment decisions in the

HRES, expressing metrics of interest and feasibility

constraints as a function of investment and operation

decision variables. We also developed an HRES

Decision Guidance System (DGS) to support the

formal performance model, relying on Decision

Guidance Analytics Language (DGAL). As part of

the HRES DGS, we created an extensible Knowledge

Base (KB) of reusable Performance Models based on

the different energy resources associated with a

municipal utility example. Finally, we provided a

case study based on this example for a microgrid

application, utilizing a combination of real and

synthetic data, to demonstrate the applicability of the

model to derive actionable recommendations on

investments on selected technologies.

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

344

There are several potential ways to expand the

model. One promising addition is to add elements of

complexity on the customer level, including

stochasticity of demand, net-metering models (where

customers produce solar energy for own consumption

and charge back excess to utility), and dynamic

pricing mechanism.

Another aspect of expansion would be to support

decisions that go beyond the operations of the

network, and to include infrastructure/ capital

investment recommendations to achieve long term

goals, based on Total Cost of Ownership.

A promising potential for the model is to define

multiple stakeholders, for example adding regulators,

consumers, and other utilities, each with their own

specific objectives, translated into Key Performance

Indicators (KPIs), which would include a variety of

goals (including environmental impact, total cost of

ownership, system reliability, etc.). The problem

could be set as what is known as Bi-level

Optimization, in which a ‘leader’ decision maker (in

this case a regulator) who has its defined KPIs, has

to define the optimal portfolio of policies (e.g. tax

incentives, emissions regulations), to affect utilities

and consumers behavior, which in turn optimize their

own KPIs (potentially different from the leader).

REFERENCES

Hoffman, K. and Ralphs, T., 2012. Integer and

Combinatorial Optimization, Encyclopaedia of

Operations Research and Management Sciences. Eds.

Saul Gass and Michael Fu. Kluwer Academic

Publishers.

Levy, R., Brodsky, A. and Luo, J., 2016. Decision Guidance

Approach to Power Network Analysis and

Optimization. Proceedings of the 18th International

Conference on Enterprise Information Systems

(ICEIS), pp 109-117.

Levy, R., Brodsky, A. and Luo, J., 2016. Decision guidance

framework to support operations and analysis of a

hybrid renewable energy system, Journal of

Management Analytics, 3:4, pp 285-304

Brodsky, A. and Wang, X., 2008. Decision-guidance

management systems (DGMS): Seamless integration of

data acquisition, learning, prediction and optimization,

in Proc. 41st Annual Hawaii Intl. Conf. System Sciences

(HICSS), pp. 71–71.

Brodsky, A. and Luo, J., 2015. Decision guidance analytics

language (DGAL): Toward reusable knowledge base

centric modeling, in 17th International Conference on

Enterprise Information Systems (ICEIS), Barcelona,

Spain.

Martin, R., 2002. A Short Introduction to OPL-

Optimization Programming Language. under:

https://www.informatik.tu-

darmstadt.de/fileadmin/user_upload/Group_ALGO/pd

f/AlgMod/AlgMod_OPL.pdf

Fourer, R., Gay, D. M., and Kernighan, B. W., 1990. A

modeling language for mathematical programming.

Management Science, 36(5), 519-554.

Omu, A., Choudhary, R., Boies A., 2013. Distributed

energy resource system optimization using mixed

integer linear programming, Energy Policy 61, 249-

266.

Wouters, C., Fraga, E., James, A., 2015. An energy

integrated, multi-microgrid, MILP (mixed-integer

linear programming) approach for residential

distributed energy system planning – A South

Australian case-study, Energy 85, 30-44.

Barbata, A., and Capone, A., 2014. Optimization Models

and Methods for Demand-Side Management of

Residential Users: A Survey. Energies; 7, 5787-5824.

Chauhan, A. and Saini, R., 2014. A review on Integrated

Renewable Energy System based power generation for

stand-alone applications: Configurations, storage

options, sizing methodologies and control, Renewable

and Sustainable Energy Reviews 38: 99–120.

Erdinc, O. and Uzunoglu, M., 2012. Optimum design of

hybrid renewable energy systems: Overview of

different approaches, Renewable and Sustainable

Energy Reviews 16: 1412– 1425.

Tenfen, D. and Finardi, E., 2015. A mixed integer linear

programming model for the energy management

problem of microgrids, Electric Power Systems

Research, 122, 19-28.

Yang, Y., Zhang, S., Xiao, Y., 2015. An MILP (mixed

integer linear programming) model for optimal design

of district-scale distributed energy resource systems,

Energy 90, 1901-1915.

Papavasiliou, A. and Oren, S., 2013. Multi-area stochastic

unit commitment for high wind penetration in a

transmission constrained network, Operations

Research, vol. 61, no. 3, pp. 578–592.

Gilman, P., Lambert, T., and Lilienthal, P., 2006 Chapter

15: Micropower System Modelling with Homer.

Nachawati, M., Brodsky, A. and Luo, J. Unity Decision

Guidance Management System: Analytics Engine and

Reusable Model, 2017. Proceedings of the 19th

International Conference on Enterprise Information

Systems (ICEIS) - Volume 1, 312-323.

APPENDIX

Formal Model for Initial Library of Components.

To exemplify how the individual components in the

library are modelled, we show here the formal model

for a Diesel Generator. A similar methodology is

applied to batteries, solar panels, households, and

external generation contracts.

Decision Guidance Framework for a Hybrid Renewable Energy System Investment Model

345

Based on our general model, we define the Fuel-

Based Generators Structure tuple as:

𝐺𝑆:𝑃



,𝑉



,𝐶𝑚𝑝



,𝑀



,𝐼𝐶





and we decompose each element of the tuple:

𝑃



= (G, fPr, gCap, gEff, NGC, GLC, GMC,

availG) as generators parameters

where:

 G is the set of generator ids;

 𝑓𝑃𝑟: 𝐺  1,….,𝑛𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠 → 𝑅



is the

price function that for each generator g 𝜖 𝐺 and

time interval 𝑡∈1,…,𝑛𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠, gives

the expected fuel (Diesel) price fPr(g,t) in

$/Gallon

 𝑔𝐶𝑎𝑝: 𝐺→𝑅



is a function that gives for each

generator g 𝜖 𝐺, the maximal load of generation

gCap(g) in kw

 𝑔𝐸𝑓𝑓: 𝐺→𝑅



is the function that gives for each

generator g 𝜖 𝐺 , the efficiency gEff(g) in

Gallon/kwh

 NGC: 𝐺𝑇𝐻→𝑅



is the cost cash flow

function associated with a new generator (either

through one-time disbursement at the beginning,

or through leasing), that gives for each generator

g 𝜖 𝐺 and day 𝑑 𝜖 𝑇𝐻, the investment daily cost

NGC(g,t)

 GLC: 𝐺→𝑅



is the generator Lifecycle

function, that gives for each generator g 𝜖 𝐺 the

expected total life GLC(g) in years

 GMC:G →𝑅



is the monthly maintenance cost

function that gives, for each generator g 𝜖 𝐺 , the

estimated monthly maintenance cost GMC(g) for

the time horizon

 availG: G→ 0,1 𝑖s the binary (flag) function

that indicates if a diesel generator g 𝜖 𝐺 was

present at the beginning of the planning horizon

𝑉



= (iG, kw) as Generators variables,

where:

 iG: G→ 0,1 is the binary (flag) function that

indicates if a new generator g 𝜖 𝐺 is being

purchased

 kw: 𝐺1,…,𝑛𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠→𝑅



is the

decision variable matrix of elements kw[g, t],

where for every time interval t

𝜖 1,….,𝑛𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠, kw[g,t] gives the

amount of kilowatts generated by the diesel

generator g 𝜖 𝐺

𝐶𝑚𝑝



corresponds to all the computations

performed for the generator, to obtain the applicable

metrics and constraints, given the parameters and

variables.

The metrics are given by 𝑀



:𝑘𝑤



,𝐶𝐹





where 𝑘𝑤



is already determined by the decision

variable kw[g, t].

𝐶𝐹



is obtained by calculating the operational and

investment costs associated with the purchase and

operation of the generator at each time interval, and

translating into cash flow entries on a daily basis.

 We assume only output flows from a Diesel

Power Generator. The cost of operating a power

generator (if it was available or purchased at the

start of the planning period) equals the total fuel

cost and the monthly maintenance cost.

 We compute the Fuel Cost for ∀𝑔𝜖 𝐺,𝑡 𝜖 𝑇,

𝐺𝑒𝑛𝐹𝑢𝑒𝑙𝐶𝑜𝑠𝑡



𝑔,𝑡



, based on the fuel unit cost

(Dollars per Gallon), the generator efficiency

(Gallon per kwh), and the amount of output flow

in kwh during the given time interval:

𝐺𝑒𝑛𝐹𝑢𝑒𝑙𝐶𝑜𝑠𝑡𝑔, 𝑡  𝑓𝑃𝑅𝑔,𝑡  𝑔𝐸𝑓𝑓 𝑔

 𝑘𝑤𝑔, 𝑡  𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝐿𝑒𝑛𝑔𝑡ℎ

(8)

 We compute GenOpCostg,t , the total

Operational Cost for the Power generator g at

time t, as:

GenOpCostg,t  



𝐺𝑒𝑛𝐹𝑢𝑒𝑙𝐶𝑜𝑠𝑡



𝑔,𝑡





𝐺𝑀𝐶



𝑔





 𝑎𝑣𝑎𝑖𝑙𝐺



𝑔



 𝑖𝐺



𝑔



(9)

 We compute the Investment cost for a new

generator GenInvestmentCost[g,t] , ased on the

given cash expenditures, and on the purchase

decision:

GenInvestmentCost[g,t] = 𝑁𝐺𝐶



𝑔,𝑑



 𝑖𝐺



𝑔



(10)

For 𝐼𝐶



, we consider the constraints for total power

output, and the condition to purchase a new

generator:

 We compute the constraint for the power output

based on the generator’s maximal operating

capacity:

𝐼𝐶





: kwg,t  gCap𝑔

(11)

∀𝑔𝜖𝐺,𝑡𝜖1,…,𝑁𝑢𝑚𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑠

● We compute the constraint for the purchase of a

new generator based on the consideration that we will

only buy a new generator g if it was not yet available

at the start of the planning horizon, i.e.

𝐼𝐶





: availB 𝑔  𝑖𝐺𝑔  1

(12)

∀𝑔𝜖 𝐺

● We compute the overall constraint for the

generator as:

𝐼𝐶



 𝐼𝐶



Λ 𝐼𝐶



(13)

ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems

346