
An Improved Cuckoo Search Algorithm for Multiple Odor Sources
Localization
Yuqing Wu
1a
and Zhipu Wang
2
1
Stuyvesant High School, New York City, U.S.A.
2
School of Automation Science and Electrical Engineering, Beihang University, Beijing, China
Keywords: Cuckoo Search Algorithm, Odor Source Localization, Multi-robot Cooperation.
Abstract: This work presents an improved Cuckoo Search Algorithm (CSA) for multiple odor sources localization. The
idea of forbidden areas is introduced to the CSA as territories of the cuckoo colonies, preventing the cuckoos
from being trapped into local optimal solutions. A source is declared when a certain number of cuckoos are
located in close proximity with each other, and a territory is formed around the declared source centered at
the local best among those cuckoos. When territories overlap, they are merged into one territory to prevent
the same source from being found multiple times. Simulation results show that the proposed method can
locate multiple odor sources with high accuracy.
1 INTRODUCTION
Odor source localization, a problem of retrieving the
source of an odor based on its traces emitted from the
source, has various applications in our lives,
including searching for locations of toxic gas
leakages, survivors, sources of fires, and explosives.
Currently, people mainly solve this problem by using
either static robots or trained animals. However, these
approaches have certain constraints that limit their
performances in certain environments. Static robots are
inflexible and hard to setup in an unknown
environment. Trained animals can’t get close to places
with toxic gas and gets tired easily. To overcome these
constraints, source localization with active robots
becomes more prevalent (Chen and Huang, 2019).
Compared to static robots, active robots can
collaborate with each other flexibly without the
limitations of their locations. Compared to trained
animals, active robots are able to work in a variety of
environments for prolonged periods of time.
Solving the odor source localization problem with
multiple active robots can have two different cases:
single source localization and multiple sources
localization. When solving single source localization
problem with multiple active robots, maintaining
diversity and handling problems with local optimal
a
https://orcid.org/0000-0002-1628-6459
solutions during the search can be challenging. When
solving multiple sources localization problem with
multiple active robots, researchers tend to divide the
robots into groups. Group formation, group
aggregation maintenance, following the same plume
by more than one group, and avoiding re-finding the
same odor source are the main challenges of multiple
odor sources localization problem with multiple
robots. Therefore, researchers have been exploring
different algorithms in respond to these challenges.
These algorithms can be classified into three types:
collaborating with a team of robots in nature-inspired
ways (Shida, et al., 2005; Marques, Nunes, Almeida,
2002) calculating the distribution of the plume (Pang,
2010), and visualizing the search area (Wang, Meng,
Zeng, 2011). One subcategory of the nature-inspired
algorithms is swarm intelligence where robots highly
collaborate with each other. Swarm intelligence based
algorithms convert the odor localization problem into
an optimization problem that doesn’t require precise
information about the gas distribution to solve the
problem. However, the algorithms that are used to
solve for the source localization problems face some
limitations. For example, the Genetic Algorithm
(Marques, Nunes, Almeida, 2002) and the Particle
Swarm Optimization (PSO) (Feng, et al., 2019) can
easily fall into local optimal solutions when solving
the single source localization problem, while some
708
Wu, Y. and Wang, Z.
An Improved Cuckoo Search Algorithm for Multiple Odor Sources Localization.
DOI: 10.5220/0010231707080715
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 708-715
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

multi-modal optimization algorithms such as the
Glowworm Optimization Algorithm (Thomas and
Ghose, 2009) and the Ant Colony Optimization (Cao,
et al., 2013) require large number of robots and might
not be able to find all the sources accurately when
solving the multiple source localization problem.
Attempting to address these issues, we proposed an
improved Cuckoo Search Algorithm (CSA) for
multiple odor sources localization problem.
The CSA is proposed by Yang and Deb (2009,
2010). Modelled after the cuckoos’ parasitic
reproduction strategy, the CSA uses the coevolution
between the parasitic cuckoos and their hosts to
maintain diversity of the cuckoo population. The
cuckoo population would migrate toward the best nest
for a certain distance determined by the Lévy Flight,
a flying strategy by a lot of birds, in each generation,
hoping to encounter a better solution around the best
nest while the best nest stays at the same location in
case the plume is lost. Solving the odor source
localization problem with CSA requires high
collaboration between the robots (represented as
cuckoos in the algorithm) and captures the global
scope well. It is simple and efficient, requiring little
number of inputs to operate. Nevertheless, it can
easily fall into local optimal solutions and has a slow
rate of convergence. Some improvements have been
made to deal with these drawbacks of the CSA. For
example, Valian, Mohanna, and Tavakoli (2011)
modified the algorithm such that it can adjust its
parameters, such as the step size, by itself depending
on its environment; Ghodrati and Lotfi (2012)
combined the Cuckoo Search with PSO to improve
the efficiency of the algorithm; In Srivastava, et al.
(2012), the CSA was mixed with the Tabu Search to
prevent the Cuckoos from falling into local optima
and flying repeated paths.
In this paper, an improved CSA is proposed to
solve the multiple odor sources localization problem,
where the idea of territories and group based
strategies are introduced such that once some robots
are in close proximity, the area is declared as a
territory containing the source. If the newly declared
territory overlaps with previously declared territories
the new territory would merge with the territories it
overlaps with. Unlike the work of Srivastava, et al.
(2012), which marks the very place the cuckoos
landed on as a forbidden area, our algorithm actively
predicts the forbidden area that might contain a good
solution. Moreover, Srivastava, et al. (2012) stores
the flying paths of the past cuckoos to prevent
repeated flying paths, while we only store the areas
where cuckoos are concentrated in. Simulation results
show the effectiveness of the improved CSA in the
multiple sources localization problem, and its
superiority over the classical CSA in single source
localization problem in a particular case.
For the rest of the article, Section 2 states the
problem. Section 3 states the details about the
improved CSA, and Section 4 gives the simulation
results. At Section 5, the conclusions are discussed.
2 PROBLEM FORMULATION
The Gaussian Dispersion Models (GDMs) are used in
this paper as they are the most commonly used
models in regulatory air dispersion modelling
(Visscher, 2013). They are easy to use, able to
accurately predict the concentrations around a source
when the surrounding landscape of the source is fairly
simple. It is valid under the assumptions below:
- The wind field is stable.
- The release source is a point source.
- The release rate is constant.
- The atmospheric turbulence is constant in space
and time.
The three-dimensional GDM can be described as
,
,
;
θ
,
,
;
,
,
,
2σ
σ
exp
2σ
exp
2σ
exp
2σ
(1)
where represents the concentration of the targeted
gas at point
,
,
given the location of the
source
,
,
). is the wind speed, is the
dispersion parameter in the horizontal direction and
is the dispersion parameter in the vertical direction.
σ
and σ
are the standard deviation in the horizontal
and vertical directions, respectively. is the effective
source height.
To further simplify the GDM, formula (1) can be
converted to a two-dimensional space, resulting in
,
;
θ
,
;
,
,
2π
exp
2
(2)
where represents the concentration of the targeted
gas at point (
,
) given the location of the source
(
,
). is the gas diffusion coefficient.
An Improved Cuckoo Search Algorithm for Multiple Odor Sources Localization
709
The dispersion model for multiple point sources
can be found based on the two-dimensional GDM
under two assumptions:
- There is no chemical reaction and interactions
between the substances released from the point
sources
- The distance between the point sources are great
enough to consider each point source separate
from another.
Once these assumptions are satisfied, the gas
dispersion model for multiple sources becomes a
linear addition of formula (2), as represented below:
;
θ
,
;
,,,
,
;
,
,
(3)
where C is the gas concentration at
,
,
contributed by multiple point sources.
is the
number of point sources.
1,2,…,
and
1,2,…,
contains the and
coordinates of the
point sources
1,2,…,
where
is the emission rate for the point
source located at (
,
).
Multiple odor sources localization can be
challenging as the number of sources to be found is
unknown and it is easy to find the same source
multiple times. While the classical CSA is only used
to locate a single source, it searches for sources
efficiently and requires a small number of parameters
to function. Therefore, an improved CSA is proposed
to solve the multiple odor sources localization
problem, that is, to find all the relative maxima of
formula (3) within bounds.
3 THE CSA
Being the best known brood parasite, cuckoos never
build their own nests and lay their eggs in other birds’
nests, leaving the host birds to take care of their young.
The cuckoo mother would remove one egg laid by the
host mother, laying her own egg as a substitute and
flying away quickly. Cuckoos can mimic the color and
pattern of their eggs to match the eggs of the hosts, with
each female specializing in one host species. Many
host species learn to recognize cuckoo eggs in their
nest and throw the eggs out of their nest, so the cuckoos
have to constantly improve their mimicry to avoid
being detected by the host birds.
For simplicity, three idealized rules are applied to
the CSA (Yang and Deb, 2009, 2010):
- Each cuckoo lays one egg at a time, dumping it in
a random nest;
- The best nests with high quality of eggs
(solutions) carry over to the next generation;
- The number of available nests is fixed. A host can
discover a cuckoo egg with a probability
∈
0,1. In this case, the host bird can either throw
away the egg or abandon the nest and build a
completely new nest. For simplicity, the
assumption is that the egg is thrown away and the
nest stays in the same place.
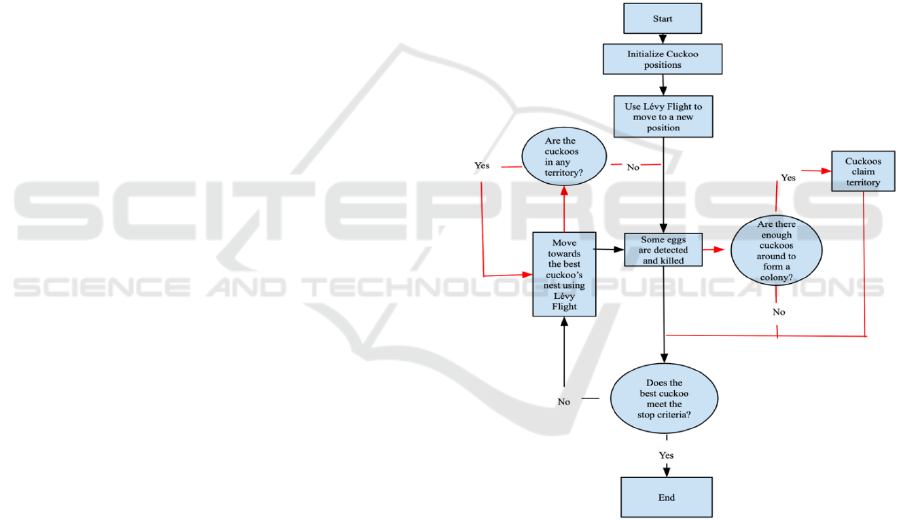
As shown in Fig. 1, the CSA starts out with an
initial population of cuckoos (robots in the context of
odor source localization), having laid some eggs in the
host bird’s nest. The eggs that are more similar to the
host’s eggs have an opportunity to grow up and enter
the next generation. Other eggs are killed by the hosts.
Figure 1: A flowchart of the classical and improved CSAs.
The red lines represent the procedures added during the
improved CSA while the black lines are the steps in the
classical CSA.
To maximize the eggs’ survival rates, the cuckoos
search for the most suitable habitat and immigrate
toward it using Lévy Flight, a flight style of a lot of
birds. They will end up inhabiting somewhere near
the best habitat and lay their egg within a certain
distance from their position. In the classical CSA, this
process would continue until most cuckoos gather at
one position. However, in the proposed improved
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
710

CSA, this process continues until some cuckoos
gather around the same position, forming a colony in
that area and occupying that area as their territory.
Any cuckoo that lands on a territory is kicked out
using Lévy Flight with a large step size. After the
program terminates, each territory would be declared
as a source.
3.1 The Improved CSA
The cuckoos are distributed at random positions on
the coordinate plane.
1,2,⋯, contains the
positions of the cuckoos on the coordinate plane
where is the number of cuckoos and
,
is the position of the i-th cuckoo with
being the x-
coordinate of the i-th cuckoo and
being the y-
coordinate of the i-th cuckoo.
The cuckoos would be flying and forming
colonies in , the entire area, where
,| ∈0,,∈0,
(4)
The Lévy Flight random walk is used to update
the position of the cuckoos given a step size. While
the targeted gas still remain undiscovered, the i-th
cuckoo during the g-th generation would update its
position based on the following formula:
,
,
(5)
where
,
is the position the i-th cuckoo would fly
to in the next generation, and
,
is the i-th cuckoo’s
current position.
⊕λ for the i-th cuckoo
where is the step size, λ satisfies the Lévy
distribution, and ⊕ means entry-wise multiplication.
The Lévy Flight provides a random walk with a
random step length drawn from a Lévy distribution.
é~
,1
λ
3
(6)
Because Lévy distribution (6) has an infinite
variance with infinite mean, the solution generated by
the Lévy distribution can be too far away from the old
solution and jump outside of the bounds when is too
small. The random step length is generated using
Mantegna's algorithm which follows the symmetric
Lévy distribution. A simplified version of Mantegna
algorithm in Yang and Deb (2010) is used in this
study as it does not apply nonlinear transformation to
generate Lévy Flight, making Lévy Flight easier to
calculate.
After traces of the targeted gas is discovered, the
i-th cuckoo during the g-th generation would update
its position based on the following formula:
,
i
f
i
f
(7)
where
is the current best solution, being
-
th cuckoo in the population.
Every time the position of the cuckoo is updated,
a random number is generated and compared with a
discovery rate
, such that if
, the current egg
is discarded. The cuckoos would attempt to declare
territories after a certain number of generations
(defined by the user) to determine
, the area the
cuckoos will be flying in during the next generation,
which is
/
(8)
where is the number of existing groups
1,2,..., in .
, the territory of
, is a square with
a side length of such that
,
|
∈
,
,
,
,
∈
,
,
,
(9)
where
,
is the local best within
.
If
overlaps with
, the territory of
,
and
would share territories such that
∪
(10)
The foreign cuckoos in the
1,2,⋯,)
would be chased out with a large step size Lévy
Flight.
The complete improved CSA can be described as
the following Algorithm 1. In which, the parameters
and
need special attention when implementing
the algorithm. If is too large, the algorithm runs the
risk of combining multiple sources into one source,
while if is too small, the algorithm might
considering different parts of one source as two
different sources. Theoretically speaking, should be
approximately the average length of each plume’s
shortest secant passing through the plume’s center in
a two-dimensional plane. However, this can be hard
to calculate in the real world when the distribution of
the sources is unknown. If
is too large, some
sources might never be found and the algorithm might
get stuck when multiple groups of robots are each
located at a different source while none of them is
greater than
, while if
is too small, the algorithm
might not be able to locate the sources accurately.
Generally speaking, a large
means slower
searching speed and higher searching accuracy. The
number of sources, and should be considered
An Improved Cuckoo Search Algorithm for Multiple Odor Sources Localization
711
when setting
. A larger and require a
larger
to maintain the accuracy of the algorithm.
However, a
larger than optimum increases the
searching time of the algorithm. As the number of
sources increases in the area,
should decrease so
there are enough robots to spread between different
sources at the same time. In order for the algorithm to
search with great accuracy, the sources should be
distant enough such that parts from multiple plumes
can’t be contained by a square.
When the initial position of the robots are far
away from the largest source, the improved CSA can
actually find all the sources more quickly and more
accurately than the classical CSA can find the largest
source. This means when the boundaries of the area
to be searched remains unknown, the improved CSA
can be more suitable for the task of searching for the
largest source than the classical CSA.
Algorithm 1: Improved CSA.
4 SIMULATION RESULTS
In this section, the searching time and accuracy of the
classical CSA and the improved CSA are compared
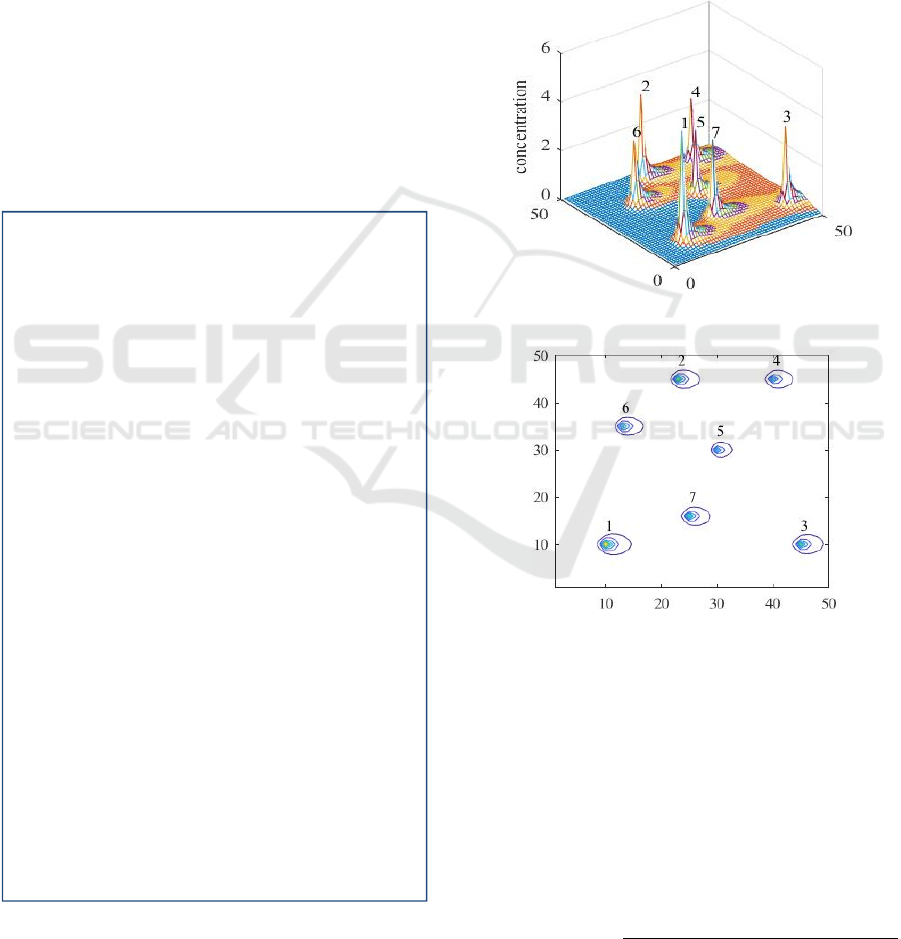
with different initial positions of the nests. We setup
sources 1-7 in the designated area, located at (10,10),
(23,45), (45,10), (40,45), (30,30), (13,35), and
(25,16) respectively, with source 1 being the largest
source. Figs. 2 and 3 show the concentration of the
odor around the designated area calculated by the
GDM.
Figure 2: 3D graph of odor sources.
Figure 3: Countour graph of odor sources.
In the following simulation, N is set to be 50. The
max CPU time (max_CPUTime) is set to be 0.15, but
this can give various results depending on the
computer’s running speed.
is set to be 5 and b is
set to be 6. For classical CSA the requirement is to
find the largest source, while for the improved CSA
the requirement is to find all sources in the designated
area. Each case is run 100 times. In order to estimate
the total searching time, we assume that the searching
time in the g-th generation is given as
max
,
/
where
,
,
,
,
,
denotes the i-th cuckoo’s flying distance in the g-th
1. Initialization
Initialize the positions of the cuckoos
Find current best
2. Iterative Process
while (current_Timemax_CPUTime)
for every nest
Use Lévy Flight to immigrate to new
location
if
Egg is thrown away.
Find new best
end if
end for
if cuckoos found within a square of side
length of a cuckoo
Find the local best in these cuckoos.
Create territory centered at
,
.
if
new territory overlaps with pre-
existing territories
Combine territory based on (10)
end if
end if
while
,
is in
1,2,⋯,
Use Levy Flight with a larger step
to relocate.
end while
end while
return current best
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
712
generation and speed is set to be 3600 meters/hour in
this simulation. Then the total searching time can be
estimated as
∑
_
.
(a)
(b)
(c)
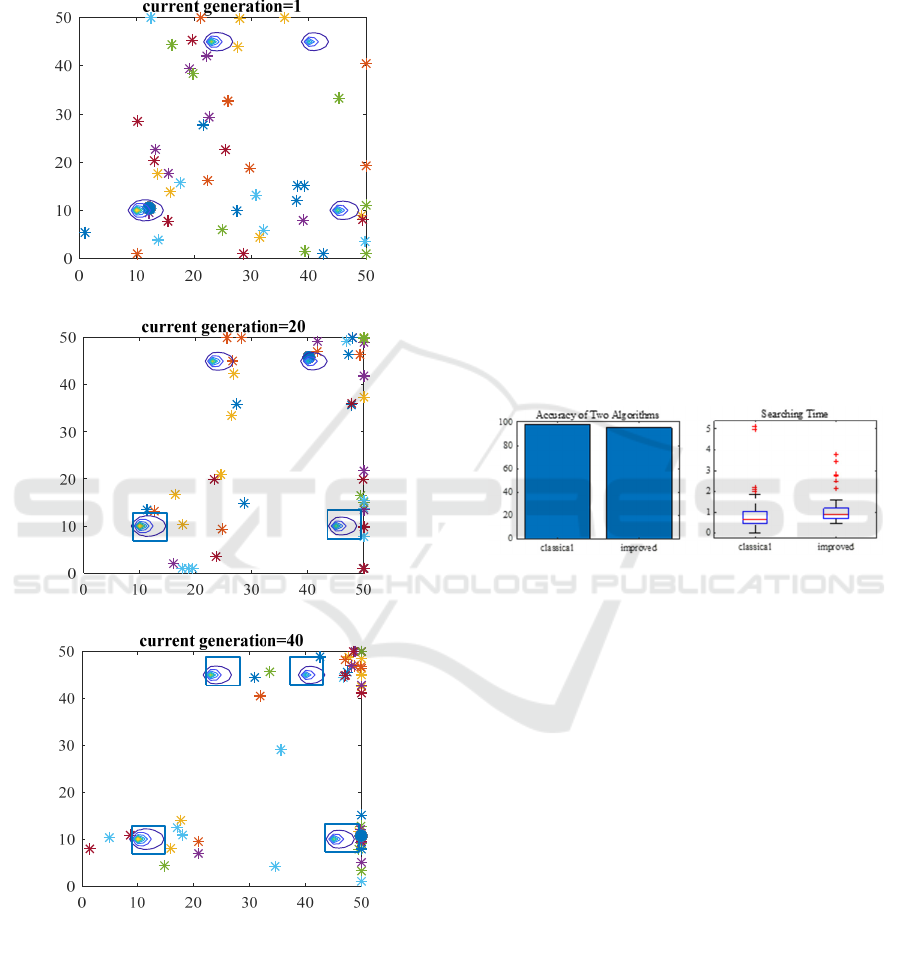
Figure 4: Searching procedure of improved CSA.
Fig. 4 shows the searching procedure of the
improved CSA. In Fig. 4(a), the initial cuckoo
population is uniformly distributed. In Fig. 4(b), two
sources are found by the cuckoos in twenty
generations. In Fig. 4(c), all four sources are found by
the cuckoos in forty generations, with the location of
the source located within the squares, and for most of
the time relatively near the center of the square.
4.1 The Initial Cuckoo Distribution
Two different initial distributions, one is uniform and
the other is far from largest source, are experimented
to compare the efficiency of the conventional Cuckoo
Search and the Improved Cuckoo Search.
When the cuckoos are distributed uniformly
across the area (shown in Fig. 4(a)), the classical CSA
achieves its requirement only slightly faster than the
improved CSA most of the time. This is because the
improved CSA would have to cover extra distance to
find all the sources while the classical CSA only
needs to find the main source. However, the time it
takes for the improved CSA to find all four sources is
generally within the range of time the classical CSA
takes to find the largest source. From Fig. 5, we can
see that the accuracies of the CSAs are similar, with
the classical CSA having 98% accuracy and the
improved CSA having 95% accuracy.
Figure 5: Accuracy and searching time of classical and
improved CSA when cuckoos are uniformly distributed.
When the initial distribution of the cuckoos are far
from the main source (shown in Fig. 6), the improved
CSA can outperform the classical CSA. This is
because the cuckoos can get trapped in local sources
that are not the largest source in the classical CSA
while the idea of territories in the improved CSA
eliminates that problem.
It can be seen from Fig. 7 that, the accuracy of the
classical CSA is 16% when the cuckoos’ initial
positions are far from the largest source while the
accuracy of the improved CSA is 85%. Even though
both algorithms have increased searching time and
decreased searching accuracies, the change in initial
positions has a minor impact on the improved CSA
when compared to its impact on the classical CSA.
This shows that the improved CSA is not as restricted
to its initial positions as the classical CSA and
therefore when the area of search remains unknown
and the robots cannot be uniformly distributed, using
the improved CSA to find the absolute maximum can
be faster than using the classical CSA.
An Improved Cuckoo Search Algorithm for Multiple Odor Sources Localization
713
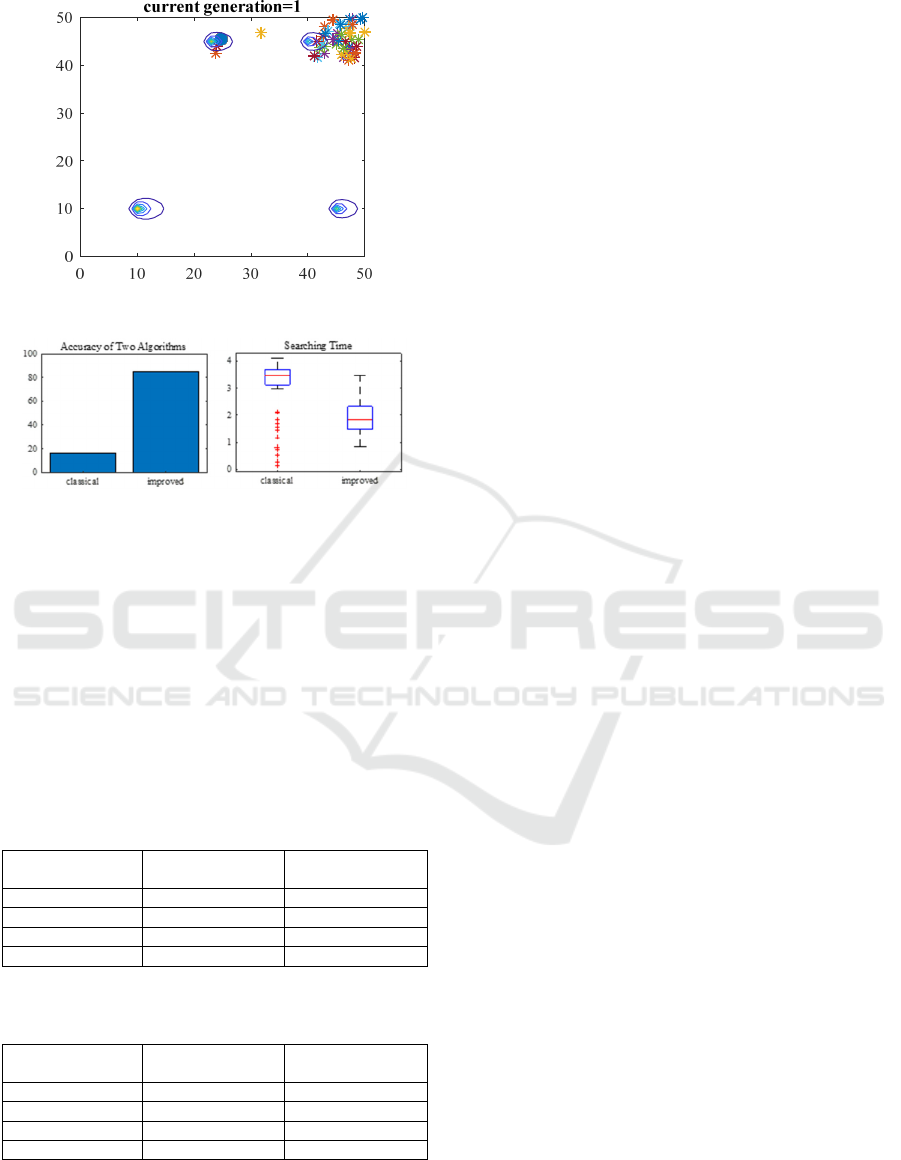
Figure 6: Initial distribution far from the largest source.
Figure 7: Accuracy and searching time of classical and
improved CSAs when cuckoos population is distributed far
from the largest source.
4.2 The Number of Sources
In this subsection, the performances of the classical
CSA and the Improved CSA are compared with
different number of sources set up in the designated
area. Table 1 records the median of the searching time
of the algorithms in 100 trials while Table 2 records
the accuracy of the algorithms in those trials.
Table 1: Searching time of the algorithms with different
number of sources.
Sources in the
area
Classical CSA
Time
Improved CSA
Time
1-2 0.4508 0.4467
1-4 0.8376 0.8294
1-6 0.9926 1.3213
1-7 1.1013 2.6410
Table 2: Accuracy of the algorithms with different number
of sources.
Sources in the
area
Classical CSA
accuracy
Improved CSA
accuracy
1-2 100% 98%
1-4 100% 97%
1-6 98% 98%
1-7 97% 96%
From Table 1 we can conclude even though both
algorithms search at increased time as the number of
sources increases, the improved CSA’s searching
time increases at a faster rate compared to that of the
classical CSA. This is because the improved CSA has
to search for all the sources and therefore the more
sources there are the more time it needs to find all of
them while for the classical CSA the sources only add
distractions to finding the largest source. From Table
2 we can conclude that the accuracy of both
algorithms are mostly maintained. Because of the
uniform distribution of the initial nest positions in this
simulation, the increase in the sources did not affect
the accuracy of the CSAs by much since they can
easily spot the different sources.
4.3 The Number of Cuckoos
In this subsection, the classical CSA and the
Improved CSA are simulated with different number
of cuckoos. Because is significantly changed,
needs to change accordingly to maintain the accuracy
and speed of the improved CSA. We set
to be
12% in this experiment because it gives us a
relatively good
to work with most of the time.
However, there can be a
that gives better results in
the different cases. In the case of 50 cuckoos, a better
to use is 5 instead of the output of the formula
which is 6, and that’s why we set
5 in the previous
simulations with 50 nests. Nonetheless, in this
subsection we would use the number calculated by
the formula as our
such that there’s less confusion.
Table 3 records the median of the searching time
of the algorithms in 100 trials while Table 4 records
the accuracy of the algorithms in those trials. Table 3
shows the number of cuckoos has a large effect on the
speed of the improved CSA. While the speed of the
improved CSA slightly increases with an increase in
number of cuckoos, the number of cuckoos during the
search has a larger impact on the classical CSA than
the improved CSA. From Table 4 we can see that
while the number of cuckoos generally don’t have a
big effect on the accuracy of both algorithms, the
accuracy and speed for the improved CSA decreased
sharply with the case of 10 cuckoos. This is because
there is no good
for the case with 10 cuckoos.
While according to our calculation
should be 2 in
the case of 10 cuckoos, it is really not a good
because this means once two cuckoos meet they
would declare that area as a source, leading to
declaration of incorrect areas as sources. However, a
larger than 2 would mean that the cuckoos have to
be less dispersed which means when the cuckoos
encounter a source, they might have to move away
from it to meet other cuckoos at another source
located further away from them, which greatly
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
714

increases the searching time. Nonetheless, if
improvements in accuracy is needed, a
of 4 is able
to increase the accuracy to around 85%, but with a
tradeoff in time for as long as 4.4918.
Table 3: Searching time of the algorithms with different
number of cuckoos.
Number of
Cukoos
Classical CSA
Time
Improved CSA
Time
10 1.9161 1.7611
30 1.1818 1.2394
50 0.7873 1.1571
70 0.3717 1.0639
Table 4: Accuracy of the algorithms with different number
of cuckoos.
Nummber of
Cuckoos
Classical CSA
accuracy
Improved CSA
accuracy
10 89% 72%
30 99% 95%
50 100% 93%
70 100% 93%
5 CONCLUSIONS
In this paper, an algorithm for the multiple odor
sources localization problem based on an improved
CSA has been proposed. The improved CSA uses the
ideas of territories and colonies to solve multiple odor
sources localization problem and is able to accurately
find all the sources in a relatively short period of time
with great accuracy. Simulation results show that the
improved CSA can successfully search for all the
odor sources in the area for mostly above 90% of the
times. In future work, we will try to shorten the
searching time this algorithm takes and possibly
derive a formal formula to use for
.
REFERENCES
Chen, X., Huang, J., 2019. Odor source localization
algorithms on mobile robots: A review and future
outlook. Robotics and Autonomous Systems, vol. 112,
pp. 123-136.
Shida, H., Nakayama, G., Nakamoto, T., et al., 2005.
Controlling a gas/odor plume-tracking robot based on
transient responses of gas sensors. IEEE Sensors
Journal, vol. 5, no. 3, pp. 537-545.
Marques, L., Nunes, U., Almeida, A. T., 2002. Cooperative
odour field exploration with genetic algorithms. In
Proceedings of the Fifth Portuguese Conference on
Automatic Control, pp. 138-143.
Pang, S., 2010. Plume source localization for AUV based
autonomous hydrothermal vent discovery. In
Proceedings of the OCEANS 2010 MTS/IEEE
SEATTLE Conference & Exhibition, Washington, USA,
pp. 1-8.
Wang, Y., Meng, Q. H., Zeng, M., 2011. Vision-aided
spiral-surge algorithm for odor source localization in
indoor natural ventilated environments. Mechanical
Engineering and Technology, vol. 125, no.1, pp. 751-
755.
Feng, Q., Cai, H., Li, F., et al., 2019. An improved particle
swarm optimization method for locating time-varying
indoor particle sources. Building and Environment, vol.
147, pp. 146-157.
Thomas, J., Ghose, D., 2009. Strategies for locating
multiple odor sources using glowworm swarm
optimization. In Proceedings of the Fourth Indian
International Conference on Artificial Intelligence, pp.
842-861.
Cao, M., Meng, Q. H., Wang, X., et al., 2013. Localization
of multiple odor sources via selective olfaction and
adapted ant colony optimization algorithm. In
Proceedings of the IEEE International Conference on
Robotics and Biomimetics, Shenzhen, China, pp.1222-
1227.
Yang, X. S., Deb, S., 2009. Cuckoo search via Lévy flights.
In Proceedings of World Congress on Nature &
Biologically Inspired Computing, pp. 210-214.
Yang, X. S., Deb, S., 2010. Engineering optimisation by
cuckoo search. International Journal of Mathematical
Modeling and Numerical Optimization, vol. 1, no. 4, pp.
330-343.
Valian, E., Mohanna, S., Tavakoli, S., 2011. Improved
Cuckoo search algorithm for global optimization.
International Journal of Communications and
Information Technology, vol. 1, no. 4, pp. 31-44.
Ghodrati, A., Lotfi, S., 2012. A hybrid CS/PSO algorithm
for global optimization. In Proceedings of the Asian
Conference on Intelligent Information and Database
Systems, pp. 89-98.
Srivastava, P. R., Khandelwal, R., Khandelwal, S., et al.,
2012. Automated test data generation using cuckoo
search and tabu search (CSTS) algorithm. Journal of
Intelligent Systems, vol. 21, no. 2, pp. 195-224.
Visscher, A. D., 2013.
Air dispersion modeling:
Foundations and applications, NJ, USA: Wiley.
An Improved Cuckoo Search Algorithm for Multiple Odor Sources Localization
715
