
Modeling and Simulation of Associative Reasoning
Jiří Jelínek
a
Institute of Applied Informatics, Faculty of Science, University of South Bohemia,
Branišovská 1760, České Budějovice, Czech Republic
Keywords: Associative Memory, Graph Structures, Human Reasoning, Knowledge Representation, Retrieval,
Processing.
Abstract: Modeling human behavior is a popular area of research. Special attention is then focused on activities related
to knowledge processing. It is the knowledge that has a fundamental influence on an individual's decision-
making and its dynamics. The subject of research is both the representation of knowledge and the procedures
of their processing. The processing also comprises associative reasoning. Associations significantly influence
the knowledge base used in processing stimuli and thus participate in creating a knowledge context that is
further used for knowledge derivation and decision making. This paper focuses on the area of associative
knowledge processing. There are already classical approaches associated with developing probabilistic neural
networks, which can also be used with modifications at a higher abstraction level. This paper aims to show
that associative processing of knowledge can be described with these approaches and simulated. The article
will present a possible implementation of the model of knowledge storage and associative processing on the
individual's knowledge base. The behavior of this model will be demonstrated in experiments.
1 INTRODUCTION
Modeling of human beings' behavior is a popular area
of research. The main goal here is to understand and
imitate human behavior to be further investigated and
eventually implemented in artificial systems to use its
positives. Special attention is then logically focused
on processes related to the individual's knowledge
and its use in processing external stimuli and realizing
decision-making processes. One possible way to learn
more about them is modeling brain activities focused
on creating and storing information and knowledge.
The subject of research is both the representation of
knowledge itself and the procedures of their
processing.
An essential part of these activities is associative
reasoning because it acts as a modifier in selecting
and processing knowledge. When processing the
external stimulus, this reasoning participates in
creating the knowledge context used for this
processing.
The internal representation of knowledge in the
brain is the active subject of intense research. The
theory about this topic can be found already in the 80s
(Warrington & McCarthy, 1983, 1987; Warrington &
a
https://orcid.org/0000-0002-1842-2055
Shallice, 1984).
The research of conceptual memory
and processing changes can also be found in
(Patterson et al., 2007), based on the study of neural
deceases. Other sources focus on examining sensory
data's internal representations on low-level (Smith et
al., 2012).
However, at a low level, it is clear that the brain
activities are based on massive parallelism in
a network of nodes (neurons), which have
a reasonably simple functionality. These nodes are
interconnected by many links of the same type with
unequal significance or permeability (influence of
synapses). The structure of these interconnections in
the brain is not flat, and we can find specialized areas
with a specific connection and purpose, but (to get
a notion) the above description is sufficient. The
number of neurons is in the hundreds of billions, and
the number of links is many times larger.
We do not know the concrete way of storing
knowledge in the above structure. However, if we use
knowledge about artificial neural network models, it
is probably a combination of a suitable
interconnection and setting the throughput (weights)
of connections. Thus, a very large-scale graph
structure is used.
716
Jelínek, J.
Modeling and Simulation of Associative Reasoning.
DOI: 10.5220/0010234707160723
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 716-723
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

If we use a certain degree of abstraction, the same
form of knowledge representation can represent
concepts and their links. However, other approaches
could also be used, e.g., formal logic tools with
temporal and spatial extensions. Some principles,
known from database technologies, can also be used,
such as relational data representation. Also, a possible
way is to use the objects; this is understandable to
people due to its similarity to the environment in
which people live, and we can find it in (Caramazza
& Mahon, 2006). Others use the object-attribute-
relation approach to describe this representation
(Wang, 2007).
However, all these structures can be implemented
at a lower level using graphs with the appropriate
node and link types. The idea of graph knowledge
representation can be found, e.g., in (Hayes, 2003).
Therefore, in our paper, we will prefer a graph
representation of knowledge in the form of concepts
and their relationships.
The rest of the article is organized as follows. In
Section 2, we look at the basics of associative
knowledge processing. In Section 3, the proposed
simulation model will be presented. In Section 4,
some experiments performed with the model are
discussed. At the end of the article, we will
summarize the findings and discuss the results.
2 RELATED WORK
The human brain's associative abilities in working
with data can be viewed from different angles. They
can also be categorized as a part of the knowledge
retrieval area. If we focus on modeling human
behavior, then, based on the human brain structures,
it seems that a suitable universal basis for storing
knowledge is graph representation. That also allows,
among other things, a very variable application of
higher formal knowledge representations.
Modeling the process of associative reasoning has
a relatively long history in the field of artificial
intelligence. As early as 1982, Hopfield came up with
its single-layer artificial neural network (Hopfield,
1982), sometimes referred to as auto-associative
memory. It is a recurrent neural network, where the
information is stored in dynamically stable attractors
of the network state. The network is assumed to be
symmetric (weights from node i to j are the same as
from node j to node i, w
ii
= 0). However, this is not
always the case with human reasoning. The network
learning mechanism then has two development
variants, binary and continuous. A continuous variant
is closer to our goals, whose dynamics can be
described according to formula (1).
𝑠
=𝑤
.𝑠
−𝜃
(1)
In formula (1), Ø
j
is the threshold of node j, w
ij
is the
weight of the link between nodes i and j, and s
j
and s
i
are states (activations) of nodes j and i. The use of the
above formula for network state updates can be
synchronous (in a single moment for all network
nodes) or asynchronous (at a given time or step, one
selected node's status is updated).
If we want to use the Hopfield network as
associative memory, we will first teach it to represent
a stored pattern (information, knowledge). The stored
information could then be entirely recalled by setting
(activating) any node within the respective attractor
range. For the network learning, the generalized Hebb
learning rule (Hebb, 1949) described by formula (2)
can be used, based on the neurobiological observation
that the bond strength increases when neurons at both
ends are activated simultaneously. For this basic
learning algorithm, it was empirically found that it is
possible to store about 0.15 N patterns in the binary
Hopfield network, which can then be called by
association (the number of nodes in the network is
denoted as N) (Jain, 1996).
𝑤
=𝑤
.+α 𝑠
𝑠
(2)
In formula (2), w
ij
is the weight of the link between
nodes i and j, s
i,
and s
j
are both end neurons'
activations. The learning parameter α has a standard
meaning and allows us to adjust the learning speed
and strength. Formula (2) is one of the oldest
algorithms for learning neural networks.
The above-described approach shows that the
graphs or networks are not new structures when
examining associative behavior. The proposed model
also uses them but assumes asymmetric links and
their weights (w
ij
≠
w
ji
). Our model also uses
modifications of the formulas mentioned above. An
interesting application of associative processes is
mentioned in (Diehl, 2009), where they are used for
information management on PDA.
Another approach to using graphs for associative
reasoning is to move up on a higher level of
abstraction and examine the links between concepts
in the knowledge base. Here, a stochastic approach is
often applied, where the weights of nodes and edges
in the graph are interpreted as probabilities of
occurrence of these elements. So, we are talking
about so-called probabilistic networks, also referred
to as Bayesian networks.
Modeling and Simulation of Associative Reasoning
717

These networks also apply probabilistic
reasoning. The basis here is formula (3) for
conditional probability, where P(i) is the probability
of the concept represented by node i. The notation
P(j | i) is then the probability of concept j with the
condition of concept i and thus relates to the oriented
edge between the two nodes.
𝑃
(
𝑗
|
𝑖
)
=𝑃(
𝑗
,𝑖) 𝑃(𝑖)
⁄
(3)
For several currently valid independent conditions,
the relationship can be adjusted to formula (4).
𝑃
(
𝑗
|
𝑖,𝑘,𝑙
)
=𝑃(
𝑗
,𝑖,𝑘,𝑙) 𝑃(𝑖,𝑘,𝑙)
⁄
(4)
When having the number of occurrences c of
individual nodes, the given formula can be modified
to formula (5).
𝑃
(
𝑗
|
𝑖,𝑘,𝑙
)
=
𝑐(
𝑗
∧𝑖∧𝑘∧𝑙)
𝑐
(
𝑖∧𝑘∧𝑙
)
(5)
The precondition for using these formulas is the
independence of the concepts i, k, and l. This
condition is problematic and hard to meet in networks
with the complex interconnection of nodes. However,
we can learn from that. A similar approach is used in
the presented model, but the specific formulas for
calculating the weights of edges are modified.
Procedures from fuzzy logic are also applied.
The social contextual influence on perceptual
processes is discussed in (Otten et al., 2017). The
importance of context for knowledge processing is
also the base idea of our model.
2.1 Graphs and Terms
For a graph representation, the key is what the nodes
of the graph represent. At a higher level of
abstraction, these can be concepts with which the
individual works. With their help, the individual (or
agent simulating him) describes himself and his
surroundings. This assumption of concept nodes is
followed up by using links between them representing
different types of interrelationships.
The concepts can be described in various ways.
Their minimal description is the identification of the
concept (term). If we use the WordNet terminology
(Miller, 1995), this will be a so-called synset. If we
assume that a textual description of a term is uniquely
tied to a single synset, this synset can be identified by
this textual description. Otherwise, the text can be
extended with a unique part to meet the above-
assumed condition. The text is then the primary
identification of the term. Other data can further
extend the description of the concept. In different
representations, the added information may differ.
For example, in the object representation, it may be
properties or behavior associated with the object
identified by the term. The extension may also
involve the addition of metadata, i.e., spatial and
temporal data linked to the concept's observation.
The graphical representation used in the paper
allows supplementing these extensions; in the form of
other concepts and interconnections. Thus, this
representation is very flexible and will enable us to
work in a single knowledge base with several higher
knowledge representation paradigms.
3 PROPOSED MODEL
The presented model is based on a graph
representation of concepts and uses only a single type
of link necessary to simulate associative reasoning
(association relation). The model uses a general
approach and has only a very few requirements on
stored concepts; it just needs their text identification.
It aims to show the abilities of humans' associative
reasoning based on the simultaneous observation of
individual concepts. Concurrence can be in temporal
and spatial dimensions and, based on others, at first
glance, invisible connections. The agent does not
know how the observed concepts are ontologically
linked and therefore treats them in the same general
way.
3.1 Model Principles
The basis of the model's operation is the assumption
that the individual uses its sensors to receive stimuli
from the environment at a given point in time. In these
stimuli, he can recognize concrete perceptions,
objects, or entities (concepts) identified by their name
or at least by temporary identification (for new and as
yet unknown concepts). Information about concepts
is stored in the knowledge base, together with
numbers of concepts' occurrence and activation
levels. The counts of occurrences enable us to respect
the probabilistic relations. The activation is the
primary tool when modeling the dynamics of the
whole simulation. Its values for nodes and links are
updated in each step according to previous data and
current observation.
The model is based on the assumption that an
individual, when using his knowledge, does not
always use his entire knowledge base, but only a part
of it, which is currently activated by the observed
concepts. So, a specific knowledge context is creating
for subsequent work with knowledge. It is this
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
718
knowledge context creation process that the model
tries to implement.
The model's input is an observation represented
by a list of terms that describe concepts
simultaneously observed. However, some of these
terms (concepts) may not express what the individual
recorded but may also represent other metadata
(individual's position at the time of observation,
current time, source of observation, and others); these
metadata are then considered as separate concepts.
The count of occurrence is incremented for each
observed concept.
All simultaneously observed concepts are fully
interconnected by oriented relationships (links,
edges) whose certainty (probability) is continually
adjusted in the simulation, based on several factors
(see below). Based on observations, the individual
creates his internal knowledge base and a model of
the world around him.
3.2 Model Details
The activity of the model can be (similarly as for
artificial neural networks or other models from the
machine learning area) divided into two phases: the
reasoning phase (production) and the setting's
modification phase (learning). However, these two
phases cannot be separated from each other; even the
reasoning brings up changes in the activation of nodes
and connections, and the model thus modifies at the
same time.
Actions from both the above phases repeatedly
proceed within the simulation. Each simulation step
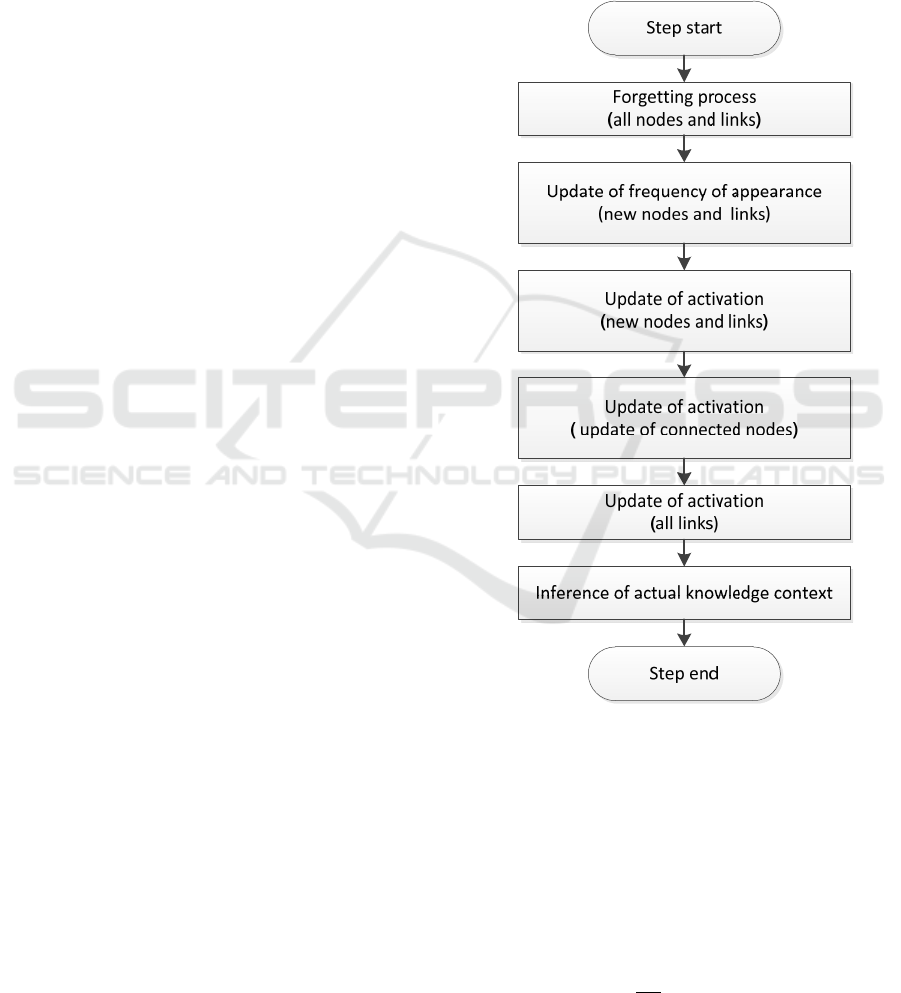
includes the activities shown in Fig. 1.
The activities in the picture can be divided into
four categories:
• Implementation of the forgetting process
• Management of the counts of occurrence
• Node and edge activation settings
• Derivation of the current context
The first action in each step is to model forgetting,
which considers the simulation time course. The
model assumes that the previously observed concepts
gradually lose their importance after a new
observation and are overlapped with the new ones.
Therefore, the activation of these nodes decreases.
A similar process takes place for links. However,
several aspects must be respected when adjusting link
activations. The forgetting is then realized by
calculation according to formulas (6).
𝑙
=𝑙
.
𝑓
𝑠
=𝑠
.
𝑓
(6)
Separate parameters (f
t
for concepts and f
l
for
relationships) were used for nodes and connections,
both with values in (0; 1). One means that the
forgetting process is excluded, and the zero value
represents a state where the individual forgets all
activation values from previous observations. Two
separate parameters are used due to their different
influence on the model's operation and thus the
possibility of their different settings in experiments.
Figure 1: Actions in one step of the simulation.
The next phase of each simulation step is to
update the counts of occurrence of nodes and edges.
This action only applies to newly observed objects
and their interconnections. Counts are then used for
setting the primary activations of the links.
The value of the new link activation must consider
more factors. Therefore, it is calculated in several
steps. Here, the lowest (basic) value p
ij
of link activity
is calculated according to formula (7).
𝑝
=
𝑛
𝑛
=𝑃(
𝑗
|𝑖)
(7)
Modeling and Simulation of Associative Reasoning
719

In formula (7), n
ij
denotes the occurrences of a given
link, and n
i
occurrences of the concept i. The p
ij
values
are considered long-term and static, representing the
relationship's certainty or probability.
If nodes or edges with the same identification
already exist in the knowledge base, their occurrence
count is incremented. Otherwise, new objects are
added to the database with an occurrence of 1. Next,
the activations s
i
and l
ij
of the newly observed
concepts and connections are set to 1.0 (very actual),
both for nodes and links.
The following phase of the simulation is the most
computationally demanding part of the model. Its
effectiveness depends very much on the appropriate
representation of the entire collection of nodes and
their connections. The activations of all nodes in the
knowledge base are being modified here using the
breadth-first search mechanism for selecting the
nodes with a start on currently observed ones. The
new values are calculated according to formula (8). If
the new activation value is lower than the original
one, the higher value is used. This procedure
guarantees that the new activation value will be the
highest possible, respecting all the links that point to
the node.
𝑠
=max
∈
𝑠
,𝑠
.𝑙
(8)
In formula (8), s
j
is the activation of the term j, s
i
the
activation of the term i, from which there is a direct
link to the term j, and l
ij
the reliability of this link. The
P is a set of nodes preceding (in terms of existing
connections) the term j. The logic of using the highest
value of certainty of occurrence is based on the fact
that each manipulation with a given term causes its
reactivation. As a result of this step and disseminating
information about the new observation, the activation
of all terms associated with the observed ones by
correctly oriented links (also by multiple links across
other nodes) will be adjusted.
The next phase of the simulation step is the update
of the link activations. This step must respect both the
static probability of the link according to formula (7),
the process of forgetting according to formula (6) and
also it is necessary to respect the neurobiological
observation and Hebb's rule of learning expressed by
formula (2). Activation is then calculated according
to relation (9).
𝑙
=max𝑝
,𝑠
𝑠
,𝑙
(9)
In the formula, 𝑙
is the actual value of link activity
from the previous step after using the forgetting
mechanism, 𝑙
is the new link activation, p
ij
is the
value of the conditional link probability. The s
i
and s
j
are the current activations of nodes i and j and product
s
i
. s
j
represents the Hebb rule.
All of the previous actions in the simulation step
result in the current setting of activations in the
knowledge base. Then only nodes and links with
activation higher than the selected threshold are
considered relevant and used in following cognitive
and decision-making processes (not presented in this
paper). These objects thus form the so-called
knowledge context. The thresholds may (according to
our needs) differ for nodes and links. Therefore, two
limit parameters a
t
and a
l
are used. Thus, only nodes
that satisfy the relationship are included in the current
context (10).
𝑠
>= 𝑎
(10)
For links, the fulfillment of the formula (11) is
required. The limit of link activation must be reached,
but both its ends must also be in the context.
𝑙
>= 𝑎
⋀
(
𝑠
>= 𝑎
)
⋀ 𝑠
>= 𝑎
(11)
The presented model works primarily with the
temporal concurrence of concepts. However, thanks
to the possibility of including other metadata (e.g., the
place of observation) as the additional concepts in
observation, the spatial and possible other
concurrences can also be respected.
3.3 Model Implementation
The described model was implemented in Java and
took full advantage of the running program threads in
parallel.
Two ways of working with the model were tested.
The first operation mode implements only a subset of
the activities of Fig. 1 and allows the model to be run
only in the input observation processing mode. In it,
only the counts of the occurrence of nodes and edges
are stored. Therefore, the created graph base is
focused on capturing long-term and statistically based
information, which, however, does not capture the
dynamics of the associative reasoning process. This
mode can thus be used to create a basis for the graph
knowledge base. The activation of objects is not set,
and the base is thus ready for further use without the
influence of its creation on the association process.
The mode can be therefore referred to as initial. This
mode may or may not be used, but its main advantage
is the high-speed processing of a large volume of
input observations.
There are many solutions for implementing graph
data storage from relational through various NoSQL
databases to their specific type, graph databases. An
internal representation storing the data in the working
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
720
memory was used to achieve the maximum speed of
data processing.
However, the model's primary operating mode is
the full mode implementing for each observation the
set of activities shown in Fig. 1. It ensures complete
capture of knowledge base development dynamics
and the activation of individual relationships and
concepts during the simulation. This mode can be
used right from the beginning of working with the
model, and during it, a graph base is created from
scratch. However, it can be used even after the initial
mode, and then it will work with the already prepared
basis of the knowledge base, and it will expand it
further. This operation mode of the model is thus
significantly oriented to the current state of
knowledge. It evokes a certain resemblance to short-
term memory, where nodes and links that do not have
a significant number of occurrences can be very
active during some time after we observe them.
4 EXPERIMENTS
The FreeBase dataset (Kuznetsova et al., 2018) was
used to test the model. It includes a database of
approximately 5.6 million annotated images. The
annotation is created both expertly and with the help
of automatic derivation. It is in the form of a list of
entities (concepts) identified in a particular image.
This description corresponds with the model's
requirements on input data. Every image was
supposed to be one observation of the world.
The dataset mentioned above was used in two
ways. The first one was testing of the model
performance, where the entire dataset was used.
During the initial mode was imported 19,508 nodes
and 79,399,030 links between them. A computer with
a minimum of 32 GB RAM was used to process this
volume of data. All data were imported within a few
tens of seconds.
The second way of using the dataset was to
examine the dynamics of association processes. The
following experiments were carried on the subset of
1,000 image annotations from the dataset with 2,304
nodes and 113,496 links.
The first experiment was focused on examining
the dynamics of knowledge base creation using the
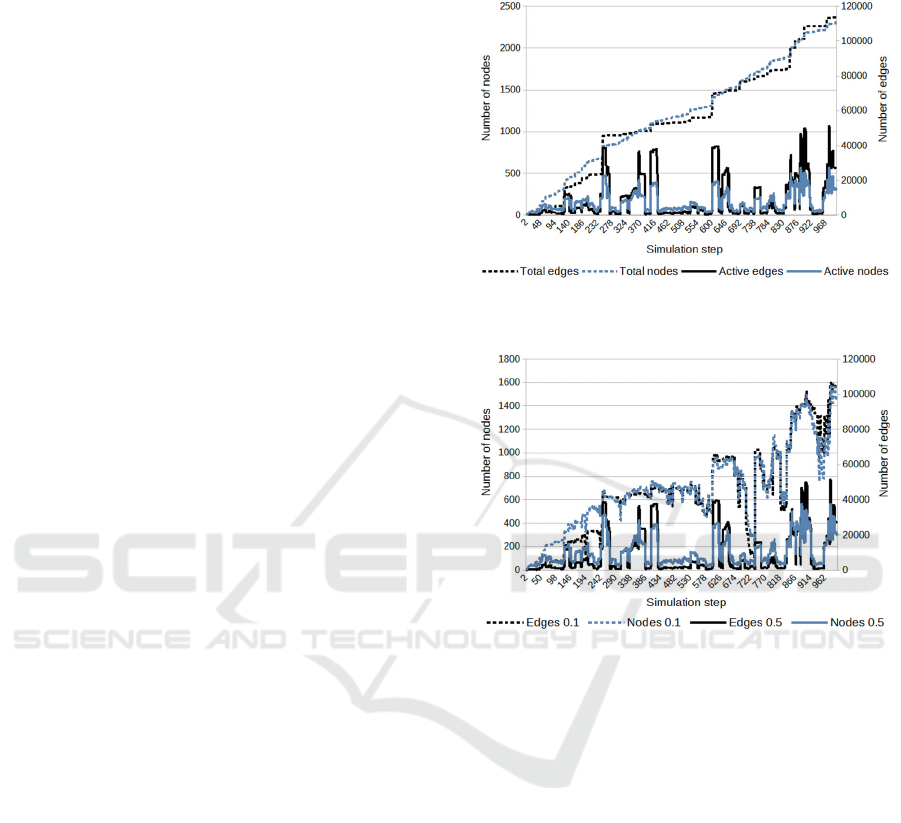
model's main mode. The results can be seen in Fig. 2,
where both the total numbers of nodes and edges
(totals) and their numbers in the current context
(active objects) are displayed. The simulation was
performed in 1000 steps; in each step, an annotation
of one image from the above set (observation) was
used as input. The values a
t
= a
l
= 0.5 were used to
generate the context. Forgetting parameters were set
to f
t
= 0.95 and f
l
= 0.97.
Figure 2: Creation of graph base.
Figure 3: Comparison of contexts created with activation
limits of 0.1 and 0.5.
The previous experiment's context sizes were
compared with setting a
t
= a
l
= 0.1 to examine the
effect of the activation limit values on the context
size. The results are in Fig. 3, and the difference is
visible here; the lower values of limit cause more
nodes and edges in the context.
The next experiment was performed to verify the
influence of the initiation mode on the created
context. The initiation mode was followed by the
submission of all 1000 image annotations as in
previous experiments. The results are given in Fig. 4,
comparing this experiment with the first one (Fig. 2).
The differences in numbers of objects in contexts
are minimal both for nodes and edges. When using
the initiation mode, the counts of occurrence were
already set, and the following main mode further
increased them gradually. That caused the small
differences. The forgetting parameters' values did not
change; the activation limit values a
t
and a
l
were 0.5
both.
Modeling and Simulation of Associative Reasoning
721
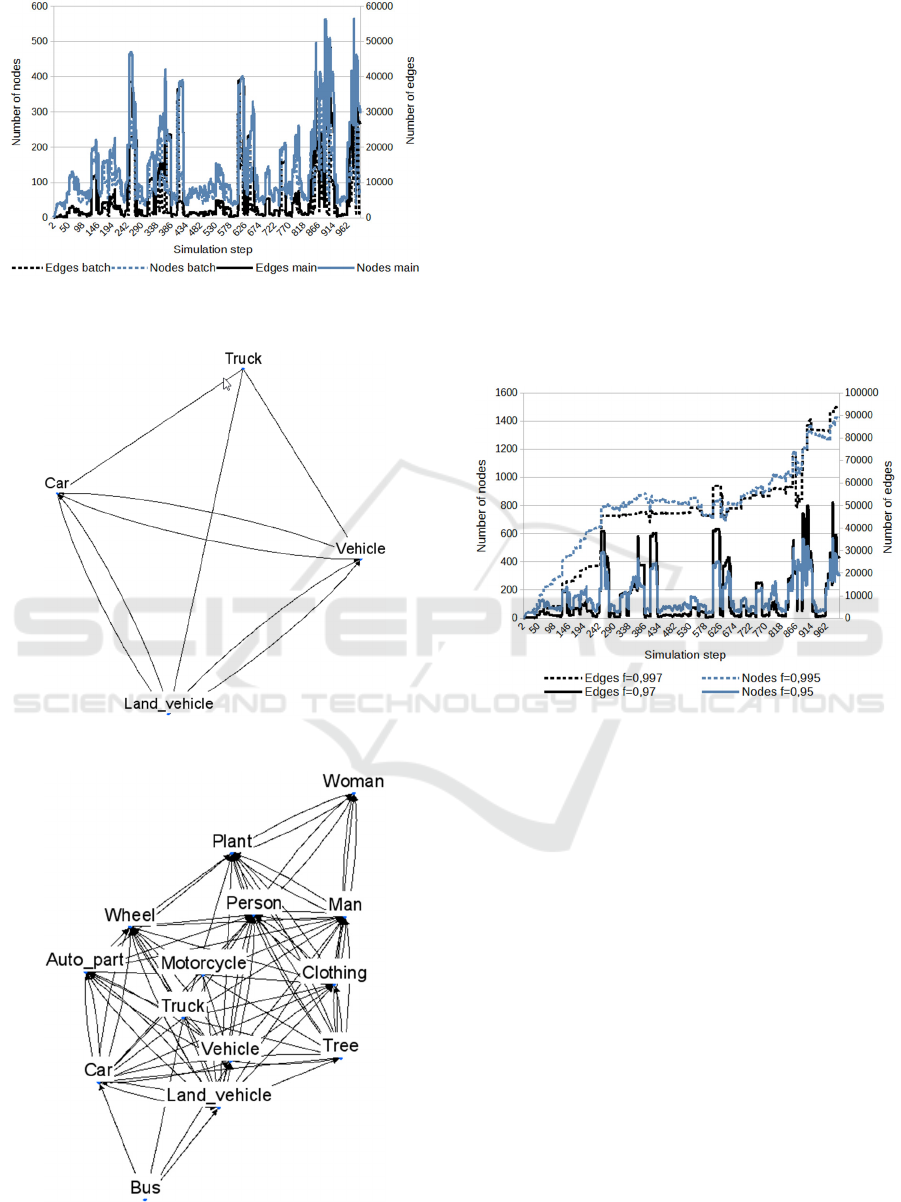
Figure 4: Comparison of contexts created with initiation
mode (init) and without it (main).
Figure 5: The context based on a single term "Truck."
Figure 6: The context based on a sequence of terms ended
with the term "Truck."
Another experiment focused on examining the
internal composition of the context. The starting point
was the same knowledge base, as in the previous
cases created using the model's initial mode. The
model's main mode was subsequently used on the
knowledge base. Separate concepts were introduced
so that no new interconnections were added. In the
first case, the only term "Truck" was entered, and the
created context is shown in Figure 5.
The influence of the previous observations on the
context can be seen in Fig. 6, where before the term
"Truck," the words "Bus," "Motorcycle," "Man," and
"Plant" were entered. The context is much broader
and also contains terms not directly connected to the
word "Truck." The activation limit here was again
0.5.
Figure 7: The influence of forgetting factors f
t
and f
l
.
Both forgetting factors f
t
and f
l
also have a
significant influence on the context. This effect can
be demonstrated in Figure 7, where two different
settings are used: the original f
t
= 0.95 and f
l
= 0.97
used in previous experiments and the adjusted
f
t
= 0.995 and f
l
= 0.997. Less influence of forgetting
leads to compensation of fluctuations in context
creation dynamics and a more significant number of
included nodes and links.
5 CONCLUSIONS
The presented paper introduces a model of associative
reasoning used by humans, which simulates this
process, including its dynamics. The model works
with the individual's observations. These define the
concepts and their interconnections, which both have
to be stored. With the help of the knowledge context
created during associative reasoning, it is then
possible, in information and multiagent systems, to
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
722

consider the agent's personal history and thus better
capture the agent's individuality.
In its processes, the model respects long-term and
short-term links between concepts. Functionally the
model is partly based on Hopfield's auto-associative
memory and Hebb's rules of learning, whose it
modifies for given conditions and goals.
The model was tested on a dataset of annotated
images. The results demonstrate the model's ability to
perform associative reasoning and create a current
knowledge context usable for other agent processes.
That was the main goal of the work. The results also
show that the whole process is significantly affected
by global parameters, mainly forgetting coefficients
and limiting objects' activation when generating
context.
Future research will focus on further testing the
model, both in terms of its efficiency and
performance in processing large graph structures and
its compliance with the observed human behavior. In
a longer perspective, the goal is to use the model in
other projects focused on multiagent systems and
behavioral simulations.
Work on the model will also focus on the
possibilities of processing data of a different nature.
The annotation of the images probably best
demonstrates the model activity, but time series or,
more generally, data captured in relational structures
can also be processed. The model can then provide a
different view of this data and the possibilities of its
processing.
REFERENCES
Caramazza, A., Mahon, B.Z., 2006. The organisation of
conceptual knowledge in the brain: The future's past
and some future directions. Cognitive
Neuropsychology, 23(1), pp. 13-38.
Diehl, J., 2009. Associative personal information
management. CHI '09 Extended Abstracts on Human
Factors in Computing Systems (CHI EA '09). ACM,
New York, NY, USA, pp. 3101–3104.
Hayes, P. J., 2003. Knowledge representation.
Encyclopedia of Computer Science. John Wiley and
Sons Ltd., GBR, 947–951.
Hebb, D. O., 1949. The organization of behavior. John
Wiley & Sons, New York.
Hopfield, J. J., 1982. Neural networks and physical systems
with emergent collective computational abilities.
Proceedings of the national academy of sciences, 79(8),
pp. 2554-2558.
Jain, A. K., Mao, J., Mohiuddin, K. M., 1996. Artificial
neural networks: A tutorial. Computer, 29(3),
pp. 31- 44.
Kuznetsova, A., Rom, H., Alldrin, N., Uijlings, J., Krasin,
I., Pont-Tuset, J., Kamali, S., Popov, S., Malloci, M.,
Kolesnikov, A., Duerig, T., Ferrari, V. (2018). The
open images dataset v4: Unified image classification,
object detection, and visual relationship detection at
scale. arXiv preprint arXiv:1811.00982.
Miller, G. A., 1995. WordNet: A Lexical Database for
English. Communications of the ACM, Vol. 38, No. 11:
pp. 39-41.
Otten, M., Seth, A.K., Pinto, Y., 2017. A social Bayesian
brain: How social knowledge can shape visual
perception. Brain and cognition, 112, pp. 69-77.
Patterson, K., Nestor, P.J., Rogers, T.T., 2007. Where do
you know what you know? The representation of
semantic knowledge in the human brain. Nature
reviews neuroscience, 8(12), pp. 976-987.
Smith, M.L., Gosselin, F., Schyns, P.G., 2012. Measuring
internal representations from behavioral and brain
data. Current Biology, 22(3), pp. 191-196.
Wang, Y., 2007. The OAR model of neural informatics for
internal knowledge representation in the
brain. International Journal of Cognitive Informatics
and Natural Intelligence (IJCINI), 1(3), pp. 66-77.
Warrington, E.K., McCarthy, R., 1983. Category specific
access dysphasia. Brain, 106(4), pp. 859-878.
Warrington, E.K., McCarthy, R.A., 1987. Categories of
knowledge: Further fractionations and an attempted
integration. Brain, 110(5), pp. 1273-1296.
Warrington, E.K., Shallice, T., 1984. Category specific
semantic impairments. Brain, 107(3), pp. 829-853.
Modeling and Simulation of Associative Reasoning
723
