Decoupling State Representation Methods from Reinforcement Learning
in Car Racing
Juan M. Montoya
1
, Imant Daunhawer
2
, Julia E. Vogt
2
and Marco Wiering
3
1
Department of Computer Science, University of Konstanz, Germany
2
Department of Computer Science, ETH Zurich, Switzerland
3
Bernoulli Institute for Mathematics, Computer Science and Artificial Intelligence, University of Groningen, The Netherlands
Keywords:
Deep Reinforcement Learning, State Representation Learning, Variational Autoencoders, Constrastive Learning.
Abstract:
In the quest for efficient and robust learning methods, combining unsupervised state representation learning
and reinforcement learning (RL) could offer advantages for scaling RL algorithms by providing the models
with a useful inductive bias. For achieving this, an encoder is trained in an unsupervised manner with two state
representation methods, a variational autoencoder and a contrastive estimator. The learned features are then fed
to the actor-critic RL algorithm Proximal Policy Optimization (PPO) to learn a policy for playing Open AI’s
car racing environment. Hence, such procedure permits to decouple state representations from RL-controllers.
For the integration of RL with unsupervised learning, we explore various designs for variational autoencoders
and contrastive learning. The proposed method is compared to a deep network trained directly on pixel inputs
with PPO. The results show that the proposed method performs slightly worse than directly learning from pixel
inputs; however, it has a more stable learning curve, a substantial reduction of the buffer size, and requires
optimizing 88% fewer parameters. These results indicate that the use of pre-trained state representations has
several benefits for solving RL tasks.
1 INTRODUCTION
In reinforcement learning (RL), decoupling image pro-
cessing and policy learning could allow scaling RL
algorithms to a multiplicity of (cheap) hardware, as
well as to speed up learning by providing the agent
with a good inductive bias. Instead of training an agent
using high-dimensional pixel data as input, in this pa-
per we investigate how self-supervised learned state
representations generalize to solving an RL task. This
approach has several advantages such as the need to
adapt fewer parameters when RL is used and more
possibilities to use transfer learning.
The benefits of training state representations and
combining these with RL has been explored before
(e.g., Hafner et al., 2019, 2020; Ha and Schmidhuber,
2018; Wahlstr
¨
om et al., 2015; Zhang et al., 2018; Lee
et al., 2019). Variational autoencoders (VAE) (Kingma
and Welling, 2014) have been used to enable efficient
planning in latent space in model-based RL, heavily
reducing the number of experiences required for learn-
ing a good policy (Hafner et al., 2019, 2020). Fur-
thermore, generative recurrent neural networks have
been used for learning to model the environment and
train an agent entirely by using “hallucinated” experi-
ences generated from its learned world model (Ha and
Schmidhuber, 2018).
More recently, contrastive learning (Smith and Eis-
ner, 2005; Gutmann and Hyv
¨
arinen, 2010; Oord et al.,
2018) was shown to be a promising, decoder-free
approach for self-supervised representation learning.
Hjelm et al. (2019) demonstrate that across many Atari
environments contrastive learning is effective in cap-
turing detailed state information, without needing su-
pervision from rewards. Srinivas et al. (2020) used off-
policy control based on representations learned with
contrastive learning; their approach performed well on
complex tasks in the DeepMind Control Suite and on
Atari games. Furthermore, Ding et al. (2019) used con-
trastive learning with model-based RL for improving
robustness against perturbed visual backgrounds.
In this paper, we investigate the transfer of pre-
trained self-supervised state representations to an RL
agent. Most previous work has focused on either as-
sessing the quality of learned representations through
known generative factors (such as the locations of
objects in an image) or on end-to-end RL. Previous
work (Lange and Riedmiller, 2010; Lange et al., 2012)
752
Montoya, J., Daunhawer, I., Vogt, J. and Wiering, M.
Decoupling State Representation Methods from Reinforcement Learning in Car Racing.
DOI: 10.5220/0010237507520759
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 752-759
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

implemented Deep Reinforcement Learning using au-
toencoders for image processing with a two-step proce-
dure. Raffin et al. (2019) decoupled feature extraction
from policy learning for goal-based robotics tasks im-
proving the results compared to end-to-end training,
whereas others (Srinivas et al., 2020; Stooke et al.,
2020) researched auxiliary tasks with contrastive es-
timators to decouple state representations from RL-
controllers. In the same spirit, our approach decouples
these components—state-representation learning and
reinforcement learning—yet, our approach freezes the
pre-trained representations unlike previous approaches
(Lange and Riedmiller, 2010; Lange et al., 2012). Con-
trary to Raffin et al. (2019) our model feeds the rep-
resentations to the RL controller without adding ad-
ditional models or using auxiliary tasks to improve
sample efficiency (Srinivas et al., 2020; Stooke et al.,
2020). This allows us to examine more systematically
what makes a good representation and provides a fair
comparison of different methods for self-supervised
state representation learning.
Summarizing, this work provides an empirical
study on how self-supervised state representation learn-
ing can provide a useful inductive bias for RL. As a
proof of concept, we study the OpenAI environment
CarRacingV0. Our study led to the following observa-
tions:
• An agent that is trained on pre-trained state rep-
resentations reaches a slightly worse performance
than an agent that learns from raw pixels, but bene-
fits from a significant increase in training stability.
• The learned state representations are improved
considerably by training a sequential VAE with
frameskip and a contrastive estimator with infor-
mation about performed actions.
• Saving state representations instead of images dur-
ing an episode considerably reduces memory over-
head and the amount of trainable parameters.
This paper is structured as follows. Section 2 explains
the proposed two-step approach for combining RL and
State Representation Learning. In Section 3, related
literature is reviewed in detail. Section 4 describes the
experimental set-up and in Section 5 the experimental
results are shown. Section 6 discusses implications
and possibilities for future research. Finally, Section 7
provides our conclusion.
2 METHODS
Proximal Policy Optimization (PPO). RL agents
receive feedback on their actions in the form of
rewards from interacting with an environment. An
agent aims to solve a sequential decision-making
problem by optimizing the cumulative future reward
intake (Sutton and Barto, 2018). PPO (Schulman
et al., 2017) is a popular on-policy algorithm with
an actor-critic architecture for continuous spaces.
PPO performs not just one but multiple mini-batch
gradient steps with the experience of each iteration.
One reuses the same data to make more progress
per iteration, while stability is ensured by limiting
the divergence between the old and updated policies.
From the two proposed variants of the original paper,
we implemented the clipped surrogate loss function.
State Representation Learning. The environment
provides an agent with a typically high-dimensional
input, such as the frame of a video sequence, at each
time step. As part of the agent, the role of an en-
coder is to compress a high-dimensional input to a
lower-dimensional representation that is useful for the
task at hand. To train an encoder from observational
data, we consider two different self-supervised learn-
ing algorithms, a variational autoencoder (VAE) and
contrastive learning:
• VAE (Kingma and Welling, 2014) is a generative
model that is trained by maximizing a variational
lower bound on the log-likelihood of the training
data. It learns a lower-dimensional representation
that is useful for reconstructing the original input,
while also matching a prior distribution. Since the
VAE optimizes the reconstruction loss, the learned
representations typically encode information about
large salient objects.
• Contrastive Learning is a self-supervised method
for learning representations based on noise con-
trastive estimation (Smith and Eisner, 2005; Gut-
mann and Hyv
¨
arinen, 2010) that does not require
a decoder. Intuitively, it is based on learning an
encoding that maximizes the similarity between
positive pairs and the dissimilarity between neg-
ative pairs. In particular, we use the InfoNCE
estimator (Oord et al., 2018) and, analogous to
previous work, define positive pairs by different
data-augmentations of the same image and nega-
tive pairs by random pairs of images, obtained by
permuting a mini-batch.
Figure 1 illustrates how state representation learning
and reinforcement learning are combined. First,
an encoder is trained through self-supervision and
then the pre-trained encoder is used for training the
reinforcement learning agent. We aim to analyze
possible advantages by separating these compo-
nents. In the following, we describe the individual
components and formalize the benefits of such a
decoupling. Afterward, we discuss the advantages
Decoupling State Representation Methods from Reinforcement Learning in Car Racing
753

Policy
Reinforcement
Learning
Algorithm
Agent
Policy
Update
Observation
o
t
Action
a
t
z
t
Reward
r
t
Policy Nets
Encoder
g(o
t
)
Environment
a
t
Figure 1: Illustration of an RL framework where the encoder
is decoupled from the agent’s policy network. Notice that
the policy updates are not propagated back into the encoder.
of our two-step approach for decoupling RL agents.
Then, we introduce our task-specific modifications to
the VAE and InfoMax models: VAE-Frameskip and
InfoMax-Action.
Encoder. The encoder g maps a high-dimensional
observation o
t
∈ R
m×n
, observed at time t , to a lower
dimensional representation z
t
∈ R
d
. As previously
discussed, we consider two different types of encoders,
VAE as well as the encoder of a constrastive estimator.
Policy Networks. The policy networks map from la-
tent space to the values required to learn a policy. For
PPO, there is one function for the critic, v(z
t
;θ
v
) =
v
t
∈R , and one for the actor, π(z
t
;θ
π
) = a
t
∈R , where
θ denotes the respective network parameters.
2.1 Advantages of Decoupled RL
Agents
The use of pre-trained state representations provides
several advantages for training an RL agent, com-
pared to training it on raw inputs. First, PPO re-
quires a large memory replay buffer consisting of tu-
ples (o
t+1
, o
t
, a
t
, r
t
) . By using low-dimensional em-
beddings z
t
instead of high-dimensional observations
o
t
, the memory footprint is reduced at least
√
mn in
the regular case of d equal or smaller than m and n .
Second, when training the agent, we freeze the weights
of the pre-trained encoder, which accounts for the ma-
jority of weights in the model. For instance, in the
considered architecture for CarRacingV0, the policy
network has around 13K weights, while the encoder
has around 142K weights—a significant reduction of
about 88% in the number of free parameters, compared
to an agent that is trained directly on pixels.
Figure 2: Illustration of the input for VAE-Frameskip.
2.2 VAE-Frameskip and
InfoMax-Action
VAE-Frameskip. The VAE uses multiple frames as
input. In particular, we found that it is important to use
the same frameskip (i.e., the same spacing between
observed frames) as for the RL agent. We chose
heuristically the same frameskip as in the baseline:
frameskip of size eight with a stack of four images,
so the VAE takes (o
t
, o
t+8
, o
t+16
, o
t+24
) as input as
illustrated in Figure 2.
InfoMax-Action. InfoMax-Action is an extended ver-
sion of spatiotemporal InfoMax (Hjelm et al., 2019),
where, in addition to spatial and temporal contrasting,
we add contrasting between observations and actions.
Thus, there are three contrasting objectives: (1) spa-
tial contrasting with random patches from the same
image and random pairs of patches from different im-
ages, (2) temporal contrasting with consecutive images
and random pairs shuffled across time, as well as (3)
contrasting between corresponding image-action pairs
and random image-action pairs. The different types of
contrasting objectives are illustrated in Figure 3.
The InfoNCE loss, that is being minimized, is de-
fined as
L
InfoNCE
:= −E
"
1
K
K
∑
i=1
log
e
f (z
i
,z
0
i
)
1
K
∑
K
j=1
e
f (z
i
,z
j
)
#
(1)
where (z
i
, z
0
i
) is a positive pair of embeddings, (z
i
, z
j
)
a negative pair, K the batch size, K −1 the number of
negative samples (the sum in the denominator includes
the positive example), and f is a critic that maps a
pair of embeddings to a real-valued score. The critic
is typically a shallow neural network or a simple dot
product of the two embeddings (see, e.g., Tschannen
et al., 2019, for a detailed discussion).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
754

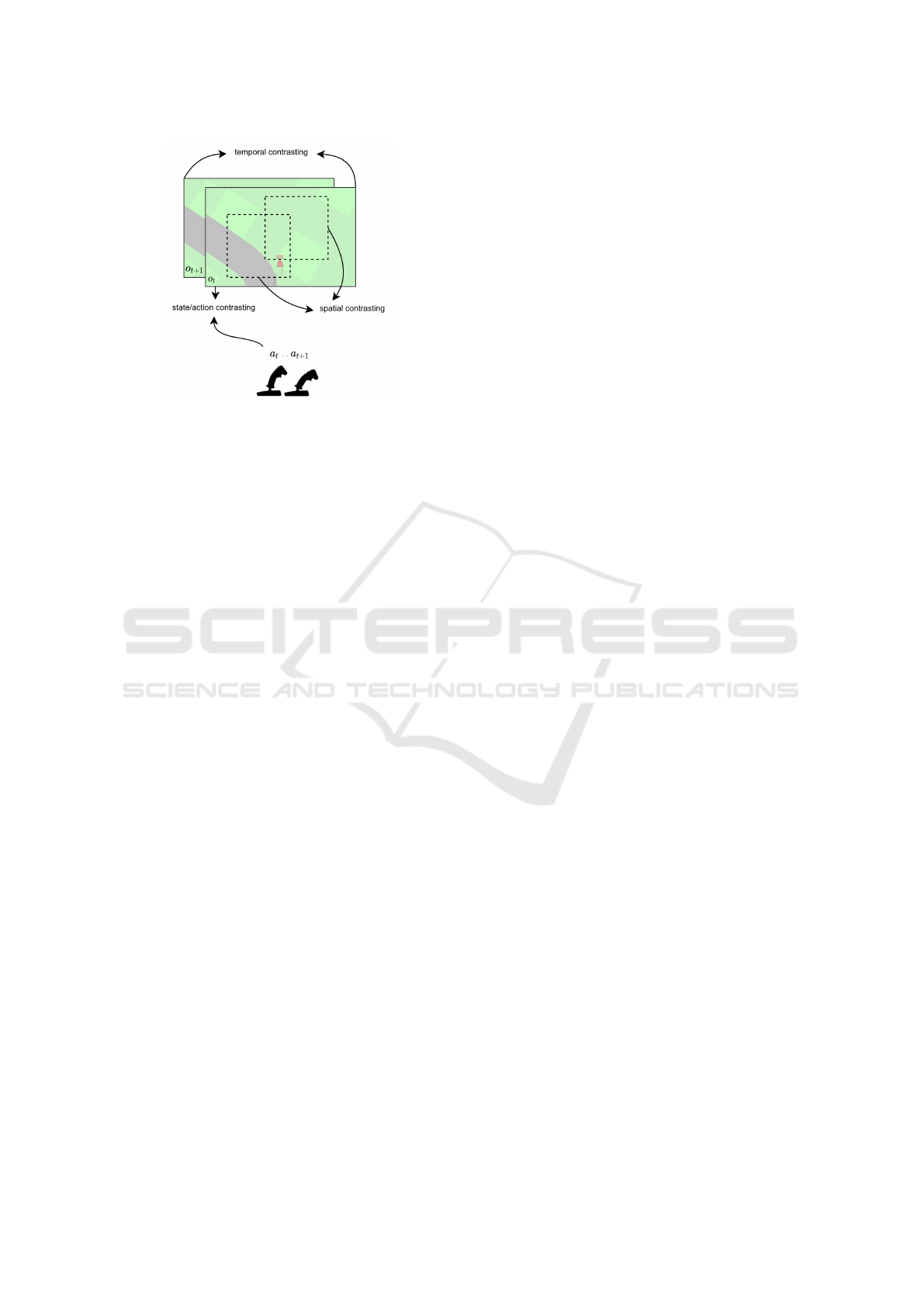
Figure 3: Illustration of the 3 contrastive objectives.
3 RELATED WORK
In Deep Reinforcement Learning, early work employ-
ing autoencoders for image processing used a two-step
procedure (Lange and Riedmiller, 2010; Lange et al.,
2012). This work aimed first to extract rich features
from images using autoencoders and then implement
the representation for control by deploying batch-mode
RL algorithms. Lange and Riedmiller (2010) showed
that RL agents using autoencoder representations can
learn near-optimal policies in a grid-world task. In
Lange et al. (2012), the same approach was extended
to autonomously learn to control a real slot car better
than humans.
Raffin et al. (2019) decoupled feature extraction
from policy learning for goal-based robotics tasks us-
ing a two-step procedure, which outperformed the pol-
icy obtained through end-to-end training. First, the au-
thors combine the reconstruction loss of the VAE with
a reward prediction and an inverse dynamics model.
This allows them to create a rich assembled model
that learns the state representation for the robotic tasks.
Second, they used these learned state representations
as input for the reinforcement learning algorithm that
trained the controller. The results show better sample
efficiency, an acceleration of the learning curve, as
well as a similar or better performance compared to
end-to-end training.
Stooke et al. (2020) show that contrastive estima-
tors can be pre-trained and their low-dimensional state-
representations used to train an RL-controller effec-
tively. The authors train the contrastive encoder with
an auxiliary task approach similar to (Srinivas et al.,
2020), but adding a temporal aspect. The implementa-
tion consists mainly of an exponential moving average
for the auxiliary task combined with an additional pre-
diction layer. The results show their method to have
better or similar results to end-to-end RL in several
benchmarks of the DeepMind Control Suite, Deep-
Mind Lab, and Atari games.
Similarly to above studies, our approach decouples
state-representation learning and reinforcement learn-
ing. However, in this paper the state representations of
the VAE and InfoMax are generated after one training
session and the representations do not have the pos-
sibility of being fine-tuned further as in (Lange and
Riedmiller, 2010; Lange et al., 2012). Unlike (Raffin
et al., 2019), we do not add extra models to the state
representation and freeze the pre-trained representa-
tions instead. Furthermore, we do not use auxiliary
tasks or add any prediction layer as in (Stooke et al.,
2020). Thus, our approach allows us to focus entirely
on the effectiveness of using learned state representa-
tions and on comparing this approach to directly using
raw pixel data as input of the RL algorithm.
4 EXPERIMENTAL SETUP
CarRacingV0. OpenAI’s CarRacing Environment
is a continuous control task to learn from pixels
in a racing environment viewed from a bird’s eye
perspective. Observations consist of 96 ×96 pixels.
The reward is -0.1 every frame and +1000/N for
every track tile visited, where N is the total number
of tiles in a track. The possible actions are braking,
accelerating and steering. CarRacing-v0 is defined
as being ’solved’ when the agent gets an average
cumulative reward of 900 over 100 consecutive trials.
RL Algorithm. All agents use PPO as their RL
algorithm. We use a standard implementation
without any modifications to the architecture or
loss function. Both actor and critic networks
consist of two fully connected layers on top of the
encoder. We use TD(0)-learning for training the critic
and the advantage is estimated using a single time step.
Baselines. The Raw-Pixel agent is trained end-to-end
given the original images, but does not decouple the
training of encoder and policy networks. The Random-
CNN agent provides an ablation on the Raw-Pixel
agent, where the encoder weights are frozen in their
random initial state, whereas the policy networks are
trained. We use a total of six convolutional layers
and one fully connected layer for the critic and actor.
In general, we use the same hyperparameters across
all models, the only exception being the size of the
memory replay buffer and frameskip, which were
found to be important hyperparameters to speed up
learning. For more concrete information about the
Decoupling State Representation Methods from Reinforcement Learning in Car Racing
755

hyperparameters, see the appendix.
Encoder. The used encoder is a convolutional neural
network with six convolutional layers that map the
input image to a latent space of size 64. It uses the
same architectures as described above. For a fair
comparison between state representation learning
methods, we use the same encoder architecture for
both VAE and contrastive learning.
Data Collection. The data collected for self-
supervised learning of state representations is
extracted during the training of a single PPO agent
from the RawPixel baseline. Therefore, the dataset is
comprised of mostly random episodes among which
there are a few mediocre and good episodes. Thereby,
we seek to replicate the variety of data that is usually
available for real-world applications. In particular, we
take 1000 frames out of every 300 episodes of our
PPO agent that is trained for 3000 episodes. In total,
this process generates 10,000 frames for training the
representation learning models.
Autoencoders. The variational autoencoders (VAE
and VAE-Frameskip) use a decoder with transpose
convolutions that is approximately symmetric to the
encoder and comparable in the number of parameters.
For the variational autoencoders, the decoder is only
required for the stage of state representation learning;
for reinforcement learning, all encoder weights are
frozen and the decoder can be discarded.
Contrastive Learning. For contrastive learning,
no decoder is necessary. The critic network for
contrasting consists of two fully-connected layers
of the same dimensionality as the latent space. As
with the VAE decoder, the critic is only required for
the stage of state representation learning and it can
be discarded for reinforcement learning. For more
concrete information about the hyperparameters, see
the appendix.
Methodology. The hyperparameters and architecture
of our agents are based on the RawPixel baseline. We
found these hyperparameters heuristically by deter-
mining a set of values that solved the CarRacingV0
environment with an average cumulative reward of
900 over 100 consecutive trials. Afterwards, we an-
alyzed the effects of using the frozen encoder VAE
and InfoMax to feed the RL-agent without altering
any other variables. Then we repeat the same pro-
cedure using the altered versions of VAE(-Skip) and
InfoMax(-Action) without changing the original hy-
perparameters. Finally, we tuned two hyperparameters
Figure 4: Learning curves for the OpenAI’s Car Racing
continuous control task. The shaded region represents the
standard deviation of the average evaluation over 10 trials for
each of the six random seeds. VAE-Frameskip and InfoMax-
Action obtain considerably better performances compared
to standard VAE and InfoMax.
in our new state representation methods. The tuned hy-
perparameters are: PPO’s buffer is reduced from 5000
to 2000 and the frame-skip is reduced from eight to
six. Thus, except for the last step, we attempt to isolate
the cause of different performances by altering only
the state representation methods in our experiments.
5 RESULTS
In this section, we first compare the representa-
tion learning methods InfoMax-Action and VAE-
Frameskip to VAE and InfoMax without altering any
hyperparameters. Later, we experiment with two hy-
perparameters within our state representation methods
with RL that improves the learning curve of our decou-
pled RL-agents.
5.1 Testing Learning Representation
Methods
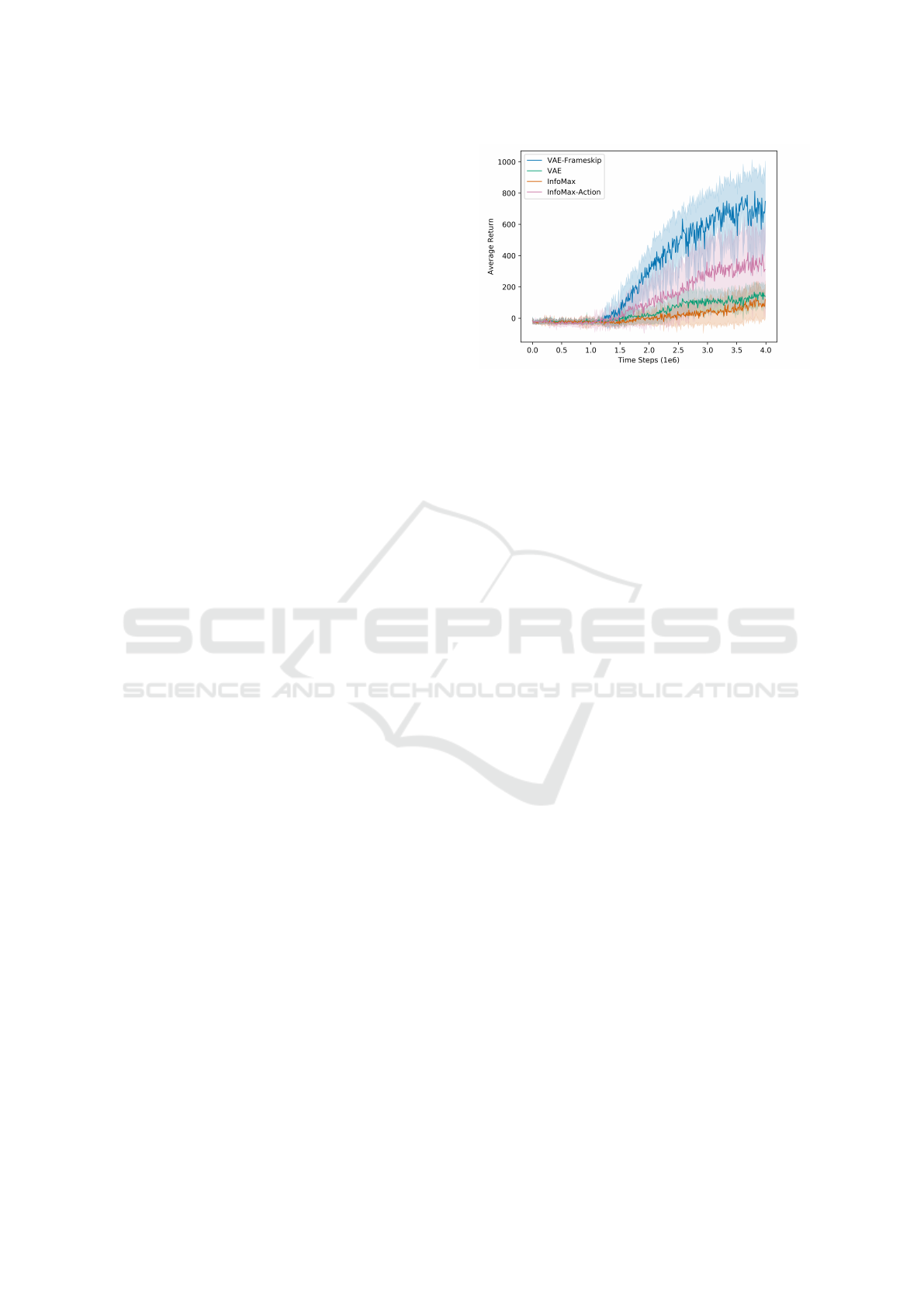
Figure 4 shows the comparison between the learning
curves of our proposed decoupled agents InfoMax-
Action and VAE-Frameskip and the corresponding
traditional approach in OpenAI’s Car Racing environ-
ment. Each run is made for 4 million time steps with
evaluations every 40,000 time steps, where each eval-
uation reports the average cumulative reward over 10
episodes with no exploration noise. The results are
reported over 6 random seeds of the simulator and
different network initializations.
InfoMax-Action reaches an average of 350 points
and VAE-Frameskip about 700. In contrast, spatiotem-
poral InfoMax without action contrasting and VAE
have a similar result of around 150 points.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
756

Table 1: Best average scores and standard deviations computed over 100 consecutive trials without exploration for the 6 random
seeds. The agent that achieved the best score during the evaluation phase (over 10 trials) of training was saved as the best agent.
Agent
Exp. no Raw-Pixel VAE-Frameskip InfoMax-Action InfoMax-Action-FS1 Random-CNN
1 901 ±36 644 ±66 604 ±188 727 ±171 −55 ±10
2 883 ±30 782 ±190 646 ±164 762 ±103 4 ±35
3 904 ±22 625 ±301 397 ±166 485 ±151 45 ±34
4 886 ±82 786 ±169 40 ±43 30 ±23 43 ±43
5 897 ±34 782 ±174 75 ±38 93 ±43 72 ±38
6 896 ±39 604 ±235 270 ±132 271 ±125 −84 ±5
Total 895 ±46 704 ±218 355 ±274 429 ±306 4 ±65
5.2 Final Results
Figure 5 shows the learning curves for Car Racing
with the baseline agents and the decoupled agents.
Compared to the previous experiment, we made two
modifications to the agents that improved the learning
speed of the proposed methods. The buffer is reduced
from 5000 to 2000 and frame-skip from eight to six.
We found these parameters by testing a range of hyper-
parameters of our PPO agents.
The Raw-Pixel agent reaches the best results—
more than 800 points on average. Up to almost 1.5
million frames, the agent shows little volatility, but af-
ter 3.5 million frames we observe a significant drop in
performance. In contrast, the random-CNN agent per-
forms close to random, which indicates that although
random convolutions can lead to good performance
for object detection (Hjelm et al., 2019; Ulyanov et al.,
2018), such a representation does not suffice for train-
ing an RL agent. The VAE agent obtains an average
of 650 points at the end of the training, while the Info-
Max agent reaches almost 400 points. The difference
between VAE and the Raw-Pixel agent is consistently
around 200 points. Notably, the VAE and InfoMax
agents obtain much better results than the Random-
CNN agent, suggesting that the inductive bias learned
Figure 5: Learning curves for the OpenAI’s Car Racing
continuous control task. The shaded region represents the
standard deviation of the average evaluation over 10 trials
for each of the six random seeds.
by self-supervised methods transfers reasonably well
to the considered RL task.
Table 1 shows the best results of each of the ran-
dom seeds for each of our agents. The best agent
is saved after achieving the best-averaged outcome
over ten consecutive trials without exploration dur-
ing the training. This evaluation is effectuated ev-
ery 100 episodes. Four raw-pixel agents are less than
20 points away from crossing the 900 points, while
two agents manage to do so. VAE-Frameskip has the
highest results among the decoupled representation
learning methods. The agents achieve an average out-
come of around 700 points. InfoMax-Action shows
results of over 300 points less than VAE. Here we
see that the drastic difference depends mainly on two
agents that give poor results comparable to Random-
CNN. We added an ablation of InfoMax-Action agent:
InfoMax-Action-FS1. This ablation implements the
lowest frameskip of one (FS1) during testing. This
modification improves the results around 70 points
for the best agent. The Random-CNN has an average
close to zero.
In line with the official evaluation for OpenAI’s
leaderboard
1
, Table 2 reports the average reward over
100 evaluations of the best agent from Table 1. We
compare to the official results from DQN (Prieur,
2017), A3C (Jang et al., 2017), and world models (Ha
and Schmidhuber, 2018), which is the best performing
agent on OpenAI’s public leaderboard. We also in-
clude the results of the ablation of the InfoMax-Action
agent for which we test the lowest frameskip of one
(FS1). This ablation is implemented during testing.
The training is exactly the same as InfoMax-Action
(except for the frameskip: 1 vs 6). This modification
improves the results around 120 points.
The Raw-Pixel agent’s score is on par with the
state-of-the-art results from OpenAI’s public leader-
board. The best VAE agent reaches a score of almost
790 points, whereas the InfoMax agent reaches an av-
erage score of 646, which can be improved by around
120 points by using a frameskip of one. Therefore, the
1
https://github.com/openai/gym/wiki/Leaderboard
Decoupling State Representation Methods from Reinforcement Learning in Car Racing
757

Table 2: Best agents scores and standard deviations averaged
over 100 consecutive trials without exploration. The result
of the Raw Pixel agent using PPO ranks among the top 3
leaderboard scores of OpenAI. The best decoupled agent
reaches 87% of the performance of our state-of-the-art agent
with 88% fewer trained parameters and a large reduction of
memory usage.
AGENT
AVERAGE SCORE
WORLD MODELS: HA AND SCHMIDHUBER (2018) 906 ±21
RAW-PIXEL 904 ±22
VAE-FRAMESKIP 786 ±169
INFOMAX-ACTION-FS1 762 ±103
AC3: JANG ET AL. (2017) 652 ±10
INFOMAX-ACTION 646 ±164
DQN: PRIEUR (2017) 343 ±18
RANDOM-CNN 72 ±38
agents using fixed pre-trained representations perform
better than the best DQN and A3C agents. Notably, our
agents achieve around 87% of the performance of the
state-of-the-art with 88% fewer trainable parameters
than the respective PPO agent.
6 DISCUSSION
This single-environment experiment using a pre-
trained agent seeks to test the viability of our two-step
methodology. Our next step is to confirm our results
with a radio-controlled (RC) car and adding more en-
vironments. Our next step consists of analyzing:
1. Different environments: having tested in only one
environment makes it challenging to know if the
results can be generalized. For this reason, it is
necessary to validate the model in additional envi-
ronments, such as Atari games and the DeepMind
Control Suite.
2. Transfer learning: an agent driving a real car could
first learn representations with real images. After-
ward, a policy can be trained with this represen-
tation in a simulator, and finally, the agent can be
transferred and adjusted to the real world.
7 CONCLUSIONS
We have investigated how well pre-trained representa-
tions, learned by self-supervised methods, transfer to
RL agents in the CarRacingV0 environment. We con-
sidered two self-supervised methods for learning rep-
resentations: variational autoencoders and contrastive
learning. Based on frozen pre-trained representations,
RL agents achieve a significant share of the perfor-
mance obtained by RL agents trained directly on pixel
inputs while requiring significantly fewer trainable pa-
rameters. The decoupled agents reach up to 87% of
the performance of unconstrained agents with a reduc-
tion of 88% in the number of parameters optimized by
the RL agent. Furthermore, our approach leads to a
significant reduction in the space requirements of the
memory replay buffer, and using pre-trained represen-
tations also exhibits more stable training behavior.
These outcomes demonstrate that self-supervised
representations can provide a useful inductive bias for
knowledge transfer in RL tasks. In future work, we
want to study this approach using more environments
such as the Atari games and real-world implementa-
tions of autonomous robotic cars.
ACKNOWLEDGEMENTS
Thanks deeply to Vassilios Tsounis and Katia Bouder.
ID is supported by the SNSF grant #200021 188466.
REFERENCES
Ding, Y., Clavera, I., and Abbeel, P. (2019). Mutual informa-
tion maximization for robust plannable representations.
In ICML 2015 Workshop on Robot Learning: Control
and Interaction in the Real World.
Gutmann, M. and Hyv
¨
arinen, A. (2010). Noise-contrastive
estimation: A new estimation principle for unnormal-
ized statistical models. In Proceedings of the Thir-
teenth International Conference on Artificial Intelli-
gence and Statistics, pages 297–304.
Ha, D. and Schmidhuber, J. (2018). Recurrent world mod-
els facilitate policy evolution. In Advances in Neural
Information Processing Systems 31, pages 2451–2463.
Curran Associates, Inc.
Hafner, D., Lillicrap, T. P., Ba, J., and Norouzi, M. (2020).
Dream to control: Learning behaviors by latent imagi-
nation. In 8th International Conference on Learning
Representations.
Hafner, D., Lillicrap, T. P., Fischer, I. C., Villegas, R., Ha,
D., Lee, H., and Davidson, J. (2019). Learning latent
dynamics for planning from pixels. In ICML.
He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. (2019).
Momentum contrast for unsupervised visual represen-
tation learning. arXiv preprint arXiv:1911.05722.
Hjelm, D., Fedorov, A., Lavoie-Marchildon, S., Grewal,
K., Bachman, P., Trischler, A., and Bengio, Y. (2019).
Learning deep representations by mutual information
estimation and maximization. In ICLR 2019. ICLR.
Jang, S. W. d., Lee, C., and Kim, J. H. (2017). Reinforcement
car racing with a3c. Scribd preprint: 358019044.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. In Proceedings of the 3rd In-
ternational Conference on Learning Representations.
Kingma, D. P. and Welling, M. (2014). Auto-encoding vari-
ational bayes. In Proceedings of the 3rd International
Conference on Learning Representations.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
758

Lange, S. and Riedmiller, M. (2010). Deep auto-encoder
neural networks in reinforcement learning. In The 2010
International Joint Conference on Neural Networks
(IJCNN), pages 1–8.
Lange, S., Riedmiller, M., and Voigtlander, A. (2012). Au-
tonomous reinforcement learning on raw visual input
data in a real world application. pages 1–8.
Lee, A. X., Nagabandi, A., Abbeel, P., and Levine, S.
(2019). Stochastic latent actor-critic: Deep reinforce-
ment learning with a latent variable model. CoRR,
abs/1907.00953.
Oord, A. v. d., Li, Y., and Vinyals, O. (2018). Representa-
tion learning with contrastive predictive coding. arXiv
preprint:1807.03748.
Prieur, L. (2017). Deep-q learning using simple feedfoward
neural network. Github Gist in https://goo.gl/VpDqSw.
Raffin, A., Hill, A., Traor
´
e, K. R., Lesort, T., D
´
ıaz-Rodr
´
ıguez,
N., and Filliat, D. (2019). Decoupling feature extrac-
tion from policy learning: assessing benefits of state
representation learning in goal based robotics. SPiRL
Workshop ICLR.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and
Klimov, O. (2017). Proximal policy optimization algo-
rithms. CoRR, abs/1707.06347.
Smith, N. A. and Eisner, J. (2005). Contrastive estimation:
Training log-linear models on unlabeled data. In Pro-
ceedings of the 43rd Annual Meeting on Association
for Computational Linguistics, pages 354–362. Asso-
ciation for Computational Linguistics.
Srinivas, A., Laskin, M., and Abbeel, P. (2020). CURL: con-
trastive unsupervised representations for reinforcement
learning. CoRR, abs/2004.04136.
Stooke, A., Lee, K., Abbeel, P., and Laskin, M. (2020). De-
coupling representation learning from reinforcement
learning. arXiv:2004.14990.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. MIT Press, Cambridge, MA,
USA, second edition.
Tschannen, M., Djolonga, J., Rubenstein, P. K., Gelly, S.,
and Lucic, M. (2019). On mutual information maxi-
mization for representation learning. In International
Conference on Learning Representations.
Ulyanov, D., Vedaldi, A., and Lempitsky, V. (2018). Deep
image prior. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition, pages
9446–9454.
Wahlstr
¨
om, N., Sch
¨
on, T. B., and Deisenroth, M. P. (2015).
From pixels to torques: Policy learning with deep dy-
namical models. In ICML 2015 Workshop on Deep
Learning.
Zhang, M., Vikram, S., Smith, L., Abbeel, P., Johnson, M. J.,
and Levine, S. (2018). SOLAR: deep structured latent
representations for model-based reinforcement learn-
ing. CoRR, abs/1808.09105.
APPENDIX: HYPERPARAMETERS
RL Agent
Model Architecture. The input to the neural network
consists of a 96 ×96 ×4 grayscale image. There are a
total of six convolutional layers with ReLU activation
functions. The first hidden layer convolves 8 filters of
4 ×4 with stride 2 with the input image. The second
hidden layer convolves 16 filters of 3 ×3 with stride 2.
The third hidden layer convolves 32 filters of 3 ×3
with stride 2. The fourth hidden layer convolves 64
filters of 3 ×3 with stride 2. The fifth hidden layer
convolves 128 filters of 3 ×3 with stride 1. The sixth
hidden layer convolves 64 filters of 3 ×3 with stride 1.
The critic’s final hidden layer is fully-connected with
100 rectifier units using the described ConvLayers.
The output layer is a fully-connected linear layer
with only one single output. The actor also has a
fully-connected layer with 100 rectifier units after the
described ConvLayers. The final layer consists of two
parallel fully connected layers with 100 units to three
outputs for each valid action with a tanh activation
function. From these layers, we sample the continuous
actions using the beta distribution.
PPO’s Hyperparameters. Frameskip = 8. Discount
Factor = 0.99. Value Loss Coefficient = 2. Image Stack
= 4. Buffer Size = 5000. Adam Learning Rate = 0.001.
Batch Size = 128. Entropy Term Coefficient = 0.0001.
Clip Parameter = 0.1. PPO Epoch = 10.
State Representation Learning
Variational Autoencoder. The VAE is trained using
the same encoder as the PPO agent described above.
We train for 2000 epochs using a batch size of 64, a
KL-divergence weight (beta) of 1.0 which is annealed
over the first 10 epochs, and the Adam optimizer
(Kingma and Ba, 2014) with learning rate 0.0003.
Contrastive Learning. For contrastive learning, we
also use the same encoder as the PPO agent described
above and Adam optimizer with learning rate 0.001.
We train the model for 5000 epochs using a large batch
size of 1024 which provides a large number of negative
samples through batch-wise permutations, which has
been shown to be beneficial in previous work (Oord
et al., 2018; He et al., 2019).
Decoupling State Representation Methods from Reinforcement Learning in Car Racing
759