
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and
Expressive Lambda Functions
B
´
alint Gyarmathy
a
, B
´
alint Mucs
´
anyi
b
,
´
Ad
´
am Czapp
c
, D
´
avid Szil
´
agyi
d
and Bal
´
azs Pint
´
er
e
ELTE E
¨
otv
¨
os Lor
´
and University, Faculty of Informatics, Budapest, Hungary
Keywords:
Program Synthesis, Programming by Examples, Beam Search, Recurrent Neural Network, Gated Recurrent
Unit.
Abstract:
We introduce a flexible program synthesis model to predict function compositions that transform given in-
puts to given outputs. We process input lists in a sequential manner, allowing our system to generalize to a
wide range of input lengths. We separate the operator and the operand in the lambda functions to achieve
significantly wider parameter ranges compared to previous works. The evaluations show that this approach is
competitive with state-of-the-art systems while it’s much more flexible in terms of the input length, the lambda
functions, and the integer range of the inputs and outputs. We believe that this flexibility is an important step
towards solving real-world problems with example-based program synthesis.
1 INTRODUCTION
There are two main branches of program synthesis
(Gulwani et al., 2017). In the case of deductive prog-
ram synthesis, we aim to have a demonstrably correct
program that conforms to a formal specification. In
the case of inductive program synthesis, we demon-
strate the expected operation of the program to be
synthesized with examples, or a textual representation
(Yin et al., 2018).
Programming by Examples (PbE) is a demonstra-
tional approach to program synthesis to specify the
desired behavior of a program. These examples con-
sist of an input and the expected output (Gulwani,
2016). The two main targets of such PbE tools are
string transformations (Parisotto et al., 2016; Lee
et al., 2018; Kalyan et al., 2018) and list manipula-
tions (Balog et al., 2016; Zohar and Wolf, 2018; Feng
et al., 2018).
In order to tackle the otherwise combinatorial
search in the space of possible programs that satisfy
the provided specification, early program synthesis
systems used theorem-proving algorithms and care-
a
https://orcid.org/0000-0002-1818-611X
b
https://orcid.org/0000-0002-7075-9018
c
https://orcid.org/0000-0001-9576-2080
d
https://orcid.org/0000-0001-6161-7328
e
https://orcid.org/0000-0003-3431-0667
fully hand-crafted heuristics to prune the search space
needed to be considered (Shapiro, 1982; Manna and
Waldinger, 1975). With the rising popularity of deep
learning, program synthesis experienced great break-
throughs in both accuracy and speed (Balog et al.,
2016). One of the most prominent approaches in in-
tegrating machine learning algorithms into the syn-
thesis process was to complement popular heuristics
used in the search with the predictions of such algo-
rithms (Kalyan et al., 2018; Lee et al., 2018).
The seminal work in the field is DeepCoder (Ba-
log et al., 2016), which serves as a baseline for several
more recent papers (Zohar and Wolf, 2018; Kalyan
et al., 2018; Feng et al., 2018; Lee et al., 2018). For
instance, PCCoder (Zohar and Wolf, 2018) showed
great advances in the performance of the synthesis
process on the Domain Specific Language (DSL) de-
fined by DeepCoder, reducing the time needed by the
search by orders of magnitude while achieving re-
markably better results on the same datasets.
In spite of these great advances in program syn-
thesis, there have not yet been many examples of suc-
cessful application of state-of-the-art program synthe-
sis systems in a real-world environment.
We think the cause of this is mainly (i) the limita-
tion of static or upper-bounded input vector sizes, (ii)
the agglutination of grammar tokens, such as treat-
ing operators and their integer parameters jointly in
lambda functions (e.g. (+1) and (∗2)), (iii) the limi-
386
Gyarmathy, B., Mucsányi, B., Czapp, Á., Szilágyi, D. and Pintér, B.
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions.
DOI: 10.5220/0010237803860395
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 386-395
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ted integer parameter ranges of the lambda operators,
and (iv) the limited integer ranges of inputs, interme-
diate values, and outputs.
As a consequence of (ii), the number of lambda
functions required is a product of the number of
lambda operators and the number of their possible
parameters. For example, there is a separate lambda
function required for each (+1), (+2), . . . (+n). The
number of possible function combinations is greatly
reduced. The consequence of (i) is that the system
does not generalize well to input lengths beyond a
constant maximum length L.
In this paper, we would like to resolve these lim-
itations. We implement a DSL with similar func-
tions to the ones used by DeepCoder using a function-
composition-based system, in which we treat lambda
operators and their parameters separately. This allows
us to reduce the number of lambda functions required
from the product of the number of lambda operators
and their parameters to the sum of them (considering
the parameters as nullary functions), and so broaden
the range of possible lambda expressions: we extend
the allowed numerical values from [-1, 4] to [-8, 8].
We also extend the range of the possible integers
in the outputs and intermediate values fourfold from
[-256, 256] to [-1024, 1024], so less programs are fil-
tered out because of these constraints. More impor-
tantly, we do not embed the integers as that would
impose restrictions to the range of inputs and outputs.
We use a deep neural network to assist our search
algorithm similarly to DeepCoder and PCCoder. The
neural network accepts input-output pairs of any
length and predicts the next function to be used in
the composition that solves the problem. Thus the
network acts as a heuristic for our search algorithm
based on beam search, which uses predefined, opti-
mized beam sizes on each level. In these first experi-
ments, we use function compositions where functions
take only a single list as an input in addition to their
fixed parameters, and the next function is applied to
the list output of the previous function. In this sense
our DSL is less expressive than DeepCoder: for ex-
ample, it does not contain ZipWith or Scan1l.
Our contributions are:
• We introduce a recurrent neural network archi-
tecture that generalizes well to different input
lengths.
• We treat the operators in lambda functions sepa-
rately from their parameters. This allows us to
significantly extend the range of their parameters.
• Our architecture does not pose artificial limits on
the range of integers acceptable as inputs, inter-
mediate results, or outputs. We extend the range
of intermediate results and outputs fourfold com-
pared to previous works.
These design choices serve to increase the flexi-
bility of the method to take a step towards real-world
tasks. We named our method FlexCoder.
2 RELATED WORK
As the seminal paper in the field, DeepCoder is a
baseline for several systems in neural program syn-
thesis. Its neural network predicts which functions are
present in the program, and so helps guide the search
algorithm. However, their network is not used step by
step throughout the search, only at the beginning.
PCCoder implemented a step-wise search which
uses the current state at each step to predict the next
statement of the program, including both the function
(operator) and parameters (operands). They use Com-
plete Anytime Beam Search (CAB) (Zhang, 2002)
and cut the runtime by two orders of magnitude com-
pared to DeepCoder.
As the neural networks used by DeepCoder and
PCCoder do not process the input sequentially, they
can only handle inputs with a maximum length of L
(or shorter because of the use of padding). The default
maximum length is L = 20 for both systems. Flex-
Coder solves this problem by using GRU (Cho et al.,
2014) layers to process the inputs, so it can work with
a large range of input sizes.
We separate the lambda function parameters of
our higher-order functions into numeric parameters
and operators to significantly widen the operand range
compared to DeepCoder and PCCoder. This approach
resolves the bound nature of their parameter func-
tions, where they only have a few predefined func-
tions with the given operator and operand (eg. (+1),
(∗2)). Similarly to PCCoder, FlexCoder also uses the
neural network in each step of the search process.
A good example of the successful use of function
compositions to synthesize programs is (Feng et al.,
2018). Its conflict-driven learning-based method can
learn lemmas to gradually decrease the program space
to be searched. They outperform a reimplementation
of DeepCoder.
The work of (Kalyan et al., 2018) introduces real-
world input-output examples for their neural guided
deductive search, combining heuristics with neural
networks in the synthesizing process. Their ranking
function serves the same role as our network in their
approach to synthesize string transformations.
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions
387
2,-2,4,3,1
2,6,8
Neural
network
reverse([2,-2,4,3,1])
2,6,8
2,6,8
=
1,3,4,-2,2
Neural
network
2,6,8,-4,4
Neural
network
map(*2,[1,3,4,-2,2])
take(3,[2,6,8,-4,4])
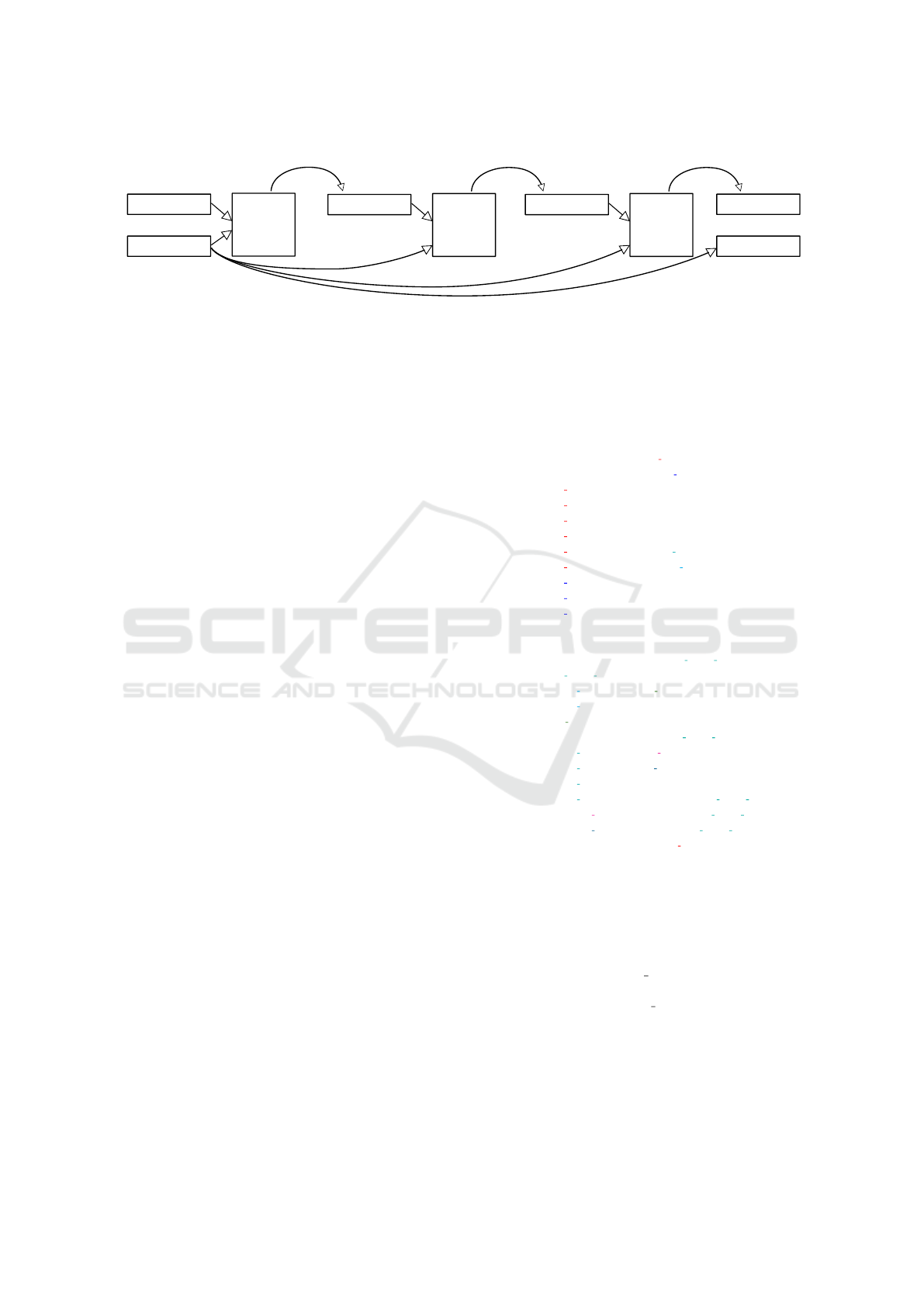
Figure 1: The process of program synthesis. The task is to find a composition which transforms the input vector into the
output vector. In this case, the input is [2,−2,4, 3,1] and the output is [2,6, 8]. This figure shows how the predicted function is
applied to the input then the result is fed back into the neural network. The reverse function reverses the order of the elements
in a list. The map function applies the function constructed from the given operator and numeric parameter (in this example
’∗’ and ’2’) for every element of its input list. The take function takes some elements (in this case ’3’) from the front of the
list and returns these in a new list. After executing these functions in the right order on the input vector, we can see that the
current input vector equals the output vector, which means we found a solution: take(3,map(∗2,reverse(input))).
3 METHOD
We introduce our neural-guided approach to program
synthesis based on beam search with optimized beam
sizes. Every step of the beam search is guided by the
neural network. The DSL of function compositions is
built of well known (possibly higher-order) functions
from functional programming. The two main parts
of FlexCoder are the beam search algorithm, and the
neural network. Another important part is the gram-
mar which defines the DSL.
Figure 1 shows an overview of the system. In each
step, an input-output pair is passed to the neural net-
work, which predicts the next function of the compo-
sition. This predicted function is applied to the input
producing the new input for the next iteration of the
algorithm. This is continued until a solution is found
or the iteration limit is reached.
3.1 Example Generation and Grammar
We represent the function compositions using
a context-free grammar (CFG) (Chomsky and
Sch
¨
utzenberger, 1959). The clear-cut structure makes
our grammar easily extensible with new functions and
more parameters. We implemented the context-free
grammar (CFG) using the Natural Language Toolkit
(Bird et al., 2009). The full version with short de-
scriptions of each function can be seen in Figure 2.
The numeric parameters are taken from the
[−8, 8] interval. This range is larger than the one used
by PCCoder as they use a range of [−1, 4]. The ele-
ments in the intermediate values and output lists are
taken from the [−1024, 1024] range ([−256, 256] in
PCCoder), while the input lists are sampled from the
[−256, 256] range (same as PCCoder).
S → ARRAY FUNCT ION
S → NU MERIC FU NCT ION
ARRAY FUNCT ION → sort(ARRAY)
ARRAY FUNCT ION → take(POS, ARRAY )
ARRAY FUNCT ION → drop(POS, ARRAY )
ARRAY FUNCT ION → reverse(ARRAY )
ARRAY FUNCT ION → map(NUM LAMBDA, ARRAY)
ARRAY FUNCT ION → f ilter(BOOL LAMBDA, ARRAY )
NUMERIC FU NCT ION → max(ARRAY ) | min(ARRAY )
NUMERIC FU NCT ION → sum(ARRAY ) | count(ARRAY )
NUMERIC FU NCT ION → search(NUM, ARRAY )
NUM → NEG | 0 | POS
NEG → −8 | − 7 | ... | − 2 | − 1
POS → 1 | GREATER T HAN ONE
GREAT ER T HAN ONE → 2 | 3 | ... | 8
BOOL LAMBDA → BOOL OPERATOR NU M
BOOL LAMBDA → MOD
BOOL OPERATOR → == | < | >
MOD → % GREAT ER T HAN ONE == 0
NUM LAMBDA → ∗ MUL NUM
NUM LAMBDA → / DIV NU M
NUM LAMBDA → + POS
NUM LAMBDA → − POS | % GREATER T HAN ONE
MUL NUM → NEG | 0 | GREATER T HAN ONE
DIV NU M → NEG | GREATER T HAN ONE
ARRAY → list | ARRAY FUNCT ION
Figure 2: The grammar used to generate the function com-
positions in CFG notation. The functions don’t modify the
input array; they return new arrays. The sort function sorts
the elements of ARRAY in ascending order. Take keeps,
drop discards the first POS elements of ARRAY. The re-
verse function reverses the elements of the input. Map and
filter are the two higher-order functions used in the gram-
mar. Map applies the NUM LAMBDA function on each
element of its parameter. Filter only keeps the elements of
ARRAY for which the BOOL LAMBDA function returns
true. The min and max functions return the smallest and the
largest element of ARRAY. The sum function returns the
sum of, count returns the number of elements of ARRAY.
Search returns the index of the element of ARRAY which is
equal to NUM. In the generated examples, we only accept
cases where the NUM is present in ARRAY.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
388

Table 1: The functions with their operators, parameter
ranges, and the buckets used for the weighted random se-
lection for building the compositions.
map filter take drop search
operators +,-,/,*,% <,>,==,% - - -
parameters [-8,8] [-8,8] [1,8] [1,8] [-8,8]
bucket map filter takedrop takedrop search
Table 2: The parameterless and operatorless functions, and
their corresponding bucket.
min max reverse sort sum count
bucket one param
The lambda functions are divided into two cate-
gories based on their return type: boolean lambda
functions used by filter and numeric lambda functions
used by map. We defined rules for the lambda func-
tions to avoid errors or identity functions, such as di-
viding by 0, or the (+0) and the (∗1) functions.
The CFG is used to generate the possible func-
tions which are then combined into compositions. As
the functions in the grammar have a different num-
ber of possible parameterizations, we have to ensure
that each type of function occurs approximately the
same number of times in the dataset. To tackle this
problem, the compositions are generated by weighted
random selections from the 151 possible functions.
We divide the functions into five buckets based on
how many different parameterizations of the function
exist in the grammar. As Tables 1 and 2 show, the
functions in different buckets contain different num-
bers of parameters and the range of the numerical
parameters also varies. As we would like to sam-
ple functions uniformly at random, we choose one of
the five buckets with weights based on the number of
functions in the corresponding bucket (Equation 1),
then we take a parameterized function from the cho-
sen bucket uniformly at random.
weight( f unction) =
6/11, if f unction ∈ one param
2/11, if f unction ∈ takedrop
1/11, if f unction ∈ map ∪ f ilter ∪ search
(1)
We use several filters on the generated functions
to remove or fix redundant functions and suboptimal
parameterizations.
The first filter optimizes the parameters of func-
tions:
• map(+ 1, map(+ 2, [1, 2])) → map(+ 3, [1, 2])
• filter(> 2, [1, 6, 7]) → filter(> 5, [1, 6, 7])
The second filter removes the identity functions
on the concrete input-output pairs:
• sum(filter(> 5, [6, 7, 8])) → sum([6, 7, 8])
Identity functions that don’t affect the outcome for
any input are prohibited by the grammar. An example
is map(+ 0, [2, 3, 5])).
The third filter deletes compositions resulting in
empty lists:
• filter(< 1, [2, 3, 4]) → [ ]
• drop(4, [1, 2, 3]) → [ ]
The fourth filter removes the examples which
contain integers outside the allowed range of
[−1024,1024]:
• map(∗ 8, [1, 2, 255]) → [8, 16, 2040]
3.2 Beam Search
As previously mentioned, we think about the prob-
lem of program synthesis as searching for an optimal
function composition. We build the composition one
function at a time. The beam search is implemented
based on Complete Anytime Beam Search (CAB).
The algorithm builds a directed tree of node ob-
jects. Each node has 3 fields: a function, the result of
that function applied to the output of its parent node,
and its rank. On each level of the search algorithm, we
sort all possible parameterized functions in descend-
ing order based on the rank values of the functions
and their parameters predicted by the neural network.
For each node of the tree, the network uses the
current state of the program input and output stored in
the parent node to predict the next possible function
of the synthesized composition. If there are multiple
input-output examples we pass them in a batch to the
network, then we take the mean of the predictions.
After generating all the child nodes we keep the
first ν
i
∈ N (i ∈ 1..ϑ) nodes (where ν
i
denotes the
beam size on the current level and ϑ is the depth limit)
from the sorted list of the nodes and fill their result
fields by evaluating them. We repeat this step until a
solution is found or the algorithm reaches the itera-
tion limit (or optionally the time limit). If a solution
is found, we follow the parent pointers until we reach
the root of the tree to get the composition. When the
depth limit ϑ is reached without finding a solution,
each ν
i
value is doubled and the search is restarted.
Since the network is called multiple times during the
search, we use caching to save the ranks for every
unique input-output pair to speed up the process. This
is possible because the network is a pure function.
Algorithm 1 uses previously optimized beam sizes
for each depth. The first step is to remove programs
that violate the range constraints of the evaluated out-
put list mentioned in 3.1 or a length constraint. The
length constraint in the case of list outputs ensures
that we only keep nodes where the output list has as
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions
389

root
[2,-2,4,3,1]
R=1
map(+2)
[4,0,6,5,3]
R=0.63
reverse()
[1,3,4,-2,2]
R=0.95
filter(<0)
[-2]
R=0.21
filter(>4)
[6,5]
R=0.17
sort()
[0,3,4,5,6]
R=0.5
map(%4)
[0,0,2,1,3]
R=0.42
take(3)
[1,3,4]
R=0.78
map(*2)
[2,6,8,-4,4]
R=0.91
drop(2)
[4,-2,2]
R=0.34
map(-2)
[-1,1,2]
R=0.02
map(+2)
[3,5,6]
R=0.73
search(3)
1
R=0.34
take(3)
[2,6,8]
R=0.83
take(2)
[2,6]
R=0.65
max()
8
R=0.2
Figure 3: This figure shows a successful beam search, where we are looking for a function composition which produces the
output sequence [2,6, 8] when given the input [2,−2, 4,3, 1]. Each node has 3 fields: a function, the result of that function
applied to the output of its parent node, and its rank. The gray rectangles are the nodes considered; these are selected based
on their rank marked by R. The highlighted ones show the result take(3, map(∗2, reverse(input))).
Algorithm 1: Beam search.
i = 0;
found = false;
while i < max iter and not found do
depth = 0;
nodes = [root];
while depth < ϑ and not found do
// beam sizes are predefined
for each depth
// we double the beam sizes
in each iteration of the
outer loop
beam size = ν[depth]∗2
i
;
// filter removes logically
incorrect function calls
// process assigns a rank to
every node
output nodes = process(filter(nodes));
found =
check solution(output nodes);
nodes = take best(beam size,
output nodes);
depth += 1;
end
i += 1;
end
many as or more elements than the original output list.
After this filtering step, a rank is assigned to all the
remaining programs by the neural network.
The programs are also executed to check whether
they satisfy the solution criteria. If a solution is found,
the algorithm ends. Otherwise, the first beam size
compositions with the highest rank are selected and
are further extended with a new function on the next
iteration of the inner loop. If the inner loop exits,
the beam sizes are doubled, but the previously com-
puted ranks are not computed again due to the caching
method mentioned previously.
We optimized the beam sizes based on experimen-
tal runs on the validation set: we approximated the
minimum beam size ∈ {ν
1
,ν
2
,...,ν
n
} on each level
that contains the next function in the composition.
This gives a higher chance to find the solution in the
first or early iterations. We chose the beam size for
each level that included the original solution 90% of
the time. This seems to be an ideal trade-off between
accuracy and speed.
3.3 Neural Network
The input to the network is a list of input and output
examples of a single program. The outputs are 6 vec-
tors that contain the ranks for each function, parame-
ter, and lambda function. The rank of a parameterized
function is determined by the geometric mean of the
ranks of its components.
We define F as the set of functions, where ev-
ery element is a tuple ( f
class
, f
arg
), where f
class
is the
function name and f
arg
is the list of its arguments. Us-
ing this definition the rank of a function is determined
using the formula
R( f ) =
n+1
s
R( f
class
) ∗
n
∏
i=1
R( f
arg
i
), (2)
where n ∈ N denotes the number of parameters.
3.3.1 Architecture
The input of the network is a list of program input-
output examples. Inputs and outputs are separately
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
390
Input
Output
G
R
U
G
R
U
D
e
n
s
e
D
e
n
s
e
D
e
n
s
e
Dense
Block
GRU
Block
Functions
Numeric Operators
N
u
m
e
r
i
c
p
a
r
a
m
e
t
e
r
s
Boolean Operators
Dense
Blocks
G
R
U
G
R
U
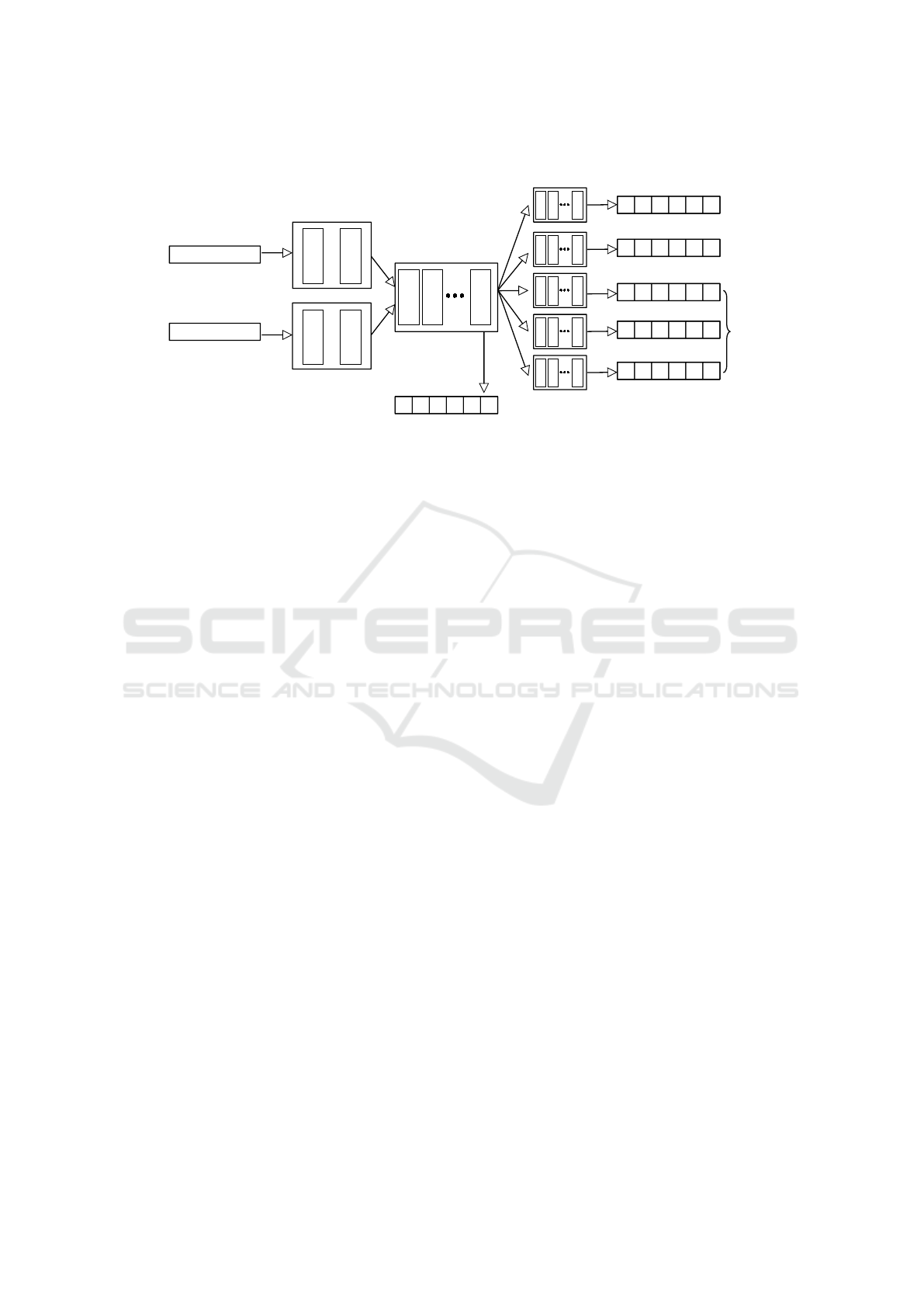
Figure 4: The general architecture of the neural network. Each input example to the network is passed to the GRU block
generating a representation which is passed through the dense block then split into six parts, five of which pass through
another dense block.
passed to two blocks of recurrent layers, which makes
it possible to use variable-size input. These blocks
each consist of two layers of GRU cells, each con-
taining 256 neurons.
The GRU representations of the input and the out-
put are concatenated and then given to a dense block
consisting of seven layers with SELU (Klambauer
et al., 2017) activation function and 128, 256, 512,
1024, 512, 256, 128 neurons in order. With SELU ac-
tivations we experienced a faster convergence while
training the network, due to the internal normaliza-
tion these functions provide.
SELU(x) = λ
(
x, if x > 0
α(e
x
− 1), if x ≤ 0
(3)
After this block we have an output layer predict-
ing the probabilities of the possible next functions us-
ing sigmoid activation for each function. This layer is
also fed into five smaller dense blocks. Each of these
contains five layers using the SELU activation func-
tion with 128, 256, 512, 256, 128 neurons.
These smaller dense blocks produce the remaining
five outputs of the model. They are vectors, each rep-
resenting the probabilities of parameters associated
with the next parameterized function of the compo-
sition. These five vectors are corresponding to (1) the
bool lambda operator, (2) the numeric lambda oper-
ator, (3) the bool lambda numeric argument, (4) the
numeric lambda numeric argument, and (5) the pa-
rameter for non-higher-order functions with only one
numeric argument, e.g. the value used in take. We use
the sigmoid activation function for each entry of all
output vectors. The smallest output vector has 4 ele-
ments, whereas the largest one has 17. The network’s
loss (L) is the sum of the 6 output components’ loss
values marked with L
i
, each denoting a cross-entropy
loss function.
L(Y,
ˆ
Y ) =
6
∑
i=1
L
i
(Y
i
,
ˆ
Y
i
) (4)
3.3.2 Training
Before training, we break down the compositions into
functions and turn each parameterized function into
six separate one-hot vectors to obtain a single label
used for training the network. Out of the generated
examples, 98% is used as the training set, and the re-
maining 2% serves the role of the validation set. The
test sets are generated on a per-experiment basis.
We use the Adam optimization algorithm
(Kingma and Ba, 2014) with the default hyperpa-
rameters: β
1
= 0.9, β
2
= 0.999 and ε = 10
−8
. We
trained the neural network on a computer with an
Intel i5-7600k processor and an NVIDIA GTX 1070
GPU using a standard early stopping method with
a patience of five. We trained the network for a
maximum of 30 epochs or 6 hours.
4 EXPERIMENTS
All of the experiments below were run on a c2-
standard-16 (Intel Cascade Lake) virtual machine on
the Google Cloud Platform with 16 vCores, 64 GB
RAM, and no GPU. For these experiments, the neu-
ral network was trained on compositions of 5 func-
tions, and the length of the input array was between
15 and 20. We provided 1 input-output example for
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions
391

boolean lambda operator
boolean lambda argument
numeric lambda operator
numeric lambda argument
function
numeric argument
71.28%
94.8%
88.02%
96.82%
87.62%
92.93%
97.94%
99.51%
98.03%
99.3%
95.42%
98.86%
Unfiltered
Filtered
Figure 5: The improvements in the neural network’s output
accuracies after applying filtering to the training data. After
filtering the problem is more learnable. The results were
measured during the training of the GRU model. Each row
shows the final validation accuracy of the network’s outputs
at the end of training.
each program in the training process. In all of the ex-
periments, we created the test datasets by sampling
the original program space uniformly at random, with
a sample size of 1000.
4.1 Filtering the Datasets
Filtering the datasets using the method described in
Section 3.1 made the problem more learnable for
the neural network, resulting in improvements in the
case of each output head of the network. The exact
changes can be seen in Figure 5.
This filtering is used on all datasets in all experi-
ments.
4.2 Different Recurrent Layers
In this section, we compare the effect of different re-
current layers on accuracy. We ran experiments with
LSTM (Hochreiter and Schmidhuber, 1997), bidirec-
tional LSTM (Schuster and Paliwal, 1997), GRU, and
bidirectional GRU.
In the first experiment, we looked at the accuracy
of the different layers as the composition length in-
creased (Figure 6). The bidirectional layers proved to
be suboptimal, as these – somewhat surprisingly – did
not make the system more accurate for longer func-
tion compositions, but training and testing both took
considerably more time.
Despite the fact that bidirectional LSTM achieves
better accuracy for shorter compositions, its accuracy
falls below regular LSTM and GRU cells as the com-
position length increases. It is also the slowest of the
three in terms of execution time. The bidirectional
GRU model is the second slowest, and its accuracy is
the worst of the layers tested for longer compositions.
2 3 4
5
50
60
70
80
90
100
Composition length
Accuracy [%]
Bidirectional GRU
Bidirectional LSTM
GRU
LSTM
Figure 6: The performance of different recurrent layers in
relation to the number of functions used in the composi-
tion. In the case of both bidirectional models and the LSTM
model, we used a hidden state consisting of 200 neurons.
For the GRU model, we increased this amount to 256, as the
GRU cells require less computation. Although the bidirec-
tional LSTM performs the best with shorter compositions,
its performance decreases remarkably as the composition
length increases, and it is also the slowest. Considering
speed and accuracy the GRU model is the most favorable.
Between the regular LSTM and GRU cells, GRU is
preferred as it performs well in terms of both execu-
tion time and accuracy.
In the second experiment, we checked how Flex-
Coder scales based on the length of the input-output
examples in terms of accuracy. We generated prog-
ram input-output vectors with a length of 10 to 50
in increments of five for testing purposes. Figure 7
shows that FlexCoder with GRU was capable of gen-
eralizing well to longer inputs.
Similarly to the first experiment, GRU was the
most accurate while being the best in terms of ex-
ecution time. Both bidirectional models performed
similarly, but the bidirectional LSTM was markedly
slower. The GRU model performed consistently bet-
ter than the LSTM-based network on longer example
lengths.
Based on the results of these two experiments, we
elected to use GRU as the recurrent layer of the archi-
tecture.
4.3 Accuracy and Execution Time
Tables 3 and 4 show the accuracy and the time needed
to find a solution in terms of the number of input-
output pairs and the composition length. By increas-
ing the number of input-output pairs the problem be-
comes more specific: finding a program that fits all
the pairs becomes a more complex task because the
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
392

10 20 30 40
50
50
60
70
80
90
100
Length of input examples
Accuracy [%]
Bidirectional GRU
Bidirectional LSTM
GRU
LSTM
Figure 7: The accuracy of FlexCoder using four different re-
current layers as a function of the length of the input. GRU
generalizes best to longer input lengths.
Table 3: Relation between composition length, the number
of input-output pairs, and the accuracy. Increasing compo-
sition length or the number of pairs almost always decreases
the accuracy.
comp.
length
#I/O
pairs
1 2 3 4 5
2 97% 97% 97% 96% 97%
3 99% 94% 92% 95% 93%
4 97% 89% 86% 83% 85%
5 96% 88% 81% 79% 78%
set of possible solutions narrows. Similarly, as we in-
crease the composition length the space of possible
programs also increases.
The accuracy achieved by FlexCoder is compara-
ble to PCCoder with the time limit replaced by the
same iteration limit as in FlexCoder. In terms of exe-
cution time FlexCoder sometimes falls behind, but the
performance of the two systems is generally similar.
Table 4: Relation between composition length, the number
of input-output pairs, and the execution time in seconds. In-
creasing either composition length or the number of inputs
almost always also increases execution time.
comp.
length
#I/O
pairs
1 2 3 4 5
2 211s 255s 264s 277s 274s
3 524s 1082s 1239s 1141s 1291s
4 1224s 2900s 3250s 3923s 3620s
5 1520s 3445s 4986s 5537s 5530s
4.4 Comparison with PCCoder
We compare our system to PCCoder which has out-
performed DeepCoder by orders of magnitude (Zohar
and Wolf, 2018).
Our approach to program synthesis is quite dif-
ferent from the approach of PCCoder (see Sec-
tions 1 and 3.1). We synthesize a function compo-
sition, they synthesize a sequence of statements. The
expressiveness of the grammars is also different: On
the one hand, our grammar is missing some func-
tions like ZipWith or Scan1l. On the other hand,
our grammar is much more expressive in terms of pa-
rameter values.
Our grammar is capable of expressing 151 diffe-
rent functions, 130 of which can be anywhere in the
sequence and 21 can only appear as the outermost
function as these return a scalar value. The DSL used
by PCCoder can express 105 different functions. The
number of possible programs with a length of five is
about 43.13 million for FlexCoder and about 12.76
million for PCCoder, resulting in our program space
being 3.38 times larger when considering programs
with a length of five.
To make fair comparisons despite these differen-
ces, we run experiments where both systems run on
their own dataset, and we also compare them by run-
ning them on the dataset of the other system.
In the first experiment, we examine what we con-
sider a crucial aspect of any program synthesis tool:
how well it generalizes with respect to the length of
the input-output lists. We trained both PCCoder and
FlexCoder on input-output vectors of length 15 to 20
with composition length 5. For PCCoder we set the
maximum vector length to 50. We tested the systems
on input-output vectors with a length of 10 to 50 in in-
crements of five, having 5 input-output examples per
program, each on their own dataset. The results can
be seen in Figure 8.
In the second experiment, we compare the accu-
racy of FlexCoder and PCCoder in a less realistic sce-
nario when PCCoder performs best: on the same in-
put lengths the systems have been trained on. In this
experiment, PCCoder does not have to generalize to
different input lengths. We compare the systems both
on their own dataset and on the datasets of each other
in Figure 9.
Our approach defines a depth limit for the search
algorithm, while the search used by PCCoder has a
time limit. To make the experiment fair, we changed
our algorithm’s depth limit to a time limit, and chose a
timeout of 60 seconds like PCCoder. The introduction
of a time limit in our search algorithm makes our sys-
tem’s accuracy go down by a couple of percent com-
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions
393
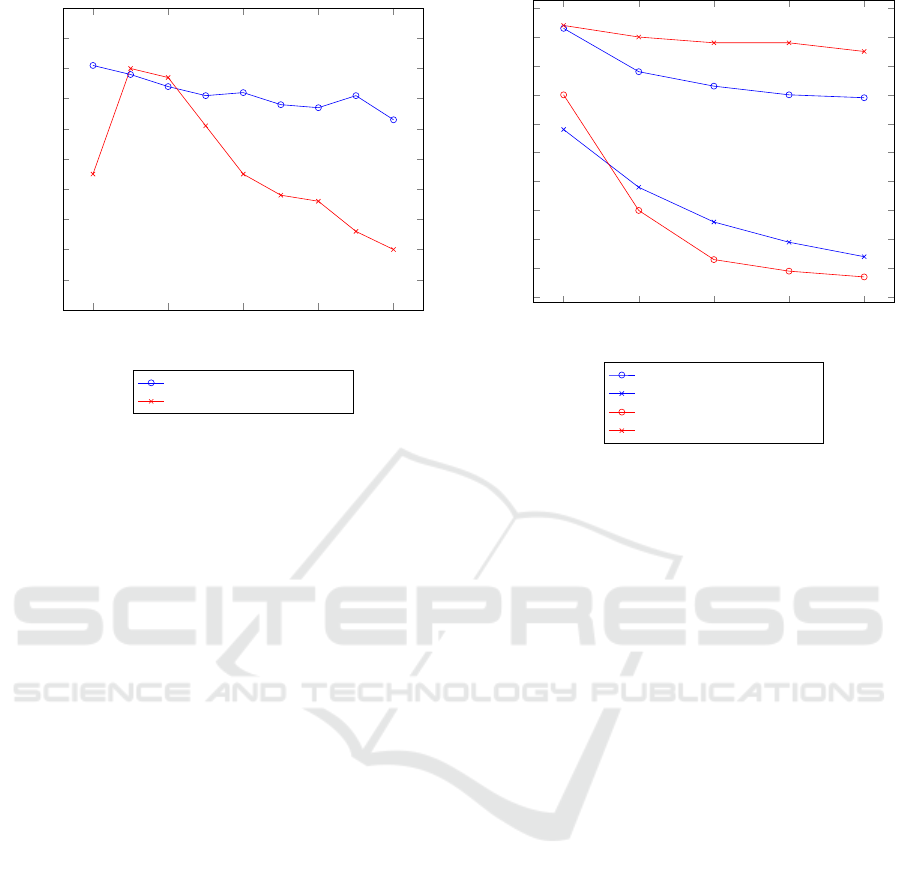
10 20 30 40
50
0
10
20
30
40
50
60
70
80
90
100
Length of input vectors
Accuracy [%]
FlexCoder on FlexCoder data
PCCoder on PCCoder data
Figure 8: The accuracy of FlexCoder and PCCoder in rela-
tion to the length of the input. Both systems were trained
on input-output vectors of length 15 to 20 with composition
length 5. For PCCoder we set the maximum vector length
to 50. We tested the systems on input-output vectors with
a length of 10 to 50 in increments of five, having 5 input-
output examples per program, each on their own dataset.
pared to Figure 7, so FlexCoder could perform even
better with the original depth limit. The parameters
in this experiment are the same as in the first exper-
iment, except for the length of the input lists which
is the same as for training, and the number of input-
output examples which range from 1 to 5.
5 DISCUSSION
FlexCoder generalized well with respect to the input
length in contrast to PCCoder. PCCoder only excelled
on vector lengths it was trained on. PCCoder has an
upper limit on the length of the input-output vectors;
we set the maximum vector length of PCCoder to 50
to accommodate this experiment. Applying PCCoder
to longer inputs would require retraining with a larger
maximum vector length.
We also compared the two systems when the in-
puts are the same length for testing as for training,
so PCCoder does not need the generalize to diffe-
rent input lengths. In this easier and less realistic
scenario, both systems beat the other on their own
dataset. Also, both systems perform notably worse
on the DSL of the other system.
We suspect that the reason behind the worse per-
formance of FlexCoder in this scenario is that in
these first experiments, we used function composi-
1 2 3 4
5
0
10
20
30
40
50
60
70
80
90
100
Number of I/O pairs
Accuracy [%]
FlexCoder on FlexCoder data
PCCoder on FlexCoder data
FlexCoder on PCCoder data
PCCoder on PCCoder data
Figure 9: The accuracy of FlexCoder and PCCoder on their
own and the other’s dataset. The parameters are the same
as in the first experiment, except that no generalization over
the input length is needed: the length of the input lists is
the same as for training. The number of input-output pairs
range from 1 to 5.
tions where – apart from the fixed parameters – each
function had only a single list as input and output.
Relaxing this constraint would raise the expressive-
ness of FlexCoder to a much higher level, and could
allow FlexCoder to outperform PCCoder in most ex-
periments.
One strength of FlexCoder in contrast to PCCoder
is the separation of operators and operands in the
lambda functions. Currently only two higher-order
functions (map and filter) are using these lambda
functions. We expect that FlexCoder would perform
better relatively to PCCoder if we extended the gram-
mar with more higher-order functions.
6 CONCLUSION
The DSL of DeepCoder is limited in terms of expres-
sivity as stated by the authors themselves in their sem-
inal DeepCoder paper. The main motivation of our
paper is to extend it and move towards real-world app-
lications.
We presented FlexCoder, a program synthesis sys-
tem that generalizes well to different input lengths,
separates lambda operators from their parameters, and
increases the range of integers in the input-output
pairs.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
394

The main limitation and the most promising fu-
ture work seems to be allowing function compositions
where each function can take more than one non-fixed
parameter. This would allow our grammar to exp-
ress ZipWith, Scan1l, and other interesting compo-
sitions, like the composition that takes the first n ele-
ments of a list where n is the maximum element of the
list. This could be expressed as take(max(arr),arr),
if we allowed expressions as parameters.
Further experimenting with our neural network
might include using NTM cells (Graves et al., 2014)
instead of GRU cells, as NTM cells are shown to work
exceptionally well when learning simple algorithms,
such as sorting which is also present in our set of used
functions.
FlexCoder proved to be accurate and efficient even
when generalizing to input vectors with a length of
50, with much wider parameter ranges than current
systems. We hope that it represents a step towards the
wide application of program synthesis in real-world
scenarios.
ACKNOWLEDGEMENTS
The authors would like to express their gratitude to
Zsolt Borsi, Tibor Gregorics and Ter
´
ez A. V
´
arkonyi
for their valuable guidance. The materials were
produced as part of EFOP-3.6.3-VEKOP-16-2017-
00001: Talent Management in Autonomous Vehicle
Control Technologies. The Project is supported by the
Hungarian Government and co-financed by the Euro-
pean Social Fund.
REFERENCES
Balog, M., Gaunt, A. L., Brockschmidt, M., Nowozin, S.,
and Tarlow, D. (2016). Deepcoder: Learning to write
programs. arXiv preprint arXiv:1611.01989.
Bird, S., Klein, E., and Loper, E. (2009). Natural language
processing with Python: analyzing text with the natu-
ral language toolkit. ” O’Reilly Media, Inc.”.
Cho, K., Van Merri
¨
enboer, B., Gulcehre, C., Bahdanau, D.,
Bougares, F., Schwenk, H., and Bengio, Y. (2014).
Learning phrase representations using rnn encoder-
decoder for statistical machine translation. arXiv
preprint arXiv:1406.1078.
Chomsky, N. and Sch
¨
utzenberger, M. P. (1959). The al-
gebraic theory of context-free languages. In Studies
in Logic and the Foundations of Mathematics, vol-
ume 26, pages 118–161. Elsevier.
Feng, Y., Martins, R., Bastani, O., and Dillig, I. (2018).
Program synthesis using conflict-driven learning.
SIGPLAN Not., 53(4):420–435.
Graves, A., Wayne, G., and Danihelka, I. (2014). Neural
turing machines. arXiv preprint arXiv:1410.5401.
Gulwani, S. (2016). Programming by examples: App-
lications, algorithms, and ambiguity resolution. In
Olivetti, N. and Tiwari, A., editors, Automated Rea-
soning, pages 9–14, Cham. Springer International
Publishing.
Gulwani, S., Polozov, O., and Singh, R. (2017). Program
synthesis. Foundations and Trends
R
in Programming
Languages, 4(1-2):1–119.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9(8):1735–1780.
Kalyan, A., Mohta, A., Polozov, O., Batra, D., Jain, P., and
Gulwani, S. (2018). Neural-guided deductive search
for real-time program synthesis from examples. arXiv
preprint arXiv:1804.01186.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Klambauer, G., Unterthiner, T., Mayr, A., and Hochre-
iter, S. (2017). Self-normalizing neural networks. In
Advances in neural information processing systems,
pages 971–980.
Lee, W., Heo, K., Alur, R., and Naik, M. (2018).
Accelerating search-based program synthesis using
learned probabilistic models. ACM SIGPLAN Notices,
53(4):436–449.
Manna, Z. and Waldinger, R. (1975). Knowledge and rea-
soning in program synthesis. Artificial intelligence,
6(2):175–208.
Parisotto, E., rahman Mohamed, A., Singh, R., Li, L., Zhou,
D., and Kohli, P. (2016). Neuro-symbolic program
synthesis.
Schuster, M. and Paliwal, K. K. (1997). Bidirectional re-
current neural networks. IEEE transactions on Signal
Processing, 45(11):2673–2681.
Shapiro, E. Y. (1982). Algorithmic program debugging.
acm distinguished dissertation.
Yin, P., Zhou, C., He, J., and Neubig, G. (2018). Struct-
vae: Tree-structured latent variable models for semi-
supervised semantic parsing.
Zhang, W. (2002). Search techniques. In Handbook of data
mining and knowledge discovery, pages 169–184.
Zohar, A. and Wolf, L. (2018). Automatic program syn-
thesis of long programs with a learned garbage col-
lector. In Advances in Neural Information Processing
Systems, pages 2094–2103.
Flexcoder: Practical Program Synthesis with Flexible Input Lengths and Expressive Lambda Functions
395
