Prediction of Cotton Field on Integrated Environmental Data

Sarthak Mishra

, Long Ma

and Nischal Aryal

Department of Computer Science, University of Illinois at Urbana Champaign, Urbana, IL, U.S.A.

Department of Computer Science, Troy University, Troy, AL, U.S.A.

Keywords: Agriculture, Crop Production, Cotton Yield, Prediction, Regression.

Abstract: The agriculture and farming industry plays a vital role in the economy. However, the importance of agriculture

cannot be fully quantified in terms of its economic profit. Agriculture affecting global hunger is a much more

sensitive and vital topic. One of the leading reasons for this is un-improvised crop production. Crop production

is affected by various factors, and monitoring those factors is the key to solving the problem. This paper

describes a comprehensive experiment predicting the cotton yield under various environments, such as Acres

Harvested, Acres Planted, Soil pH, Bulk Density, Clay-High, Clay-Low, Organic-Carbon, and Water-Area.

1 INTRODUCTION

Agriculture production is known to be affected by

various factors, such as temperature. With a slight

change of these factors, there can be considerable

variations on the crop’s net yield. Most of these

factors are environmental; for instance, rainfall and

temperature change seasonally, whereas factors like

Bulk Density and water-area of the soil change

slowly. To accurately quantify the effects of the

environmental factors on crop yield, type of crop and

the irrigation practices of the chosen crop must

remain constant.

The problem then reduces to predicting the amount

of crop yield based on the environmental factors.

Statistically, this problem boils down to a regression

task. Hence, our research focuses on discovering any

quantifiable co-relations between these

environmental factors and the yield of the crop.

Intuitively there seems to be a cause-and-effect

relation between these environmental factors and the

crop yield. This paper aims to verify a presence

statistical relationship between these factors and the

crop yield.

One of state-of-art machine learning classifiers has

been applied to the research to improve the

performance of the model, we will have to choose the

dependent entities carefully. The dependent entities

chosen for our study are Acres Harvested, Acres

Planted, Soil pH, Bulk Density, Clay-High, Clay-

Low, Organic-Carbon, and Water-Area.

The rest of the paper is organized as follows. Next

section discusses the data collection. In the third

section, we describe the data preparation and

proposed method. The fourth section illustrates

several comprehensive experiments for crop yield

prediction. At last, our work is concluded, and future

work is presented.

2 DATA PREPARATION

The data is collected from several web databases

(ISRIC WOSIS). The primary source we used in our

research is the USDA (United States Department of

Agriculture) database. The weather data is derived

from the weather API. The goal of this project is to

predict the cotton yield using soil type and weather

data. By profiling the column and the row of the

extracted data, two master tables and five child tables

were created.

2.1 Parent Table

The sources of data of these tables are the USDA

database and ISRIC WOSIS database. After

exhaustively collecting the data from the

websites www.ers.usda.gov/data-products and

https://websoilsurvey.sc.egov.usda.gov/App/WebSoi

lSurvey.aspx.

We divided the records into two main tables. These

tables stored the exact copy of online data. The two

master tables planned are soil table and crop table.

Mishra, S., Ma, L. and Aryal, N.

Prediction of Cotton Field on Integrated Environmental Data.

DOI: 10.5220/0010240707810786

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 781-786

ISBN: 978-989-758-484-8

781

▪ Soil table: stores the bulk of information

extracted from the given data sources.

▪ Crop table: the cotton plant is one of the most

complex structured plants. The life cycle of

cotton is found to be significantly changing

based on environmental conditions. Thus,

making this plant uniquely suitable for our

project. The root length of the cotton plant

varies from 30inch to 38 inches. Hence for the

analysis of this paper, the standard length of

80cm (31.50 inches) is taken. The information

stored in this table is the yield of cotton in

various counties of the united states of

America. This data is extracted from the USDA

database. This table also stores the Acres

Harvested and Acres Planted of cotton.

2.2 Child Table

The grain of data for these tables are derived from the

master tables. For the informational extraction and

consistency in the data lineage, a child table only has

one Master table as the source. There were 6 child

tables to store seven of our labels used for regression

analysis. All the below mentioned table are derived

from Soil Table:

▪ Soil Classification table: stores the place’s

location, namely Latitude and longitude

with the soil type. The metadata for this table

is Latitude, Longitude, and Soil Type.

▪ Site Characteristic table: stores the location,

namely Latitude and longitude with Soil

organic carbon stock in tonnes per hectare.

The metadata for this table is Latitude,

Longitude, Depth to bedrock.

▪ Soil Water: the metadata of the Soil Water

table is Latitude, Longitude, and Volumetric

water content at wilting point pF 4.2(WWP).

▪ Climate Data: the metadata of the Climate

Data is Latitude, Longitude, High

Temperature in Degrees, Low Temperature

in Degrees, and Average rainfall in inch.

▪ Physical Soil Properties table: the physical

soil properties of a location are divided into

four different types. These tables store the

location of the place namely Latitude and

longitude with different Physical attributes.

o Bulk density: The metadata of

the bulk density table is

Latitude, Longitude, and bulk

density.

o Coarse fragments: the metadata

of the Coarse fragments table is

Latitude, Longitude, and the

volumetric percent of the

fragments in 80cm depth.

o Bulk density: the metadata of

the bulk density table is

Latitude, Longitude, and bulk

density.

o Soil texture fraction silt in

percentage: the metadata of the

Soil texture slit table is

Latitude, Longitude, and the slit

in percentage at 80cm depth.

o Soil texture fraction sand in

percentage: the metadata of the

Soil texture sand table is

Latitude, Longitude, and the

sand in percentage at 80 cm

depth.

▪ Chemical Soil Properties: the chemical

Soil properties tables store the

information about the place like

Latitude, Longitude, and several

chemical properties.

o Cation exchange capacity: the

Cation exchange capacity

table's metadata is Latitude,

Longitude, and fine earth

fraction in cmolc/kg at 80cm

o Total nitrogen: the metadata of

the Total nitrogen table is

Latitude, Longitude, and the

fine earth fraction (80cm).

o Soil organic carbon content:

the metadata of the soil organic

carbon content table is Latitude,

Longitude, and fine earth

fraction in permilles at 80cm.

o Soil pH in H2O: the metadata

of the Soil pH in the H2O table

is Latitude, Longitude, and pH

in H2O at 80cm.

o Soil pH in Kcl: the metadata of

the Soil pH in the Kcl table is

Latitude, Longitude, and pH in

Kcl at 80cm.

2.2.1 Association Table

Association Table is the penultimate table for this

project. The models were created as part of this

project feed of the association table. There was a

significant challenge to meet the purpose of this table.

The challenge was to bind the data between the child

table and the crop master table. The content of child

tables was uniquely identified using the latitude and

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

782

longitude of a place, whereas the crop table was being

uniquely identified using the county's name. This

structure created a lack of shared key columns

between these tables. To mitigate this problem, we

took the average of all the child table's data in the

rough square boundary of a county and took this as

the final data.

The lack of information derived from the weather

table is not being included in our association table.

The latitude and longitude of the weather table were

missing for many counties. The metadata of this table

is County Name, State, Acres Harvested, Acres

Planted, Yield, Soil pH, Bulk Density, Clay-High,

Clay-Low, Organic-Carbon, and Water-Area.

2.2.2 Data Definition

▪ Soil-pH: indicates the acidity or alkalinity of

the soil. The PH unit is called the pH unit, and

it represents the negative logarithm of the

hydrogen ion concentration. The pH ranges

from 0 to 14. The pH of the soil is known to

affect the yield to a great degree. The

measurement of soil acidity or alkalinity is like

a doctor's measurement of a patient's

temperature. Changes in the acidity of soils

may change the availability to plants of

different nutrients in different ways

(Allaway,1957).

▪ Bulk Density: the calculation of the

compactness of the soil. It is the dry weight of

soil divided by its volume. The unit of Bulk

Density is g/cm3. The bulk density of the soil

affects the growth of the roots thereby affecting

the overall yield of the crop. Roots growing in

compacted soils can traverse otherwise

impenetrable soil using bio pores and cracks

and thus gain access to a more extensive

reservoir of water and nutrients (Stirzaker,

Passioura, and Wilms, 1996).

▪ Organic-Carbon: a measurable component of

soil organic matter. Organic Carbon is the

primary source of energy for soil

microorganisms.

▪ Water-Area: the number of miles of water body

contained in that area. The unit of measurement

is in miles.

▪ Crop yield: the quantification of the amount of

produce harvested per unit land.

▪ Acres Planted: the acres of land used for cotton

plantation.

▪ Acres Harvested: the acres of land where cotton

was harvested.

▪ Clay-High: represents the percentage of clay

with high plasticity. A clay–water system of

high plasticity requires more force to deform it

and deforms to a greater extent without

cracking than one of low plasticity, which

deforms more easily and ruptures sooner

(Brownell, 1977)

▪ Clay-Low: represents the percentage of clay

with high plasticity. The hydraulic conductivity

of the soil is known to be affected by the

plasticity of clay (Allen, 2005)

3 PROPOSED METHOD

3.1 Data Profiling and Modelling

After brief profiling, a supervised learning model will

be appropriately applied. There are two types of

learning approaches in supervised learning.

▪ Regression Analysis

▪ Classification Problem

The problem of our interest falls under the realm of

regression learning.

3.2 Regression Analysis

The central concept of this method is to find an

algebraic relationship between the dependent and the

independent variables. A model of the relationship is

hypothesized and estimates of the parameter values

are used to develop an estimated regression equation

(

Ostertagováa, 2012). This experiment will be using

Linear Regression.

Linear regression is a statistical tool for forming

the relationship between some "explanatory"

variables and some real-valued outcome (Shalev-

Shwartz and Ben-David, 2014). This research uses

nonlinear polynomial predictors. A nonlinear

polynomial predictor is a one-dimensional

polynomial function of degree n, that is

p(x) = a

+ a

x + a

+ ꞏ ꞏ ꞏ + a

(1)

where (a

, a

, ꞏ ꞏ ꞏ, a

) is a vector of coefficients of

size n + 1(Shalev-Shwartz and Ben-David, 2014).

To implement this method, we have used [Acres

Harvested, Acres Planted, Soil pH, Bulk Density,

Clay-High, Clay-Low, Organic-Carbon, and Water-

Area] as our independent variable and [crop yield] as

our dependent variable. The dichotomy of data was

created to separate the test and train data. Out of all

50 states, 'Alabama's data was used to test the

Prediction of Cotton Field on Integrated Environmental Data

783

hypothesis. The experiment uses a training set that is

better fitted using a 5th-degree polynomial predictor

than using a linear predictor.

y=a

+...+a

n-2

n-1

(2)

For this experiment: y is the Yield of cotton; a

the intercept; a

, a

... a

is the coefficient for Acres

Harvested, Acres Planted, Soil pH, Bulk Density,

Clay-High, Clay-Low, Organic-Carbon, and Water-

Area in 5th degree polynomial predictor. These are

called model coefficients. These values are generated

during model fitting and can be used for making

predictions.

This experiment used the linear regression

function that was packaged in the scikit-learn to

create the model. The scatter plots were generated

using Matplotlib.

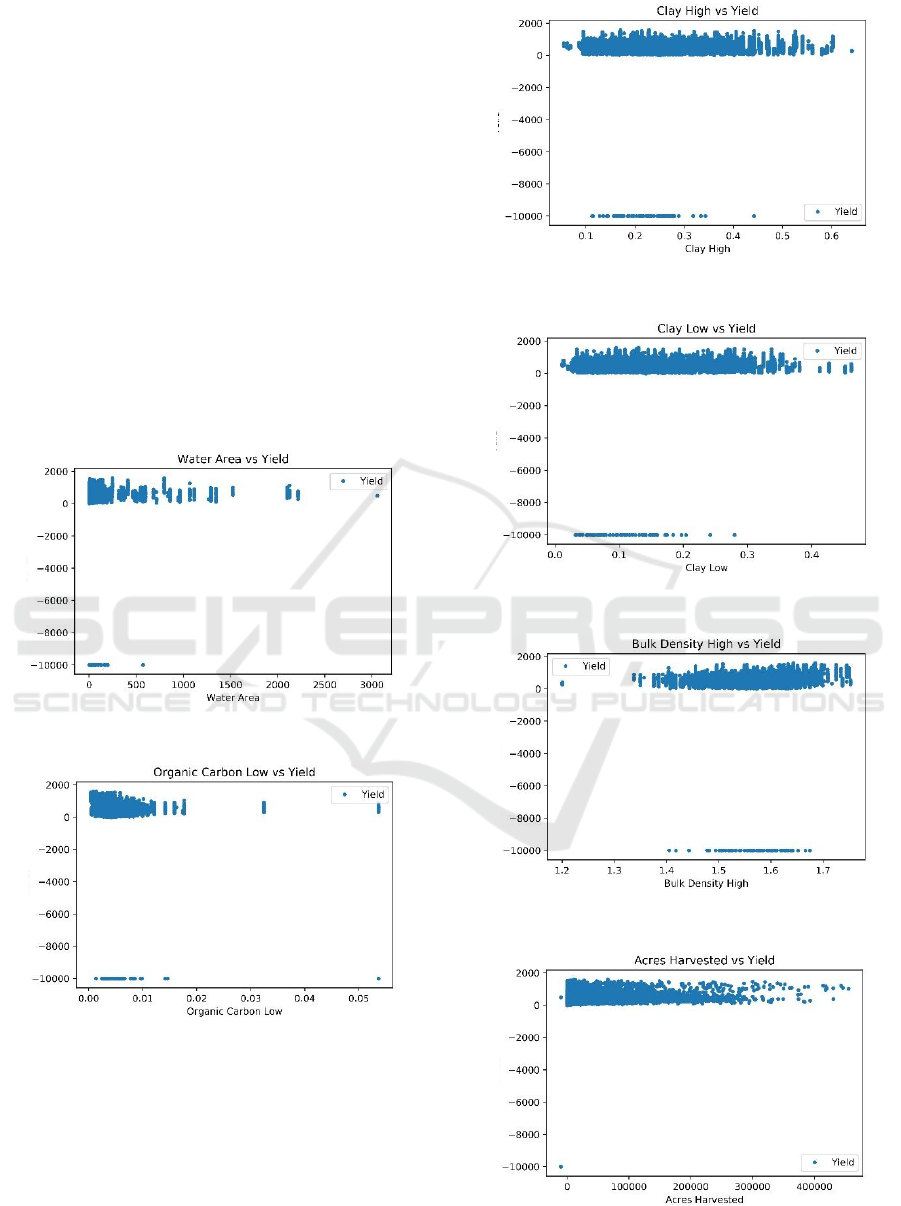
Figure 1: Scatterplot Water area vs Yield.

Figure 2: Organic Carbon vs Yield.

Figure 3: Scatterplot Clay High vs Yield.

Figure 4: Scatterplot Clay Low vs Yield.

Figure 5: Scatterplot Bulk Density vs Yield.

Figure 6: Scatterplot Acres Harvested vs Yield.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

784

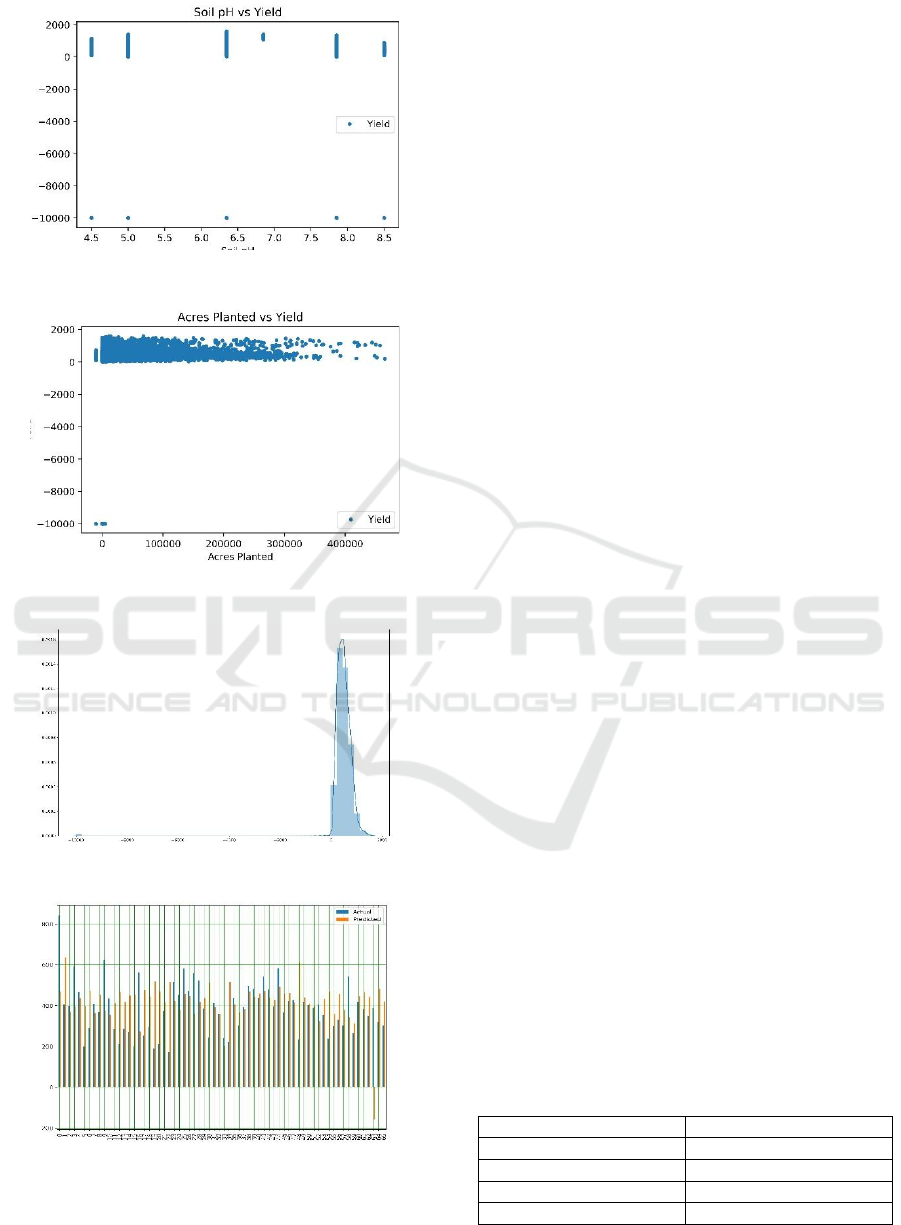
Figure 7: Scatterplot Soil pH vs Yield.

Figure 8: Scatterplot Acres Planted vs Yield.

Figure 9: Distribution of Yield.

Figure 10: Actual Data VS Predicted Data.

The first figure has the data that is cultured

between 0-250 units. In Figure 2, our data is

concentrated between 0-0.01 units for organic carbon.

We can infer that cotton's yield is maximized when

organ carbon is less than 0.01 units. Figure 3 and

figure 4 display that data on clay high and clay low is

spread around 0.1-0.6 units and 0.0-0.4 units,

respectively. Next, figure 5 shows that our data is

concentrated around 1.5 to 1.65 units. We can infer

that the precision of prediction will be in this region.

Also, figure 6 presents cotton harvested in less than

100000 acres; our data yield is more concentrated. In

the following figure, we find bands of 6 ph. values

that are affecting the yield. Figure 8 includes cotton

planted in less than 100000 acres; our data yield is

more concentrated. Figure 9 illustrates that our data

of cotton yield is distributed around 800 units.

Figure 10 compares the actual data and the

predicted data. The mean accuracy of this comparison

was 82%. It also tells the actual value of the

dependent variable [Yield] and the dependent

variable [Yield] predicted by the model created in this

experiment.

3.3 Results Analysis

For the experiment, we are using the coefficient of

Determination as the evaluation metric. The

coefficient of determination, a.k.a. R2, is well-

defined in linear regression models and measures the

proportion of variation in the dependent variable

explained by the predictors included in the model

(Zhang, 2017). The value of R2 ranges from 0 to 1- 0

being the worst and 1 being the best value.

R-squared measures of 0.86 represent the model

used for this experiment was of high accuracy. Hence,

using the knowledge from the above several

experiments we find that there is a quantifiable

correlation between environmental factors and the

yield of cotton. This experiment also finds that it is

feasible to predict the return of cotton-based on

several environmental factors. Hence, we conclude

that there is enough evidence to support our initial

hypothesis that there is a quantifiable relationship

between environmental parameters like pH, bulk

density, acres harvest, and planted with the Yield.

Table 1: Results of the Experiment.

Absolute Mean 128.51

Root Mean square

171.18

Absolute Median 87.65

Variance score 0.78

R2 score 0.86

Prediction of Cotton Field on Integrated Environmental Data

785

4 CONCLUSIONS

From the experiments above we conclude that it is

convincing to predict the yield of crops with good

accuracy based on environmental factors. Introducing

new factors will expand the model as well as improve

the accuracy of the model.

In the future, we are planning to collect more data

for several countries and improvise the model. We

plan to include weather data in the model as we

suspect this will improve the accuracy of the model.

REFERENCES

Allaway, W. H. 1957. pH, soil acidity and plant growth.

Pp. 67–79 in Soils: the 1957 yearbook of agriculture.

United States Department of Agriculture

Allen, Whitney M., 2005. The relationship between

plasticity ratio and hydraulic conductivity for bentonite

clay during exposure to synthetic landfill

leachate. Graduate Theses and Dissertations.

https://scholarcommons.usf.edu/etd/2772

Brownell W.E., 1977. Structural clay products Applied

Mineralogy, Springer, Berlin, vol. 9.

Zhang (2017) A Coefficient of Determination for

Generalized Linear Models, The American Statistician,

71:4, 310-316, DOI: 10.1080/00031305.2016.1256839

ISRIC WOSIS.https://data.isric.org/geonetwork/srv/eng/

catalog.search#/home.

Laliberte, G.E. and Corey, A.T. (1966) Hydraulic

properties of disturbed and undisturbed clays, ASTM,

STP. 417.

Ostertagováa, E. (2012). Modelling using polynomial

regression.

Shalev-Shwartz, S., & Ben-David, S. (2014).

Understanding Machine Learning - From Theory to

Algorithms, Cambridge University Press. Cambridge

Stirzaker, R. J., Passioura, J. B. & Wilms, Y. 1996., Soil

structure and plant growth: Impact of bulk density

and biopores. PlantSoil 185, 151–162.

https://doi.org/10.1007/BF02257571

USDA. data-products. United States Department of

Agriculture. www.ers.usda.gov/data-products.

Websoilsurvey.https://websoilsurvey.sc.egov.usda.gov/Ap

p/WebSoilSurvey.aspx.

Weather API. https://openweathermap.org/api.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

786