
Effective Area Partitioning in a Multi-Agent Patrolling Domain
for Better Efficiency
Katsuya Hattori and Toshiharu Sugawara
a
Department of Computer Science and Communications Engineering, Waseda University, Shinjuku, Tokyo 1698555, Japan
Keywords:
Multi-Agent System, Patrolling Problem, Division of Labor, Negotiation, Cooperative Agent.
Abstract:
This study proposes a cooperative method for a multi-agent continuous cooperative patrolling problem by par-
titioning the environment into a number of subareas so that the workload is balanced among multiple agents
by allocating subareas to individual agents. Owing to the advancement in robotics and information technology
over the years, robots are being utilized in many applications. As environments are usually vast and compli-
cated, a single robot (agent) cannot supervise the entire work. Thus, cooperative work by multiple agents,
even though complicated, is indispensable. This study focuses on cooperation in a bottom-up manner by fairly
partitioning the environment into subareas, and employing each agent to work on them as its responsibility.
However, as the agents do not monitor the entire environment, the decentralized control may generate unrea-
sonable shapes of subareas; the area are often unnecessarily divided into fragmented enclaves, resulting in
inefficiency. Our proposed method reduced the number of small and isolated enclaves by negotiation. Our
experimental results indicated that our method eliminated the minute/unnecessary fragmented enclaves and
improved performance when compared with the results obtained by conventional methods.
1 INTRODUCTION
In recent years, robotic applications have attracted
attention in many fields due to the development of
advanced hardware, such as high-functional sensors
and actuators related to robot technology and infor-
mation technology. Robots are particularly required
to play an active role in fields that entail repetitive
tasks or operations in inaccessible areas. However,
if the workspace is vast and/or complicated and re-
quires various abilities, it is not realistic to work only
with a single robot owing to physical and performance
limits, such as battery capacity, movement speed, and
limited work capability. The advancement in mobile
wireless communication technology enables efficient
real-time communication among robots and coordina-
tion and cooperation among multiple robots.
To control the collaborative activities of multiple
agents, which are the abstraction of robots in a gen-
eral framework, we consider the multi-agent contin-
uous cooperative patrolling problem. Possible appli-
cations of this problem are area cleaning and secu-
rity/surveillance patrolling by multiple agents. In this
problem, agents are required to divide the given task
a
https://orcid.org/0000-0002-9271-4507
so that the burden on each agent is as fair as possi-
ble; this also improves overall efficiency and results
in uniform quality of task outputs. To achieve fair
and effective division of labor, we consider a method
of explicitly partitioning a working responsible area
(RA) to a number of smaller areas and assigning
each agent to the partitioned area through communi-
cation/negotiation between agents. One of the diffi-
culties in fair partition of areas is that simple parti-
tion into equal sizes may not be appropriate because,
for example, (1) some partitioned area/room is dis-
tant from the charging/storage locations of agents, (2)
some rooms are more important than others so agents
have to visit them more frequently than others, (3)
some areas contain obstacles/slopes that makes pa-
trolling inefficient, and (4) the shape of a partitioned
area is complicated so it takes longer time to cover
the area. Nevertheless, agents have to consider these
factors to fairly partition the working area in a decen-
tralized manner.
Several studies have attempted to achieve collab-
orative work by dividing work areas (Kato and Sug-
awara, 2013; Ahmadi and Stone, 2006; Elor and
Bruckstein, 2009; Nasir et al., 2016). One disadvan-
tage of such distributed methods is that there is no
agent that manages the entire area; hence, the shapes
Hattori, K. and Sugawara, T.
Effective Area Partitioning in a Multi-Agent Patrolling Domain for Better Efficiency.
DOI: 10.5220/0010241102810288
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 281-288
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

of the divided areas are left unattended. For exam-
ple, agents proposed in Kato and Sugawara (Kato
and Sugawara, 2013) may generate split (and often
chopped) RAs due to the local decision. This kind of
inefficient division leads to a decrease in overall per-
formance. Conversely, agents often have to generate
disconnected RAs. For example, if rooms have nar-
row entrance doors or are led by narrow passages that
must be allocated to only one agent (an actual exam-
ple is shown later), the splitting of RAs is mandatory.
Therefore, in such an environment, if we introduce
a constraint that each RA must be connected, the di-
vided working areas cannot be balanced.
Therefore, we propose a method for partition-
ing the entire area into a number of RAs for indi-
vidual agents to obtain a balanced workload with-
out unnecessarily splitting the areas. We experimen-
tally demonstrated that our proposed method exhib-
ited better performance than that by the conventional
method (Kato and Sugawara, 2013). We also inves-
tigated the performance when the environment had
many obstacles and when the environment character-
istics are not uniform and show that in all such cases,
our method outperformed the conventional method.
2 RELATED WORK
There are a number of studies on multi-agent contin-
uous patrolling problems (Huang et al., 2019). We
can classify them roughly into two based on the meth-
ods for solving them. In the first type of method, the
agents share the entire area to move around without
dividing the area into smaller subareas. Carrillo and
Rapp (Carrillo and Rapp, 2020) proposed a method
to identify patrolling policies for multiple agents with
limited visibility regions and non-deterministic pa-
trolling paths. Yoneda et al. (Yoneda et al., 2013)
propose a method in which agents individually de-
termine their exploration algorithms using reinforce-
ment learning to contribute more toward the shared
goal. They also assumed that agents’ intermittent be-
haviors depend on the battery charge and agents de-
cide to explore the environment further or return to
their charging base depending on their battery capac-
ity. Our study also assumes the charging base, and
that agents have to return to the base before run-out.
Sugiyama et al. (Sugiyama et al., 2019), who also
used the model of cyclic charging activities, consider
the cycle of agent patrolling while shifting the time
phase to visit each location. However, because en-
vironments are not partitioned, there is a possibility
that more than two agents patrol the same area, which
may be redundant and hence, unnecessary actions in-
crease.
In the second type of method for solving continu-
ous patrolling problems, the environment is fairly di-
vided into a number of subareas and each of them is
allocated to an agent to move around in a balanced
manner. In the method proposed by Nasir et al. (Nasir
et al., 2016), the leader agent divides the environment
and determines and allocates the exploring area to in-
dividual member agents. However, this requires cen-
tralized control by the leader agent, and hence, its fail-
ure affects the entire system. Ahmadi and Stone (Ah-
madi and Stone, 2006) introduced area division based
on boundary relationships between agents. If there
were overlapping locations, they were transferred to
the agents which frequently visited those areas. Elor
and Bruckstein (Elor and Bruckstein, 2009) proposed
a model based on balloon expansion so that individual
agents can fairly divide the environment into subareas
of the same size in a bottom-up manner. However,
given the obstacles and non-uniform structures in the
environment, divisions of the same size are not always
fair from the viewpoint of agents’ workload. More-
over, these methods did not consider the constraints
due to battery capacity.
By contrast, Kato et al. (Kato and Sugawara,
2013) introduced the constraint on the battery ca-
pacity and proposed the partitioning method for fair
workload among agents. Their method for area par-
titioning is based on the expansion power, like the
current study, that reflects the degree to which the
agent has completed the work in its RA. However,
because their method generated many fragments of
RAs (Kato and Sugawara, 2013), the performance
often decreased or could not be applied in a compli-
cated environment. In this study, agents divide their
RAs according to the shape of the environment so
that agents with the method can be applied to even
complex environments. We also reduce the unneces-
sary fragments of the area of responsibility to improve
the efficiency of event collection/observation in multi-
agent patrolling problem.
3 BACKGROUND AND PROBLEM
3.1 Environment
We introduce discrete time t ≥ 0, whose unit is a
step. The multi-agent continuous cooperative pa-
trolling problem can be expressed by (G,A,P ), where
A = {1,·· · ,N} is a set of agents, G = (V, E) is a con-
nected graph embeddable into two-dimensional Eu-
clidean space, V = {v
1
,· ·· ,v
x
} is the set of nodes,
E is the set of edges e
v
i
,v
j
connecting two nodes
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
282

v
i
,v
j
∈ V , and P = {p
v
}
v∈V
(0 ≤ p
v
≤ 1) is the distri-
bution of event probability, i.e., a collection of proba-
bilities of event occurrence at v ∈ V . An event at node
v is required to be observed or monitored by one of the
agents, and thus, agents are necessary to visit these
nodes in proportion to the values of these probabili-
ties. For example, nodes where high security levels
are required has higher event probabilities in a secu-
rity patrolling domain and nodes with higher proba-
bilities are more likely to get dirty in a vacuum clean-
ing domain. Therefore, we assume that P is given to
all agents.
We assume that events are accumulated if no
agents have monitored/observed them. Therefore, for
∀v ∈ V , the amount of accumulated events L
t
(v), is
incremented by one with p
v
at t, that is,
L
t+1
(v) =
L
t
(v) + 1 with probability p
v
L
t
(v) otherwise
(1)
If the agent visits node v at time t, it has observed or
monitored v, and so the amount of accumulated event
at v is cleared (L
t+1
(v) = 0). However, agents cannot
know the actual values of L
t
(v); hence, they estimate
L
t
(v) using the expected value E(L
t
(v)) using p
v
∈ P .
We can assume that the length of an edge is 1 by
adding dummy nodes whose event probabilities are
zero. Therefore, agents at any node can move to its
adjacent node in one step. Agent i has a charging base
v
i
base
(∈ V ) that is specified initially and that it has to
return to before run-out. Agent i has its own RA V
i
t
at time t, which is a subset of V including v
i
base
, and
where it must move around to maintain. For a fair
workload, i has to adjust its own RA by negotiation
with its collaborative agents.
3.2 Model of Agent
We introduced three assumptions in the model of
agents. First, agents have the map where they patrol.
We believe that in many applications, the map of the
environment is often known; hence, this assumption
is plausible. Furthermore, many map creation algo-
rithms have been proposed so far. As we focus on
the fair workload by appropriate area partitioning, we
assume that maps can be made by using these algo-
rithms if necessary. Second, multiple agents can exist
in the same node and collision is not possible. In re-
ality, a collision may occur when multiple agents try
to move to the same node if it is narrow. However
again, because we focus on fair workload, we assume
that collision avoidance algorithms will be used for
actual applications. Finally, each agent has a battery
with a finite capacity. Therefore, it cannot continue
patrolling forever, and alternately repeats the explor-
ing state and the charging state.
Agents have two states: the active state and charg-
ing state. Agents in the active state move around the
environment (or their own RA) to find unobserved
events in accordance with their exploring strategies,
whereas agents in the charging state charge at their
charging base. The states of the battery in agent i is
specified by parameters B
i
max
B
i
drain
B
i
t
, where B
i
max
is the maximal charge capacity, B
i
drain
is the battery
consumption per step when i is moving, and B
i
t
is the
remaining battery capacity. Therefore, the charging
time t
i
ch
to make the battery full is proportional to the
consumed energy; hence, it is
t
i
ch
= k
i
ch
(B
i
max
− B
i
t
), (2)
k
i
ch
> 0 is the charging constant. For simplicity,
agents start from their base after full charge.
For ∀v ∈ V , we define the potential Pot
i
(v) of v as
the required amount of energy to reach the charging
base. Let Len(v,u) be the shortest distance from node
v to node u, i.e., the number of edges in the shortest
path between them. It can then be defined by
Pot
i
(v) = Len(v, v
i
base
) × B
i
drain
(3)
When i attempts to move from node v
1
to node v
2
, it
compares B
i
t
and Pot
i
(v
2
) and if
B
i
t
< Pot
i
(v
2
) + Len(v
1
,v
2
) × B
i
drain
(4)
is satisfied, i gives up on v
2
and returns to its charging
base v
i
base
to prevent battery run-out.
The purpose of agents is to visit nodes in their
RA V
i
t
as frequently as possible by considering the
event probability of nodes using a certain exploring
algorithm. In this paper, because we focus on the
method of area partitioning, we used a simple al-
gorithm for exploring, the directed depth-first search
(DDFE) (Kato and Sugawara, 2013), which is briefly
described as follows.
When agent i leaves the charging base at t, it
sets the node v
0
which has the largest expected value
E(L
t
(v)) in V
i
t
and moves to v
0
along the shortest
route. When i reaches v
0
, v
0
is pushed into the in-
ternal stack and its unvisited adjacent nodes in V
i
t
are
added to the open list. Then, i selects one of them
randomly and moves there. Agent i pushes the cur-
rent node into the stack and the adjacent nodes that
are unvisited and are not in the open list are added
to the open list. This is repeated as long as i can se-
lect unvisited adjacent nodes. When i cannot select
an unvisited node, it pops the top node from the stack
and moves back to that node, and then i selects an un-
visited node from the open list. After repeating this
operation if i returns to v
0
and cannot select another
unvisited node, it returns to the charging base along
the shortest path. Note that when it moves along the
Effective Area Partitioning in a Multi-Agent Patrolling Domain for Better Efficiency
283

shortest path, all nodes in this path may not be in V
i
t
;
therefore, i may pass through the areas that are the
responsibility of other agents.
3.3 Deciding RA
We will briefly explain how agents coordinate with
each other to decide their RAs in the environment us-
ing the conventional method. Please see (Kato and
Sugawara, 2013) for details. Initially, agent i ∈ I has
a small area within the distance d
init
from its charging
base v
i
base
as an initial RA V
i
0
= {v ∈ V |Len(v,v
i
base
) ≤
d
init
}. We assume that v
i
base
∈ V
i
t
for ∀t.
First, agent i calculates the sum of all expected
values
E(L(V
i
t
)) =
∑
v∈V
i
t
E(L(v)).
This value also indirectly shows how completely an
agent has patrolled its area of responsibility. The re-
ciprocal of this value, ε(i,t), is called the expansion
power of i at time t. Agents calculate the expansion
power whenever they return to the charging base, and
retain the values until the next change in calculation.
When agents expand their RAs, they attempt to in-
clude some boundary nodes {u
1
,. .. ,u
K
} of V
i
t
(where
u
i
6∈ V
i
t
) and nodes that are not too far from the base
v
i
base
. Then, if u
i
is not included, in other RAs, u
i
is
added to V
i
t
. If u
i
∈ V
j
t
for j ∈ I (i 6= j), they begin
to negotiate and the agent whose expansion power is
larger includes the nodes into their RA.
3.4 Isolated Enclaves
One significant drawback of the conventional method
is that agents will have their RAs unnecessarily split
by others’ expansion behaviors; there will be many
isolated enclaves. We define an enclave as follows.
For the current RA V
i
t
, let us consider G
i
t
= (V
i
t
,E
i
t
)
where E
i
t
= {e
uv
∈ E|u,v ∈ V
i
t
}. Then, for v ∈ V
i
t
,
the connected nodes V
i
conn
(v) of i is the set of nodes
in V
i
t
reachable from v only along the edges in E
i
t
.
Similarly, we can define the connected component
G
i
conn
(v) = (V
i
conn
(v),E
i
conn
(v)), where E
i
conn
(v) =
{e
uv
∈ E|u,v ∈ V
i
conn
(v)}. Let G
i
conn
be the set of all
connected components of i. Then, G
i
conn
(v) is an en-
clave if it does not include i’s base (v
i
base
6∈ V
i
conn
(v)).
Obviously, connected components are exclusive and
their union is equal to V
i
t
. As mentioned before, some
enclaves are indispensable to cover the entire environ-
ment, but unnecessary enclaves, especially small and
scattered enclaves, will significantly reduce the sys-
tem’s performance.
3.5 System Evaluation Criteria
The purpose of this research is to allow agents to pa-
trol the environment and more frequently visit impor-
tant nodes by appropriately partitioning the environ-
ment into RAs, so that their workload is fair and bal-
anced. Because our target applications are, for ex-
ample, patrolling for security surveillance, large area
cleaning, and environmental/sensor data collection,
agents should visit the nodes in their RA without leav-
ing any nodes unattended for a long time. For this pur-
pose, we evaluate the systems performance using the
average value D
t
s
,t
e
(V ) of the number of remaining
events of all nodes in period [t
s
,t
e
], which is defined
by
D
t
s
,t
e
(V ) =
t
e
∑
t=t
s
L
t
(V )/(t
e
−t
s
+ 1). (5)
Therefore, the smaller the value of D
t
s
,t
e
(V ), the better
is the performance of the method.
The target of the proposed method is efficient pa-
trolling by reducing the number of enclaves, and so,
we also investigate the number of enclaves of their
RAs. Note that t
s
and t
e
in D
t
s
,t
e
(V ) is often omitted
(so D(V )).
4 PROPOSED METHOD
We propose a method for multiple autonomous agents
to individually decide their own RA by partitioning
the environment without small isolated enclaves. This
method consists of the determination of expansion
nodes, which is almost identical to the conventional
method (Kato and Sugawara, 2013), and two negoti-
ation phases for the arrangement of overlapped area
assignments to maintain a balanced workload and del-
egate isolated enclaves to reduce small and isolated
areas.
4.1 Determination of Expansion Nodes
Agent i ∈ A attempts to gradually expand the RA by
including a number of nodes that are not in but at
the boundaries of V
i
t
, when it has almost finished the
work in the RA and still has enough battery capacity
to move more. First, when i leaves the charging base
v
i
base
at the time t
b
, it calculates the estimated value
E(L
t
b
+γ
(V
i
t
b
)) of the remaining amount of the event
after γ (> 0) steps from t
b
. The reason for calculating
the estimated number of unobserved events at time
t
b
+ γ instead of at t
b
is that (1) i tries to expand the
RA at a certain time after leaving the base and (2) it
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
284

wants to compare the state of unobserved events if it
does not move after it works actually.
After agent i starts from v
i
base
at t
b
, it records
N
vis
(t), which is the number of nodes visited by t
(> t
b
), and N
d
(t), which is the sum of the observed
events. Then, when conditions (6) and (7) are satis-
fied, the agent tries to expand the RA.
N
vis
(t) ≥ R
1
· |V
i
t
| (6)
N
d
(t) ≥ R
2
· E(L
t
b
+γ
(G
i
t
b
)), (7)
where R
1
and R
2
are the parameters to adjust expan-
sion activity (0 ≤ R
1
,R
2
≤ 1). To avoid excessive area
expansion, agents attempt to expand the RA only once
after leaving their bases.
When agent i tries to expand its own area, it deter-
mines the set of nodes to be included I
i
.
(1) Agent i selects a set of nodes B that is adjacent to
its own RA.
(2) i selects k
inc
(> 0) nodes from B that are not in-
cluded in I
i
exp
(explained later) and have the short-
est distance from its charging base v
i
base
, and sets
them as I
i
inc
, where k
inc
is an integer.
(3) Nodes in I
i
inc
and nodes adjacent to an element in
I
i
inc
\ I
exp
are defined as the set I
i
.
Thus, if I
i
= ∅, i does not expand the area.
4.2 Arrangement of Overlapped Areas
After determining the expansion nodes, agents decide
which agent should work for individual nodes in I
i
.
For every v ∈ I
i
, when v ∈ V
j
t
, i requests ε( j,t), from
j and i includes v to V
i
t+1
only when ε( j,t) < ε(i,t).
If ε( j,t) ≥ ε(i,t), then v is added to I
i
exp
.
I
i
exp
is the set of nodes that should not be included
in I
i
for a while to prevent frequent challenges and
failures. Hence, once a node is included in I
i
exp
, it
will be excluded from I
i
exp
after the area expansion is
performed k
avoid
(> 0) times. Furthermore, in Step (2)
of the expansion node determination, i adds all nodes
that are not included in other’s RA and are omitted
from counting k
avoid
nodes.
4.3 Reducing Isolated Small Enclaves
To reduce the occurrence of unnecessary enclaves,
agent i negotiates with other agents to delegate iso-
lated enclaves to more appropriate agents. To decide
an enclave that should be delegated to other agents, i
will select small enclaves distant from the base.
For ∀G
i
conn,k
∈ G
i
conn
, we calculate the mean dis-
tance from the base v
i
base
by
dis(G
i
conn,k
) =
1
|V
i
conn,k
|
∑
v∈G
i
conn,k
Len(v, v
i
base
) (8)
Then, the enclaves, which are the connected compo-
nents that do not contain v
i
base
, and satisfy the follow-
ing condition become the candidates to be delegated.
dis(G
i
conn,k
) >
|V
i
conn,k
|
R
3
· |V
i
t
|
, (9)
where R
3
is a small positive number to decide the bal-
ance between the size and distance of the connected
components. An enclave G
i
conn,k
will be delegated to
agent j that has the largest number of nodes adjacent
V
i
conn,k
to its RA. This calculation can be done during
i charges.
Then, agent i communicates with agent j so that
i delegates G
i
conn,k
to j, without considering their ex-
pansion powers. Therefore, j may temporally have a
large RA. However, its expansion power decreases so
that j’s RA is gradually diminished by other agents;
eventually, the overall load will become fair. Note
that all enclaves are not deleted; only small enclaves
far from v
i
base
will be delegated. Finally, when agent
i moves from enclave G
i
conn,k
to another G
i
conn,k
0
, it
takes the shortest path between two enclaves. There-
fore, i finds the pair (v,v
0
) ∈ G
i
conn,k
× G
i
conn,k
0
s.t.
Len(v, v
0
) is the smallest (if there are more than two
pairs, one of the pairs is selected randomly), and i fol-
lows the shortest path between v and v
0
. Note that the
pair of length Len(v, v
0
) is defined as the distance be-
tween two areas and denoted by dist(G
i
conn,k
,G
i
conn,k
0
),
We can clearly define the distance between any sub-
areas in the same way.
5 EXPERIMENTAL RESULTS
We conducted three experiments using three differ-
ent environments (Fig. 1) to verify that our proposed
method does not generate unnecessary fragments of
RAs in various environments. We set A = {1,2,3,4}
(agent i is indicated as Agent+i in all figures below).
Other initial parameters in this experiment are listed
in Table 1. All data shown below are averages for
every 3600 steps (because the maximum cycle of op-
eration and charging is 3600 steps) taken from 100
independent experimental runs.
To compare the performance with those of the
conventional method (Kato and Sugawara, 2013), we
adopted the DDFE method to explore. Because the
Effective Area Partitioning in a Multi-Agent Patrolling Domain for Better Efficiency
285
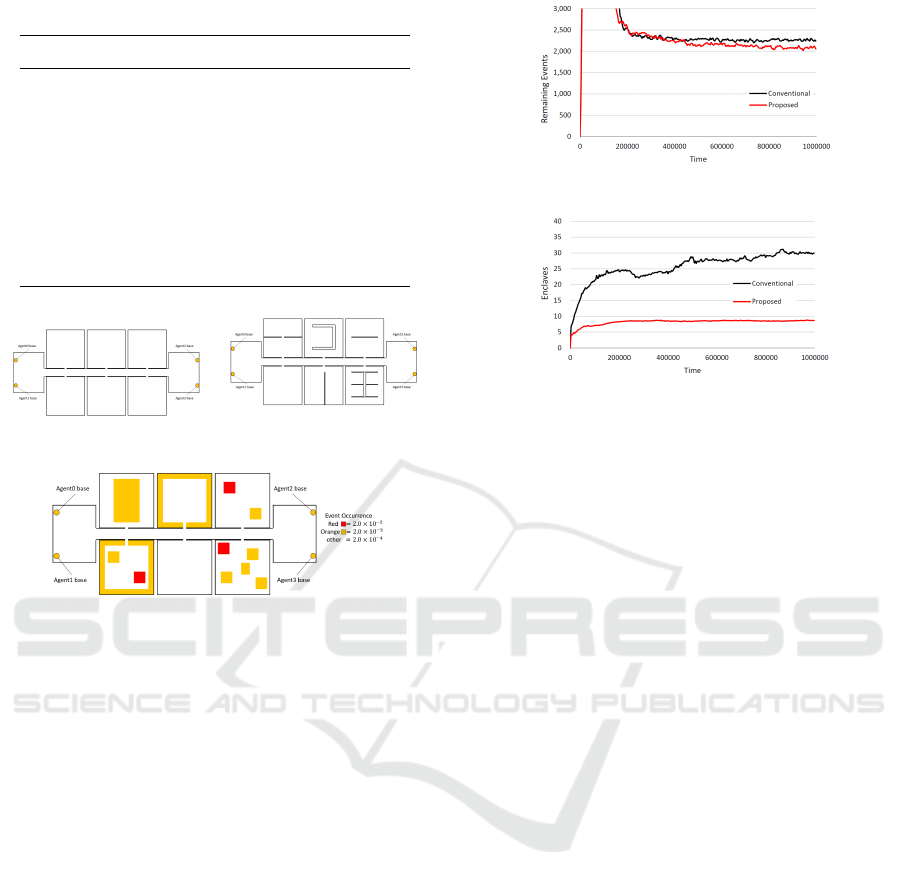
Table 1: Agent’s Parameters.
Description Parameter Value
Parameters for area expansion R
1
0.4
R
2
0.4
γ 300
k
avoid
90
Ratio for enclave negotiation R
3
0.005
Battery consumption per step B
drain
1
Battery capacity B
max
900
Charging constant k
ch
= k
i
ch
3
Radius of initial RA d
init
2
(a) Uniform environment
(b) Environment with obsta-
cles
(c) Biased environment
Figure 1: Three Environments.
DDFE assumes that the RA is connected (its perfor-
mance considerably decreases if not), we connected
the fragmented RAs with paths between the nearest
area; then, the agent moves in its RA with the con-
nected paths. Let us set G
temp
= G
i
conn
. Agent i
selects two connected components G
i
1
and G
i
2
from
G
i
temp
, whose distance is the smallest and connects
them with one of the shortest path. Then, G
i
1
and
G
i
2
are removed from G
temp
and instead, union of
G
i
1
∪G
i
2
∪{n ∈ V |n is on the connected path} is added
to G
temp
. Agent i repeats this process until G
temp
be-
comes a singleton. The generated area consisting of
G
temp
is used as the connected RA of i.
5.1 Uniform Environment
In the first experiment, we evaluate the proposed
method by comparing its performance with that by
the conventional method in the uniform environment
where the event probability is identical in all nodes
and defined as p
v
= 2×10
−4
for ∀v ∈V . The structure
of the environment is shown in Fig. 1a, in which there
is only one connection node between the corridor and
each of the six rooms. Therefore, assuming that the
Figure 2: Remaining events D(V ) in uniform environment.
Figure 3: Number of enclaves (uniform environment).
RA must be connected, each room must be patrolled
by one agent, whereas the number of agents is four,
making fair assignment of responsibilities impossible.
Conversely, if we exclude this assumption, many en-
claves are generated because no agent is looking at
the whole state of the RAs, resulting in undesirable
division in the conventional method. The locations of
the battery charging bases for individual agents are in
one of the wide spaces at the ends of the corridor as
shown in Fig. 1a.
Figure 2 plots the number of remaining events in
the environment every 3,600 steps over time. Note
that the smaller the number of events, the better is
the method. This figure indicates that the proposed
method exhibited slightly better performance than the
conventional method. In earlier steps, the perfor-
mance of the proposed method seems lower, but this
is caused by reallocating the enclaves to other agents,
so agents’ workloads are temporally not balanced.
We counted the number of enclaves (including the
connected component containing v
i
base
) of the RA of
each agent; this is shown in Fig. 3. This figure indi-
cates that the number of enclaves of the conventional
method gradually increased over time because in the
area expansion, agents tried to include nodes that is
decided only by the local viewpoint; thus, this expan-
sion process may split the RA of other agents. Con-
versely, agents with the proposed method allocated
the fragmented enclaved areas to other agents, even
if such areas were generated, and thus, they can sup-
press the increase of the number of RAs. It should
be noted that because |A| = 4, at least four connected
components are necessary. Furthermore, in the exper-
imental environment, the disconnected enclaves are
mandatory to cover the entire environment.
Finally, we investigated how environment is di-
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
286
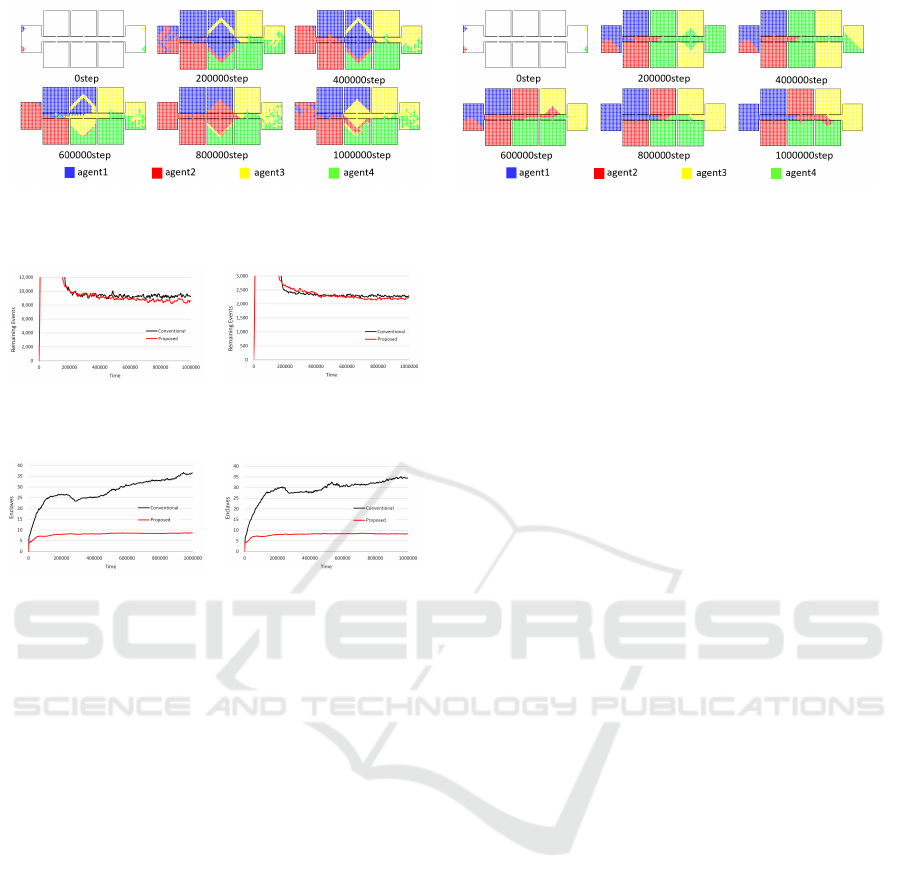
(a) Conventional method
(b) Proposed method
Figure 4: Distribution map of RAs (uniform environment).
(a) Biased event probabilities
(b) With obstacles
Figure 5: Number of remaining events (D(V )).
(a) Biased event probabilities
(b) With obstacles
Figure 6: Number of enclaves.
vided into the RAs and how they are allocated to
agents over time. The distribution maps of the en-
claves of the RAs of all agents are shown in Fig. 4.
Figure 4a indicates that RAs were fragmented in the
whole environment, especially spaces near the battery
bases, throughout the experiment. This was probably
because the competition of RAs occurred frequently
there, even if the size of the allocated areas were al-
most identical. By contrast, Fig. 4b shows the RAs are
not unnecessarily divided, and thus, no fragmented ar-
eas seemed to exist. Note that the RAs were always
varying. Of course, we can suspend the behavior of
area expansion at a sufficient point if the environment
is static. However, if the environment is dynamic and
unexpected events, such as failure of an agent, intro-
duction of new agents and deployment of obstacles,
occur, agents should continue to perform the area ex-
pansion behavior to adapt to the changes.
5.2 Non-uniform Environment
We conducted the same experiments in two differ-
ent types of environments. First, is the biased en-
vironment (Fig. 1c), where there are a number of
specific regions where more events are likely to oc-
cur or which are more important regions that agents
must visit more frequently. The second environment
(Fig. 1b) has a number of walls and obstacles in all
rooms. The purpose of these experiments are to check
if the proposed method can avoid the unnecessary,
small, and disconnected RAs even in more compli-
cated environments. Note that the event probabilities
of white orange and red nodes are p
v
= 2.0 × 10
−4
,
p
v
= 2.0 × 10
−3
and p
v
= 2.0 × 10
−2
in Fig. 1.
Their performances, i.e., the values of D(V ), are
plotted in Fig. 5. This figure shows that the pro-
posed method outperformed the conventional method
in both environments by suppressing unnecessary
fragmented enclaves; we can also see this fact in both
cases from Fig. 6. Actually, the number of enclaves
was stable in the proposed method whereas it gradu-
ally increased over time in the conventional methods.
Figure 5 also indicates that the convergence speed of
agents with the proposed method was slightly slower;
this is also the result of the negotiation to allocating
enclaves to more appropriate agents because, in ear-
lier stages, agents generated more enclaves aggres-
sively by their area expansion processes.
Finally, we generated maps to see how all RAs
changed over time in these experiments; these maps
are shown in Figs. 7 and 8. They show that the pro-
posed method considerably reduces the number of en-
claves by eliminating unnecessary fragments even if
there are no global observers that monitor the entire
environment. We have to note that because the pro-
posed method suppressed the number of unnecessary
enclaves, the degree of balance in the sizes of RAs of
four agents slightly decreased; however, this is quite
small and the resulting efficiency was improved, so
we believe that it can be ignorable.
6 CONCLUSION
In this paper, we discuss a method to cover a large en-
vironment using multiple agents by partitioning it in a
bottom-up manner to achieve fair and efficient coop-
erative executions of the continuous multi-agent pa-
trolling problem. Although there are some studies to
Effective Area Partitioning in a Multi-Agent Patrolling Domain for Better Efficiency
287
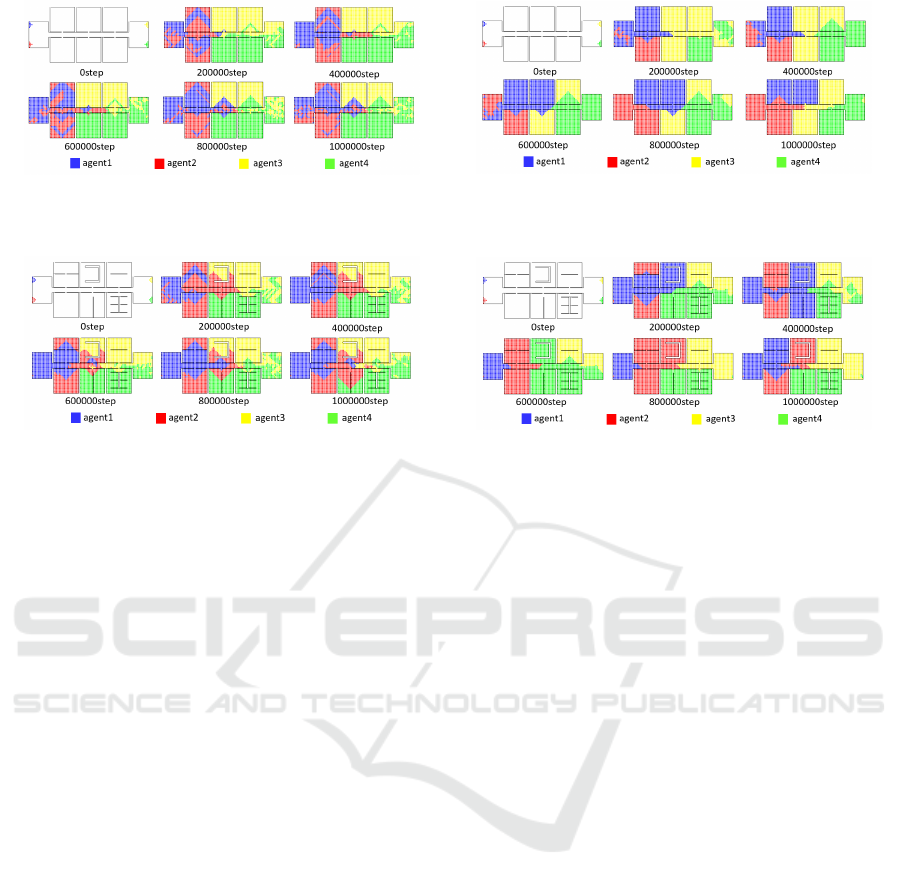
(a) Conventional method
(b) Proposed method
Figure 7: Distribution map of RAs (biased environment).
(a) Conventional method
(b) Proposed method
Figure 8: Distribution map of RAs (biased environment).
achieve the balanced collaboration by area division,
they often generated fragmented RAs due to the de-
centralized control wherein no one agent can see the
entire situation, thus, resulting in inefficient coopera-
tive work. We proposed a method in which agents do
not generate unnecessary enclaves of RAs by allocat-
ing fragmented parts of the RA to more appropriate
agents through communication. The results indicated
that our proposed method could reduce the unneces-
sary enclaves of the RAs and thus, could achieve effi-
cient cooperative work in the various environments.
We would like to examine more complicated en-
vironments to apply our method to more realistic do-
mains. We also plan to further improve the shape of
RAs, especially eliminating enclaves or fill recesses
in concave areas, for more efficiency.
ACKNOWLEDGEMENT
This paper is partly supported by JSPS KAKENHI
grant number 17KT0044.
REFERENCES
Ahmadi, M. and Stone, P. (2005). Continuous area sweep-
ing: A task definition and initial approach. In Proc.
of 12th Int. Conf. on Advanced Robotics (ICAR 2005),
IEEE, pages 316–323.
Ahmadi, M. and Stone, P. (2006). A multi-robot system
for continuous area sweeping tasks. In Proc. of 2006
IEEE Int. Conf. on Robotics and Automation (ICRA
2006), pages 1724–1729.
Carrillo, P. and Rapp, B. (2020). Stochastic multi-robot pa-
trolling with limited visibility. Journal of Intelligent
& Robotic Systems, 97(2):411–429.
Elor, Y. and Bruckstein, A. (2009). Multi-a(ge)nt graph
patrolling and partitioning. In Proc. of the 2009
IEEE/WIC/ACM Int. Joint Conf. on Web Intelligence
and Intelligent Agent Technology, Vol. 2, IEEE Com-
puter Society, pages 52–57.
Huang, L., Zhou, M., Hao, K., and Hou, E. (2019). A sur-
vey of multi-robot regular and adversarial patrolling.
IEEE/CAA Journal of Automatica Sinica, 6(4):894–
903.
Kato, C. and Sugawara, T. (2013). Decentralized area parti-
tioning for a cooperative cleaning task. In Proc. of the
16th Int. Conf. on Principles and Practice of Multi-
Agent Systems (PRIMA-2013), pages 470–477.
Nasir, A., Salam, Y., and Saleem, Y. (2016). Multi-
level decision making in hierarchical multi-agent
robotic search teams. The Journal of Engineering,
2016(11):378–385.
Sugiyama, A., Wu, L., and Sugawara, T. (2019). Improve-
ment of multi-agent continuous cooperative patrolling
with learning of activity length. Agents and Artificial
Intelligence, pages 270–292, Cham. Springer Int. Pub-
lishing.
Yoneda, K., Kato, C., and Sugawara, T. (2013). Au-
tonomous learning of target decision strategies
without communications for continuous coordinated
cleaning tasks. In IEEE/WIC/ACM Int. Confs. on Web
Intelligence and Intelligent Agent Technology, pages
216–223.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
288
