
Single Stage Class Agnostic Common Object Detection:
A Simple Baseline
Chuong H. Nguyen
1 a
, Thuy C. Nguyen
1
, Anh H. Vo
1
and Yamazaki Masayuki
2
1
Cybercore, Marios 10F, Morioka Eki Nishi Dori 2-9-1, Morioka, Iwate, Japan
2
Toyota Research Institute-Advanced Development, 3-2-1 Nihonbashi-Muromachi, Chuo-ku, Tokyo, Japan
Keywords:
Common Object Detection, Open-set Object Detection, Unknown Object Detection, Contrastive Learning,
Deep Metrics Learning.
Abstract:
This paper addresses the problem of common object detection, which aims to detect objects of similar cat-
egories from a set of images. Although it shares some similarities with the standard object detection and
co-segmentation, common object detection, recently promoted by (Jiang et al., 2019), has some unique advan-
tages and challenges. First, it is designed to work on both closed-set and open-set conditions, a.k.a. known
and unknown objects. Second, it must be able to match objects of the same category but not restricted to the
same instance, texture, or posture. Third, it can distinguish multiple objects. In this work, we introduce the
Single Stage Common Object Detection (SSCOD) to detect class-agnostic common objects from an image
set. The proposed method is built upon the standard single-stage object detector. Furthermore, an embedded
branch is introduced to generate the object’s representation feature, and their similarity is measured by cosine
distance. Experiments are conducted on PASCAL VOC 2007 and COCO 2014 datasets. While being simple
and flexible, our proposed SSCOD built upon ATSSNet performs significantly better than the baseline of the
standard object detection, while still be able to match objects of unknown categories. Our source code can be
found at (URL).
1 INTRODUCTION
The ability to find similar objects across different
scenes is important for many applications, such as
object discovery or image retrieval. Different from
the standard object detection, which can only make
correct predictions on a close-set of predefined cate-
gories, common-object detection (COD) aims to lo-
cate general objects appearing in both scenes, regard-
less of their categories.
The COD problem (Jiang et al., 2019) is closely
related to co-segmentation, co-detection, and co-
localization tasks. Although they all attempt to pro-
pose the areas belonging to common object cate-
gories, there are several key differences. Concretely,
co-segmentation does not distinguish different in-
stances. Co-detection finds the same object instance
in a set of images, while co-localization is restricted to
finding one category that appears in multiple images.
The COD problem hence is much more challenging,
due to (1) it must be able to localize potential areas
a
https://orcid.org/0000-0002-2860-3159
containing objects, (2) be able to work in open-set
condition, i.e. detect unseen categories, (3) be able
to match those of same categories and not limited to
the same instance, texture or posture.
In this work, we focus on a similar COD problem,
which is applied for 2D images domain, as illustrated
in Fig. 1. The objective is to find a set of bound-
ing box pairs from two input images, such that each
pair contains objects of the same category. Also, there
should be no restriction on the number of classes, seen
or unseen categories, and the number of instances in
the images. Our direct application is to detect suspi-
cious objects in surveillance cameras, hence the abil-
ity to detect unknown objects is critical. Moreover,
since we need to perform detection in real-time, we
select an FPGA as our target hardware. This limits
the type of kernels we can perform to standard oper-
ations, i.e. some operators such as ROI-Align are not
supported. Concretely, we introduce a Single Stage
Common Object Detection (SSCOD), in which our
contributions are summarized as follows:
• Single Stage Common Object Detector is pro-
posed. The framework is simple and can be
396
Nguyen, C., Nguyen, T., Vo, A. and Masayuki, Y.
Single Stage Class Agnostic Common Object Detection: A Simple Baseline.
DOI: 10.5220/0010242303960407
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 396-407
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Illustrated results of common object detection.
adapted to any standard Single Stage Object De-
tection. Hence, the standard training pipeline can
be used, except that the classification branch is
trained in a class-agnostic manner. This helps the
network generalize the concept of objectness seen
in training set to detect similar categories that are
unseen.
• An embedded branch is introduced to extract an
object’s representation feature, using its cosine
similarity to detect common object pairs. We in-
vestigate different loss functions for metric learn-
ing, such as classwise and pairwise losses, and
then propose a unified function named Curricu-
lum Contrastive Loss to deal with inherent prob-
lems of object detection, such as class imbalance
and small batch-size. Our proposed loss yields the
best results in our experiments.
• The model is evaluated on two dataset PASCAL
VOC 2007 and COCO 2014. Our SSCOD model
can achieve better results than the baseline of stan-
dard object detection, for both known and un-
known categories. For unknown cases, our SS-
COD can achieve comparable results with previ-
ous work.
2 LITERATURE REVIEW
2.1 Object Detection
Since the COD problem is developed based on Object
Detection framework, we review general techniques
for Object detection in this section. Object Detec-
tion framework can be separated into two main ap-
proaches, namely two stages and one stage.
Benchmarks in two-stage approach can be named
as Regional-based convolutional neural network (Gir-
shick et al., 2014), (Girshick, 2015), Faster R-CNN
(Ren et al., 2015) and Mask R-CNN (He et al., 2017).
This approach is based on a backbone CNN to ex-
tract features, which is then attached to two CNN
modules. The first one proposes possible regions con-
taining objects, and the second module contains two
sub-nets: a classification head to classify the object
and a regression head to predict bounding boxes off-
set from the anchor. Since Region Proposal is the core
component, recent works, such as Iterative RPN (Gi-
daris and Komodakis, 2016) or Cascade RCNN (Cai
and Vasconcelos, 2017), (Cai and Vasconcelos, 2019)
attempt to enhance its performance by adding more
stages to refine the predictions. Recently, Cascade
RPN (Vu et al., 2019) improves the quality of region
proposal by using Adaptive Convolution and combine
anchor-based and anchor-free criteria to define posi-
tive boxes. (Song et al., 2020) improves the spatial
misalignment between classification and regression
heads by using two disentangled proposals, which are
estimated by the shared proposal. In general, two-
stage approaches can achieve higher accuracy by cas-
cading more stages and refine modulators. However,
it is often slower due to the framework complexity.
Single-stage detectors were developed later to im-
prove speed, and the representative works can be
named as SSD (Liu et al., 2016), YOLO (Redmon
and Farhadi, 2017), (Redmon and Farhadi, 2018),
and RetinaNet (Lin et al., 2017b). The key advan-
tage of this approach is to omit the proposal region
but use a sliding-window to produce dense predic-
tions directly. Specifically, at each cell in a feature
map, a set of default anchors with different scales
and ratios are predefined. Classification and bound-
ing box regression are then predicted directly on each
anchor. Recently, research shifts attention to re-
move the anchor-box step and propose a new kind
of framework name “anchor-box-free” approach. In
general, anchor-box-free approaches, such as FCOS
(Tian et al., 2019)), CenterNet (Duan et al., 2019),
Object-as-Points (Zhou et al., 2019), CornerNet (Law
and Deng, 2018) are designed to be simpler and more
efficient. (Zhang et al., 2020) investigates the fac-
tors constituting the performance gap between anchor
and free-anchor approaches, and discover that the
main factor is how to assign positive/negative training
samples. Consequently, they propose adaptive train-
ing sample selection (ATSS) improvement to Retina
net, which surpasses all anchor and free-anchor ap-
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
397

proaches without introducing any overhead. In short,
single-stage detectors currently achieve comparable
or even better accuracy than two-stages, while signif-
icantly simpler and faster.
2.2 Co-segmentation
The co-segmentation has been studied for many years
(Joulin et al., 2010), (Vicente et al., 2011) (Quan
et al., 2016), where the main goal is to segment
common foreground in the pixel level from multi-
ple images. (Yuan et al., 2017) introduced a deep
dense conditional random field framework and used
handcrafted SIFT and HOG features to establish co-
occurrence maps. (Quan et al., 2016) proposed a
manifold ranking method that combines low-level ap-
pearance features and high-level semantic features ex-
tracted from an Imagenet pre-trained network.
However, the application of previous works is
quite restricted, since it assumes only a single com-
mon object, which also must be salient in the im-
age set. Recently, (Li et al., 2019a) proposed a deep
Siamese network to achieve object co-segmentation
from a pair of images. (Chen et al., 2019a) pro-
posed an attention mechanism to select areas that have
high activation in feature maps for all input images.
(Zhang et al., 2019) proposed a spatial-semantic mod-
ulated network, in which the spatial module roughly
locates the common foreground by capturing the cor-
relations of feature maps across images, and the se-
mantic module refines the segmentation masks. A
comprehensive review of co-segmentation methods
can be found in the recent work of (Xu et al., 2019),
(Merdassi et al., 2019). The co-segmentation setting,
however, works with pixel-level rather than object in-
stance level. Hence, the objective is different from the
COD problem.
2.3 Common Object Detection
(Bao et al., 2012) introduce a problem named object
co-detection aiming to detect if the same object is
present in a set of images. It is based on the intuition
that an object should have a consistent appearance re-
gardless of observation viewpoints. (Guo et al., 2013)
follow the principle to exploit the consistent visual
patterns from the objects. The goal then is to recog-
nize whether objects in different images correspond to
the same instance, and estimate the viewpoint trans-
formation.
Co-localization (Le et al., 2017), (Li et al., 2019b)
defines the problem as localizing categorical objects
using only a positive set of sample images. The gen-
eral approach is to utilize a classification activation
map from a pre-trained Imagenet network to localize
the common areas. This problem is weaker since it
requires a set of positive images as input, hence the
application is limited to a single instance only.
(Jiang et al., 2019) recently extend the idea of co-
detection and co-localization and introduce common
object detection, which removes the aforementioned
limitations. In their approach, Faster-RCNN is used
as the base detector to propose foreground areas. The
object proposals are then passed to an ROI align layer
to extract object features in the second stage. Siamese
Network and Relation Matching subnet are proposed
to estimate the similarity between objects. Compared
to (Jiang et al., 2019) solution, our proposed method
is based on a Single-Stage Detector with an embedded
branch network, which is more simple and flexible.
Moreover, our proposed method can achieve higher
accuracy in both seen and unseen categories, as pre-
sented in the following sections.
3 METHODOLOGY
3.1 Network Architecture
Our proposed framework, Single Stage Common Ob-
ject Detection Network (SSCOD), is illustrated in
Figure 2. The framework is built upon the standard
Single Stage Object detection, such as Retina (Lin
et al., 2017b) or FCOS (Tian et al., 2019). Specif-
ically, the network includes a Backbone to extract
features from an input image, and a Feature Pyra-
mid Network (FPN) (Lin et al., 2017a) to fuse fea-
tures from different scales. Features extracted from
P3-P7 of FPN, i.e. with resolution (H/2
3
,W /2
3
) to
(H/2
7
,W /2
7
), are passed to the detection head.
We design the SSCOD head based on the Retina
Head with ATSS (Zhang et al., 2020) sampling thanks
to its efficiency, although other modules such as
FCOS (Tian et al., 2019) or Centerness (Zhou et al.,
2019), (Duan et al., 2019) can be easily substituted. In
particular, the detection head has 3 branches, namely
Regression, Objectness, and Embedded Head, as il-
lustrated in Figure 2. The regression branch regresses
to bounding box location B = (x,y,w,h), and also pre-
dicts the object’s center p
c
, a.k.a centeredness (Zhang
et al., 2020). The objectness predicts the probability
p
o
that a bounding box contains an object. This is
similar to the classification branch in Retina, but in
a class-agnostic manner, e.g only predict foreground
vs. background. A bounding box centering at (i, j) is
considered as a valid object if its score
s(i, j) = p
o
(i, j)p
c
(i, j) (1)
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
398

Backbone
+FPN
RegressionHead
(4convs)
BoundingBoxB
CenternessP
c
ObjectnessHead
(4convs)
ObjectnessP
o
EmbeddedHead
(4convs)
Score
s
Image
Threshold,
NMS
Out:
(B(i,j),s(i,j),x(i,j))
Embedvectorx
Figure 2: Single Stage Common Object Detection Network (SSCOD).
is greater than a threshold.
To perform common class matching, we add an
embedded branch to produce a representation vector
x ∈ R
d
, where d is the embedded dimension and x is
normalized kxk = 1. Hence, a predicted box b
i
is rep-
resented by a tuple b
i
= (B
i
,s
i
,x
i
), and the similarity
between two predicted bounding boxes b
1
and b
2
is
measured by
sim(b
1
,b
2
) = s
1
s
2
cos(x
1
,x
2
) = s
1
s
2
x
T
1
x
2
(2)
Following the ATSS sampling strategy (Zhang
et al., 2020), we only use a single scale, square an-
chor, for anchor setting. To keep it simple, similar
to Retina or Mask-RCNN, each branch has 4 con-
volution layers kernel 3 × 3, although other add-on
blocks such as Deformable Conv (Zhu et al., 2019),
Nonlocal Block (Wang et al., 2018b) can be easily
added. To accommodate for small batch size, we use
Convolution with Weight Standardized (Qiao et al.,
2019) followed by a Group Normalization (GN) (Wu
and He, 2018) and a ReLu activation. Each branch
ends by a convolution layers kernel 3 × 3 without the
normalization layer. For the objectness and centered-
ness branch, the features are passed through a Sig-
moid layer.
3.2 Loss Functions
The Generalized IoU (GIoU) (Rezatofighi et al.,
2019) and the Cross-Entropy losses are utilized to
train the bounding box regression and the centered-
ness branch. To train the objectness branch, we
adopt an adaptive version of Focal Loss proposed
by (Weber et al., 2019). For the embedded branch,
we consider two types of loss functions for metric
representation learning, namely class-wise and
pair-wise losses.
Class-wise losses, such as Angular Loss (Wang et al.,
2017), SphereFace (Liu et al., 2017), CosFace (Wang
et al., 2018a), ArcFace (Deng et al., 2019), use a lin-
ear layer W ∈ R
d×n
to map the embedded feature di-
mension to the number of classes n, followed by a
softmax layer:
L = −
1
N
N
∑
i=1
log
e
W
T
y
i
x
i
∑
n
j=1
e
W
T
y
j
x
i
(3)
where N is the batch size, and W
j
∈ R
d
denotes the
j-th column of W , corresponding to class y
j
. To en-
force feature learning, the weight W and features are
normalized, e.g. kW
j
k = 1 kx
i
k = 1, which leads to
W
T
j
x
i
= kW
j
kkx
i
kcos(θ
j
) = cos(θ
j
). Hence, optimiz-
ing the loss function (3) only depends on the angle
between the feature and the weight, where W
j
can be
associated as the center of class y
i
. To smoothen the
loss, the cosine value is often multiplied with a scale
s before computing softmax.
Let T (θ
y
i
) and N(θ
j
) be functions that modulate
the angles between positive and negative samples re-
spectively. In the simplest case (no manipulation),
T (θ
y
i
) = cos(θ
y
i
), and N(θ
j
) = cos(θ
j
), and (3) can
be rewritten as:
L = −
1
N
N
∑
i=1
log
e
sT (θ
y
i
)
e
sT (θ
y
i
)
+
∑
n
j=1, j6=y
i
e
sN(θ
j
)
(4)
Many approaches focus on modulating positive sam-
ples; for example, in ArcFace Loss, a margin m is
added to the angle of positive samples:
T (θ
y
i
) = cos(θ
y
i
+ m), N(θ
j
) = cos(θ
j
) (5)
However, negative samples are also important. In
metric representation learning, a negative sample can
be classified as: (a) hard if θ
j
< θ
y
i
, (b) semi-hard if
θ
y
i
≤ θ
j
< θ
y
i
+ m, and (c) easy if θ
y
i
+ m ≤ θ
j
. Cur-
riculum Loss (Huang et al., 2020) further imposes a
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
399

modulation to the negative samples:
T (θ
y
i
) = cos(θ
y
i
+ m),
N(θ
j
) =
(
cos(θ
j
) if θ
y
i
+ m ≤ θ
j
cos(θ
j
)(t + cos(θ
j
)) otherwise
(6)
That is, the weights of hard and semi-hard are ad-
justed during training by a modular w = t + cos(θ
j
).
Here, t is set to the average of positive cosine similar-
ity
t =
∑
N
i
cos(θ
y
i
)
N
. (7)
At the beginning, t ≈ 0, thus w < 1 and the effect of
hard negatives lessens, letting the model learn from
the easy negative samples first. As the model be-
gins to converge, it can detect negative samples bet-
ter. Therefore, the number of easy negative samples
increases, i.e. θ
y
i
→ 0, hence increasing the weight t,
and switching the model’s focus from easy to the hard
negative samples.
We adopt the Curriculum Loss to compare in our
experiments. Furthermore, to deal with typical class-
imbalance problem of object detection, we also im-
pose a focal term:
L = −
1
N
N
∑
i=1
(1 − p
i
)
γ(t)
log(p
i
), (8)
where
p
i
=
e
sT (θ
y
i
)
e
sT (θ
y
i
)
+
∑
n
j=1, j6=y
i
e
sN(θ
j
)
(9)
Inspired by Automated Focal Loss (Weber et al.,
2019), we set γ(t) = −log(max(t,10
−5
)). In practice,
t is computed through Exponential Moving Average
of (7).
Pair-wise losses, such as Max Margin Contrastive
Loss (Hadsell et al., 2006), Triplet Loss (Weinberger
and Saul, 2009) (Schroff et al., 2015), (Hermans
et al., 2017), Multi-class N-pair loss (Sohn, 2016),
directly minimize the distances between different
samples having same classes (positive pairs) and
maximizes the distance between those of different
labels (negative pairs).
For an anchor sample x
i
in a data batch, we can
find a set of positive pairs U
i
and negative pairs V
i
. Let
N
+
i
and N
−
i
as the size of U
i
and V
i
respectively, and
d
+
i j
(d
−
i j
) be the distance between two positive (neg-
ative) samples x
i
and x
j
, where d(x
i
,x
j
) = −x
T
i
x
j
1
1
The exact formula is d(x
i
,x
j
) = 1 −
x
T
i
x
j
kx
i
kkx
j
k
, but we
require kx
i
k = kx
j
k = 1 and drop constant 1 for notation
convenience since it does not affect the loss value.
for Cosine distance or d(x
i
,x
j
) = kx
i
− x
j
k
2
2
for Eu-
clidean distance. When N
+
i
= 1 (or N
−
i
= 1 ), we
denote d
+
i
(or d
−
i
) as the only distance in the set. The
general form of pairwise loss is:
L =
N
∑
i
F( d
+
i j
j∈U
i
, d
−
ik
k∈V
i
) (10)
In Triplet Loss (Hermans et al., 2017), for exam-
ple, F = max(0, m + max
j∈U
i
d
i j
− min
k∈V
i
d
ik
), where m is
the margin. In Multi-class N-pair loss (Sohn, 2016),
the loss function is defined as:
F = log(1 +
∑
k∈V
i
exp(d
+
i
− d
−
ik
))
= −log
exp(−d
+
i
)
exp(−d
+
i
) +
∑
k∈V
i
exp(−d
−
ik
)
(11)
(11) is also extended by using a temperature, as
named NT-Xent by (Chen et al., 2020), and applied
to general case where N
+
i
≥ 1, as named Supervised
Contrastive loss by (Khosla et al., 2020):
F = −
1
N
+
i
∑
j∈U
i
log
exp(−d
+
i j
/τ)
exp(−d
+
i j
/τ) +
∑
k6=i
exp(−d
−
ik
/τ)
(12)
Note that, the difference between (11) and (12)
also lie in the denominator. In N-Pair loss (11), only
the negative pairs are considered ( j ∈ V
i
), while in
(12), all positive and negative are used (k 6= i). This is
because the NT-Xent and Supervised Contrastive loss
are originally designed for transfer learning, aiming to
learn general visual representation. In our case, since
we aim for both class intra compactness and inter sep-
arability, we also consider the negative pairs only as
in (11).
Finally, let s = 1/τ and using the Cosine distance,
(12) is rewritten as:
F = −
1
N
+
i
∑
j∈U
i
log
exp(scos(θ
i j
))
exp(scos(θ
i j
)) +
∑
k6=i
exp(scos(θ
ik
))
(13)
Note that (4) and (13) share the same structure. There-
fore, we can adopt the modulation defined in (5) or (6)
to rewrite (13) as:
F = −
1
N
+
i
∑
j∈U
i
log
e
sT (θ
i j
)
e
sT (θ
i j
)
+
∑
k∈V
i
e
sN(θ
ik
)
(14)
We name the former combination as Arc Con-
trastive (ArcCon) loss and the later as Curriculum
Contrastive (CurCon) loss. For CurCon Loss, we
compute t =
1
N
∑
N
i=1
min
j∈U
i
(cosθ
i j
). Table 1 summarizes
the loss functions proposed in this paper.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
400

Table 1: Summary of Loss Functions for embedded matching.
Loss
Focal Curriculum
(FocalCur)
Arc Contrastive
(ArcCon)
Arc Contrastive -Negative
(ArcCon-Neg)
Curriculum Contrastive
(CurCon)
Formular Equ. (8) (14), k 6= i as in (13) (14), k ∈ V
i
as in (11) (14), k 6= i as in (13)
T (θ),N(θ) (6) (5) (5) (6)
4 EXPERIMENTS
4.1 Experimental Setup
Our experiments are conducted on the popular PAS-
CAL VOC (Everingham et al., 2010) and the large-
scale detection benchmarks COCO 2014 (Lin et al.,
2014). Following the common practice (Zhang et al.,
2018), (Zoph et al., 2019), (Zhang et al., 2019), we
use both the trainval VOC 2007 and VOC 2012 for
training (21.5k images and replicate 3 times), and
evaluate on VOC2007 (5K images) test set. For the
COCO dataset, we use the trainval35k split (115K im-
ages) for training and report the results on the minival
split (5K images). Our code is implemented based on
MMDetection opensource (Chen et al., 2019b).
Training Details. We conduct the experiments using
the standard setup with backbone Resnet50 (R50) pre-
trained from ImageNet. The stem convolution, the
first stage, and Batch Norm layers of backbone R50
are frozen. For FPN and Head, we use Weight Stan-
dardized Convolution (Qiao et al., 2019) and Group
Norm (Wu and He, 2018). The model is trained with
stochastic gradient descent (SGD) with momentum
0.9 and weight decay 10
−4
, with batch sizes (BS)
equal 16. We train the models with 12 epochs for
both VOC and COCO datasets.
We evaluate the effectiveness of both class-wise
losses and pair-wise losses presented in Section. 3.2.
If a pair-wise loss is used, for each image in the batch,
we also randomly sample another image that has at
least one common object to form a valid pair. Hence
the number of images in the batch is doubled. There-
fore, we reduce the batch size a haft to make con-
sistent training setting, but still keep the notation of
batch size unchanged. In addition, we use auto policy
V0 (Zoph et al., 2019) for data augmentation. For the
VOC dataset, the shorter side of the input images is
resized to 600 pixels, while ensuring the longer side
is smaller than 1000 pixels, and the aspect ratio is
kept unchanged. In short, we denote it as resize to
(1000,600). For the COCO dataset, the images are
set to a size of (1333,800). All images after resizing
are padded to be divisible by 32.
We investigate different losses presented in Table
1. To find appropriate parameters for the loss func-
tions, we first train and evaluate the model on the val-
idation set of VOC2007. We observe that ArcFace
and CurricularFace are sensitive to parameter s, and
s = 4,m = 0.5 yields the best result. For pair-wise
losses, s ∈ [1,4], m = 0.5 yields quite equivalent re-
sults, and select s = 1,m = 0.5 as the default value for
our experiments.
Inference and Evaluation Details. We first forward
the input image through the network and obtain the
predicted bounding boxes with a confidence score
and embedded feature vector. We use the same post-
processing parameters with RetinaNet (threshold 0.05
and NMS with maximum of 100 bounding boxes per
image). For inference, two bounding boxes are con-
sidered belonging to a common class if their similar-
ity score is greater than a threshold.
For evaluation, we extract the top 100 pairs that
have the highest matching scores from all possible
matching pairs of two images. We evaluate the model
using both Recall and Average Precision (AP) with
the VOC evaluation style. Specifically, among the
top 100 pairs, a predicted pair is true positive if it
satisfies both conditions: (a) Each bounding box
has IoU > 0.5 with ground-truth boxes. (b) Their
ground-truth boxes have the same object categories.
Otherwise, it is a false positive. To generate ground
truth, although arbitrary number of pairs can be
used, we follow (Jiang et al., 2019) to randomly
sample p = 6 valid pairs for each image in the
validation dataset, where the random seed is set to 0
for reproducibility.
Baseline Model. The easiest solution for common
object detection is to use the standard object detection
approach, then a common pair can be estimated by:
• Hard matching (HM): Object category of each
bounding box can be inferred as the class having
the highest probability. Two bounding boxes form
a valid pair if they predict the same class.
• Soft matching (SM): The probability score is used
as a description vector, and matching score can be
computed as their cosine similarity. The inference
hence follows the same setup of our solution.
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
401
4.2 Pascal VOC
The learning rate is linearly increased using warm-up
strategy to 0.5e
−2
in the first 300 iterations, and then
gradually reduced by the cosine annealing to 0.5e
−4
.
Experiment Type 1. First, to verify if our SSCOD
degrades the accuracy for known categories, we train
the standard model ATSS with R50 backbone by com-
mon setting, and infer the Hard-matching (HM) and
Soft-Matching (SM) baseline. In this experiment,
our baseline model without test-time augmentation
or complex structure achieves 0.774 mAP, which is
similar or higher than several benchmark results (Ren
et al., 2015), (Liu et al., 2016) (Fu et al., 2017). This
validates that our model can be a strong baseline.
Similarly, we train the proposed SSCOD model with
different losses. The experiments are conducted using
all samples of 20 classes, and the result is presented
in Table 2.
As seen from Table 2, results of SSCOD are
asymptotic to those of the baseline. Specifically,
SSCOD trained with FocalCur loss achieves 0.5986
AP, which is closely matched to the HM baseline of
0.6052 AP and higher than SM baseline of 0.5746 AP.
The CurCon loss obtains the best result in this case,
which is 0.6141AP and higher than both baselines.
The ArcCon loss yields slightly worse result than the
HM baseline, but still better than SM baseline.
Note that, images in VOC dataset often has
only one or two classes. Hence, the performance
of baseline for VOC is quite predictable from its
mAP, since the precision when predicting a pair is
conditional on the precision of each box component,
e.g. mAP
2
= 0.774
2
≈ 0.6. The hard matching yields
higher accuracy than soft-matching because it can
suppress the noise better through the post processing.
Nevertheless, our SSCOD using cosine similarity can
achieve comparable or better results. Surprisingly,
ArcCon-Neg yields the worst result. This is possibly
due to insufficient number of negative pairs, which
is even more severe due to small batch size used in
object detection.
Experiment Type 2. Second, to evaluate the ability to
detect common pairs of unseen categories, we remove
the five classes from the training set. For simplic-
ity and reproducibility, we chose the last five classes,
namely: potted plant, sheep, sofa, train and tv mon-
itor, and repeat similar experiments on the truncated
training set. Different from the known-category case,
the unseen case depends on both the localization abil-
ity of the objectness branch and the matching accu-
racy of embedded features. Hence, to independently
evaluate the matching module, we train the object-
ness branch using all samples from the dataset. We
emphasize that this is solely to learn foreground and
background concept, hence no object category infor-
mation is used. Follow (Jiang et al., 2019), we denote
unseen classes as Only Novel Categories (ONC) and
seen classes as Excluded ONC (EONC), and the ex-
periment results are shown in Table 3.
As seen from Table 3, although the baseline
model yields the highest results for EONC test,
it can’t detect novel classes in ONC test. This is
expected due the standard object detection is only
designed for close-set condition. In contrast, our
SSCOD is still able to match objects from unseen
classes. Specifically, ArcCon loss yields the best
result for ONC test, 0.2765AP. On the other hand,
CurCon loss gets a better balance between EONC
and ONC tests, 0.5857AP, and 0.2663AP for objects
of seen and unseen categories respectively. Focal-
Cur loss yields worse results for ONC test in this case.
Experiment Type 3. Finally, we evaluate the models
in the most restricted case, where both objectness and
embedded branches are trained with samples from
only 15 seen classes. In practice, since one image may
contain several objects, simply dropping samples of
unknown classes will force the network treating them
as background, thus harm the network generalization.
To overcome this problem, we simply set the weight
for samples of unknown classes equal 0 during com-
puting the loss for objectness branch and regression
branches. Note that, this setting does not restrict real
application because in practice all samples are used
to train the network, and unlabeled objects are often
not interesting. For the embedded branch, these sam-
ples are totally ignored. The highest results of each
experiment are presented in Table 4.
As seen from Table 4, ArcCon and CurCon per-
form best in this case, while FocalCur and ArcCon-
Neg perform worst. The CurCon loss still yields the
best balance between EONC and ONC test, 0.5593AP
and 0.1212AP for seen and unseen categories respec-
tively. However, different from previous experiments,
we observe the trade-off between EONC and ONC’s
performance.
Figure 3: Trade-Off between EONC and ONC test in Ex-
periment Type 3 using CurCon Loss.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
402

Table 2: Comparison between the baseline model and SSCOD model for Experiment Type 1 on VOC dataset . Bold and Both
Italic represent the best results of baseline and SSCOD, respectively.
Eval.
Metrics
Baseline SSCOD
HM SM FocalCur ArcCon ArcCon-Neg CurCon
Recall 0.7922 0.7976 0.7208 0.7771 0.6356 0.8090
AP 0.6052 0.5746 0.5986 0.5832 0.5326 0.6141
Table 3: Comparison between the baseline model and SSCOD model for Experiment Type 2 on the VOC dataset. Bold and
Both Italic represent the best results of baseline and SSCOD, respectively.
Type
Eval.
Metrics
Baseline SSCOD
HM SM FocalCur ArcCon ArcCon-Neg CurCon
EONC
Recall 0.8128 0.8123 0.8078 0.8232 0.7752 0.8385
AP 0.6278 0.6001 0.5443 0.5505 0.4798 0.5857
ONC
Recall 0.0699 0.0850 0.5925 0.6211 0.5936 0.6267
AP 0.0012 0.0014 0.1906 0.2765 0.2510 0.2663
Table 4: Comparison between the baseline model and SSCOD model for Experiment Type 3 on the VOC dataset. Bold and
Both Italic represent the best results of baseline and SSCOD, respectively.
Type
Eval.
Metrics
Baseline SSCOD
HM SM FocalCur ArcCon ArcCon-Neg CurCon
EONC
Recall 0.8128 0.8123 0.7347 0.7509 0.4103 0.8105
AP 0.6278 0.6001 0.4262 0.4595 0.2572 0.5593
ONC
Recall 0.0699 0.0850 0.3563 0.4060 0.3418 0.3810
AP 0.0012 0.0014 0.066 0.1391 0.0567 0.1212
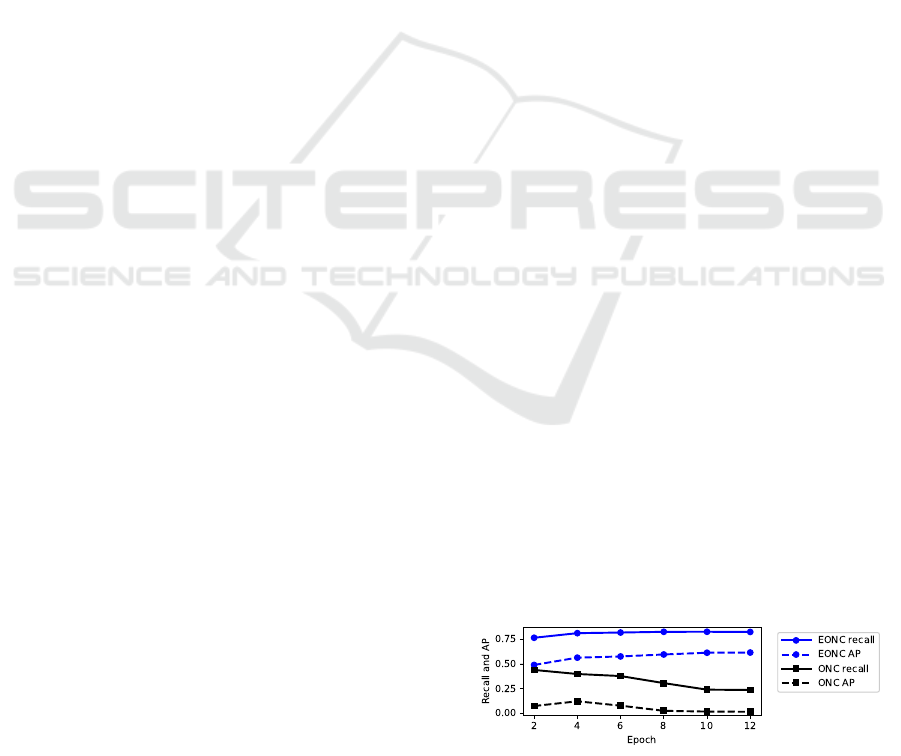
As illustrated in Fig. 3, the longer training, the
better EONC test but the worse ONC test. This is be-
cause the objectness and regression branches start to
overfit to the seen classes, hence decrease the local-
ization ability for unseen classes. This effect does not
happen in Type 2 experiments.
4.3 COCO 2014
We conduct similar experiments on the COCO dataset
for type 1 and 2 as done in VOC.
Experiment Type 1. The learning rate is linearly in-
creased using warm-up strategy to 1e
−2
in the first
500 iterations, and then gradually reduced by the co-
sine annealing to 1e
−4
. Since ArcCur-Neg loss does
not yield comparable results with other, we exclude it
for COCO experiments. For the baseline, we use the
checkpoint
2
provided by MMDetection, which has
39.4 box mAP.
The results are shown in Table 5. In this case, Cur-
Con loss yields the best performance and surpasses
the base-line with a large margin for both recall and
AP, 0.5862 and 0.3811 respectively. FocalCur loss
also yields closely matching results with the baseline.
These results are consistent with VOC’s results, hence
confirm the effectiveness of our proposed approach.
2
https://github.com/open-
mmlab/mmdetection/tree/master/configs/atss
Experiment Type 2. Unlike VOC, COCO dataset
has many fine-granded classes in each meta-classes,
namely: person, vehicle, outdoor, animal, accessory,
sports, kitchen, food, furniture, electronics, appli-
ance, and indoor. Therefore, selecting seen and un-
seen categories for training and evaluation can have
a significant effect on the AP score. For example, if
both car and bus are in unseen classes, their high score
matching is reasonable but false-positive. Therefore,
we conduct two experiments:
• Case A: Follow (Jiang et al., 2019), we select 30
classes to train the model. However, since they do
not specify the class names, reproducing is hard.
Here, we choose the training classes as: person,
bicycle, car, airplane, boat, fire hydrant, stop sign,
dog, horse, elephant, umbrella, handbag, snow-
board, sports ball, baseball bat, skateboard, bot-
tle, fork, bowl, apple, carrot, cake, chair, toilet,
laptop, cell phone, microwave, sink, book, and
hair drier.
• Case B: We split 75% classes for training, and
25% other for testing. Concretely, 20 unseen
classes are: motorcycle, bus, cat, horse, sheep,
backpack, tie, skis, sports ball, surfboard, tennis
racket, cup, banana, hot dog, pizza, donuts, re-
mote, toaster, clock, teddy bear.
We report the results using only CurCon loss in Ta-
ble 6, since we found it yields the best results in all
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
403
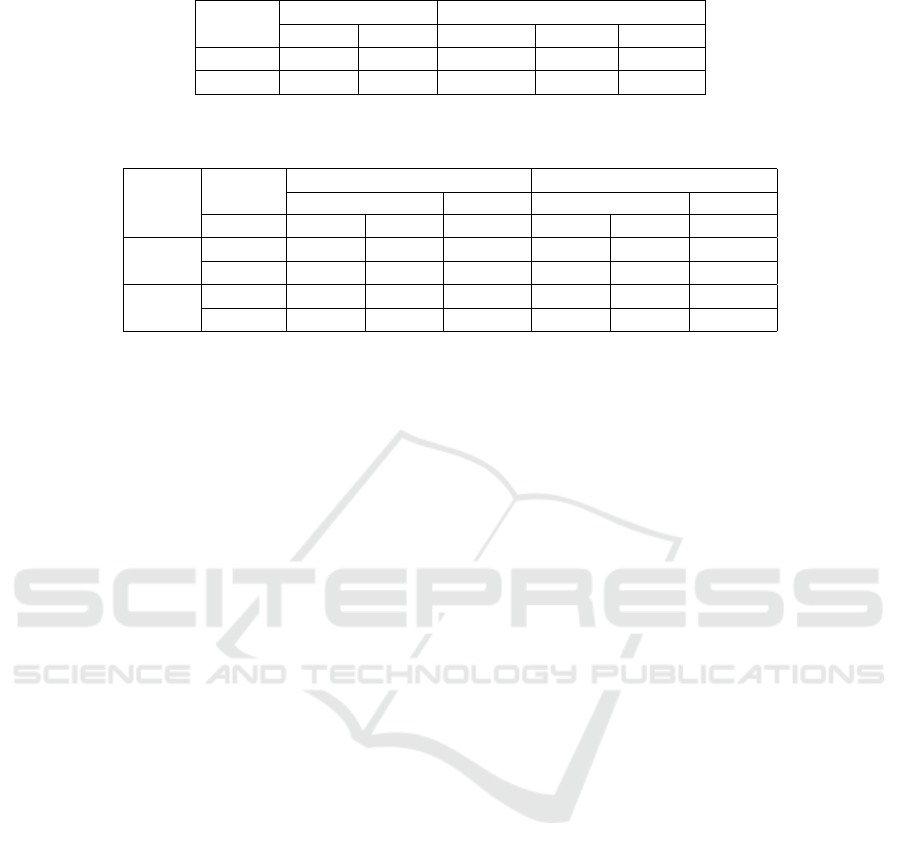
Table 5: Comparison between the baseline model and SSCOD model for Experiment Type 1 on the COCO dataset. Bold and
Both Italic represent the best results of baseline and SSCOD, respectively.
Eval
Metrics
Baseline SSCOD
HM SM FocalCur ArcCur CurCon
Recall 0.5128 0.5102 0.5101 0.5473 0.5862
AP 0.3688 0.3515 0.3615 0.3160 0.3811
Table 6: Comparison between the baseline model and SSCOD model for Experiment Type 2 on the COCO dataset. Bold and
Both Italic represent the best results of baseline and SSCOD, respectively.
Type
Eval
Metrics
Case A Case B
Baseline SSCOD Baseline SSCOD
Metrics HM SM CurCon HM SM CurCon
EONC
Recall 0.5141 0.5075 0.5862 0.5247 0.5206 0.6201
AP 0.3676 0.3501 0.3811 0.3781 0.3603 0.4074
ONC
Recall 0.0545 0.0595 0.4202 0.0739 0.0540 0.4587
AP 0.0003 0.0003 0.0643 0.0003 0.0003 0.1213
previous experiments. For EONC test, SSCOD yields
higher results than the baseline with a large margin,
0.3811AP and 0.4074AP for case A and B respec-
tively. As previously mentioned, the baseline can not
work for ONC test. For Case A, the performance is
poor due to the shortage of training samples. For Case
B, the results are better, e.g. 0.1213AP, due to a larger
number of training samples.
4.4 Discussion
4.4.1 Comparison of Loss Functions
Although the class-wise and pairwise losses have
been used for Face-ID or unsupervised learning, this
work adopts them for (unseen) object detection. In
our experiments, the pairwise losses are more effec-
tive than the classwise loss. We hypothesize that this
is because in classwise loss, the number of contrastive
pairs in the denominator is limited to the number of
known classes (the centroid of each class) from the
train set. In contrast, the number of pairs in the de-
nominator of pairwise losses is essentially all possi-
ble object pair combinations, governed by the num-
ber of bounding boxes in a minibatch. This helps in-
crease the interaction between the sample pairs, and
especially useful for the case of unknown classes de-
tection. Our results are in-line with recent research
of contrastive learning (Chen et al., 2020) (He et al.,
2020), who also finds the importance of using a large
training batch size to increase the number of negative
pairs for good performance.
Our proposed Curriculum Contrastive Loss per-
forms best in most of experiments, since it unifies
both approaches by adding the adaptive angular mar-
gins to the contrastive loss formulation.
4.4.2 Comparison to Previous Works
To compare with previous works, we attempt to re-
produce the results of (Jiang et al., 2019). How-
ever, this is challenging, due to missing information.
Specifically, in our reproducing attempt, their pro-
posed Siamese Network was unstable during train-
ing, e.g. when sim(p
1
, p
2
) < 0 in their Equ (7), the
loss is NaN. Also for the Siamese network, sampling
strategy is critical for convergence but unmentioned.
Similarly, in their proposed Relation Matching net-
work, concat( f
1
, f
2
) and concat( f
2
, f
1
) can yield dif-
ferent results. Furthermore, missing information such
as how to select 20 images pair for training, how
to select seen/unseen classes, and setup optimization
makes the reproducing process very difficult. Hence,
we use their reported results for direct comparison,
albeit possibly different settings.
As seen from Tab. 7 and Tab. 8, their EONC re-
sults are always worse then the baseline, while ONC
is better. This is questionable, since the model is
trained on seen classes, it should perform better for
EONC case. This is contrast with our results. In
the Type 1 experiments, our SSCOD always performs
better the baseline, which also has much higher AP
than the Faster-RCNN baseline used by (Jiang et al.,
2019). This confirms the effectiveness of our pro-
posed methods.
For ONC test, our results on VOC is still higher
than the Siamese and Relation Network methods re-
ported by (Jiang et al., 2019). In addition, our pro-
posed approach does not require complicated training
setup, offline sampling mechanism or extra matching
modulation, therefore can serve as a good baseline.
In contrast, our proposed method perform worse on
COCO dataset, which is likely due to missing detec-
tion for unknown objects.
However, there are still ample room to improve
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
404

Table 7: Comparison between the proposed method and previous works on the VOC dataset. Bold represents the best results.
Type
Ours Jiang et al. 2019
FocalCur ArcCon ArcCon-Neg CurCon Best Baseline Siamese Relation
EONC 0.5443 0.5505 0.4798 0.5857 0.4481 0.3269 0.3774
ONC 0.1906 0.2765 0.251 0.2663 0.1638 0.2187 0.2535
Table 8: Comparison between the proposed method and previous works on the COCO dataset. Bold represents the best
results.
Type
Ours Jiang et al. 2019
CurCon Best Baseline Siamese Relation
EONC 0.3811 0.2107 0.141 0.1773
ONC 0.0643 0.1247 0.1398 0.1824
the results. As showed in Tab. 4 and Fig. 3, the
network can be easily trained to optimize the perfor-
mance on seen classes, but this will reduce the ability
to generalize for unseen objects. This problem can
be partially alleviated by training on larger and more
diverse dataset. In addition, we can also treat it as
positive-unlabeled problem (Yang et al., 2020) to re-
duce the effect of missing labels. Currently, the ob-
jectness, the regression and the embedded branches
are trained independently, and this can be insufficient.
Adding an attention mechanism from embedded fea-
tures to the objectness can also enhance the results.
We leave the discussion above for future work.
4.4.3 Result Visualization
Due to space limitations, visualization of predicted re-
sults and the pretrained model to generate predictions
can be found at (URL).
5 CONCLUSION
This paper proposes a solution for common object de-
tection, which aims to detect pairs of objects from
similar categories in a set of images. While this is an
interesting problem, there are many challenges, such
as the ability to work on both closed-set and open-set
conditions, and for multiple objects. Our solution is
built upon single-stage object detection thanks to its
efficiency. To matching objects of the same category,
we add an embedded branch to the network to gener-
ate representation features. Several loss functions to
train the embedded branch are investigated. The pro-
posed Curriculum Contrastive loss, which combines
contrastive learning and angular margin losses, gives
the best performance. The experiments on both VOC
and COCO dataset demonstrate that our approach
yields higher accuracy than the base-line of standard
object detection for both seen and unseen categories.
We hope this work can serve as a strong baseline for
future research of Common Object Detection.
REFERENCES
Bao, S. Y., Xiang, Y., and Savarese, S. (2012). Object co-
detection. Lecture Notes in Computer Science, 7572
LNCS(PART 1):86–101.
Cai, Z. and Vasconcelos, N. (2017). Cascade R-CNN: Delv-
ing into High Quality Object Detection. Proceedings
of the IEEE Computer Society Conference on Com-
puter Vision and Pattern Recognition, pages 6154–
6162.
Cai, Z. and Vasconcelos, N. (2019). Cascade r-cnn: high
quality object detection and instance segmentation.
IEEE Transactions on Pattern Analysis and Machine
Intelligence.
Chen, H., Huang, Y., and Nakayama, H. (2019a). Se-
mantic Aware Attention Based Deep Object Co-
segmentation. Lecture Notes in Computer Science,
11364 LNCS:435–450.
Chen, K., Wang, J., Pang, J., Cao, Y., Xiong, Y., Li, X.,
Sun, S., Feng, W., Liu, Z., Xu, J., Zhang, Z., Cheng,
D., Zhu, C., Cheng, T., Zhao, Q., Li, B., Lu, X., Zhu,
R., Wu, Y., Dai, J., Wang, J., Shi, J., Ouyang, W.,
Loy, C. C., and Lin, D. (2019b). MMDetection: Open
MMLab Detection Toolbox and Benchmark. arXiv
preprint arXiv:1906.07155.
Chen, T., Kornblith, S., Norouzi, M., and Hinton, G.
(2020). A Simple Framework for Contrastive
Learning of Visual Representations. arXiv preprint
arXiv:2002.05709.
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019). Ar-
cFace: Additive angular margin loss for deep face
recognition. Proceedings of the IEEE Computer So-
ciety Conference on Computer Vision and Pattern
Recognition, 2019-June:4685–4694.
Duan, K., Bai, S., Xie, L., Qi, H., Huang, Q., and Tian, Q.
(2019). Centernet: Keypoint triplets for object detec-
tion. In Proceedings of the IEEE International Con-
ference on Computer Vision, pages 6569–6578.
Everingham, M., Van Gool, L., Williams, C. K., Winn, J.,
and Zisserman, A. (2010). The pascal visual object
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
405

classes (VOC) challenge. International Journal of
Computer Vision, 88(2):303–338.
Fu, C.-y., Liu, W., Ranga, A., Tyagi, A., and Berg, A. C.
(2017). DSSD : Deconvolutional Single Shot Detec-
tor. arXiv preprint arXiv:1701.06659.
Gidaris, S. and Komodakis, N. (2016). Attend Refine
Repeat : Active Box Proposal. arXiv preprint
arXiv:1606.04446v1.
Girshick, R. (2015). Fast r-cnn. In Proceedings of the IEEE
international conference on computer vision, pages
1440–1448.
Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014).
Rich feature hierarchies for accurate object detection
and semantic segmentation. Proceedings of the IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition, pages 580–587.
Guo, X., Liu, D., Jou, B., Zhu, M., Cai, A., and Chang, S. F.
(2013). Robust object co-detection. Proceedings of
the IEEE Computer Society Conference on Computer
Vision and Pattern Recognition, pages 3206–3213.
Hadsell, R., Chopra, S., and LeCun, Y. (2006). Dimension-
ality reduction by learning an invariant mapping. Pro-
ceedings of the IEEE Computer Society Conference
on Computer Vision and Pattern Recognition, 2:1735–
1742.
He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. (2020).
Momentum contrast for unsupervised visual represen-
tation learning. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition,
pages 9729–9738.
He, K., Gkioxari, G., Dollar, P., and Girshick, R. (2017).
Mask R-CNN. Proceedings of the IEEE International
Conference on Computer Vision, 2017-Octob:2980–
2988.
Hermans, A., Beyer, L., and Leibe, B. (2017). In Defense
of the Triplet Loss for Person Re-Identification. arXiv
preprint arXiv:1703.07737.
Huang, Y., Wang, Y., Tai, Y., Liu, X., Shen, P., Li, S., Li, J.,
and Huang, F. (2020). Curricularface: adaptive cur-
riculum learning loss for deep face recognition. In
Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 5901–
5910.
Jiang, S., Liang, S., Chen, C., Zhu, Y., and Li, X. (2019).
Class Agnostic Image Common Object Detection.
IEEE Transactions on Image Processing, 28(6):2836–
2846.
Joulin, A., Bach, F., and Ponce, J. (2010). Discriminative
clustering for image co-segmentation. Proceedings of
the IEEE Computer Society Conference on Computer
Vision and Pattern Recognition, pages 1943–1950.
Khosla, P., Teterwak, P., Wang, C., Sarna, A., Tian, Y.,
Isola, P., Maschinot, A., Liu, C., and Krishnan, D.
(2020). Supervised Contrastive Learning. arXiv
preprint arXiv:2004.11362, pages 1–18.
Law, H. and Deng, J. (2018). Cornernet: Detecting objects
as paired keypoints. Lecture Notes in Computer Sci-
ence, 11218 LNCS:765–781.
Le, H., Yu, C. P., Zelinsky, G., and Samaras, D. (2017). Co-
localization with Category-Consistent Features and
Geodesic Distance Propagation. Proceedings - 2017
IEEE International Conference on Computer Vision
Workshops, ICCVW 2017, 2018-Janua:1103–1112.
Li, W., Hosseini Jafari, O., and Rother, C. (2019a). Deep
Object Co-segmentation. In Lecture Notes in Com-
puter Science, volume 11363 LNCS, pages 638–653.
Li, W., Jafari, H., and Rother, C. (2019b). Localizing Com-
mon Objects Using Common Component Activation
Map. pages 28–31.
Lin, T.-Y., Doll
´
ar, P., Girshick, R., He, K., Hariharan, B.,
and Belongie, S. (2017a). Feature pyramid networks
for object detection. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 2117–2125.
Lin, T. Y., Goyal, P., Girshick, R., He, K., and Dollar,
P. (2017b). Focal Loss for Dense Object Detection.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 42(2):318–327.
Lin, T. Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ra-
manan, D., Doll
´
ar, P., and Zitnick, C. L. (2014). Mi-
crosoft COCO: Common objects in context. In Lec-
ture Notes in Computer Science, volume 8693 LNCS,
pages 740–755.
Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S.,
Fu, C. Y., and Berg, A. C. (2016). SSD: Single shot
multibox detector. Lecture Notes in Computer Sci-
ence, 9905 LNCS:21–37.
Liu, W., Wen, Y., Yu, Z., Li, M., Raj, B., and Song, L.
(2017). SphereFace: Deep hypersphere embedding
for face recognition. Proceedings - 30th IEEE Con-
ference on Computer Vision and Pattern Recognition,
CVPR 2017, 2017-Janua:6738–6746.
Merdassi, H., Barhoumi, W., and Zagrouba, E. (2019). A
Comprehensive Overview of Relevant Methods of Im-
age Cosegmentation. Expert Systems with Applica-
tions, 140:112901.
Qiao, S., Wang, H., Liu, C., Shen, W., and Yuille, A.
(2019). Weight Standardization. arXiv preprint
arXiv:1903.10520.
Quan, R., Han, J., Zhang, D., and Nie, F. (2016). Object
Co-segmentation via Graph Optimized-Flexible Man-
ifold Ranking. In 2016 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
687–695.
Redmon, J. and Farhadi, A. (2017). YOLO9000: Better,
faster, stronger. Proceedings - 30th IEEE Conference
on Computer Vision and Pattern Recognition, CVPR
2017, 2017-Janua:6517–6525.
Redmon, J. and Farhadi, A. (2018). YOLOv3:
An Incremental Improvement. arXiv preprint
arXiv:1804.02767.
Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster
r-cnn: Towards real-time object detection with region
proposal networks. In Advances in neural information
processing systems, pages 91–99.
Rezatofighi, H., Tsoi, N., Gwak, J., Sadeghian, A., Reid,
I., and Savarese, S. (2019). Generalized intersection
over union: A metric and a loss for bounding box re-
gression. In Proceedings of the IEEE Conference on
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
406

Computer Vision and Pattern Recognition, pages 658–
666.
Schroff, F., Kalenichenko, D., and Philbin, J. (2015).
FaceNet: A unified embedding for face recognition
and clustering. Proceedings of the IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition, 07-12-June:815–823.
Sohn, K. (2016). Improved deep metric learning with multi-
class N-pair loss objective. Advances in Neural Infor-
mation Processing Systems, (Nips):1857–1865.
Song, G., Liu, Y., and Wang, X. (2020). Revisiting the sib-
ling head in object detector. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition, pages 11563–11572.
Tian, Z., Shen, C., Chen, H., and He, T. (2019). Fcos: Fully
convolutional one-stage object detection. In Proceed-
ings of the IEEE international conference on com-
puter vision, pages 9627–9636.
Vicente, S., Rother, C., and Kolmogorov, V. (2011). Object
cosegmentation. Proceedings of the IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition, pages 2217–2224.
Vu, T., Jang, H., Pham, T. X., and Yoo, C. (2019). Cas-
cade rpn: Delving into high-quality region proposal
network with adaptive convolution. In Advances in
Neural Information Processing Systems, pages 1432–
1442.
Wang, H., Wang, Y., Zhou, Z., Ji, X., Gong, D., Zhou, J., Li,
Z., and Liu, W. (2018a). CosFace: Large Margin Co-
sine Loss for Deep Face Recognition. Proceedings of
the IEEE Computer Society Conference on Computer
Vision and Pattern Recognition, pages 5265–5274.
Wang, J., Zhou, F., Wen, S., Liu, X., and Lin, Y. (2017).
Deep Metric Learning with Angular Loss. Proceed-
ings of the IEEE International Conference on Com-
puter Vision, 2017-Octob:2612–2620.
Wang, X., Girshick, R., Gupta, A., and He, K. (2018b).
Non-local neural networks. In Proceedings of the
IEEE conference on computer vision and pattern
recognition, pages 7794–7803.
Weber, M., F
¨
urst, M., and Z
¨
ollner, J. M. (2019). Automated
Focal Loss for Image based Object Detection. arXiv
preprint arXiv:1904.09048.
Weinberger, K. Q. and Saul, L. K. (2009). Distance metric
learning for large margin nearest neighbor classifica-
tion. Journal of Machine Learning Research, 10:207–
244.
Wu, Y. and He, K. (2018). Group normalization. In Pro-
ceedings of the European Conference on Computer Vi-
sion (ECCV), pages 3–19.
Xu, H., Lin, G., and Wang, M. (2019). A Review of
Recent Advances in Image Co-Segmentation Tech-
niques. IEEE Access, 7:182089–182112.
Yang, Y., Liang, K. J., and Carin, L. (2020). Object Detec-
tion as a Positive-Unlabeled Problem. arXiv preprint
arXiv:2002.04672.
Yuan, Z., Lu, T., and Wu, Y. (2017). Deep-dense condi-
tional random fields for object co-segmentation. IJ-
CAI International Joint Conference on Artificial Intel-
ligence, pages 3371–3377.
Zhang, S., Chi, C., Yao, Y., Lei, Z., and Li, S. Z. (2020).
Bridging the gap between anchor-based and anchor-
free detection via adaptive training sample selection.
In Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 9759–
9768.
Zhang, S., Wen, L., Bian, X., Lei, Z., and Li, S. Z. (2018).
Single-shot refinement neural network for object de-
tection. In Proceedings of the IEEE conference on
computer vision and pattern recognition, pages 4203–
4212.
Zhang, Z., He, T., Zhang, H., Zhang, Z., Xie, J., and Li, M.
(2019). Bag of Freebies for Training Object Detection
Neural Networks. arXiv preprint arXiv:1902.04103.
Zhou, X., Wang, D., and Kr
¨
ahenb
¨
uhl, P. (2019). Objects as
Points. arXiv preprint arXiv:1904.07850.
Zhu, X., Hu, H., Lin, S., and Dai, J. (2019). Deformable
convnets v2: More deformable, better results. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 9308–9316.
Zoph, B., Cubuk, E. D., Ghiasi, G., Lin, T.-Y., Shlens,
J., and Le, Q. V. (2019). Learning Data Augmenta-
tion Strategies for Object Detection. arXiv preprint
arXiv:1906.11172.
Single Stage Class Agnostic Common Object Detection: A Simple Baseline
407
