
Reduced Precision Strategies for Deep Learning:
A High Energy Physics Generative Adversarial Network Use Case
Florian Rehm
1,2
, Sofia Vallecorsa
1
, Vikram Saletore
3
, Hans Pabst
3
, Adel Chaibi
3
, Valeriu Codreanu
4
,
Kerstin Borras
2,5
and Dirk Kr
¨
ucker
5
1
CERN, Switzerland
2
RWTH Aachen University, Germany
3
Intel, U.S.A.
4
SURFsara, The Netherlands
5
DESY, Germany
Keywords:
Reduced Precision, Quantization, Convolutions, Generative Adversarial Network Validation, High Energy
Physics, Calorimeter Simulations.
Abstract:
Deep learning is finding its way into high energy physics by replacing traditional Monte Carlo simulations.
However, deep learning still requires an excessive amount of computational resources. A promising approach
to make deep learning more efficient is to quantize the parameters of the neural networks to reduced precision.
Reduced precision computing is extensively used in modern deep learning and results to lower execution
inference time, smaller memory footprint and less memory bandwidth. In this paper we analyse the effects
of low precision inference on a complex deep generative adversarial network model. The use case which
we are addressing is calorimeter detector simulations of subatomic particle interactions in accelerator based
high energy physics. We employ the novel Intel low precision optimization tool (iLoT) for quantization and
compare the results to the quantized model from TensorFlow Lite. In the performance benchmark we gain
a speed-up of 1.73x on Intel hardware for the quantized iLoT model compared to the initial, not quantized,
model. With different physics-inspired self-developed metrics, we validate that the quantized iLoT model
shows a lower loss of physical accuracy in comparison to the TensorFlow Lite model.
1 INTRODUCTION
Simulations in High Energy Physics (HEP) have,
due to their complex physical processes, a high de-
mand for computational hardware resources and re-
quire more than half of the worldwide Large Hadron
Collider (LHC) grid resources (Albrecht, 2019). Cur-
rently, the interactions of particles in the detectors are
simulated by employing the simulation toolkit Geant4
(Agostinelli et al., 2003) which uses detailed Monte
Carlo simulation for reproducing the expected detec-
tor output. Because of their dense material and the
highly granular geometry, calorimeters are among the
detectors that take longer time to simulate. Future
simulations of the LHC in the high luminosity phase
will require around 100 times more simulated data
which exceeds drastically the expected computation
resources, even taking into account technological de-
velopment (Apollinari et al., 2017). Therefore, in-
tense research is already ongoing for seeking faster
alternatives to the standard Monte Carlo approach.
Several prototypes based on Deep Generative
Models have shown great potential, by achieving sim-
ilar accuracy than traditional simulation (de Oliveira
and Paganini, 2017; Ghosh, 2019). Generative Ad-
versarial Networks (GANs) represent an example of
such model that have proven for creating calorimeter
shower images (Khattak et al., 2018).
In this paper we describe our developments to fur-
ther enhance the GAN approach for calorimeter sim-
ulations by quantizing the trained neural network into
lower precision. Lower precision operations lead to a
reduced computation time, smaller model storage re-
quirements and fewer data movements. We assess the
impact of quantization on the computational side by
measuring the inference time and the GPU memory
footprint. On the physical side we validate the ac-
curacy by comparing the energy deposition patterns
(”shower shapes”) observed in GAN and Geant4 im-
ages. We benchmark the new Intel Low Precision
Optimization Toolkit (Feng Tian and Gong, 2020) by
quantizing our model using Integer-8 (int8) format
Rehm, F., Vallecorsa, S., Saletore, V., Pabst, H., Chaibi, A., Codreanu, V., Borras, K. and Krücker, D.
Reduced Precision Strategies for Deep Learning: A High Energy Physics Generative Adversarial Network Use Case.
DOI: 10.5220/0010245002510258
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 251-258
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
251

and compare the results to the quantized models ob-
tained using TensorFlow Light (TFL, 2020) in 16-bit
floating point (float16) and int8 formats.
Section 2 provides a description of calorimeter
simulations and the data set format. Section 3 briefly
introduces the GAN approach and the prototype we
use for this study. Section 4 covers an introduction
to reduced precision and to the quantization tools. A
brief review on related work is shown in section 5. In
section 6 results are evaluated in terms of computa-
tional resources and physical accuracy. The last sec-
tion summarizes the conclusions.
2 ELECTROMAGNETIC
CALORIMETERS
Calorimeters are one of the main components of
accelerator-based HEP experiments and detectors.
They are used to measure the energy of particles
(Brown and Cockerill, 2012) at collider experiments.
The primary particles which enter and interact with
the material of the calorimeter deposit their ener-
gies by creating showers of secondary particles as
they pass through the detector. The secondary par-
ticles in turn, create other particle showers by the
same mechanism. While the shower evolves, the
energy of the particles gradually reduces and is ab-
sorbed or measured by the calorimeter sensors. In
our work, we simulate electromagnetic calorimeters,
which are specially designed to measure energies
of electrons, positrons and photons that interact in
the detector volume via electromagnetic interactions
(mainly bremsstrahlung for electrons and pair produc-
tion for photons).
We use particle shower images, recorded by the
calorimeter, as data set for the simulations. The train-
ing and test data set are simulated using Geant4: they
represent a future electromagnetic calorimeter proto-
type. For the study in this paper, we are using 200 000
3-dimensional shower images of electrons with a pri-
mary particle energy in the range of 100-500 GeV and
a 3-dimensional shape of 25x25x25 pixels. Figure 1
shows an example shower image cutout.
It is worth noticing that we do not use any tim-
ing information: only static images of the energy de-
posits are used to train the GAN model (described in
section 3). Particle shower shapes are parameterized
according to the energy of the primary particle E
p
,
which is the energy of the electron which enters the
calorimeter volume and the ECAL value (for Elec-
tromagnetic CALorimeter), which corresponds to to-
tal energy measured by the calorimeter (summing the
estimated energy deposits over all calorimeter cells).
Figure 1: (Left): A simplified representation of the 3-
dimensional image. (right): An example shower develop-
ment at y = 13.
The relation between ECAL and E
p
depends on the
type, geometry and material of the calorimeter. For
our data we approximate it using polynomial func-
tion.
3 3D GENERATIVE
ADVERSARIAL NETWORKS
Generative Adversarial Networks (GANs) are being
successfully investigated for replacing some tradi-
tional Monte Carlo calorimeter simulations. It is
demonstrated, that GANs can achieve similar levels
of accuracy as the Monte Carlo simulations, on some
specific use case, while considerably decreasing the
simulation time (Khattak et al., 2018) (Erdmann M.,
2019). GANs were first introduced by Ian Goodfel-
low (Goodfellow et al., 2014) in 2014. They belong
to the group of unsupervised learning methods and are
nowadays used for a large variety of different gener-
ative tasks. The whole GAN model consists of two
deep neural networks. A generator network which
generates images from random numbers and a dis-
criminator which is trained to evaluate and distinguish
between the generated and the training images.
The generator network receives as input a latent
vector with 200 uniform distributed random num-
bers multiplied by an energy scalar corresponding
to the primary particle energy E
p
. It produces a
3-dimensional shower image with the same shape
25x25x25, as the images of the training dataset.
The generator network uses a mix of convolutional
2D (Conv2D) layers and transposed convolutional
2D (Conv2D transpose) layers. Additionally, we
use batch normalization (BatchNorm), leaky recti-
fied linear units activation function (LeakyReLU) and
dropout layers (Dropout). The detailed neural net-
work architecture of the generator is shown in figure
2.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
252
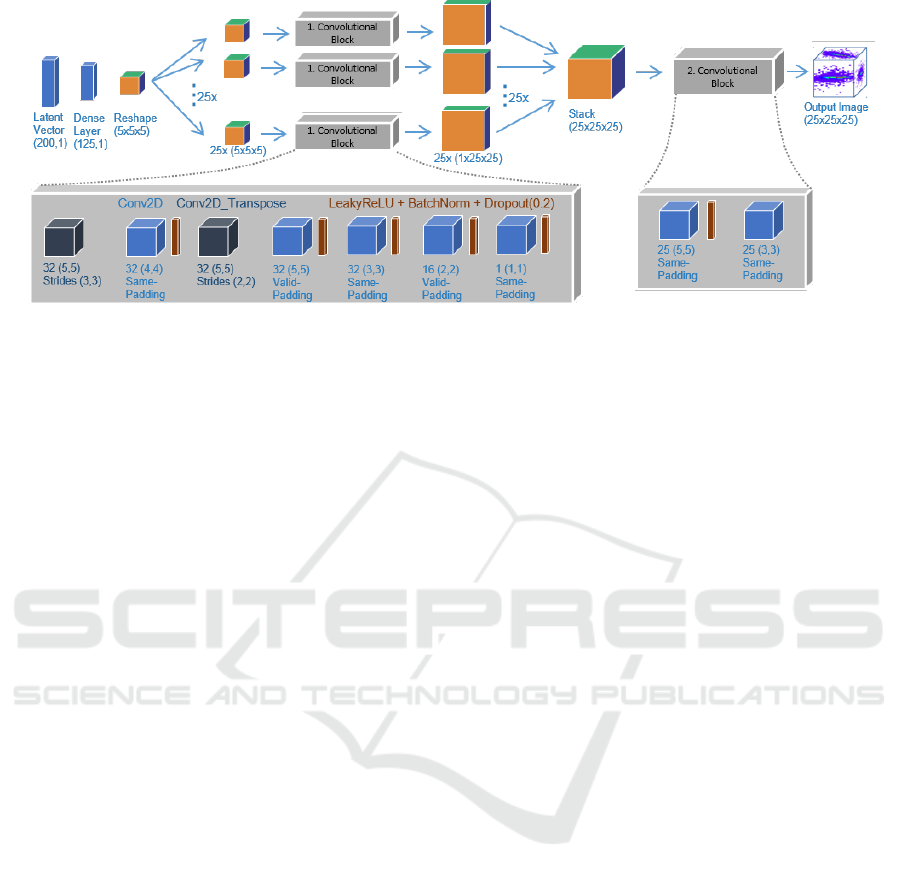
Figure 2: Generator neural network architecture. Input is a latent vector and output is the 3-dimensional shower image.
The discriminator produces three output values,
see figure 3. The first is the typical GAN true/fake
probability (Goodfellow et al., 2014). The second
and third discriminator outputs are auxiliary losses to
support the GAN model to converge during training.
We name the second loss AUX (for AUXiliary loss)
which is a regression task to compare the discrimi-
nator output with the label of the primary energy E
p
.
The third discriminator output is named ECAL and is
a self-produced lambda layer calculating the sum over
the pixels of the input image which therefore, corre-
sponds to the total energy of the input image.
In previous papers we used convolutional 3D
(Conv3D) layers in the models but here we replace
them by Conv2D layers. The Conv2D layers re-
duce the computational complexity with respect to the
Conv3D approach and we gained a reduction in com-
putation time. In addition the Conv3D layers are not
supported in any quantization tool yet. We will de-
scribe the change from Conv3D to Conv2D more de-
tailed in a future paper, since this approach is appli-
cable for any kind of convolutional models with 3D
images and comes with a significant decrease in com-
putation time.
4 REDUCED PRECISION
COMPUTATION
To achieve higher throughput and to reduce memory
bandwidth during inference we can shrink the size
of activations and weights of the trained neural net-
work to lower precision. This approach is named re-
duced precision computing and the process of con-
verting numbers from higher to lower precision is
named quantization. The standard number format in
machine learning is floating point 32 (float32) or sin-
gle precision, specified in IEEE 754 (IEEE, 2008).
The format which uses just half of the bits of float32
is floating point 16 (float16) and is therefore called as
half precision, specified in IEEE 754 (IEEE, 2008).
The smallest format in which we want to quantize our
model is integer-8 (int8). Integer numbers can be ei-
ther signed int8 (sint8) with a range of [−127, 127] or
unsigned int8 (uint8) with a range of [0, 255].
Intel Low Precision Optimization Tool. The Intel
Low Precision Optimization Tool (iLoT) (Feng Tian
and Gong, 2020) is an open-source python library
for quantizing deep learning models and running low
precision inference across multiple frameworks. It
uses the Intel oneAPI Deep Neural Network Library
(oneDNNL) (Intel, ), which contains building blocks
for deep learning applications to improve the perfor-
mance on Intel processors. This paper presents results
of the first test of the brand new iLoT tool on a real
use case.
Quantization of a trained model requires identify-
ing the best order of magnitude across pixels cover-
ing an entire layer instead of a single pixel. Once the
order of magnitude of an entire layer is known, it is
possible to drop single bits, named ”outliers”, which
are far away from the other values within this layer.
Dropping outliers, the choice of different statistical
means and repeated refinement of the topology makes
quantization a delicate process rather than just a one-
step deployment task. iLoT tunes the quantization
process automatically with accuracy-driven strategies
for computational performance, model size and mem-
ory footprint (Feng Tian and Gong, 2020). During
the iterative and automatic quantization process iLoT
can keep a few single nodes in the neural network
in float32 precision in order to increase the accuracy.
This is the advantage of iLoT compared to any other
recent quantization tool. The accuracy is measured
using a physics-inspired validation metric introduced
in section 6.
Reduced Precision Strategies for Deep Learning: A High Energy Physics Generative Adversarial Network Use Case
253

Figure 3: Discriminator neural network architecture. Input are the 3-dimensional shower images and output the loss values.
Previously, quantization in deep learning was
mainly applied to classification problems which em-
ploy simpler neural network outputs (probability val-
ues of classes) compared to the complex shower im-
ages of our network. Moreover, our generator net-
work uses LeakyReLU activation functions instead
of standard ReLU. Since LeakyReLU can generate
negative weights, they require sint8 operations after
quantization. As the sint8 operations are not needed
for classification networks with standard ReLU acti-
vations, sint8 are by default not yet implemented in
TensorFlow. Similarly no recent quantization tool im-
plements LeakyReLU activations functions. In this
study we make use of an Intel-customized Tensor-
Flow version supporting sint8 operations and an ad-
hoc implementation of LeakyReLU activations in the
iLoT tool.
Layers fusion is another strategy that can be used
to accelerate deep neural networks inference: iLoT
implements [Conv2D + LeakyReLU] fused operation
followed by a FusedBatchNorm layer. In its next re-
lease, iLoT (included in oneDNNL) will support a full
[Conv2D + LeakyReLU + BatchNorm] fuse, which
could further improve the performance.
TensorFlow Lite. TensorFlow Lite (TFL, 2020) is
part of the TensorFlow library and is created for de-
ploying machine learning models on mobile and in-
ternet of things (IoT) devices. It contains packages
for converting TensorFlow models to TensorFlow Lite
models and packages to quantize and deploy models.
It can quantize networks, layer-wise, from float32 into
float16 and int8 (TFL, 2020).
Because TensorFlow does not support sint8 opera-
tions yet, TensorFlow Lite does not support quantized
LeakyReLU activation functions as well. Addition-
ally, we do not have the compatible hardware for run-
ning quantized TensorFlow Lite models available for
this study, therefore we use TensorFlow Lite only for
measuring the accuracy of the quantized models and
not inference speed-up.
5 RELATED WORK
Generative Adversarial Networks. xz GANs are
today extensively used in a wide range of applications
(Brownlee, 2020).
In the field of High Energy Physics, a lot of re-
search is ongoing to understand how to replace Monte
Carlo simulations by employing GANs. For example
in (Salamani et al., 2018) Variational Auto-Encoders
(VAEs) and GANs are proposed to simulate the out-
put of the ATLAS liquid Argon calorimeter. The first
proof of concept, using 3D convolutional GANs for
electromagnetic calorim eters is represented by the
3DGAN prototype (Khattak et al., 2018) and (Val-
lecorsa et al., 2019) based on a simple auxiliary GAN
model. Other approaches investigated Wasserstein
GAN (Arjovsky et al., 2017) for improving the model
convergence (Erdmann M., 2019).
Int8 Quantization. Quantizing trained deep learn-
ing models to a reduced precision is being actively
researched in the recent years to allow, in particular,
fast inference on mobile devices where the compu-
tational power is strongly constrained. In more gen-
eral, with increasing model size and complexity, con-
straints on computing time and memory consumption
become relevant for other architectures, CPUs and ac-
celerators alike.
In most cases, quantization techniques are tar-
geted to int8, because it is a data format that most
modern hardware supports and because it maintains
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
254
almost the same level of accuracy, compared to lower
precision formats (Jain et al., 2020). Most of the ex-
isting benchmarks represent classification problems
(Wu et al., 2020), while in our case, we require an
accurate description of simulated data. There are
two main quantization techniques. The first is post-
training quantization, where the model is trained in
float32. Afterwards, it uses a calibration dataset to
calculate the maxima of the weights and activations
which are needed for the quantization process into
a lower precision. This is commonly the first ap-
proach which is chosen and leads mostly to a satis-
fying level of accuracy (Wu, 2019), hence we use this
approach for the research in this paper. An alternative
method, named quantization-aware training, directly
trains models using lower precision formats.
Mixed Precision Training. One can go even fur-
ther and train models with mixed precision formats:
for example, using both float32 and int8. In this case,
some weights are represented in int8 format to gain
a speed-up, but others are kept as float32, to main-
tain the level of accuracy. Choosing which weights
are represented in higher or lower precision is done
by intelligent algorithms.
Different studies have evaluated mixed precision
for training (Micikevicius et al., 2017) (Nandakumar
et al., 2020): In particular (Osorio, ) applies a mixed
precision approach to the training of 3DGANs.
6 EVALUATION
This section describes the evaluation process in terms
of computational performance and physics accuracy
and discusses results in details.
6.1 Computational Evaluation
The computational throughput depends in practice on
the model and the hardware on which it runs. We per-
form all computational performance tests on an In-
tel 2S Xeon Processor 8280 with Cascade Lake ar-
chitecture and 28 cores (56 virtual cores or threads)
which supports int8 format. As explained above, the
iLoT int8 model is benchmarked against the original
float32 model.
Multiple flows of different input data are pro-
cessed concurrently on affinitized threads (and taking
advantage of memory locality), which is referred to
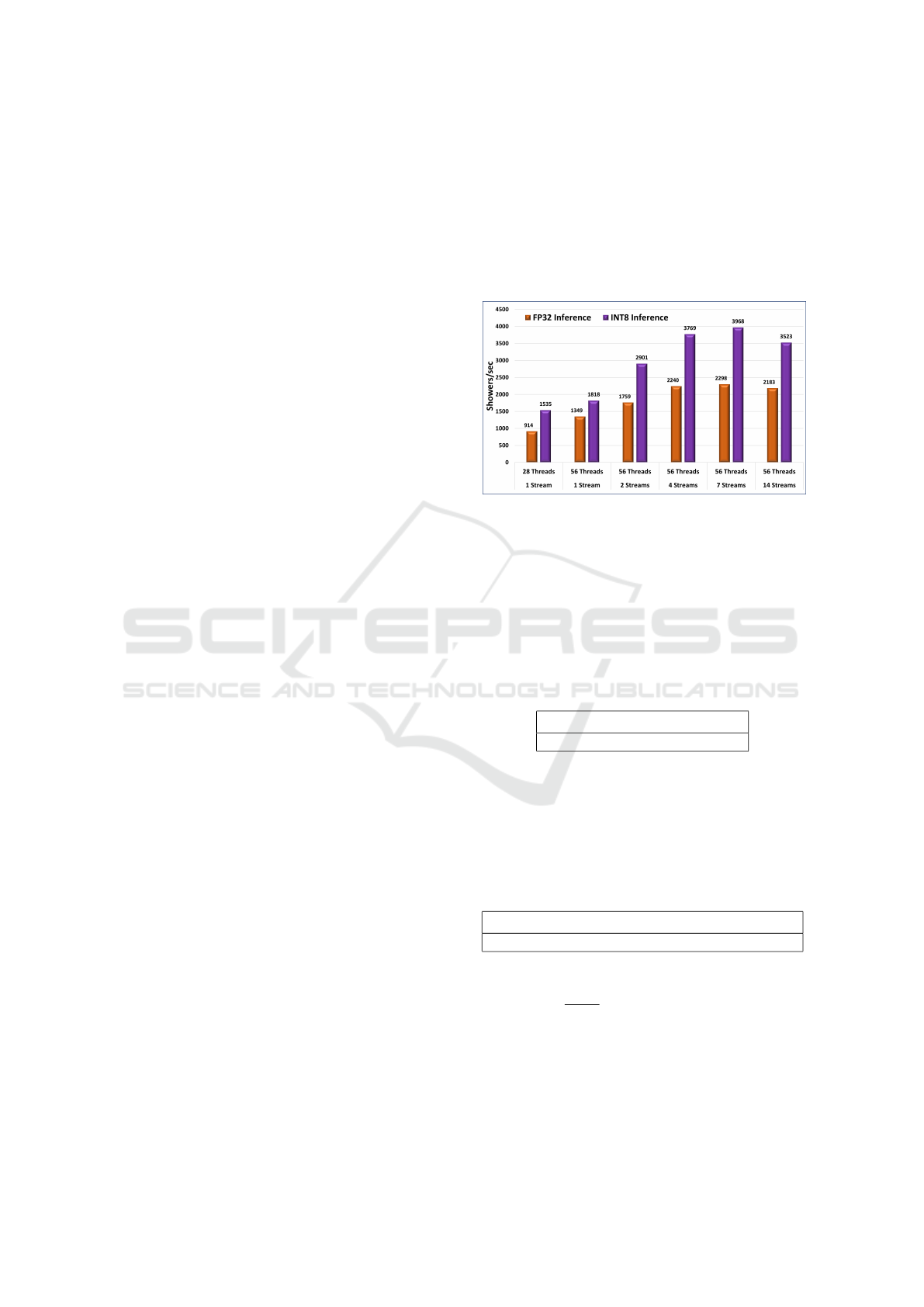
multiple streams. We measured the total time and the
throughput by parallelising the inference process us-
ing multiple threads and multiple data streams: The
results are shown in figure 4. As expected, the number
of showers per seconds increases with the number of
streams and threads for both the int8 and float32 mod-
els. In particular the best performance is achieved us-
ing 56 threads and 7 data streams. Beyond this point
the performance becomes worse, most probably be-
cause the memory bandwidth limit is exceeded and
the CPU gets oversubscribed. All tests were run in-
cluding a warm-up time with TensorFlow version 2.3.
Figure 4: Inference throughput in showers per seconds for
the float32 and int8 model for different number of stream
and thread configurations.
Using 7 streams and 56 threads for both mod-
els we measure an inference time of 55.7 ms for the
float32 model and 32.3 ms for the int8 model, as
shown in table 1, corresponding to a 1.73x speed-up
using the iLoT quantized model.
Table 1: Inference times in milliseconds [ms] for float32
and INT8 GAN model measured on Cascade Lake CPU.
float32 int8 Speed-up
55.7 ms 32.3 ms 1.73x
Details about the runtimes of some operations are
shown in table 2. It can be seen, that the FusedBatch-
Norm yields about 30% of the total runtime: replacing
this operation with a fused [Conv2D + LeakyReLU +
BatchNorm] will bring a significant speed-up.
Table 2: Times in milliseconds (ms) for some operations of
the quantized int8 iLoT model.
Total FusedBatchNorm De-/Quantization
32.3 ms 9.37 ms 6.06 ms
Table 2 also shows the time needed by the de-
quantize operation, which is non negligible as it cor-
responds to
6.06 ms
32.3 ms
= 18.3% of the total runtime.
The dequantization step takes care of converting the
float32 input data to int8 and then converting back the
model output data (int8) to float32, expected for the
simulation output.
An additional effect is due to the fact that, a low-
precision unit internally demands higher bandwidth,
Reduced Precision Strategies for Deep Learning: A High Energy Physics Generative Adversarial Network Use Case
255

i.e. scratch memory bandwidth or cache bandwidth,
and this demand can limit operations depending on
the specific hardware implementation. Therefore,
practical implementations of low-precision in hard-
ware and software are challenged to speed-up infer-
ence by the full ratio of type-width.
Generally speaking, larger models might exhibit
a larger inference acceleration, simply thanks to the
relatively smaller weight represented by the quanti-
zation/dequantization steps with respect to the quan-
tized operations runtime. As an example, ResNet-
50 (He et al., 2015) has over 23 million parameters,
Inception-v3 (Szegedy et al., 2015) over 24 million
parameters whereas our model has only around 2 mil-
lion parameters. Being 10 times smaller, our GAN
network is more sensitive to the size of the quan-
tization and dequantization steps (10.5 ms) with re-
spect to the total run time (32.3 ms). In other words,
the smaller the model, the stronger the impact of the
quantization and dequantization functions at the be-
ginning and end of the model.
In any case, running inference using int8 preci-
sion, further increases the advantage with respect to
running standard Monte Carlo simulation. With re-
spect to the original Geant4 benchmarks quoted in
(Vallecorsa et al., 2019), the int8 quantized models
reaches a huge 67 000x speed-up. In terms of mem-
ory consumption, the iLoT int8 model decreases by a
factor 2.26x the total utilised physical memory (from
8 KB to 3.6 KB) with respect to the initial float32.
6.2 Physical Evaluation
Evaluating performance of a Generative Model is not
an easy task, several methods have been proposed de-
pending on the specific applications (Borji, 2018).
In this work, we rely on physics inspired valida-
tion, visually inspecting the energy patterns across
the calorimeter volume by measuring the accuracy on
specific physics quantities, the energy deposits distri-
butions along the calorimeter y- and z-axis.
We compare the quantised models in three dif-
ferent formats (int8 iLoT, int8 TFLite and float16
TFLite) to the baseline GAN model (float32) and the
Geant4 validation set.
1. Particle Shower Shapes. Figure 5 represents
the first visual validation method and shows the 2-
dimensional particle shower shapes along the y- and
the z-axis for the different models. The particle en-
ters the detector at the coordinates x = 13, y = 13
and z = 0, orthogonally to its surface: the larger en-
ergy depositions, in the transverse (x, y) plane, clus-
ter around the middle of the image while the patterns
along the z-axis develops as discussed in section 2.
For simplicity, we report only the energy distribu-
tion along the y-axis, since the patterns along the two
transverse directions are very similar. In figure 5 we
compare all models to the Geant4 prediction.
Figure 5: Generated shower shapes along y- (top) and z-axis
(bottom) of Geant4 (red), the TF float32 model (blue), the
iLoT int8 model (pink), the TFLite float16 model (green),
and the TFLite int8 model (orange). Horizontal we plot the
single pixels of the respective axis and vertical the average
energies contained in the single pixels. The vertical lines
corresponds to the statistical errors for the single pixels.
The float32 prediction (our baseline) is very close
to the Geant4 test data. The quantized iLoT int8
and TFLite float16 models are close to initial float32
model and remain mostly within the range of the sta-
tistical error bars. However, the TFLite int8 model
is slightly off. This effect is larger at the edges of
the distribution, where the energy deposits are much
smaller (see figure 5).
Table 3 summarizes the statistical mean and stan-
dard deviation for the particle shower distributions in
figure 5. The TFLite int8 seems to yield worse predic-
tion with respect to both the GAN baseline (float32)
and Geant4.
This can be visually confirmed by looking at the
same shower shapes in logarithmic scale in figure 6.
In the y-axis plot we can see that TFLite float16, and
especially TFLite int8 struggles with the low energies
at the tails. Tails we name the first and last five pixels
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
256

Table 3: Statistical values mean and standard deviation
(STD) for the different models.
Model: Mean: STD:
y-axis Geant4 12.00 1.45
y-axis float32 12.02 1.46
y-axis iLoT int8 12.03 1.45
y-axis TFLite float16 12.05 1.13
y-axis TFLite int8 12.10 1.19
z-axis Geant4 13.85 4.62
z-axis float32 13.81 4.50
z-axis iLoT int8 13.91 4.48
z-axis TFLite float16 13.78 4.50
z-axis TFLite int8 14.25 4.62
of the y-axis shower shape plot. On the other hand,
the iLoT int8 model has no troubles in representing
the low energy pixels at the tails. However, a more de-
tailed performance analysis is needed to confirm this
result.
Figure 6: Logarithmic Shower Shapes.
2. Single Validation Number. In order to sim-
plify results evaluation, we define a composite accu-
racy value, calculated by building 2-dimensional pro-
jections of the particle shower distributions for the
GAN and Geant4 samples and then measuring the to-
tal mean squared error (MSE) between the two pro-
jections. The MSE-based metric values for the vari-
ous models are shown in table 4.
The iLoT model seem to reach a better accuracy
than the initial float32 model. However, this is an arti-
Table 4: MSE-based values for the different models. The
lower the value, the better the accuracy.
float32 iLoT TFLite float16 TFLite int8
0.061 0.053 0.254 0.340
fact of the quantization process that relies on the same
metric to determine which weights are kept in float32
format in a similar fashion as an architecture hyper-
parameter search. In contrast, both quantized TFLite
models loose accuracy.
3. Pixel-wise Image Comparison. In addition we
perform a pixel-wise image comparison, by fixing the
input latent vector and generating a synthetic image.
We subtract then element-wise the entries of the sin-
gle pixels of the output image of the quantized model
from the baseline model and sum up the absolute val-
ues. The pseudo code for the pixel-wise comparison
looks like:
mean ( sum ( abs ( X_float32 - X_int8 ) ) )
With the corresponding values we can directly
compare how different the created images are. The
smaller the pixel-wise validation value, the closer are
the images and the better the model. We performed
the pixel-wise validation for all our quantized models
compared to the baseline float32 model. The results
are shown in table 5. One can see that the TFLite
float16 model performs best and the iLoT int8 model
is approximately three times better than the TFLite
int8 model in the pixel-wise comparison.
Table 5: Pixel-Wise validation values for the different quan-
tized models.
Model: Mean: STD:
TFLite float16 0.133 0.291
TFLite int8 4.054 0.721
iLoT int8 1.550 0.191
All in all the iLoT tool reaches a better level of
physics accuracy in all our shown validation metrics
compared to TFLite int8.
7 CONCLUSION AND FUTURE
WORK
In this paper we studied the impact of int8 quantiza-
tion on a convolutional GAN model developed for
High Energy Physics detector simulation. Prelimi-
nary results seem to suggest that the iLoT tool per-
forms better than TFLite, in terms of physics accu-
racy. Additional studies are on-going in order to con-
firm these findings. We are interested, in particular,
Reduced Precision Strategies for Deep Learning: A High Energy Physics Generative Adversarial Network Use Case
257

in understanding what is the effect of the optimisa-
tion metric used by the iLoT tool on the overall output
quality.
Thanks to the quantization we obtain a 1.73x
speed-up on inference time compared to the initial
float32 model. This brings the total speed-up with re-
spect to the standard Monte Carlo approach to several
orders of magnitude (67 000x). These results make
the proposed reduced precision strategies on GAN
models an attractive approach for future researches on
the detector simulations and could help to save large
computing resources in view of the future High Lu-
minosity LHC runs.
With this paper we hope to inspire colleagues to
follow us and to apply quantization to deep learning
models with more complex outputs than classification
tasks. More use cases, in turn, will lead to an im-
provement of quantization methods and tools leading
to possible further decrease of inference times in the
future.
ACKNOWLEDGEMENTS
This work has been sponsored by the Wolfgang Gen-
tner Programme of the German Federal Ministry of
Education and Research.
REFERENCES
(2020). TensorFlow Lite. TensorFlow For Mobile & IoT.
Agostinelli, S. et al. (2003). GEANT4–a simulation toolkit.
Nucl. Instrum. Meth. A, 506:250–303.
Albrecht, Alvesand, A. e. a. (2019). A roadmap for hep
software and computing r&d for the 2020s. Comput-
ing and Software for Big Science, 3.
Apollinari, G., B
´
ejar Alonso, I., Br
¨
uning, O., Fessia, P., La-
mont, M., Rossi, L., and Tavian, L. (2017). High-
Luminosity Large Hadron Collider (HL-LHC): Tech-
nical Design Report V. 0.1. 4/2017.
Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-
stein gan.
Borji, A. (2018). Pros and cons of gan evaluation measures.
Brown, R. and Cockerill, D. (2012). Electromagnetic
calorimetry. Nuclear Instruments and Methods in
Physics Research Section A, 666:47 – 79. Advanced
Instrumentation.
Brownlee, J. (2020). 18 Impressive Applications of Gener-
ative Adversarial Networks (GANs).
de Oliveira, L. and Paganini, Michela, B. (2017). Learning
particle physics by example: Location-aware genera-
tive adversarial networks for physics synthesis. Com-
puting and Software for Big Science, 1(1).
Erdmann M., G. J. . Q. T. (2019). Precise simulation of
electromagnetic calorimeter showers using a wasser-
stein generative adversarial network. Comput Softw
Big Sci 3.
Feng Tian, Chuanqi Wang, G. Z. P. C. P. Y. H. S. and Gong,
J. (2020). Intel
R
low precision optimization tool.
Ghosh, A. (2019). Deep generative models for fast shower
simulation in ATLAS. Technical Report ATL-SOFT-
PROC-2019-007, CERN, Geneva.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial networks.
He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep resid-
ual learning for image recognition.
IEEE (2008). Ieee standard for floating-point arithmetic.
IEEE Std 754-2008, pages 1–70.
Intel. oneapi deep neural network library (onednn).
Jain, A., Bhattacharya, S., Masuda, M., Sharma, V., and
Wang, Y. (2020). Efficient execution of quantized
deep learning models: A compiler approach.
Khattak, G., Vallecorsa, S., and Carminati, F. (2018). Three
dimensional energy parametrized generative adversar-
ial networks for electromagnetic shower simulation.
In 2018 25th IEEE International Conference on Im-
age Processing (ICIP), pages 3913–3917.
Micikevicius, P., Narang, S., Alben, J., Diamos, G., Elsen,
E., Garcia, D., Ginsburg, B., Houston, M., Kuchaiev,
O., Venkatesh, G., and Wu, H. (2017). Mixed preci-
sion training.
Nandakumar, S. R., Le Gallo, M., Piveteau, C., Joshi, V.,
Mariani, G., Boybat, I., et al. (2020). Mixed-precision
deep learning based on computational memory. Fron-
tiers in Neuroscience, 14.
Osorio, J. Evaluating mixed-precision arithmetic for 3d
generative adversarial networks to simulate high en-
ergy physics detectors.
Salamani, D., Gadatsch, S., Golling, T., Stewart, G., Ghosh,
A., Rousseau, D., Hasib, A., and Schaarschmidt, J.
(2018). Deep generative models for fast shower sim-
ulation in atlas. pages 348–348.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna,
Z. (2015). Rethinking the inception architecture for
computer vision.
Vallecorsa, S., Carminati, F., and Khattak, G. (2019). 3d
convolutional gan for fast simulation. EPJ Web of
Conferences, 214:02010.
Wu, H. (2019). Inference at reduced precision on gpus.
Wu, H., Judd, P., Zhang, X., Isaev, M., and Micikevicius, P.
(2020). Integer quantization for deep learning infer-
ence: Principles and empirical evaluation.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
258
