
Deep Learning based Model Identification System Exploits the Modular
Structure of a Bio-inspired Posture Control Model for Humans and
Humanoids
Vittorio Lippi
a
Neurological University Clinic, University of Freiburg, Freiburg im Breisgau, Germany
Keywords:
Posture Control, Deep Learning, System Identification, Parametric Nonlinear System.
Abstract:
This work presents a system identification procedure based on Convolutional Neural Networks (CNN) for
human posture control using the DEC (Disturbance Estimation and Compensation) parametric model. The
modular structure of the proposed control model inspired the design of a modular identification procedure, in
the sense that the same neural network is used to identify the parameters of the modules controlling different
degrees of freedom. In this way the presented examples of body sway induced by external stimuli provide
several training samples at once.
1 INTRODUCTION
The application of convolutional neural networks
(CNN) in human movement analysis has produced
promising results in recent experiments (Batchuluun
et al., 2018; Karatzoglou et al., 2018; Abdu-Aguye
and Gomaa., 2019a; Abdu-Aguye and Gomaa., 2019b),
and in general deep learning is starting to be applied to
system identification (De la Rosa and Yu, 2016; Ander-
sson et al., 2019; Miriyala and Mitra, 2020; De la Rosa
et al., 2015; Ljung et al., 2020). This work aims to ap-
ply CNN to the identification of human posture control
models, that are used in several studies for the analy-
sis of human data and the control of humanoids, e.g.
(van der Kooij et al., 2007; van der Kooij et al., 2005;
van Asseldonk et al., 2006; Goodworth and Peterka,
2018; Mergner, 2010; Engelhart et al., 2014; Pasma
et al., 2014; Jeka et al., 2010; Boonstra et al., 2014).
Most of the studies on posture control use linear mod-
els like the independent channel (IC) model (Peterka,
2002), and make the assumption of linear and time-
invariant behavior (Engelhart et al., 2016). In this work
a nonlinear model will be considered. This makes the
use of deep learning more interesting, as the identifi-
cation of nonlinear systems is more complex and in
general it is performed using computationally expen-
sive iterative algorithms as in (Assl
¨
ander et al., 2015).
In a previous work, CNNs proved to be suitable to iden-
tify the parameters of a human posture control model
a
https://orcid.org/0000-0001-5520-8974
(Lippi. et al., 2020). Specifically, the CNN presented
in (Lippi. et al., 2020) was applied to a single inverted
pendulum (SIP) model, but it proved to work also in
identifying the parameters of a double inverted pendu-
lum system. In this work a triple inverted pendulum
(TIP) model of posture control will be used to show
how the identification process can be extended to an ar-
bitrary number of degrees of freedom. The model used
here, the Disturbance Estimation and Compensation
(DEC) has a modular structure (Lippi and Mergner,
2017), i.e. each degree of freedom is controlled by a
module and all the modules share the same structure.
Exploiting this characteristic, one CNN is used to iden-
tify the parameters of the three modules controlling the
three degrees of freedom. In this way each simulation
provides three training samples at once.
2 METHODS
2.1 Posture Control Scenario
The scenario considered here models a human (or hu-
manoid) balancing on a tilting support surface as a TIP.
The three degrees of freedom considered in the sagittal
plane are the ankles, the knees and the hips (Fig. 1A).
The support surface tilt
α
FS
represents the input of the
system and it is the same for all the simulations. The
profile of the tilt of the support surface is the pseudo-
random ternary sequence, PRTS, shown in Fig. 1B.
540
Lippi, V.
Deep Learning based Model Identification System Exploits the Modular Structure of a Bio-inspired Posture Control Model for Humans and Humanoids.
DOI: 10.5220/0010245405400547
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 540-547
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Balance scenario and posture control system. (A)
The triple inverted pendulum model used to simulate human
posture control together with the control modules. The
α
BS
represent the sway of the body COM around the ankle joint.
(B) The Pseudo-Random Ternary Signal, PRTS, the time
profile for support surface tilt. (C) Schema of a control
module. The disturbances are compensated feeding them
in the form of an angle equivalent as input to the servo
controller (PID).
Such stimulus is used in human experiments because
it is not predictable for the subject (Peterka, 2002). It
is composed by a sequence of velocity steps suitable
to excite the dynamics of the system over several fre-
quencies. The output of the system is the sway of the
body segments: shank, thigh (leg) and trunk addressed
as α
SS
, α
LS
, and α
T S
respectively.
2.2 Human and Humanoid Posture
Control: The DEC Model
The DEC is a model of the human postural con-
trol mechanisms (Mergner, 2010; Lippi and Mergner,
2017). It has a modular structure that can be applied
to multiple DoF robots (Lippi and Mergner, 2017;
Zebenay et al., 2015; Ott et al., 2016; Lippi, 2018;
Hettich et al., 2013; Hettich et al., 2015). Here it
is implemented specifically on the TIP model, using
three control modules. A block diagram of the DEC
control is shown in Fig.1. A complete description of
the model is beyond the scope of this paper and can
be found in (Lippi and Mergner, 2017). In the fol-
lowing a general description of the model is provided
with particular emphasis on the components that have
an impact on the definition of the machine learning
problem. A control module based on the DEC concept
is implemented as servo loop, here implemented as
a PID controller (the neural controller in Fig. 1C).
The controlled variable can consist in the COM sway
of all the segments above the joint controlled by the
module with respect to the gravitational vertical pass-
ing through the controlled joint (e.g.
α
BS
in Fig 1 for
the ankle joint). The sensory channels shown in Fig.1
(C) as Vestibular, Proprioceptive, and Force are used
for disturbance estimation. The disturbance estimates
are fed into the servo so that the joint torque on-line
compensates for the disturbances. The lumped delay
in Fig. 1 (C) represents all the delay effects that are
distributed in humans, and humanoids (Antritter et al.,
2014; Hettich et al., 2014). The model used in this
work considers gravity and support surface tilt as dis-
turbances. The gravity torque to be compensated is
assumed to be proportional to the sway of the COM
of groups of segments above the controlled joints. Ide-
ally the gain required to compensate gravity is
mgh
,
where
m
and
h
are the total mass and the COM height
of the controlled segments respectively, and
g
is the
gravity acceleration. The integral component of the
PID controller is not applied to the compensation as
in (Ott et al., 2016). The support surface tilt estimator
includes a non-linearity, introduced to represent the
behavior observed in humans (Mergner et al., 2009;
Mergner et al., 2003), defined as:
α
FS
=
Z
t
0
f
θ
d
dt
α
vest
BS
+
d
dt
α
prop
BF
(1)
where
α
prop
BF
is the ankle joint angle signal from propri-
oception.
BF
stands for Body-to-Foot. The function
f
θ
is a dead-band threshold defined as
f
θ
(α) =
α + θ i f α < −θ
0 i f −θ < α < θ
α − θ i f α > θ
(2)
The estimated
α
FS
is then up-channeled through the
control modules and used to control body position.
In this work the threshold is set as
θ = 0.0003rad/s
.
The disturbance compensation and the total torque
commanded by the servo controller for the ankle joint
is:
τ(s) = −e
−s∆
K
p
+ sK
d
+ K
i
1
s
(ε) + (K
p
+ sK
d
)T
g
(3)
where
K
p
and
K
d
is the derivative coefficient for the
PD controller, and
∆
is the lump delay. Notice that
the derivative component is also acting on gravity
T
g
,
representing a sort of anticipation of the disturbance.
Deep Learning based Model Identification System Exploits the Modular Structure of a Bio-inspired Posture Control Model for Humans and
Humanoids
541
There is also a passive torque acting on the joints rep-
resented as a spring-damper model:
τ
passive
= −(K
pass
p
+ sK
pass
d
)
α
prop
BF
(4)
The coefficients
K
pass
p
and
K
pass
d
are kept fixed for all
the simulations. The standard parameters are shown
in Table 1. In general the gains are proportional to the
mgh
for the groups of segments above the controlled
joint, this will be used in the next section to normalize
the parameters. The anthropometric of the TIP model
is taken from previous works (Lippi et al., 2019b;
Lippi and Mergner, 2020).
2.3 The Training Set
Control Parameters and Target Set.
The training
set has been generated simulating the posture control
scenario with different parameters, these parameters
represent the target for the neural network and the
sway of the segments represents the input. In order
to exploit the modular structure of the DEC control
the CNN has been designed to identify the parame-
ters of a specific module. In this way each simulation
provides three training samples associated with the
three control modules. As explained in the previous
section, the gains of the controllers are proportional
to the
mgh
of the segments above the controlled joint,
and the lumped delay is larger for the ankle module
and smaller for the hip module. In order to use such
parameters for the training of the same CNN their
value is expressed as deviation from the default value
and normalized dividing it by the default value, e.g.
˜
K
p
= (K
sample
p
− K
p
)/K
p
in Table 1. Besides the PID
gains the target vector includes the lumped delay and
a variable
C
that is set to
−1
when the controlled vari-
able is the joint angle and to
+1
when the controlled
variable is the COM. This leads to a sample with the
following form:
˜
T =
˜
K
p
˜
K
i
˜
K
d
˜
∆ C
(5)
where the˜indicates that the values are normalized.
The training samples are generated with random
parameters from normal distributions
X ∼ N (0, 0.5)
that is summed to the normalized parameters. The
variable
C
is sampled with equal probability (
0.5
) be-
tween the two cases. In order to avoid negative values
the absolute value of the obtained parameters is used
”‘warping”’ the normal distribution on positive values.
A set of parameters is used as a sample only if the
behavior it produces is stable: simulations with body
sway larger than
6
◦
are not considered realistic balanc-
ing scenarios and are discarded. Overall the obtained
data consist of
20730
samples,
14000
used as training
set,
3000
as validation set and
3730
as test set. The
three sets are normalized subtracting the average di-
vided by the variance of the training set. The resulting
distribution of the normalized
˜
K
p
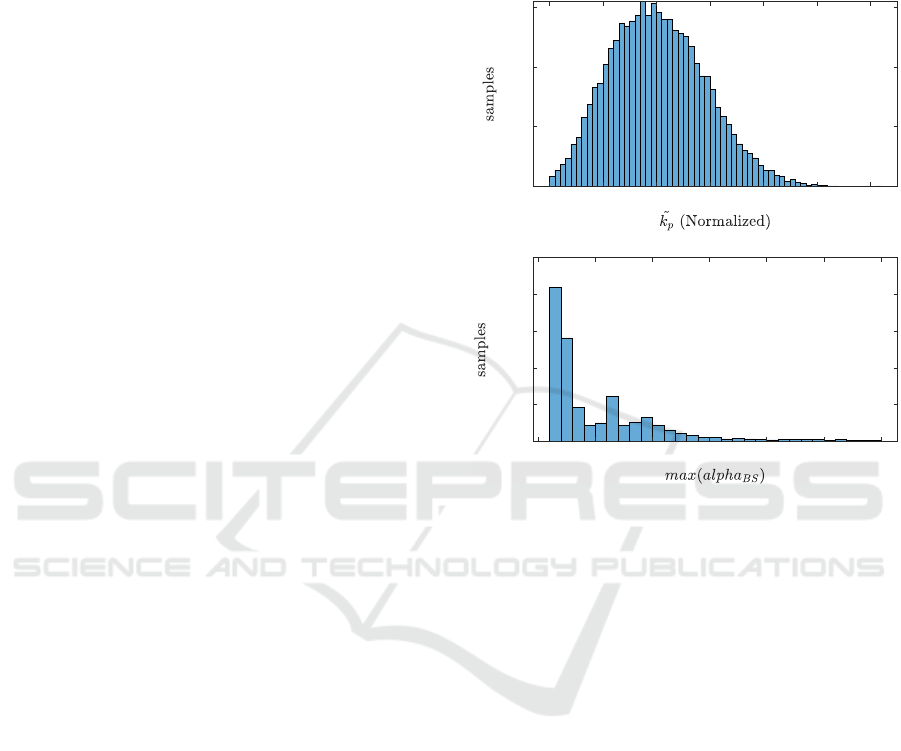
is shown in Fig. 2
together with the distribution of maximum body sway
amplitudes.
-2 -1 0 1 2 3 4
0
200
400
600
0 1 2 3 4 5 6
0
500
1000
1500
2000
2500
Figure 2: Output of the performed simulations. Above the
distribution of the normalized
˜
K
p
parameter produced during
the stable simulations. Below the distribution of the body
sway amplitudes. The last column of the histogram on the
right includes the simulations that were aborted because the
body sway reached the threshold of 6
◦
.
The CNN Input.
The Input is a representation of
the system output, i.e the sway of the segments. The
simulation was performed with a fixed integration step
of
2ms
and sampled at
50 Hz
, producing
6051
samples
with a resolution of
20 ms
. In order to adapt the signal
to the CNN the input was transformed into an image.
The data considered were the sway with respect to
the vertical of the two segments under and above the
controlled joint, e.g. for the ankle module they are
α
FS
and
α
LS
. The Spectrogram of the two signals is com-
puted with short-time Fourier transform over windows
of 250 samples overlapping for 135 computing 250
frequency points. This results in a 51 ×250 matrix of
complex values. The first 51 columns of the matrix
are here considered, corresponding to a bandwidth of
approximately
10 Hz
. Due to the low-pass dynamics
of the body sway, the power spectrum of the signal
at higher frequency is very poor and hence not giving
important informations (i.e. almost black images inde-
pendently of the parameters) . The resulting
51 × 51
matrix is used to define the input image as follows: the
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
542

Table 1: Default parameters.
Parameter Symbol Ankle Knee Hip unit
Active proportional gain K
p
465.98 245.25 73.575
N·m
rad
Active derivative gain K
d
116.49 18.394 18.394
N·m·s
rad
Active integrator gain K
i
11.649 6.1312 1.8394
N·m
rad·s
Passive stiffness K
p
pass
232.5000 61.2500 36.5000
N·m
rad
Passive damping K
d
pass
145.000 11.2500 11.2500
N·m·s
rad
Foot rotation velocity threshold θ
v f s
0.03 rad/s
Lumped delay ∆ 0.10 0.07 0.1210 s
module and the phase of the matrices associated to the
two segments sway are computed. The first channel of
the image is the module of the matrix describing the
sway of the segment above, the second is the matrix
describing the segment below and the third channel is
the difference between the phases. The process is sum-
marized in Fig 3. Also the input images are normalized
subtracting the average and dividing by the variance
of the training set through element-wise operation (i.e.
pixel by pixel, channel by channel).
2.4 CNN Architecture
The neural network architecture is schematized in Fig
4. The network is implemented with Matlab
TM
Deep
Learning Toolbox
TM
. The network has been trained
using stochastic gradient descent with momentum as
policy. The training was set to a limit of 200 epochs.
The loss function is the Mean Squared Error MSE as
expected with a regression task, although the target
vector includes a categorical feature, the controlled
variable, that implies a classification problem. The cat-
egorical variable produced by the CNN is interpreted
considering the sign (positive = COM sway, negative =
joint angle). The performance in regression and classi-
fication is discussed separately in the Results section.
3 RESULTS
3.1 Training and Test
The results of the training set are reported in Table 2.
Notice that there is a total RMSE on the training set,
including the error on the categorical variable, and a
Figure 3: Design of the input features for the CNN. In A the
spectrogram of a signal is given, the dashed line shows where
it is cut. In B it is shown how the spectrograms associated
with the sway of two body segments are combined to form
a three channel
51 × 51
pixel image. The image C shows
the normalization of the samples using the mean and the
variance of the training set, computed element-wise (pixel
by pixel).
fit RMSE computed on the continuous variables. The
average absolute error and absolute variance is shown
in Fig. 5. The error is larger on
K
i
. The identification
Deep Learning based Model Identification System Exploits the Modular Structure of a Bio-inspired Posture Control Model for Humans and
Humanoids
543
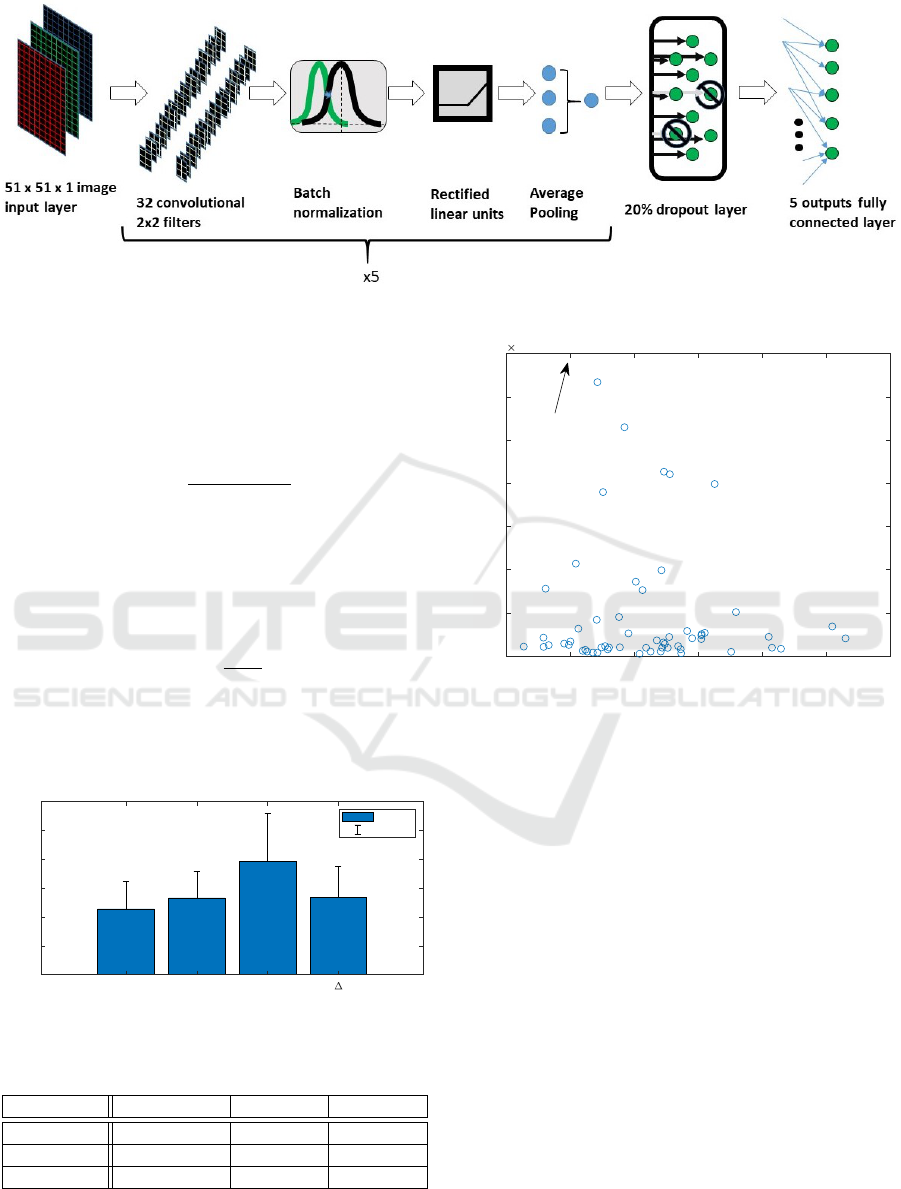
Figure 4: Neural Network architecture. The group of layers addressed with x 5 is repeated 5 times.
error in this context can be defined as the norm of
the difference between body sway obtained with the
target parameters (
α
α
α
BS
) and the one associated with
the identified parameters (
˜
α
α
α
BS
) divided by the number
of samples N = 6051,
E
id
=
k
α
α
α
BS
−
˜
α
α
α
BS
k
N
(6)
, where the bold text represents the fact that
α
BS
is
a vector of samples. The MSE on the single sample
is computed considering the target error on the three
control modules used in the simulation. The prediction
error
ε
p
on the 15 normalized parameters is computer
for each sample, leading to an MSE of
MSE =
q
ε
T
p
ε
p
/15 (7)
. The identification error plotted versus the MSE is
shown in Fig. 6. On average the identification error on
the training set is 0.0024
◦
K
p
K
d
K
i
0
0.2
0.4
0.6
0.8
1
1.2
average absolute error
Mean
Variance
Figure 5: Average and variance of the error on the parame-
ters.
Table 2: Training Results.
Dataset total RMSE fit RMSE Accuracy
Training 1.3664 1.3296 85.79%
Validation 1.5186 1.4810 83.90%
Test 1.4846 1.4486 84.72%
0 0.1 0.2 0.3 0.4 0.5 0.6
MSE (by sample)
0
1
2
3
4
5
6
7
Average identification error [°]
10
-3
(0.1, 0.07)
Figure 6: Identification Error for a set of 60 training sam-
ples. The identification error is plotted versus the MSE error
on the parameters (target output). The arrow addresses a
point that is out of the scale of the axes (i.e MSE = 0.1,
error=0.07). The correlation between the two measures of
errors is
−0.1265
, which means in general larger MSE on
the parameters are not associated to the larger identification
errors. This may suggest a certain degree of redundancy in
the model, allowing the system to reproduce a similar output
with different sets of parameters.
3.2 Identification of Human Posture
Control Parameters
The neural network is used to identify the control pa-
rameters from a human experiment performed with
the same scenario simulated in the training set. The
human experiment had the user stand with straight
legs and hence the simulation was applied just to the
ankle and the hip module. The identified parameters
are reported in table 3 and the simulated sways of the
segments are shown in Fig. 7, the result shows a good
similarity between the simulation and the original data.
For both the control modules, i.e. hip and ankle, the
network proposed the sway in space of the segments
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
544

as controlled variable, in according to previous studies
on support surface tilt (Hettich et al., 2014).
Table 3: Parameters identified for an example from a human
experiment.
Module K
p
K
i
K
d
∆ Var
Ankle 421.8574 74.6664 12.0254 0.0685 Sway Angle
Hip 74.5148 8.2559 1.8854 0.0219 Sway Angle
0 20 40 60 80 100
Time [s]
-1.5
-1
-0.5
0
0.5
1
1.5
2
Sway [°]
LS
simulated
TS
simulated
LS
human
TS
human
Figure 7: Human data compared with simulated responses.
3.3 Identification with a Monolithic
Model
In order to evaluate the impact of the modular ap-
proach the experiment is repeated with a network that
considers the three DOF together. The target vector
incorporates the parameters for the 3 control modules,
i.e. 15 values; the input is encoded as a 5 channel
picture with with spectrograms as described in
§
2.3.
Support surface tilt
α
FS
is not taken in account as it is
the same for all the samples. The channels represent
the modulus of the spectrogram for
α
LS
,
α
MS
, and
α
T S
,
and the phase difference between
α
LS
and
α
MS
as well
as between
α
MS
and
α
T S
. The dataset, rearranged in
this way accounted for
2264
samples, i.e. one third of
the original set. The dataset was split into a training
set and a validation set of
1000
samples and a test set
of
264
samples.The network had the same structure
of the one used in the modular case, but the input and
the output layers were modified according to the di-
mensionality of the new dataset. Such network has
the disadvantage of having less training samples and
more parameters, but potentially the advantage of in-
tegrating more information about the global structure
of the system (e.g. distinguishing explicitly between
different DOFs). The results are shown in Table 4.
The performance is overall worse than in the modular
case, especially for the classification accuracy, sug-
Table 4: Training Results with a monolithic model.
Dataset total RMSE fit RMSE Accuracy
Training 4.0731 3.2723 60.20%
Validation 4.1597 3.3297 53.50%
Test 4.0531 3.2586 51.51%
gesting that a modular approach is advantageous with
this problem.
4 CONCLUSIONS AND FUTURE
WORK
In this work a method for posture control parameter
identification based on CNN is presented. The sys-
tem provides an efficient way to fit a model of the
non-linear bio-inspired control system DEC on experi-
mental data. This represents an advantage with respect
to previous solutions relying on iterative methods. the
training set is produced with parameters from normal
distributions (although only the parameters producing
a stable simulation are selected). Future work will fo-
cus on the distribution of human data. An a posteriori
test can be performed comparing the distribution of the
parameters identified on the test set with the expected
distribution on real data. This can help the process of
choosing between different possible network hyperpa-
rameters sets as shown in (Sforza et al., 2011; Sforza
and Lippi, 2013).
Some parameters were better identified than others
as shown in Fig. 5. This may be due to the kind of
experimental set up or due to the choice of the input
features. For example the effect of
K
i
is mainly visible
just in the low pass components of the spectrogram.
Furthermore, simulations and robot experiments are
able to reproduce human behavior in the considered
set up (PRTS support surface tilt) without the integral
component of the neural controller (Mergner, 2010;
Hettich et al., 2015; Hettich et al., 2014). The inte-
gral component of the controller is more important in
analyzing transient behavior, e.g. reaching a desired
position, where it can be used to guarantee zero track-
ing error (Ott et al., 2016). A tracking task may be
better to identify K
i
more precisely.
The proposed CNN for posture control modeling
can find application in bio-inspired humanoid control,
e.g. (Choi and Kim, 2007; Abedi and Shoushtari,
2012; Zebenay et al., 2015; Mergner and Lippi, 2018).
The CNN can also be helpful in setting up wearable
robots using the control parameters identified on the
user (Chugo et al., 2019; Mergner and Lippi, 2019).
The parameters can be a tool to benchmark humanoids
and wearable devices (Torricelli et al., 2020), in partic-
ular, in the framework of the COMTEST project (Lippi
Deep Learning based Model Identification System Exploits the Modular Structure of a Bio-inspired Posture Control Model for Humans and
Humanoids
545

et al., 2019a; Lippi et al., 2020) that aims to make
a posture control testbed available for the humanoid
robotics community, and to define performance met-
rics.
ACKNOWLEDGEMENTS
C
O
M
T
T
S
E
This work is supported by the project
COMTEST, a sub-project of EUROBENCH
(European Robotic Framework for
Bipedal Locomotion Benchmarking,
www.eurobench2020.eu) funded by H2020
Topic ICT 27-2017 under grant agreement number
779963.
REFERENCES
Abdu-Aguye, M. G. and Gomaa., W. (2019a). On the fea-
sibility of on-body roaming models in human activity
recognition. In Proceedings of the 16th International
Conference on Informatics in Control, Automation and
Robotics - Volume 1: ICINCO,, pages 507–516. IN-
STICC, SciTePress.
Abdu-Aguye, M. G. and Gomaa., W. (2019b). Versatl: Ver-
satile transfer learning for imu-based activity recogni-
tion using convolutional neural networks. In Proceed-
ings of the 16th International Conference on Informat-
ics in Control, Automation and Robotics - Volume 1:
ICINCO,, pages 507–516. INSTICC, SciTePress.
Abedi, P. and Shoushtari, A. L. (2012). Modelling and
simulation of human-like movements for humanoid
robots. In Proceedings of the 9th International Con-
ference on Informatics in Control, Automation and
Robotics - Volume 1: ICINCO,, pages 342–346. IN-
STICC, SciTePress.
Andersson, C., Ribeiro, A. H., Tiels, K., Wahlstr
¨
om, N., and
Sch
¨
on, T. B. (2019). Deep convolutional networks in
system identification. In 2019 IEEE 58th Conference
on Decision and Control (CDC), pages 3670–3676.
IEEE.
Antritter, F., Scholz, F., Hettich, G., and Mergner, T. (2014).
Stability analysis of human stance control from the
system theoretic point of view. In Control Conference
(ECC), 2014 European, pages 1849–1855. IEEE.
Assl
¨
ander, L., Hettich, G., and Mergner, T. (2015). Visual
contribution to human standing balance during support
surface tilts. Human movement science, 41:147–164.
Batchuluun, G., Naqvi, R. A., Kim, W., and Park, K. R.
(2018). Body-movement-based human identification
using convolutional neural network. Expert Systems
with Applications, 101:56–77.
Boonstra, T. A., van Vugt, J. P., van der Kooij, H., and Bloem,
B. R. (2014). Balance asymmetry in parkinson’s dis-
ease and its contribution to freezing of gait. PLoS One,
9(7):e102493.
Choi, Y. and Kim, D. (2007). On the balancing control of
humanoid robot. In Proceedings of the Fourth Inter-
national Conference on Informatics in Control, Au-
tomation and Robotics - Volume 2: ICINCO,, pages
248–252. INSTICC, SciTePress.
Chugo, D., Koyama, M., Yokota, M., Kawazoe, S., Mu-
ramatsu, S., Yokota, S., Hashimoto, H., Katayama,
T., Mizuta, Y., and Koujina, A. (2019). Sitting assis-
tance that considers user posture tolerance. In Proceed-
ings of the 16th International Conference on Informat-
ics in Control, Automation and Robotics - Volume 2:
ICINCO,, pages 489–496. INSTICC, SciTePress.
De la Rosa, E. and Yu, W. (2016). Randomized algorithms
for nonlinear system identification with deep learning
modification. Information Sciences, 364:197–212.
De la Rosa, E., Yu, W., and Li, X. (2015). Nonlinear system
identification using deep learning and randomized al-
gorithms. In 2015 IEEE International Conference on
Information and Automation, pages 274–279. IEEE.
Engelhart, D., Boonstra, T. A., Aarts, R. G., Schouten, A. C.,
and van der Kooij, H. (2016). Comparison of closed-
loop system identification techniques to quantify multi-
joint human balance control. Annual reviews in control,
41:58–70.
Engelhart, D., Pasma, J. H., Schouten, A. C., Meskers, C. G.,
Maier, A. B., Mergner, T., and van der Kooij, H. (2014).
Impaired standing balance in elderly: a new engineer-
ing method helps to unravel causes and effects. Jour-
nal of the American Medical Directors Association,
15(3):227–e1.
Goodworth, A. D. and Peterka, R. J. (2018). Identifying
mechanisms of stance control: a single stimulus multi-
ple output model-fit approach. Journal of neuroscience
methods, 296:44–56.
Hettich, G., Assl
¨
ander, L., Gollhofer, A., and Mergner, T.
(2014). Human hip—ankle coordination emerging
from multisensory feedback control. Human Movement
Science, 37:123–146.
Hettich, G., Lippi, V., and Mergner, T. (2013). Human-like
sensor fusion mechanisms in a postural control robot.
In Londral, A. E., Encarnacao, P., and Pons, J. L., ed-
itors, Proceedings of the International Congress on
Neurotechnology, Electronics and Informatics. Vilam-
oura, Portugal, pages 152–160.
Hettich, G., Lippi, V., and Mergner, T. (2015). Human-like
sensor fusion implemented in the posture control of a
bipedal robot. In Neurotechnology, Electronics, and
Informatics, pages 29–45. Springer.
Jeka, J. J., Allison, L. K., and Kiemel, T. (2010). The dynam-
ics of visual reweighting in healthy and fall-prone older
adults. Journal of motor behavior, 42(4):197–208.
Karatzoglou, A., Schnell, N., and Beigl, M. (2018). A convo-
lutional neural network approach for modeling seman-
tic trajectories and predicting future locations. In In-
ternational Conference on Artificial Neural Networks,
pages 61–72. Springer.
Lippi, V. (2018). Prediction in the context of a human-
inspired posture control model. Robotics and Au-
tonomous Systems.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
546

Lippi, V. and Mergner, T. (2017). Human-derived distur-
bance estimation and compensation (dec) method lends
itself to a modular sensorimotor control in a humanoid
robot. Frontiers in neurorobotics, 11:49.
Lippi, V. and Mergner, T. (2020). A challenge: Support of
standing balance in assistive robotic devices. Applied
Sciences, 10(15):5240.
Lippi., V., Mergner., T., and Maurer., C. (2020). Deep learn-
ing for posture control nonlinear model system and
noise identification. In Proceedings of the 17th In-
ternational Conference on Informatics in Control, Au-
tomation and Robotics - Volume 1: ICINCO,, pages
607–614. INSTICC, SciTePress.
Lippi, V., Mergner, T., Maurer, C., and Seel, T. (2020).
Performance indicators of humanoid posture control
and balance inspired by human experiments. In
The International Symposium on Wearable Robotics
(WeRob2020) and WearRAcon Europe.
Lippi, V., Mergner, T., Seel, T., and Maurer, C. (2019a).
COMTEST project: A complete modular test stand
for human and humanoid posture control and balance.
In 2019 IEEE-RAS 19th International Conference on
Humanoid Robots (Humanoids) Toronto, Canada. Oc-
tober 15-17.
Lippi, V., Molinari, F., and Seel, T. (2019b). Distributed
bio-inspired humanoid posture control. In 2019 41st
Annual International Conference of the IEEE Engineer-
ing in Medicine and Biology Society (EMBC), pages
5360–5365. IEEE.
Ljung, L., Andersson, C., Tiels, K., and Sch
¨
on, T. B. (2020).
Deep learning and system identification. In 21st IFAC
World Congress, page 8.
Mergner, T. (2010). A neurological view on reactive human
stance control. Annual Reviews in Control, 34(2):77–
198.
Mergner, T. and Lippi, V. (2018). Posture Control–Human-
Inspired Approaches for Humanoid Robot Benchmark-
ing: Conceptualizing Tests, Protocols and Analyses.
Frontiers in Neurorobotics, 12:21.
Mergner, T. and Lippi, V. (2019). Integrating posture control
in assistive robotic devices to support standing bal-
ance. In Carrozza M., Micera S., P. J., editor, Wearable
Robotics: Challenges and Trends. WeRob 2018., vol-
ume 22 of Biosystems & Biorobotics. Springer, Cham.
Mergner, T., Maurer, C., and Peterka, R. J. (2003). A multi-
sensory posture control model of human upright stance.
Progress in Brain Research, 142:189–201.
Mergner, T., Schweigart, G., and Fennell, L. (2009). Vestibu-
lar humanoid postural control. Journal of Physiology -
Paris, 103:178–194.
Miriyala, S. S. and Mitra, K. (2020). Deep learning based
system identification of industrial integrated grinding
circuits. Powder Technology, 360:921–936.
Ott, C., Henze, B., Hettich, G., Seyde, T. N., Roa, M. A.,
Lippi, V., and Mergner, T. (2016). Good posture, good
balance: Comparison of bioinspired and model-based
approaches for posture control of humanoid robotsg.
IEEE Robotics & Automation Magazine, 23(1):22–33.
Pasma, J., Engelhart, D., Schouten, A., Van der Kooij, H.,
Maier, A., and Meskers, C. (2014). Impaired standing
balance: the clinical need for closing the loop. Neuro-
science, 267:157–165.
Peterka, R. (2002). Sensorimotor integration in human pos-
tural control. Journal of neurophysiology, 88(3):1097–
1118.
Sforza, F. and Lippi, V. (2013). Support vector machine clas-
sification on a biased training set: Multi-jet background
rejection at hadron colliders. Nuclear Instruments and
Methods in Physics Research Section A: Accelerators,
Spectrometers, Detectors and Associated Equipment,
722:11–19.
Sforza, F., Lippi, V., and Chiarelli, G. (2011). Rejection
of multi-jet background in pp e
ν
+ jj channel through
a svm classifier. In Journal of Physics: Conference
Series, volume 331, pages 32–45. IOP Publishing.
Torricelli, D., Mizanoor, R. S., Lippi, V., Weckx, M., Mathi-
jssen, G., Vanderborght, B., Mergner, T., Lefeber, D.,
and Pons, J. L. (2020). Benchmarking human likeness
of bipedal robot locomotion: State of the art and fu-
ture trends. In Metrics of Sensory Motor Coordination
and Integration in Robots and Animals, pages 147–166.
Springer.
van Asseldonk, E. H., Buurke, J. H., Bloem, B. R., Ren-
zenbrink, G. J., Nene, A. V., van der Helm, F. C., and
van der Kooij, H. (2006). Disentangling the contri-
bution of the paretic and non-paretic ankle to balance
control in stroke patients. Experimental neurology,
201(2):441–451.
van der Kooij, H., van Asseldonk, E., and van der Helm, F. C.
(2005). Comparison of different methods to identify
and quantify balance control. Journal of neuroscience
methods, 145(1-2):175–203.
van der Kooij, H., van Asseldonk, E. H. F., Geelen, J., van
Vugt, J. P. P., and Bloem, B. R. (2007). Detecting
asymmetries in balance control with system identifica-
tion: first experimental results from parkinson patients.
Journal of Neural Transmission, 114(10):1333.
Zebenay, M., Lippi, V., and Mergener, T. (2015). Human-
like humanoid robot posture control. In 2015 12th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO), volume 2, pages
304–309. INSTICC, SciTePress.
Deep Learning based Model Identification System Exploits the Modular Structure of a Bio-inspired Posture Control Model for Humans and
Humanoids
547
