Improvements to Increase the Efﬁciency of the AlphaZero Algorithm:

A Case Study in the Game ’Connect 4’

Colin Clausen

, Simon Reichhuber

, Ingo Thomsen

and Sven Tomforde

Intelligent Systems, Christian-Albrechts-Universit

at zu Kiel, 24118 Kiel, Germany

PCT Digital GmbH, Fleeth

orn 7, 24103 Kiel, Germany

Keywords:

AlphaZero, Connect 4, Evolutionary Process, Tree Search, Network Features.

Abstract:

AlphaZero is a recent approach to self-teaching gameplay without the need for human expertise. It suffers

from the massive computation and hardware requirements, which are responsible for the reduced applicability

of the approach. This paper focuses on possible improvements with the goal to reduce the required compu-

tation resources. We propose and investigate three modiﬁcations: We model the self-learning phase as an

evolutionary process, study the game process as a tree and use network-internal features as auxiliary targets.

Then behaviour and performance of these modiﬁcations are evaluated in the game Connect 4 as a test scenario.

1 INTRODUCTION

Computer games have ever been a fantastic play-

ground for research on artiﬁcial intelligence (AI).

With the increasing availability of computing re-

sources and platforms of the last decade, ground-

breaking developments in human-like and even super-

human game playing behaviour have been wit-

nessed. Especially the presentation of AlphaGo (Sil-

ver, Huang et al., 2016) that defeated a world-class

human go player in 2016 (Gibney, 2016) is a mile-

stone towards fully sophisticated games AI.

Subsequently to the breakthrough caused by Al-

phaGo, the AlphaZero algorithm (Silver, Hubert et

al., 2018) signiﬁcantly simpliﬁed the initial AlphaGo

approach. The basic idea was to allow for a learning

concept that starts with a random network and obvi-

ates human expert input of any kind. Despite the suc-

cess of these concepts, we face a massive challenge

that inhibits ubiquitous utilisation of the approach:

The dramatic requirements of computation power.

The goal of this paper is to investigate possibilities

for improvements of AlphaZero’s efﬁciency, expect-

ing a reduction of hardware and computational cost,

while simultaneously maintaining the generic concept

and the success of AlphaZero. We therefore propose

and investigate three different extensions, which re-

sult in a changed behaviour of the basic AlphaZero

algorithm: We model the self-learning phase as an

evolutionary process, study the game process as a tree

and use network-internal features as auxiliary targets.

The remainder of this article is organised as fol-

lows: Section 2 describes the background of this pa-

per by brieﬂy summarising the state-of-the-art. Sec-

tion 3 develops a baseline for AlphaZero for the game

Connect 4. Afterwards, Section 4 provides the key

contributions of this paper by proposing three dif-

ferent reﬁnements and extensions to the current Alp-

haZero approach and analyses the behaviour. Finally,

Section 5 concludes the article.

2 BACKGROUND

2.1 Monte Carlo Tree Search

With Monte Carlo Tree Search (MCTS) (Br

ugmann,

1993) a large (game) tree is randomly searched to

assess the expected reward for moves starting at the

tree root. The variant UTC (’UCB applied to trees’)

(Kocsis and Szepesv

ari, 2006) is used in AlphaZero:

the Upper Conﬁdence Bounds (UCB) algorithm of

the multi-armed bandit problem (Auer et al., 2002)

is used to choose the next move in tree node: Possible

episodes (root to the end of game) are sampled and

the results are propagated back. When playing only

to a ﬁxed tree depth, the positions can be evaluated by

averaging over results from a number of random play-

throughs to the end. Weighting exploitation against

exploration is applied for episode sampling, which in-

crementally improves overall move evaluation.

Clausen, C., Reichhuber, S., Thomsen, I. and Tomforde, S.

Improvements to Increase the Efﬁciency of the AlphaZero Algorithm: A Case Study in the Game ’Connect 4’.

DOI: 10.5220/0010245908030811

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 803-811

ISBN: 978-989-758-484-8

803

2.2 From AlphaGo to AlphaZero

AlphaGo used a complex system initialisation with

example games, random rollouts during tree searches

and two networks (prediction of position values and

of promising moves). AlphaGo Zero (Silver, Schrit-

twieser et al., 2017) is much simpler by using only

single network without rollouts: The network evalua-

tion for a position is directly used. AlphaZero is ap-

plied to games other than Go and offers further sim-

pliﬁcation: Instead of comparing the currently trained

network with the previously known best player us-

ing evaluation games, AlphaZero always bases new

games on the current network. The main advantage

of the ’Zero’ versions is the independence from prior

human knowledge (apart from rules). This promotes

strategies without human bias and even enables re-

search on games without human expertise.

2.3 The AlphaZero Algorithm

AlphaZero combines the UTC variant with a deep

neural network to bias tree search and evaluate unﬁn-

ished games. The network is trained to predict ﬁnal

results of the MCTS and self-play games by MCTS

against itself. This tends to be slower at ﬁrst, but the

network is trained to make ”good decisions”. This is

subsequently faster due to using just a single forward

pass. The network creates two outputs from the en-

coded game situation: a policy describing move like-

lihoods and the expected value of the situation. Un-

like plain UTC, AlphaZero does not randomly select

episodes, which besides are not played out until a ter-

minal game state is reached. To steer the MCTS to-

wards moves estimated to be promising by the net-

work, the following statistics are gathered for each

node:

N(s, a) times action a was chosen in state s

W (s, a) total action value

Q(s, a) average action value, equal to

W (s,a)

N(s,a)

P(s, a) probability to play action a in state s

When the analysis of an episode is propagated up-

wards the tree, these statistics are updated. They are

used in the next tree search until it reaches again an

unknown node. When a ﬁxed number of nodes are

created, the output is a distribution of node visits: A

high count implies a worthwhile and thoroughly eval-

uated move. The action a is selected as follows:

argmax

(Q(s, a) +U(s, a)) (1)

U(s, a) = C

puct

P(s, a)

N(s)

(1 + N(s, a))

(2)

Equation 2 is weighted against exploitation and is

based upon plain UTC, but biased by the network pol-

icy. C

puct

is a game-dependent constant, typically in

[0.5, 5]. Dirichlet noise is added for further explo-

ration in self-play games, pushing the MCTS cau-

tiously to evaluate some random moves more than

others. Games are played out using this tree search:

The policy, resulting game states and outcome are

stored to train the network to predict the ﬁnal result

and policy. A policy, based upon network and MCTS,

is expected to outperform one produced by only the

network.

A drawback is the massive computational cost. In

practice for playing a single move, the search tree has

to grow to at least hundreds of nodes, each with a cor-

relating forward pass through the network.

2.4 Extensions to AlphaZero

Many proposed enhancements focus on reducing the

computational cost and several of those listed below

originate from the Leela Chess Zero project (LCZero,

2020), a distributed effort to implement AlphaZero

for Chess. Some approaches do not rely on domain-

speciﬁc game knowledge, and those denoted by *

were implemented to form a strong AlphaZero base-

line for comparison (see Section 3.3 and 3.4).

Network and Training Modiﬁcations. Improving

the neural network design to speed up training, while

retaining the original tower of 20 or 40 residual net-

work blocks with 256 convolutional ﬁlters:

1. * The network blocks themselves can be enhanced

with Squeeze-and-Excitation elements (Hu et al.,

2018). A similar approach is used by (Wu, 2020).

2. * Cyclic learning rates as in (Smith, 2017) can be

used to improve the network ﬁtting to the data.

3. Increasing the number of convolutional ﬁlters in

the policy head and values from 3 to 32, speeding

up the training (Young, 2019).

Modiﬁcation of the Tree Search. Different spend-

ing of the available time for analysing game positions.

1. With ’Playout Caps’ (Wu, 2020) the number of

MCTS playouts is randomly and drastically re-

duced for most moves. An acceleration of the

training by 27% is stated.

2. The handling of the search tree can be improved.

One example is the propagation of terminal moves

to simplify the search (Videodr0me, 2019), mod-

erately improving the playing strength.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

804

3. (Lan et al., 2019) use two networks instead of one.

Unequal sizes (10 resp. 5 residual blocks with 128

resp. 64 convolutional ﬁlters), allow the smaller,

faster network to do more search steps in most po-

sitions. This at least doubles the training speed.

4. With constant computational effort, the playing

strength can be increased (Tilps, 2019a) by em-

ploying the Kullback-Leibler divergence of the

policy to identify and focus on complex positions.

Learning Target Modiﬁcations. Reducing overﬁt-

ting and regulating the network training.

1. * (Gao et al., 2020) add a third output head to pre-

dict the win probability for every move. This es-

timate might be of worse quality. Small improve-

ments are claimed.

2. * (Wu, 2020) predict the opponent’s reply to reg-

ularise training – showing modest improvement.

3. * They also argue to add some domain-speciﬁc

targets to regularise the learning process, which

shows major improvements.

4. Finally, they guarantee selected nodes a mini-

mum number of further ”Forced Playouts” to pro-

mote exploration. ”Policy Target Pruning” then

removes those from the ﬁnal policy distribution.

The training speed is shown to increase by 20%.

5. The LCZero project modiﬁes the value target

(Tilps, 2019b) to explicitly predict drawing prob-

abilities: The network can discern between very

likely and unlikely positions.

6. (Young, 2019) proposes to combine the game re-

sults as a learning target with the average value

of the MCTS node, reducing the inﬂuence of few

bad moves at the end of the game.

Training Data Enhancements. Improved handling

of the numerous training examples by (Young, 2019).

1. * In some games, like Connect 4, positions can be

duplicated. Averaging the respective targets and

combining them into a single example is useful.

2. * A sudden increase of playing strength occurs

when removing the ﬁrst training examples, which

were very likely generated by a random network.

Modifying the training windows ﬁxes this.

3 A BASELINE: AlphaZero FOR

CONNECT 4

Connect 4 is a board game where two players, in turn,

let their discs fall straight down to the lowest avail-

able space of a column in a vertical grid, typically of

size 6 × 7. The goal is to create a horizontal, verti-

cal or diagonal line of four of one’s own discs. It is a

game with known a solution for which strong solvers

exists (Prasad, 2019). Therefore, we can evaluate the

strength of AlphaZero by comparing the accuracy on

a set of solved test positions. The network can also be

trained on solved games for maximum performance.

The state space was a 6 × 7 matrix with 4 possible

cell values: 3 (unoccupied), (player) 2 or 1. Also, 0 is

used for padding during convolution. The base imple-

mentation of AlphaZero uses a different network tar-

get for game results, encoding a dedicated value for a

draw. Therefore, the 3 possible outcomes are a win of

either player or a draw. This differs from the output

between zero and one of the original implementation.

There might be a slight change in learning efﬁciency

caused by this change. However, due to the technical

requirements in the context of the abstraction-driven

framework (to keep the generic capability and not re-

focus it to Connect 4), we changed the implementa-

tion to this additional state.

We started with a basic version of AlphaZero and

adapted it for Connect 4. With a given training set

of played games for a certain state s representing the

state of the game, a neural network directly learns

the move probabilities m

pred

∈ [0, 1]

#moves

. This states

how likely one of the seven possible moves leads to

a win. Furthermore, it learns the outcome of the

game’s test set o

test

. Since the outcome also includes

draws, we extended the test set outcome to a tuple

test

= (o

test

win

, o

test

draw

, o

test

loose

) and the predicted outcome

analogously to o

pred

= (o

pred

win

, o

pred

draw

, o

pred

loose

). The vec-

tors of the optimal move were ”one-hot-encoded”:

Only the optimal move and the true outcome are set to

1. With these the the network f

(s) = (m

pred

, o

pred

)

aims to guarantee (m

pred

, o

pred

) ≈ (m

test

, o

test

) w.r.t.

to an output weighting and regularised loss function

as in (Silver, Schrittwieser et al., 2017):



pred

, m

pred

), (o

test

, m

test

)



− c

out put

∗

∑

i=1

test

[i] ∗ log (o

pred

[i])

−

∑

j=1

test

[ j] ∗ log(m

pred

[ j]) + c

reg

∗

(3)

The weights were c

out put

= 0.01 and c

reg

= 0.0001

3.1 Experimental Setup

The main goal of this paper is to identify ways to

reduce the substantial costs of training using Alp-

haZero. The majority of GPU capacity is spent on

Improvements to Increase the Efﬁciency of the AlphaZero Algorithm: A Case Study in the Game ’Connect 4’

805

self-playing games to create training data for the neu-

ral network. This fact was used to simplify the train-

ing cost measurement by ignoring the costs of net-

work training. Instead, only the cost of self-playing

workers was measured. In all experiments, neural net-

work training were done on a single GPU and newly

produced networks were evaluated on another single

GPU. Self-play workers are run on a P2P cloud ser-

vice2 using up to 20 GPUs of various types to com-

plete full training runs for Connect 4 in 2 to 6 hours,

depending on the number of workers. For each exper-

iment a benchmark was run on a reference machine

using the produced networks, measuring how much

time is needed on average to play a single move. This

value was then used to estimate the cost of the ac-

tual number of moves played by the self-play work-

ers during the experiments. The reference machine

uses a single Nvidia RTX 2070S, which was saturated

(100% load) by the benchmark. Thus, all self-play

cost of experiments is stated as estimated time spent

on that machine, limited by its GPU capacity.

3.2 Supervised Training

The generation of the testing set for the learning pro-

cess is an important step that determines how compa-

rable results are to previous work. An important deci-

sion is what should be considered a correct move in a

given situation. In Connect 4, a player has many posi-

tions where she has multiple ways to force a win, but

some lead to a longer game before the win is forced.

To evaluate this (Young, 2019) deﬁnes two test sets:

• The strong test set only considers a move correct

if it yields the fastest win resp. the slowest loss.

• The weak test set only cares about the move pro-

ducing the same result as the best move, no matter

how much longer the win will take or how much

faster the loss will occur.

For training a dataset of 1 million game positions

was generated by playing 50% random moves and

50% perfect moves determined by a solver (Pons,

2020). This is substantially harder than a dataset cre-

ated using 90% perfect and only 10% random moves,

which appears to be mainly a result of the distribu-

tion of game length as fewer random moves produce

a dataset with more positions late in the game, while

more random moves cause more positions to be in the

early game. No duplicates, without trivial positions

and only the strongest possible moves were accepted

as correct. Two versions of the dataset were gener-

ated. In version 1, all positions of played games are

used for training, while in version 2, only one single

position is randomly picked from each played game.

This substantially increased the number of distinct

games played. For both dataset versions, 800 000 ex-

amples were used as training data and 100 000 exam-

ples as validation data. The remaining 100 000 exam-

ples were utilised as test data. We achieved the high-

est accuracy of correctly assigned outcomes by using

a network with 20 ResNet blocks (see Table 1).

Table 1: Results of supervised training and accuracy com-

pared to a Connect 4 solver. The column named N lists the

number of used ResNet blocks, Pr

move, win

are the move and

win probabilities of training set version 1 v

resp. 2 v

N # params Pr

move

win

move

win

5 1.57e6 91.63% 77.47% 92.44% 79.23%

10 3.05e6 92.37% 77.87% 93.00% 79.67%

20 6.01e6 92.68% 78.23% 93.49% 79.93%

3.3 Extended AlphaZero

We analysed known AlphaZero extensions (see Sec-

tion 2.4) in addition to Connect 4 speciﬁc modiﬁca-

tions from (Prasad, 2019). In detail, successful exten-

sions are presented in the remainder of this section.

Remove Duplicate Positions. Merging duplicate

positions is proposed by (Prasad, 2019). We imple-

mented this by using the training worker. Only new

positions are added to the pool of training examples;

previously known positions instead update the target

value for that position. A z

duplicate

produced by a self-

play worker is sent to the training worker, which up-

dates the new target values z

new

with the duplicate’s

old target values z

old

, weighted by w

duplicate

new

= z

old

∗ (1 − w

duplicate

) + z

duplicate

∗ w

duplicate

(4)

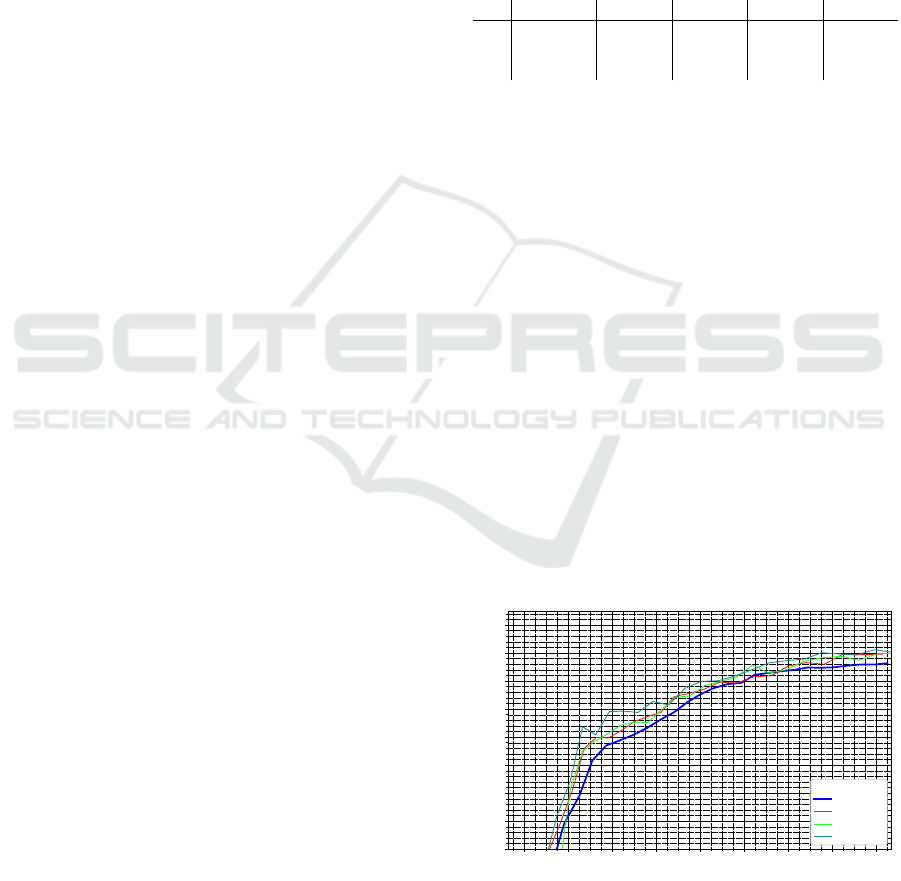
Figure 1 shows tests for some w

duplicate

= 0.2, 0.5, 0.8:

2 4 6 8 10 12 14 16 18

Estim at ed cost in h ours

MCTS accuracy %

Dedu p licat ion with different weight fact ors

Accuracy

base

weight 0.2

weight 0.5

weight 0.8

Figure 1: Comparison of different choices for w

duplicate

. For

all further experiments 0.8 was chosen.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

806

Cyclic Learning Rate. To speed up general neu-

ral network training, (Smith, 2017) proposed cycli-

cal learning rates. (Prasad, 2019) suggests some im-

provements in the context AlphaZero. Based on these

claims, cyclic learning rates and cyclic momentum

were used for AlphaZero as a potential addition to the

extended baseline. The cycles are spread over a single

training iteration. The values are updated by previous

runs to determine the maximum and minimum useful

learning rates. Their curve can be seen in Figure 2.

0.0 0.2 0.4 0.6 0.8 1.0

0.000

0.025

0.050

0.075

0.100

0.125

0.150

0.175

0.200

Learning rat e

0.86

0.88

0.90

0.92

0.94

Mom entum

Cyclic learnin g rat e and m om ent um

Mom entum

Figure 2: Change of learning rate and momentum over the

training of a new network when using cyclic learning rates.

Additionally, the learning rate is annealed down with

a multiplicative factor that drops linearly with the

number of network iterations. It starts at 1 in iteration

1 and reaches 0.4 in iteration 20. Beyond that, the

factor stays at 0.4: At iteration 20 and later, the maxi-

mum learning rate is 0.08. This annealing accommo-

dates the fact that in later parts of training the learning

rate should be smaller in general. This improvement

accelerated the learning as seen in Figure 3.

2 4 6 8 10 1 2 14 1 6 18

Estim at ed cost in hou rs

MCTS accuracy %

Cyclic learn ing r ate

Accuracy

base

cy clic_lr

Figure 3: Comparison of the usage of cyclic learning rates

and momentum with the baseline.

Improved Training Window. Similar to (Prasad,

2019) a slow training window starts with a size of

500000 examples, growing between iteration 5 and 12

up to the maximum size of 2 million examples. This

causes early examples to be removed by iteration 3.

This is useful as those are very close to random play.

The slow window was added to the extended base-

line, since it seemed to have no harmful effect (see

Figure 4) and follows a sound idea. As the extended

baseline uses a training window without duplicate po-

sitions, the parameters were modiﬁed to grow from it-

eration 5 to 15, since the number of new examples per

iteration is lower.

2 4 6 8 10 12 14 16 18

Estim at ed cost in h ours

MCTS accuracy %

Slow tr aining window

Accuracy

base

slow window

Figure 4: Comparison of the usage of a slow training win-

dow with the baseline.

Predicting the Reply of the Opponent. (Wu,

2020) also, show that predicting an opponent’s reply

to a position produces a modest but clear beneﬁt, by

adding a term to the loss function to regularise train-

ing:

−w

opp

∑

m∈moves

opp

(m)log (

opp

(m)) (5)

opp

is the policy target for the turn after the current

turn,

opp

is the network prediction of π

opp

and w

opp

is a weight for the loss term. Based on preliminary

experiments, 0.35 was used. Figure 5 shows the re-

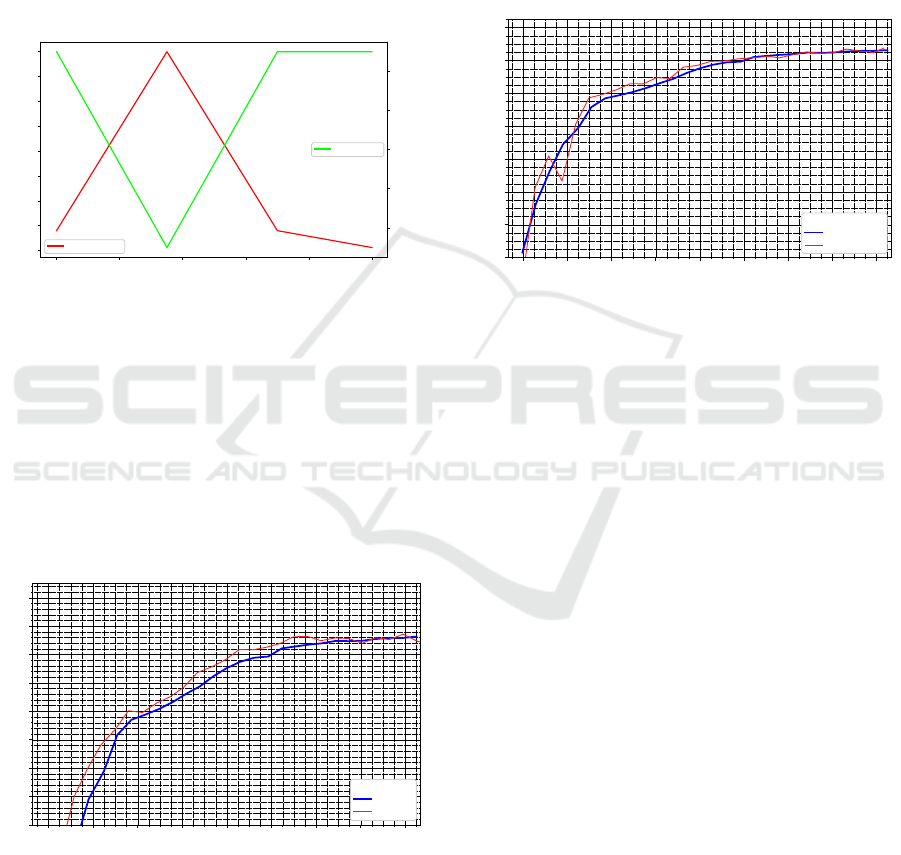
sults of testing this on Connect 4. There appears to be

a small advantage for some parts of the run, which is

why this was made part of the extended baseline.

Improved Network Structure. The Leela Chess

Zero project proposes using squeeze-and-excitation

elements in the network. This is a general devel-

opment of deep neural networks (Hu et al., 2018)

and shall improve the accuracy of correctly predicted

game outcomes compared to the baseline. A result

of a test run can be seen in Figure 6. There might

be some gains early during the training and possibly

some small losses later on.

Since this did not seem to reduce performance

much – and intuitively should help, especially given

more distinct training data from de-duplication – the

Improvements to Increase the Efﬁciency of the AlphaZero Algorithm: A Case Study in the Game ’Connect 4’

807

2 4 6 8 10 12 14 16 18

MCTS accuracy %

Predict the op ponent's reply

Accuracy

base

Playout Caps

Figure 5: Results of implementing the predictions of the

opponent’s reply.

2 4 6 8 10 1 2 14 1 6 18

Estim at ed cost in hours

MCTS accuracy %

Squ eeze and Excite ResNet

Accuracy

base

Squ eeze and Excite

Figure 6: Results of predictions of squeeze-and-excitation.

squeeze-and-excite elements were added to the ex-

tended baseline. The network structures can be seen

in Table 2.

3.4 Establishing the Baselines

Various baselines needed to be deﬁned and imple-

mented for the comparison. Using supervised train-

ing for the networks allowed for the exploration of

the maximum possible performance: A plain Alp-

haZero baseline showed how the original algorithm

performed and a baseline of AlphaZero, extended

with a set of previously known improvements, shows

the progress compared to the original algorithm.

As our goal is to ﬁnd AlphaZero extensions low-

ering the training costs of such an algorithm, we pro-

vided a baseline measurement on how much time is

needed on average to play a single move. This value

was then used to estimate the cost of the actual num-

ber of moves played by the self-play workers during

the experiments (see Figure 7).

Table 2: The ﬁnal architecture, including the modiﬁcations

of (Silver, Hubert et al., 2018). Squeeze-and-excite add

pooling to the residual blocks, which averages every fea-

ture map to a single scalar value. These are then processed

by fully connected layers without bias, activated by ReLU

and Sigmoid. x × y × z describes a convolution with ker-

nel size x × y and z ﬁlters. FC : x denotes a fully connected

layer with x neurons. Addition describes the addition with

the input of the residual block forming the residual structure

of the block. Both the win prediction and the move policy

output are connected to the output of the last residual block.

Description base extended

Initial block





3 × 3 × 64

BatchNorm

ReLU





—’—

Adaptor convolution



1 × 1 × 128



—’—

Residual block,

repeated N times







3 × 3 × 128

BatchNorm

ReLU

3 × 3 × 128

BatchNorm

Addition

ReLU













3 × 3 × 128

BatchNorm

ReLU

3 × 3 × 128

BatchNorm

AVGPooling

FCnb : 8

ReLU

FCnb : 128

Sgmoid

Addition

ReLU







Move policy output





3 × 3 × 32

FC : 7

LogSoftMax





—”—

Win prediction

output





3 × 3 × 32

FC : 3

LogSoftMax





—”—

5 10 15 20 25

MCTS accuracy %

Baselines, hard d ataset

Accuracy

ex t ended

base

Figure 7: Comparison of the baseline and the extended

baseline. Mean was only calculated until either run stops

showing improvements.

4 THREE EXTENSIONS FOR

AlphaZero

4.1 Playing Games as Trees

The ﬁrst extension focuses on how AlphaZero plays

games and implements a distributed approach: In-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

808

stead of many machines playing independent games,

only one plays all the games and requests from a ser-

vice an MCTS evaluation, which is distributed across

multiple machines instead. This service can easily ﬁl-

ter out duplicate evaluations, increasing the efﬁciency

compared to the extended baseline (see Figure 8).

Figure 8: The MCTS evaluation service is more efﬁcient

compared to the AlphaZero baseline.

This ﬁltering allows for further tuning: For a lost

game the position can be reset, tweaking the search

for alternatives: In case of a bad path (due to losing),

we want to identify more promising strategies from

here. However, the experiments showed that this did

not result in signiﬁcant improvements.

With a focus on the tree size, we grew one large

MCTS tree and used its nodes as learning positions

– again to explore more alternative paths for better

coverage. However, the results showed no signiﬁcant

improvement: MCTS seems to gets stuck on certain

typical games and stops exploring. It nevertheless ex-

plores quite well during the early training phase (see

Figure 9). More precisely, using MCTS in this way

causes a quick spike in game diversity. It then quickly

drops as it settles into a certain style of play, from

which it never shifts away again. Seemingly, a short

boost is possible but long-term success is not visible.

Section 5 will outline how to combine these two steps

in future work.

4.2 Network-internal Features as

Auxiliary Targets

The second approach uses network-internal features

as auxiliary targets. Generally, domain-speciﬁc fea-

tures can be beneﬁcial but are not easy to obtain with-

out human design. So, we tried to automate this and

applied deep neural networks, which are known to

learn good features in other tasks (e.g. image recog-

nition). We performed a full AlphaZero training run

Figure 9: Replacing self-play with one large MCTS which

tends to get stuck on a few game paths and stops exploring.

This reduces the diversity of encountered game positions

and even massively increasing C

puct

does not prevent this.

with a tiny network on a single machine and used

its internal features to regulate the training targets.

For additional beneﬁt, we analysed them using two

features from the future: The playout of full games

and applying the small network to all the states in the

game, with which the features for each position can be

found. A larger network can be trained for a limited

prediction of the smaller network’s feature output.

The small network uses only a single ﬁlter in the last

convolutional layer, that has two distinct output-heads

(of the 6 × 7 network ﬁelds): Policy and game output

prediction with 42 features each. These features, that

correspond to the future (single player) moves 2 and

4, are then to regulate the bigger network: A squared

error is added to the training loss for calculating the

mean squared error between auxiliary feature and an

internal layer of the big network, to which no addi-

tional parameters are added – only the internal layer

from which the features in the small network were

taken is regularised to get the same features in the

bigger network. For evaluation, we performed a set

of supervised runs and identiﬁed the most promising

candidates – which turned out to provide a very small

0.2% absolute improvement in test accuracy, which

outside the typical run-to-run variance. Within the

full AlphaZero setting the improvements could not be

generalised: The extended baseline mostly remained

better than the novel variant as shown in Figure 10.

Since the novel approach was surprisingly inef-

fective we examined more closely: The 2 hours train-

ing time for the small network, to obtain the features,

was rather expensive and made a huge difference. As

this can explain the effect, we tried to ﬁx it by growing

the network during the run (see Figure 11). However,

the effect remains. Additionally, we can observe that

using the small network to regularise the large one

causes consistent issues later in the training, reducing

the ﬁnal accuracy. This seems to be the root of the

limited applicability of the approach. Again, future

Improvements to Increase the Efﬁciency of the AlphaZero Algorithm: A Case Study in the Game ’Connect 4’

809

Figure 10: Using auxiliary features from a smaller network.

Figure 11: Growing the network as the run progresses in-

creases efﬁciency, but the steps up to a bigger network cause

a temporary drop in accuracy, especially towards the end.

work will focus on ways to tackle these inconsisten-

cies to harvest the potential beneﬁts.

4.3 Self-playing Phase as Evolutionary

Process

The third extension focuses on the self-playing phase

of AlphaZero: Using played games to evaluate differ-

ent hyperparameter sets on the ﬂy. This re-utilisation

comes without any extra computational costs. There-

fore, we modelled the hyperparameter sets as play-

ers, which play in a league with Elo rating: The most

promising candidates (’best players’) are evolved us-

ing Gaussian mutation. We use the MCTS-related hy-

perparameters as a basis for the investigation as they

can be changed easily for every game played.

In future work, we will further investigate which

other hyperparameters can be handled and show

promising results. Here, we investigated how to con-

trol the reasoning period of the algorithm using a

threshold on the Kullback-Leibler divergence on the

development of the policy found by MCTS with the

initial results outlined in Figure 12, although no sig-

niﬁcant improvements were found.

Figure 12: Initial results of evolving hyperparameters.

Consequently, we analysed if the evolution itself

works. To verify the implementation of the evolu-

tion, we added an ’artiﬁcial’ additional hyperparam-

eter with a known value. This artiﬁcial parameter

was perfectly optimised, meaning that the evolution

itself works. Issues occurred with optimising towards

winning games since this does not correlate with the

metric used to determine the training progress and

the accuracy against the Connect 4 solver. Therefore,

we compared different hyperparameter sets found in

1000 matches: The hyperparameters found by the

evolution won more games, but in turn, played worse

according to the Connect 4 solver.

Motivated by this observation, we investigated us-

ing novelty search as an evolution ﬁtness function.

This novelty-driven process identiﬁes marginally

more new game-play than the parameters found by

the original baseline, which was determined with

Bayesian hyperparameter optimisation. From these

outcomes, it can be stated that the original hyperpa-

rameters have already been optimised rather for game

novelty. Figure 13 illustrates the achieved results.

5 CONCLUSIONS

This paper motivated the need for efﬁcient and scal-

able modiﬁcations of the state-of-the-art technique

AlphaZero with the observation of a limited applica-

tion due to the massive hardware demands.

We, therefore, reviewed the most prominent algo-

rithm extensions to develop a baseline for further ex-

periments. Based on this, we presented three differ-

ent concepts for reducing the necessary efforts: We

proposed to model the self-learning phase as an evo-

lutionary process, we studied the game process as a

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

810

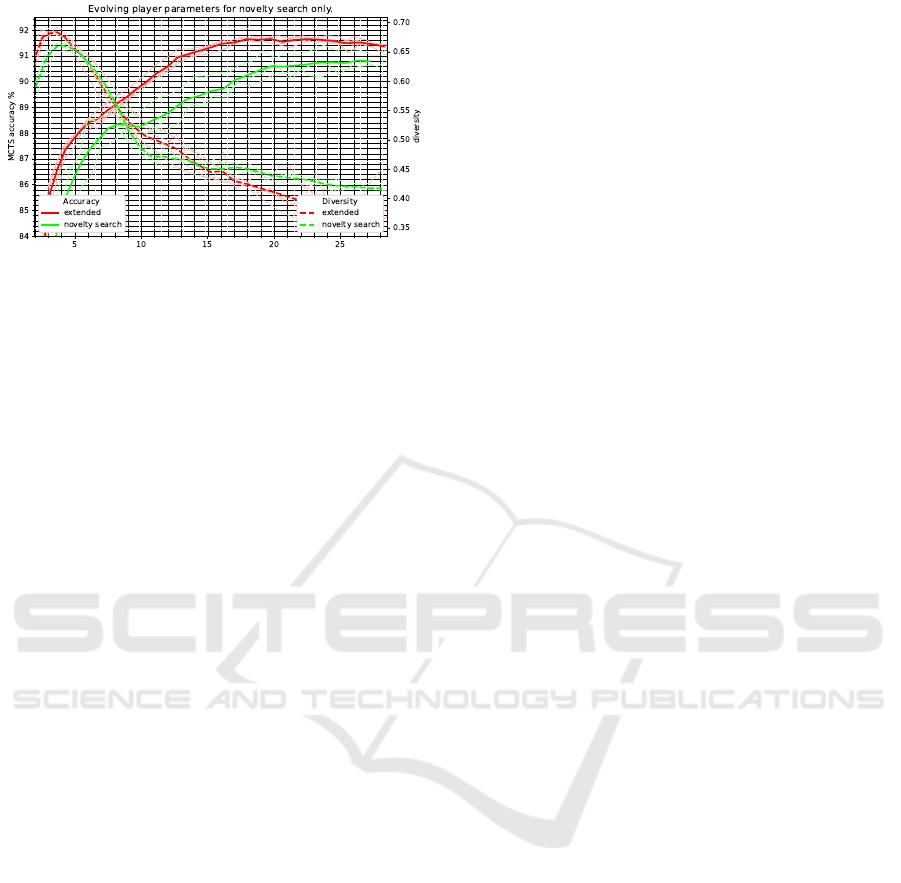
Figure 13: Even pure novelty search only produces more

novel games towards the end of the training. The baseline

parameters were likely to be already implicitly optimised

for game diversity by the initial Bayesian hyperparameter

optimisation aiming to learn efﬁciently.

tree and used network-internal features as auxiliary

targets. We showed that, although the effort could be

decreased slightly, the beneﬁt is mostly only small.

Our future work follows two directions: We want

to further analyse possible improvements of Alp-

haZero, e.g. based on the Connect 4 scenario, and

we want to investigate the applicability to real-world

control problems. For the ﬁrst path, we identiﬁed

an approach of growing the network more system-

atically as a possibly beneﬁcial extension. Alterna-

tively, a more sophisticated ﬁtness function for the

evolutionary self-playing phase could provide a more

suitable trade-off between heterogeneity and conver-

gence. For the second path, we will investigate if such

a technique is applicable to real-world control prob-

lems ( D’Angelo, Gerasimou, Gharemani et al., 2019)

as given by self-learning trafﬁc light controller (Som-

mer et al., 2016) or smart camera networks (Rudolph

et al., 2014).

REFERENCES

D’Angelo, Gerasimou, Gharemani et al. (2019). On learn-

ing in collective self-adaptive systems: state of prac-

tice and a 3D framework. In Proc. of SEAMS@ICSE

2019, pages 13–24.

Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-

time analysis of the multiarmed bandit problem. Ma-

chine learning, 47(2–3):235–256.

ugmann, B. (1993). Monte Carlo Go. www.ideanest.com

/vegos/MonteCarloGo.pdf .

Gao, C., Mueller, M., Hayward, R., Yao, H., and Jui, S.

(2020). Three-Head Neural Network Architecture for

AlphaZero Learning. https://openreview.net/forum?i

d=BJxvH1BtDS.

Gibney, E. (2016). Google AI algorithm masters ancient

game of Go. Nature News, 529(7587):445.

Hu, J., Shen, L., and Sun, G. (2018). Squeeze-and-

excitation networks. In Proc. of IEEE CVPR, pages

7132–7141.

Kocsis, L. and Szepesv

ari, C. (2006). Bandit based Monte-

Carlo planning. In European conference on machine

learning, pages 282–293. Springer.

Lan, L.-C., Li, W., Wei, T.-H., Wu, I., et al. (2019). Multiple

Policy Value Monte Carlo Tree Search. arXiv preprint

arXiv:1905.13521.

LCZero (2020). Leela Chess Zero. http://lczero.org/.

Pons, P. (2020). https://connect4.gamesolver.org and

https://github.com/PascalPons/connect4. accessed:

2020-10-02.

Prasad, A. (2019). Lessons From Implementing AlphaZero.

https://medium.com/oracledevs/lessons-from-imple

menting-alphazero-7e36e9054191. accessed: 2019-

11-29.

Rudolph, S., Edenhofer, S., Tomforde, S., and H

ahner, J.

(2014). Reinforcement Learning for Coverage Opti-

mization Through PTZ Camera Alignment in Highly

Dynamic Environments. In Proc. of ICDSC’14, pages

19:1–19:6.

Silver, Huang et al. (2016). Mastering the game of Go

with deep neural networks and tree search. Nature,

529(7587):484–489.

Silver, Hubert et al. (2018). A general reinforcement

learning algorithm that masters chess, shogi, and Go

through self-play. Science, 362(6419):1140–1144.

Silver, Schrittwieser et al. (2017). Mastering the

game of Go without human knowledge. Nature,

550(7676):354.

Smith, L. N. (2017). Cyclical learning rates for training

neural networks. In 2017 IEEE Winter Conference on

Applications of Computer Vision (WACV), pages 464–

472. IEEE.

Sommer, M., Tomforde, S., and H

ahner, J. (2016). An Or-

ganic Computing Approach to Resilient Trafﬁc Man-

agement. In Autonomic Road Transport Support Sys-

tems, pages 113–130. Springer.

Tilps (2019a). https://github.com/LeelaChessZero/lc0/pull

/721. accessed: 2019-11-29.

Tilps (2019b). https://github.com/LeelaChessZero/lc0/pull

/635. accessed: 2019-11-29.

Videodr0me (2019). https://github.com/LeelaChessZero/lc

0/pull/700. accessed: 2019-11-29.

Wu, D. J. (2020). Accelerating Self-Play Learning in Go.

Young, A. (2019). Lessons From Implementing AlphaZero,

Part 6. https://medium.com/oracledevs/lessons-from

-alpha-zero-part-6-hyperparameter-tuning-b1cfcbe

4ca9a. accessed: 2019-11-29.

APPENDIX

The framework and the experimental platform

for distributed job processing are available at:

https://github.com/ColaColin/MasterThesis.

Improvements to Increase the Efﬁciency of the AlphaZero Algorithm: A Case Study in the Game ’Connect 4’

811