
Few-Shot Class Incremental Learning with Generative Feature Replay
Abhilash Reddy Shankarampeta
1 a
and Koichiro Yamauchi
2 b
1
Department of EEE, Indian Institute of Technology Guwahati, India
2
Department of Informationn Science, Chubu University, Japan
Keywords:
Few-Shot Learning, Incremental Learning, Catastrophic Forgetting, Generative Feature Replay.
Abstract:
The humans can learn novel concepts from only a few examples effortlessly and learn additional tasks without
forgetting previous ones. Making machines to learn incrementally from only a few instances is very challenging
due to catastrophic forgetting between new and previously learned tasks; this can be solved by generative image
replay. However, image generation with only a few examples is a challenging task. In this work, we propose
a feature replay approach instead of image replay for few-shot learning scenarios. A feature extractor with
feature distillation is combined with feature replay at the classifier level to tackle catastrophic forgetting.
1 INTRODUCTION
Convolutional Neural Networks (CNNs) (Krizhevsky
et al., 2012; Chen et al., 2017; He et al., 2016; Liu
et al., 2017; Simonyan and Zisserman, 2014) have
achieved impressive results broad range of Computer
Vision tasks like object recognition (Russakovsky
et al., 2015), image restoration (Tai et al., 2017), pose
estimation (Newell et al., 2016). The availability of
accurately annotated large scale datasets such as Im-
ageNet (Deng et al., 2009), CIFAR 10 (Krizhevsky
et al., 2014), played a significant role in the recent suc-
cess of deep learning. In image recognition tasks set of
categories that the CNN model can recognize is fixed,
to accommodate the new set of categories not seen in
training requires recollecting data which may not be
feasible for large scale cases. Moreover, re-training
these network decreases models performance abruptly
on previous tasks due to the problem of catastrophic
forgetting (McCloskey and Cohen, 1989) and severely
overfit if there only a few training images. These mod-
els assume that the training data is independent and
identically distributed, but it is valid only for fixed
environments with stationary data distributions (tasks
does not change). However, in real-world problems,
this may not be true.
An episodic memory system that stores past data
(Robins, 1995) can be used to diminish catastrophic
forgetting. However, these memory-based approaches
a
https://orcid.org/0000-0001-6711-7789
b
https://orcid.org/0000-0003-1477-0391
have a significant drawback as they require large work-
ing memory to store and replay past inputs. On the
contrary, humans can learn novel classes effortlessly
with only a few examples and also continuously ac-
quire and update information without effecting previ-
ous knowledge. The complementary learning systems
(CLS) theory, illustrates that intelligent agents must
possess dual learning systems, instantiated in mam-
malians in neocortex and hippocampus. Hippocampus
would quickly learn specific experiences using non-
parametric representations of information, and neocor-
tex would more slowly learn generalizable structured
knowledge using a parametric representation. Over
time, the information in the first system is consoli-
dated and transferred to the second through a process
called reply (McClelland et al., 1995). In CLS the-
ory, the fast-learning hippocampal system acts as a
complement to the slow neocortical system to support
continual learning in the neocortex (Kumaran et al.,
2016). These separate interacting memory systems
are the most apparent distinction between humans and
artificial neural networks in continual learning tasks.
Inspired by the biological systems, several ap-
proaches have been proposed to alleviate catastrophic
forgetting (Shin et al., 2017). Generative models are
used for generating images samples of previous tasks
and these synthetic images are replayed (Nguyen et al.,
2017; Wu et al., 2018; Ostapenko et al., 2019; Zhang
et al., 2018). Using generative models to replay images
of previous tasks has various limitations. The com-
plexity of images makes deep generators difficult to
train computationally expensive. For few-shot learning
Shankarampeta, A. and Yamauchi, K.
Few-Shot Class Incremental Learning with Generative Feature Replay.
DOI: 10.5220/0010246602590267
In Proceedings of the 10th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2021), pages 259-267
ISBN: 978-989-758-486-2
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
259

problems, it is even more challenging to train genera-
tive models as the complexity of the image distribution
of a particular task increases and gets narrower. There
are other approaches like Learning without Forgetting
(LwF) (Li and Hoiem, 2017), which is a combination
of distillation networks (Hinton et al., 2015) and fine-
tuning. The copy of the model trained on the previous
task is stored. Before learning the new task old model
distils its predicted probabilities into the new model.
For a new task, nodes to the existing model are added
in the fully connected layers.
In this paper, to mitigate catastrophic forgetting,
we proposed a novel approach for few-shot class incre-
mental learning using generative feature replay. As im-
age generation might be a complicated process when
the number of images is limited, so we adopted to use
feature generation instead of image generation as it is
easier than accurately generating images. Our model
divided into two parts a feature extractor and a classi-
fier. Generative feature replay (in the classifier) with
feature distillation on the feature extractor are com-
bined to overcome forgetting in the network. We con-
duct extensive experiments on the popular CIFAR100
(Krizhevsky et al., 2014), miniImageNet (Deng et al.,
2009) datasets. Experimental results demonstrate the
effectiveness of our proposed approach.
Our main contributions can be summarized as fol-
lows: We design a hybrid model for few-shot class-
incremental learning which combines generative fea-
ture replay at the classifier level and distillation in the
feature extractor.
2 RELATED WORK
2.1 Few-Shot Learning
Few-Shot Learning is the ability of the model to learn
from a limited number of examples. The general idea
is to train a model on classes with enough training sam-
ples and generalize to new classes with few samples
without learning new parameters. A naive approach
to re-train the model on the new data would have a
high risk of over-fitting. In the past years, there is
an accelerated surge of interest in Few-Shot Learning
(Koch et al., 2015; Santoro et al., 2016b; Vinyals et al.,
2016; Snell et al., 2017; Munkhdalai and Yu, 2017;
Ravi and Larochelle, 2017). Among the many algo-
rithms proposed, there were grouped into three main
categories:
2.1.1 Metric based Learning
The core idea of this approach is to learn embedding
vectors of input data explicitly and use them to de-
sign proper kernel functions. This approach is used
in (Koch et al., 2015) formulated a method for per-
forming one-shot image classification with a siamese
neural network. The siamese network is trained as a
verification task to identify input pairs according to the
probability that they belong to the same or different
class. During test time images from the novel classes
are evaluated in a pairwise manner against test images.
Matching Networks (Vinyals et al., 2016) com-
bine both embedding and classification to form an
end-to-end differentiable nearest neighbours classifier.
Matching Networks first embed a high dimensional
sample into a low dimensional space. The output is
defined as a sum of labels of support samples weighted
by attention kernel.
Prototypical Networks (Snell et al., 2017) learn a
metric space to perform classification by computing
distances to prototype representations of each class. A
prototype feature vector is defined as the mean vector
of the embedded support data samples in this class.
2.1.2 Model-based Learning
A model which updates its parameters swiftly with
only a few training steps is explicitly designed for
fast learning with only a few samples. Memory-
Augmented Neural Networks (MANN) (Santoro et al.,
2016a) use external memory storage to facilitate the
learning process of neural networks, including Neural
Turing Machines (Graves et al., 2014) and Memory
Networks (Weston et al., 2015). In (Santoro et al.,
2016b), the authors modified the memory to encode
and capture information on new tasks fast and to ac-
cess quickly. The authors argue that NTM is a perfect
candidate for meta-learning and low-shot prediction,
as it is capable of both long-term storage via slow
updates of its weights, and short-term storage via its
external memory module.
Meta Networks (Munkhdalai and Yu, 2017) uses
fast weights for rapid generalization across tasks. It
employs an embedding network to encodes raw inputs
into feature vectors, a base learner model to complete
the actual learning task, an LSTM network for learn-
ing fast weights of the embedding network and a neu-
ral network for learning the fast weights for the base
learner from its loss gradients. The learner’s loss gradi-
ents are used as meta information to populate models
that learn fast weights.
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
260

2.1.3 Optimization-based Learning
Here the key idea is obtaining task-specific parameters
through optimization. There is an inner-loop optimiza-
tion process to optimize for a set of meta parameters
such that optimization procedure for the task-specific
parameters leads to excellent performance.
Methods like (Ravi and Larochelle, 2017) pro-
posed an LSTM meta learner to update the learner’s
parameters using a small support set so that the learner
can adapt to the new task quickly. The key idea of the
LSTM meta-learner is to train an LSTM cell to learn
an update rule for the primary task. Moreover, the
LSTM network also learns the parameter initialization
of the learner model.
MAML (Finn et al., 2017) is a general optimiza-
tion algorithm, compatible with any model that learns
through gradient descent. To achieve optimal fast
learning on a new task, MAML provides a good ini-
tialization of a model’s parameters with only a small
number of gradient steps. For each task from the batch,
the model is trained using a few examples of that task
(k-shot learning) and the feedback from loss function.
The model is improved by considering how the test er-
ror on new data changes w.r.t the parameters. The test
error on the batch of tasks is the training error of the
meta-learning process. Now, the meta-optimization
across tasks is performed via stochastic gradient de-
scent.
2.2 Class-incremental Learning
Class-incremental learning is the ability to learn the
new classes incrementally using a unified model. In In-
cremental learning methods, the performance dramati-
cally degrades due to the missing data of old classes.
To prevent catastrophic forgetting knowledge distill-
ing techniques are used to store old knowledge in the
external memory. In iCARL (Rebuffi et al., 2017),
a small number of training samples from previous
tasks is stored, and the nearest-neighbour classifier
is learned incrementally for the new classes. A de-
crease in performance is observed when the number
of classes increases because the number of samples
stored per class is decreased within a memory budget.
FearNet (Kemker and Kanan, 2017) uses a genera-
tive autoencoder for memory replay inspired from the
brain. To mitigate the unfavourable effects of the im-
balance between the old and new classes is addressed
in (Wu et al., 2019) by learning a linear bias correction
layer whereas in (Hou et al., 2019) bias is addressed
by adopting a cosine normalization to eliminate the
bias in the output layer.
2.3 Multi-task Incremental Learning
we group the multi-task incremental learning into three
classes: architectural, rehearsal, and regularization
methods
2.3.1 Architecture based Methods
To mitigate forgetting, network morphology is modi-
fied by using techniques such as dynamic expansion,
network pruning, and parameter masking. In Pack-
net (Mallya and Lazebnik, 2018), an iterative network
pruning technique is used to create free parameters for
the new task. In HAT (Serra et al., 2018) and Ternary
Feature Masks (Masana et al., 2020) the masks on
activations for old tasks are learned to constrain the
parameters when learning the new task. In (Yoon et al.,
2017) network capacity is dynamically expanded as
it trains on a sequence of tasks. In progressive nets
(Rusu et al., 2016), a new neural network is created for
each task and transfer learning is enabled via lateral
connections to features of previously learned network.
2.3.2 Rehearsal-based Methods
Two main strategies are used in the existing ap-
proaches. One is to store a few exemplars from pre-
vious tasks using an external memory and constrain
their losses while learning the new task (Rebuffi et al.,
2017). A similar approach GEM (Lopez-Paz and Ran-
zato, 2017) the gradients of old tasks are preserved. In
A-GEM (Chaudhry et al., 2018) average gradients of
previous tasks are stored in the memory. Another strat-
egy is to use a generative mechanism to sample data
and use it for replay (Lesort et al., 2019). In (Shin et al.,
2017) a generative model and a task solving model is
used for learning data distributions and learning tasks
respectively, then the training data for previous tasks
is sampled and interleaved with data for the new task.
2.3.3 Regularization-based Methods
These methods focus on regularizing network parame-
ters which show significant changes between the tasks.
In Elastic Weight Consolidation (Kirkpatrick et al.,
2017) slows the learning rate of those weights that
are accountable for old tasks. In Continual Learn-
ing Through Synaptic Intelligence (Zenke et al., 2017),
task-relevant information is accumulated and exploited
to store new memories without forgetting old ones
rapidly. In (He and Jaeger, 2018) gradients are shielded
against degradation of previously learned tasks, i.e.
gradients of parameters are guided during the back-
propagation procedure so that a new task interferes
only minimally with previously learned tasks.
Few-Shot Class Incremental Learning with Generative Feature Replay
261
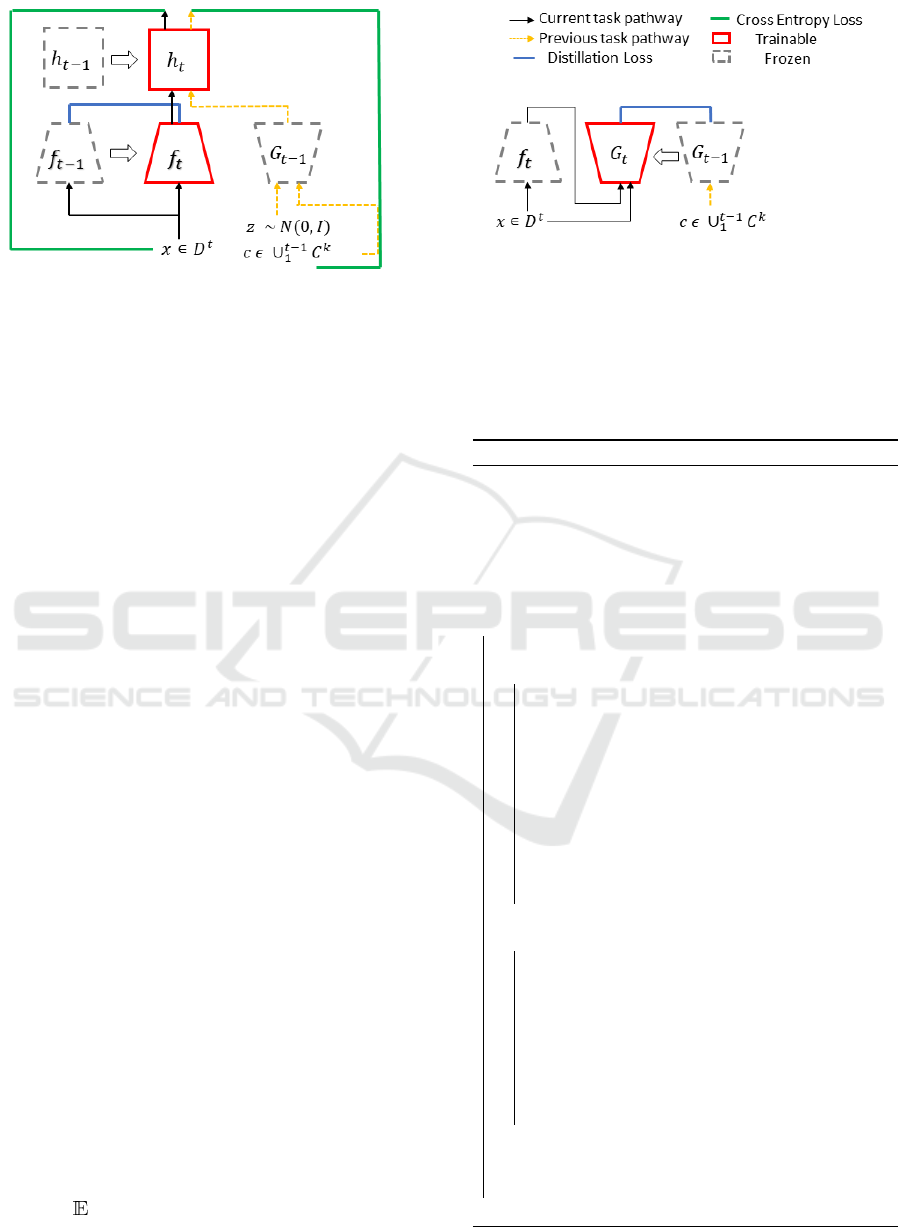
Figure 1: (Left) Learning task
t
without forgetting previous tasks, (right) Training feature generator for task
t
;
C
k
is a set of all
classes for a task k. Here t is the incremental task (T ).
3 METHODOLOGY
In this section, we define the setup of few-shot class
incremental few-shot learning, and then we introduce
our new model with generative feature replay.
We define the few-shot class-incremental-learning
setting as follows. Suppose
T
classification tasks
are learned independently from labelled training sets
D
(1)
, D
(2)
, . . . , D
(T )
where
D
(t)
= {(x
(t)
i
, y
(t)
i
)}
N
(t )
i=1
and
N
(t)
is size of
D
(t)
.
C
(t)
be list of all classes in
D
(t)
for task
T
. We assume that the classes in each task
are disjoint, i.e.
C
(i)
∩ C
( j)
= φ ∀i 6= j
. On datasets
D
(1)
, D
(2)
, . . . , D
(T )
model
Θ
is trained incrementally
with unified classification layer while
D
(t)
is only avail-
able at
t
-th training session. For
D
(t)
,
t > 1
, we denote
the setting with C classes and K training samples per
class as the C-way K-shot Few-Shot Class incremental
Learning. These C classes are randomly sampled from
L
(t)
.
3.1 Feature Extraction and Feature
Distillation
We define a feature extractor
f (., θ
f
)
based on CNNs.
The feature extractor defines the feature space
F ⊆ R
n
.
To prevent forgetting a copy feature extractor from
previous tasks
f
t−1
(., θ
f
)
is stored. At the start we train
f
1
(., θ
f
)
on
D
(1)
and stored. Then we incrementally
train on
D
(2)
, . . . , D
(T )
using feature distillation and
feature replay (section 3.2).
To prevent forgetting in
f
T
(., θ
f
)
, it is distilled
by features of
f
T −1
(., θ
f
)
i.e.
θ
f
T −1
. Where
T
is
the current task. L2 loss is used for calculating the
distillation loss.
L
FD
f
T
=
x∼D
(T )
[k f
T
(x, θ
f
T
) − f
T −1
(x, θ
f
T −1
)k
2
] (1)
As the feature extracted is shared among tasks, we are
not using a separate loss for each head (Li and Hoiem,
2017).
Algorithm 1: Conditional WGAN with MAML.
Data: Sequence D
(1)
, D
(2)
, . . . , D
(T )
where
D
T
= ∪
T
b
t=0
(D
s
t
∪ D
q
t
), D
t
= (x
t
, c
t
)
,
T
b
= no. of small
tasks
Require
: Feature extractor
f
1
, Classifier
h
1
, Genera-
tor G
1
. All trained end-to-end in few-shot setting.
For a incremental task T
for T = 2,. . . ,T do
Initialize G
T
with parameters of G
T −1
for t = 1,. . . ,T
b
do
Get K real samples from D
s
t
Sample
K
g
generated samples
D
s
f
from
G
T
(c, z), c ∈ C
s
t
, z ∼ p
z
Evaluate discriminator and generator loss
l
t
D
T
and l
t
G
T
Evaluate Distillation loss L
RD
G
T
Compute adapted parameters
θ
0
d
, θ
0
g
using
∇
θ
d
l
t
D
T
, ∇
θ
g
(l
t
G
T
+ L
RD
G
T
) respectively
end
for t = 1,. . . ,T
b
do
Get K
0
real samples from D
q
t
Sample
K
0
g
generated samples
D
q
f
from
G
T
(c, z), c ∈ C
q
t
, z ∼ p
z
Compute loss gradients
∇
θ
d
L
t
D
T
,
∇
θ
g
(L
t
G
T
+
L
RD
G
T
)
with adapted parameters
θ
0
d
, θ
0
g
using
(K
0
) real and (K
0
g
) generated samples.
end
Update parameters
θ
g
,
θ
d
with accumulated loss
gradients, and store G
T
, D
T
end
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
262

3.2 Feature Generation
To prevent forgetting in the classifier we propose a
feature generator to model the conditional distribution
of features and sample from it when learning future
tasks. Inspired from MetaGAN (Zhang et al., 2018),
we use the Wasserstein GAN (Arjovsky et al., 2017)
with MAML (Finn et al., 2017) to train a transferable
initialization that is able to quickly adapt to any spe-
cific task with only few gradient steps.
For a few-shot N-way classification task
T
on the
dataset
D
(T )
, we split
D
(T )
into small task batches
t
and each small batch sets consists of support set
D
s
t
and query set
D
q
t
and
D
is the discriminator. Formally
the discriminator
D(θ
d
)
is parameterized by param-
eters
θ
d
. For a specific small task
t
, we update the
parameters using
∇
θ
d
l
t
D
, where is
l
t
D
is loss defined as
l
t
D
T
=
z∼p
z
,c∈C
t
[D
T
(c, G
T
(c, z)] −
x∼D
s
t
[D
T
(c, f
T
(x))]
(2)
Similarly we update generator parameters
θ
0
g
using
∇
θ
g
l
t
G
, where l
t
G
is loss defined as
l
t
G
T
= −
z∼p
z
,c∈C
t
[D
T
(c, G
T
(c, z))] (3)
Here feature vector
u = G
T
(c, z)
,
c
is one of the
class in
D
t
and
G
T
(c, z)
generator conditioned on
c
and takes noise input
z
which is sampled from dis-
tribution
p
z
(usually Gaussian). The transferable ini-
tialization learned quickly with few gradient steps on
the support set
D
s
t
. Then we minimize the expected
loss on query set
D
q
t
with adapted discriminator
D(θ
0
d
)
across task
T
to train the discriminator with initial
parameters
θ
d
. Then we minimize the expected loss
on query set
D
q
t
with adapted generator
G(θ
0
g
)
across
task
t
to train the discriminator with initial parameters
θ
g
. The loss functions on query set is defined as
L
t
D
T
=
z∼p
z
,c∈C
t
[D
T
(c, G
T
(c, z)]−
x∼D
q
t
[D
T
(c, f
T
(x))]
(4)
L
t
G
T
= −
z∼p
z
,c∈C
t
[D
T
(c, G
T
(c, z))] (5)
To make the present generator
G
T
to replay similar
features as
G
T −1
when conditioned on a given previ-
ous class
c
and a given latent vector
z
. A distillation
loss (Wu et al., 2018) is defined as follows:
L
RD
G
T
= Σ
T −1
i=1
Σ
t
j=1
Σ
c∈C
t
z∼p
z
[kG
T
(c, z) − G
T −1
(c, z)k
2
]
(6)
See Algorithm 1
3.3 Few-Shot Class Incremental
Learning
The last layer is the classification layer
h(u, θ
h
)
is an
MLP, with the parameter set
θ
h
is defined to produce
the output vector followed by a softmax. Here
u
is
the feature vector (can be real or generated). During
training we combine the real features extracted from
available real data for the current task with generated
features of the classes from the previous tasks and
fed into classifier to predict the probability p over all
classes. When the feature extractor and classifier are
trained, we then freeze them and then train the feature
generator. For task-k-agnostic predictions we extend
the last linear layer in classifier by increasing g its size
to accommodate the new classes. The classification
layer learns new classes with pseudo-samples gener-
ated to prevent overfitting on new classes and to retain
performance on previous classes.
3.4 Algorithm
Algorithm 2: Few-Shot Class Incremental Learning.
Data: Sequence D
(1)
, D
(2)
, . . . , D
(T )
where
D
T
= ∪
T
b
t=0
(D
s
t
∪ D
q
t
), D
t
= (x
t
, c
t
) = D
s
t
∪ D
q
t
, T
b
= no.
of small tasks
Require : Feature extractor f
1
, Classifier h
1
, Generator
G
1
. All trained end-to-end in few-shot setting.
For a incremental task T
for T = 2,. . . ,T do
for t = 1,. . . ,T
b
do
Get K real samples from D
s
t
⊂ D
t
Sample K
g
generated samples D
s
f
from
G
T −1
(c, z), c ∈ C
T −1
Evaluate classification loss and distillation
loss with real (K) and fake (K
g
) features
generated.
L
t
f
T
,h
, L
FD
f
T
θ
c
= {θ
f
, θ
h
}
Compute adapted parameters θ
0
c
using
∇
θ
c
(L
t
f
T
+ L
FD
f
T
)
end
for t = 1,. . . ,T
b
do
Get K
0
real samples from D
q
t
Evaluate classification and distillation loss
L
t
f
T
,h
, L
FD
f
T
Compute loss gradients ∇
θ
c
(L
f
T
,h
+L
FD
f
T
) with
adapted parameters using real K
0
samples
end
Update parameters θ
c
with accumulated loss gradi-
ents
end
Few-Shot Class Incremental Learning with Generative Feature Replay
263

Table 1: Overall Accuracy is the overall joint accuracy on base + novel classes, each task has 10 novel classes. Weighted
acc(
4
w
↓
) decrease is (weights depending on no.of classes in the task) decrease in accuracy of each task when compared to
previous task. Also, Model does not information on task boundary (miniImageNet Data).
5-way 5-shot Task 1 Task 2 Task 3 Task 4
Overall Accuracy 49.9 45.1 42.3 41.3
Weighted Acc(4
w
↓) decrease -11.7 -6.1 -5.9 -6.9
Table 2: Overall Accuracy Decrease is the overall joint accuracy on base + novel classes. Weighted acc(
4
w
↓
) decrease is
(weights depending on no.of classes in the task) decrease in accuracy of each task when compared to previous task. Also,
Model does not information on task boundary (miniImageNet Data).
5-way 1-shot Task 1 Task 2 Task 3 Task 4
Overall accuracy decrease (4
o
↓) -2.5 -5.1 -1.9 -1.8
Weighted acc decrease (4
w
↓) -8.2 -7.1 -6.3 -2.6
4 EXPERIMENTS
We conduct comprehensive experiments on two
image classification datasets miniImageNet (Vinyals
et al., 2016), CIFAR-100 (Krizhevsky et al., 2014).
MiniImageNet.
dataset is the 100-class subset
of the ImageNet (Deng et al., 2009) dataset which has
1000 classes. Each class contains 480 training images
and 120 test images (we chose 80%-20% split). The
images are in RGB format of the size
84 × 84
. This
dataset is popular in few-shot learning (Vinyals et al.,
2016; Finn et al., 2017)
CIFAR-100.
dataset contains 60,000 RGB images of
100 classes, where each class has 480 training images
and 120 test images (we chose 80%-20% split). Each
image has the size
32 × 32
. This dataset is popular in
class incremental learning (Castro et al., 2018; Rebuffi
et al., 2017)
For CIFAR100 and miniImageNet datasets, we
choose 60 and 40 classes as the base and new classes,
respectively, and adopt the 5-way 5-shot setting and
5-way 1-shot setting. These 40 new classes are learned
in incremental steps of 10 classes per step. In each
incremental step (
T
), data (
D
T
) is into small tasks
(
T
b
) which containes batches
N ∗ K
images for N-way
K-shot learning. In both datasets, for each task’s (in-
cremental step) training set is constructed by randomly
picking
K
training samples per class from the original
dataset, while the test set remains to be the original
one, which is large enough to evaluate the generaliza-
tion performance for preventing overfitting. Here is
K
is decided based the setting for learning (K-shot).
We use a modified version of ResNet-18 (He et al.,
2016) as the feature extractor. The extracted feature
vector is a 512 dimensional vector. To see the true po-
tential we trained both base and new classes in K-shot
way, instead of training the base classes in the normal
supervised pre-training way and new classes in K-shot
way. Because in reality obtaining 600 images per class
might be difficult. After training on base classes we
fine tune
Θ
c
on each subsequent training set of new
classes
D
(t)
, where t > 2
(See Algorithm 2 in Section
3.4), with learning rate
1e − 3
with a decay of 0.1 for
feature extractor. Both Discriminator and Generator
are consists sequential linear layers with a intial learn-
ing rate of
1e − 4
for outer update steps and a intial
learning rate of
1e − 2
for inner update steps in GAN,
this learning rate for GAN is adaptive for a better op-
timization. After training on
D
(t)
, we test
Θ
t
c
on the
union of the test sets of all encountered classes. Noise
input for generator is a 200 dimensional vector which
is sampled from a gaussian distribution zero mean and
unit variance. Now, features of the current task and
generated features of the previous task (as replay) are
given to the classifier
h
, which outputs the probabil-
ities of input features. When finetuning ResNet-18,
as we only have very few new class training samples
, it would be difficult to compute batchnorm. Thus,
we use the batchnorm statistics computed on
D
(1)
and
fix the batchnorm layers during finetuning. For data
augmentation, we perform standard random rotation
and flipping. We used ADAM (Kingma and Ba, 2014)
optimizer for both feature extraction and feature gen-
eration.
4.1 Comparative Studies
We implemented and compared our method with Proto-
typical Networks (Snell et al., 2017),Weights Imprint-
ing (Qi et al., 2018), LWF (Gidaris and Komodakis,
2018). In Prototypical Networks, for each base class
we store a base representation (prototype), which is
the average representation over all images belonging
to the base class. In the few-shot learning stage, av-
erage the representation of the few-shot classes are
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
264

learned and stored. In testing representation of a test
image is compared with the stored representations and
nearest neighbor is retrieved. In Weights Imprint-
ing, the base classes are learned regularly through
supervised pre-training, and novel classes are learned
through prototypical averaging. In LWF, base classes
are learned through episodic meta-learning and novel
classes through prototypical averaging.
Table 3: 60 (base) + 5 (Novel) in 1 shot setting on miniIma-
geNet.
Model 4
o
↓
ProtoNet (Snell et al., 2017) −20.43
Imprint (Qi et al., 2018) −22.64
LWF (Gidaris and Komodakis, 2018) −13.39
Ours -4.95
Table 4: 64 (base) + 5 (Novel) in 5 shot setting on miniIma-
geNet.
Model 4
o
↓
ProtoNet (Snell et al., 2017) −32.01
Imprint (Qi et al., 2018) −27.36
LWF (Gidaris and Komodakis, 2018) −14.33
Ours -6.9
Here in Table 1,2,3,4,
4
o
↓
decrease in the ac-
curacy on predicting jointly on both base and novel
classes. In Table 1,2,
4
w
↓
is weighted decrease in
accuracy of each task when compared to previous task
i.e for current task
t
which has no. of novel classes
n
t
, decrease in the accuracy in predicting classes in
the previous tasks is calculated and with weights of
n
t−1
, n
t−2
, . . .
weighted arithmetic mean of accuracy
is evaluated.
Similar analysis on CIFAR100 shows a decrease
of 9.7% on jointly predicting 70 (base) + 10 (novel)
classes in 5-way, 5-shot setting.
4.2 Comparison of Storage
Requirements
Our feature generator only need a 4.6MB of mem-
ory,when compared to the memory usage of exemplar
based methods like iCARL (Rebuffi et al., 2017), Re-
balance (Hou et al., 2019) generally stores around 20
exemplar images per class and memory needed in-
creases drastically from 7MB to greater than 300MB
for 100 classes. It is also difficult for exemplar-based
method to learn only with roughly 20 images and gen-
eralize well. Generative image replay techniques like
MeRGAN(Wu et al., 2018) requires only a constant
memory of 8.5MB but has difficulty generating realis-
tic images in few-shot setting.
5 CONCLUSION
We proposed a novel few-shot incremental learning
approach by combining feature replay and feature dis-
tillation. The fact that the distribution of high-level
features is notably simpler than the distribution at the
pixel level distribution drives our approach by effec-
tively modelling with simpler generators and trained
on limited samples. From the experiments performed
on the miniImageNet and CIFAR-100 datasets, we
outperformed other methods without exemplars. We
also showed that our model is efficient and scalable.
For future work, with advances in adversarial learning
method for few-shot setting, it is interesting to extend
this kind of approach to large scale data containing
many classes.
ACKNOWLEDGEMENTS
We acknowledge the support of Biomimetic Intelli-
gent System Laboratory, Chubu University, Japan for
providing resources for conducting this research.
REFERENCES
Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-
stein gan. ArXiv, abs/1701.07875.
Castro, F. M., Mar
´
ın-Jim
´
enez, M., Mata, N. G., Schmid,
C., and Karteek, A. (2018). End-to-end incremental
learning. ArXiv, abs/1807.09536.
Chaudhry, A., Ranzato, M., Rohrbach, M., and Elhoseiny, M.
(2018). Efficient lifelong learning with a-gem. arXiv
preprint arXiv:1812.00420.
Chen, L.-C., Papandreou, G., Schroff, F., and Adam, H.
(2017). Rethinking atrous convolution for semantic
image segmentation. arXiv preprint arXiv:1706.05587.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei,
L. (2009). Imagenet: A large-scale hierarchical image
database. In 2009 IEEE conference on computer vision
and pattern recognition, pages 248–255. Ieee.
Finn, C., Abbeel, P., and Levine, S. (2017). Model-agnostic
meta-learning for fast adaptation of deep networks.
ArXiv, abs/1703.03400.
Gidaris, S. and Komodakis, N. (2018). Dynamic few-shot
visual learning without forgetting. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, pages 4367–4375.
Graves, A., Wayne, G., and Danihelka, I. (2014). Neural
turing machines. arXiv preprint arXiv:1410.5401.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Few-Shot Class Incremental Learning with Generative Feature Replay
265

He, X. and Jaeger, H. (2018). Overcoming catastrophic
interference using conceptor-aided backpropagation.
In International Conference on Learning Representa-
tions.
Hinton, G. E., Vinyals, O., and Dean, J. (2015). Dis-
tilling the knowledge in a neural network. ArXiv,
abs/1503.02531.
Hou, S., Pan, X., Loy, C. C., Wang, Z., and Lin, D. (2019).
Learning a unified classifier incrementally via rebal-
ancing. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition, pages 831–
839.
Kemker, R. and Kanan, C. (2017). Fearnet: Brain-
inspired model for incremental learning. arXiv preprint
arXiv:1711.10563.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Des-
jardins, G., Rusu, A. A., Milan, K., Quan, J., Ramalho,
T., Grabska-Barwinska, A., et al. (2017). Overcoming
catastrophic forgetting in neural networks. Proceedings
of the national academy of sciences, 114(13):3521–
3526.
Koch, G., Zemel, R., and Salakhutdinov, R. (2015). Siamese
neural networks for one-shot image recognition. In
ICML deep learning workshop, volume 2. Lille.
Krizhevsky, A., Nair, V., and Hinton, G. (2014). The cifar-10
dataset. online: http://www. cs. toronto. edu/kriz/cifar.
html, 55.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Kumaran, D., Hassabis, D., and McClelland, J. L. (2016).
What learning systems do intelligent agents need? com-
plementary learning systems theory updated. Trends
in Cognitive Sciences, 20(7):512 – 534.
Lesort, T., Caselles-Dupr
´
e, H., Garcia-Ortiz, M., Stoian,
A., and Filliat, D. (2019). Generative models from the
perspective of continual learning. In 2019 International
Joint Conference on Neural Networks (IJCNN), pages
1–8. IEEE.
Li, Z. and Hoiem, D. (2017). Learning without forgetting.
IEEE transactions on pattern analysis and machine
intelligence, 40(12):2935–2947.
Liu, W., Wen, Y., Yu, Z., Li, M., Raj, B., and Song, L. (2017).
Sphereface: Deep hypersphere embedding for face
recognition. In Proceedings of the IEEE conference on
computer vision and pattern recognition, pages 212–
220.
Lopez-Paz, D. and Ranzato, M. (2017). Gradient episodic
memory for continual learning. In Advances in neural
information processing systems, pages 6467–6476.
Mallya, A. and Lazebnik, S. (2018). Packnet: Adding mul-
tiple tasks to a single network by iterative pruning.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 7765–7773.
Masana, M., Tuytelaars, T., and van de Weijer, J. (2020).
Ternary feature masks: continual learning without any
forgetting. arXiv preprint arXiv:2001.08714.
McClelland, J. L., McNaughton, B. L., and O’Reilly, R. C.
(1995). Why there are complementary learning systems
in the hippocampus and neocortex: insights from the
successes and failures of connectionist models of learn-
ing and memory. Psychological review, 102(3):419.
McCloskey, M. and Cohen, N. J. (1989). Catastrophic in-
terference in connectionist networks: The sequential
learning problem. In Psychology of learning and moti-
vation, volume 24, pages 109–165. Elsevier.
Munkhdalai, T. and Yu, H. (2017). Meta networks. Proceed-
ings of machine learning research, 70:2554–2563.
Newell, A., Yang, K., and Deng, J. (2016). Stacked hourglass
networks for human pose estimation. In European con-
ference on computer vision, pages 483–499. Springer.
Nguyen, C. V., Li, Y., Bui, T. D., and Turner, R. E.
(2017). Variational continual learning. arXiv preprint
arXiv:1710.10628.
Ostapenko, O., Puscas, M. M., Klein, T., J
¨
ahnichen, P., and
Nabi, M. (2019). Learning to remember: A synap-
tic plasticity driven framework for continual learning.
2019 IEEE/CVF Conference on Computer Vision and
Pattern Recognition (CVPR), pages 11313–11321.
Qi, H., Brown, M., and Lowe, D. G. (2018). Low-shot
learning with imprinted weights. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 5822–5830.
Ravi, S. and Larochelle, H. (2017). Optimization as a model
for few-shot learning. In ICLR.
Rebuffi, S.-A., Kolesnikov, A., Sperl, G., and Lampert, C. H.
(2017). icarl: Incremental classifier and representation
learning. In Proceedings of the IEEE conference on
Computer Vision and Pattern Recognition, pages 2001–
2010.
Robins, A. (1995). Catastrophic forgetting, rehearsal and
pseudorehearsal. Connection Science, 7(2):123–146.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein,
M., et al. (2015). Imagenet large scale visual recog-
nition challenge. International journal of computer
vision, 115(3):211–252.
Rusu, A. A., Rabinowitz, N. C., Desjardins, G., Soyer, H.,
Kirkpatrick, J., Kavukcuoglu, K., Pascanu, R., and
Hadsell, R. (2016). Progressive neural networks. ArXiv,
abs/1606.04671.
Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D., and
Lillicrap, T. (2016a). Meta-learning with memory-
augmented neural networks. In International confer-
ence on machine learning, pages 1842–1850.
Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D.,
and Lillicrap, T. (2016b). One-shot learning with
memory-augmented neural networks. arXiv preprint
arXiv:1605.06065.
Serra, J., Suris, D., Miron, M., and Karatzoglou, A. (2018).
Overcoming catastrophic forgetting with hard attention
to the task. arXiv preprint arXiv:1801.01423.
Shin, H., Lee, J. K., Kim, J., and Kim, J. (2017). Continual
learning with deep generative replay. In Advances in
ICPRAM 2021 - 10th International Conference on Pattern Recognition Applications and Methods
266

Neural Information Processing Systems, pages 2990–
2999.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Snell, J., Swersky, K., and Zemel, R. (2017). Prototypical
networks for few-shot learning. In Advances in neural
information processing systems, pages 4077–4087.
Tai, Y., Yang, J., Liu, X., and Xu, C. (2017). Memnet: A
persistent memory network for image restoration. In
Proceedings of the IEEE international conference on
computer vision, pages 4539–4547.
Vinyals, O., Blundell, C., Lillicrap, T., Wierstra, D., et al.
(2016). Matching networks for one shot learning. In
Advances in neural information processing systems,
pages 3630–3638.
Weston, J., Chopra, S., and Bordes, A. (2015). Memory
networks. CoRR, abs/1410.3916.
Wu, C., Herranz, L., Liu, X., Wang, Y., van de Weijer, J.,
and Raducanu, B. (2018). Memory replay gans: learn-
ing to generate images from new categories without
forgetting. ArXiv, abs/1809.02058.
Wu, Y., Chen, Y., Wang, L., Ye, Y., Liu, Z., Guo, Y., and Fu,
Y. (2019). Large scale incremental learning. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 374–382.
Yoon, J., Yang, E., Lee, J., and Hwang, S. J. (2017). Lifelong
learning with dynamically expandable networks. arXiv
preprint arXiv:1708.01547.
Zenke, F., Poole, B., and Ganguli, S. (2017). Continual
learning through synaptic intelligence. Proceedings of
machine learning research, 70:3987.
Zhang, R., Che, T., Ghahramani, Z., Bengio, Y., and Song, Y.
(2018). Metagan: An adversarial approach to few-shot
learning. In NeurIPS.
Few-Shot Class Incremental Learning with Generative Feature Replay
267
