
A New Parking Space Allocation System based on a
Distributed Constraint Optimization Approach
Atik Ali
1
, Souhila Arib
2
and Samir Aknine
3
1
Research Center on Scientific and Technical Information, CERIST, Higher National School of Computer Science,
ESI ex INI, Algeria
2
CY Tech Cergy Paris Universit
´
e, 33 Boulevard du port 95000 Cergy, France
3
Laboratoire LIRIS, Universit
´
e Claude Bernard Lyon 1, UCBL 69622 Villeurbanne, France
Keywords:
Parking Allocation, DCOPs, Max-Sum Algorithm.
Abstract:
This paper develops and evaluates a new decentralized mechanism for the allocation of parking slots in down-
town, using a distributed constraints optimization approach (DCOP). Our mechanism works with the multi-
parking/multi-zone model, where vehicles are connected and can exchange information with the distributed
allocation system. This mechanism can reach the minimal allocation costs where vehicles are assigned to the
parking lots with the best possible aggregated user costs. The cost is calculated based on driver’s aggregated
preferences over slots. We empirically evaluated the performance of our approach with randomly generated
costs and tested on three different configurations. The evaluation shows the performance of each configuration
in terms of runtime and volume of exchanged data.
1 INTRODUCTION
Parking demand is determined by the attractiveness
of the destination, with city centers being the most
attractive areas. These areas are experiencing a grow-
ing shortage of parking places, and drivers generally
need to spend a significant amount of time circling the
blocks around their destination searching and waiting
for available parking spaces. In this problem, the dif-
ficulty lies in the fact that the requirements and the
destinations of the drivers vary from one driver to an-
other. Many works have been carried on to deal with
this last issue. For instance, (Zeenat et al., 2018) pro-
posed a multiple criteria based parking space reser-
vation algorithm that can be used to reserve a space
for users, and to deal with their requirements in a fair
way by using the normalized weighting of each cri-
teria score for all options relating to each user’s pro-
file. In (Boudali and Ouada, 2017), the authors pro-
posed a system that handles user’s preferences by en-
suring an online space allocation based on real-time
information and by optimizing driver’s preferences
with respect to a set of operational constraints, such
as, the bound on parking fees, bounds on distances,
time interval that have to be satisfied for each reser-
vation, etc. In (Ayala et al., 2011), the authors pro-
posed to allocate parking slots via negotiations. This
work uses a game theoretic approach to allocate the
suitable place for the suitable vehicle, or the short-
est way to the suitable spot via a routing algorithms
(Hedderich et al., 2017), or via smart reservation sys-
tem as in (Kazi et al., 2018). All these works, each
in its own way, claim to reduce the traffic in urban ar-
eas, and to alleviate its negative related effects, from
the reduction of air pollution, the reduction of fuel
consumption, to the reduction of cursing time, social
anxiety, etc. Besides, with the advent of IoT technol-
ogy, the proliferation of smart-phones, and on-board
navigation systems, it is already possible for a user to
be linked in a real-time with parking space allocation
applications that lead their users to the best possible
spot to park. In this paper, we study the setting up
of a parking management system to respond without
a centralized control to parking requests in downtown
parking areas, with the aim of limiting both the time
of response and the cost of communication. Indeed,
commercial fleet management solutions that require
real-time data collections and exploitation, especially
in the Cloud like parking allocation, carpooling, be-
come rapidly costly depending on the rate of the data
collections and the volume of data to be processed
(Picard et al., 2018). We thus focus on finding effi-
cient solutions for the allocation of parking slots. To
that end, we formulate the problem as a distributed
196
Ali, A., Arib, S. and Aknine, S.
A New Parking Space Allocation System based on a Distributed Constraint Optimization Approach.
DOI: 10.5220/0010249201960204
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 196-204
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

constraint optimization problem which has shown to
be effective in vehicle routing optimization (L
´
eaut
´
e
et al., 2010), auctions and resource allocation prob-
lems (Weiss et al., 2017). The decentralized approach
has the benefit of distributing the main computations
across all available devices, thus giving more com-
putation power to the system. Here we do not claim
to propose a solution that is faster than the central-
ized models but rather a solution that requires less
volume of data to be processed than the centralized
ones
1
. Our main contributions are:
1. We propose a new distributed parking allocation
model that we test in three architectural shapes for
a set of n connected vehicles.
2. We choose the best DCOP solver, and show how
to extend the model from the static case to the dy-
namic case.
This article is organized as follows: section 2 presents
the related work. Section 3 presents DCOPs in gen-
eral, then our problem formulation and solution in
subsections 3.1, 3.2 and 3.3. An illustrative example
is given in subsection 3.4, whereas subsections 3.5,
3.6 and 3.7 are devoted to the presentation of our three
approaches. Section 4 shows experimentation we car-
ried on our three approaches. Finally, the conclusion
is presented in section 5.
2 RELATED WORK
Among distributed approaches, we can mention phys-
ically distributed multi-agent systems. As an exam-
ple of the latter we can cite (Chou et al., 2008) in
which the authors proposed an agent-based intelligent
parking negotiation and guidance system which acts
as a bargaining platform between parks and drivers.
The platform facilitates the search for available park-
ing spaces, the dynamic negotiation of parking fees,
the reservation of parking spaces, and the derivation
of optimal paths from the current location to the in-
tended car park as well as from the car park to the
final destination. This approach presents some short-
comings due to the increasing number of exchanged
messages during the negotiation process as well as the
possibility of non-convergence of the negotiation to-
ward a viable solution. Distributed systems could be
self-coordinated car parking methods like in (Bess-
ghaier et al., 2012), in which the authors propose a
decentralized multi-agent paradigm with one of the
1
For technical reasons, and with respect to the context,
we only focus on optimizing the calculation time, and min-
imizing the data volume to be processed without physically
using a real distributed hardware.
objectives being the coordination of distributed enti-
ties based on inter-vehicular communication (V2V)
which allows vehicles to receive and broadcast infor-
mation on space availability to the other vehicles of
the same community. The system works without prior
information on the parking spots and without central
storage of information. In fact, vehicles of the same
district update their local knowledge by exchanging
messages which include the list of occupied and free
spots at each parking and each discharge. In these
categories, the vehicle has a trade-off between coop-
erating to collect information or competing to find a
suitable parking slot. Indeed, to improve the coop-
eration between vehicles, a recent work (Chou et al.,
2018), proposed a decentralized car parking approach
for vast car park areas. Their approach called Co-
park is based on cooperation among vehicles through
vehicle-to-vehicle communication. Their system uses
a cooperation algorithm which optimizes the level of
satisfaction in terms of individual and social benefits
in large car parking areas. In our work, we propose
a new decentralized multi-agent paradigm with dis-
tributed optimizer and using VANETs network and
investigate the impact of our model on communica-
tion costs.
3 PROBLEM FORMULATION
Distributed constraint optimization problem is used
in decentralized approaches. It gives more computa-
tional power to the system by distributing the compu-
tational load over multiple computation nodes. DCOP
gives better scalability and adaptability, since the fail-
ure/maintenance in any node doesn’t affect the whole
system. Finally, it gives more power to the system by
allowing it to operate in highly dynamic environment
such as car park environment. A DCOP is a tuple
{A,X,D,C,µ}, where: A = {a
1
,a
2
,...,a
|A|
} is a set
of agents; X = {x
1
,x
2
,..,x
n
} is a set of decision vari-
ables, each decision variable x
i
being controlled by
an agent a(x
i
); and the domain D = {d
1
,d
2
,...,d
n
} is
a set of finite discrete domains for the decision vari-
ables such that x
i
takes values in the sub-domain d
i
.
C = {c
1
,...,c
θ
} is a set of constraints that assign costs
where c
i
∈ R. Each c
i
is assumed to be known to all
involved agents. The µ defines a mapping function
between agents and variables from X . A solution to
the DCOP is an assignment to all variables that mini-
mizes the sum
∑
θ
i=1
c
i
.
In our model, we consider car parks disseminated
in a random manner in a given area portioned into
several zones. We assume that each locality (zone)
contains from 0 to λ car parks. Each single car park
A New Parking Space Allocation System based on a Distributed Constraint Optimization Approach
197

belongs to a single locality (zone) z
i
from the set
Z = {z
0
,z
1
,z
2
,. . . ,z
|Z|
}. In what follows, we present
some notations relative to the vehicles (or users) and
to the car parks. In our model, we consider N users
requesting parking in this area. We define V as the
set of vehicles (or users) who are searching for a
place to park: V = {v
x
,x | x = {1,2,3,...,N}}. We
define P as the set of car parks in our downtown,
P = {p
k
,k | k = {1,2,3,...,|P|}, |P| ≤ λ. Let us de-
note Dest
x
as the destination of the vehicle v
x
, and let
us define D
max
x
as the maximum distance allowed by
the vehicle v
x
from the elected car park space to the
vehicle’s destination Dest
x
. We define the parameter
q(p
k
) as the capacity of the parking number k. We
define zv
x
/zp
k
as the zone number where is located
the destination of the vehicle v
x
respectively the car
park p
k
. We define the set of the candidate car parks
C
D
(x) for the user x or the vehicle v
x
who is seeking
to park in a given zone z ∈ Z. The c(p
k
,v
x
) is the cost
when the vehicle v
x
parks in that car park p
k
. The
c(p
k
,v
x
) 6= ∞ means that the car park p
k
has a pro-
posal to our user.
We define the set C
D
(x)
6=z
to design the car parks
which do not belong to the user’s zone destination
but are near to the user’s destination (i.e. the tolera-
ble walking distance of user x, D
max
x
is respected and
C
D
(x)
6=z
⊆ P).
C
D
(x) = {p
k
| p
k
∈ P,walking(p
k
,v
x
) ≤ D
max
x
∧c(p
k
,v
x
) 6= ∞ ∧ p
k
∈ zv
x
} (1)
C
D
(x)
6=z
= {p
k
| p
k
∈ P ∧ p
k
/∈ C
D
(x),
walking(p
k
,v
x
) ≤ D
max
x
∧ zv
x
6= zp
k
} (2)
Where walking(p
k
,v
x
) returns the time that the user
needs to reach the parking. We define toc
x
as the ap-
proximate occupancy time claimed by the user x and
we define t
s
x
and t
e
x
as the start and end time interval re-
lating to the user x. t
s
x
,t
e
x
∈ [1,τ] where τ = {1,2...,T },
designates the iteration current time.
toc
x
= t
e
x
− st
s
x
+ 1 (3)
We define τ
k.x
the estimated walking time between the
vehicle x current car park slot and the user destina-
tion Dest
x
. We define Est
x.k
as the average estimated
travel time between the vehicle x current position and
the car park of number k. We define the Pdur
x.k
as a
calibration quantity which includes the stay, the trav-
eling and the walking time parameters via the follow-
ing formula:
Pdur
x.k
= toc
x
+ Est
x.k
+ 2τ
k.x
− 1 (4)
We define the subset X
π.k
⊂ X as the allocation vari-
ables for the car park p
k
where:
X
π.k
= {x
i.k
,..,x
a.k
,..,x
n.k
,..,x
s.k
..} (5)
x
i.k
designates an allocation variable for an ordinary
user.
x
a.k
is the allocation variable for the elderly.
x
n.k
is the allocation variable for the commuter.
x
s.k
is the allocation variable for the sick users.
We define our allocation function X
x.k
as follows
2
:
X
x.k
=
1 if vehicle x is assigned at car park k.
0 otherwise.
For a given allocation X
x.k
, we associate a cost func-
tion C
x.k
, where each allocation must be able to derive
the cost from the parking. For any user x, the c
x.k
rep-
resents the cost of a certain user x if he chooses to
park in a car park k.
3.1 Objective
Our objective is to propose to each vehicle of our set
of vehicles a place to park, (i.e. to propose a set of
identifiers of car parks where each vehicle can park),
This set of car parks is called a configuration. Let t
be the current time step and V the set of all vehicles
seeking to park in the system. A configuration is a
set φ = {p
1
, p
2
,.., p
N
} where each p
i
is the car park
number assigned to each v
i
∈ V . We aim to build, for
each time step t, a configuration φ
t
for all vehicles in
V that minimises their total cost of allocation. The
input is the set of vehicles V
t
presented in the system
at the current time step and the configuration at the
last time step φ
t−1
. Let c
x
be the allocation cost of
vehicle v
x
(this cost is influenced by every vehicle’s
priority, location and destination). Let Φ be the set of
all possible configurations. Our goal is to search for a
minimisation of the function f :
f : (t,V
t
,φ
t−1
) 7→ Arg min
φ
t
∈Φ
∑
v
i
∈V
t
c
i
(6)
3.2 Structural Constraints
Structural constraints are bunch of hard constraints
that represent the compliance of the resource with the
basic spatial allocation rules which must be respected
together in order to satisfy the consumers. These
structural constraints are as follow:
3.2.1 The Single Slot Constraint
The constraint (7) ensures that, at most only one ve-
hicle is allocated to a single car park slot.
O(X) =
∑
p
k
∈P
X
x.k
≤ 1,∀v
x
∈ V (7)
2
For ease of writing x ∈ {i,a,n,s}.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
198

It enforces that v
x
must be assigned to at most one
car park.
3.2.2 Car Park Capacity Constraint
This constraint ensures that the sum of all allocations
for a given parking area never exceeds its capacity.
C(X ) =
∑
v
x
∈V
X
x.k
≤ q(p
k
),∀p
k
∈ P (8)
3.3 The Soft Constraints
These constraints serve to favor the users on the basis
of their profile, these may be violated but their viola-
tion is monetized by a given cost.
3.3.1 The Priority Constraint
For that, we define in (9) the binary relation
Typc(x
i.k
,x
x.k
) of tuples of elements of X
π.k
where the
x
i.k
, as previously explained in (5), is a variable allo-
cation for an ordinary user. c
i.k
− c
x.k
is a cost differ-
ence between the user i and the user x
x.k
∈ X
π.k
\x
i.k
pertaining to the car park k. The triple equality x
i.k
=
x
x.k
= 1 means that for every car park p
k
in the system
there are four levels of priority, one for the ordinary
users, another one for the sick and the elderly persons
and finally another one for the commuters.
Typc(x
i.k
,x
x.k
) = {(x
i.k
,x
x.k
) | x
i.k
∈ X
π.k
,
x
x.k
∈ X
π.k
\x
i.k
, x
i.k
= x
x.k
= 1 ∧ c
i.k
− c
x.k
> 0} (9)
We define the binary priority constraint ∆(x,x
0
) as
follows:
∆(x
i.k
,x
x.k
) =
0 i f (x
i.k
,x
x.k
) ∈ Typc(x
i.k
,x
x.k
)
1 otherwise.
(10)
3.3.2 The Travel Time Constraint
The binary relation (11) is between two users heading
to a given car park k, this relation assigns a lower cost
to the vehicle having estimated travel time between its
current position and the car park in question.
Tr(x
x.k
,x
x
0
.k
) = { (x
x.k
, x
x
0
.k
) ∈ X
2
π.k
, (11)
x
k
= x
x.k
= 1 ∧ Est
x.k
> Est
x
0
.k
∧ c
x
0
.k
− c
x.k
> 0}
then the equation (12) defines the travel time con-
straint as follows:
Λ(x
x.k
,x
x
0
.k
) =
0 i f (x
x.k
,x
x
0
.k
) ∈ Tr(x
x.k
,x
x
0
.k
)
1 otherwise.
(12)
3.3.3 The Parking Duration Constraint
The relation (13) is another soft binary relation that
gives a lower cost to the user who is claiming to stay
no longer than his competitor (again if both users are
heading to the same car park) this constraint is to en-
courage the users to minimize their parking time.
E(x
x.k
,x
x
0
.k
) = { (x
x.k
,x
x
0
.k
) ∈ X
2
π.k
, (13)
x
x
0
.k
= x
x.k
= 1 ∧ Pdur
x.k
< Pdur
x
0
.k
∧ c
x.k
− c
x
0
.k
> 0}
The parking duration constraint will be the equation
(14):
ρ(x
x.k
,x
x
0
.k
) =
0 i f (x
x.k
,x
x
0
.k
) ∈ E(x
x.k
,x
x
0
.k
)
1 otherwise.
(14)
We define our allocation objective function as fol-
lows:
Argmin
X
f (X) =
N
∑
x=1
λ
∑
k=1
(C
x.k
X
x.k
) (15)
subject to: (7), (8), (10), (12) and (14)
We let the binary relation X from a set V × P to a
set G, where G is a subset of:
V × P, X : V × P → G ⊆ V × P
An allocation X is optimal if it minimizes the
objective function f (X) and respects all the hard
constraints (7) and (8) and the remaining soft con-
straints (10), (12) and (14) listed above. Now we
define our DCOP as the tuple {A, X,D,C,µ}, where
the set A is a finite set of m agents that manage
the zones and the users, A = {a
0
,a
1
,..,a
m
}. This
means that certain agents are assigned for the con-
trol of the different users or car parks or zones of
the area. We define the set D as a set of finite dis-
crete domains: D = {d
0
,d
1
,..,d
ε
} and the set X =
{X
π.1
,X
π.2
,..,X
π.λ
} ∪ {n
1
,n
2
,..,n
δ
} as the finite set
of variables owned by all the agents a
i
∈ A. The
subset of variables {X
π.1
,X
π.2
,..,X
π.λ
}
3
takes values
from the domain [0, 1] ; the variables n
δ
take values
from another set of discrete domains: d
x
⊂ D where
d
x
= C
D
(x)
6=z
∪ C
D
(x). Here the set D is nothing
else than the whole car parks subsets of the system
plus the two element set {0, 1}. We define the set of
constraints C = {c
0
,c
1
,..,c
θ
} as the set of constraints
over the variables of X where each constraint c
θ
∈ C
defines a cost ∈ R∪{∞} and for each possible alloca-
tion we associate a cost corresponding to it. A solu-
tion to our DCOP consists in the optimization of the
equation (15) subject to the set of constraints. Finally,
µ the last element of our tuple’s DCOP problem, is a
3
See equation (5)
A New Parking Space Allocation System based on a Distributed Constraint Optimization Approach
199
mapping function that assigns for every variable from
X an agent a
i
∈ A so that no variable from X is as-
signed to more than one agent and µ : X → A. The
mapping function µ will be explained in more detail
in the next sub-sections 3.5, 3.6 and 3.7.
In our formulation, we assume that the agents have
the following capabilities: (1) Agents are capable of
communicating with each other via the network in a
cooperative manner with respect to a communication
radius. (2) Users are capable to communicate with the
bargaining agents which are in charge of negotiating
slots via a central server. (3) Requests are sent via
the communication infrastructure which can be global
(e.g. cellular network, embedded system) and sent to
a central server.
3.4 Illustration of Our DCOP Model
with an Example
In this example, we are assuming that each car is mon-
itored by an agent, and each agent holds four param-
eters: the car’s destination, the car’s user type, the
user walking distance threshold, and the user’s esti-
mation of his occupation time. We consider a global
area divided into 2 zones (central, peripheral), with
3 car parks in the central zone and one car park in
the peripheral zone (illustrated by the red squared
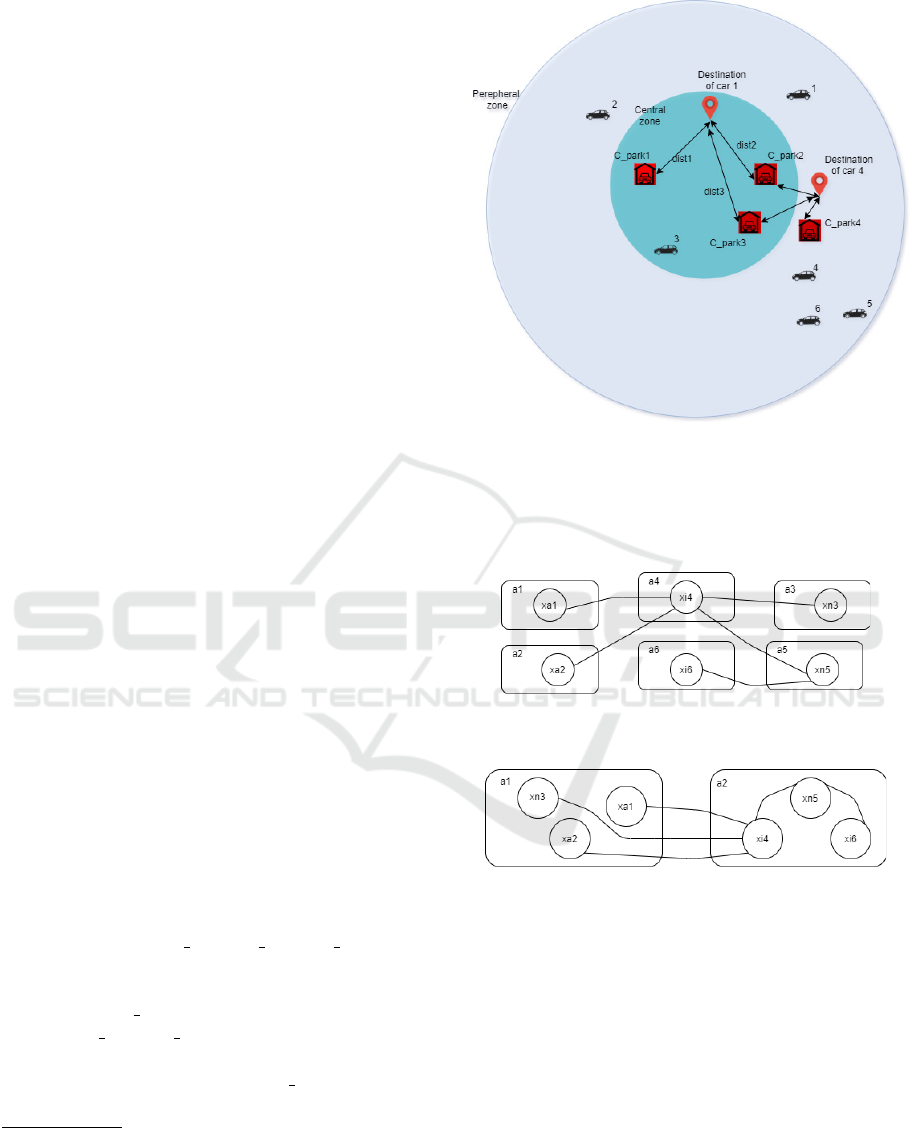
houses (See Fig. 1). We consider 6 users requesting
to park, three cars requesting to park in the central
zone and three cars requesting to park at the periph-
eral zone. Every car agent calculates the cost of the
candidate car park of its own user: for instance the
cost calculated via the agent of the car number 2 if
he chooses to park at car park number 1 is 71, the
agent of the user number 4 knows that there is no
place in the same car park (cost = ∞). The agent of
the user number 5 calculated the cost 44 with refer-
ence to car park number 4 (see Table 1)
4
. For sim-
plicity, the set of users y = {1,2,3} requesting to park
in the central zone will have the same set of candidate
car parks C
D
(y) = {C park
1
,C park
2
,C park
3
}(i.e.
their respective destinations are inside the central area
zone as shown in the Fig. 1
5
. The user{4} has the
set C
D
(4) = {C park
4
} of candidate car parks and
C
D
(4) = {C park
2
,C park
3
} as illustrated in Fig. 1.
For the remaining users {5,6}, the set of the candi-
date car parks is the singleton {C park
4
} (see Ta-
ble 2). Looking at the constraint graph (Fig. 2),
4
Each cost cell is calculated on the basis of the cost ac-
cumulations of the constraints (7), (8), (10), (12), (14).
5
This simplification is made to help explain the model.
In a complete example, every single user will have a set of
candidate car parks which could be calculated according to
the distance D
max
x
relating to each user, see equation (1).
Figure 1: The red squares represent the car parks. The dist1,
dist2 and dist3 represent the three distances between the car
number 1 destination and the three car parks (1, 2 and 3).
Circles are zones delimiters illustrating the division of the
car park area into sectors based on the distance from down-
town center.
Figure 2: Constraint graph of our example with the vehicle
based approach.
Figure 3: Constraint graph of our example with the zone
based approach.
we can see that each single agent a
i
is responsi-
ble of exactly one allocation variable. The figure
3 illustrates the constraint graph of the same prob-
lem with this time every zone is monitored by an
agent, here we have two agents responsible for two
zones. The first agent a
1
is responsible of the cen-
tral zone, subsequently in charge of the variables
{x
a.1
,x
a.2
,x
n.3
} representing respectively the alloca-
tion variables for the users {1, 2, 3}. The agent a
1
is
responsible for the satisfaction of the set of constraints
C = {(7), (8),(10),(12),(14)}. Similarly, agent a
2
is responsible for the peripheral zone and is thus in
charge of the variables {x
n.5
,x
i.6
,x
i.4
} respectively
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
200
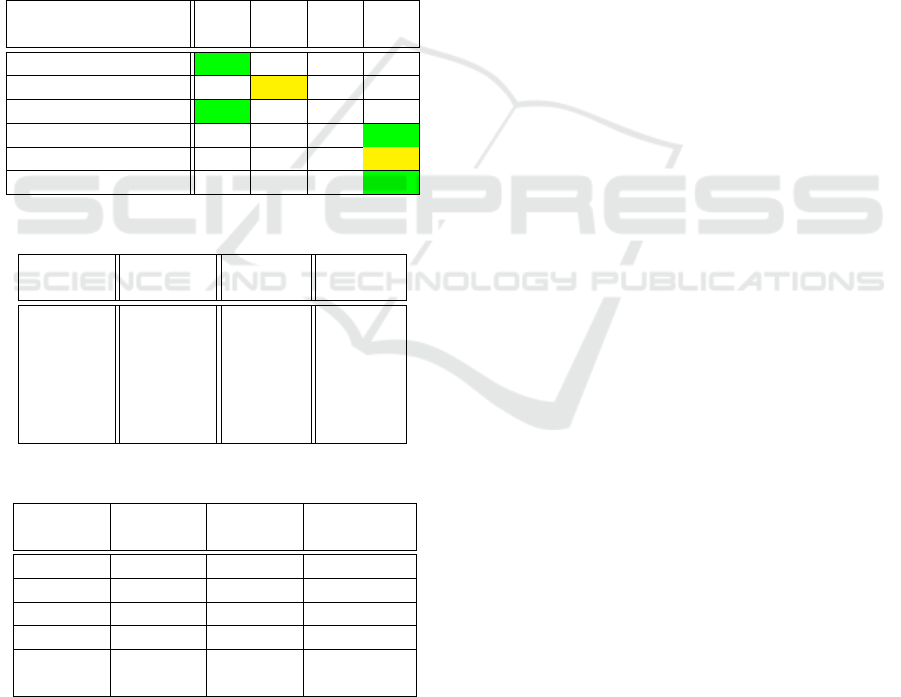
pertaining to users {4, 5, 6}. Similarly agent a
2
is re-
sponsible for the satisfaction of the set of constraints
C = {(7), (8), (10),(12),(14)}. We wrote the prob-
lem formulation in XML format, and launched the re-
solver using the Max-Sum algorithm from the frodo
platform (L
´
eaut
´
e et al., 2009), applying the equation
(15) and with the respect of the set of constraints C
cited above which generated the cost grid (see Ta-
ble 1). Arg min
X
f (X) =
∑
6
x=1
∑
4
k=1
(C
x.k
X
x.k
) = c
1.1
×
x
a.1
+c
2.2
×x
n.2
+c
3.1
×x
n.3
+c
4.4
×x
i.4
+c
5.4
×x
n.5
+
c
6.4
× x
i.6
= c
1.1
× 1 + c
2.2
× 1 + c
3.1
× 1 + c
4.4
× 1 +
c
5.4
× 1 + c
6.4
× 1 = 33 + 42 + 23 + 35 + 44 + 17 =
194. We obtained the optimized results (i.e. the allo-
cations of the six users with the minimal cost). Here
the best cumulative cost is equal to 194 and a total of
47 exchanged messages (see Tables 2 and 3).
Table 1: The costs table.
X
X
X
X
X
X
X
X
X
X
User
Car park
1 2 3 4
1 33 71 77 ∞
2 71 42 75 ∞
3 23 82 45 ∞
4 ∞ 52 55 35
5 ∞ ∞ ∞ 44
6 ∞ ∞ ∞ 17
Table 2: The candidate car park table.
user
number
user’s
variable
C
D
(x) C
D
(x)
6=z
1 x
a.1
{1,2,3} {
/
0}
2 x
a.2
{1,2,3} {
/
0}
3 x
n.3
{1,2,3} {
/
0}
4 x
i.4
{4} {2,3}
5 x
n.5
{4} {
/
0}
6 x
i.6
{4} {
/
0}
Table 3: The candidate car park table.
user
number
user’s
variable
Allocated
car park
Costs
1 x
a.1
1 (c
1.1
= 33)
2 x
a.2
2 (c
2.4
= 42)
3 x
n.3
1 (c
3.4
= 23)
4 x
i.4
4 (c
4.2
= 35)
5 x
n.5
4 (c
5.2
= 44)
6 x
i.6
4 (c
6.4
= 17)
3.5 Vehicles based Approach
The vehicles based approach consists in modeling
all the vehicles as agents. Each agent holds four
parameters: the agent’s destination, the agent’s user
type, the user walking distance threshold, and the
user’s estimation occupation time (i.e. how much
time does the user requests to occupy the parking
space). The number of agents corresponds to the
number of vehicles to monitor. We then map the
following constraints:
The first constraint combines two equations (7), (8).
Each single vehicle in the system must be assigned
to exactly one car park, while respecting the capacity
of each car park, those are structural constraints (hard
constraints) and should be respected in any allocation
in order to satisfy the consumers.
C
1
(x) =
0 if O(X)∧C(X) are true.
∞ otherwise.
The C
1
(x) = ∞ means that at least one of the two
structural constraints are violated for the user x.
The second constraint is about the respect of the
walking distance from a candidate car park for every
single user. This constraint is needed to check that at
least there is one eligible car park to make proposal
for the user.
C
2
(x) =
0 if C
D
(x) 6=
/
0
∞ otherwise.
The C
2
(x) = ∞ means that the system has no place to
propose for the user x.
The third constraint favors the elderly and com-
muters and the sick over the ordinary user. This
constraint serves to vehicles which move towards the
same parking several times. Each time this constraint
is violated, it will cost a unit. From the equation
(10) we define the constraint C
3
(x
i.k
) as follows:
C
3
(x
i.k
) =
∑
x
0
∈X
π.k
\x
i.k
∆(x
i.k
,x
0
).
The fourth constraint favors the vehicle which
has an estimated travel time lower than that of
its opponents this constraint finds its application
between the permutations (x, x
0
) of each subset of the
set X
π.k
which are heading to the car park k. From the
equation (12), we define the travel time constraint for
the user x as follows: C
4
(x) =
∑
x
0
∈X
π.k
\x
Λ(x,x
0
).
The fifth constraint gives a priority to the user who
is claiming to stay no longer than his competitor.
This constraint finds its application between the
A New Parking Space Allocation System based on a Distributed Constraint Optimization Approach
201
permutations (x, x
0
) of each subset of X
π.k
heading to
the same parking slot k at the same time. From the
equation (14), we define the fifth constraint C
5
(x) for
the user x as follows: C
5
(x) =
∑
x
0
∈X
π.k
\x
ρ(x,x
0
).
The sixth constraint makes sure that when agents ne-
gotiate slots between different zones (i.e. when both
C
D
(x)
6=z
and C
D
(x) are not empty) the cost is even
lower for the user x.
C
6
(x) =
0 i f C
D
(x)
6=z
∧C
D
(x) 6=
/
0 ∧
∑
5
j=1
C
j
(x)
≤
h
∑
5
j=1
C
j
(x) | ∀p
k
∈ {C
D
(x)\C
D
(x)
6=z
}
i
1 otherwise.
3.6 Car Park Approach
Instead of considering each vehicle as an agent, we
can consider each car park as an agent. The num-
ber of agents corresponds to the number of car parks
to monitor. We consider that every car park has the
knowledge of all vehicles seeking to park in its zone.
A car park agent holds an array variable T
k
that con-
tains the type, the trip time estimation and parking
time of every vehicle heading to its zone. To model
these vehicles, we use the six constraints of the previ-
ous approach.
3.7 Zone based Approach
In this approach, we consider that there is an agent
per zone, where each agent zone has the knowledge
of all vehicles on it . Thus the number of agents cor-
responds to the number of zones to monitor. We con-
sider that each agent zone has the knowledge of all ve-
hicles seeking to park on it. A zone agent contains an
array variable T
z
which contains the type, the trip time
estimations and park duration estimations of each ve-
hicle heading to it.
4 EXPERIMENTATION
4.1 The Choice of the Solver
The choice of the solver depends on the problem and
the environment characteristics. DCOP algorithms
can be classified as being either complete or incom-
plete, based on whether they can guarantee the opti-
mal solution or they trade optimally for shorter ex-
ecution times (Fioretto et al., 2018). In addition,
DCOP algorithms are classified as synchronous or
asynchronous (Farinelli et al., 2008). In our case and
considering our constraints, we need a synchronous
algorithm, since our constraints are strongly linked
and need to be satisfied at the same time. We have
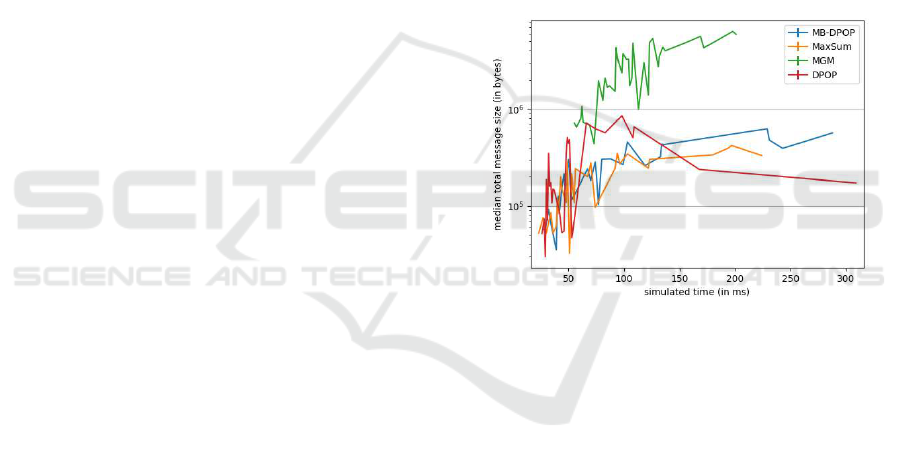
conducted different experiments to determine the best
solver for our model (among 12 solvers see Fig. 4).
These allowed us to confirm that the Max-Sum al-
gorithm is the fastest one in term of run times and
number of messages generated followed by the DPOP
algorithm. The Max-Sum is an incomplete, syn-
chronous, inference-based algorithm based on belief
propagation. It operates on factor graphs by perform-
ing a marginalization process of the cost functions,
and optimizing the costs for each given variable. This
process is performed by recursively propagating mes-
sages between variable nodes and factor nodes . The
value assignments take into account their impact on
the marginalized cost function. Max-Sum is guar-
anteed to converge to an optimal solution in acyclic
graphs, but convergence is not guaranteed on cyclic
graphs (Farinelli et al., 2008).
Figure 4: The illustration of the performances of the four
most efficient solvers. Here we show the median total mes-
sage size per simulated time (in ms) by each solver.
4.2 The Solution in the Dynamic
Environment
Parking spaces during all day are either occupied or
free, and their status changes in a volatile way over
time and on a system needs to know the occupation
status of each car park. Besides in the real environ-
ment vehicles continuously approach their destina-
tion, at each time step, we must define the new posi-
tions of the vehicles that take part in our DCOP prob-
lem, we mean the vehicles for which the DCOP will
eventually maintain their previous allocations or re-
vise certain according to the new updates in the en-
vironment. A way to cope with this issue is to sim-
ply solve the problem with the new current input, and
consider starting a new instance only after the solver
finishes executing the current instance. Our system
needs a faster execution model by providing solutions
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
202

of the static model more frequently. At every call of
the solver the system might find a better allocation
for already allocated vehicles, or provide a new allo-
cation for vehicles that would have been left without
allocation.
Figure 5: The sum of the simulation times per approach in
(ms).
Figure 6: The total number of messages exchanged by ap-
proach (in bytes).
Figure 7: The median simulated time per zone (in ms) by
approach.
4.3 Empirical Evaluation
In this section, we propose the Max-Sum algorithm
as a resolver and frodo2 as a platform (L
´
eaut
´
e et al.,
2009), the experiments were performed using ora-
cle VM virtual BOX with 24 GB RAM, under Linux
18.04(64 bit) with Intel core i5-7400 (six cores). We
compare values from at least 1442 simulations, from 6
car parks to 16 car parks spread over [3,4,.., 6] zones
per time. The range of requests varies on a domain
[120,130, .., 180] per experimentation. We evaluate
the performance of our mechanism on the three ap-
proaches described before. The first vehicle based
Figure 8: The median simulated time per number of car
parks (in ms) by approach.
Figure 9: The median simulated time per number of agents
(in ms) by approach.
Figure 10: The median agent’s number per simulated time
(in ms) by approach.
approach is denoted by CBA. The second one, the
car park based approach is denoted by PBA. The
last one, the zone based approach is denoted by ZBA.
From Fig. 5, we can infer that the fastest model is the
model CBA approach followed by the PBA approach,
the slowest one is the ZBA approach. From Fig. 6, we
can see that the CBA exchanged the biggest volume
data followed by the PBA. The smallest data is used
by ZBA. From Fig. 7, it can be seen that the more the
A New Parking Space Allocation System based on a Distributed Constraint Optimization Approach
203

number of sectors (or zones) we use the more faster is
the ZBA approach. On the other hand, CBA remains
insensitive to the change of number of zones, however
PBA becomes slower. From Fig. 8, we could say that
as the number of car parks increases, the possibility of
finding a parking space increases more. From Fig. 9
and Fig. 10, we can deduce that even though CBA
approach is the fastest of the three approaches, the
agents of the CBA start to run out of steam compared
to the PBA, certainly because the number of agents is
more important. From these approaches we can infer
that the most suitable approach for the Cloud environ-
ment is the PBA. It is a model which is not the slow-
est amid the three approaches and which exchanges a
volume of data which is not the highest.
5 CONCLUSION
As mentioned, our distributed model uses the
VANETs that connect agents both for relaying the
parking status and for inter-agent negotiations. The
reservations are then relayed to a central server. By
doing so, we decrease the volume of data exchanged
in the Cloud. Contrarily, in the centralized case,
there is a central server which gathers parking re-
quests, real-time information (i.e., vehicle location,
traffic condition, users preferences), etc. At every pe-
riod of time T (related to the lifetime of the informa-
tion on the availability of spots) the central server re-
ceives thousands of variables about the status of all
car parks of the system, which could be excessively
time-consuming and potentially incur high cost and
slow-downs if there are huge amounts of data ex-
changed via the Cloud like in large car parks area. As
a perspective, our next task will be to investigate the
impact of our process on communication costs, and
show that our model transfers less data and is there-
fore less expensive than the centralized one.
REFERENCES
Ayala, D., Wolfson, O., Xu, B., Dasgupta, B., and Lin, J.
(2011). Parking slot assignment games. In Proceed-
ings of the 19th ACM SIGSPATIAL International Con-
ference on Advances in Geographic Information Sys-
tems, pages 299–308.
Bessghaier, N., Zargayouna, M., and Balbo, F. (2012). On-
line localized resource allocation application to urban
parking management. In 2012 IEEE/WIC/ACM Inter-
national Conferences on Web Intelligence and Intelli-
gent Agent Technology, volume 2, pages 67–74. IEEE.
Boudali, I. and Ouada, M. B. (2017). Smart parking reser-
vation system based on distributed multicriteria ap-
proach. Applied Artificial Intelligence, 31(5-6):518–
537.
Chou, S.-Y., Arifin, Z., and Dewabharata, A. (2018). Opti-
mal decision of reservation policy for private parking
sharing system. In 2018 International Conference on
Computer, Control, Informatics and its Applications
(IC3INA), pages 66–71. IEEE.
Chou, S.-Y., Lin, S.-W., and Li, C.-C. (2008). Dynamic
parking negotiation and guidance using an agent-
based platform. Expert Systems with applications,
35(3):805–817.
Farinelli, A., Rogers, A., Petcu, A., and Jennings, N. R.
(2008). Decentralised coordination of low-power em-
bedded devices using the max-sum algorithm. In 7th
International Joint Conference on Autonomous Agents
and Multiagent Systems (AAMAS 2008), Estoril, Por-
tugal, Volume 2, pages 639–646.
Fioretto, F., Pontelli, E., and Yeoh, W. (2018). Distributed
constraint optimization problems and applications: A
survey. Journal of Artificial Intelligence Research,
61:623–698.
Hedderich, M., Fastenrath, U., Isaac, G., and Bogenberger,
K. (2017). Adapting the a* algorithm for park spot
routing. Transportation Research Procedia, 27:1066–
1073.
Kazi, S., Nuzhat, S., Nashrah, A., and Rameeza, Q. (2018).
Smart parking system to reduce traffic congestion.
In 2018 International Conference on Smart City and
Emerging Technology (ICSCET), pages 1–4. IEEE.
L
´
eaut
´
e, T., Ottens, B., and Faltings, B. (2010). Ensuring
privacy through distributed computation in multiple-
depot vehicle routing problems. In Proceedings of the
ECAI’10 Workshop on Artificial Intelligence and Lo-
gistics (AILog’10).
L
´
eaut
´
e, T., Ottens, B., and Szymanek, R. (2009). Frodo 2.0:
An open-source framework for distributed constraint
optimization. In Proceedings of the IJCAI’09 Dis-
tributed Constraint Reasoning Workshop (DCR’09),
pages 160–164.
Picard, G., Balbo, F., and Boissier, O. (2018). Approches
multiagents pour l’allocation de courses
`
a une flotte de
taxis autonomes. Rev. d’Intelligence Artif., 32(2):223–
247.
Weiss, M., Lubin, B., and Seuken, S. (2017). Sats: A uni-
versal spectrum auction test suite. In Proceedings of
the 16th Conference on Autonomous Agents and Mul-
tiAgent Systems, pages 51–59.
Zeenat, R., Ashifuddin, M., and Marijn, J. (2018). A
multiple-criteria algorithm for smart parking: mak-
ing fair and preferred parking reservations in smart
cities. In Proceedings of the 19th Annual International
Conference on Digital Government Research: Gover-
nance in the Data Age, pages 1–9.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
204
