Information-theoretic Cost of Decision-making in Joint Action

Dari Trendaﬁlov

, Daniel Polani

and Alois Ferscha

Institute of Pervasive Computing, Johannes Kepler University, Linz, Austria

Adaptive Systems Research Group, University of Hertfordshire, Hatﬁeld, U.K.

Keywords:

Collective Behavior, Information Dynamics, Complex Systems, Information Theory.

Abstract:

We investigate the information processing cost relative to utility, associated with joint action in dyadic

decision-making. Our approach, built on the Relevant Information formalism, combines Shannon’s Infor-

mation Theory and Markov Decision Processes for modelling dyadic interaction, where two agents with in-

dependent controllers move an object together with fully redundant control in a grid world. Results show

that increasing collaboration relaxes the pressure on required information intake and vice versa, antagonistic

behavior takes a higher toll on information bandwidth. In this trade-off the particular embodiment of the envi-

ronment plays a key role, demonstrated in simulations with informationally parsimonious optimal controllers.

1 INTRODUCTION

Individual agents with limited information-

processing capabilities can successfully coordinate

their behavior and make well-informed collective

decisions. Examples include collective behaviors,

such as coordinated motion of birds and ﬁshes

(Couzin et al., 2005), bees and ants (Franks et al.,

2002), or coordination of individual cells (Pezzulo

and Levin, 2015), which are complex collective

phenomena studied from various perspectives, e.g.,

population models (Couzin et al., 2005; Marshall

et al., 2009), game-theoretic (Challet and Zhang,

1997), or multi-agent simulations (Goldstone and

Janssen, 2005).

When agents interact socially, sometimes they act

in a complete agreement towards a shared goal, and

other times their goals may diverge or be completely

incompatible with each other. Over time, the inter-

action dynamics could alternate between cooperative

and antagonistic behavior and the ﬂow of informa-

tion could reveal a given player’s contribution for the

emergence of a particular strategy. In certain cases,

limitations in the perception–action loop or in the

decision-making capabilities of agents could make

them behave irrationally while coordinating their joint

activities (e.g. autistic behavior).

In our study, we explore the information-

processing burden imposed on a completely ratio-

nal agent by its irrational (or adverse) partner. We

examine the trade-off between the level of compli-

ance (i.e. cooperative coordination) within a dyad

and the information processing cost incurred by the

cooperative agent while aiming to achieve a pre-

deﬁned goal (i.e. utility level). Our framework, built

on Shannon’s information theory (Shannon, 1949),

imposes certain information processing constraints,

while not assuming any intrinsic dynamics nor a par-

ticular metabolism in providing necessary and sufﬁ-

cient environmental conditions and invariants. This

approach allows to characterize causal relationships

in Bayesian networks. For this purpose, information

theory provides a universal language for quantifying

conditions and invariants for a large class of models in

a generic and principled way. Furthermore, it allows

comparison of models that are otherwise not directly

comparable.

To study agent coordination from an information-

theoretic perspective towards a predictive and quan-

titative theory of agent interactions, we look at em-

bodied agent dyads interacting in a grid-world. The

agents have independent controllers and a fully re-

dundant set of actions for controlling the same ob-

ject in the grid. Using information-theoretic tools, we

explore the information processing constraints of an

agent in achieving a speciﬁc goal, depending on the

level of cooperation by its partner.

2 BACKGROUND

Initially, social interaction and coordination have

been studied by (Walter, 1950) in natural and artiﬁ-

cial agents, and more recently by (Ikegami and Iizuka,

2007; Paolo et al., 2008; Goldstone and Janssen,

2005). The study of coordination has applications

304

Trendaﬁlov, D., Polani, D. and Ferscha, A.

Information-theoretic Cost of Decision-making in Joint Action.

DOI: 10.5220/0010252303040311

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 1, pages 304-311

ISBN: 978-989-758-484-8

in ethology, where it helps to understand collec-

tive tasks like foraging, ﬂocking or group decision-

making (Couzin et al., 2005; Nabet et al., 2009). Stig-

mergy in coordinated behavior of ant-like agents was

investigated by (Meyer and Wilson, 1991) in a study

based on cellular models of morphogenesis. Stig-

mergy and local observation are common ways for

modelling agent communication and coordinated be-

havior (Castelfranchi, 2006). In both cases, commu-

nication is ‘channeled’ through the environment, in

the case of stigmergy in a very explicit way by alter-

ing the environment. In these models communication

is spatially bound and limited by the amount of infor-

mation that can be ‘stored’ in the environment.

The study of collective behavior has traditionally

relied on a variety of different methodological tools,

ranging from more theoretical methods such as popu-

lation or game-theoretic models to empirical ones like

Monte Carlo or multi-agent simulations. More recent

approaches use information theory as a methodolog-

ical framework to study the ﬂow of information and

the statistical properties of collectives of interacting

agents. Several general purpose tools provide efﬁ-

cient information-theoretic analysis, including classi-

cal information-theoretic measures, measures of in-

formation dynamics and information-based methods

to study the statistical behavior of collective systems

(Moore et al., 2018; Lizier et al., 2014; Lindner et al.,

2011). A study by (Valentini et al., 2018), using

simulated agents, applies transfer entropy (Schreiber,

2000) to measure the ﬂow of information generated in

collective decision-making mechanisms. The appli-

cation of complexity measures, and information the-

ory metrics in general, to support the automatic design

and analysis of collaborative dynamics, have recently

attracted the interest of multi-agent and robotics com-

munities, owing to their capability to capture relevant

features of robot behaviors while abstracting from im-

plementation details (Roli et al., 2019). In a study of a

homeokinetic dyad (Martius et al., 2008) suggest the

fundamental role of the maximal integration of the en-

vironment into the sensorimotor loop. Building on the

free energy principle of the brain (Friston, 2010), in

conjunction with the theory of sense-making, (Davis

et al., 2017) proposed a method to quantify interac-

tion dynamics of creative collaboration, e.g. rhythm

of interaction or turn-taking style, in order to charac-

terize collaborations over time. Multi-objective rein-

forcement learning has been applied with respect to

fairness (Matsui, 2019) and dyadic trust models have

been investigated by (Callebert et al., 2016).

Information theory has been successfully em-

ployed to models of embodied agents in a grow-

ing body of scientiﬁc literature starting from (Ashby,

1956). It provides a quantitative framework for as-

sessing how information is exchanged and processed

in collectives and has been explored in studies of nat-

ural (Zenil et al., 2015; Meyer, 2017; Butail et al.,

2016; Mwaffo et al., 2017) and artiﬁcial systems

(Sperati et al., 2011; Boedecker et al., 2011; Walker

et al., 2012; Kim et al., 2015). The premise is that

information is a key resource for organisms, which

is costly to process and affects the way information-

theoretic models of agents are investigated (Polani

et al., 2007). This idea has received an increased

attention due to new techniques by (Touchette and

Lloyd, 2000; Klyubin et al., 2007), and there are now

broad applications of information theory (Shalizi and

Crutchﬁeld, 2002). The concept of relevant informa-

tion, introduced by (Polani et al., 2001; Polani et al.,

2006), builds on the Information Bottleneck princi-

ple (Tishby et al., 1999), extended to the perception–

action loop. Building on the relevant information for-

malism, (Harder et al., 2010) introduced a measure

of individuality (or autonomy) in a collaborative task

under information processing constraints.

3 INFORMATION THEORY

Shannon’s Information Theory deﬁnes entropy by

H(X) = −

∑

p(x)log p(x)

where X denotes a discrete random variable taking

values from X , and p(x) the probability of X taking

on the value x ∈ X . Entropy can be interpreted as the

average amount of information gained when a vari-

able’s value is revealed. When multiple random vari-

ables are correlated, then knowing the value of one

reduces the uncertainty about the other. The average

uncertainty about Y left after revealing the value of X

is quantiﬁed by the conditional entropy

H(Y |X) = −

∑

x,y

p(x, y)log p(y|x).

The average reduction in uncertainty, interpreted as

the amount of information that knowing X gives about

Y , is deﬁned as the mutual information between the

two variables

I(X;Y ) = H(Y ) − H(Y |X).

In this study we apply and adapt the Relevant Infor-

mation method originally introduced in (Polani et al.,

2006), to joint action. It provides a measure depend-

ing only on the stochastic model and independent of

the topology of the environment. The measure quan-

tiﬁes the minimal amount of information an agent

needs to process in order to achieve a certain level

Information-theoretic Cost of Decision-making in Joint Action

305

of utility as speciﬁed by a reward function. It reﬂects

an information parsimony principle, suggesting that

processing information has a metabolic cost (Polani

et al., 2007) and complies with ﬁndings that certain

neurons work at informational limits, minimising the

bandwidth to just maintain their function (Laughlin,

2001). In theory, the relevant information can be

much lower than the bandwidth of the sensor, that is,

different sensory inputs lead to the same distribution

of actions. An algorithm, proposed in (Polani et al.,

2006), computes the information-utility trade-off us-

ing a utility in terms of a reward structure.

4 SCENARIO

In our experimental scenario two agents perform the

task of achieving a particular goal conﬁguration to-

gether (under information processing constraints) us-

ing controls from the same set of actions and alternat-

ing their moves on even (agent A) and odd (agent B)

steps. We can compute the optimal policy for each

agent using the Relevant Information method, assum-

ing we have a prediction for the policy of the other

agent. Our goal is to investigate how the behavior of

agent B inﬂuences the optimal policy and the infor-

mation constraints of agent A, and how that affects

the joint action.

The experimental setup consists of two agents

jointly moving an object in a 2-D grid-world by us-

ing four actions (up, down, left, right). The goal is

to move the object from one corner of the grid to the

opposite corner along the diagonal. The state of the

environment is denoted with the random variable S.

The scenario uses deterministic state transition model

p(s

t+1

, s

) ∈ {0, 1}, which reﬂects the movement of

the object in the grid-world constrained by the walls.

In every step the agents get a reward determined by a

reward function r(s

t+1

), which depends on the

current state, the action taken and the state of the

world after the action is executed. The reward func-

tion of agent A is −1 for all states except the goal

state where it is 0. Thus, a policy that maximises the

expected utility of agent A is one that takes the short-

est path to the goal conﬁguration. Note that due to the

particular action set there are many different shortest

paths to the goal, which however differ in informa-

tional cost as will be demonstrated later.

The underlying Markov Decision Process (MDP)

deﬁnes a reinforcement learning problem in which a

state value function V

(s) speciﬁes the expected fu-

ture reward at some state s following the policy π, and

a utility function U

(s, a) that gives the expected re-

ward incorporating the action chosen at state s and

following the policy π, deﬁned as

(s, a) =

∑

p(s

|s, a)[r(s, a, s

) + γV

)]. (1)

The discount factor γ ∈ [0, 1] controls the trade-off be-

tween long-term and short-term rewards – if γ is large,

future rewards weigh more in the expected sum, and

if it is small immediate rewards have higher relative

weight.

Finding an expected future reward maximising

policy is equivalent to solving the following optimiza-

tion problem:

∗

= argmax

(s),

where the optimal policy π

∗

is not necessarily unique.

Moreover, any convex combination απ

∗

+ (1 − α)π

∗

(α ∈ (0, 1)) of two optimal policies π

∗

and π

∗

results

in a new optimal policy. Having multiple optimal

policies poses the question of whether one is preferred

over the others. One natural criterion is the cognitive

processing associated with executing a speciﬁc pol-

icy, i.e. the cost of making a decision. The standard

value iteration algorithm ﬁnds an optimal policy by

computing ﬁrst the optimal value function V

∗

(s) = max

p(s

|s, a)[r(s, a, s

) + γV

∗

)] (2)

starting from an arbitrary V and iterating Equation 2

until convergence (Bellman, 1957). From dynamic

programming this iteration is known to converge

to a global optimal solution, providing a numerical

method for its computation (Sutton et al., 1999).

If the agents have independent controllers and

their actions are interleaving, that is, if agent A makes

a move on even and agent B on odd steps, the prob-

lem boils down to optimizing one agent’s policy with

respect to the other agent’s policy. In the optimisation

we use a static prediction for agent B’s policy, which

we scale in different trials from fully cooperative to

completely antagonistic. Assuming a particular strat-

egy of agent B, agent A optimizes its own action pol-

icy in order to achieve the goal under informational

constraints.

The scenario involves two dependent MDPs that

are not deterministic anymore and whose transition

probabilities depend on a prediction of the other

agent’s action. In every iteration we use as a predic-

tor the policy of the other agent. In a scenario where

agents do not know anything about each other it is rea-

sonable to set the predictor to a uniform distribution.

In this study, we investigate how the behavior of one

agent adapts to various strategies of the other agent.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

306

5 OPTIMAL POLICIES

The relevant information represents the minimal level

of information (mutual information between states

and actions over all optimal policies) required for

achieving a certain level of performance as charac-

terised by the expected utility E[U (S, A)], which is

deﬁned as:

[U (S, A)] =

∑

s,a

π(a|s)p(s)U (s, a).

The problem of informational parsimony can be

formulated as search for a value-optimal strategy

∗

(a|s), which at the same time minimises the re-

quired relevant information I(S;A), i.e. is also

information-optimal. This double optimisation is

transformed into an unconstrained minimisation prob-

lem via Lagrange multipliers:

min

π(a|s)

(I(S; A) − βE[U(S, A)]).

The β multiplier implicitly enforces the maximisation

of U (S; A). For β → ∞ the optimisation restricts the

policy to a value-optimal one. A reduction of β, how-

ever, makes the minimisation less sensitive to a drop

in utility. This minimax optimisation problem corre-

sponds to trading in utility for a reduction of relevant

information.

To compute the policies corresponding to com-

pletely rational and completely irrational behavior we

executed the Relevant Information algorithm with a

single agent and two extreme β multipliers, β → −∞

and β → ∞, as suggested in (Ortega and Braun, 2013),

the former providing the antagonistic policy and the

latter the cooperative one. In both cases the reward

function was the same: 0 for the goal state and -1 else-

where. The task is episodic and the agents act only

until they reach the goal conﬁguration.

To obtain a policy that is optimal and informa-

tionally parsimonious (Polani et al., 2006) extended

the standard value iteration method to accommodate

for the double optimisation by adding an interleaved

Blahut-Arimoto iteration (Blahut, 1972) with the util-

ity as a distortion measure for computing the strategy

as follows:

(a) =

∑

p(s)π

(a|s)

k+1

(a|s) =

(a)exp[βU

(s, a)] (3)

where k denotes the iteration step, ζ is a normalis-

ing partitioning function and β a parameter trading

off utility and relevant information.

The policy update iteration is alternated with a

value iteration to get a consistent utility. This leads

to the following iteration:

(2)

−→ V

(1)

−→ U

(3)

−→ π

which generates a sequence of consistent policy–

utility (π–U) pairs for a speciﬁc β, by interlacing

the updates corresponding to Equations 1 and 3, and

performing these iterations until convergence of both

policy and utility.

This approach allows the computation of optimal

strategies while trading off utility and relevant infor-

mation. However, it does not address the cost in-

volved with obtaining information, but focuses only

on how much (relevant) information needs to be ac-

quired (and processed) in order to achieve a certain

level of utility, ignoring the possible acquisition cost.

It speciﬁes the amount of information an agent takes

in and processes on average per time-step in the action

selection process. This amount depends on the pol-

icy – different policies require different informational

bandwidth, i.e. processing capacity. It is hypothe-

sised that the required capacity is correlated to the

metabolic cost of information processing and consti-

tutes a quantitative measure of cognitive burden. The

parsimony pressure tries to minimise this quantity

while the efﬁciency pressure drives towards higher

performance. Therefore for β → ∞ the resulting opti-

mal policy maximizes the expected utility and at the

same time minimizes the mutual information I(S; A).

Two extensions of relevant information to multi-

ple steps provide similar algorithms unifying Value

Iteration with Blahut-Arimoto for minimizing infor-

mation quantities in Bayesian graphs under optimality

constraints (Tishby and Polani, 2011).

To adapt the relevant information algorithm for the

scenario involving two agents with independent con-

trollers we introduce the following modiﬁcation. As

the agents alternate in taking actions, the policy op-

timization of agent A needs to take into account the

policy of agent B, which we replace by a static pre-

diction. On every iteration we combine the static pre-

diction of agent B’s policy with the current policy of

agent A:

π ∼ π

+ π

and use the resulting policy

π in the utility update,

which provides the following modiﬁed iteration:

−→ V

−→ U

−→ π

This iteration optimizes the policy of agent A while

taking into consideration the implications of the co-

operative or antagonistic behavior of agent B in the

shared environment.

Information-theoretic Cost of Decision-making in Joint Action

307

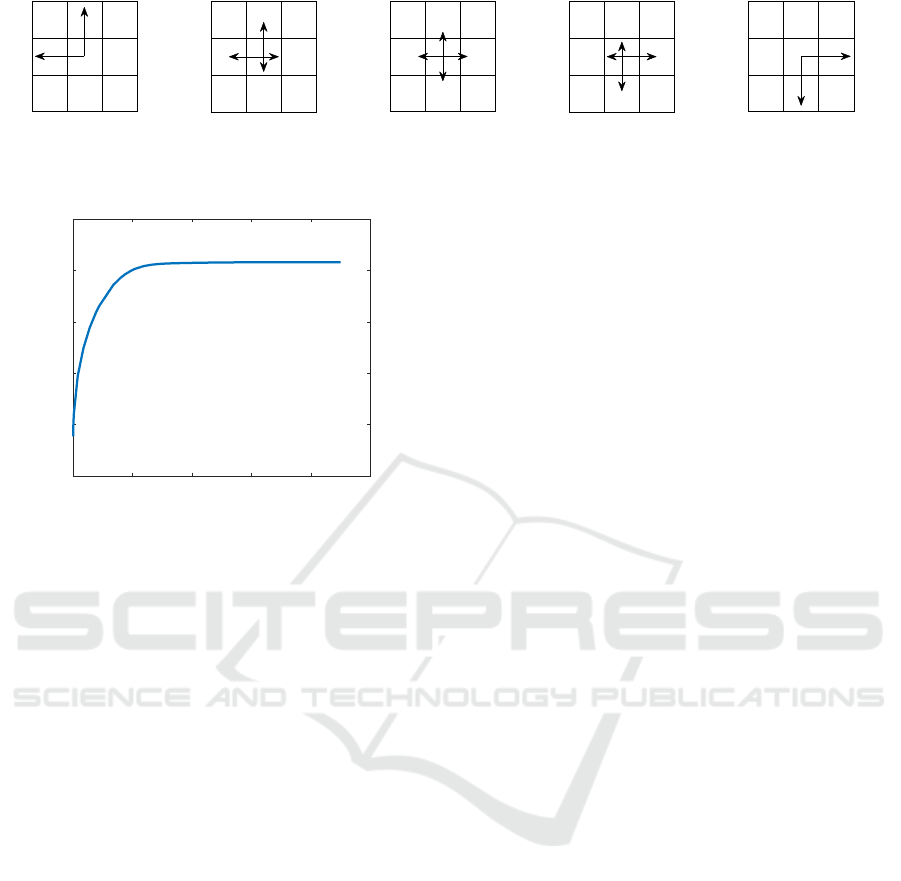
Figure 1: Various uniform strategies of agent B ranging from completely antagonistic to fully cooperative (left to right). G

denotes the goal state and the arrow length represents the action probability, which is 0.5 at the extremes (left/right) and 0.25

in the middle.

0 0.2 0.4 0.6 0.8 1

Relevant information I(S,A) (bits)

-600

-550

-500

-450

-400

-350

Utility

Figure 2: Utility vs. Relevant Information trade-off curve

of agent A corresponding to the uniform policy of agent B.

For different policies of agent B the curve has similar shape

with speciﬁc offsets in utility levels.

6 INFORMATION-UTILITY

TRADE-OFF

We computed the optimal policies of agent A for a

range of antagonistic and cooperative behaviors of

agent B (see Figure 1) and for multiple levels of the

trade-off factor β. The level of collaboration of agent

B (denoted with δ) varies in the range of (0,1) – where

0 corresponds to fully antagonistic and 1 to fully co-

operative behavior (see Figure 1. Factor of 0.5 corre-

sponds to a uniformly distributed policy over the ac-

tion space (see Figure 1). As expected, the resulting

utility vs. relevant information trade-off curves have

similar shapes, with speciﬁc offsets in utility levels,

increasing with the level of cooperation of agent B.

For brevity, Figure 2 presents only the trade-off curve

of agent A corresponding to the uniform policy of

agent B (see Figure 1).

A theoretic upper limit on the amount of relevant

information is given by the cardinality of the action

space, which in this case is log |A | = 2 bits. However,

the required information is below 1 bit on average (see

Figure 2), since partitioning the state space by only

two actions (right and down) provides an optimal so-

lution. As β tends to 0 so is the amount of relevant

information, since in every state of the grid a uniform

action policy over the two actions (right and down)

provides a solution, however with a lower utility.

Figure 5 reveals the change in the optimal policy

of agent A corresponding to a uniform policy of agent

B for two levels of β, low and high. The size of the ar-

rows reﬂects the probability of dominant actions. For

low β the (soft) policy is close to a uniform distribu-

tion over two actions (right and down), while for high

β most states have deterministic action probabilities.

A characteristic policy transition can be observed in

the upper-left corner of the grid in the form of rectan-

gle.

The simulated trajectories generated when apply-

ing the optimal policies of agent A for two levels of

β – high (see Figure 3) and low (see Figure 4) – are

demonstrated for ﬁve levels of collaboration. Figure 3

reveals how increasing cooperation (left to right) in-

ﬂuences the optimal path of agent A. For antagonistic

behaviors of agent B, agent A prefers to stick to the

wall, which protects the object from moving back and

decrease utility. As cooperation of agents increases,

agent A gradually moves away from the wall towards

the diagonal, which represents the optimal informa-

tionally parsimonious policy. In this particular sce-

nario the collaboration rate plays the role of a trade-

off factor between following the wall and the diago-

nal. Initially, the agent feels more conﬁdent by the

wall before switching to the diagonal, and this period

of initial uncertainty gets shorter as the agent can in-

creasingly rely on its partner. Figure 4 reveals that the

trends for lower β are similar with the typical blur,

which relaxes the required level of relevant informa-

tion. Interestingly, even with a lower pressure on the

utility level, agent A still tends to stick to the wall,

which shows how the embodiment in this scenario

helps the agent tackle excess uncertainty and stabilize

performance.

Figure 6 demonstrates similar shapes of the utility

as a function of the collaboration rate for two levels

of β (high and low). The normalized distance between

the two utility curves reveals that increased collabora-

tion rates emphasize the utility gap between different

levels of β. This suggests that decreasing the collab-

oration level has a damping effect on the inﬂuence β

has on utility, i.e., for antagonistic policies utility lev-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

308

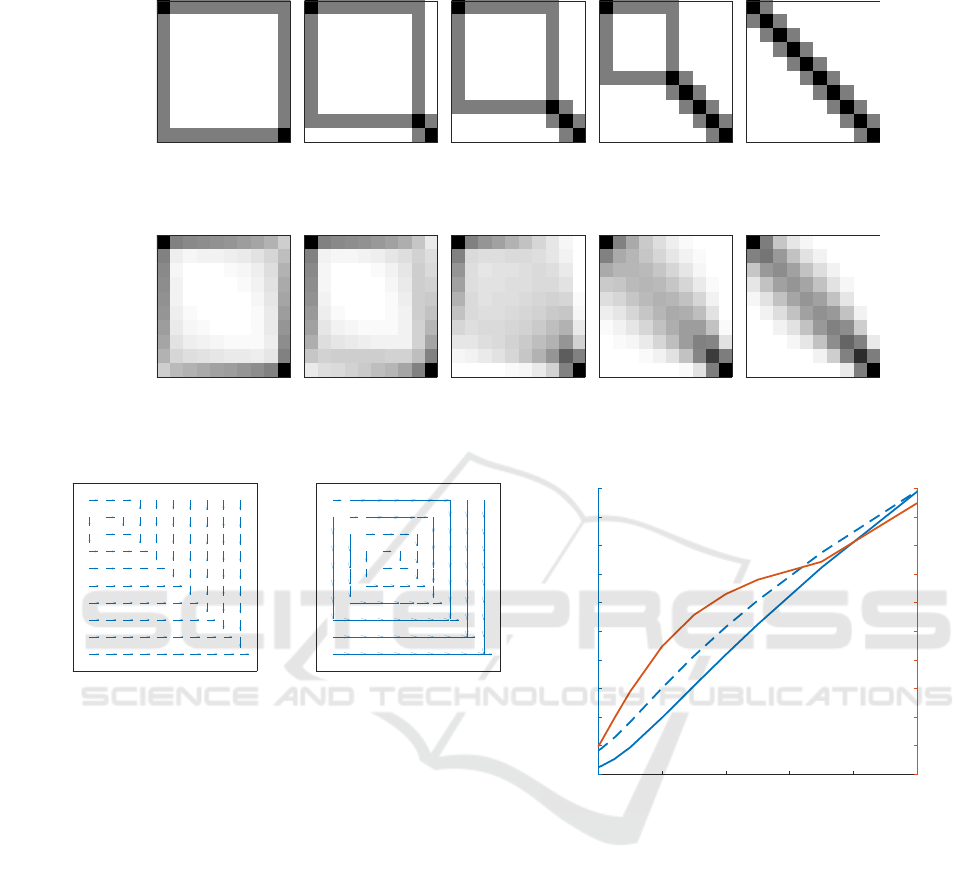
Figure 3: Simulated trajectories of agent A’s optimal policies for ﬁve collaboration rates increasing from left to right (high β).

Darker color denotes higher recurrence. For antagonistic behaviors of agent B agent A initially sticks to the wall to mitigate

risk, before gradually moving towards the diagonal as cooperation increases.

Figure 4: Simulated trajectories of agent A’s optimal policies for ﬁve collaboration rates increasing from left to right (low β).

Darker color denotes higher recurrence. Regardless of lower pressure on utility level agent A sticks to the wall to gain control

over uncertainty, revealing the role of embodiment in this scenario.

Figure 5: Optimal policies of agent A corresponding to a

uniform policy of agent B for low (a) and high (b) β. Arrow

size reﬂects dominant action probability. A policy transition

propagates from the upper-left corner along the diagonal.

els are relatively close to each other across different β.

This trend can also be observed in Figures 3/a and 4/a,

which reveal similar trajectory paths.

7 DISCUSSION

We explored a dyadic collaborative scenario in a 2-

D grid-world, where two memoryless agents with in-

dependent controllers interact using fully redundant

control. We applied a variation of the relevant in-

formation method to compute the optimal policies of

one of the agents under information processing con-

straints. Our study investigated how the behavior of

one agent inﬂuences the optimal strategy of the other

in a range of different conﬁgurations. The results

demonstrate that when the agents cooperate towards a

common goal they achieve a higher utility at a lower

informational cost. However, when their behavior is

0 0.2 0.4 0.6 0.8 1

Collaboration rate

-1000

-900

-800

-700

-600

-500

-400

-300

-200

-100

Utility

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

0.22

0.24

Normalized distance

Figure 6: Utility as a function of collaboration rate for high

(dashed) and low (solid) levels of β (blue). The normal-

ized distance between these utility curves (red) reveals how

higher collaboration emphasize the utility gap in β levels.

antagonistic to each other, the utility level drops sig-

niﬁcantly and the informational cost increases. One

could think of various situations where this scenario

could arise, for example, if the controllers are stochas-

tic, or the precise knowledge of the other agent’s

model is unavailable or compromised, or the other

agent is adverse or autistic.

The results reveal that when facing an antagonis-

tic partner, the cooperative agent exploits the partic-

ular embodiment of its environment in order to max-

imize its control abilities. This suggests that the ap-

plied method of relevant information is able to iden-

tify salient features of the state space and beneﬁt from

them in order to provide an optimal informationally

Information-theoretic Cost of Decision-making in Joint Action

309

parsimonious strategy in various environmental con-

ditions. This initial study did not reveal further in-

terplay between the informational cost and the rate

of collaboration, however, future work could explore

this trade-off with more elaborate and focused scenar-

ios. The optimal policies derived in our study operate

with relevant information intake in the range of [0,1]

bits on average per step, which is considerably lower

than the theoretical limit of 2 bits, suggesting that a

different embodiment could result in a higher infor-

mation burden and provide deeper insights.

In this particular scenario, our approach highlights

two types of optimal trajectories, one following the

walls and another one traversing the diagonal, and

trades off these two paths on the base of cooperation

level. Furthermore, the results demonstrate that high

cooperation rates (δ) emphasize the role of β in re-

inforcing high performance levels, which suggests a

speciﬁc trade-off between δ and β and is an interest-

ing topic for future research.

The key beneﬁts of the applied information-

theoretic treatment are that it is universal, general and

could enable the direct comparison of scenarios with

different computational models. The proposed ap-

proach reframes the problem into a trade-off between

the reward achieved and the informational cost of per-

forming a task by incorporating limits on the informa-

tion processing capacity, which are fundamental prop-

erties of agent–environment systems. The framework

can be further extended to tackle issues of time shifts

and turn-taking in the decision process.

8 CONCLUSION

This paper presents an application of an information-

theoretic framework to a reward driven decision

process in the perception–action cycle of a dyad.

We demonstrate interesting behaviors generated in

robotic agents based on self-organization following

the principle of homeokinesis. Driven by this prin-

ciple through the interaction with its environment, the

agent shows preferences for states where its control

actions are most effective in avoiding unpredictable

and undesired situations. We believe that theories and

tools from complex systems and information theory

may successfully be applied in the future for facili-

tating the automated design of robot collectives and

for the analysis of their dynamics. The proposed ap-

proach could provide a framework supporting the cre-

ation of artiﬁcial agents, which not only act optimally,

but optimize also their computational resources in the

decision-making process. Further work is required to

evolve this methodology into the continuous action

domain and showcase its application in more realis-

tic practical scenarios.

ACKNOWLEDGEMENTS

The authors would like to acknowledge support by

H2020-641321 socSMCs FET Proactive and FFG-

6112792 Pro

Future projects.

REFERENCES

Ashby, W. R. (1956). An Introduction to Cybernetics. Chap-

man & Hall Ltd.

Bellman, R. E. (1957). Dynamic Programming. Princeton

University Press.

Blahut, R. (1972). Computation of channel capacity and

rate distortion functions. IEEE Transactions on Infor-

mation Theory, 18(4):460–473.

Boedecker, J., Obst, O., Lizier, J., Mayer, N., and Asada, M.

(2011). Information processing in echo state networks

at the edge of chaos. Theory in biosciences, 131:205–

13.

Butail, S., Mwaffo, V., and Porﬁri, M. (2016). Model-free

information-theoretic approach to infer leadership in

pairs of zebraﬁsh. Physical Review E, 93.

Callebert, L., Lourdeaux, D., and Barth

es, J.-P. (2016).

A trust-based decision-making approach applied to

agents in collaborative environments. In Proceedings

of the 8th International Conference on Agents and Ar-

tiﬁcial Intelligence, pages 287–295.

Castelfranchi, C. (2006). Silent agents: From observation

to tacit communication. Advances in Artiﬁcial Intelli-

gence - IBERAMIA-SBIA, (4140):98–107.

Challet, D. and Zhang, Y.-C. (1997). Emergence of co-

operation and organization in an evolutionary game.

Physica A: Statistical Mechanics and its Applications,

246(3):407 – 418.

Couzin, I., Krause, J., Franks, N., and Levin, S. (2005).

Effective leadership and decision-making in animal

groups on the move. Nature, 433 (7025):513–516.

Davis, N., Hsiao, C., Singh, K. Y., Lin, B., and Magerko, B.

(2017). Quantifying collaboration with a co-creative

drawing agent. ACM Transactions on Interactive In-

telligent Systems (TiiS), 7:1–25.

Franks, N., Pratt, S., Mallon, E., Britton, N., and Sumpter,

D. (2002). Information ﬂow, opinion-polling and col-

lective intelligence in house-hunting social insects.

Philosophical Transactions B: Biological Sciences,

357 (1427):1567–1583.

Friston, K. (2010). The free-energy principle: a uniﬁed

brain theory? Nature reviews. Neuroscience, 11:127–

38.

Goldstone, R. and Janssen, M. (2005). Computational mod-

els of collective behavior. Trends in Cognitive Sci-

ences, 9(9):424–430.

Harder, M., Polani, D., and Nehaniv, C. L. (2010). Two

agents acting as one. In Artiﬁcial Life, pages 599–606.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

310

Ikegami, T. and Iizuka, H. (2007). Turn-taking interaction

as a cooperative and co-creative process. Infant Be-

havior and Development, (30):278–288.

Kim, H., Davies, P., and Walker, S. (2015). New scal-

ing relation for information transfer in biological

networks. Journal of the Royal Society, Interface,

12(113):20150944.

Klyubin, A. S., Polani, D., and Nehaniv, C. L. (2007). Rep-

resentations of space and time in the maximization of

information ﬂow in the perception-action loop. Neural

Computation, 19(9):2387–2432.

Laughlin, S. B. (2001). Energy as a constraint on the cod-

ing and processing of sensory information. Current

Opinion in Neurobiology, 11:475–480.

Lindner, M., Vicente, R., Priesemann, V., and Wibral, M.

(2011). Trentool: A matlab open source toolbox

to analyse information ﬂow in time series data with

transfer entropy. BMC neuroscience, 12:119.

Lizier, J. T., Prokopenko, M., and Zomaya, A. Y. (2014).

A Framework for the Local Information Dynamics of

Distributed Computation in Complex Systems, pages

115–158.

Marshall, J. A. R., Bogacz, R., Dornhaus, A., Planqu

R., Kovacs, T., and Franks, N. R. (2009). On

optimal decision-making in brains and social insect

colonies. Journal of the Royal Society, Interface,

6(40):1065—1074.

Martius, G., Nolﬁ, S., and Herrmann, J. (2008). Emergence

of interaction among adaptive agents. In 10th Interna-

tional Conference on Simulation of Adaptive Behav-

ior, pages 457–466.

Matsui, T. (2019). A study of joint policies considering

bottlenecks and fairness. In Proceedings of the 11th

International Conference on Agents and Artiﬁcial In-

telligence, pages 80–90.

Meyer, B. (2017). Optimal information transfer and

stochastic resonance in collective decision making.

Swarm Intelligence, 11:1–24.

Meyer, J. A. and Wilson, S. W. (1991). The Dynamics of

Collective Sorting Robot - Like Ants And Ant - Like

Robots, pages 356–363.

Moore, D. G., Valentini, G., Walker, S. I., and Levin, M.

(2018). Inform: Efﬁcient information-theoretic anal-

ysis of collective behaviors. Frontiers in Robotics and

AI, 5:60.

Mwaffo, V., Butail, S., and Porﬁri, M. (2017). Analysis of

pairwise interactions in a maximum likelihood sense

to identify leaders in a group. Frontiers in Robotics

and AI, 4:35.

Nabet, B., Leonard, N., Couzin, I., and Levin, S. (2009).

Dynamics of decision making in animal group mo-

tion. journal of nonlinear science. Proceedings of the

National Academy of Sciences of the United States of

America, 19(4):399–435.

Ortega, P. and Braun, D. (2013). Thermodynamics as a the-

ory of decision-making with information-processing

costs. Royal Society: Mathematical, Physical and En-

gineering Sciences, 469(2153).

Paolo, E. D., Rohde, M., and Iizuka, H. (2008). Sensitivity

to social contingency or stability of interaction? mod-

elling the dynamics of perceptual crossing. New Ideas

in Psychology, 26(2):278–294.

Pezzulo, G. and Levin, M. (2015). Re-membering the body:

applications of computational neuroscience to the top-

down control of regeneration of limbs and other com-

plex organs. Integr. Biol., 7:1487–1517.

Polani, D., Martinetz, T., and Kim, J. T. (2001). An

information-theoretic approach for the quantiﬁcation

of relevance. 6th European Conference on Advances

in Artiﬁcial Life, pages 704–713.

Polani, D., Nehaniv, C., Martinetz, T., and Kim, J. T.

(2006). Relevant information in optimized persistence

vs. progeny strategies. In 10th International Confer-

ence on the Simulation and Synthesis of Living Sys-

tems, pages 337–343. MIT Press.

Polani, D., Sporns, O., and Lungarella, M. (2007). How in-

formation and embodiment shape intelligent informa-

tion processing. In 50 Years of Artiﬁcial Intelligence,

pages 99–111.

Roli, A., Ligot, A., and Birattari, M. (2019). Complex-

ity measures: Open questions and novel opportunities

in the automatic design and analysis of robot swarms.

Frontiers in Robotics and AI, 6:130.

Schreiber, T. (2000). Measuring information transfer. Phys.

Rev. Lett., 85(2):461–464.

Shalizi, C. R. and Crutchﬁeld, J. P. (2002). Information bot-

tlenecks, causal states, and statistical relevance bases:

How to represent relevant information in memoryless

transduction. Advances in Complex Systems, (5):91.

Shannon, C. E. (1949). The mathematical theory of com-

munication. The University of Illinois Press, Urbana.

Sperati, V., Trianni, V., and Nolﬁ, S. (2011). Self-organised

path formation in a swarm of robots. Swarm Intelli-

gence, 5:97–119.

Sutton, R., Precup, D., and Singh, S. (1999). A frame-

work for temporal abstraction in reinforcement learn-

ing. Artiﬁcial intelligence, 112(1-2):181–211.

Tishby, N., Pereira, F. C., and Bialek, W. (1999). The

information bottleneck method. In The 37th annual

Allerton Conference on Communication, Control, and

Computing, pages 368–377.

Tishby, N. and Polani, D. (2011). Information theory of de-

cisions and actions. In Cutsuridis, V., Hussain, A., and

Taylor, J., editors, Perception-Action Cycle: Models,

Architecture and Hardware, pages 601–636. Springer.

Touchette, H. and Lloyd, S. (2000). Information-theoretic

limits of control. Phys. Rev. Lett., 84(6):1156–1159.

Valentini, G., Moore, D. G., Hanson, J. R., Pavlic, T. P.,

Pratt, S. C., and Walker, S. I. (2018). Transfer of in-

formation in collective decisions by artiﬁcial agents.

Artiﬁcial Life Conference Proceedings, (30):641–648.

Walker, S., Cisneros, L., and Davies, P. (2012). Evolution-

ary transitions and top-down causation. 13th Interna-

tional Conference on the Simulation and Synthesis of

Living Systems, pages 283–290.

Walter, W. (1950). An imitation of life. Scientiﬁc American,

May:42–45.

Zenil, H., Marshall, J. A. R., and Tegn

er, J. (2015). Ap-

proximations of algorithmic and structural complexity

validate cognitive-behavioural experimental results.

CoRR, abs/1509.06338.

Information-theoretic Cost of Decision-making in Joint Action

311