Novelty Detection in Physical Activity

Bernardo Leite, Amr Abdalrahman, Jo

ao Castro, Julieta Frade, Jo

ao Moreira and Carlos Soares

Department of Informatics Engineering, Faculty of Engineering, University of Porto,

R. Dr. Roberto Frias, 4200-465, Porto, Portugal

Keywords:

Artiﬁcial Intelligence, Machine Learning, Activity Recognition, Novelty Detection.

Abstract:

Artiﬁcial Intelligence (AI) is continuously improving several aspects of our daily lives. There has been a

great use of gadgets & monitoring devices for health and physical activity monitoring. Thus, by analyzing

large amounts of data and applying Machine Learning (ML) techniques, we have been able to infer fruitful

conclusions in various contexts. Activity Recognition is one of them, in which it is possible to recognize and

monitor our daily actions. The main focus of the traditional systems is only to detect pre-established activities

according to the previously conﬁgured parameters, and not to detect novel ones. However, when applying

activity recognizers in real-world applications, it is necessary to detect new activities that were not considered

during the training of the model. We propose a method for Novelty Detection in the context of physical

activity. Our solution is based on the establishment of a threshold conﬁdence value, which determines whether

an activity is novel or not. We built and train our models by experimenting with three different algorithms and

four threshold values. The best results were obtained by using the Random Forest algorithm with a threshold

value of 0.8, resulting in 90.9% of accuracy and 85.1% for precision.

1 INTRODUCTION

There are many applications which are required to de-

cide whether a new observation belongs to the same

distribution as existing observations (inlier), or should

be considered as different (outlier)

. We, therefore,

make this important distinction:

• Outlier Detection: Aims to detect outlier(s),

i.e., an observation which deviates so much from

the other observations as to arouse suspicions

that it was generated by a different mechanism

(Hawkins et al. (2002)).

• Novelty Detection: Aims to detect novel classes,

i.e., classes that were not seen in the training set.

Typically a classiﬁcation problem.

Novelty detection is the identiﬁcation of new or un-

known classes that a machine learning system is not

aware of during training (Miljkovi

c, 2010). More-

over, this can also be deﬁned as the task of discover-

ing that test data differ in some respect from the data

available from the training step. The main goal is to

try to recognize/identify these new observations that

are different (or not consistent) with the original train-

ing data.

https://scikit-learn.org/stable/modules/outlier

detection.html

Novelty detection has its impact in many practi-

cal and real-life applications regarding different do-

mains. In concrete, these application areas can be di-

vided into 6 distinct categories: (a) Information and

Technology (IT) Security, (b) Industrial Monitoring,

Mining, (e) Sensor Networks and, ﬁnally, (f) Health-

care Informatics and Medical Diagnosis. Research in

IT Security systems mainly includes fraud detection

to avoid malicious programs and the identiﬁcation of

intrusions (Helali, 2010). Studies in Industrial Mon-

itoring try to identify deterioration in industrial as-

sets as early as possible (Surace and Worden, 2010).

The use of novelty detection techniques for Image

and Video (Markou and Singh, 2006; Yong et al.,

2013) allow us to identify novel objects in images and

video streams. Regarding Text Mining, the goal is to

detect novel topics, new stories, and events (Zhang

et al., 2005). Research in Sensor Networks (Has-

san et al., 2011) mainly focuses on discovering faults

and malicious attacks on these networks. Lastly, re-

search in Healthcare Informatics and Medical Diag-

nosis (Clifton et al., 2011) has great importance since

it helps to identify clinically relevant changes in pa-

tient health. Thus, it facilitates a more timely inter-

vention by doctors.

By studying Novelty Detection for Physical Activ-

Leite, B., Abdalrahman, A., Castro, J., Frade, J., Moreira, J. and Soares, C.

Novelty Detection in Physical Activity.

DOI: 10.5220/0010254908590865

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 2, pages 859-865

ISBN: 978-989-758-484-8

859

ity we will process data records from vital signs. For

such, we use the PAMAP2 dataset (Reiss and Stricker,

2012a,b), from UCI Machine Learning Repository

This dataset contains data of 18 different physical ac-

tivities (such as walking, cycling, playing soccer, etc),

performed by 9 subjects wearing 3 inertial measure-

ment units (IMU) and a heart rate monitor. We select

three of the available activities to train our classiﬁ-

cation models. For that, we experiment with three

algorithms: Decision Tree, Random Forest, and K-

Nearest Neighbors (k-NN). To detect novel activities,

the main idea is to insert new activities (the original

three plus two) into the test data (that were not in the

training data) and, by comparing the model’s predic-

tion conﬁdence with a certain threshold (tested with

0.5, 0.6, 0.7 and 0.8), classify them as a novel or not.

We emphasize the fact that we propose this approach

in a little-explored context of novelty detection, which

is Activity Recognition.

The rest of the paper is structured as follows. Sec-

tion 2 presents previous research in Novelty Detec-

tion and Activity Recognition. Section 3 describes in

detail our methodology and Section 4 outlines the re-

sults from evaluation. Conclusions and future work

are exposed in Section 5.

2 LITERATURE REVIEW

One of the most signiﬁcant reviews in the con-

text of novelty detection was conducted by Pimentel

et al. (2014). They provided a structured investiga-

tion of novelty detection approaches that have ap-

peared in the Machine Learning literature. These ap-

proaches fall into ﬁve different categories: probabilis-

tic, distance-based, reconstruction-based, domain-

based, and information-theoretic techniques. We use

that study as a reference to the methodologies that we

will now synthesize.

Starting with the probabilistic techniques (Clifton

et al., 2012; Hazan et al., 2012), these mainly use

probabilistic methods that involve a density estima-

tion of the normal/usual/standard class. Also, they

consider that low-density areas from the training set

indicate that these areas have a low probability of in-

cluding normal objects. Distance-based techniques

are related to the Nearest Neighbor approach (Ghot-

ing et al., 2008) in which a certain point is consid-

ered as a novelty if its distance to a k-NN neighbor

surpasses the predeﬁned threshold. Also, distance-

based techniques include the concept of clustering

analysis (Viegas et al., 2018) where is the assump-

https://archive.ics.uci.edu/ml/index.php

tion that normal data belong to dense (and large)

clusters, whereas novel objects don’t belong to any

of these clusters. By using reconstruction-based ap-

proaches (Marchi et al., 2015; Xia et al., 2015), the

main idea is to map the unusual data using the train-

ing model and then, the error (reconstruction error)

between the regression target and the values that are

actually observed causes a higher novelty value (or

score). Domain-based approaches (Le et al., 2010;

Peng and Xu, 2012) have the main goal of describ-

ing and characterize a domain in which is the nor-

mal/usual data is present, by creating a boundary

around the normal/usual class. Regarding Informa-

tion Theoretic techniques (Filippone and Sanguinetti,

2010; Wu and Wang, 2011), these are methods that

compute information content from the training data

by using information-theoretic measures, e.g. en-

tropy, relative entropy, and kolmogorov complexity.

The main idea is that unusual (or novel) data signiﬁ-

cantly alter the information content from the dataset.

More recently, new studies have emerged with

new advances in the ﬁeld of Deep Learning (DL). In

this context, Mello et al. (2018) propose a novelty de-

tector based on Stacked AutoEncoders (SAE) to de-

tect unknown arriving patterns in a passive sonar sys-

tem. Sabokrou et al. (2018), inspired by the success

of Generative Adversarial Networks (GANs), propose

an end-to-end architecture for one-class classiﬁcation.

The authors make use of two deep networks: One of

them works as the novelty detector, while the other

supports it by enhancing the inlier samples and dis-

torting the outliers. Finally, in the scope of object

recognition, Lee et al. (2018) have studied informa-

tive novelty detection schemes based on a hierarchi-

cal classiﬁcation framework. They propose top-down

and ﬂatten methods, and their combination as well.

The authors claim that one of the essential ingredients

of their methods are conﬁdence-calibrated classiﬁers

for modeling novel classes.

As previously mentioned, our study is in the scope

of Activity Recognition. In this context, Sprint et al.

(2016) formalize the problem of unsupervised Phys-

ical Activity Change Detection (PACD). The authors

compare the abilities of three change detection algo-

rithms from the literature and one proposed algorithm

to capture different types of changes as part of PACD.

Rossi et al. (2018) present a two-step framework im-

plementing a strategy for the detection of Activities

of Daily Living (ADL) that are divergent from normal

ones. This strategy uses a deep learning technique to

determine the most probable ADL class related to a

certain action and a Gaussian Mixture Model to com-

pute the likelihood that the action is normal or not.

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

860

3 APPROACH

In this section, we present our approach that fol-

lows roughly the CRISP-DM methodology (Shearer,

2000). First, we start with Data Understanding (Sec-

tion 3.1), where we describe and explore the acquired

data from the chosen dataset. Still at this step, we ver-

iﬁed the quality of the same data. Then, we proceed

to Data Preparation (Section 3.2) where we apply the

necessary pre-processing steps, namely the selection,

cleaning, and integration of our data. In Modelling

and Novelty Detection (Section 3.3), we explain the

modeling selection technique, in which we build our

model and describe its parameter settings. Finally, we

present the applied technique to detect novel activi-

ties. To accomplish all these steps we made use of the

RapidMiner

3.1 Data Understanding

As stated previously, we use the information from the

PAMAP2 dataset to train and build our models. It

holds data of 18 distinct corporal activities performed

by a group consisting of 8 males and 1 female with

ages between 24 and 32. The dataset comprises the

subsequent activities with the corresponding activity

IDs: 1 (lying), 2 (sitting), 3 (standing), 4 (walking), 5

(running), 6 (cycling), 7 (nordic walking), 9 (watch-

ing TV), 10 (computer work), 11 (car driving), 12

(ascending stairs), 13 (descending stairs), 16 (vac-

uum cleaning), 17 (ironing), 18 (folding laundry), 19

(house cleaning), 20 (playing soccer), 24 (rope jump-

ing) and 0 (other/transient activities).

Also, within this dataset we were able to retrieve

a total of 2,872,533 examples (rows) equivalent to 10

hours of information along one data ﬁle per individ-

ual, comprising the following 54 columns per row:

• 1: timestamp (s);

• 2: activityID;

• 3: heart rate (bpm);

• 4-20: IMU hand;

• 21-37: IMU chest;

• 38-54: IMU ankle.

The IMU sensory data contains the following

columns attributes:

• 1: temperature (ºC);

• 2-4: 3D-acceleration data (ms

-2

), scale: ±16g;

• 5-7: 3D-acceleration data (ms

-2

), scale: ±6g;

• 8-10: 3D-gyroscope data (rad/s);

https://rapidminer.com/

• 11-13: 3D-magnetometer data (µT);

• 14-17: orientation (invalid in this data collection).

In terms of data quality, three situations for future

treatment were found. Firstly, the data examples con-

cerning activity ID 0 mainly cover transient activities

between performing different activities, e.g. going

from one location to the next activity’s location. For

this reason, it is necessary to discard these examples.

Secondly, 90% of the heart rate attribute values were

missing. Also, there is an average of 8,528 missing

values for the remaining attributes. Third and last, the

dataset is not perfectly balanced, e.g, 238,753 exam-

ples for activity ID 4 vs 98,192 examples for activity

ID 5. In the next Section 3.2, the goal is to explain

what we did to deal with the referred situations.

3.2 Data Preparation

To solve data-related problems, we start by removing

examples from activity ID 0 since they were not ac-

tual activities but yet transient ones. Regarding the

missing values, we completely removed the heart rate

attribute (ID 3) since a substantial part (90%) of the

values were missing. Timestamp (ID 1) was also ex-

cluded since we did not consider it as a relevant at-

tribute for the classiﬁcation model. Orientation (IDs

14-17) was dropped since it was invalid in this data

collection. The IMU (IDs 2-4 and 5-7) columns were

removed as they were highly related to acceleration.

After that, the examples that contained missing val-

ues were dismissed considering that they only repre-

sent 0.5% of the whole dataset. It was not necessary

to create new attributes or change/modify the existing

ones.

At the end of this phase, we are left with a total

of 1,929,578 examples (from the 2,872,533 examples

mentioned in Section 3.1), each of them containing

16 attributes (or features). In Section 3.3 we will ex-

plain the modeling and novelty detection techniques,

starting by deﬁning how many of these last examples

are used for training and testing.

3.3 Modelling and Novelty Detection

In Figure 1 it is possible to observe our experimental

setup scheme that represents the modeling and nov-

elty detection processes. Throughout this section, we

describe all the steps involved.

Previously, in Section 3.2, from the (1) Data

Preparation phase, we obtained a total of 1,929,578

examples to be used in the following steps. Thus,

from (2) Data Splitting, we separate the training and

test data by applying a split size value of 0.5 (50% for

each one) using the stratiﬁed sampling type. Stratiﬁed

Novelty Detection in Physical Activity

861

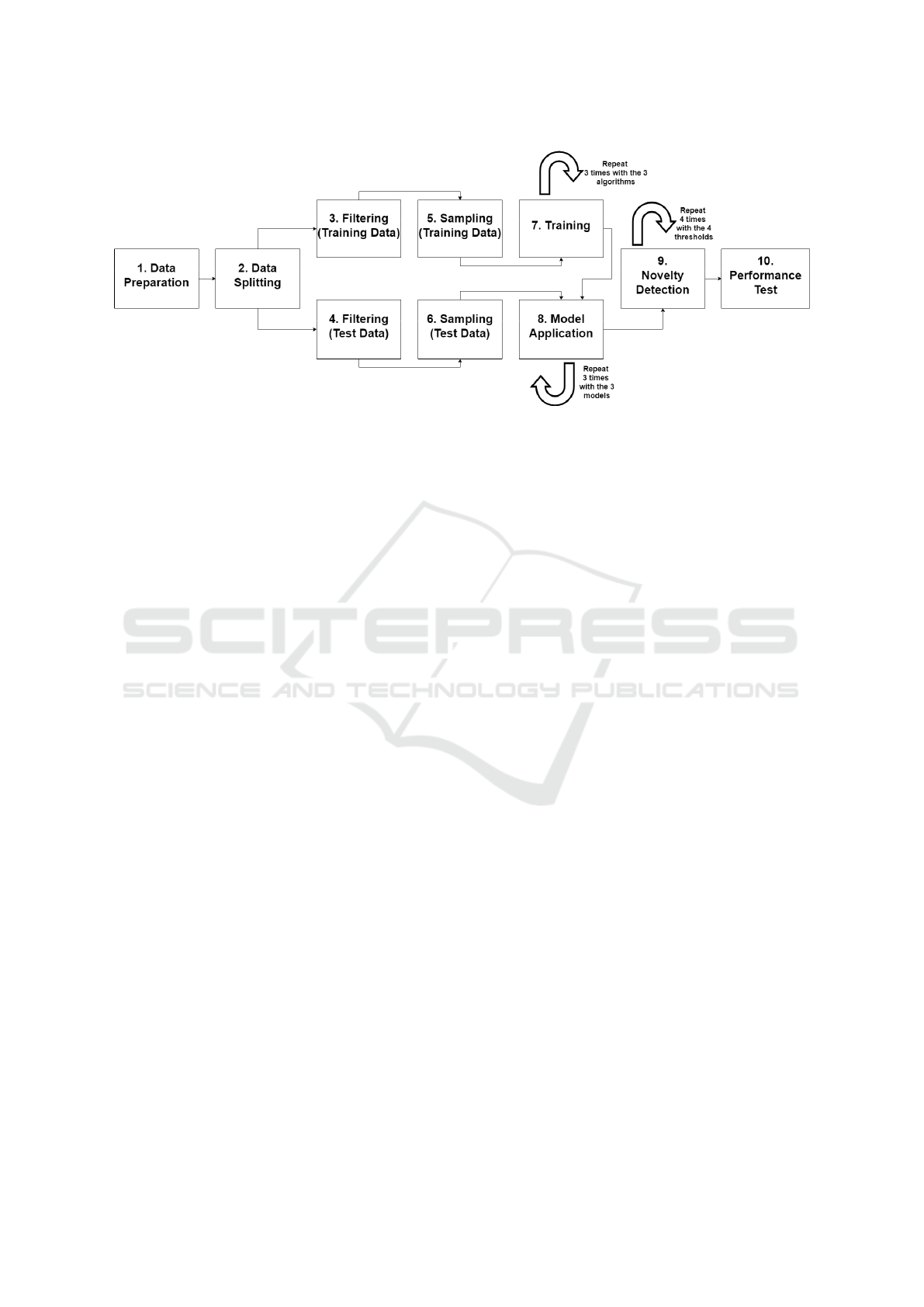
Figure 1: Modeling and Novelty Detection - Experimental Setup.

sampling builds random subsets and ensures that the

class distribution in the subsets is the same as in the

whole example set. Through this splitting, we have

964,789 examples for training and another 964,789

examples for testing. We decided to create our mod-

els to perform multiclass classiﬁcation. We consider

the ﬁrst three activities from the example set as our

classes: lying (ID 1) sitting (ID 2), and standing (ID

3). So, we use the (3) Filtering (Training Data) to

ﬁlter only the examples corresponding to ID 1, 2, or

3. This gives a total of 283,677 examples for training.

On the other hand, we use (4) Filtering (Test Data)

to ﬁlter the examples corresponding to ID 1, 2, 3 but

also two other activities: walking (ID 4) and running

(ID 5). This gives a total of 447,242 examples for

testing. This then allows us, when later applying the

novelty detection method, to classify the ﬁve activi-

ties as a novel or not (walking and running should be).

In order to adjust the dimension and class distribution

of our dataset, we use (5) Sampling (Training Data)

and (6) Sampling (Test Data) to obtain the following

ﬁnal examples:

• Number of Training Examples (1,800): lying

(600), sitting (600) and standing (600);

• Number of Testing Examples (1,250): lying

(250), sitting (250), standing (250), walking

(250), and running (250).

To train the models, we experimented with three dif-

ferent algorithms:

A Decision Tree: This uses a tree-like model of de-

cisions and their possible consequences, including

chance event outcomes, resource costs, and util-

ity;

B Random Forest: This is an ensemble of a certain

number of trees (random forest), speciﬁed by the

number of trees parameters. These trees are cre-

ated/trained on bootstrapped sub-sets of the exam-

ple set provided;

C k-NN: This is based on comparing an unknown

example with the k training examples which are

the nearest neighbors of the unknown example.

Regarding the Decision Tree, for the criterion on

which attributes are selected for splitting, we use gain

ratio that adjusts the information gain for each at-

tribute to allow the breadth and uniformity of the at-

tribute values. Also, we set the value of 100 for the

maximal depth. This parameter is used to restrict the

depth of the decision tree. The depth of a tree varies

depending upon the size and characteristics of the ex-

ample set. As for Random Forest, we set the value

of 100 for the number of trees. This parameter spec-

iﬁes the number of random trees to generate. For the

criterion on which attributes are selected for splitting,

we use information gain in which the entropies of all

the attributes are calculated and the one with the least

entropy is selected for the split. Finally, we select 50

as being the maximal depth of the trees. Concerning

k-NN, we set the value of 5 for ﬁnding the k train-

ing examples that are closest to the unknown example

(this is the ﬁrst step of the k-NN algorithm).

From (7) Training we are training our data using

each of the three algorithms. Thus, we produce three

different models after training the data with each of

the referred algorithms. Before assessing the ability

of the approach proposed here for novelty detection

(on the test set), we need to understand how good the

model is at predicting the classes it was trained with.

To do this, we estimate the predictive performance of

the algorithms using cross-validation (10 folds) on the

training data. For each algorithm, the cross-validation

produces 10 iterations, with each of the 10 subsets

used exactly once as the test data. The 10 results from

the 10 iterations are averaged to produce a single es-

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

862

timation. The performance results can be analyzed in

Table 1. These results represent the average perfor-

mance of the 10-fold cross-validation for each algo-

rithm.

Table 1: Performance Results: Accuracy (Acc), Macro-

average Precision (P), Macro-average Recall (R) and

Macro-average F1-Score (F1) for each algorithm, consid-

ering the multiclass classiﬁcation.

Algorithm

Performance

Measure (%)

Acc P R F1

Decision

Tree

94.4 94.5 94.4 94.4

Random

Forest

96.7 96.7 96.7 96.7

k-NN 95.0 95.1 95.0 95.0

We recall that these models were trained consid-

ering only three classes (lying, sitting and standing).

When we apply each model to the new data, two new

classes (walking and running) are mixed with the oth-

ers. Therefore, with (8) Model Application we are

now predicting whether a given example belongs to

one of the three classes used in the training data. For

each prediction (1, 2 or 3), the model presents the con-

ﬁdence value [0-1] for its respective decision. Also

note that each example, in addition to prediction and

conﬁdence, it has the activityID attribute that repre-

sents the correct/real activity (1, 2, 3, 4 or 5) for that

given example. In these conditions, everything is pre-

pared for the next step, (9) Novelty Detection. The

Novelty detection method can be enumerated with

three essential steps, they are:

1. Create novelty attribute which will be true or

false based on this condition:

(if conﬁdence<threshold, then novelty=true, else

novelty=false);

2. Set the novelty attribute with the target role of

prediction label;

3. Create isNovel attribute from activityID using

this condition:

(if activityID == (1 or 2 or 3), then isNovel=false,

else isNovel=true);

From item 1 the idea is to create a new attribute (nov-

elty) that can take only two values: true (it is novel)

or false (it is not novel). For that, we deﬁne the re-

ferred condition. The threshold acts as a comparison

value that will deﬁne whether the conﬁdence value for

a given prediction corresponds to a navel/non novel

activity. We experimented with four distinct thresh-

old values: 0.5, 0.6, 0.7 and 0.8. Also, note that we

now deﬁne the novelty attribute with the target role of

prediction label (item 2). Finally, from item 3 we are

creating the isNovel attribute, setting it as false (not

novel) when activityID is equal to 1, 2 or 3 and with

the value of true (is novel) when activityID is equal

to 4 or 5. This is done since we now want to compare

whether the predictions established in the new novelty

attribute (that can be true or false) correspond to the

truth, by comparing it with what is deﬁned in isNovel

attribute (also can be true or false). In other words,

we just created the (10) Performance Test, which is

our test environment for novelty detection.

4 RESULTS AND DISCUSSION

FOR NOVELTY DETECTION

In Section 3.3 we explain the modeling mechanism

and the novelty detection method. For the latter, we

end up with two important attributes: isNovel and

novelty. novelty is our prediction label, in which we

predict whether a given example is novel or not (true

or false). On the other hand, isNovel is the attribute

that contains the correct answer, that is, whether the

activity is novel or not (true or false). By compar-

ing these two values for each example, we are able to

evaluate the performance for novelty detection. The

results are shown in Table 2.

Table 2: Performance Results: Accuracy (Acc), Precision

(P), Recall (R) and F1-Score (F1) for each Algorithm (Alg)

and Threshold (T), considering our novelty detection tech-

nique.

Alg. T.

Performance

Measure (%)

Acc P R F1

Decision

Tree

0.5 60.0 50.0 0.60 1.2

0.6 59.9 47.8 2.2 4.2

0.7 59.8 47.7 4.2 7.7

0.8 59.8 57.7 4.2 7.8

Random

Forest

0.5 76.2 95.6 42.6 58.9

0.6 85.7 92.1 70.2 79.7

0.7 89.9 90.5 83.6 86.9

0.8 90.9 85.1 93.8 89.3

k-NN

0.5 63.3 93.6 8.8 16.1

0.6 70.2 88.0 29.4 44.1

0.7 74.5 83.4 45.2 58.6

0.8 80.2 84.9 61.6 71.4

We consider that reasonable accuracy values are

achieved for the Random Forest and k-NN, which

are increased as the threshold values increase, except

when using the Decision Tree which does not seem to

improve its correctly predicted observations ratio. In

general, the best results go for Random Forest, when

Novelty Detection in Physical Activity

863

using a threshold value of 0.8. In fact, this algorithm

has some advantages such as reducing overﬁtting and

being extremely ﬂexible. However, Random Forests

(depending on the dataset) are time-consuming.

Random Forest presents the best recall value

(93.8%). If the scope of this research was related to

health-related systems (e.g, a person has a disease or

not), the recall would be a better measure than preci-

sion. That is, it is far preferable to not miss any person

with the disease even if that means “signaling” some

patients as having a disease that actually do not have

it. As here we study the detection of new physical ac-

tivities, false-negatives are less of a concern. Then,

precision is preferable here.

We highlight that the precision values for Random

Forest and k-NN are indeed very close (85.1% and

84.9%). This means that they both are good at detect-

ing novelty activities of all activities that were pre-

dicted as a novelty.

5 CONCLUSIONS

In order to put our research in retrospect, we recall

that our motivation is to study novelty detection in

the context of activity recognition and be able to de-

tect new activities. To achieve this goal, we propose a

method that involves experimenting with three differ-

ent algorithms by creating three classiﬁcation models

in a example set that contained three classes (or activ-

ities). We apply these models in a test set that con-

tained ﬁve classes, two of which were new, not being

present in the original training set. When comparing

the model’s conﬁdence predictions with four thresh-

old values, we are able to detect how many of these

ﬁve activities were in fact novel (or not). We now

point some general observations.

Firstly, by increasing the threshold value, it means

that more activities are classiﬁed as a novel, which

leads to higher accuracy, recall but in a lower pre-

cision. Furthermore, lowering the threshold means

that fewer activities are classiﬁed as a novel, which

leads to lower recall and higher precision. Finally, by

choosing a threshold bigger than 0.8 would make it

possible to detect more novel activities. However, it

would make the model less precise. The best results

go for the Random Forest algorithm with a threshold

value equal to 0.8. However, k-NN is not far behind,

as both of them achieve a very close precision.

For future work, it would be relevant to study a

mechanism that would allow us to divide novel activ-

ities into different categories. Although we are detect-

ing if these examples are novel or not, it does not nec-

essarily mean that they belong to the same activity.

Another improvement would be using a clustering-

based technique to take into account outliers, to avoid

classifying an example as a novelty activity since it

also is a detached occurrence. Besides that, the use of

the latest deep learning techniques can help improve

the performance of novelty detection.

To sum up, we see a promising outlook for this re-

search area in the future, as novelty detection can help

us by recognizing and monitor our daily actions with

the fruitful purpose of providing useful information.

REFERENCES

Clifton, D. A., Clifton, L., Hugueny, S., Wong, D., and

Tarassenko, L. (2012). An extreme function theory for

novelty detection. IEEE Journal of Selected Topics in

Signal Processing, 7(1):28–37.

Clifton, L., Clifton, D. A., Watkinson, P. J., and Tarassenko,

L. (2011). Identiﬁcation of patient deterioration in

vital-sign data using one-class support vector ma-

chines. In 2011 federated conference on computer sci-

ence and information systems (FedCSIS), pages 125–

131. IEEE.

Filippone, M. and Sanguinetti, G. (2010). Information

theoretic novelty detection. Pattern Recognition,

43(3):805–814.

Ghoting, A., Parthasarathy, S., and Otey, M. E. (2008). Fast

mining of distance-based outliers in high-dimensional

datasets. Data Mining and Knowledge Discovery,

16(3):349–364.

Hassan, A., Mokhtar, H. M., and Hegazy, O. (2011). A

heuristic approach for sensor network outlier detec-

tion. Int J Res Rev Wirel Sens Netw (IJRRWSN), 1(4).

Hawkins, S., He, H., Williams, G., and Baxter, R. (2002).

Outlier detection using replicator neural networks. In

International Conference on Data Warehousing and

Knowledge Discovery, pages 170–180. Springer.

Hazan, A., Lacaille, J., and Madani, K. K. (2012). Extreme

value statistics for vibration spectra outlier detection.

In International Conference on Condition Monitoring

and Machinery Failure Prevention Technologies, page

p.1, Londres, United Kingdom.

Helali, R. G. M. (2010). Data mining based network intru-

sion detection system: A survey. In Novel Algorithms

and Techniques in Telecommunications and Network-

ing, pages 501–505. Springer.

Le, T., Tran, D., Ma, W., and Sharma, D. (2010). An op-

timal sphere and two large margins approach for nov-

elty detection. In The 2010 International Joint Confer-

ence on Neural Networks (IJCNN), pages 1–6. IEEE.

Lee, K., Lee, K., Min, K., Zhang, Y., Shin, J., and Lee,

H. (2018). Hierarchical novelty detection for visual

object recognition. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1034–1042.

Marchi, E., Vesperini, F., Eyben, F., Squartini, S., and

Schuller, B. (2015). A novel approach for automatic

ICAART 2021 - 13th International Conference on Agents and Artiﬁcial Intelligence

864

acoustic novelty detection using a denoising autoen-

coder with bidirectional lstm neural networks. In

Proceedings 40th IEEE International Conference on

Acoustics, Speech, and Signal Processing, ICASSP

2015, pages 5–pages.

Markou, M. and Singh, S. (2006). A neural network-based

novelty detector for image sequence analysis. IEEE

transactions on pattern analysis and machine intelli-

gence, 28(10):1664–1677.

Mello, V., Moura, N., and Seixas, J. (2018). Novelty detec-

tion in passive sonar systems using stacked autoen-

coders. In 2018 International Joint Conference on

Neural Networks (IJCNN), pages 1–7.

Miljkovi

c, D. (2010). Review of novelty detection methods.

In The 33rd International Convention MIPRO, pages

593–598. IEEE.

Peng, X. and Xu, D. (2012). Efﬁcient support vector data

descriptions for novelty detection. Neural Computing

and Applications, 21(8):2023–2032.

Pimentel, M. A., Clifton, D. A., Clifton, L., and Tarassenko,

L. (2014). A review of novelty detection. Signal Pro-

cessing, 99:215–249.

Reiss, A. and Stricker, D. (2012a). Creating and bench-

marking a new dataset for physical activity monitor-

ing. In Proceedings of the 5th International Confer-

ence on PErvasive Technologies Related to Assistive

Environments, pages 1–8.

Reiss, A. and Stricker, D. (2012b). Introducing a new

benchmarked dataset for activity monitoring. In 2012

16th International Symposium on Wearable Comput-

ers, pages 108–109. IEEE.

Rossi, S., Bove, L., Di Martino, S., and Ercolano, G. (2018).

A two-step framework for novelty detection in activ-

ities of daily living. In International Conference on

Social Robotics, pages 329–339. Springer.

Sabokrou, M., Khalooei, M., Fathy, M., and Adeli, E.

(2018). Adversarially learned one-class classiﬁer for

novelty detection. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 3379–3388.

Shearer, C. (2000). The crisp-dm model: the new blueprint

for data mining. Journal of data warehousing,

5(4):13–22.

Sprint, G., Cook, D. J., and Schmitter-Edgecombe, M.

(2016). Unsupervised detection and analysis of

changes in everyday physical activity data. Journal

of biomedical informatics, 63:54–65.

Surace, C. and Worden, K. (2010). Novelty detection

in a changing environment: a negative selection ap-

proach. Mechanical Systems and Signal Processing,

24(4):1114–1128.

Viegas, J. L., Esteves, P. R., and Vieira, S. M. (2018).

Clustering-based novelty detection for identiﬁcation

of non-technical losses. International Journal of Elec-

trical Power & Energy Systems, 101:301–310.

Wu, S. and Wang, S. (2011). Information-theoretic out-

lier detection for large-scale categorical data. IEEE

transactions on knowledge and data engineering,

25(3):589–602.

Xia, Y., Cao, X., Wen, F., Hua, G., and Sun, J. (2015).

Learning discriminative reconstructions for unsuper-

vised outlier removal. In Proceedings of the IEEE In-

ternational Conference on Computer Vision (ICCV).

Yong, S.-P., Deng, J. D., and Purvis, M. K. (2013). Wildlife

video key-frame extraction based on novelty detection

in semantic context. Multimedia tools and applica-

tions, 62(2):359–376.

Zhang, J., Ghahramani, Z., and Yang, Y. (2005). A proba-

bilistic model for online document clustering with ap-

plication to novelty detection. In Advances in neural

information processing systems, pages 1617–1624.

Novelty Detection in Physical Activity

865