
Explaining Inaccurate Predictions of Models through
k-Nearest Neighbors
Zeki Bilgin
1 a
and Murat Gunestas
2 b
1
Arcelik Research, Istanbul, Turkey
2
Cyphore Cyber Security and Forensics Initiative, Istanbul, Turkey
Keywords:
XAI, Explainable AI, Deep Learning, Nearest Neighbors, Neural Networks.
Abstract:
Deep Learning (DL) models exhibit dramatic success in a wide variety of fields such as human-machine
interaction, computer vision, speech recognition, etc. Yet, the widespread deployment of these models partly
depends on earning trust in them. Understanding how DL models reach a decision can help to build trust
on these systems. In this study, we present a method for explaining inaccurate predictions of DL models
through post-hoc analysis of k-nearest neighbours. More specifically, we extract k-nearest neighbours from
training samples for a given mispredicted test instance, and then feed them into the model as input to observe
the model’s response which is used for post-hoc analysis in comparison with the original mispredicted test
sample. We apply our method on two different datasets, i.e. IRIS and CIFAR10, to show its feasibility on
concrete examples.
1 INTRODUCTION
Explainable Artificial Intelligence (XAI) is an emerg-
ing and popular research topic in AI community,
which aims to understand and explain underlying
decision-making mechanism of AI-based systems
(Arrieta et al., 2020). Being able to explain how AI
systems reach a decision in an understandable way for
human beings is crucial to build trust on these sys-
tems (Barbado and Corcho, 2019; Chakraborti et al.,
2020; Ribeiro et al., 2016). This is particularly im-
portant for some use cases such as autonomous ve-
hicles, security, finance, defense, and medical diag-
nosis, where an inaccurate decision could cause non-
recoverable damages (Arrieta et al., 2020; Tjoa and
Guan, 2019; Holzinger et al., 2019). Due to the im-
portance of the issue, DARPA decided to launch an
XAI program in May 2017, with the objective of cre-
ating AI systems whose learned models and decisions
can be understood and appropriately trusted by end
users (Gunning and Aha, 2019). The need for an ex-
planation of an algorithmic decision that significantly
affects human beings is also mentioned in European
Union regulations (Goodman and Flaxman, 2017).
The problem actually arises from the black-box
a
https://orcid.org/0000-0002-8613-4071
b
https://orcid.org/0000-0001-8096-689X
characteristics displayed by advanced AI models.
Particularly, the rise of neural network-based Deep
Learning (DL) models that exhibit dramatic success
in a wide range of tasks from load forecasting (Us-
tundag Soykan et al., 2019) to vulnerability prediction
(Bilgin et al., 2020), by relying on efficient learning
algorithms with huge parametric space, makes them
be considered as complex black-box models (Arri-
eta et al., 2020; Castelvecchi, 2016). Therefore, to
be considered practical, a model’s decision-making
mechanism either needs to be more transparent, or
provides hints on what could perturb the model (Hall,
2018). In this study, we focus on this issue and seek
to understand why a model makes inaccurate pre-
dictions by performing experimental analysis on two
different datasets from two different domains. The
first dataset we consider is IRIS dataset (Dua and
Graff, 2017), which consists of 50 samples from each
of three species of Iris, and the second one is CI-
FAR10 (Krizhevsky et al., 2009), which consists of
60000 32x32 colour images in 10 different classes,
with 6000 images per class. Our approach is a kind
of post-hoc analysis of mispredictions based on k-
nearest neighbours of training samples corresponding
to inaccurately predicted test instance. Our motiva-
tion for focusing on inaccurate predictions is that ex-
plaining a model’s mispredictions may be more criti-
cal with respect to accurate predictions in some situa-
228
Bilgin, Z. and Gunestas, M.
Explaining Inaccurate Predictions of Models through k-Nearest Neighbors.
DOI: 10.5220/0010257902280236
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 228-236
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tions that require responsibility.
In our proposed method, when a model makes a
misprediction for a certain test input, we first extract
k-nearest neigbours from the training set based on a
specific distance calculation approach, and then feed
these extracted samples into the model as input to get
auxiliary predictions which will be used for post-hoc
analysis. Considering the original misprediction to-
gether with auxiliary predictions, we perform both
sample-based individual analyses and collective sta-
tistical analysis on them. The main contribution of
this study is that it provides a methodology, with
supportive experimental results, based on the analy-
sis of the model’s behaviour on k-nearest neighbors
of the mispredicted sample to understand the reasons
for the model’s inaccurate estimations, by presenting
more appropriate distance calculation method in near-
est neighbour search when dealing with image data.
The rest of the paper is organized as follows: First,
in Section 2, we give an overview of related work
and explain how our work differs from prior studies.
Then, in Section 3, we present our post-hoc analysis
method to explain inaccurate decisions of deep learn-
ing models. Section 4 includes our experimental anal-
ysis for two different datasets. Finally, we conclude
our work by giving final remarks.
2 RELATED WORK
There are certain concepts that are highly related with
model explainability, and some studies provide well-
defined meanings of these concepts and discuss their
differences. For example, in (Roscher et al., 2020),
the authors review XAI in view of applications in the
natural sciences and discuss three main relevant el-
ements: transparency, interpretability, and explain-
ability. Transparency can be considered as the oppo-
site of the “black-boxness” (Lipton, 2018), whereas
interpretability pertains to the capability of making
sense of an obtained ML model (Roscher et al., 2020).
The work (Holzinger et al., 2019) introduces the no-
tion of causability as a property of a person in contrast
to explainability which is a property of a system, and
discusses their difference for medical applications.
Some other studies providing comprehensive outline
of the different aspects of XAI are (Chakraborti et al.,
2020), (Arrieta et al., 2020) and (Cui et al., 2019).
Rule Extraction. One common and longstand-
ing approach used to explain AI decisions is the rule
extraction, which aims to construct a simpler coun-
terpart of a complex model via approximation such
as building a decision tree or linear model leading
to similar predictions of the complex model. An
early work in this category belongs to Ribeiro et
al. (Ribeiro et al., 2016), who present a method
to explain the predictions of any model by learning
an interpretable sparse linear model in a local re-
gion around the prediction. In another work (Bar-
bado and Corcho, 2019), the authors evaluate some
of the most important rule extraction techniques over
the OneClass SVM model which is a method for
unsupervised anomaly detection. In addition, they
propose algorithms to compute metrics related with
XAI regarding the “comprehensivility”, “representa-
tiveness”, “stability” and “diversity” of the rules ex-
tracted. The works (Bologna and Hayashi, 2017;
Bologna, 2019; Bologna and Fossati, 2020) present
a few different variants of a similar propositional
rule extraction technique from several neural network
models trained for various tasks such as sentiment
analysis, image classification, etc.
Post-hoc Analysis. Another widely adopted ap-
proach is the post-hoc analysis, which involves dif-
ferent techniques trying to explain the predictions of
ML models that are not transparent by design. In
this category, the authors of (Petkovic et al., 2018)
develop frameworks for post-training analysis of a
trained random forest with the objective of explaining
the model’s behavior. Adopting a user-centered ap-
proach, they generate an easy to interpret one page ex-
plainability summary report from the trained RF clas-
sifier, and claim that the reports dramatically boosted
the user’s understanding of the model and trust in the
system. In another study (Hendricks et al., 2016),
the authors bring a visual explanation method that fo-
cuses on the discriminating properties of the visible
object, jointly predicts a class label, and explains why
the predicted label is appropriate for the image.
A model explanation technique relevant to our
proposed method is the explanation by example as a
subcategory of the post-hoc analysis approach (Arri-
eta et al., 2020). As an early work in this category,
Bien et al. (Bien and Tibshirani, 2011) develop a Pro-
totype Selection (PS) method, where a prototype can
be considered as a very close or identical observation
in the training set, that seeks a minimal representa-
tive subset of samples with the objective of making
the dataset more easily “human-readable”. Aligned
with (Bien and Tibshirani, 2011), Li et al. (Li et al.,
2018) use prototypes to design an interpretable neural
network architecture whose predictions are based on
the similarity of the input to a small set of prototypes.
Similarly, Caruena et al. (Caruana et al., 1999) sug-
gest that a comparison of the representation predicted
by a single layer neural network with the represen-
tations learned on its training data would help iden-
tify points in the training data that best explain the
Explaining Inaccurate Predictions of Models through k-Nearest Neighbors
229

prediction made. The work (Papernot and McDaniel,
2018) exhibits a particular example of classical ML
model enhanced with its DL counterpart (Deep Near-
est Neighbors DkNN), where the neighbors consti-
tute human-interpretable explanations of predictions
including model failures. Our own study differs from
these studies in that (i) we focus on diagnosing pos-
sible root causes of a model’s inaccurate predictions
and thus try to explain what perturbs the model, (ii)
we do not design a new neural network structure (e.g.
on contrary to (Li et al., 2018)), (iii) we perform
post-hoc analyses based on the model’s extra predic-
tions when the k-nearest neighbors of training sam-
ples of the mispredicted test inputs are entered into
the model, and (iv) we find k-nearest neighbors based
on the distance calculated according to the features
extracted at internal layer of convolutional neural net-
work (CNN) used.
3 EXPLAINING INACCURATE
PREDICTIONS VIA k-NEAREST
NEIGHBORS
Our objective is to understand why a model makes in-
accurate prediction on a certain test sample. If this
goal is achieved, the model can be improved by tak-
ing appropriate actions based on revealed root causes
of the inaccurate predictions. To this end, we present
a post-hoc analysis method based on analysis of the
model’s prediction response on k-nearest neighbors of
the training samples corresponding to the test sample
in question. To put it another way, we first extract
the k-nearest neighbors from the training dataset for
a given mispredicted test input, and then feed these
extracted k-nearest neighbors into the same model
and get the auxiliary predictions for these extracted k-
nearest neighbors. Then, we perform post-hoc analy-
ses on these additional predictions together with orig-
inal inaccurate test prediction by seeking to reveal
what could perturb the model. Figure 1 depicts high-
level schema of our methodology.
As depicted in Figure 1, our method relies on ex-
tracting k-nearest neighbors from training dataset for
a given test input, and therefore, it is highly crucial
for our method how to calculate distance between two
samples, which forms the basis of the nearness crite-
rion between the two samples. In the following sub-
section, we discuss this issue in detail from the per-
spective of two different datasets in two different do-
mains.
Table 1: Sample instances from IRIS dataset.
Flower Attributes
Name sepal
length
(cm)
sepal
width
(cm)
petal
length
(cm)
petal
width
(cm)
Setosa 5.1 3.5 1.4 0.2
Setosa 4.9 3.0 1.4 0.2
Versicolor 7.0 3.2 4.7 1.4
Versicolor 5.5 2.3 4.0 1.3
Virginica 6.3 3.3 6.0 2.5
Virginica 5.8 2.7 5.1 1.9
Table 2: 3-nearest neighbours of a sample based on eu-
clidean distance in IRIS dataset.
Flower Attributes Nearest
Neighbors
Name sepal
length
(cm)
sepal
width
(cm)
petal
length
(cm)
petal
width
(cm)
euclidean
distance
(cm)
Setosa 5.1 3.5 1.4 0.2 -
Setosa 5.1 3.5 1.4 0.3 0.100
Setosa 5.0 3.6 1.4 0.2 0.141
Setosa 5.1 3.4 1.5 0.2 0.141
3.1 Extracting k-Nearest Neighbors
There are many alternative metrics that can be used
to measure distance between two samples. For exam-
ple, one of the most widely used metric is euclidean
distance, which calculates element-wise distance be-
tween corresponding elements of two item to be com-
pared as formulated in Equation 1.
L(x, y) =
s
n
∑
i=1
(x
i
− y
i
)
2
(1)
where x and y are a pair of samples in an n-
dimensional feature space.
Euclidean distance can be safely used to measure
distance between two samples especially when these
samples are constituted of features with numeric val-
ues. For example, in IRIS dataset, each instance is
represented with four features as indicated in Table 1.
These are sepal length, sepal width, petal length, and
petal width in cm of the iris flower. The euclidean-
based 3-nearest neighbours of the first instance in Ta-
ble 1 are given in Table 2. For this particular case,
it is easy to observe the similarity between the given
instance and its nearest neighbours as there are small
deviations on some of the feature values.
However, when we deal with an image dataset
such as CIFAR10, calculating euclidean distance di-
rectly between two images may not be appropriate to
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
230

Figure 1: Overview of the method.
find nearest neighbours. This is because the similar-
ity between two images is something complicated and
requires sophisticated analysis. For example, con-
sider two images consisting of the same object but
in different locality in the images (e.g. the object is
located in top-left of the first image, whereas it is
in the bottom-right of the second image). In such a
case, the euclidean distance between these two im-
ages could be a large number, implying that these two
images have not any common property, although the
opposite is the case. To illustrate this, as an example,
we found 3-nearest neighbours of an image from CI-
FAR10 dataset based on euclidean distance between
images, and demonstrate them in Figure 2a.
As seen in Figure 2a, the 3-nearest neighbours
(a)
(b)
Figure 2: The 3-nearest neighbours of the training set for the
very first sample of the test set in CIFAR10 dataset based
on (a) euclidean distance directly between images and (b)
euclidean distance on the extracted features at the internal
layers of the neural network.
of the given test sample (index=0 in the original CI-
FAR10 test dataset) are images of deer, bird, and bird
respectively, which validates our claim that similarity
between images is a bit more complicated than simi-
larity between vectoral data. Therefore, while finding
nearest neighbours in CIFAR10 dataset, instead of di-
rectly applying euclidean distance calculation on im-
ages, we first get the extracted image features at inter-
nal layers of the utilized convolutional neural network
as depicted in Figure 3, and then calculate euclidean
distance on these features which is in the form of a
vector consisting of numeric data. We hypothesise
that this approach could give more meaningful and
appropriate nearest neighbours. To validate this, for
the same test sample given in Figure 2a, we found the
3-nearest neighbours based on the euclidean distance
between the extracted features at the internal layers
of the neural network as demonstrated in Figure 2b.
As seen in Figure 2b, the 1
st
and 3
rd
nearest neigh-
bours are images of a cat, which really look like the
test sample, and the 2
nd
nearest neighbour is an image
of deer, which is also meaningful as it has observable
similar patterns (e.g. curves) with the test sample. As
a result, when dealing with CIFAR10 dataset, we find
nearest neighbours based on euclidean distance be-
tween the extracted features at internal layers of the
neural network to be used.
3.2 Post-hoc Analysis
When we encounter an incorrect prediction of the
model, we first extract the k-nearest neighbours in
the training set based on the incorrectly predicted test
sample as described in the previous part, and then give
them as input to the model in order to obtain auxiliary
Explaining Inaccurate Predictions of Models through k-Nearest Neighbors
231

Figure 3: Getting the features extracted at the internal layers
of CNN, which is used for distance calculations in k-nearest
neighbor search.
predictions. In the post-hoc analyses, we compare the
original inaccurate prediction with the auxiliary pre-
dictions with the objective of revealing possible cause
of the misprediction in question. There may appear
different cases as explained below:
• Case-I: A sample of k-nearest neighbour is
belong to same category with the correspond-
ing inaccurately predicted test sample, and the
model makes accurate prediction when this near-
est neighbour is given the model as input. This
situation is a sign that the model actually fits well
and inaccurate prediction of the test sample is an
unexpected circumstance.
• Case-II: A sample of k-nearest neighbour is be-
long to same category with the corresponding in-
accurately predicted test sample, but the model
makes inaccurate prediction when this nearest
neighbour is given the model as input. This sit-
uation implies that the model may not be fitted
very well which could also be the root cause of
the original misprediction of the test sample.
• Case-III: A sample of k-nearest neighbour is
belong to different category with respect to the
corresponding inaccurately predicted test sample,
and the model makes accurate prediction when
this nearest neighbour is given the model as in-
put. This situation can imply that this nearest
neighbour may have some disruptive effect on the
model’s prediction performance on the test sam-
ple in question, because the fact that the model
makes accurate prediction on a nearest neighbour
in different category means that the model learnt
to yield this nearest neighbour’s category when
identical inputs are given, which would be an in-
accurate prediction for the corresponding test in-
put. On the other hand, if the majority of the near-
est neighbours falls in this case, then the mispre-
dicted test instance is likely to be an outlier or lo-
cated near the boundaries of data points.
• Case-IV: A sample of k-nearest neighbour is be-
long to different category with respect to the
corresponding inaccurately predicted test sam-
ple, and the model makes inaccurate prediction
when this nearest neighbour is given the model
as input. How this situation affects the model’s
behaviour on the related test sample partly de-
pends on whether this misprediction of the near-
est neighbour is the same with the original inac-
curate test prediction or not. For Case IV, suppose
the model’s prediction for the nearest neighbour is
different than the original test misprediction. This
situation does not give any clue about the model’s
inaccurate prediction for the test sample.
• Case-V: A sample of k-nearest neighbour is be-
long to different category with respect to the
corresponding inaccurately predicted test sample,
and the model makes inaccurate prediction when
this nearest neighbour is given the model as input.
Moreover, this misprediction is the same with the
original test misprediction. Such a situation im-
plies that the model behaves in harmony with the
nearest neighbours, and may also point that the
test sample is outlier of its own category.
4 EXPERIMENTAL ANALYSIS
We realized our implementation in the scikit-learn
machine learning platform (Pedregosa et al., 2011),
and applied our explanation method on two different
datasets as described in detail in the following subsec-
tions.
4.1 IRIS Dataset
IRIS dataset (Fisher, 1936) contains 3 classes of 50
instances each, where each class refers to a type of iris
plant, with four attributes as shown in Table 1. This
is a pretty simple dataset for classification task and
can be successfully handled by using simple machine
learning algorithms, without requiring any neural net-
work implementation. However, we intentionally pre-
ferred to use this dataset in our neural network based
experimental analysis because we believe it can serve
our purpose well thanks to its simplicity.
In our neural network implementation, we in-
cluded 1 hidden layer with 12 neurons, and split-
ted whole dataset into training and test sets with 2/3
and 1/3 ratio respectively. We trained the model up
to the optimal epoch where minimum validation loss
is achieved, which allows us to avoid underfitting or
overfitting situations.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
232
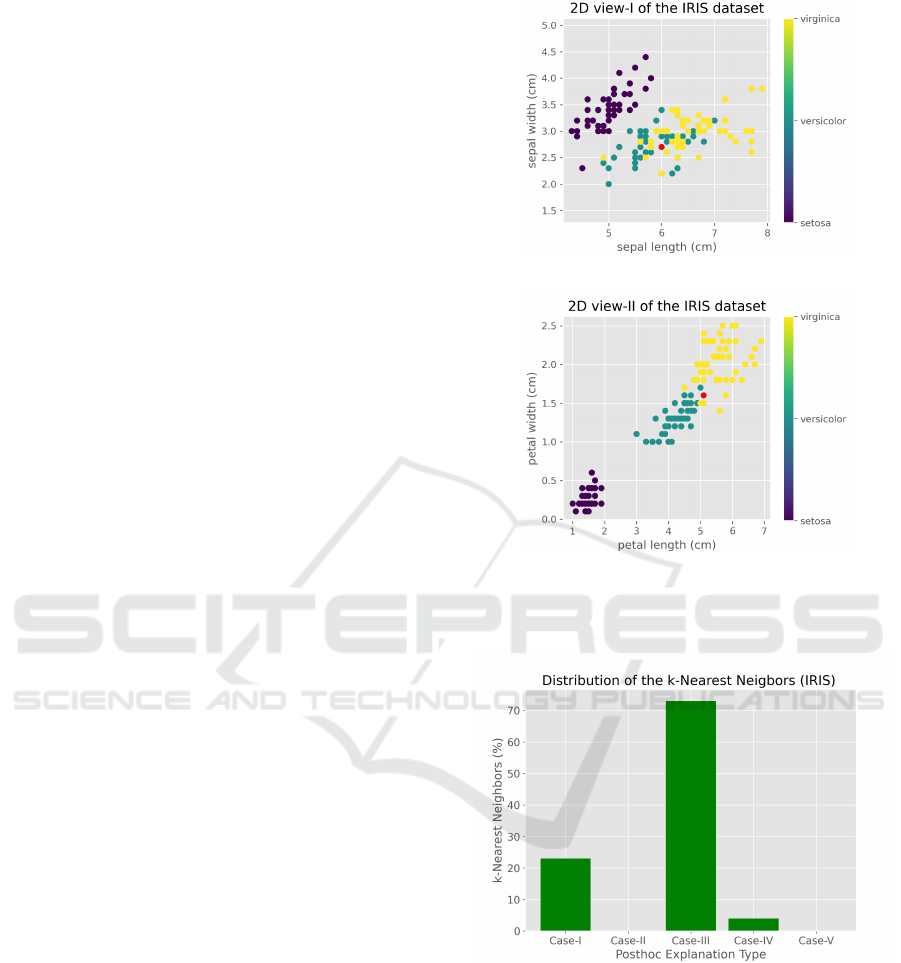
4.1.1 Sample-based Analysis
After completing the model training, we performed
predictions on test dataset, and picked an inaccu-
rate prediction for post-hoc analysis. Table 3 shows
mispredicted test instance along with associated 11-
nearest neighbor instances from training dataset. As
seen in Table 3, the majority of the 11-nearest neigh-
bours fall into Case III, which implies that the mis-
predicted test sample is likely to be an outlier or lo-
cated near the boundaries of data points as justified
in Section 3.2. To examine this issue a little more,
we plotted 2D views of IRIS dataset as seen in Figure
4. Figure 4a shows 2D view of IRIS data from the
perspective of the attribute pair of “sepal width” and
“sepal length”, where the mispredicted sample, which
is normally belong to the category of “versicolor”, is
colored red. It is seen from Figure 4a that the mis-
predicted sample is located among “versicolor” and
“virginica” samples that makes it difficult to distin-
guish. On the other hand, Figure 4b shows 2D view
of IRIS data from the perspective of the attribute pair
of “petal width” and “petal length”, where the mispre-
dicted sample is again colored red. It is seen from Fig-
ure 4b that the mispredicted sample is located near the
boundary between “versicolor” and “virginica” sam-
ples, which makes it clear why the model made in-
accurate prediction on this specific sample. This is
compatible with our posthoc analysis and interpreta-
tions that we have done above.
4.1.2 Statistical Analysis
In our experiments, 2 test samples out of 50 were mis-
predicted by the model, one of which have been ex-
plained in the previous part. In this part, we provide
statistical distribution of k-nearest neighbors based
posthoc analysis of these two mispredicted test sam-
ples. Figure 5 shows distribution as percentage of
the 11-nearest neighbors of the two mispredicted test
samples according to the cases in our posthoc analy-
sis. As seen in Figure 5, the majority of the 11-nearest
neighbors fall into Case-III, which implies that the
mispredicted test samples are either outliers or located
near boudaries.
4.2 CIFAR10 Dataset
The CIFAR-10 dataset consists of 60000 32x32
colour images in 10 different classes, with 6000 im-
ages per class, which are splitted as 50000:10000 for
training and test purposes. The 10 classes in CIFAR-
10 represent airplanes, cars, birds, cats, deer, dogs,
frogs, horses, ships, and trucks.
(a)
(b)
Figure 4: 2D views of IRIS dataset based on pairs of at-
tributes. The red circle represents the mispredicted sample
which is normally belong to category of “versicolor”.
Figure 5: Distribution of the 11-nearest neighbours of the
training set corresponding to inaccurate test samples when
they are given as input to the model.
In our experimental analysis, we implemented a CNN
which has similar architecture with VGG as follows:
Two successive 2D convolutional layers with 32 fil-
ters and kernel size of (3,3), followed by pooling layer
and flatten layer. Then a dense layer with 128 neu-
rons followed by a droput layer and finally final dense
layer with softmax function. We trained the model up
to the optimal epoch where minimum validation loss
Explaining Inaccurate Predictions of Models through k-Nearest Neighbors
233

Table 3: 11-nearest neighbours of a sample based on euclidean distance in IRIS dataset.
Instance Attributes Distance Prediction True Label Explanation
Type sepal
length
(cm)
sepal
width
(cm)
petal
length
(cm)
petal
width
(cm)
euclidean
(cm)
Test 6.0 2.7 5.1 1.6 - virginica versicolor
1
st
NN 6.3 2.8 5.1 1.5 0.450 versicolor virginica Case IV
2
nd
NN 6.3 2.7 4.9 1.8 0.462 virginica virginica Case III
3
rd
NN 5.8 2.7 5.1 1.9 0.463 virginica virginica Case III
4
rt
NN 5.8 2.7 5.1 1.9 0.463 virginica virginica Case III
5
th
NN 6.3 2.5 4.9 1.5 0.612 versicolor versicolor Case I
6
th
NN 6.4 2.7 5.3 1.9 0.635 virginica virginica Case III
7
th
NN 5.7 2.8 4.5 1.3 0.676 versicolor versicolor Case I
8
th
NN 6.3 2.9 5.6 1.8 0.703 virginica virginica Case III
9
th
NN 6.3 2.5 5.0 1.9 0.709 virginica virginica Case III
10
th
NN 5.9 3.0 5.1 1.8 0.749 virginica virginica Case III
11
th
NN 6.0 3.0 4.8 1.8 0.758 virginica virginica Case III
is achieved, which allows us to avoid underfitting or
overfitting situations.
4.2.1 Sample-based Analysis
After completing the model training, we performed
predictions on test dataset, and picked an inaccurate
prediction for post-hoc analysis. Figure 6 shows the
mispredicted test sample along with its 11-nearest
neighbours from training dataset. The caption under
each subfigure indicates true label of the given figure
and the model’s prediction when this image is given
as input.
As seen in Figure 6, the original test image con-
tains a frog, but the model inaccurately classified this
sample as an deer image. When we look at the 11-
nearest neighbours, 1st, 2nd, 3rd, 4rt, 7th, 8th, 9th,
10th and 11th nearest neigbours (9 out of 11) fall into
Case III according to explanations given in Section
3.2, which implies that the model behaved in harmony
with the nearest neighbors for this specific test sam-
ple.
4.2.2 Statistical Analysis
In our experiments, the validation accuracy of the
model was about 68.61%, which corresponds to 3139
inaccurate predictions given that there are 10000 test
instances in CIFAR10 datasets. Taking k=3 in k-
nearest neighbors, we find k-nearest neighbors for
all mispredicted test instances, and then performed
posthoc analysis according to explanations given in
Section 3.2. Figure 7 shows statistical distribution of
k-nearest neighbors according to the cases given in
our posthoc analysis.
As seen in Figure 7, almost 50% of the k-nearest
neighbors fall into Case-III, which implies that the
mispredicted test instances are likely to be outliers or
located near the boundaries of data points.
Figure 6: The 11-nearest neighbours in the training set for
a mispredicted test sample based on euclidean distance on
the extracted features at the internal layers of the neural net-
work.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
234
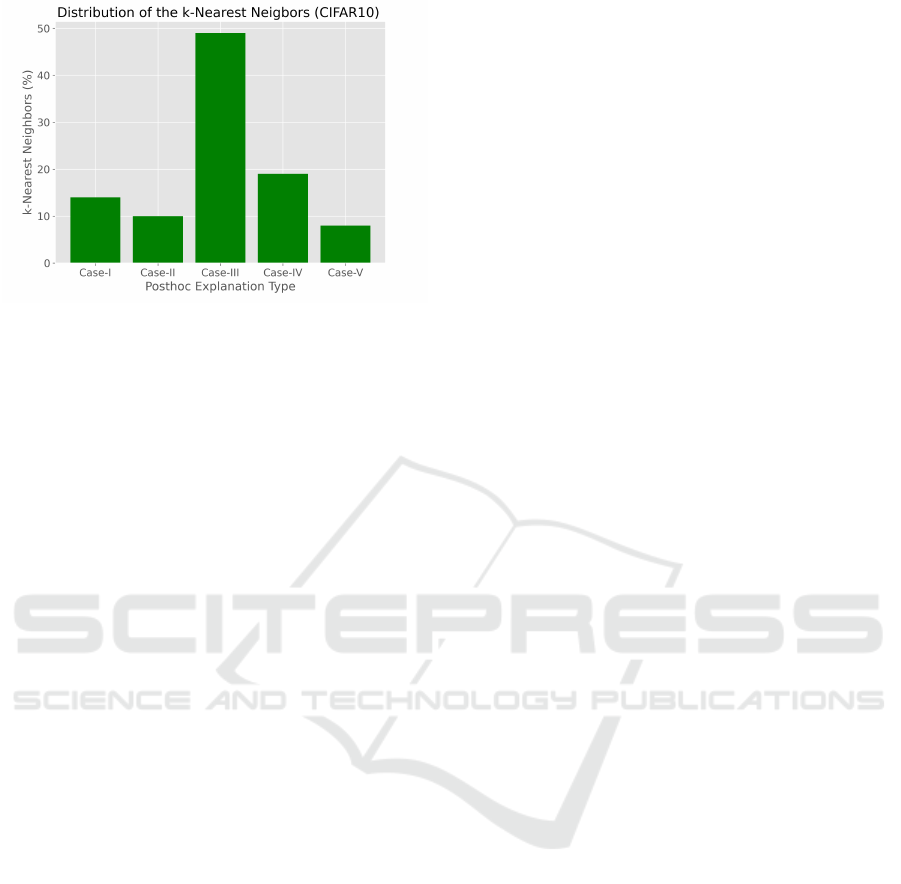
Figure 7: Distribution of the 3-nearest neighbours of the
training set corresponding to inaccurate test samples when
they are given as input to the model.
5 CONCLUSION
We studied the root causes of inaccurate decisions
reached particularly by deep learning models, which
is an important issue for many use cases that require
responsibility for the actions taken by AI. We devel-
oped a method for finding k-nearest neighbours in
training set for a given test instance, which were en-
hanced for finding similar images such that we calcu-
late euclidean distance not directly on the compared
images, but instead, on the features extracted from in-
ternal layers of the convolutional neural network. To
reveal possible root cause of an inaccurate prediction,
we thus find k-nearest neighbours from training sam-
ples and re-entered them into the model to observe
its behaviour for further analysis. By comparing the
model’s responses on the k-nearest neighbours and
the associated test input, we estimated possible root
cause of the mispredictions. We validated our pro-
posed method on both IRIS and CIFAR-10 datasets,
and experimentally showed that our proposed method
can be used to understand why a model makes inac-
curate misprediction.
REFERENCES
Arrieta, A. B., D
´
ıaz-Rodr
´
ıguez, N., Del Ser, J., Bennetot,
A., Tabik, S., Barbado, A., Garc
´
ıa, S., Gil-L
´
opez, S.,
Molina, D., Benjamins, R., et al. (2020). Explainable
artificial intelligence (xai): Concepts, taxonomies, op-
portunities and challenges toward responsible ai. In-
formation Fusion, 58:82–115.
Barbado, A. and Corcho,
´
O. (2019). Rule extraction in
unsupervised anomaly detection for model explain-
ability: Application to oneclass svm. arXiv preprint
arXiv:1911.09315.
Bien, J. and Tibshirani, R. (2011). Prototype selection for
interpretable classification. The Annals of Applied
Statistics, pages 2403–2424.
Bilgin, Z., Ersoy, M. A., Soykan, E. U., Tomur, E., C¸ omak,
P., and Karac¸ay, L. (2020). Vulnerability prediction
from source code using machine learning. IEEE Ac-
cess, 8:150672–150684.
Bologna, G. (2019). A simple convolutional neural network
with rule extraction. Applied Sciences, 9(12):2411.
Bologna, G. and Fossati, S. (2020). A two-step rule-
extraction technique for a cnn. Electronics, 9(6):990.
Bologna, G. and Hayashi, Y. (2017). Characterization of
symbolic rules embedded in deep dimlp networks: a
challenge to transparency of deep learning. Journal of
Artificial Intelligence and Soft Computing Research,
7(4):265–286.
Caruana, R., Kangarloo, H., Dionisio, J., Sinha, U., and
Johnson, D. (1999). Case-based explanation of non-
case-based learning methods. In Proceedings of the
AMIA Symposium, page 212. American Medical In-
formatics Association.
Castelvecchi, D. (2016). Can we open the black box of ai?
Nature News, 538(7623):20.
Chakraborti, T., Sreedharan, S., and Kambhampati, S.
(2020). The emerging landscape of explainable
ai planning and decision making. arXiv preprint
arXiv:2002.11697.
Cui, X., Lee, J. M., and Hsieh, J. (2019). An integrative 3c
evaluation framework for explainable artificial intelli-
gence.
Dua, D. and Graff, C. (2017). UCI machine learning repos-
itory.
Fisher, R. A. (1936). The use of multiple measurements in
taxonomic problems. Annals of eugenics, 7(2):179–
188.
Goodman, B. and Flaxman, S. (2017). European union reg-
ulations on algorithmic decision-making and a “right
to explanation”. AI magazine, 38(3):50–57.
Gunning, D. and Aha, D. W. (2019). Darpa’s explainable ar-
tificial intelligence program. AI Magazine, 40(2):44–
58.
Hall, P. (2018). On the art and science of machine learning
explanations. arXiv preprint arXiv:1810.02909.
Hendricks, L. A., Akata, Z., Rohrbach, M., Donahue, J.,
Schiele, B., and Darrell, T. (2016). Generating visual
explanations. In European Conference on Computer
Vision, pages 3–19. Springer.
Holzinger, A., Langs, G., Denk, H., Zatloukal, K., and
M
¨
uller, H. (2019). Causability and explainability of
artificial intelligence in medicine. Wiley Interdisci-
plinary Reviews: Data Mining and Knowledge Dis-
covery, 9(4):e1312.
Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple
layers of features from tiny images.
Li, O., Liu, H., Chen, C., and Rudin, C. (2018). Deep learn-
ing for case-based reasoning through prototypes: A
neural network that explains its predictions. In Thirty-
second AAAI conference on artificial intelligence.
Lipton, Z. C. (2018). The mythos of model interpretability.
Queue, 16(3):31–57.
Explaining Inaccurate Predictions of Models through k-Nearest Neighbors
235

Papernot, N. and McDaniel, P. (2018). Deep k-nearest
neighbors: Towards confident, interpretable and ro-
bust deep learning. arXiv preprint arXiv:1803.04765.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Petkovic, D., Altman, R. B., Wong, M., and Vigil, A.
(2018). Improving the explainability of random for-
est classifier-user centered approach. In PSB, pages
204–215. World Scientific.
Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). ” why
should i trust you?” explaining the predictions of any
classifier. In Proceedings of the 22nd ACM SIGKDD
international conference on knowledge discovery and
data mining, pages 1135–1144.
Roscher, R., Bohn, B., Duarte, M. F., and Garcke, J. (2020).
Explainable machine learning for scientific insights
and discoveries. IEEE Access, 8:42200–42216.
Tjoa, E. and Guan, C. (2019). A survey on explainable ar-
tificial intelligence (xai): towards medical xai. arXiv
preprint arXiv:1907.07374.
Ustundag Soykan, E., Bilgin, Z., Ersoy, M. A., and Tomur,
E. (2019). Differentially private deep learning for load
forecasting on smart grid. In 2019 IEEE Globecom
Workshops (GC Wkshps), pages 1–6.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
236
